Perbandingan interpolasi dalam metode spline

(1)

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh :

Anastasia Vrysca Jayanti NIM : 013114014

PROGRAM STUDI MATEMATIKA

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(2)

(3)

(4)

When Jesus Say That He Love Me

I feel that I am lonely It doesn’t prove that I am alone

I listen to the words He say That He will always be by my side

I mean everything to Him And He will never leave me

‘cause He love me so

When He say that He love me It means He give the best for me

When He say that He love me He will give everything for me No more fear about the future

And the blame for the past He will give everything When He say that He love me

He died for me He give His life for me

When He say that He love………. Say that He love me

(5)

Apa yang kuberikan untuk Mama Untuk Mama tersayang Tak kumiliki sesuatu berharga

Untuk Mama tercinta

Hanya ini kutuliskan

Tugas Akhir dari tanganku untuk Mama Hanya sebuah tugas akhir sederhana

Tugas akhirku untuk Mama

Walau tak dapat lagi kuungkapkan Rasa cintaku untuk Mama

Namun dengarlah hatiku selalu berkata

Sungguh kusayang padamu Mama

Mama . . . . . . .

Yogyakarta, 28 Maret 2007

(6)

“Janganlah gelisah hatimu; percayalah kepada Allah,

percayalah juga kepada-Ku. ”

- Yohanes 14 : 1 -

Kupersembahkan untuk :

My Sweet Heart Jesus

My Beautiful Life

My Be Loved Mom

(7)

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 28 Maret 2007 Penulis,

(8)

ABSTRAK

Metode Spline adalah salah satu metode Interpolasi yaitu dengan memakai pendekatan fungsi-fungsi Spline sebagai polinom penghubung. Fungsi Spline ter-diri Spline Linear, Spline Kuadrat dan Spline Kubik.

Pada skripsi ini akan dibuat perangkat lunak untuk membandingkan Spline Linear, Spline Kuadrat dan Spline Kubik. Perbandingan dilakukan dalam hal galat dan waktu komputasi. Proses perhitungan galat dihasilkan dari harga mutlak nilai sebenarnya dikurangi nilai hampiran dibagi nilai sebenarnya dikali seratus persen. Lama tidaknya waktu komputasi ditunjukkan dari banyaknya data yang dicari dalam proses perhitungan.

(9)

ABSTRACT

Spline method is one of Interpolation method that with make approxima-tion Spline funcapproxima-tions as connected polynom. Spline funcapproxima-tion consist of Linear Spline, Quadrate Spline and Cubic Spline.

In this thesis, will make a program to compare Linear Spline, Quadrate Spline ang Cubic Spline, on particular the error and the time computation. Process error computation is shown by absolute value from exact value minus approxima-tion value divide exact value and multiply one hundred percent. While the compu-tation processing duration by determining how many times the time compucompu-tation from data quantity in computation process.

(10)

KATA PENGANTAR

Puji syukur kepada Allah Bapa Yesus Kristus atas Roh Kudus dan segala kasih-Nya yang berlimpah, sehingga skripsi yang berjudul Perbandingan Interpo-lasi Dalam Metode Spline, sebagai salah satu syarat untuk memperoleh gelar Sar-jana Sains (S.Si) Program Studi Matematika, dapat terselesaikan dengan baik.

Penyusunan skripsi ini tidak terlepas dari bantuan dan dukungan dari ber-bagai pihak, baik yang terlibat secara langsung maupun tidak langsung. Oleh karena itu, dalam kesempatan ini dengan segala kerendahan hati, penulis ingin menyampaikan rasa terima kasih yang mendalam kepada :

1. My Be Loved Mom…………..Love u, Miss u, Need u,Want u so much.

2. Keluarga yang selalu memberi semangat dan segenap doa : Babeh Nano, Mas Chemi, Ade Luchia dan Tante Lusi. Terima kasih atas segala-segalanya………Kakak lulus!!

3. Bapak Drs. Jong Jek Siang, M.Sc., selaku dosen pembimbing skripsi dan pani-tia penguji yang telah memberi bimbingan, pengarahan, saran dan koreksi dalam penyusunan skripsi penulis.

4. Bapak Y. G. Hartono, S. Si, M. Sc, selaku Kaprodi Fakultas MIPA Univer-sitas Sanata Dharma, dosen penguji dan dosen pembimbing akademik. Terima kasih atas pencarian judul skripsi, telah memberikan yang terbaik sebagai dosen, berbagi canda seperti teman dan memahami seperti ayah.

(11)

6. Dosen-dosen Program Studi Matematika yang memberi dukungan kepada pe-nulis baik selama kuliah maupun dalam penyusunan skripsi ini.

7. Bapak Z. Tukijo yang telah membantu dalam urusan administrasi dan persia-pan ujian akhir.

8. Sahabat-sahabat tersayang di Tangerang:

• Elly yang selalu menemani saat-saat yang paling menyakitkan dan yang selalu bisa diandalkan untuk bertukar fikiran.

• Olla yang selalu menemani saat-saat yang paling hancur dan selalu men-jadi teman yang paling manja.

• Linda yang selalu menemani saat-saat langkah kaki terasa sangat berat dan yang selalu bisa diandalkan untuk jalan-jalan.

Sahabat termanis di Yogyakarta :

• Cece yang selalu mencoba mendekatkan pada Kristus, tempat berbagi suka dan duka. Terima kasih atas persahabatan yang manis dan yang selalu melarang pergi ke luar paingan saat fikiran penulis sedang kacau.

Kehadiran kalian membuat penulis percaya bahwa Tuhan tidak meninggalkan saat-saat penulis merasa tidak dapat lagi melangkah.

9. Angkatan 2001 yang teristimewa (urut abjad) : Ajeng, Andre, Ariel, Alam , Agnes, April, Bita, Dani, Deta, Daniel, Erika, Fanya, Indah, Maria, Ray, Rita, Tedi,Yuli, Upik, Veri, Wiwit. Terima kasih untuk semua kisah yang sudah dilewati bersama.

(12)

11.- Fanya dan kostnya yang selalu menjadi tempat pelarian dikala stress. - Eko yang selalu siap membantu, menyupir dan mentraktir, he....he....

Cayoo Fanya & Eko, Semangat !!!

12.Catur Prasdianto tempat bertukar fikiran, thanks for everything, Koko Satijan, Robet Tampa, Moko, Mba Sumi, Bruder Koko, Mba Dwi, Mba Nia.

13.Keluarga kost 99999 : Bora, Diana, Maria, Okta, Grace, Emi, Desi, Cicil, Lia, Nana, Juli, Hanny, Vivi. Terima kasih kalian telah menjadi keluarga inti di jogja. Terima kasih untuk Welly, Olive dan lainnya. You All always be My Friends!! Bapak dan ibu kost atas nasihat-nasihatnya dan penjagaannya. 14.Kediaman DED : Rm. Sari Jatmiko...terima kasih atas setiap doa dan paksaan

untuk mengerjakan skripsi, Mba Tika, Mba Vivi, Septi, Eko, Siska, Theo, Mas Adhit.

Penulis berharap agar Tugas Akhir ini dapat berguna bagi penulis maupun pi-hak lain sebagai wahana pembelajaran interpolasi dengan Metode Spline. Tak ada gading yang tak retak dan tak ada langit yang tak berawan. Demikian juga penelitian dan penulisan Tugas Akhir ini masih jauh dari kesempurnaan. Oleh karena itu, penulis siap menerima dengan mata, tangan dan hati yang terbuka akan segala macam kritik dan saran demi peningkatan kualitas penelitian di kemudian hari.

Yogyakarta, 28 Maret 2007 Penulis,

(13)

DAFTAR ISI

Halaman HALAMAN JUDUL……….

HALAMAN PERSETUJUAN PEMBIMBING…………... HALAMAN PENGESAHAN……… HALAMAN PERSEMBAHAN……… HALAMAN KEASLIAN KARYA……… ABSTRAK……… ABSTRACT……… KATA PENGANTAR………. DAFTAR ISI………... DAFTAR TABEL………. DAFTAR GAMBAR………... BAB I PENDAHULUAN……….1

A. Latar Belakang Masalah………..…………

B. Rumusan Masalah………..

C. Tujuan Penulisan………

D. Manfaat Penulisan………

E. Metode Penelitian ………

F. Pembatasan Penulisan ………

G. Sistematika Penulisan ………..…

(14)

BAB II LANDASAN TEORI

A. Interpolasi………..…………

B. Galat……… ………

C. Metode Spline ………

1. Spline linear………..…

2. Spline Kuadrat……….………

3. Spline Kubik ……….

BAB III PERANCANGAN DAN IMPLEMENTASI………

A. Perancangan Umum………

B. Perancangan Antarmuka...

1. Layar Sampul………

2. Layar Masukan Spline………..….…

C. Rancangan Proses……….…

D. Implementasi………..………

1. Spline Linear ……….……

2. Spline Kuadrat………

3. Spline Kubik………

BAB IV ANALISIS………...……… A. Hasil Implementasi...

1. Layar Sampul... 2. .Layar Spline... B. Pengujian Program Spline...

(15)

C. Percobaan Dan Analisis... 1. Galat...

a. Percobaan 1... b. Percobaan 2………... c. Percobaan 3... 2. Waktu Komputasi... a. Percobaan 1…... b. Percobaan 2... BAB V PENUTUTUP………...….

A. Kesimpulan………...…….

B. Saran………...……….

DAFTAR PUSTAKA... LAMPIRAN...

(16)

DAFTAR TABEL

Halaman Tabel 2.1...

Tabel 2.2 Hasil Perhitungan Spline Linear... Tabel 2.3 Hasil Perhitungan Spline Kuadrat……….. Tabel 2.4 Hasil Perhitungan Spline Kubik……….. Tabel 4.1 Data Percobaan 1……… Tabel 4.2 Hasil Galat Percobaan 1………. Tabel 4.3 Data Percobaan 2……….. Tabel 4.4 Hasil Galat Percobaan 2……… Tabel 4.5 Data Percobaan 3……….. Tabel 4.6 Hasil Galat Percobaan 3……… Tabel 4.7 Hasil Waktu Komputasi Percobaan 1……… Tabel 4.8 Hasil Waktu Komputasi Percobaan 2………. Tabel 4.9 Rata-rata Waktu Komputasi………

(17)

DAFTAR GAMBAR

Halaman Gambar 3.1 Rancangan Layar Sampul………. Gambar 3.2 Rancangan Layar Spline……… Gambar 3.3 Flowchart Spline Linear... Gambar 3.4 Flowchart Spline Kuadrat... Gambar 3.5 Flowchart Spline Kubik……… Gambar 4.1 Hasil Implementasi Layar Sampul……….. Gambar 4.2 Hasil Implementasi Spline……… Gambar 4.3 Hasil Perhitungan Spline……….. Grafik 4.1 Galat Percobaan 1………. Grafik 4.2 Galat Percobaan 2………. Grafik 4.3 Galat Percobaan 3………. Grafik 4.3 Waktu Komputasi Percobaan 1……… Grafik 4.4 Waktu Komputasi Percobaan 2……… Grafik 4.5 Rata-rata Waktu Komputasi……… Grafik 4.6 Rata-rata Waktu Komputasi dalam Persen………..

(18)

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Seringkali harus mencari nilai antara titik-titik data yang telah diketahui dan itu menjadi masalah yang cukup rumit. Metode numerik merupakan cabang atau bidang ilmu matematika yang masalah penaksiran nilai antara titik-titik data yang telah diketahui diformulasikan sedemikian rupa sehingga dapat diselesaikan menggunakan pencocokan kurva. Fungsi-fungsi dalam pencocokan kurva mampu memecahkan berbagai persoalan mengenai penaksiran nilai antara titik-titik data yang telah diketahui. Taksiran nilai antara titik-titik data yang telah tepat dinamakan Interpolasi.

Interpolasi Spline merupakan interpolasi sepotong-sepotong. Ini berarti bahwa suatu fungsi f(x) tertentu pada selang a ≤ x ≤ b, jika ingin menghampiri f(x) pada selang ini dengan sebuah fungsi lain g(x). Fungsi g(x) yang diperoleh ini dinamakan Spline. Nama Spline sendiri diambil dari batang tipis yang telah digunakan sejak lama oleh para insinyur untuk mengepaskan kurva me-lalui titik tertentu.

(19)

menurunkan polinom orde kedua dan Spline Kubik yang menurunkan polinom orde ketiga. Prediksi yang digunakan yaitu nilai x natural logaritma

Dari Fungsi-fungsi Spline yang ada maka akan diketahui Spline mana yang dapat mencapai hasil yang optimal, yaitu errornya kecil dan waktu perhitungan yang singkat.

B. Rumusan Masalah

Pokok permasalahan yang akan dibahas dalam skripsi ini dapat ditu-lis dengan beberapa pertanyaan berikut :

1 Bagaimana mencari nilai antara titik-titik data yang telah diketahui dengan Spline Linear, Spline Kuadrat, dan Spline Kubik?

2 Bagaimana menganalisis Fungsi-fungsi Spline sehingga menghasilkan Fungsi Spline yang baik untuk mencari nilai antara titik-titik data yang telah diketa-hui?

3 Fungsi Spline mana yang lebih baik di antara Spline Linear, Spline Kuarat dan Spline Kubik dalam hal akurasi dan waktu untuk memprediksi nilai x natural logaritma dengan menggunakan bahasa pemprograman Delphi 7.0?

C. Tujuan Penulisan

(20)

D. Manfaat Penulisan

Manfaat yang diharapkan dalam skripsi ini adalah penulis dapat me-nentukan Fungsi Spline mana yang paling baik untuk memprediksi nilai x natural logaritma sehingga errornya kecil dan waktu perhitungan yang singkat.

E. Metode Penelitian

Metode Penelitian :

1. Masukan data natural logaritma.

2. Terapkan persamaan Fungsi Spline Linear untuk memprediksi nilai x

yang tidak terdapat dalam tabel dan catat kesalahannya.

3. Terapkan persamaan Fungsi Spline Kuadrat untuk memprediksi nilai x

4. Terapkan persamaan Fungsi Spline Kubik untuk memprediksi nilai x

5. Bandingkan kesalahan yang terjadi pada masing-masing Fungsi Spline.

F. Pembatasan Penulisan

Dalam skripsi ini dilakukan beberapa batasan sebagai berikut :

1. Interpolasi dengan Metode Spline yaitu Spline Linear, Spline Kuadrat , Spline Kubik .

2. Faktor untuk membandingkan yaitu galat dan running time. 3. Data yang dipakai adalah tabel natural logaritma.

(21)

G. Sistematika Penulisan

Sistem penulisan laporan skripsi ini terdiri dari 6 bab dengan urutan sebagai berikut :

BAB I PENDAHULUAN

Menjelaskan uraian mengenai hal-hal yang menjadi dasar dalam pembahasan skripsi ini. Uraian tersebut mengenai latar belakang masalah, rumusan masalah, tujuan penulisan, manfaat penulisan, metode penelitian dan sistematika penulisan.

BAB II LANDASAN TEORI

Pada bab ini, penulis membahas dasar-dasar teori yang mendukung penyusunan skripsi ini secara terperinci, sehingga mudah dimengerti.

BAB III PERANCANGAN DAN IMPLEMENTASI

Menjelaskan perencanaan dalam rancangan program untuk implementasi. Serta melakukan implementasi dari rancangan program yang telah dibuat.

BAB IV ANALISIS

(22)

BAB V PENUTUTUP

(23)

BAB II

LANDASAN TEORI

A. Interpolasi

Terdapat n + 1 data pasangan bilangan

(

x₀,f₀

) (

, x₁, f₁

)

,. . .,

(

x_n,f_n

)

denganx0, x1, . . . ,xn nilainya berbeda, jika ingin memperoleh sebuah

polinomP_n

( )

x yang bernilai fjdi xj, dengan kata lain

dan berderajat n atau kurang. Polinom Pn sering dinamakan polinom penginterpolasi. Nilai xj sering dinamakan simpul. Besaran fj mungkin saja merupakan nilai fungsi matematis f(x) tertentu sehingga f(xj) = fj dan dengan demikian Pn

( )

x merupakan suatu hampiran bagi f(x) dengan sifat bahwa Pn

bernilai sama dengan f di semua simpul. Polinom P_n

( )

x ini digunakan untuk memperoleh nilai bagi semua x yang merupakan nilai hampiran bagi f(x). Jika x

yang ingin dicari terletak di antara simpul-simpul tersebut maka dinamakan Interpolasi.

B. Galat

Perhitungan numerik tidak terlepas dari kesalahan atau galat. Terdapat dua bentuk galat yang utama di dalam metode numerik yaitu galat pembulatan yang dapat terjadi akibat keterbatasan mesin hitung dan galat pemotongan yang dapat terjadi karena keterbatasan proses komputasi. Kedua galat tersebut mempengaruhi

Galat Mutlak dan Galat Relatif Persen.

1 1 0

0) ( ) ( )

( _n _n _n _n

n x f , P x f, . . ., P x f

(24)

Definisi 2.1 :

Andaikan p~ adalah nilai hampiran dari p maka Galat Mutlak didefinisikan

sebagai Em= p−~p dan Galat RelatifPersen 100%, 0. ~

≠ ∗

−

= p

p p p Er

C. Metode Spline

Metode Spline adalah salah satu metode numerik yang dapat digunakan untuk pencarian interpolasi. Interpolasi Spline merupakan polinom sepotong-sepotong. Suatu fungsi f(x) yang sudah diketahui pada selang a≤ x≤b di hampiri dengan sebuah fungsi lain g(x) dengan cara menyekat selang a≤ x≤bmenjadi beberapa anak selang a= x1 < x2 <. . .< xn =b. Fungsi g(x) yang didapat

dinamakan spline. Akan dibahas Spline Linear, Spline Kuadrat dan Spline Kubik. Besar kesalahan Metode Spline dapat diketahui dengan cara mereduksi nilai eksak dari tabel natural logaritma dengan pendekatan yang dihasilkan dari Metode Spline.

1. Spline Linear

(25)

sekelompok titik data terurut (x_i,f(x_i)), i=1,2,. . .,n dinyatakan sebagai berikut : Contoh 2.1

Diberikan sebuah tabel yang berisi 5 himpunan data logaritma natural

Tabel 2.1

Gunakan Tabel 2.1 untuk mencari nilai Interpolasi saat x = [1.11 1.22 1.33 1.44 1.49] menggunakan Spline Linear.

(26)

Penyelesaian :

Dari persamaan di atas didapat

2. Spline Kuadrat

Spline Kuadrat menyediakan sebuah persamaan kuadrat yang men-ghubungkan sedikitnya tiga pasangan data yang berdekatan di dalam

him-x f(x) 1.11 1.22 1.33 1.44 1.49 0.104 0.1983 0.2846 0.3641 0.3986 1.2 1.1 ) 1 . 1 ( 1 . 1 2 . 1 ) 0953 . 0 1823 . 0 ( 0953 . 0 ) (

1 ₋ − ≤ ≤

− +

= x x

x f 1.3 1.2 ) 2 . 1 ( 2 . 1 3 . 1 ) 1823 . 0 2624 . 0 ( 1823 . 0 ) (

2 ₋ − ≤ ≤

− +

= x x

x f 1.4 1.3 ) 3 . 1 ( 3 . 1 4 . 1 ) 2624 . 0 3365 . 0 ( 2624 . 0 ) (

3 ₋ − ≤ ≤

− +

= x x

x f 1.4 1.3 ) 3 . 1 ( 3 . 1 4 . 1 ) 2624 . 0 3365 . 0 ( 2624 . 0 ) (

4 ₋ − ≤ ≤

− +

= x x

x f 1.5 1.4 ) 4 . 1 ( 4 . 1 5 . 1 ) 3365 . 0 4055 . 0 ( 3365 . 0 ) (

5 ₋ − ≤ ≤

− +

= x x

x f

(27)

punan data (xi,f(xi)), i=1,2, . . . ,n . Bentuk umum dari persamaan kuadrat

diantara titik

(

x_i,f

( )

x_i

)

dan

(

x_i₊₁,f

( )

x_i₊₁

)

adalah

i i i

i x a x bx c

f ( )= 2 + + i=1,2,. . ., n−1 (2.2) oleh karena itu, setiap dua titik-titik data yang berdekatan mempunyai sebuah persamaan interpolasi yang diberikan oleh (2.2) dengan 3 konstanta

i i

i b c

a , ,dan .

Untuk n titik data terdapat n-1 selang, maka ada 3(n-1) konstanta yang harus-dicari dan yang memenuhi 3(n-1) persamaan atau kondisi sebagai berikut : 1. Spline harus melalui titik-titik data. Nilai-nilai fungsi harus sama pada simpul-simpul dalam untuk i = 1 sampai n dimana i=1,2, . . . ,n−1. Kondisi ini dapat dinyatakan sebagai berikut :

f_i(x_i)=a_ix_i2 +bx_i +c_i= f

( )

x_i i=1,2,3,...,n−1 (2.3) f_i(x_i₊₁)=a_ix_i₊₁2 +b_ix_i₊₁ +c_i= f

( )

x_i₊₁ i=1,2,3,...,n−1 (2.4)

2. Spline harus kontinu pada bagian dalam titik-titik data. Kondisi ini dapat dinyatakan menggunakan derivatif pertama dari spline kuadrat.

2a_ix_i +b_i =2a_i₊₁x_i₊₁ +b_i₊₁ i=1,2,3,...,n−1 (2.5) 3. Kondisi terakhir yang dapat dibentuk bebas sebagai turunan kedua dari spline diantara dua titik data pertama menjadi nol. Sejak turunan pertama untuk spline pertama adalah 2a_i, kondisi ini dapat dinyatakan

(28)

Contoh 2.2

Gunakan Tabel 2.1 untuk mencari nilai Interpolasi saat x = [1.11 1.22 1.33 1.44 1.49] menggunakan Spline Kuadrat.

Penyelesaian :

Data tabel terdapat 5 titik data. Dengan menggunakan persamaan (2.3) sampai dengan persamaan (2.6) dihasilkan 3(5-1) = 12 kondisi yang dibutuhkan untuk mendapatkan 3(5-1) = 12 konstanta yang dibutuhkan.

Persamaan (2.3) menghasilkan :

. = c b . a . . = c b . a . . = c b . a . . = c b . a . 3365 0 4 1 96 1 2624 0 3 1 69 1 1823 0 2 1 44 1 0953 0 1 1 21 1 4 4 4 3 3 3 2 2 2 1 1 1 + + + + + + + +

. c b . a . . c b . a . . c b . a . . c b . a . 4055 0 5 1 25 2 3365 0 4 1 96 1 2624 0 3 1 69 1 1823 0 2 1 44 1 4 4 4 3 3 3 2 2 2 1 1 1 = + + = + + = + + = + +

b a . b a . b a . b a . b a . b a . 4 4 3 3 3 3 2 2 2 2 1 1 8 2 8 2 6 2 6 2 4 2 4 2 + = + + = + + = +

Persamaan (2.6) menyatakan :

(29)

Dengan menggunakan pensubtitusian didapatkan

8895 1 43 2 6 0 5371 0 498 0 09 0 8553 1 526 2 69 0 8617 0 87 0 0 4 4 4 3 3 3 2 2 2 1 1 1 . c . b . a . c . b . a . c . b . a . c . b a − = = − = − = = = − = = − = − = = =

Maka persamaan Spline Kuadrat yang dihasilkan adalah

5 . 1 4 . 1 8895 . 1 43 . 2 6 . 0 ) ( 4 . 1 3 . 1 5371 . 0 498 . 0 09 . 0 ) ( 3 . 1 2 . 1 8553 . 1 526 . 2 69 . 0 ) ( 2 . 1 1 . 1 8617 . 0 87 . 0 ) ( 2 4 2 3 2 2 1 ≤ ≤ − + − = ≤ ≤ − + = ≤ ≤ − + − = ≤ ≤ − = x x x x f x x x x f x x x x f x x x f

Dari persamaan di atas didapat

3. Spline Kubik

Spline kubik adalah menurunkan polinom orde ketiga untuk setiap selang di antara simpul,seperti dalam :

f

( )

x =a_ix3 +b_ix2 +c_ix+d_i.

x f(x) 1.11 1.22 1.33 1.44 1.49 0.104 0.1994 0.2844 0.3655 0.3991

(30)

Jadi untuk n + 1 titik data (i = 0, 1, 2, . . . , n), terdapart n interval maka diperlukan 4n konstanta yang harus dicari yang persamaan-persamaannya di-cari dengan mengikuti definisi 2.2.

Definisi 2.2

Diberikan fungsi f pada

[ ]

a,b dan suatu himpunan angka yang disebut simpul a=x₀ <x₁ <. . .< x_n =b. Suatu interpolasi spline kubik S, untuk f(x)adalah suatu fungsi yang memenuhi kondisi :

a. S

( )

x adalah polinom kubik, S_k

( )

x menyatakan polynomial pada segmen

[

xk,xk+1

]

untuk k = 0, 1, . . . , n-1 ;

b. S

( )

x_k = f

( )

x_k k = 0, 1, . . . , n-1 ;

c. S_k₊₁

( )

x_k₊₁ =S_k

( )

x_k₊₁ k = 0, 1, . . . , n-2 ;

d. S'k+1

( )

x_k₊₁ =S'k

( )

x_k₊₁ k = 0, 1, . . . , n-2 ; e. S"k+1

( )

xk₊₁ =S"k

( )

xk₊₁ k = 0, 1, . . . , n-2 ; f. Memenuhi salah satu kondisi

(i) S''

( )

x₀ =S''

( )

x_n =0 ( Batas Natural ) (ii) S'

( )

x₀ = f'

( )

x₀ dan S'

( )

x_n = f'

( )

x_n ( Batas Apitan )

Bentuk Interpolasi Spline Kubik untuk fungsi f , dengan mengikuti kondisi-kondisi dalam Definisi 2.1

a. S_k

( )

x =a_k +b_k(x−x_k)+c_k(x−x_k)2 +d_k(x−x_k)3 k = 0, 1, . . . , n-1 ;

(31)

b. )S(x_k)= f(x_k

S_k

( )

x_k =a_k +b_k(x_k −x_k)+c_k(x_k −x_k)2 +d_k(x_k −x_k)3 =aK +bk*0+ck*0+dk*0

=a_k

∴a_k = f

( )

x_k (2.8)

c. S_k₊₁

( )

x_k₊₁ =S_k(x_k₊₁) maka

S_k(x_k₊₁)=a_k +b_k(x_k₊₁ −x_k)+c_k(x_k₊₁ −x_k)2 +d_k(x_k₊₁−x_k)3 dan

3

1 1

2 1 1

1 1

1

1( ) + + ( + ) + ( + ) + ( + )

+ = k + k − k + k − k + k − k

k x a b x x c x x d x x

S

S_k₊₁(x_k₊₁)=a_k₊₁ +b_k₊₁(x_k₊₁−x_k₊₁)+c_k₊₁(x_k₊₁−x_k₊₁)+d_k₊₁(x_k₊₁ −x_k₊₁) =a_k₊₁++b_k₊₁*0+c_k₊₁*0+d_k₊₁*0

=ak₊₁

S_k₊₁

( )

x_k₊₁ =S_k(x_k₊₁) maka

a_k₊₁ =a_k +b_k(x_k₊₁−x_k)+c_k(x_k₊₁−x_k)2 +d_k(x_k₊₁−x_k)3 jika x_k₊₁−x_kdi ganti h_k maka

(32)

3 2

1 1

1( k ) k k k k k k k k

k x a a b h c h d h

S ₊ ₊ = ₊ = + + + (2.9)

d. S'k+1

( )

x_k₊₁ =S'k(x_k₊₁)

perhatikan S_k

( )

x =a_k +b_k(x−x_k)+c_k(x−x_k)2 +d_k(x−x_k)3

( )

2

' ) ( 3 ) (

2 _k _k _k _k

k

k x b c x x d x x

S = + − + −

( )

2

' ) ( 3 ) (

2 _k _k _k _k _k _k

k k

k x b c x x d x x

S = + − + −

0 * 3 0 *

2 _k _k

k c d

b + +

=

k

b

=

( )

2

1 1

1

' ₂ ₍ ₎ ₃ ₍ ₎

k k k k k k k k

k x b c x x d x x

S ₊ = + ₊ − + ₊ −

dan Sk₊₁(x)=ak₊₁+bk₊₁(x−xk₊₁)+ck₊₁(x−xk₊₁)2 +dk₊₁(x−xk₊₁)3

( )

2

1 1 1 1 1 ' ) ( 3 ) (

2 ₊ ₊ ₊

+

+ = _k + _k − _k + _k − _k

k x b c x x d x x

S

( )

2

1 1 1 1 1 1 1 1 ' ) ( 3 ) (

2 ₊ ₊ ₊ ₊ ₊

+ +

+ _k = _k + _k _k − _k + _k _k − _k

k x b c x x d x x

S 0 * 3 0 * 2 ₁

1 k k

k c d

b + +

= ₊ ₊

1 +

=bk

( )

₁ ' ( ₁)

1 '

+ +

+ _k = k _k

k x S x

S

maka b_k₊₁ =b_k +2c_k(x_k₊₁ −x_k)+3d_k(x_k₊₁−x_k)2 jika x_k₊₁ −x_kdi ganti h_k maka

S'k+1(x_k₊₁)=b_k₊₁ =b_k +2c_kh_k +3d_kh_k2 (2.10)

e. S"k+1

( )

x_k₊₁ =S"k(x_k₊₁)

(33)

( )

2 6 ( )

''

k k k

k x c d x x

S = + −

( )

2 6 ( )

''

k k k k k

k x c d x x

S = + −

=2c_k +6d_k*0 =2c_k

S''k

( )

x_k₊₁ =2c_k +6d_k(x_k₊₁−x_k)

dan S'k+1

( )

x =bk₊₁+2ck₊₁(x−xk₊₁)+3dk(x−xk₊₁)2

S''k+1

( )

x_k₊₁ =2c_k₊₁ +6d_k₊₁(x_k₊₁−x_k₊₁) =2c_k₊₁+6d_k₊₁*0

=2c_k₊₁

S"k+1

( )

x_k₊₁ =S"k(x_k₊₁)

maka )2ck+₁ =2ck +6dk(xk+₁−xk

jika x_k₊₁ −x_kdi ganti h_k maka

k k k

k c d h

c 2 6

2 ₊₁ = +

c_k₊₁ =c_k +3d_kh_k (2.11) dari (2.11) didapat

k k k k

h c c d

3

1−

= + _(2.12)

Dari (2.9) dan (2.12) diperoleh :

2 1

1

3 3

2 _k

k k k k k k

k h

h c c h c b

b ₊ = + + + −

k k k k k k

k c h c h c h

b + + −

= 2 ₊₁

(34)

Dari (2.9) dan (2.12) di peroleh :

3 2

1 k k k k k k k

k a b h c h d h

a ₊ = + + +

3 1

2 1

3 _k k

k k k k k k k k h h c c h c h b a

a ₊ = + + + + −

2 1 2 1 3 ) ( k k k k k k k k k k k k h h c c h h c h a h a

b = + − + + + −

k k k k k k k k k k k h h c h c h c h a a b 3

3 2 ₁ 2 2

1 − − − +

= + +

(

1

)

(

2 1

)

3 1

+

+ − − +

= k k

k k k k

k c c

h a a h

b (2.14) dengan pengurangan indeks

(

)

(

k k

)

k k

k c c

h a

a h

b = − ₋ − − ₋ +

− − 1 1 1 1 1 2 3 1 (2.15)

Dari (2.13) dan (2.14) di peroleh :

(

k k

)

k

k b h c c

b = ₋₁ − ₋₁ ₋₁ +

(

1

)

(

2 1

)

3 1

+

+ − − +

= k k

k k k k

k c c

h a a h b

jadi

(

)

(

2

)

( )

3 1 1 1 1 1

1 k k k k k

k k k k

k c c h c c

h a a h

b ₋ = ₊ − − + ₊ − ₋ ₋ + (2.16) Persamaan (2.15) dan (2.16) menghasilkan

(

)

(

)

(

)

(

2

)

( )

(35)

(

)

(

k k

)

k k k k a a h a a

h ₋₁ − −1 − +1−

1 1

(

)

3 3 2 2 3 1 1 1 1 1 1 1 1 k k k k k k k k k k k k

k h c h c

c h c h c h c c

h ₋ ₋ ₋

− − − − + − − + + + − =

(

)

(

k k

)

k k k k a a h a a

h ₋₁ − −1 − +1−

1 1

(

)

3 3 3 2 3 2 3 1 1 1 1 1 1 1 k k k k k k k k k k

k h c h c h c h c

c c

h ₋ ₋ ₋ ₋ ₋ ₋

+ + − + − + − =

(

)

(

k k

)

k k k k k k k

k k k k c h c h c c h a a h a a

h ₁ 1 1 (2 1) 1 1 2 1

3 3 − − − + + − − − − + − = − − −

(

)

(

k k

)

k k k k k k k

k k k k c h c c h c h a a h a a

h 1 1 ₁ 1 1 1 (2 1) 2 1

3 3 − + − − − − − + − − − = + + +

(

)

(

1

)

1 1 1 1

1

1 (2 )

3 3 + − − − − −

+ − − k − k = k k + k k + k + k k

k k k k c h c c h c h a a h a a

h (2.17)

untuk k = 1, 2, . . ., n-1

dari persamaan-persamaan yang telah didapat di atas, sudah didapatkan per-samaan-persamaan untuk mencari koefisien-koefisien a, b, dan d. Untuk men-cari koefisien c akan digunakan persamaan (2.17) dengan mengikuti teorema yang memenuhi kondisi dari (i) atau (ii).

Teorema 2.1

Jika f di definisikan pada a= x0 < x1 <. . .<xn =b, maka f adalah

interpolasi spline natural tunggal pada simpul x₀ < x₁ <. . .<x_n, interpo-lasi spline natural memenuhi keadaan S''(a)=0 dan S''(b)=0.

(36)

0 ) (

'' =

a

S dan S''(b)=0 menyatakan secara tidak langsung 0 2 ) ( '' = = _n

n S x

c dan )0=S''(x₀)=2c₀ +6d₀(x₀ −x₀

jadi 0c₀ = .

Dua pernyataan c₀ =0 dan c_n =0 dalam persamaan

(

)

(

1

)

1 1 1 1

1

1 (2 )

3 3 + − − − − −

+ − − k − k = k k + k k + k + k k

k k k k c h c c h c h a a h a a h

menghasilkan sistem linear dengan persamaan Ax=b, A adalah (n+1) dengan matriks (n+1).

(

)

(

)

(

)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = − − − − 1 0 0 0 2 0 2 0 2 0 0 0 1 1 1 2 2 2 2 1 1 1 1 0 0 n n n

n h h h

h h h h h h h h h A ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − = − − − − − 0 ) ( 3 ) ( 3 ) ( 3 ) ( 3 0 2 1 2 1 1 0 1 0 1 2 1 n n n n n n a a h a a h a a h a a h M b

Dari persamaan Ax = b akan didapat penyelesaian tunggal dan dapat dicari dengan Eliminasi Gauss.

(37)

Teorema 2.2

Jika f didefinisikan pada a=x₀ <x₁ <. . .< x_n =bdan turunan pada a dan b, maka f adalah Interpolasi Spline Apitan pada simpul

n

x x

x₀ < ₁ <. . .< , Interpolasi Spline dinyatakan S'(a)= f'(a) dan ) ( ) ( ' ' b f b

S = .

Bukti :

Menggunakan S'(a)=S'(x₀)=b₀

implementasi

(

₁

)

(

2 ₁

)

3 1

+

+ − − +

= k k

k k k k

k c c

h a a h

b dengan k = 0

(

0 1

)

0 0 0 1 ' 2 3 )

( h c c

h a a a

f = − − +

(

)

( ) 3 2 ' 0 1 0 1 0 0

0 a a f a

h c h c

h + = − −

) (

)

( ₁ ₁ ₁

'

n n n n

n b h c c

b b

f = = ₋ + ₋ ₋ +

persamaan

(

₁

)

(

2 ₁

)

3 1

+

+ − − +

= k _k _k

k k k

k c c

h a a h

b dengan k =n−1

(

2

)

( )

3 )

( 1 ₁ ₁ ₁

1 1 ' n n n n n n n n n c c h c c h h a a b

f = − − − ₋ + + ₋ ₋ −

− − ) 2 ( 3 1 1 1 1 n n n n n n c c h h a a + − − = − ₋ − −

dan 2 3 ( ) 3 ( ₁)

1 ' 1 1 1 − − − −

− + = − n − n

n n

n a a

(38)

Persamaan

(

)

(

₁

)

₁ ₁ ₁ ₁

1

1 (2 )

3 3 + − − − − −

+ − − k − k = k k + k k + k + k k

k k k k c h c c h c h a a h a a h

dengan persamaan 2 3

(

₁ ₀

)

'( )

0 1 0 0

0 a a f a

h c h c

h + = − −

dan 2 3 ( ) 3 ( ₁)

1 ' 1 1 1 − − − −

− + = − n − n

n n

n a a

h b f c h c h

menghasilkan sistem linear dengan persamaan Ax = b .

(

)

(

)

(

)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + = − − − − − − 1 1 1 1 2 2 2 2 1 1 1 1 0 0 0 0 2 0 0 2 0 2 0 2 0 0 2 n n n n n n h h h h h h h h h h h h h h h h A ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − − − − = − − − − − − − ) ( 3 ) ( 3 ) ( 3 ) ( 3 ) ( 3 ) ( 3 ) ( 3 ) ( 3 1 1 ' 2 1 2 1 1 0 1 0 1 2 1 ' 0 1 0 n n n n n n n n n a a h b f a a h a a h a a h a a h a f a a h M b

Dari persamaan Ax = b akan didapat penyelesaian tunggal dan dapat dicari dengan Eliminasi Gauss.

(39)

Gunakan Tabel 2.1 untuk mencari nilai Interpolasi saat x = 1.11 menggunakan Spline Kubik.

Penyelesaian :

Persamaan Spline Kubik dari persamaan (2.7)

Sk

( )

x =ak +bk(x−xk)+ck(x−xk)2 +dk(x−xk)3 k = 1, 2, . . ., n-1

Dari (2.8) didapat koefisien a

S(xk) = f(xk) = ak

S(x1) = f(x1) = 0.0953 = a1 S(x2) = f(x2) = 0.1823 = a2 S(x3) = f(x3) = 0.2624 = a3 S(x4) = f(x4) = 0.3365 = a4 S(x5) = f(x5) = 0.4055 = a5

Untuk h_k = xk+1 −xk

h1 = x2 – x1 = 1.2 – 1.1 = 0.1 h2 = x3 – x2 = 1.3 – 1.2 = 0.1 h3 = x4 – x3 = 1.4 – 1.3 = 0.1 h4 = x5 – x4 = 1.5 – 1.4 = 0.1

Untuk mencari koefisien c menggunakan Teorema 2.1 yaitu Batas Natural

(40)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − − − = 0 153 . 0 18 . 0 207 . 0 0 0 ) ( 3 ) ( 3 ) ( 3 ) ( 3 ) ( 3 ) ( 3 0 3 4 3 4 5 4 2 3 2 3 4 3 1 2 1 2 3 2 a a h a a h a a h a a h a a h a a h b ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 4 3 2 1 1 0 0 0 0 1 . 0 4 . 0 1 . 0 0 0 0 1 . 0 4 . 0 1 . 0 0 0 0 1 . 0 4 . 0 1 . 0 0 0 0 0 1 c c c c c ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = 0 153 . 0 18 . 0 207 . 0 0

Dengan Eliminasi Gauss untuk persaman sistem linear Ax = b

Koefisien ck yang di dapat

0 4468 . 0 2571 . 0 5818 0 0 5 4 3 2 1 = − = = − = = c c c . c c

(41)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

2

)

0.69 ( 0.0298) 0.7198 3 1 7388 . 0 0022 . 0 741 . 0 2 3 1 8312 . 0 ) 0302 . 0 ( 801 . 0 2 3 1 8894 . 0 ) 0194 . 0 ( 87 . 0 2 3 1 2 3 1 5 4 4 4 5 4 4 4 3 3 3 4 3 3 3 2 2 2 3 2 2 2 1 1 1 2 1 1 1 1 = − − = + − − = = − = + − − = = − − = + − − = = − − = + − − = + − − = ₊ ₊ c c h a a h b c c h a a h b c c h a a h b c c h a a h b c c h a a h

b k k

k k k k k

Dari persamaan (2.12) didapat koefisien untuk dk

4893 . 1 3 3463 . 2 3 7963 . 2 3 9393 . 1 3 3 4 4 5 4 3 3 4 3 2 2 3 2 1 1 2 1 1 = − = − = − = = − = − = − = − = + h c c d h c c d h c c d h c c d h c c d k k k k

Persamaan Spline Kubik Sk(x)

(42)

Dari Persamaan Spline Kubik di atas maka didapat

BAB III

PERANCANGAN DAN IMPLEMENTASI

A. Perancangan Umum

Untuk mengetahui seberapa besar galat yang dihasilkan dalam metode Spline yaitu Spline Linear, Spline Kuadrat dan Spline Kubik maka akan dilakukan percobaan. Percobaan dilakukan menggunakan sebuah program dengan bahasa pemrograman Delphi versi 7.0. Program yang akan dibuat adalah program dengan masukan spline. Sebagai dasar perbandingannya adalah galat yang dihasilkan masing-masing Spline dengan data pada tabel natural logaritma.

Program masukan spline digunakan untuk mencari Interpolasi dalam metode Spline yaitu Spline Linear, Spline Kuadrat dan Spline Kubik. Dari hasil percobaan dapat diketahui nilai Interpolasi yang dilakukan oleh Spline Linear, Spline Kuadrat dan Spline Kubik. Perbandingan Interpolasi dari data masukan

x f(x) 1.11

1.22 1.33 1.44 1.49

0.1042 0.1989 0.2853 0.3647 0.3987

(43)

dianalisis dengan menggunakan grafik dan hasilnya dianalisis untuk ditarik ke-simpulan.

B. Perancangan Antarmuka

Program yang dibuat terdiri dari 2 layar, yaitu :

1. Layar Sampul

Gambar 3.1 Rancangan Layar Sampul

LOGO

Perbandingan Interpolasi dalam Metode Spline

Oleh :

Anastasia Vrysca Jayanti 013114014

Jurusan Matematika

Fakultas Matematika Dan Ilmu Pengetahuan alam Universitas Sanata Dharma

Yogyakarta

(44)

Dalam layar ini berisi text judul, nama penyusun beserta NIM, nama fakultas dan nama universitas serta 2 tombol pilihan.

2. Layar Masukan Spline

Dalam layar ini terdapat pilihan spline, edit text untuk jumlah data masukan, jumlah data yang dicari, kolom baris untuk dihapus dan kolom baris untuk ditambah, stringgrind untuk masukan nilai-nilai data, 2 tabsheet yang masing-masing terdapat stringgrid untuk hasil pencarian dan galat, chart untuk grafik spline yang dipilih dan 11 tombol pilihan.

(45)

C. Rancangan Proses

Proses yang dilakukan untuk membandingkan Interpolasi dalam metode Spline yaitu Spline Linear, Spline Kuadrat dan Spilne Kubik, dilakukan percobaan dengan memasukan nilai-nilai data. Pertama kali yang dilakukan yaitu memilih spline yang akan digunakan, kemudian memasukan nilai-nilai data, jum-lah data, jumjum-lah pencarian dan nilai yang akan dicari. Selanjutnya program mela-kukan proses perhitungan sebanyak nilai yang dicari. Hasil yang ditampilkan dari perhitungan berupa nilai interpolasi. Dari hasil perhitungan ketiga spline tersebut akan ditampilkan galat untuk masing-masing nilai yang didapat. Dari hasil perco-baan kemudian dianalisis dan dibandingkan galatnya untuk setiap spline.

D. Implementasi

Dalam program masukan spline ini terdapat tiga bagian penting dalam me-tode Spline yaitu perhitungan Spline Linear, Spline Kuadrat dan Spline Kubik. 1. Spline Linear

(46)

(47)

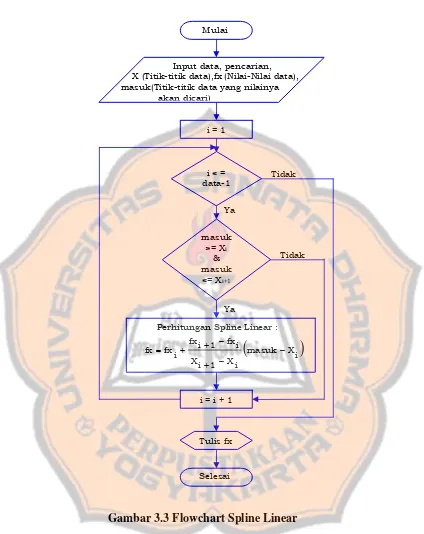
i = 1

i < = data-1

i = i + 1 masuk

>= Xi & masuk <= Xi+1

Selesai

Tidak

Tidak Ya

Ya

Tulis fx

Perhitungan Spline Linear :

(

masuk X_i

)

i X 1 i X

i fx 1 i fx i fx

fx −

− +

− + + =

Input data, pencarian, X (Titik-titik data),fx (Nilai-Nilai data), masuk(Titik-titik data yang nilainya akan dicari)

Mulai

(48)

Setelah user memasukan banyaknya data yang diketahui, banyaknya data yang dicari, titik-titik data dan nilai-nilai data yang diketahui, titik-titik data yang nilainya yang akan dicari, selanjutnya dengan menekan tombol Spline maka pro-gram menjalankan proses perhitungan dengan Spline Linear.

Potongan programnya sebagai berikut :

for i :=1 to data-1 do begin

if(masuk[w]>=strtofloat(cells[1,i]))and (masuk[w]<=strtofloat(cells[1,i+1]))then begin

fx:=strtofloat(cells[2,i])+(((strtofloat(cells[2,i+1])-

strtofloat(cells[2,i]))/(strtofloat(cells[1,i+1])- strtofloat(cells[1,i])))*(masuk[w]-strtofloat(cells[1,i])));

with StringGrid1 do begin

Cells[2,w]:= FloatToStr(fx); end;

end; end;

Nilai Spline Linear digunakan untuk pencarian galat. Saat tombol galat diklik maka program akan menjalankan nilai galat untuk Spline Linear. Untuk pembuatan grafik yang pertama dilakukan adalah menghitung selisih titik data yang diketahui yang terakhir dengan titik data yang diketahui yang pertama dan dibagi 1000. Hasilnya merupakan penambahan titik data yang diketahui yang pertama sampai titik data yang diketahui yang terakhir. Kemudian program melakukan perhitungan nilai data dengan alur perhitungan Spline Linear.

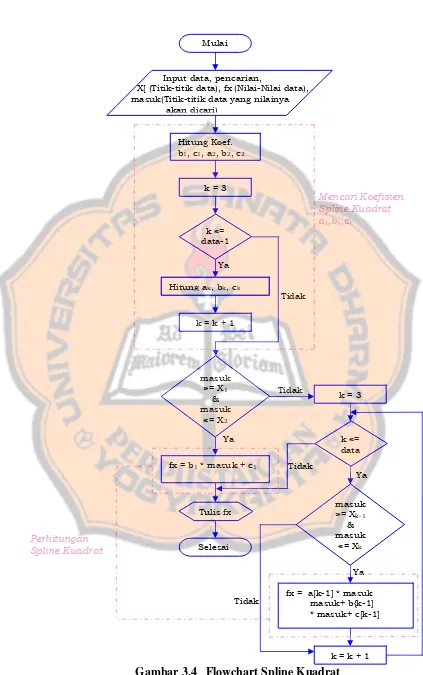
2. Spline Kuadrat

(49)

Hitung Koef. b1, c1, a2, b2, c2

Ya Tidak

Tidak

Ya k <= data-1

k = 3

k = k + 1 Input data, pencarian,

X[ (Titik-titik data), fx (Nilai-Nilai data), masuk(Titik-titik data yang nilainya akan dicari)

Hitung ak, bk, ck Mulai

masuk >= X1

& masuk

<= X2

Tulis fx

Selesai Ya

fx = b1 * masuk + c1

k = 3

k <= data

masuk >= Xk-1

& masuk

<= Xk

fx = a[k-1] * masuk masuk+ b{k-1] * masuk+ c[k-1]

k = k + 1 Tidak

Ya

Tidak

Mencari Koefisien Spline Kuadrat ak,bk,ck

Gambar 3.4 Flowchart Spline Kuadrat

(50)

Spline Kuadrat membutuhkan membutuhkan 3(n-1) buah konstanta yang dicari dengan mengikuti kondisi yang ada di bab II. Setelah user memasukan ban-yaknya data yang diketahui, banban-yaknya data yang dicari, titik-titik data dan nilai-nilai data yang diketahui, titik-titik data yang nilai-nilainya yang akan dicari maka pro-gram akan mencari 3(n-1) konstanta yang dibutuhkan. Pencarian konstanta dilakukan pensubtitusian. Potongan program berikut merupakan pencarian konstanta ak, bk, ck:

for k:=3 to data-1 do begin

r[k]:=StrToFloat(Cells[1,k])-StrToFloat(Cells[1,k+1]); t[k]:=StrToFloat(Cells[2,k])-StrToFloat(Cells[2,k+1]); end;

b[1]:=(StrToFloat(Cells[2,1])-StrToFloat(Cells[2,2]))/ (StrToFloat(Cells[1,1])-StrToFloat(Cells[1,2])); c[1]:=StrToFloat(Cells[2,1])-b[1]*StrToFloat(Cells[1,1]);

a[2]:=(StrToFloat(Cells[2,2])-StrToFloat(Cells[2,3]))- (b[1]*(StrToFloat(Cells[1,2])-StrToFloat(Cells[1,3])))/

(2*StrToFloat(Cells[1,2])*StrToFloat(Cells[1,3])- StrToFloat(Cells[1,2])*StrToFloat(Cells[1,2])-StrToFloat(Cells[1,3])*StrToFloat(Cells[1,3])); b[2]:=b[1]-2*a[2]*StrToFloat(Cells[1,2]);

c[2]:=StrToFloat(Cells[2,2])-a[2]*StrToFloat(Cells[1,2])* StrToFloat(Cells[1,2])-b[2]*StrToFloat(Cells[1,2]);

for k:=3 to data-1 do begin

j[k]:=2*StrToFloat(Cells[1,k])*StrToFloat(Cells[1,k+1])- StrToFloat(Cells[1,k])*StrToFloat(Cells[1,k])- StrToFloat(Cells[1,k+1])*StrToFloat(Cells[1,k+1]); end;

for k:= 3 to data-1 do begin

a[k]:= ((StrToFloat(Cells[2,k])-StrToFloat(Cells[2,k+1]))- (((2*a[k-1]*StrToFloat(Cells[1,k]))+b[k-1])*r[k]))/j[k]; b[k]:= ((2*a[k-1]*StrToFloat(Cells[1,k]))+b[k-1])-

(2*a[k]*StrToFloat(Cells[1,k]));

(51)

Potongan program berikut untuk mencari nilai Spline Kuadrat :

if(masuk[w]<StrToFloat(Cells[1,2]))and (masuk[w]>=StrToFloat(Cells[1,1]))then begin

fx:=b[1]*masuk[w]+c[1]; With StringGrid1 do begin

end;

for k:=3 to data do begin

if(masuk[w]>=StrToFloat(Cells[1,k-1]))and (masuk[w]<=StrToFloat(Cells[1,k]))then begin

fx :=a[k-1]*masuk[w]*masuk[w]+b[k-1]*masuk[w]+c[k-1]; with StringGrid1 do

begin

end; end;

Nilai Spline Kuadrat digunakan untuk pencarian galat. Saat tombol galat dik-lik maka program akan menjalankan nilai galat untuk Spline Kuadrat. Untuk pembuatan grafik yang pertama dilakukan adalah menghitung selisih titik data yang diketahui yang terakhir dengan titik data yang diketahui yang pertama dan dibagi 1000. Hasilnya merupakan penambahan titik data yang diketahui yang per-tama sampai titik data yang diketahui yang terakhir. Kemudian program melakukan perhitungan nilai data dengan alur perhitungan Spline Kuadrat.

3. Spline Kubik

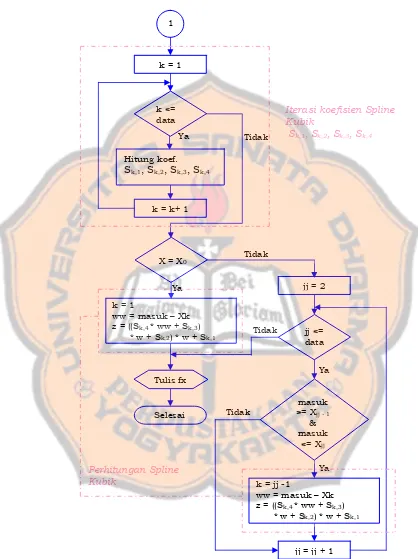
Alur Spline Kubik digambarkan secara singkat pada gambar 4.3. Titik-titik data yang diketahui dianggap X dan nilai-nilai data yang diketahui dianggap fx dan titik-titik data yang akan dicari nilainya dianggap masuk.

(52)

Tidak

Tidak Ya

k <= data k = 2

k = k + 1 Input data, pencarian,

X[ (Titik-titik data), fx (Nilai-Nilai data), masuk(Titik-titik data yang nilainya akan dicari)

Mulai

Ya

Turunan kedua ujung simpul m1 = 0 & mdata = 0

mk = ( vk-ck * mk+1 )

/ bk

k = k - 1 k <= 2 k = data - 1

1 Hitung

Selisih titik (h1)& nilai data (d1]

Hitung

Selisih titik (hk)& nilai data (dk]

Selisih titik data hk & nilai

data dk

Turunan Kedua mk

(53)

Tidak

Tidak Tidak Tidak 1

k = k+ 1 k = 1

Hitung koef.

Sk,1, Sk,2, Sk,3, Sk,4

jj = 2

jj = jj + 1 masuk >= Xjj - 1

& masuk

<= Xjj k <=

data

X = X0

jj <= data k = 1

ww = masuk – Xk z = ((Sk,4 * ww + Sk,3) * w + Sk,2) * w + Sk,1

Tulis fx

Selesai

k = jj -1

ww = masuk – Xk z = ((Sk,4 * ww + Sk,3) * w + Sk,2) * w + Sk,1 Ya

Ya

Iterasi koefisien Spline Kubik

Sk,1, Sk,2, Sk,3, Sk,4

Perhitungan Spline Kubik

Ya

(54)

Spline Kuadrat membutuhkan membutuhkan 4n buah konstanta yang dicari dengan mengikuti kondisi yang ada di bab II. Setelah user memasukan banyaknya data yang diketahui, banyaknya data yang dicari, titik-titik data dan nilai-nilai data yang diketahui, titik-titik data yang nilainya yang akan dicari maka program akan mencari 4n konstanta yang dibutuhkan. Pencarian konstanta dilakukan dengan eliminasi Gauss. Potongan program berikut merupakan pencarian konstanta Sk,1, Sk,2, Sk,3, Sk,4.

cells[1,data+1]:=floattostr(0); cells[2,data+1]:=floattostr(0);

h[1] := strtofloat(cells[1,2])-strtofloat(cells[1,1]);

d[1] := (strtofloat(cells[2,2])-strtofloat(cells[2,1]))/h[1];

for k :=2 to data do begin

h[k] := strtofloat(cells[1,k+1])-strtofloat(cells[1,k]);

d[k] := (strtofloat(cells[2,k+1])-strtofloat(cells[2,k]))/h[k]; a[k] := h[k];

b[k] := 2*(h[k-1]+h[k]); c[k]:= h[k];

end;

for k := 2 to data do begin

v[k] :=6*(d[k]-d[k-1]); end;

m[1] := 0; m[data] := 0;

tt := a[k-1]/b[k-1]; v[k] := v[k]-tt*v[k-1]; b[k] := b[k]-tt*c[k-1]; end;

m[data] := v[data]/b[data];

for k:= data-1 downto 2 do begin

m[k] := (v[k]-c[k]*m[k+1])/b[k]; end;

(55)

s[k,1] := strtofloat(cells[2,k]);

s[k,2] := d[k]-((h[k]*((2*m[k])+m[k+1]))/6); s[k,3] := m[k]/2;

s[k,4] := (m[k+1]-m[k])/(6*h[k]); end;

Potongan program berikut untuk mencari nilai Spline Kubik :

for jj := 2 to data do begin

if(masuk[w]>=strtofloat(cells[1,jj-1]))and

(masuk[w]<=strtofloat(cells[1,jj]))then begin

k := jj-1;

ww := masuk[w]-strtofloat(cells[1,k]);

z := ((s[k,4]*ww+s[k,3])*ww+s[k,2])*ww+s[k,1]; with stringgrid1 do

begin

cells[4,w] := FloatToStr(z); end;

end; end;

if (masuk[w] = strtofloat(cells[1,1])) then begin

k := 1;

ww := masuk[w]-strtofloat(cells[1,k]);

z := ((s[k,4]*ww+s[k,3])*ww+s[k,2])*ww+s[k,1]; with stringgrid1 do

begin

cells[4,w] := FloatToStr(z); end;

end;

(56)

BAB IV

ANALISIS

A. Hasil Implementasi

1. Layar Sampul

Layar sampul berisi 2 tombol yaitu : a. Spline : Untuk menuju layar spline b. Exit : Untuk Keluar dari program.

(57)

2. Layar Spline

Layar Spline terdapat 2 tabsheet yang pertama untuk pencarian dan yang kedua untuk galat. Layar Spline keseluruhannya terdiri dari :

a. CheckBox

Digunakan untuk memilih Spline yang akan digunakan b. Edit Text

Tempat masukan untuk jumlah data masukan, jumlah data yang dicari, kolom baris yang ingin dihapus, dan kolom baris yang ingin ditambah. c. BitBtn

- No : Digunakan untuk memberi nomor baris.

- Reset : Digunakan untuk membersihkan semua tampilan.

- Delete : Digunakan untuk menghilangkan kolom baris yang di-inginkan.

(58)

- Spline : Digunakan untuk mencari nilai Spline. - Clear : Digunakan untuk menghapus grafik. - Grafik : Digunakan untuk menggambar grafik. - Close : Untuk kembali ke layar sampul.

d. StringGrid

- Data : Digunakan untuk masukan nilai data.

- Pencarian : Digunakan untuk masukan nilai data yang dicari dan hasil pencarian.

- Galat : Digunakan untuk hasil perhitungan galat. e. PageControl

- Pencarian : Digunakan untuk StringGrid Pencarian. - Galat : Digunakan untuk StringGrid Galat.

(59)

B. Pengujian Program Spline

Contoh 4.1

Mencari nilai Interpolasi terhadap data pada tabel 2.1 sebagai data yang diketahui untuk mencari x = [1.11 1.22 1.33 1.44 1.49]

C. Percobaan dan Analisis

Percobaan yang dilakukan untuk menganalisis galat dan waktu komputasi. Percobaan dilakukan sebanyak dua kali yaitu dengan 5 pasangan data. Beda jauh data untuk percobaan pertama yaitu 0.1 dan percobaan kedua 0.3. Untuk menganalisis galat dilakukan dengan mencari 20 nilai data yang ti-tik datanya diketahui. Setelah melakukan percobaan untuk Spline Linear, Spline Kuadrat dan Spline Kubik, hasil yang diperoleh akan dianalisis dengan galat dan grafik.. Untuk menganalisis waktu komputasi, percobaan dilakukan dengan jumlah data pencarian yang berbeda-beda.

(60)

Tabel 4.1 Data Percobaan 1 1. Galat

a. Percobaan 1

No x y

1 1.1 0.0953 2 1.2 0.1823 3 1.3 0.2624 4 1.4 0.3365 5 1.5 0.4055

Data Nilai Tabel Galat (%)

No

x y Spline Linear Spline Kuadrat Spline kubik

1 1.11 0.1044 0.38 0.38 0.19 2 1.12 0.1133 0.52 0.52 0.26 3 1.13 0.1222 0.55 0.55 0.33 4 1.14 0.1310 0.69 0.69 0.31 5 1.15 0.1398 0.72 0.72 0.29 6 1.21 0.1906 0.16 0.16 0 7 1.22 0.1989 0.30 0.25 0 8 1.23 0.2070 0.34 0.39 0.05 9 1.24 0.2151 0.37 0.42 0.05 10 1.25 0.2231 0.31 0.45 0.04 11 1.31 0.2700 0.07 0.11 0.04 12 1.32 0.2776 0.14 0.18 0.04 13 1.33 0.2852 0.21 0.28 0.04 14 1.34 0.2927 0.24 0.31 0.03 15 1.35 0.3001 0.23 0.30 0.07 16 1.41 0.3436 0.06 0.09 0 17 1.42 0.3507 0.11 0.17 0 18 1.43 0.3577 0.14 0.22 0 19 1.44 0.3646 0.14 0.25 0.03 20 1.45 0.3716 0.16 0.24 0.03

(61)

Grafik Galat Percobaan 1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

1.11 1.13 1.15 1.22 1.24 1.31 1.33 1.35 1.42 1.44

Tititk Data Pencarian

Ga

la

t

( %

)

Spline Linear Spline Kuadrat Spline Kubik

Grafik 4.1 Galat Percobaan 1

Dari tabel 4.2 dan grafik 4.1 diperoleh keterangan :

a. Galat yang dihasilkan Spline Linear dan Spline Kuadrat bisa sama.

b. Dari grafik 4.1 diketahui bahwa Spline Linear yang merupakan orde yang lebih kecil dibandingkan Spline Kuadrat, menghasilkan galat yang lebih kecil. Dengan kata lain orde yang lebih tinggi tidak menjamin akan menghasilkan galat yang lebih kecil.

c. Galat yang dihasilkan Spline Kubik lebih kecil dari galat yang dihasilkan Spline Linear dan Spline Kuadrat.

(62)

b. Percobaan 2

Tabel 4.3 Data Percobaan 2

Nilai Data Tabel Galat (%)

No

x y Spline Linear Spline Kuadrat Spline Kubik

1 1.11 0.1044 1.05 1.05 0.67 2 1.12 0.1133 1.68 1.68 1.06 3 1.13 0.1222 2.30 2.30 1.39 4 1.14 0.1310 2.67 2.67 1.60 5 1.15 0.1398 3.08 3.08 1.86 6 1.21 0.1906 3.62 3.62 1.78 7 1.22 0.1989 3.57 3.57 1.76 8 1.23 0.2070 3.49 3.49 1.64 9 1.24 0.2151 3.35 3.35 1.53 10 1.25 0.2231 3.23 3.23 1.43 11 1.31 0.2700 2.18 2.18 0.74 12 1.32 0.2776 1.95 1.95 0.65 13 1.33 0.2852 1.75 1.75 0.56 14 1.34 0.2927 1.50 1.50 0.44 15 1.35 0.3001 1.27 1.27 0.37 16 1.41 0.3436 0.17 0.26 0.06 17 1.42 0.3507 0.37 0.48 0.09 18 1.43 0.3577 0.50 0.70 0.11 19 1.44 0.3646 0.60 0.88 0.16 20 1.45 0.3716 0.75 1.02 0.16

Tabel 4.4 Hasil Galat Percobaan 2

No x y

(63)

Grafik Galat Percobaan 2

0 0.5 1 1.5 2 2.5 3 3.5 4

1.11 1.13 1.15 1.22 1.24 1.31 1.33 1.35 1.42 1.44

Titik Data Pencarian

Gal

a

t (

%

)

Spline Linear Spline Kuadrat Spline Kubik

Grafik 4.2 Galat Percobaan 2

Dari tabel 4.4 dan grafik 4.2 diperoleh keterangan :

a. Dari grafik 4.2 diketahui bahwa semakin besar beda jauh data maka galat yang dihasilkan Spline Linear dan Spline Kuadrat relatif sama.

b. Galat yang dihasilkan Spline Kubik tetap lebih kecil dibandingkan galat yang dihasilkan Spline Linear dan Spline Kuadrat meskipun beda jauh data bertambah.

(64)