BAB I PENDAHULUAN I. Latar Belakang
Pengujian hipotesis adalah suatu prosedur yang akan menghasilkan suatu keputusan, yaitu keputusan menerima atau menolak hipotesis itu. Dalam pengujian hipotesis, keputusan yang dibuat mengandung ketidakpastian, artinya keputusan bisa benar atau salah, sehingga menimbulkan risiko. Besar kecilnya risiko dinyatakan dalam bentuk probabilitas.
Jenis – jenis pengujian hipotesis yakni berdasarkan jenis distribusi nya. Berdasarkan jenis distribusi, pengujian hipotesis dibedakan atas empat jenis yaitu pengujian hipotesis dengan distribusi Z, pengujian hipotesis dengan distribusi t, pengujian hipotesis dengan distribusi X 2 (kai kuadrat), pengujian hipotesis dengan distribusi F(F-ratio). Salah Satu contoh pengujian hipotesis dengan distribusi Z dan distribusi t yaitu pengujian hipotesis satu rata-rata dan pengujian hipotesis beda dua rata. Pengujian hipotesis satu rata adalah pengujian yang memiliki satu rata-rata. Sedangkan pengujian hipotesis dua rata-rata adalah pengujian yang memiliki dua rata-rata.
II. Tujuan Praktikum
a. Memahami dan mampu menerapkan langkah-langkah pengujian hipotesis statistik untuk mengambil suatu kesimpulan atau keputusan. b. Mampu melakukan pengujian hipotesis khususnya uji rata-rata untuk
mengestimasi besaran parameter rata-rata pada populasi. III. Pengantar Praktikum
1.
Statistik Inferensi2. Pengujian Hipotesis a. Hipotesis statistik
Hipotesis statistik ialah suatu anggapan atau pernyataan, yang mungkin benar atau tidak, mengenai suatu populasi atau lebih. Benar atau salahnya suatu hipotesis tidak akan pernah diketahui dengan pasti kecuali bila seluruh populasi diamati. Hal ini tentunya dalam kebanyakan keadaan tidak praktis. Karena itu, kita mengambil sampel acak dari populasi yang ingin diselidiki dan menggunakan data sampel ini untuk mencari kenyataan yang akan mendukung hipotesis tadi. Struktur pengujian hipotesis dirumuskan dengan istilah hipotesis nol. Ini menyatakan setiap hipotesis yang ingin diuji dinyatakan dengan H0. Penolakan H0 menjurus pada penerimaan hipotesis tandingan, dinyatakan H1.
b. Pengujian hipotesis statistik
Pengujian hipotesis adalah langkah atau prosedur untuk menentukan apakah menerima atau menolak hipotesis. Dalam pengujian hipotesis statistik terdapat empat kemungkinan keadaan yang menentukan apakah keputusan kita benar atau keliru. Keempat hal ini disarikan pada tabel berikut
Keputusan Keadaan Sebenarnya
Ho benar Ho salah
Terima Ho Keputusan benar Galat tipe II Tolak Ho Galat tipe I Keputusan benar
Penolakan hipotesis nol padahal hipotesis itu benar disebut galat jenis I. Sedangkan penerimaan hipotesis nol padahal hipotesis itu salah disebut galat jenis II. Peluang melakukan galat jenis I, juga disebut taraf keberartian (level of
significane), yang dinyatakan dengan α (baca: alfa) dan peluang membuat galat tipe
rangka pengujian hipotesis, jelas kiranya bahwa kedua tipe galat ini harus dibuat sekecil mungkin yang dinyatakan dalam peluang (probability).
c. Uji satu-pihak dan dua-pihak
Suatu uji hipotesis statistik dengan tandingan yang bersifat satu-pihak, seperti H0 : θ = θ0,
H0 : θ > θ0, atau mungkin
H0 : θ = θ0, H0 : θ < θ0,
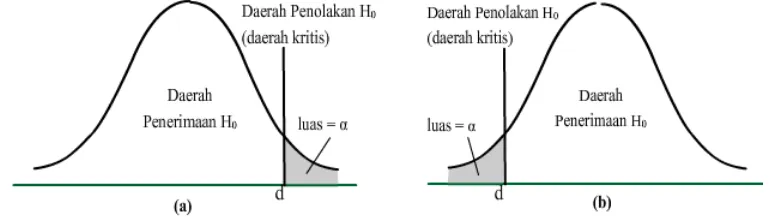
disebut uji satu-pihak. Umumnya, daerah kritis untuk hipotesis tandingan θ > θ0 terletak di sisi kanan distribusi uji statistik (lihat gambar 1.a), sedangkan daerah kritis hipotesis tandingan θ < θ0 terletak seluruhnya di sisi kiri (lihat gambar 1.b). Jadi, tanda ketidaksamaan menunjukkan arah letaknya daerah kritis.
Gambar 1. Daerah kritis untuk uji satu-pihak Suatu uji hipotesis statistik dengan tandingan berpihak dua seperti
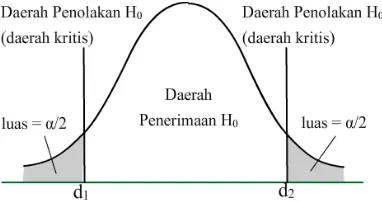
disebut uji dua-pihak, karena daerah kritis terbagi atas dua bagian, seiring dengan peluang yang sama yang diberikan pada setiap sisi atau ujung dari distribusi uji statistik tersebut. Hipotesis tandingan θ ≠ θ0 menyatakan salah satu dari θ < θ0 ataupun θ > θ0.
Gambar 2. Daerah kritis untuk uji dua-pihak d. Penggunaan nilai-P dalam pengambilan keputusan
Pendekatan nilai peluang (nilai-P) telah luas digunakan dalam statistika terapan. Pendekatan ini dirancang sebagai pilihan lain (dari segi peluang) dari pada kesimpulan hanya tolak atau tidak tolak. Pendekatan nilai-P sebagai alat bantu dalam pengambilan keputusan cukup wajar karena hampir semua paket komputer dalam perhitungan pengujian hipotesis memberikan nilai-P bersama dengan nilai yang sesuai dengan uji statistik tersebut. Definisi nilai- P adalah taraf (keberartian) terkecil sehingga nilai uji statistik yang diamati masih berarti.
Berikut ini adalah rangkuman prosedur pengujian hipotesis dengan menganggap bahwa bentuk hipotesisnya berbentuk H0 : θ = θ0,
1. Tuliskan hipotesis nol H0 bahwa θ = θ0,
2. Pilih hipotesis tandingan H1 yang sesuai dari salah satu θ < θ0, θ > θ0, atau θ = θ0
3. Pilih taraf keberartian berukuran α
5. Hitunglah nilai uji statistik dari data sampel
6. Kesimpulan : Tolak H0 bila uji statistik tersebut mempunyai nilai dalam daerah kritis (atau, bila nilai-P hitungan lebih kecil atau sama dengan taraf keberartian α yang ditentukan), sebaliknya terima H0.
3. Uji Rata-rata
Umpama kita mempunyai sebuah populasi berdistribusi normal dengan rata-rata µ dan simpangan baku σ. Akan diuji mengenai parameter rata-rata µ. Maka diambil sebuah sampel acak berukuran n, lalu kita hitung statistik x dan s. Kita kelompokkan sebagai berikut :
a. Uji satu rata-rata dengan variansi (σ) diketahui Untuk uji dua-pihak, maka pasangan hipotesis : H0 : µ = µ0
H1 : µ ≠ µ0
Dengan µ0 sebuah harga yang diketahui, digunakan statistik :
z
=
x
σ
−
μ
0/
√
n
Untuk menentukan kriteria pengujian, digunakan daftar distribusi normal baku. H0 diterima jika – zα/2 < z < zα/2, dan H0 ditolak jika z > zα/2 atau z < -zα/2. Penolakan H0 berarti penerimaan hipotesis tandingan µ ≠ µ0 . Selain menggunakan nilai z, daerah kritis juga ditulis dengan menggunakan nilai rata-rata (x), dimana tolak H0 bila x > b atau x < a, dengan :
a
=
μ
0−
z
α/2σ
√
n
danb
=
μ
0+
z
α/2untuk taraf signifikan α, nilai kritis variabel acak z dan x keduanya diperlihatkan pada gambar 1 berikut.
Gambar 3. Daerah kritis untuk hipotesis tandingan µ ≠ µ0
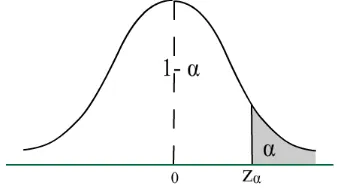
Untuk uji satu-pihak, daerah kritisnya hanya berada di satu sisi dari distribusi normal baku. Jadi, misalnya, kita ingin menguji
H0 : µ = µ0 H1 : µ > µ0
Kriteria keputusan adalah menolak H0 bila nilai hitungan z > zα dengan zα didapat dari daftar distribusi normal baku. Dalam hal lainnya H0 diterima.
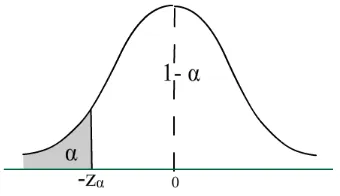
Gambar 4. Daerah kritis untuk hipotesis tandingan µ > µ0 Jika kita ingin menguji
Kriteria keputusan adalah menolak H0 bila nilai hitungan z < - zα dengan -zα didapat dari daftar distribusi normal baku. Dalam hal lainnya H0 diterima.
Gambar 5. Daerah kritis untuk hipotesis tandingan µ < µ0
b. Uji satu rata-rata dengan variansi (σ) tidak diketahui
Pada kenyataannya, simpangan baku σ sering tidak diketahui. Untuk uji rata-rata dengan σ tidak diketahui akan menggunakan distribusi t-Student. Untuk populasi normal, t berdistribusi Student dengan derajat kebebasan (v) = (n-1). Karena itu, distribusi untuk menentukan kriteria pengujian digunakan distribusi Student dengan batas-batas kriteria untuk uji dua-pihak maupun satu-pihak didapat dari Daftar Distribusi Student. Dalam hal ini, maka diambil taksirannya yaitu simpangan baku s yang dihitung dari sampel dengan menggunakan rumus :
s
2=
∑
(
x
i−¯
x
)
2n
−
1
atau menggunakan rumus s2=n
∑
xi2−(∑
xi) 2n(n−1) .
Untuk uji dua-pihak, maka pasangan hipotesis : H0 : µ = µ0
H1 : µ ≠ µ0
t
=
¯
x
s
−
μ
0/
√
n
Melampaui t α/2,n-1 atau kurang dari -t α/2,n-1. Sedangkan pada uji satu-pihak, untuk H1 : µ > µ0, penolakan diambil bila t > t α,n-1. Untuk H1: µ < µ0, daerah kritisnya adalah bila t < -t α,n-1.
c. Uji dua rata-rata dengan variansi (σ) diketahui
Banyak penelitian yang memerlukan perbandingan antara dua keadaan atau tepatnya dua populasi. Misalnya membandingkan dua cara mengajar, dua cara produksi, daya sembuh dua macam obat dan lain sebagainya.
Dua sampel acak yang bebas diambil dari dua populasi normal dengan rata-rata µ1 dan µ2 , variansi
σ
12
dan
σ
22 dan dianggap σ1 = σ2 = σ. Hipotesis untuk ujikesamaan dua rata-rata secara umum dapat ditulis sebagai H0 : µ1- µ2= do atau H0 : µ1 = µ2
Tentu hipotesis tandingannya (H1) dapat dua-pihak maupun satu-pihak. Nilai x1 dan x2 dihitung dan untuk σ1 dan σ2 diketahui, maka uji statistiknya berbentuk
z
=
( ¯
x
1−¯
x
2)−
d
0berdistribusi normal dan σ1 = σ2 = σ, maka uji t-gabungan (sering disebut uji-t dua
Distribusi-t digunakan di sini dan untuk uji dua-pihak maka hipotesis tidak ditolak bila
e. Uji dua rata untuk pengamatan berpasangan
Pengujian dua rata-rata dapat juga dilakukan untuk data yang berpasangan. Dalam tiap pasangan ini, persyaratan kedua populasi (perlakuan) dikenakan secara acak dalam satuan yang homogen. Permasalahan dua-sampel pada dasarnya dapat disederhanakan menjadi permasalahan satu-sampel dengan menggunakan selisih d1, d2, ..., dn. Jadi hipotesisnya berbentuk
H0 : µD= do
Dan uji statistik perhitungannya adalah
t
=
¯
d
s
−
d
0d
/
√
n
BAB II PEMBAHASAN 2.1. Pengumpulan Data
Berikut merupakan tabel data tinggi badan, jenis kelamin, dan nilai material teknik 30 mahasiswa jurusan teknik industri di universitas x yang diambil secara acak.
Tabel 2.1.1. Data tinggi badan, jenis kelamin, dan nilai material teknik.
167 156 160 2 65 87
168 155 165 2 67 80
170 157 166 1 78 65
175 157 158 2 65 80
170 160 145 2 56 90
169 154 160 1 67 87
165 154 168 1 45 86
170 170 170 1 50 76
Keterangan:
TBP : Tinggi badan pria TBW : Tinggi badan wanita TBM : Tinggi badan mahasiswa JK : Jenis kelamin
2.2. Pengolahan Data 2.2.1. One-Sample T Test
Ujilah hipotesis bahwa, apakah nilai rata-rata pada masing-masing sampel berbeda secara signifikan dengan nilai rata-rata pada populasinya atau nilai tinggi badan pria dan wanita berbeda dengan tinggi rata-rata pada populasinya!
4.616 cm dan 5.508 cm. Nilai Sig. (2-tailed) atau nilai-P untuk variabel Tinggi Badan Pria dan Tinggi Badan Wanita yaitu 0.000. Nilai 0.000 < nilai α = 0.05 (berada di wilayah penolakan hipotesis). Sehingga disimpulkan nilai rata-rata pada masing-masing sampel berbeda secara signifikan dengan nilai rata-rata pada populasinya atau nilai tinggi badan pria dan wanita berbeda dengan tinggi rata-rata pada populasinya.
2.2.2. Independent-Samples T Test
Ujilah hipotesis bahwa, apakah terdapat perbedaan yang signifikan antara rata-rata tinggi badan pria dan wanita?
2.2.3. Paired-Samples T Test
Ujilah hipotesis bahwa, apakah metode pengajaran baru yang diterapkan memberi pengaruh berarti pada nilai yang diraih mahasiswa?
BAB III PENUTUP 3.1. Kesimpulan
Pada pengujian hipotesis (uji rata-rata) didapatkan kesimpulan bahwa:
Pada pengujian One-Sample T Test nilai Sig. (2-tailed) atau nilai-P untuk variabel Tinggi Badan Pria dan Tinggi Badan Wanita yaitu 0.000. Nilai 0.000 < nilai α = 0.05 (berada di wilayah penolakan hipotesis). Sehingga disimpulkan nilai rata-rata pada masing-masing sampel berbeda secara signifikan dengan nilai rata-rata pada populasinya atau nilai tinggi badan pria dan wanita berbeda dengan tinggi rata-rata pada populasinya.
Pada pengujian Independent-Samples T Test nilai Sig. (2-tailed) pada t-test for Equality of Means adalah 0.06 yang berarti > nilai α = 0.05 (berada di wilayah penerimaan hipotesis). Sehingga ditarik kesimpulan terhadap variabel tinggi badan mahasiswa yaitu tidak terdapat perbedaan yang signifikan antara rata-rata tinggi badan pria dan wanita.
Pada pengujian Paired-Samples T Test nilai Sig. (2-tailed) sebesar 0.000 yang berarti < nilai α 0.05 (berada di wilayah penolakan hipotesis). Sehingga dapat ditarik kesimpulan bahwa terdapat perbedaan nilai rata-rata pada dua variabel yang diuji yaitu Nilai_1 dan Nilai_2. Sehingga dapat diinterpretasikan bahwa metode pengajaran baru yang diterapkan memberi pengaruh berarti pada nilai yang diraih mahasiswa.
Pada pengujian hipotesis ini, kita harus hati-hati dalam mengalisis nilai signifikansi yang dihasilkan. Apakah nilai sig berada pada wilayah penolakan hipotesis atau tidak, sehingga kita akan lebih mudah dalam mengambil sebuah kesimpulan.
DAFTAR PUSTAKA
Nesti, Lisa dan Syamsul Anwar. 2008. “Pengujian Hipotesis (uji rata-rata)”. Bahan Ajar. Padang: ATIP.
Walpole, Ronald E. 1995. Pengantar Statistika. Jakarta: Gramedia Pustaka Utama.
Walpole, Ronald E dan Raymond H Myers. 1995. Ilmu Peluang dan Statistika untuk