BAB 2
LANDASAN TEORI
2.1. Kriptografi
Kata Cryptography berasal dari bahasa Yunani yang terdiri dari dua kata yaitu kryptos yang berarti rahasia dan graphein yang berarti tulisan (Mollin, 2007).
Kriptografi adalah ilmu mengenai teknik enkripsi dimana data diacak menggunakan suatu kunci enkripsi menjadi sesuatu yang sulit dibaca oleh seseorang yang tidak memiliki kunci dekripsi (Kromodimoeljo, 2010).
2.1.1. Terminologi
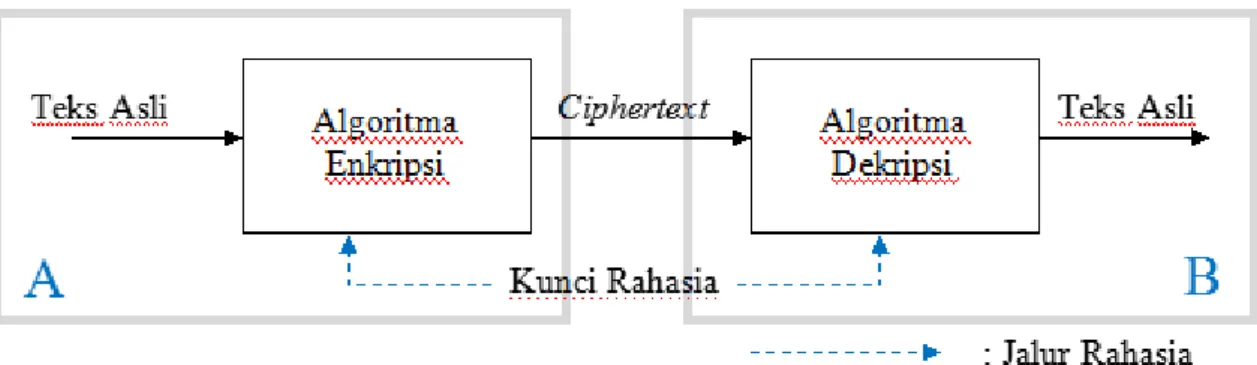
Ketika seorang pengirim (sender) ingin mengirimkan suatu pesan kepada si penerima (receiver), dimana si pengirim ingin pesan yang disampaikannya tidak dapat dibaca oleh orang lain yang ingin melakukan penyadapan (eavesdropper). Dalam kriptografi, pesan asli biasa disebut plaintext dan pesan yang disamarkan disebut ciphertext. Proses menyamarkan pesan sedemikian rupa untuk menyembunyikan substansinya disebut enkripsi. Proses untuk mengubah ciphertext kembali ke plaintext adalah dekripsi. Skema rangkaian proses enkripsi dan dekripsi ditunjukkan secara umum pada Gambar 2.1 (Schneier, 1996).
Gambar 2.1. Skema Proses Enkripsi dan Dekripsi (Schneier, 1996)
Enkripsi Dekripsi
2.1.2. Tujuan kriptografi
Kriptografi bertujuan untuk memberikan layanan keamanan sebagai berikut : (Paar&Pelzl, 2010)
1. Kerahasiaan (Confidentiality)
Informasi dirahasiakan dari semua pihak yang tidak berwenang. 2. Keutuhan Data (Inegrity)
Pesan tidak berubah dalam proses pengiriman hingga pesan diterima oleh penerima.
3. Autentikasi (Message Authentication)
Kepastian terhadap identitas setiap entitas yang terlibat dan keaslian sumber data.
4. Nirpenyangkalan (Nonrepudiation)
Setiap entitas yang berkomunikasi tidak dapat menolak atau menyangkal atas data yang telah dikirim atau diterima.
2.2. Sistem Kriptografi
Sistem kriptografi adalah algoritma, seluruh kemungkinan plaintext, ciphertext dan kunci. P adalah notasi yang digunakan untuk plaintext, C adalah ciphertext, E adalah fungsi enkripsi dan D adalah fungsi dekripsi (Schneier, 1996). Sedangkan untuk kunci dapat dinotasikan sebagai K.
Berdasarkan kunci yang dipakai, algoritma kriptografi dibagi menjadi tiga, yaitu algoritma simetri (menggunakan satu kunci untuk enkripsi dan dekripsi), algoritma asimetri (menggunakan kunci yang berbeda untuk enkripsi dan dekripsi) dan fungsi hash (Ariyus, 2008).
Selain berdasarkan kunci yang dipakai, karakteristik kriptografi juga dibagi berdasarkan tipe operasi yang dipakai untuk enkripsi dan dekripsi serta berdasarkan tipe pengolahan pesan (Sadikin, 2012).
2.3. Kriptografi Berdasarkan Kunci yang Dipakai
Algoritma Kriptografi dibagi tiga berdasarkan kunci yang dipakai, yaitu algoritma simetri (menggunakan satu kunci untuk proses enkripsi dan dekripsi), algoritma
asimetri (menggunakan kunci yang berbeda untuk proses enkripsi dan dekripsi), dan fungsi hash (Ariyus, 2008).
Karakteristik kriptografi dibagi dua berdasarkan tipe operasi yang dipakai untuk enkripsi dan dekripsi (teknik substitusi dan teknik permutasi) serta berdasarkan tipe pengolahan pesan (block cipher dan stram cipher) (Verma, 2015).
2.3.1. Sistem kriptografi simetri
Algoritma simetris adalah algoritma yang menggunakan kunci enkripsi yang sama dengan kunci dekripsinya (Kromodimoeljo, 2010). Bila mengirim pesan dengan algoritma ini, si penerima pesan harus diberitahu kunci dari pesan tersebut agar bisa mendekripsikan pesan yang dikirim. Keamanan dari pesan yang menggunakan algoritma ini tergantung pada kunci.
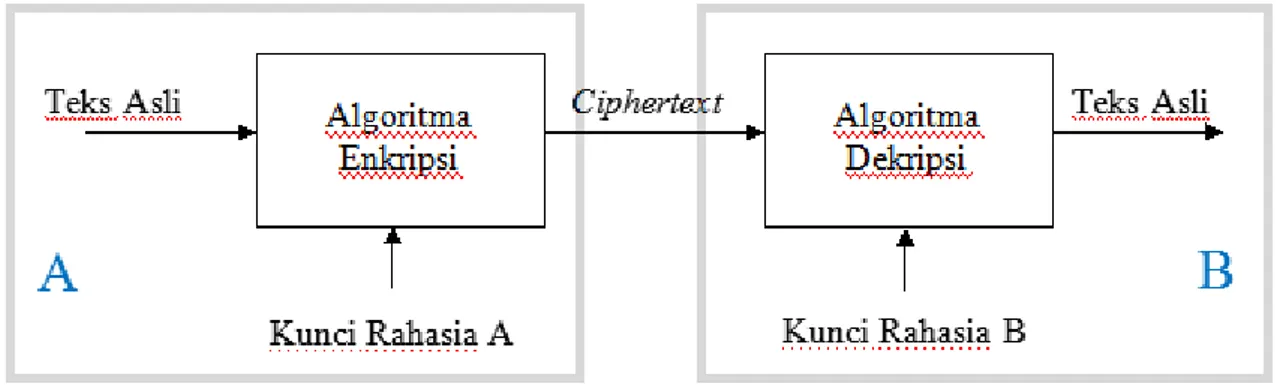
Jika kunci tersebut diketahui oleh orang lain maka orang tersebut dapat melakukan enkripsi dan dekripsi pada pesan. Yang termasuk algoritma kunci simetris adalah Hill Cipher, Affine Cipher, OTP, DES, RC2, RC4, RC5, IDEA, Twofish, Magenta, FEAL, dan lain-lainnya. Skema kriptografi simetris ditunjukkan secara umum pada Gambar 2.2.
Gambar 2.2. Skema Kriptografi Simetris (Fauzana, 2013)
2.3.2. Sistem kriptografi asimetri
Algoritma asimetris disebut juga dengan kriptografi kunci publik karena algortima ini memiliki kunci yang berbeda untuk enkripsi dan dekripsi, dimana enkripsi menggunakan public key dan untuk dekripsinya menggunakan private key. Public key dan private key harus saling berpasangan secara matematis. Dengan memberikan public key, pembuat kunci berhak memberikan dan mendapatkan public key agar pesan aman dan hanya bisa dibaca oleh si pembuat kunci. Dalam kriptografi kunci asimetri, hampir
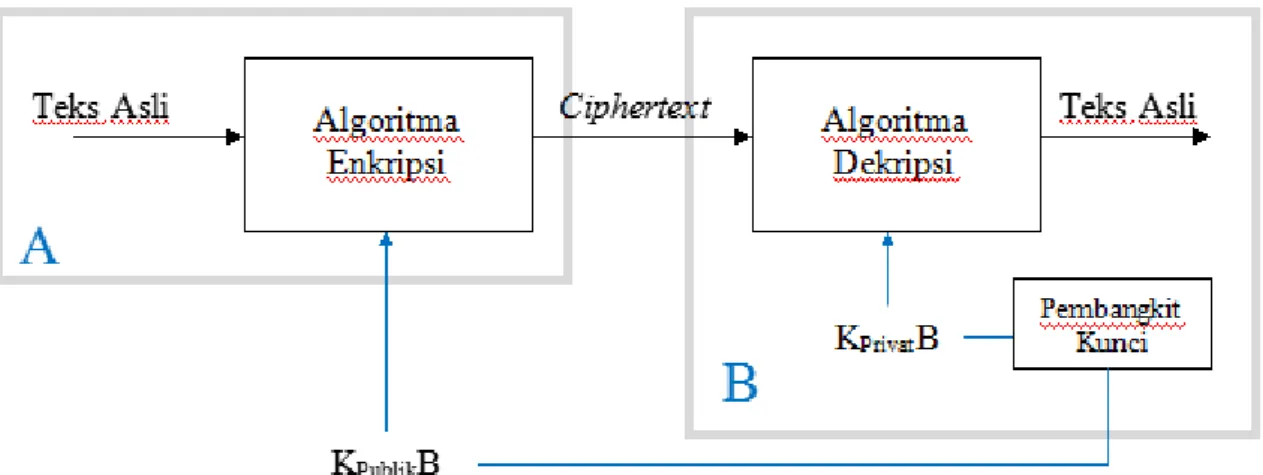
semua algoritma kriptografinya menggunakan konsep kunci publik, seperti Rivest-Shamir-Adleman (RSA), El-Gamal, Rabin dan sebagainya (Harahap, 2014). Skema kriptografi asimetris ditunjukkan secara umum pada Gambar 2.3.
Gambar 2.3 Kriptografi Asimetris (Fauzana, 2013)
Sistem kriptografi asimetri kunci publik pertama kali diusulkan oleh Diffie dan Hellman pada tahun 1976. Ide kriptografi kunci publik sebenarnya mirip dengan cara kerja kunci gembok, misalnya terdapat sebuah peti yang berisi pesan rahasia, lalu peti itu dikunci dengan gembok di mana gembok ini dimiliki oleh semua orang (gembok bekerja seperti public key). Peti terkunci tersebut kemudian dikirim ke tujuan atau penerima yang memiliki kunci untuk membuka gembok. Penerima dapat membuka gembok apabila kunci yang dipegang olehnya merupakan pasangan dari gembok tersebut. Kunci yang dipegang oleh penerima bekerja seperti private key (Sadikin, 2012).
Sistem kriptografi kunci publik memiliki kunci untuk enkripsi Ke dan kunci
untuk dekripsi Kd yang berbeda. Kunci untuk enkripsi Ke disebut juga sebagai kunci
publik (KPublik) bersifat tidak rahasia sehingga dapat didistribusikan melalui saluran
tidak aman. Sedangkan kunci dekripsi Kd disebut juga kunci privat (KPrivat) bersifat
rahasia dan harus dijaga kerahasiaannya oleh pemegang kunci. Berikut ini adalah algoritma sistem kriptografi kunci publik (Sadikin, 2012).
1. Sebelum A melakukan enkripsi, B membangkitkan sepasang kunci yaitu kunci privat dan kunci publik milik B dengan memanggil fungsi PembangkitKunci().
(KPublikB, KPrivatB) PembangkitKunci()
B memublikasikan kunci publik (KPublikB) dan menjaga kerahasiaan kunci privat
2. A melakukan enkripsi sebuah teks asli (P) dengan kunci publik B (KPublikB)
menghasilkan sebuah teks sandi (C) dengan memanggil fungsi enkripsi (E). C E(KPublikB, P)
A mengirim teks sandi (C) ke B melalui saluran tidak aman.
3. B mendekripsi teks sandi (C) dengan kunci privat B (KPrivatB) untuk
mendapatkan teks asli (P) dengan fungsi dekripsi (D). P D(KPrivatB, C)
B mendapatkan P jika teks sandi (C) dienkripsi dengan kunci publik B yang sesuai.
Jadi dalam kriptografi kunci publik, kunci publik dapat disebar-luaskan kepada umum dan sebaiknya disebar luaskan. Sebaliknya, kunci privat harus dirahasiakan oleh pemiliknya. Perlu untuk diingat, biasanya algoritma tidak dirahasiakan, bahkan enkripsi yang mengandalkan kerahasiaan algoritma dianggap sesuatu yang tidak baik (Kromodimoeljo, 2010). Hal ini sesuai dengan prinsip Kerckhoff yaitu semua algoritma kriptografi harus publik, hanya kunci yang rahasia (Munir, 2006).
Dalam kriptografi kunci asimetri, hampir semua algoritma kriptografinya menggunakan konsep kunci publik, seperti Rivest-Shamir-Adleman (RSA), El-Gamal, Rabin dan sebagainya. Kecuali algoritma Pohlig˗Hellman karena kunci enkripsi maupun kunci dekripsinya bersifat rahasia. (Fauzana, 2013). Skema algoritma kriptografi asimetri nirkunci publik (dengan asumsi kunci sudah diketahui oleh kedua belah pihak sebelumnya) dapat dilihat pada Gambar 2.4.
2.3.3. Fungsi hash
Fungsi hash adalah sebuah fungsi yang masukannya adalah sebuah pesan dan keluarannya adalah sebuah sidik pesan (message fingerprint) (Ariyus, 2008).
Fungsi hash sering disebut dengan fungsi hash satu arah (one-way function), message digest, fingerprint, fungsi kompresi dan message authentication code (MAC) yang merupakan suatu fungsi matematika yang mengambil masukan panjang variabel dan mengubahnya ke dalam urutan biner dengan panjang yang tetap. Fungsi hash biasanya diperlukan bila ingin membuat sidik jari dari suatu pesan. Sidik jari pada pesan merupakan suatu tanda bahwa pesan tersebut benar-benar berasal dari orang yang diinginkan (Ariyus, 2008). Beberapa fungsi hash yang banyak dipakai adalah MD5 dan SHA.
2.4. Teori Bilangan Integer
2.4.1. Faktor Persekutuan Terbesar (Greatest Common Divisor)
Faktor Persekutuan Terbesar atau Greatest Common Divisor (GCD) merupakan bilangan bulat terbesar yang merupakan pembagi yang sama dari dua bilangan bulat. Misalkan a dan b adalah 2 (dua) bilangan bulat yang tidak nol. GCD dari a dan b adalah bilangan bulat terbesar c sedemikian sehingga c|a dan c|b. GCD dari a dan b dapat dinotasikan dengan gcd(a,b) (Nasution, 2015).
Contoh : GCD (36,88) = … ? 36 mod 88 = 36 88 mod 36 = 16 36 mod 16 = 4 16 mod 4 = 0
Jadi, GCD dari (36,88) adalah 4
2.4.2. Aritmatika Modulo
Aritmatika modulo merupakan sisa hasil pembagian dua bilangan. Operator yang digunakan dalam aritmatika modulo adalah mod. Misalkan, jika bilangan integer a dibagi dengan bilangan integer yang lebih besar dari nol (b > 0), maka akan
menghasilkan sisa bagi r (remainder) dengan hasil bagi s (quotient). Sehingga dapat dinotasikan sebagai berikut (Lipschutz & Lipson, 2007).
a mod b = r sedemikian sehingga a = bs + r, dengan 0 ≤ b < n ... (2.1) Sebagai contoh, jika 23 mod 4 = 3, maka 23 = (4 × 5) + 3.
Jika a negatif, maka bagi |a| dengan b mendapatkan sisa bagi r’ (Munir, 2006). Sehingga didapatkan:
a mod b = b – r’, di mana r’ ≠ 0 dan a < 0 ... (2.2) Sebagai contoh, jika |-23| mod 4 = 3, maka -23 mod 4 = 4 – 3 = 1.
Cormen, et al. (2009) menuliskan di dalam bukunya, untuk setiap bilangan bulat a dan setiap bilangan bulat positif b, nilai a mod b adalah sisa (residu) dari hasil bagi a/b:
a mod b = a – b (a/b), di mana 0 ≤ a mod b < b ... (2.3) Contohnya adalah 23 mod 4 = 23 – 4(23/4) = 23 – 4(5) = 23 – 20 = 3.
2.4.3. Algoritma Extended Euclid
Teorema yang digunakan sebagai dasar dari algoritma Extended Euclid adalah sebagai berikut:
Jika = qb + r maka gcd(,b) = gcd(b,r)………….……(2.4)
Algoritma Euclid menggunakan rumus diatas secara berulang untuk men-dapatkan gcd, yaitu dengan memperkecil kedua bilangan yang dijadikan patokan untuk gcd setiap kali mengulang, tanpa merubah nilai gcd itu sendiri. Hasil dari komputasi gcd di dapat saat kedua patokan untuk gcd tidak dapat diperkecil lagi.
2.4.4. Chinese Remainder Theorem
Chinese Remainder Theorem (CRT) ditemukan oleh seorang matematikawan Cina bernama Sun-Tsu (juga disebut Sun Tse) sekitar 100 A.D (anno domini) atau 100 M (Stallings, 2011). Chinese Remainder Theorem (teorema sisa Cina) dinamai setelah masalah peninggalan Cina yang melibatkan sistem persamaan atau kekongruenan linear, menyatakan bahwa ketika modulus dari sistem kekongruenan linear yang berpasangan relatif prima, ada solusi unik dari sistem modulo produk dari modulus. Berikut ini adalah pertanyaan atau teka-teki Sun-Tsu (Rosen, 2012).
“Ada beberapa hal yang bilangannnya tidak diketahui. Bila dibagi dengan 11, sisanya adalah 2, ketika dibagi oleh 7, sisanya adalah 3, dan ketika dibagi 5, sisanya adalah 2. Berapakah bilangan itu?”
Teka-teki tersebut dapat dituliskan sebagai berikut. x ≡ 2 (mod 11)
x ≡ 3 (mod 7) x ≡ 2 (mod 5)
Apa solusi dari sistem kekongruenan berikut ini?
Sebelum menyelesaikan teka-teki tersebut, berikut ini adalah teorema sisa Cina (Chinese Remainder Theorem) (Rosen, 2012).
Misalkan m1, m2, …, mn adalah bilangan bulat positif yang relatif prima berpasangan
(pairwise relatively prime) yang lebih besar dari 1 dan a1, a2, …, an merupakan bilangan
bulat sembarang. Maka sistem kekongruenan linear x ≡ a1 (mod m1),
x ≡ a2 (mod m2),
x ≡ an (mod mn)
memiliki sebuah solusi unik modulo m = m1m2…mn. (Terdapat solusi x dengan 0 ≤ x <
m, dan semua solusi lainnya adalah kongruen modulo m untuk solusi ini).
Solusi dari penyelesaian teka-teki Sun-Tsu tersebut adalah sebagai berikut (Wandani, 2012).
1. Hitung hasil perkalian dari keseluruhan modulus.
M = m1m2…mn ………….……….……….…… (2.5)
M = 11 × 7 × 5 = 385
2. Buat himpunan penyelesaian untuk masing-masing persamaan dari bilangan terkecil hingga hasil perkalian modulus (M).
x1 = {2, 13, 24, 35, 46, 57, 68, 79, 90, 101, 112, 123, 134, 145, 156, 167, 178, 189, 200, 211, 222, 233, 244, 255, 266, 277, 288, 299, 310, 321, 332, 343, 354, 365, 376} x2 = {3, 10, 17, 24, 31, 38, 45, 52, 59, 66, 73, 80, 87, 94, 101, 108, 115, 122, 129, 136, 143, 150, 157, 164, 171, 178, 185, 192, 199, 206, 213, 220, 227, 234, 241, 248, 255, 262, 269, 276, 283, 290, 297, 304, 311, 318, 325, 332, 339, 246, 353, 360, 367, 374, 381} x3 = {2, 7, 12, 17, 22, 27, 32, 37, 42, 47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97, 102, 107, 112, 117, 122, 127, 132, 137, 142, 147, 152, 157, 162, 167, 172, 177, 182, 187, 192, 197, 202, 207, 212, 217, 222, 227, 232, 237, 242, 247, 252, 257, 262, 267, 272, 277, 282, 287, 292, 297, 302,
307, 312, 317, 322, 327, 332, 342, 347, 352, 357, 362, 367, 372, 377, 382}
3. X merupakan irisan dari keseluruhan himpunan penyelesaian tersebut. X = x1 ∩ x2 ∩ … ∩ xn ………….……….……….…… (2.6)
X = x1 ∩ x2 ∩ x3 = 332
4. Agar tercapai seluruh bilangan yang memenuhi x, maka dihitung kelipatan persekutuan terkecil (Least Common Multiple) dari ketiga modulus (interval yang memenuhi x).
Persamaan 2.7 berikut merupakan rumus untuk mencari LCM dari dua bilangan bulat positif (Rosen, 2012).
ab = GCD(a,b) . LCM(a, b) ………….…… (2.7) Dari persamaan di atas dapat disimpulkan:
GCD(11,5,7) = 1 dan LCM(11,5,7) = 385
Sehingga x memenuhi akan bilangan dalam interval 105 dimulai dari 23, yaitu x = 332 ± (k × 385). Atau interval ini dapat dituliskan x X ± (k × LCM (m1,m2, …,mn))
Cara yang dapat digunakan untuk menyelesaikan teka-teki Sun-Tsu menurut Rosen (2012) adalah sebagai berikut.
1. Hitung hasil perkalian dari keseluruhan modulus.
M = m1m2…mn ………….……….……….…… (2.8)
M = 11 × 7 × 5 = 385
2. Hitung hasil bagi dari M dengan tiap-tiap modulus.
Mn = M/mn ………….……….……….…… (2.9)
M1 = 385/11 = 35
M2 = 385/7 = 55
M3 = 385/5 = 77
3. Hitung invers modulo (yn) dari (Mn mod mn). Maka diperoleh:
y1 = 2, y2 = 6 dan y3 = 2
4. Diperoleh solusi x dari teka-teki dengan menghitung rumus berikut ini. x ≡ a1M1y1 + a2M2y2 + … + anMnyn ………….……….… (2.10)
x ≡ a1M1y1 + a2M2y2 + a3M3y3 ≡ (2.35.2) + (3.55.6) + (2.77.2)
2.4.5. Bilangan prima
Bilangan prima adalah bilangan bulat positif a, dimana a ≥ 2 hanya dapat dibagi dengan 1 dan bilangan itu sendiri. Seluruh bilangan prima adalah bilangan ganjil, kecuali 2 yang merupakan bilangan genap. Contoh bilangan prima adalah 2, 3, 5, 7, 11, 13, 17, ….
Untuk menguji apakah n merupakan bilangan prima atau bukan, kita cukup membagi n dengan sejumlah bilangan prima, dengan syarat bilangan prima ≤ √n. Jika n habis dibagi dengan salah satu dari bilangan prima tersebut, maka n bukan bilangan prima, tetapi jika n tidak habis dibagi oleh semua bilangan prima tersebut, maka n adalah bilangan prima.
Terdapat metode lain yang dapat digunakan untuk menguji keprimaan suatu bilangan bulat, yang terkenal dengan Teorema Fermat. Berikut pernyataan dari Teorema Fermat : Jika p adalah bilangan prima dan a adalah bilangan bulat yang tidak habis dibagi dengan p, yaitu GCD(a,p) = 1, maka : ap-1 ≡ 1 (mod p) (Mollin, 2007).
Teorema Fermat ini memiliki kelemahan yaitu terdapat bilangan bulat bukan prima p sedemikian sehingga ap–1 ≡ 1 (mod p). Bilangan bulat p seperti itu disebut bilangan prima semu (pseudoprimes). Bilangan bulat a yang menyebabkan ap–1 ≡ 1 (mod p),
dimana p adalah bilangan prima semu disebut dengan bilangan carmichael atau fermat’s liar. Akan tetapi, bilangan prima semu relatif jarang ditemukan.
Contoh :
Apakah p = 49 adalah bilangan prima?
a. Pilihlah sembarang bilangan bulat positif a dengan syarat 1<a<p.
b. Hitung ap-1 mod p sebanyak dua kali untuk menghindari ditemukan bilangan prima semu. Jika salah satu hasil perhitungan tidak sama dengan 1, maka bilangan bulat p bukan bilangan prima.
348 mod 49 = 43 648 mod 49 = 8
Karena ap-1 mod p ≠ 1, maka bilangan bulat p = 49 bukan bilangan prima
2.5. Sistem Kriptografi Hill Cipher
Sejak kekaisaran Romawi, kriptosistem yang lebih rumit dikembangkan oleh orang seperti ahli matematika Italia Leon Battista Alberti (lahir pada tahun 1404), matematikawan Jerman Johannes Trithernius (lahir pada tahun 1492), seorang
kriptographer dan diplomat Perancis Blaise de Vigenere (1523-1596), Lester S.Hill, yang menemukan Hill Cipher pada tahun 1929. Hill Cipher merupakan jenis lain dari Polygraphic cipher. Sandi ini mengenkripsi suatu string huruf menjadi bentuk string yang lain dengan panjang sama. Teknik Hill Cipher dikembangkan oleh Lester S.Hill pada Hunter Collage dan dipublikasikan pada American Mathematical Monthly, Volume 36, Issue 6 (Juni-Juli, 1929) halaman 106-312. Hill Cipher menggunakan matriks untuk mentransformasi string berupa blok huruf (Simamora,2015).
Hill Cipher berdasarkan pada aljabar linier dan seperti sandi Vignere, Hill Cipher merupakan Block Cipher. Sandi ini dapat dipecahkan dengan Known-Plaintext Attacks tetapi tahan melawan ciphertext-only attack. Cara kerja sandi ini berdasarkan atas perkalian matriks dengan menggunakan sebuah kunci K. Penjelasan mengenai Hill Cipher ini dapat diuraikan sebaai berikut:
Misalkan m adalah bilangan bulat positif dan 𝑃 = 𝐶 = (𝑍26)𝑚 dan misalkan K
={ 𝑚 × 𝑚 merupakan matriks yang nilai elemennya terdiri dari 𝑍26}, maka untuk suatu kunci K, dapat didefenisikan sebagai ℮𝐾(𝑋) = 𝐾 × 𝑚𝑜𝑑 26 dan 𝑑𝐾(𝑦) =
𝐾−1𝑦 𝑚𝑜𝑑 26 dimana semua operasi dilakukan dalam matriks 𝑍 26.
Karena 𝐾−1 dengan mudah dapat dihitung dari K, maka Hill Cipher merupakan
suatu kriptosistem simetris. Hill Cipher juga merupakan blok cipher linier umum. Suatu blok cipher linier dapat dengan mudah dipecahkan yang dikenal cara Known-plaintext attacks. Maka bagi penyerang yang mengetahui beberapa contoh plaintext dengan enkripsi yang berhubungan, tidaklah sulit baginya untuk mencari kunci yang dipakai untuk mengenkripsikan plaintext tersebut. Metode dari perhitungan frekuensi sering dipakai untuk usaha ini. Metode ini mengeksplorasi perulangan (redundancy) dari bahasa alami yang dipakai sebagai plaintext pada pesan.
Cara kerja Hill Cipher dapat disederhanakan dengan cara perkalian dengan matriks kunci (K). K merupakan sebuah matriks kunci 𝑚 × 𝑚 yang merupakan representasi dari suatu persamaan linier. Cara mencari matriks kunci itu sendiri adalah dengan mencari GCD dari matriks K tersebut. Cara kerja Hill Cipher dapat diuraikan sebagai berikut. Pertama tentukan matriks kunci secara acak. Misal matriks kuncinya:
𝐾 = (
4 2 3 6 3 3 3 2 1
)
Setelah matriks kunci ditentukan secara acak, lalu buktikan matriks kunci tersebut apakah mempunyai invers atau tidak. Syarat matriks punya invers yaitu
determinan matriks ≠ 0. Jika sudah memenuhi syarat, maka selanjutnya lakukan GCD (det, 26) =1
Sebagai contoh, buktikan apakah matriks kunci ini mempunyai invers : 𝐾 = (
4 2 3 6 3 3 3 2 1
) Mencari determinan matriks :
( 4 2 3 6 3 3 3 2 1 ) 4 2 6 3 3 2 = ( 12 + 18 + 36 ) – ( 27 + 24 + 12 ) = 3
Setelah dapat determinannya selanjutnya pembuktian apakah matriks kunci atau tidak dengan cara :
GCD (det,26) = 1 GCD (3,26) = 1 3 mod 26 = 3 26 mod 3 = 2 3 mod 2 = 1 2 mod 1 = 0
Maka terbukti matriks diatas merupakan matriks kunci karena memenuhi syarat. Setelah mendapatkan matrik kunci. Maka untuk menghasilkan ciphertext menggunakan persamaan sebagai berikut:
C=K.P(mod26) ………….……….……….…… (2.11) ( 𝐶1 𝐶2 𝐶3 ) = ( 𝐾11 𝐾12 𝐾13 𝐾21 𝐾22 𝐾23 𝐾31 𝐾32 𝐾33 ) ( 𝑃1 𝑃2 𝑃3 ) 𝑚𝑜𝑑 26
2.5.1. Enkripsi Hill Cipher
Langkah-langkah untuk proses enkripsi plaintext dengan Hill Cipher adalah sebagai berikut:
1. Pilih suatu matriks kunci K yang berupa matriks bujur sangkar yang dipakai sebagai kunci.
2. Transformasikan tiap huruf dalam teks ke bilangan bulat yang sesuai (A=1; B=2;...Z=26).
3. Kelompokkan barisan angka yang didapat ke dalam beberapa blok vektor P yang panjangnya sama dengan ukuran matriks K.
4. Hitung C = K. P (mod 26) untuk tiap vektor P.
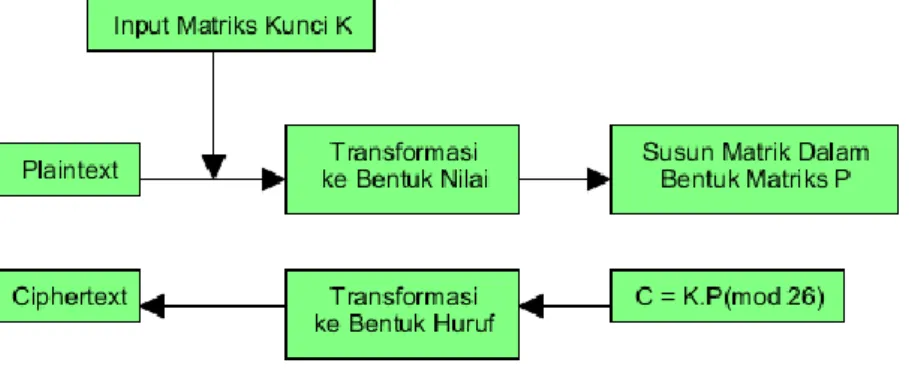
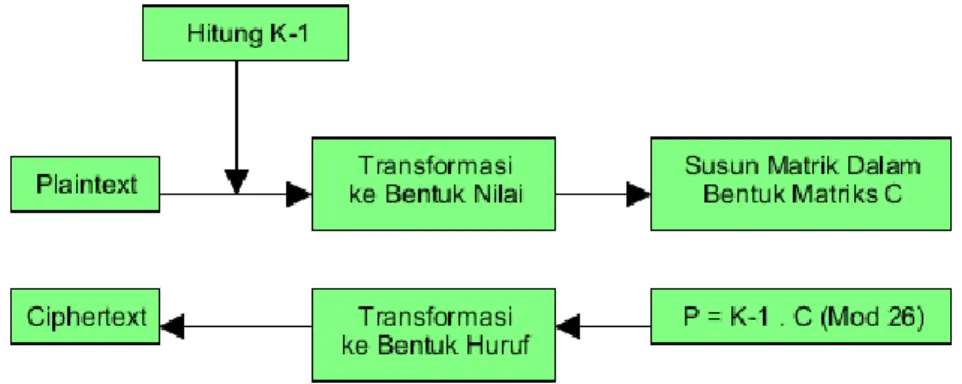
5. Kembalikan tiap angka dalam vektor sandi C ke huruf yang sesuai untuk mendapatkan teks sandi. Skema kerja enkripsi Hill Cipher dapat dilihat pada Gambar 2.5.
Gambar 2.5. Illustrasi Enkripsi Hill Cipher
Bagian ini akan menjelaskan enkripsi dengan Hill Cipher dengan memberikan contoh. Hill Cipher menggunakan matriks untuk mentransformasikan string plaintext menjadi ciphertext.
Untuk mentransformasikan plaintext maka pertama sekali semua alphanumerik dinyatakan dalam Tabel 2.1 seperti berikut:
Tabel 2.1 Transformasi alphanumerik
A B C D E F G H I J K L M N O P 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Q R S T U V W X Y Z
16 17 18 19 20 21 22 23 24 25
Contoh :
Kode Hill dengan mengunakan matriks 3×3 dengan kunci matriks : (
4 2 3
6 3 3
3 2 1
)
Diketahui teks asli adalah: “FITRIIMUT”. Perhatikan Tabel 2.2 pada proses enkripsi hill cipher.
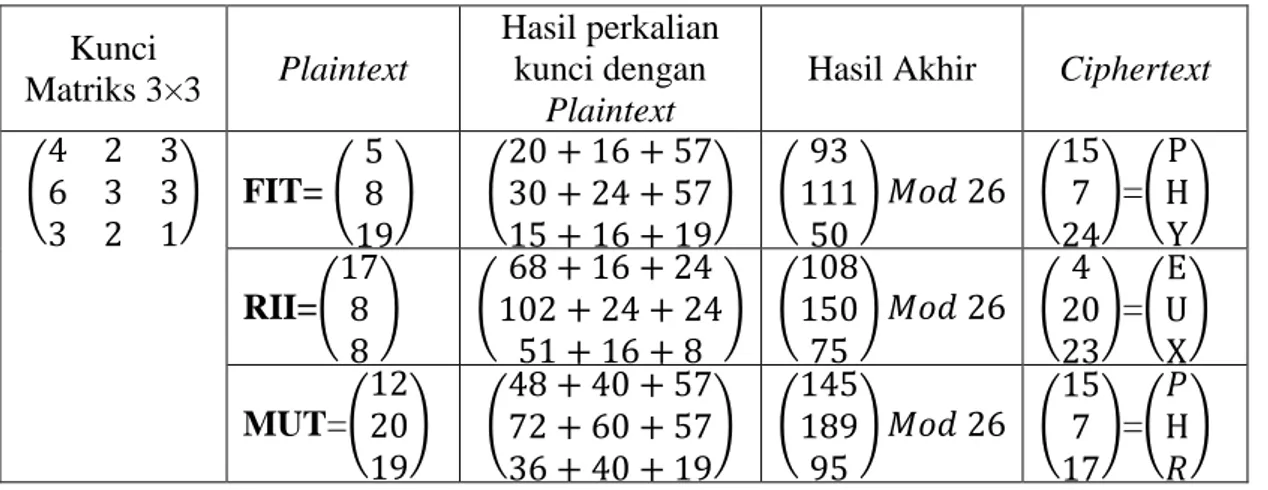
Tabel 2.2 Enkripsi Hill Cipher Kunci Matriks 3×3 Plaintext Hasil perkalian kunci dengan Plaintext
Hasil Akhir Ciphertext
( 4 2 3 6 3 3 3 2 1 ) FIT= ( 5 8 19 ) ( 20 + 16 + 57 30 + 24 + 57 15 + 16 + 19 ) ( 93 111 50 ) 𝑀𝑜𝑑 26 ( 15 7 24 )=( P H Y ) RII=( 17 8 8 ) ( 68 + 16 + 24 102 + 24 + 24 51 + 16 + 8 ) ( 108 150 75 ) 𝑀𝑜𝑑 26 ( 4 20 23 )=( E U X ) MUT=( 12 20 19 ) ( 48 + 40 + 57 72 + 60 + 57 36 + 40 + 19 ) ( 145 189 95 ) 𝑀𝑜𝑑 26 ( 15 7 17 )=( 𝑃 H 𝑅 )
Jadi, enkripsi dari “FITRIIMUT” adalah “PHYEUXPHR”
2.5.2. Dekripsi Hill Cipher
Algoritma proses pendekripsian Hill Cipher dapat diuraikan dalam bentuk langkah-langkah sebagai berikut:
1. Hitung matriks 𝐾−1 (Mod 26) sebagai kunci pembuka. 𝐾−1 ada jika GCD ((det(K),26)=1.
2. Transformasikan tiap huruf dalam teks ke bilangan bulat yang sesuai (A=1; B=2; … Z=26).
3. Kelompokkan barisan angka yang didapat ke dalam beberapa blok vektor C yang panjangnya sama dengan ukuran matriks 𝐾−1.
4. Hitung P = 𝐾−1. 𝐶 (𝑀𝑜𝑑 26) untuk tiap vector C.
5. Kembalikan tiap angka dalam vektor sandi P ke huruf yang sesuai untuk mendapatkan teks sandi. Gambar 2.6 berikut adalah ilustrasi dekripsi Hill Cipher:
Gambar 2.6. Illustrasi dekripsi Hill Cipher Contoh :
Diketahui Kode Hill dengan mengunakan matriks 3×3 dengan kunci matriks: (
4 2 3
6 3 3
3 2 1
)
Diketahui teks adalah: “PHYEUXPHR”.
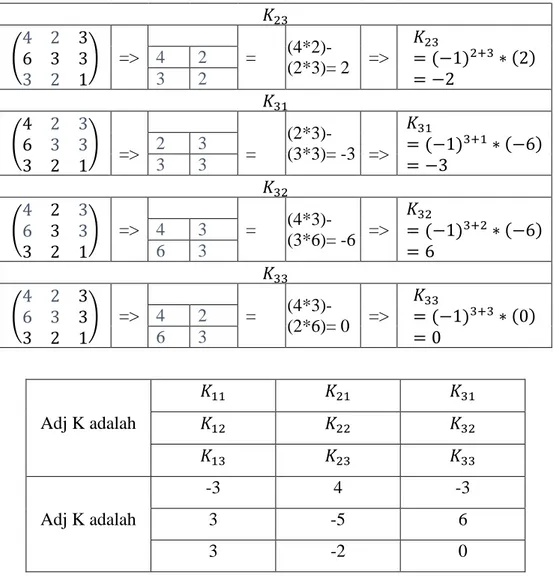
1. Cari Adjoint dari matriks K yang ditunjukkan pada Tabel 2.3 Tabel 2.3 Mencari Adjoint dari Matriks K
𝐾11 ( 4 2 3 6 3 3 3 2 1 ) => = 3*13*2= -3 => 𝐾11 = (−1)1+1∗ (−3) = (−3) 3 3 2 1 𝐾12 ( 4 2 3 6 3 3 3 2 1 ) => = (6*1)-(3*3)= -3 => 𝐾12 = (−1)1+2∗ (−3) = 3 6 3 3 1 𝐾13 ( 4 2 3 6 3 3 3 2 1 ) => = (6*2)-(3*3)= 3 => 𝐾13= (−1)1+3 ∗ 3 = 3 6 3 3 2 𝐾21 ( 4 2 3 6 3 3 3 2 1 ) => = (2*1)-(3*2)= -4 => 𝐾12 = (−1)2+1∗ (−4) = 4 2 3 2 1 𝐾22 ( 4 2 3 6 3 3 3 2 1 ) => = (4*1)-(3*3)= -5 => 𝐾22 = (−1)2+2∗ (−5) = −5 4 3 3 1
𝐾23 ( 4 2 3 6 3 3 3 2 1 ) => = (4*2)-(2*3)= 2 => 𝐾23 = (−1)2+3∗ (2) = −2 4 2 3 2 𝐾31 ( 4 2 3 6 3 3 3 2 1 ) => = (2*3)-(3*3)= -3 => 𝐾31 = (−1)3+1∗ (−6) = −3 2 3 3 3 𝐾32 ( 4 2 3 6 3 3 3 2 1 ) => = (4*3)-(3*6)= -6 => 𝐾32 = (−1)3+2∗ (−6) = 6 4 3 6 3 𝐾33 ( 4 2 3 6 3 3 3 2 1 ) => = (4*3)-(2*6)= 0 => 𝐾33 = (−1)3+3∗ (0) = 0 4 2 6 3 Adj K adalah 𝐾11 𝐾21 𝐾31 𝐾12 𝐾22 𝐾32 𝐾13 𝐾23 𝐾33 Adj K adalah -3 4 -3 3 -5 6 3 -2 0
b. Adjoint diperoleh, cari determinan matriks K yang ditunjukkan pada Tabel 2.4 berikut.
Tabel 2.4 Proses determinan matriks K
4 2 3 4 2 6 3 3 6 3 3 2 1 3 2 Det K = ((4*3*1)+(2*3*3)+(3*6*2))-((3*3*3)-(4*3*2)-(2*6*2)) = 12+18+36-27-24-12 = 66-63 = 3 c. Invers dari determinan K
Det K * X = 1 mod 26 => 3*X = 1 mod 26
=> (3*X) mod 26 = 1 => (3*9) mod 26 = 1 => 27 mod 26 = 1
d. Kemudian 𝐶𝑎𝑟𝑖 𝐾−1= det 𝐾−1∗ adj 𝐾 mod 26
𝐾−1= 9* ( −3 4 −3 3 −5 6 3 −2 0 ) 𝑚𝑜𝑑 26 = ( −27 36 −27 27 −45 54 27 −18 0 ) 𝑚𝑜𝑑 26 = ( −1 10 −1 1 −19 2 1 −18 0 )
e. Ketika adanya hasil yang negatif (-) maka, ditambahkan 26 agar tetap memperoleh bilangan Positif (+), ini dilakukan karena yang digunakan adalah bilangan 0 hingga 25 seperti yang ditunjukkan pada Tabel 2.5.
Tabel 2.5 Proses Pembulatan ( −1 10 −1 1 −19 2 1 −18 0 ) (+26)
(Hanya yang bernilai negative) ( 25 10 25 1 7 2 1 8 0 )
f. Pembuktian bahwa K saling invers dengan 𝐾−1, dengan melakukan perkalian, dan hasil akhirnya adalah matriks identitas yang ditunjukkan pada Tabel 2.6 berikut ini :
Tabel 2.6 Proses Saling Invers
K 𝐾−1 = K* 𝐾−1 ( 4 2 3 6 3 3 3 2 1 ) * ( 25 10 25 1 7 2 1 8 0 ) 4*25+2*1+3*1 4*10+2*7+3*8 4*25+2*2+3*0 6*25+3*1+3*1 6*10+3*7+3*8 6*25+3*2+3*0 3*25+2*1+1*1 3*10+2*7+1*8 3*25+2*2+3*0 100+2+3 40+14+24 100+40+0 Mod 26 = ( 105 78 104 156 105 156 78 52 79 ) 𝑚𝑜𝑑 26 ( 1 0 0 0 1 0 0 0 1 ) 150+3+3 60+21+24 150+6+0 75+2+1 30+14+8 75+2+0
g. Mendekripsikan dengan mengalikan matriks 𝐾−1 dengan Ciphertext (𝐾−1∗ 𝐶𝑖) 𝑚𝑜𝑑 26. Tabel ciphertext dapat dilihat pada Tabel 2.7 dan proses dekripsi Hill Cipher dapat dilihat pada Tabel 2.8.
Tabel 2.7 Tabel Ciphertext
P H Y E U X P H R
Tabel 2.8 Proses dekripsi Hill Cipher PHY (𝐾−1∗ 𝐶𝑖) 𝑚𝑜𝑑 26 Plaintext ( 25 10 25 1 7 2 1 8 0 ) ∗ ( 15 7 24 ) mod 26 (25*15+10*7+25*24) Mod 26 ( 1045 112 71 ) mod 26 ( 5 8 19 )=FIT (1*15+7*7+2*24) Mod 26 (1*15+8*7+0*24) Mod 26 EUX (𝐾−1∗ 𝐶𝑖) 𝑚𝑜𝑑 26 Plaintext ( 25 10 25 1 7 2 1 8 0 ) ∗ ( 4 20 23 ) mod 26 (25*4+10*20+25*23) Mod 26 ( 875 190 164 ) mod 26 ( 17 8 8 )=RII (1*4+7*20+2*23) Mod 26 (1*4+8*20+0*23) Mod 26 PHR (𝐾−1∗ 𝐶𝑖) 𝑚𝑜𝑑 26 Plaintext ( 25 10 25 1 7 2 1 8 0 ) ∗ ( 15 7 17 ) mod 26 (25*15+10*7+25*17) Mod 26 ( 870 98 71 ) mod 26 ( 12 20 19 )=MUT (1*15+7*7+2*17) Mod 26 (1*15+8*7+0*17) Mod 26
Jadi teks asli dari “PHYEUXPHR” adalah “FITRIIMUT”.
2.6. Sistem Kriptografi Rabin Public Key
Sistem kriptografi Rabin (Rabin Cryptosystem) adalah suatu teknik kriptografi asimetris atau kriptografi kunci publik yang memiliki tingkat keamanan terkait dengan masalah sulitnya faktorisasi. Sistem kriptografi Rabin termasuk dalam sistem kriptografi asimetris yang menerapkan konsep untuk mendapatkan keseluruhan plaintext dari suatu ciphertext yang diketahui berdasarkan pada kesulitan dalam melakukan faktorisasi. Seperti teknik kriptografi kunci publik atau asimetris lainnya, sistem kriptografi Rabin menggunakan suatu pasangan kunci, yaitu kunci publik dan kunci privat.
2.6.1. Pembangkit Kunci Rabin
Untuk membangkitkan bilangan prima dapat menggunakan metode Fermat. Jika p adalah bilangan prima dan a adalah bilangan bulat yang tidak habis dibagi dengan p, yaitu GCD(a,p) = 1, maka : ap-1 ≡ 1 (mod p) (Mollin, 2007).
Teorema Fermat ini memiliki kelemahan yaitu terdapat bilangan bulat bukan prima p sedemikian sehingga ap–1 ≡ 1 (mod p). Bilangan bulat p seperti itu disebut bilangan prima semu (pseudoprimes). Bilangan bulat a yang menyebabkan ap–1 ≡ 1 (mod p), dimana p adalah bilangan prima semu disebut dengan bilangan carmichael atau fermat’s liar. Akan tetapi, bilangan prima semu relatif jarang ditemukan.
2.6.2. Enkripsi Rabin Public Key
Proses enkripsi pada algoritma Rabin Public Key menggunakan kunci publik n. Pada proses dekripsi menggunakan Algoritma Rabin Public Key akan menghasilkan 4 (empat) buah kemungkinan plaintext. Oleh karena itu, diperlukan modifikasi dalam proses enkripsi dan dekripsi untuk menentukan plaintext yang sebenarnya. Berikut langkah–langkah proses enkripsi pesan rahasia menggunakan algoritma Rabin Public Key yang telah dimodifikasi adalah : (Wandani, 2012)
a. Ubah nilai plaintext m menjadi nilai biner, kemudian tambahkan dengan nilai biner m itu sendiri (redundant information) atau dengan kata lain plaintext digandakan.
b. Ubah hasil penggandaan nilai biner plaintext menjadi nilai desimalnya.
c. Hitung nilai k yang merupakan kongruen nilai desimal dari hasil penggandaan plaintext m terhadap kunci publik n dengan menggunakan rumus :
𝑘 ∗ 𝑛 = 𝑚 − (𝑚 𝑚𝑜𝑑 𝑛) ………….……….………..…… (2.12) d. Hitung nilai ciphertext c dengan menggunakan rumus :
c = m2 mod n ………….……….……….………….……… (2.13) Dengan c adalah ciphertext, n adalah kunci publik, dan m adalah nilai desimal dari hasil penggandaan nilai biner plaintext.
2.6.3. Dekripsi Kunci Public Rabin
Proses enkripsi pada algoritma Rabin Public Key menggunakan kunci privat p dan q. Berikut langkah–langkah proses dekripsi dengan menggunakan algoritma Rabin Public Key yang telah dimodifikasi : (Wandani, 2012)
a. Tentukan nilai Yp dan Yq yang merupakan pembagi GCD (Greatest Common
Divisor) dari p dan q dengan menggunakan Algoritma Extended Euclidean. Karena GCD bilangan prima adalah 1, maka dapat ditulis sebagai berikut : Yp * p + Yq * q = 1 ………….……….……….………….… (2.14) b. Hitunglah nilai akar kuadrat dari ciphertext terhadap p dan q dengan rumus:
mp = 𝑐( 𝑝+1 4 )𝑚𝑜𝑑 𝑝 ………….……….……….………….…. (2.15) mq= 𝑐( 𝑞+1 4 )𝑚𝑜𝑑 𝑞 ………….……….……….……... (2.16) Dengan mp adalah akar kuadrat dari ciphertext terhadap p dan mq adalah akar
kuadrat dari ciphertext terhadap q.
c. Hitung nilai r, s, t dan u dengan menggunakan Chinese Remainder Theorem, dengan persamaan berikut :
r = (Yp*p* mq + Yq * q* mp ) mod n ………….……….…………(2.17)
s = (Yp*p* mq - Yq * q* mp ) mod n ………….……….………….(2.18)
t = ( -Yp*p* mq + Yq * q* mp ) mod n ………….……….………..(2.19)
u = ( -Yp*p* mq - Yq * q* mp ) mod n ………….……….………..(2.20)
d. Tambahkan r,s,t,u dengan kongruen nilai desimal hasil penggandaan plaintext k yang dikalikan dengan kunci publik n.
R = (k*n)+r ………….……….………….………….……...…...(2.21) S = (k*n)+s ………….……….………...…….…… …….…… .(2.22) T = (k*n)+t ………….……….……….…….………….……...(2.23) U = (k*n)+u ………….……….………...…….…… …….…… .(2.24) e. Ubahlah nilai desimal R, S, T, U ke dalam bentuk biner. Kemudian nilai biner
R, S, T, U dibagi menjadi 2 (dua) bagian. Bandingkan kedua bagian tersebut. Jika kedua bagian tersebut menghasilkan bentuk biner yang sama, maka didapatlah hasil dekripsi ciphertext c dengan mengubah bentuk biner salah satu bagian yang telah dibagi menjadi 2 (dua) bagian yang sama.
2.7. Android
Android adalah sistem operasi untuk telepon seluler yang berbasiskan Linux (Entprise,2010). Android menyediakan platform terbuka bagi para pengembang untuk menciptakan aplikasi mereka sendiri sehingga dapat digunakan oleh bermacam peranti penggerak. Untuk mengembangkan Android di bentuklah Open Handset Alliance yang merupakan gabungan dari 34 perusahaan peranti keras, peranti lunak dan telekomunikasi termasuk Google, HTC, Intel, Motorola, Qualcomm, TMobile, dan Nvidia.
Pada saat perilisan perdana Android pada tanggal 5 November 2007, Android bersama Open Handset Alliance menyatakan mendukung pengembangan pada perangkat seluler. Pertama yang dapat dukungan penuh dari Google atau Google Mail Service (GMS) dan kedua adalah yang benar-benar bebas distribusinya tanpa dukungan langsung dari Google atau dikenal sebagai Open Handset Distribution (DHD) (Ardiansyah, 2011). Sejak April 2009, masing-masing versi android dirilis sesuai urutan alfabet. Berikut adalah rangkaian perjalanan Android dan logo dari Android pada Gambar 2.7
1. Kerjasama Android Inc. dengan Google Inc.
2. 2007-2008 perjalanan awal Android 3. Android Versi 1.1
4. Android Versi 1.5 (Cupcake) 5. Android Versi 1.6 (Donut) 6. Android Versi 2.0/2.1 (Eclair)
7. Android Versi 2.2 (Froyo) 8. Android Versi 2.3 (Gingerbread) 9. Android Versi 3.0 (Honeycomb) 10. Android Versi 4.0 (ICS)
11. Android Versi 4.1-4.3 (Jelly Bean) 12. Android Versi 4.4 (KitKat)
13. Android Versi 5.0 (Lollipop)
2.8. Penelitian Yang Relevan
Berikut ini adalah beberapa penelitian tentang kriptografi yang berkaitan dengan Algoritma Hill Cipher dan Rabin Public Key :
1. Wandani,H (2012) dengan judul “Implementasi Sistem Keamanan Data dengan Menggunakan Teknik Steganografi End of File (EOF) dan Rabin Public Key Cryptosystem” dengan kesimpulan bahwa kombinasi plaintext dan kunci tertentu. Terdapat hasil dekripsi yang berbeda dari plaintext yang sebenarnya dikarenakan pada saat sistem memeriksa 4 (empat) kemungkinan nilai plaintext, terdapat 2 (dua) atau lebih nilai kemungkinan plaintext yang memenuhi syarat sebagai plaintext yang sebenarnya. Sehingga sistem ini akan mengambil nilai kemungkinan plaintext yang pertama sekali memenuhi syarat sebagai plaintext yang sebenarnya.
2. Harahap, A.A (2014) dengan judul “Implementasi Sistem Keamanan Data Menggunakan Steganografi Teknik Pemetaan Titik Hitam dengan Pencarian Sekuensial dan Rabin Cryptosystem” dengan kesimpulan bahwa proses enkripsi relatif lebih cepat dibandingkan dengan proses dekripsi pada algoritma kriptografi Rabin dan proses ekstraksi gambar relatif lebih cepat dibandingkan dengan proses penyisipan pada steganografi teknik pemetaan titik hitam dengan pencarian sekuensial.
3. Nasution,R.N.N (2015) dengan judul “Impementasi Algoritma Hill Cipher dan RSA pada Enkripsi Hybrid Pesan SMS di Android” dengan kesimpulan bahwa kedua algoritma yang digunakan untuk melakukan proses enkripsi masing-masing algoritma memiliki kelebihan masing-masing-masing-masing.