MATHEMATICS EDUCATION
JOURNAL
VOLUME 2, NO. 2 NOVEMBER 2012 ISSN 2089-4716
Southeast Asian Ministers of Education Organization (SEAMEO)
Southeast Asian Mathematics Education Journal (SEAMEJ) is an academic journal devoted to reflect a variety of research ideas and methods in the field of mathematics education. SEAMEJ aims to stimulate discussions at all levels of mathematics education through significant and innovative research studies. The Journal welcomes articles highlighting empirical as well as theoretical research studies, which have a perspective wider than local or national interest. All papers submitted to the Journal are peer reviewed before publication.
The SEAMEJ (ISSN: 2089-4716) is the official journal of SEAMEO QITEP in Mathematics and published yearly in December. Readers wishing to submit manuscripts for publication should refer to instruction notes which can be found on the inside back cover.
All correspondence including comments, suggestions, contributions or other related inquiries should be addressed to:
The Director
SEAMEO QITEP in Mathematics
Jl. Kaliurang Km. 6, Sambisari, Condongcatur, Depok Sleman, Yogyakarta, Indonesia.
v Editorial Board Members
Subanar SEAMEO QITEP in Mathematics
Widodo PPPPTK Matematika Yogyakarta
Ganung Anggraeni PPPPTK Matematika Yogyakarta
Wahyudi SEAMEO QITEP in Mathematics
Pujiati SEAMEO QITEP in Mathematics
Sahid SEAMEO QITEP in Mathematics
Anna Tri Lestari SEAMEO QITEP in Mathematics
Punang Amaripuja SEAMEO QITEP in Mathematics
Manuscript Editors
Sriyanti SEAMEO QITEP in Mathematics
Siti Khamimah SEAMEO QITEP in Mathematics
Rachma Noviani SEAMEO QITEP in Mathematics
Marfuah SEAMEO QITEP in Mathematics
Luqmanul Hakim SEAMEO QITEP in Mathematics
Mutiatul Hasanah SEAMEO QITEP in Mathematics
Tri Budi Wijayanto SEAMEO QITEP in Mathematics
Wahyu Kharina Praptiwi SEAMEO QITEP in Mathematics
Administrative Assistants
Rina Kusumayanti SEAMEO QITEP in Mathematics
Rini Handayani SEAMEO QITEP in Mathematics
Cover Design & Typesetting
Joko Setiyono SEAMEO QITEP in Mathematics
Suhananto SEAMEO QITEP in Mathematics
Eko Nugroho SEAMEO QITEP in Mathematics
Tika Setyawati SEAMEO QITEP in Mathematics
Febriarto Cahyo Nugroho SEAMEO QITEP in Mathematics
International Advisory Panels
Mohan Chinnapan University of South Australia
Philip Clarkson Australian Catholic University
Lim Chap Sam Universiti Sains Malaysia
Cheah Ui Hock SEAMEO RECSAM Malaysia
Noraini Idris Universiti Pendidikan Sultan Idris, Malaysia
Paul White Australian Catholic University
Parmjit Singh Universiti Technology Mara Malaysia
Michael Cavanagh MacQuarie University Australia
Jaguthsingh Dindyal Nanyang University Singapore
Chair
Fadjar Shadiq SEAMEO QITEP in Mathematics
Chief Reviewer
Wahyudi & Allan Leslie White 1 Editorial
Xingfeng Huang, Jinglei Yang,
Bingxing Tang, Lingmei Gong, Zhong
Tian
3
An
Experienced
Chinese
Teacher’s
Strategies In Teaching Mathematics:
Translation of Quadratic Functions
Paul White, Sue Wilson, & Michael Mitchelmore
11
Teaching for Abstraction: Teacher
Learning
Catherine Attard 31
Transition from Primary to Secondary
School
Mathematics:
Students’
Perceptions
Sue Wilson & Steve Thornton 45
Bibliotherapy:
A
Framework
for
Understanding
Pre-Service
Primary
Teachers’
Affective
Responses
to
Learning and Teaching Mathematics
S. Kanageswari Suppiah Shanmugam
& LeongChee Kin
61
IntroducingComputer Adaptive Testing
to a Cohort of Mathematics Teachers:
The Case of Concerto
Allan Leslie White 75
What Does Brain Research Say about
Teaching and Learning Mathematics?
Ida Karnasih & Wahyudi 89
Exploring
Student
Perceptions
on
Teacher-Students Interaction
Editorial
This is the second edition of the South East Asia Mathematics Education Journal (SEAMEJ) which is an academic journal devoted to publishing a variety of research studies and theoretical papers in the field of mathematics education. SEAMEJ seeks to stimulate discussion at all levels of the mathematics education community. SEAMEJ aims to eventually publish an edition twice a year, in June and December.
SEAMEJ is supported by the Southeast Asian Ministers of Education Organization (SEAMEO), Centre for Quality Improvement of Teachers and Education Personnel (QITEP) in Mathematics situated in Yogyakarta Indonesia. Launched on July 13, 2009, there are now three QITEP SEAMEO Centres for Quality Improvement of Teachers and Education Personnel in Indonesia. One centre is in Mathematics (Yogyakarta), one in Science (Bandung) and one in Languages (English - Jakarta).
The first edition was produced using revised papers from the first International Symposium of QITEP Mathematics in November 2011, where a number of paper presenters were approached to submit their reworked papers to this journal. In this issue we are proud to state, there are papers that have been submitted by researchers from a number of countries. We hope that trend this will continue and swell as the journal becomes widely read and enable us to meet our aim of two editions in one year.
In this issue we begin with a paper that provides some insights into the mathematics teaching in Shanghai China. The paper describes the struggle of a teacher and tends to concentrate more upon the teaching issues and less upon the research issues. While researchers may not find all the information they would like, nevertheless, as this journal seeks to serve both teachers and researchers, this paper deserves to be widely read. The papers that follow cover a wide range of issues and perspectives and include research into: translating concrete understanding to the abstract by students and how to help teacher achieve this end; a further elaboration of a longitudinal study of Australian transition years and school student engagement; a further elaboration of bibliotherapy with a framework for use with pre-service teachers; a report on a professional learning workshop using a computer adaptive assessment program; the implications that brain research has for the teaching and learning of mathematics, and finishing with a study exploring on psychosocial learning environment in Indonesian mathematics classrooms. We are very thankful for this early support.
As this is only the second edition we are still refining our processes and so we wish to apologise if we have made errors or omissions. We welcome feedback and suggestions for improvement, but most of all, we welcome paper contributions.
The Journal seeks articles highlighting empirical as well as theoretical research studies, particularly those that have a perspective wider than local or national interests. All contributions to SEAMEJ will be peer reviewed and we are indebted to those on the International Advisory Panel for their support.
Wahyudi
Allan L White
3
An Experienced Chinese Teacher’s Strategies In Teaching Mathematics:
Translation of Quadratic Functions
Xingfeng Huang, Jinglei Yang, Bingxing Tang, Lingmei Gong, Zhong Tian Department of Mathematics, Changshu Institute of Technology, Jiangsu, China.
<xfhuang0729@gmail.com>
Abstract
The study selected the topic of translation of quadratic functions. In order to explore some effective instructional strategies to help students understand this topic, an experienced teacher was chosen for a case study. Based on lesson observation and semi-structure interviews, this study found that the teacher employed various strategies to facilitate students understanding of translations of quadratic functions.
Keywords experienced Chinese teacher; strategies; translation of quadratic function
Introduction
With the background of Chinese curriculum innovation, how do mathematics teachers apply teaching strategies to classroom practice? This issue aroused researchers’ interest. A lot of mathematics public lessons (in Chinese公开课) attracted their research (Huang, 2009; Huang & Fan, 2009; Li & Li, 2009, Huang & Li, 2009). The purposes of these studies were not only to promote policy-makers to understand the implementation of curriculum innovation, but also to encourage teachers to have opportunities to learn while reflecting on their own teaching (Yu, 2002; Wong, 2009). However, there has been criticism of the model lessons. Some people argued that public lessons looked like certain shows which are pretty but not practical and that these lessons did not represent the real matter (Qian, 2007). With this in mind, it became important to pay special attention to teachers’ strategies in their routine classroom practice. This study focuses on a junior school teacher with 10 years of teaching experience, and explores his teaching strategies in his routine classroom.
Focus On A Challenging Topic
As the evaluation of the teacher, as well as the evaluation of classroom teaching strategies, it is often rewarding if he completes a challenging task. It is a good opportunity for the teacher to exhibit his instructional wisdom, when he is given challenging tasks.
ones. In order to understand translation of quadratic function, first we must understand the concept of quadratic function. Because any translation of quadratic function is, by nature, an operation, students should think of quadratic function as an operational object. The order of instruction also brings obstacles to students’ learning because they are usually taught vertical translation ahead of horizontal translation (Zazics, Liljedahl, & Gadowsky, 2003). Vertical translation of quadratic functions coincides with students’ intuition. For example, students are asked to translate y=x2 to y=x2+1. Comparing the two function expressions, if they add a positive one to x2, the graph of y=x2 will be moved up one unit in the positive direction along axis y. However, horizontal translation is against intuition. If y=x2 is supposed to be translated to y=(x+1)2, x in the former expression is also added into a positive one, then the graph moved left toward in the negative direction along the axis x. Since it is so different from vertical translation, it would be quite difficult for students to understand the concept of horizontal translation. A study by Eisenberg and Dreyfus (1994) shows it would be hard for students to understand horizontal translation. Baker, Hemenway, and Trigueros (2000) used APOS theory to explain students’ learning difficulty. The vertical action is operated directly on a quadratic function, while the actions in horizontal are different, in which two operations are included, first on the variable, and then on the function.
Research Question
Recently some studies began to investigate Chinese curriculum innovation influences on mathematics classroom teaching (Huang, 2009; Huang & Fan, 2009; Li & Li, 2009, Huang & Li, 2009). The main concern of these studies was to observe some excellent mathematics lessons, which were usually isolated, in which teachers were not observed in a structured way. In order to overcome the deficiencies of these studies, this study was grounded in curriculum innovation and conducted a series of successive observations of routine lessons, in which the focus was on the experienced teacher’s strategies. In order to promote an understanding of the teacher’s strategies, we chose a challenging topic of translation of quadratic functions. The research question was: What strategies does the experienced teacher use to help students understand the concept of translation of quadratic functions?
Methodology
Participant
5
region of Jiangsu. This school has about 2,500 students divided into three grades from seven to nine. Each grade has 16 classes, and each class has 45 to 50 students mostly from local families.
We invited Mr S to participate in this study, because on the one hand he is an experienced teacher, and on the other hand, he and the researchers have a good relationship so as he can help us to complete the study successfully.
Data collection
From October to November 2009, Mr S’s class of grade 9 was studied. The content of translation of quadratic functions was divided into three lessons, each of which has about 40minutes. In each mathematics classroom, a researcher videoed, and another wrote field notes. After each lesson, the lesson plan was copied, and the teacher was interviewed by the researcher using a semi-structured process where the researcher wrote notes. At the same time, the researcher who had videoed the lesson also recorded the whole process of the interview. Videos of the lessons and interviews were translated into scripts by four assistants.
In the next section a description is presented of how the experienced teacher used effective strategies to help students understand vertical translation of quadratic functions. His strategies have been identified to be similar with the other two lessons, the result of which is set aside for an appropriate occasion.
Results
Review and foreshadowing (in Chinese铺垫)
Before the lesson, Mr S copied a mathematics task on the blackboard. The task was: If the quadratic function y=ax2 and the line y=x-1 have only one common point, then how many points of intersection do the function y=4ax2 and the line y=x+3 have?
Mr S pointed out that the quadratic function could be denoted by an algebraic expression, but also could be represented by a graph. Therefore students could access solutions using two perspectives. He said: “We have learned features of function graph for some days, so I hope that you can use the graph features to solve this problem.” Next, the problem solving process was completed under the control of him. He asked his students to draw the two possible graphs of the quadratic function y=ax2. At the same time he drew the two graphs of concave up and down on the blackboard.
The following are the teacher-student interactions. On the blackboard Mr S drew the graph, in which y = ax2 and y = x-1have only one common point. Then Mr S asked students to stretch the graph of y = ax2, and translate the graph of y = x-1 in the same system, so that they constructed the graph of y = 4ax2 and y = x+3. Finally, the teacher guided his students to solve this problem by setting up an equation system.
of the quadratic function.
Actually the teacher attempted to highlight the importance of the graph solution, although he guided his students to solve this problem by algebraic solution later. In the lesson, he gave a cue to his students: "We have learned the graph of a function, so I hope you can use graph features to solve this problem first of all." In the interviews, Mr S emphasized repeatedly that students lacked the idea of combining figures with graph (in Chinese数形结合). It is hard for students to associate the features of a function graph with its algebraic expression, and they felt it was difficult to learn quadratic functions. He also made it clear that he would always stress the idea of combining figures with graphs in teaching quadratic functions. He is convinced that if students generated this idea, they would be assured of understanding the content of quadratic functions, and be able to solve the problems related to it.
Transition
Mr S made a transit to the theme of this lesson, vertical translation of quadratic functions. He asked: "What is the relationship between the quadratic functions y = ax2 and
y = ax2+bx+c?" After a moment in silence, he told the students: “Special versus General". Then, Mr S asked his students to classify y = ax2+bx+c according to its coefficients whether it is zero or not. Then, he raised a question: "What is the relationship between the graph of y = ax2 and y = ax2+bx+c?"
In fact, it was found that the classification of the quadratic function was too difficult for the students. Although he gave his students a lot of cues, and gave them time to explore it, they did not finally succeed. The students’ performance in the lesson surprised the teacher. After the lesson he said:
I have spent too much time dealing with classification, which should not be stressed in this lesson. My intention was to enable students to realize the algebraic relation between y = ax2 and y = ax2 +c, and pilot them to consider the graph relation between them.
His comment implies that he dealt with the classification of quadratic functions because of two points. Firstly, considering the pedagogy, he wanted to strengthen the coherence of the classroom instruction. Secondly, he emphasized the connection among y=ax2+bx+c, y=ax2 and y=ax2+c, in order to encourage his students to understand the concept of quadratic functions.
Core concept
7
answered in unison: “Translate it upward or downward”. It looked like a very obvious matter for them. Mr S invited a student to make the explanation. He asked: “Yun, can you explain?”
Yun: Just like the translation on linear function. Mr S: Can you give us an example?
Yun: y=2x, y=2x+1
Yun made an analogy translation of linear function to translation of a quadratic one. Perhaps, the foreshadowing at the beginning of the lesson had an effect on their thinking. So the student could easily connect two type of translation with. Mr S said would like to hear other different answers.
Feng: Take a point on y=ax2
. Its abscissa is x, while its ordinate is ax2 . Mr S: Let(x1, y1).
Feng: Substitute x1in y=ax 2
+c, then get y1+c.
Mr S: What is the position relation between the points of (x1, y1)and(x1, y1+c)? Feng: Translate upward or downward.
In fact, the teacher emphasized the explanation of the graphical features on the algebraic perspective. In the previous lesson, he had always taken the trouble to lead his students to use point-coordinates to interpret the symmetry of y=ax2. In the interview, he said:
Algebraic explanation is the most powerful. When we see a function expression, we should think of its graphical features; when looking at function graph, we should explain it on the algebraic perspective.
It also shows that Mr S always highlighted the idea of combining figures with graphs. In this episode, he first attempted to give students an overall impression on the translation of quadratic function. He expected that students would preliminarily perceive the translation of a parabola before accessing details. This strategy which is consistent with the view of Gestalt could facilitate students to connect existing cognitive conceptions (translation of linear function) with the overall impression so as to establish the structure which can assimilate specific knowledge.
Depicting points to draw a parabola. Mr S requested his students to complete the
mathematical task: Depicting points to draw parabolas of y = ½ x2, 1 2
+1 2
y= x , and 1 2
-1 2 y= x
at the same coordinate system, then discussing their features.
In the first step, the teacher listed a table on the blackboard, took x =- 3, -2, -1, 0, 1, 2,
3symmetrically, and found the corresponding value of 1 2
2
y= x in order. He said: “Do you
think the value of 1 2
+1 2
y= x must be calculated in this way? ... Yes, don’t calculate any
longer, as long as the latter’s corresponding value of the 1 2
2
to find the corresponding value of function -1 2
y= x , he also asked the students to focus
their attention on the feature: as long as the last function’s value is same from the function
2
1 2
y= x but add negative one.
In the tabulation process, Mr S asked his students repeatedly to pay attention to the numerical relation among the three functions’ values, in which the same number was taken from. In this way, he intended to help his students to understand the relation among the function graphs.
The teacher required each student to depict the graphs of 1 2
2
y= x , 1 2
+1 2
y= x , and
2
1 -1 2
y= x on the cross-section paper. A few students drew exotic graphs: (1) The three
parabolas’ vertices coincided at the origin; (2) Parabolas intersected; (3) Parabolas extended in different directions, but did not intersect. Mr S saw several students drawing intersected parabolas, then required all students to watch the parabolas which he had drawn on the blackboard. He explained: “It is impossible for these parabolas to intersect, because each
point on the graph of 1 2
2
y= x is moved upward one unit, so as to get the graph of 1 2
+1 2 y= x .
Can the original graph intersect with the new one? No, they cannot.”
After the lesson, we told Mr S the other errors in drawing the parabolas. He felt surprised that these students drew the three parabolas with the same vertex. He said:
If so, students still have no idea of translation? I already elicited students to conjecture. The purpose is to promote them to generate a overall impression on the translation. And I stressed repeatedly the change of the values in the table. Perhaps their impression on the graph of y=ax2 is too deep -vertex must be at the origin.
Mr S had confidence that what he had done could enhance students’ understanding of translation. He just contributed a few students’ errors to their prior experience. So we can understand why the teacher employed similar strategies in the other two lessons on translation.
Because the teacher did not consider these errors in drawing before the lesson, his interpretation was confusing. In fact, a graph may intersect with the moved one. For example, a circle may intersect with the moved one. It was hard for him to make effective strategies to deal with unexpected accidents in classroom.
9
Sketch. The teacher required the students to sketch graphs of 1 2
-2
y= x , 1 2
- +1
2 y= x ,
and 1 2
- -1
2
y= x . As far as the teaching arrangement was involved, he explained:
At first, students can familiarize with the knowledge that they have just learned. At second, they have learned the parabolas of up-opening, and now they do an exercise on down-opening. Furthermore, in solving problems we usually sketch rather than depict points.
The teacher’s intention was obvious. On the one hand, he tried to make students understand the concept of translation with variation. On the other hand, he trained students’ sketch skills, which could be used to solve problems. The teacher has a further understanding of the sketch value. He believed that conceiving a graph in the mind is more important than depicting points to draw it. Here, the former means the graph of a quadratic function operated in the mind, which is the second stage of Bruner’s iconic mode, semi-concrete operation. The stage of iconic operation is important for students to understand the abstract concept of translation, the symbolic mode, which is the third learning stage defined by Brunner.
Summary
In classroom interactions, students observed similarities and differences between the graphs of y = ax2 and y = ax2+ c, and then generalized the relation between them, so that they completed the third learning stage of symbolic mode.
In the instructional process of the core concept, the teacher firstly gave his students an overall impression of the translation process, and then accessed details. Students experienced the specific--semi-specific and semi-abstract-- abstract stage, in which they depicted points to draw a graph, or sketch, and generalized vertical translation of quadratic functions.
After that, there was no time to do other exercises in the class. However, the teacher’s plan had not been completed. His intention before the lesson was to consolidate students’ concept of the translation with some mathematics exercises.
Conclusion
This research was supported by Ministry of Education (China) under GOA107014.
Reference
Baker, B., Hemenway, C., & Trigueros, M. (2000). On transformations of basic functions. In: H. Chick, K. Stacey, & J. Vincent (Eds.), Proceedings of the 12th ICMI Study Conference on the Future of the Teaching and Learning of Algebra (pp. 41-47). University of Melbourne.
Bruner, J. S. (1966). Toward a theory of instruction. Cambridge, MA: Harvard University Press.
Huang, X. F. (2009). Research on Mathematics Classroom in Shanghai. Nanning: Guangxi Education Publishing House.
Huang, X. F., & Fan, L. H. (2009). Instructional practice in mathematics classroom driven by curriculum reform: a case study of model lesson from the Shanghai Two Round
Curriculum Reform. Journal of Mathematics Education, 3, 25-30.
Huang, R., & Li, Y. (2009).Pursuing excellence in mathematics classroom instruction through exemplary lesson development in China: a case study.ZDM-The International Journal on Mathematics Education, 41, 297-309.
Eisenberg, T., & Dreyfus, T. (1994). On understanding how students learn to visualize function transformations. In: E. Dubinsky, A. Schoenfeld, & J. Kaput (Eds.), Research in collegiate mathematics education 1, (pp. 45-68). Providence, RI: American
Mathematical Society.
Leinhardt, G., Zaslavsky, O., & Stein, M. K. (1990). Function, graphs, and graphing: Tasks, learning, and teaching. Review of educational Research, 60, 1-64.
Li, Y., &Li, J. (2009). Mathematics classroom instruction excellence through the platform of teaching contests. ZDM-The International Journal on Mathematics Education, 41, 263-277.
Ministry of Education. (2001). Mathematics Curriculum Standards in Compulsory Education. Beijing: Beijing Normal University publishing House.
Qian, W. W. (2007). Commentary of several contentious issues about open class.Shanghai Research On Education, 7, 34-37.
Sajka, M. (2003). A secondary school students’ understanding of the concept of function: a case study. Educational Studies in Mathematic, 53, 229-254.
Vinner, S., & Dreyfus, T. (1989). Images and definitions for the concept of function.Journal for Research in Mathematics Education, 20, 356-366.
Wong, N. (2009). Exemplary mathematics lessons: What lessons we can learn from them? ZDM-The International Journal on Mathematics Education, 41, 379-384.
Yu, P. (2002). Briefly on dual-function of publicly-given class. Shanghai Research On Education1, 31-33.
Zaslavsky, O. (1997). Conceptual obstacles in the learning of quadratic functions.Focus on Learning Problems in Mathematics, 19, 20–44.
11
Teaching for Abstraction: Teacher Learning
Paul White, Sue Wilson Australian Catholic University
<paul.white@acu.edu.au; sue.wilson@acu.edu.au>
Michael Mitchelmore Macquarie University <mike.mitchelmore@mq.edu.au>
Working collaboratively with the researchers, a small team of teachers developed and taught two Grade 6 mathematics lessons based on the Teaching for Abstraction model (White & Mitchelmore, 2010). This paper reports how one teacher learned about the model and implemented it in practice. It was found that she assimilated several key features of the model, such as starting with several embodiments of the target concept and guiding students to look for similarities between them. However, it was more difficult for her to help students abstract and reify the target concept and link it to other mathematical concepts. It was concluded that teachers also need to abstract Teaching for Abstraction, and need more embodiments of it before they can reify and implement an effective model.
Keywords: learning by abstraction, Lesson Study, primary school education, professional growth, teacher learning
Over the past decade, the first and last author have been developing a mathematics
teaching model called Teaching for Abstraction which is based on a specific theory of
learning mathematics. However, we have repeatedly found that teachers’ ability to
comprehend the underlying theory has been a barrier to effective implementation. This paper
represents an attempt to identify more closely what aspects of the Teaching for Abstraction
model teachers find particularly difficult and to design more effective professional
development.
Background and Rationale
Learning by abstraction
One theory of mathematics learning (Dienes, 1963) holds that all elementary concepts
are the result of abstraction and generalisation from common experiences. For example,
children experience many objects that are basically linear such as the edge of a table and a
line drawn with a ruler. They see that two edges of a table top meet at a corner and they mark
points on a drawn line to indicate a particular length. However, they also experience objects
that are too wide, curved or indistinct to be called a line (such as a path across a field) and
other lines that do not meet at a point (such as railway tracks). By recognising the underlying
children may abstract the concepts of line, point and intersection and generalise that two lines
never meet in more than one point.
The role of abstraction in this theory of learning was well described by Skemp (1986)
as follows:
Abstracting is an activity by which we become aware of similarities ... among our experiences. Classifying means collecting together our experiences on the basis of these similarities. An abstraction is some kind of lasting change, the result of abstracting, which enables us to recognise new experiences as having the similarities of an already formed class. ... To distinguish between abstracting as an activity and abstraction as its end-product, we shall ... call the latter a concept. (p. 21, italics in original)
We call the formation of basic mathematical concepts in this manner empirical
abstraction because it is based on experience.
Empirical abstraction occurs both inside and outside the classroom. For example,
parents often help young children recognise similarities in their everyday experiences (e.g.,
by teaching them the names of particular classes of objects) and school children frequently
look for patterns that could simplify their learning (“Just tell us the rule, miss!”). Such
empirical abstraction is almost always superficial. Everyday concepts such as “red” and
“building” are based on surface appearances anyway, so they are necessarily superficial. But
mathematical concepts are based on deeper similarities and it is important that these deeper
similarities be learned (Mitchelmore, 2000). For example, students must go beyond thinking
that a fraction is “one number over another”.
Empirical abstraction is to be contrasted with theoretical abstraction, which is the
construction of concepts to fit into a specific mathematical theory (Davidov, 1990). For
example, the mathematical concepts of line and point are theoretical abstractions; their only
existence is in terms of axioms (such as “two lines never meet in more than one point”) that
define relations between them and other geometrical concepts. Reasoning about theoretical
points and lines must be based on such precise axioms, and no appeal can be made to the
imprecise points and lines of experience. Theoretical abstraction plays an extremely
important role in mathematics.
We have argued (Mitchelmore & White, 2004) that most abstract mathematical theories
are constructed to model empirical abstractions. For example, theoretical lines and points
only represent real linear objects and points⎯there is no such things in our world as a
perfectly straight line or a dimensionless dot. It is not until one reaches the refined
atmosphere of research mathematics that theories are invented for their own sake, but even
13
Therefore, if students are to appreciate the value of theoretical mathematics and be able to
apply abstract theory to concrete situations, they need to have a sound understanding of the
empirical abstractions on which the theoretical abstractions are based.
Teaching For Abstraction
Teaching for Abstraction (White & Mitchelmore, 2010) attempts to build on children’s
natural tendency to seek similarities and make rules in order to assist them to abstract
mathematical concepts. The Teaching for Abstraction model consists of four phases:
1. Familiarity. Students explore a variety of contexts where a concept arises, in
order to form generalisations about individual contexts and thus become familiar
with the underlying structure of each context.
2. Similarity. Teaching then focuses on helping students recognise the similarities
and differences between the underlying structures of these various contexts.
3. Reification. The general principles underpinning the identified similarities are
drawn out, and students are supported to abstract the desired concept into a
mental object that can be operated on in its own right.
4. Application. Students are then directed to new situations where they can use the
concept.
In this model, teachers start by carefully selecting situations known to the students
that embody a significant mathematical concept and ensure that students understand the
mathematics within each situation. They then deliberately focus students’ attention on the
underlying similarity between those situations and help them formulate that similarity in
abstract terms. Finally, they help students learn how to operate with those abstract concepts
and apply them to solve problems in other situations that embody that concept. Several
examples of specific skills and understandings at each level of the model are given in White
and Mitchelmore (2010).
The model is the reverse of the traditional ABC (Abstract Before Concrete) method of
teaching mathematics (Mitchelmore & White, 2000). As one teacher put it, “It is the opposite of what we’re doing in school now. It is starting with the blurred and being revealed.
Backwards. Not doing specific instructions first, more a thinking thing.”The model has many similarities to several approaches advanced in the mathematics education literature over the
past 20 years (encapsulated in such slogans as realistic learning, communities of discourse,
and teaching for understanding) in its emphasis on drawing mathematics out of familiar
relation posited between abstract ideas and familiar experience: Concepts are seen as
representing what is common among several experiences, rather than as ideas that can be
explained or justified through specific experiences. As a result, Teaching for Abstraction uses
multiple contexts for each concept, focuses on the relation between them, and constantly
links abstract ideas to the several contexts from which they were derived.
Our earliest experiments with the Teaching for Abstraction model involved teaching
the concept of angle in Years 3 and 4 (Mitchelmore & White, 2002a, 2002b). Familiar
contexts included corners, scissors, body joints, doors, clock hands, and slopes. The first
lessons concentrated on ensuring that students understood each of these contexts to the extent
that they could represent them graphically (Phase 1: Familiarity). The next lessons involved a
variety of matching exercises, both within and between contexts, leading students to
recognise that an angle (wherever it occurred) had two arms meeting at a point and that each
angle had a particular size (Phase 2: Similarity). Students then completed various activities to
develop facility in interpreting and using abstract angle diagrams (Stage 3: Reification) and
using them in new situations (Phase 4: Application). There was evidence that many students
developed a quite sophisticated concept of angle by as early as age 10.
Subsequent experiments have investigated the teaching of decimals, percentage and
ratio by abstraction. Summaries of these experiments and their effectiveness are given in
White and Mitchelmore (2010). The investigations have confirmed our conviction that the
Teaching for Abstraction model has promise in terms of student learning of key concepts and
generalisations. They have also consistently shown the vital significance of teacher learning.
Teacher learning
In the teaching studies we have undertaken, we have provided teachers with detailed
lesson outlines but many teachers have found it difficult to implement the Teaching for
Abstraction model. Because the model is so different from common teaching practice, we
have found it difficult to communicate to teachers despite revising the professional learning
activities several times. As a result, many teachers have either followed the materials
provided to the letter, not being in a position to adapt them to their particular classroom
situation, or they have subverted the whole process and reverted to the ABC method. As a
result, the model was not implemented faithfully in several of the classrooms we studied.
Nevertheless, most teachers have spoken favourably of the results in their classrooms, and
15
A possible reason for the poor implementation of the model in previous studies is that
the teachers were not involved in planning the unit or developing the teaching materials. The
literature on teacher learning repeatedly cites the importance of active teacher involvement if
innovative ideas are to be accepted (Pegg & Panizzon, 2008). In our investigations, the
researchers did all the development and simply presented lesson plans to the teachers.
Consequently, the teachers had no real ownership of the experiments. They may even have
considered us as outsiders with no knowledge of classroom realities (Jaworski, 2004).
We therefore decided to investigate a different method of implementing Teaching for
Abstraction, one in which, instead of presenting teachers with completed teaching materials,
we would work collaboratively with teachers to develop Teaching for Abstraction lessons
that would better fit their own classroom situations. We hypothesised that such a procedure
would lead to greater ownership and thus more faithful implementation, deeper student
learning and, most importantly, greater teacher learning than the previous method.
The present study
As a theoretical framework for assessing the impact of this new method of
professional development, we call on the Interconnected Model of Professional Growth
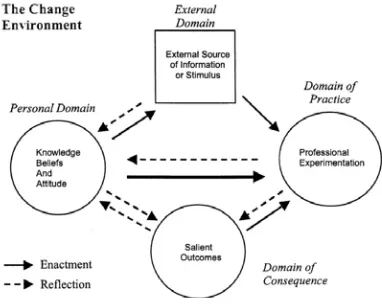
(Clarke & Hollingsworth, 2002). This model contains four domains and various interactions
between them, as shown in Figure 1. Note that most interactions are bidirectional. For
example, teachers enact a new idea, belief or practice in their classroom and then reflection
provides (positive or negative) feedback on the critical features of that innovation and its
value to them.
As an initial exploratory study, we worked with a small group of teachers in a small
regional town to prepare two unconnected lessons. The teachers then taught these lessons in a
kind of lesson study mode (Hart, Alston, & Murata, 2011). In terms of Figure 1, the External
Domain was the collaborative lesson preparation and study, the Personal Domain was
teachers’ knowledge and acceptance of Teaching for Abstraction, the Domain of Practice was
the lessons taught, and the Domain of Consequence consisted of student outcomes from the
lessons taught.
Our research question was: Can collaborative lesson development lead to faithful
implementation of the Teaching for Abstraction model?
More specifically: Which parts of the model are easier or more difficult for teachers to
implement? Can student learning be linked to the parts of the model that are implemented?
To provide answers to these questions, data were collected on all four components of
the model in Figure 1. We report a case study of one of the teachers involved.
Method
Participants
The study took place in Grade 6 at St Joseph’s1, a small primary school in regional
New South Wales. Initially, three teachers volunteered to participate: David, Bridget, and
Uarda. However, David was unwell during our visits and only participated marginally. Also,
Bridget was a part-time teacher and had several other calls on her time. Only Uarda
participated fully, and she is therefore the focus of this paper. Uarda had been teaching for 5
years, and was enrolled in a master’s degree at the time.
Procedures
The authors paid two 2-day visits to St Joseph’s. Both visits followed the same
pattern: The research team (the authors, Uarda, and whichever of the other teachers were
available) met for an initial discussion on the afternoon of Day 1 to decide on the aims for the
following day. Early on Day 2, the team developed a lesson and prepared the necessary
materials. Both sessions were guided by the principle that each participant should contribute
their particular expertise in the lesson design. Thus, the authors shared their knowledge of the
Teaching for Abstraction Model and their experience of its previous implementations while
17
Later in Day 2, Uarda taught the experimental lesson while the others observed, after
which the team discussed the lesson and modified it as they felt appropriate. Bridget then
taught the revised lesson while the others observed. On the second visit, an additional team
session was devoted to identifying the strengths and weaknesses of the Teaching for
Abstraction model and reflecting on the teacher learning that had occurred.
After the second visit, Uarda indicated that she would attempt to apply the model to
her teaching about angles in the following month. After teaching this unit, which we did not
observe, she provided the authors with written feedback.
Data collection and analysis
The research team’s discussion sessions were audio recorded and transcribed, but no
recordings were made of the lessons. Instead, one member of the research team acted as a
lesson recorder, taking detailed notes of the lessons that included time markers for the major
transitions. The other members subsequently added their individual observations to these
notes.
Because student outcomes have a significant feedback effect on teacher learning
(Clusky, 2002), an attempt was also made to assess short-term student learning. The recorder
noted students’ comments during the face-to-face teaching and all members of the team
circulated and observed students during the small group work, occasionally interacting with
them to clarify what they were attempting to do. In addition, the teachers administered a short
quiz at the end of the first visit and a short questionnaire at the end of the second visit.
The analysis of how Uarda interpreted and applied the Teaching for Abstraction
model, as well as its resulting effectiveness and potential, focussed on the four components
shown in Figure 1. Firstly, each author formed an interpretation of each of these components
on the basis of their own observations, notes and informal discussions during the site visits.
The three authors then cross-validated and synthesised their separate interpretations during
extensive discussions, frequently re-examining transcripts and field notes to reach consensus.
Results
The first visit
Initial discussions. At the first meeting of the research team, the authors outlined the Teaching for Abstraction model and gave some examples from their previous research. In
particular, they provided the teachers with copies of the instructional materials developed for
2008). They also explained the purpose of the study, and asked teachers for their reaction to
the model and its potential in their situation.
The teachers expressed interest in experimenting with the model. Uarda indicated that
she regularly trialled novel activities and approaches that she believed might be beneficial to
her students. Teaching for Abstraction had a definite resonance for her because she was
particularly keen on the use of realistic scenarios and always tried to embed the mathematics
she was teaching in contexts that she felt would be familiar to students.
The teachers then outlined a number of topics where they felt their students were
having most difficulty, and it was agreed that the next day’s lesson would focus on place
value in decimals. It was also agreed that Uarda and Bridget would both teach the same
lesson with their own classes, in that order, with time for discussion and revision between the
two lessons.
Lesson planning. The teachers reported that students had been taught about decimals but some students were still having difficulty deciding, for example, whether 0.65 was bigger
than 0.8. It was decided to focus the lesson on this topic, restricting the content to 1- and
2-place decimals. It was considered that this topic was sufficiently narrow for a single lesson,
but that it could nevertheless be of significant value to students. The teachers could extend
students’ understanding to other decimals later.
Having decided on this topic, that next task was to identify a small number of familiar
contexts involving one- or two-place decimals, which could then be compared to identify and
abstract the underlying similarity. The teachers initially had some difficulty with this task but,
after some suggestions from the authors, the team agreed on four contexts: money ($0.65 vs
$0.8), length (0.65 cm vs 0.8 cm), fractions of a box of 100 lollies (0.65 vs 0.8), and fractions
of a 10 × 10 square of chocolate (0.65 vs 0.8). It was decided to write four scenarios and to
break each class into four groups that would (after an initial introduction) circulate around the
four tasks, spending no more than 5 minutes on each. This would leave time for a final
discussion of students’ responses in which generalisations about decimal place value could be
abstracted.
It was agreed that the planned lesson included the first three phases of the Teaching
for Abstraction model applied to the concept of decimal place value: Students were already
familiar with the four contexts, they would be prompted to identify the underlying similarities
between them, and generalisation would initiate reification. Application would occur in
19
The teachers then left to collect or create materials for the lesson (counters for money
and lollies, rulers and butcher paper for measurement, and grids for the chocolate). After they
returned, discussion continued on the phrasing of the actual tasks to be used. The entire
planning session took just under an hour.
The lesson. Uarda started the lesson by writing the four scenarios on the whiteboard (see Figure 2). She explained the rotation procedure for the lesson (which was already
familiar practice in her classroom), divided the students into four approximately equally sized
groups, and instructed them to start working on their first scenario. No other introduction was
given.
Figure 2.Scenarios for the first trial lesson.
During the small group work (see Figure 3), the group working on the money task
finished first at each rotation. The lollies group took a long time to count out two lots of 100
counters, and the measurement group was slow to draw their two lines. Although the first
rotation took only 3 minutes, as planned, the group work took up 26 minutes in all because of
( 1) Money t ask ( 2) Measur em ent t ask
( 3) Chocolat e bar t ask ( 4) Lollies t ask
Figure 3.Students’ work on the four tasks.
Uarda then commenced the final discussion section of the lesson. Asked to identify
similarities between the four scenarios, students initially remarked only on superficial
aspects: They all involved Tom and Judy and the numbers 0.8 and 0.65, and Tom always
won. Asked how we know that 0.8 is bigger than 0.65, some students demonstrated
considerable insight with the responses “0.8 is 0.80”, “0.65 is 6 and a half, whereas 0.8 is 8”
and “0.8 is different from 0.08”. Uarda then gave an explanation using Dienes blocks, taking
the flat to represent 1 unit and having the students recognise that a long then represents 0.1
and a cube represents 0.01. Many students appeared to realise that 0.8 is represented by 8
longs and that 0.65 corresponds to 6 longs and 5 cubes, but others appeared bewildered. One
student suggested that a cube represented 0.1 and several students called 0.65 “point
sixty-five”.
Lesson discussion. After the lesson, Uarda remarked on how well the students enjoyed the hands-on aspect of the lesson. She was particularly struck by the fact that some
21
back a few times. She’s somebody that generally has no idea. And she was hands up
confidence. … She was the one that was explaining when the boy beside her wasn’t sure.”
Students’ tendency to notice irrelevant similarities was noted, and the authors recalled
Dienes’s (1963) dictum that “all variables need to be varied if the full generality of the
concept is to be achieved” (p. 158). It was decided for the second trial lesson to vary the
children’s names and to ask alternately for the larger or smaller number. It was also decided
to compare 0.4 and 0.25 in order to make the lollies and measurement tasks more
manageable. Bridget left to write the revised scenarios on the whiteboard in her classroom in
preparation for the second lesson.
Discussion then turned to the question of how general students’ understanding of
place value was. In particular, it was felt that the approach taken had tended to reinforce
whole number thinking (e.g., treating 0.8 as 80 out of 100 rather than a fraction of the flat).
It was decided to put more emphasis on decimals as fractions of a whole rather than numbers
of parts of the whole, even by including questions such as “What is 0.8 of a student’s pony
tail?” Ideas were canvassed on how to question students in order to take them beyond the
specific insights they had shown, by focussing more strongly on the similarities between the
four scenarios. The plan for the repeat lesson (not reported here) was modified accordingly.
As a measure of how much students had learned from the lesson, Uarda suggested a
short quiz in which students would be asked to identify the smaller of two decimals; the team
then constructed this quiz jointly. Figure 4 shows the resulting quiz.
Circle the smaller number:
(1) 0.8 (2) 0.52 (3) 0.6 (4) 0.8 (5) 1.6534 (6) 2
0.65 0.7 0.298 0.09 1.72 2.2
Figure 4.Short quiz questions.
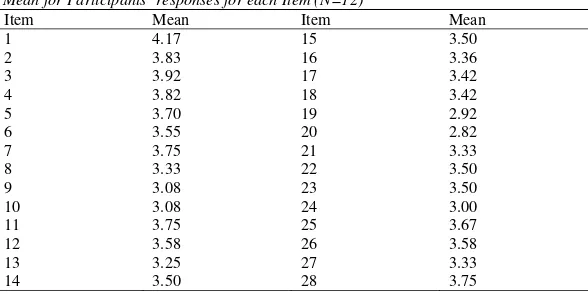
Assessment. Shortly after the lesson discussion, Uarda administered the quiz to a total of 24 students in her class. About 70% answered Items 1, 2 and 6 correctly, while Items 3, 4
and 5 were only answered correctly by just over 50% of the students. However, it was noted
that five students marked all the larger numbers correctly. It could be argued that they
instructions carefully and had proceeded as in the scenarios they had just experienced. On
this assumption, the percentages correct would have been about 20% greater.
If this assumption is correct, the result for Item 2 would suggest that the majority of
Uarda’s students had generalised their knowledge of 2-place decimals to numbers other than
the ones in the given scenarios. However, the zero in Item 4 seems to have introduced
problems for several students. Most students appeared to be able to cope with numbers with
no decimal places, as in Item 6, but it was clear from Items 3 and 4 that more work needed to
be done on decimals with more than 2 places.
In general, the assessment results confirm the post-lesson discussion that greater
emphasis needed to be put on bringing out the underlying structure of the decimal notation
system.
The second visit
Initial discussions. The teachers had decided that on this occasion they wanted the lesson to focus on percentages, where students were demonstrating continued difficulties.
The team brainstormed some typical percentage problems and possible scenarios, gradually
honing in on discounts and the generalisation “a percentage must be a percentage of
something”. After some discussion of how to approach this generalisation, it was agreed to
present two scenarios that consisted of specific calculations from which the generalisation
could be abstracted and two applications of the generalisation where no calculation was
specified. Students would be asked to predict the answers before doing the calculation in the
first type of scenario, and the two types of scenario would be separated by a brief discussion.
It was agreed that this lesson followed the Teaching for Abstraction model. Students
would learn the percentage generalisation by recognising the similarity between the two
initial scenarios, which would have to be chosen to be familiar. They would then be prompted
to apply the generalisation to two different contexts.
Uarda also suggested a “cognitive closure” exercise at the end of the lesson, to check
student understanding. Apart from this, it was agreed to follow the same procedure as on the
previous visit.
Lesson planning. Four scenarios were composed; ensuring that Scenarios 1 and 2 gave contrasting results. Figure 5 shows the four scenarios. Each scenario was written on an
A5 card (two copies of each), and the words “Don’t forget to predict which will be the better
23
materials were required for this lesson, but David created an A3 illustration to motivate each
scenario.
1. There are 2 telephone plans and your parents are going to give you a % (percentage) of money towards your plan. In which plan do your parents give YOU more money?
(a) 15% on $50 plan
(b) 10% on $60 plan
2. Electronic Store A is having their 50% mid year sale. Your favourite game is usually $110. How much will you pay now?
At Electronic Store B, the full price for your favourite game is usually $90. Their discount is 40%. How much will you now pay?
Which shop is offering the better price?
3. Pizzas Galore have a 10% surcharge on all of their purchases on a Sunday. You want 3 pizzas. Is it cheaper to buy the 3 at once or one at a time?
4. The top 2 basketball teams of the local basketball league have a success rate at goal shooting of 80% and 50%.
Which team has shot the most goals in the season?
Figure 5.Scenarios for the second trial lesson.
The lesson. Uarda began the lesson by teaching students how to use a calculator, writing the examples in Figure 6 on the whiteboard and giving students three examples of
each type to work out. However, some students seemed to be working out the percentages
mentally, and many found the resulting price by subtracting the discount from the original
price instead of using the second procedure.
5 0 x 2 5 % = [gives a 25% discount on $50]
5 0 x 2 5 % - = [gives the resulting price]
Figure 6.Uarda’s examples of using a calculator for percentages.
Fifteen minutes into the lesson, Uarda introduced the first two scenarios and explained
the rotation procedure. In one group, students’ predictions appeared to be mere guesses.
Calculation difficulties (which button to press) seemed to distract from understanding, and
several students did not seem to realise the difference between discount and discounted price.
In one group, two students showed the others how to do the calculations and told them the
vigorous discussion and general agreement that the bigger percentage does not always give
the bigger amount.
Thirty-three minutes into the lesson, students started on the second pair of scenarios.
Scenario 3 seemed rather difficult, the idea of checking a prediction by choosing values being
clearly unfamiliar to the students. The term “surcharge” was also unfamiliar to several
students. Scenario 4 seemed to be much easier, even though it also requires the choice of
specific values to test a generalisation.
There was only time at the end of this lesson to check students’ answers and discuss
how to test general predictions. Several students successfully argued in Scenario 3 that “it
doesn’t matter”, but one student was adamant that buying three separate pizzas would be
cheaper and could not be dissuaded from this view.
Lesson discussion. It was generally agreed that, in this lesson, students had been absorbed with the procedure for using a calculator and that this had interfered with the
cognitive process of generalisation. Uarda said that, in future, she would break down the
content into several lessons⎯perhaps mastering the method of calculation and a lesson on
discounts and surcharges before posing the problems in Scenarios 1 and 2. She would then
take a whole lesson on Scenarios 3 and 4.
A number of minor points were also identified. For example, it was agreed that
including the instruction “Give an example to illustrate your thinking” would help students in
responding to Scenarios 3 and 4. Minor changes were made for the repeat lesson (not
reported here).
Assessment. Figure 7 shows the cognitive closure exercise that Uarda constructed and administered shortly after teaching her lesson. Responses were obtained from 17 of her
students.
By completing these 4 exercises, what have you learnt about % (percentages)? Give me an example of your own.
Figure 7. Cognitive closure exercise.
Responses to the first question were grouped into seven categories, with some
students giving responses in more than one category. Almost 50% of the students responded
to the effect that “the smaller percentage doesn’t always make the smaller answer” and 40%
indicated that they found the scenarios thought provoking and requiring different procedures
25
percentages every day or that they had learnt nothing new, or gave a small number of other
responses.
Students’ examples were categorised as direct or open, contextual or abstract, and
calculation or comparison. Nearly 50% fell into the direct contextual comparison category
similar to Scenarios 1 and 2 and less than 25% involved an open contextual comparison as in
Scenarios 3 and 4.
These results were considered encouraging, the categories of examples proposed by
students apparently reflecting their greater familiarity with the style of Scenarios 1 and 2.
Follow-up
About a month after our second visit, Uarda taught an angles unit which she had
designed following the principles she had learnt during our earlier visits. The key ideas
addressed over four lessons were as follows (quoting from the unit outline she provided):
Angles are found everywhere; angles can be measured using a protractor; parallel lines have
equal angles; and each type of angle is useful. Apart from angle measurement, where Uarda
first showed students how to use a protractor, the lesson plans showed a similar procedure to
the earlier trial lessons: Activities in small rotational groups were followed by class
discussion and some follow-up tasks. For example, the four activities used in the first lesson
were as follows:
1. Find angles around the room.
2. Make as many angles with scissors.
3. Make as many angles with straws.
4. Draw as many different angles as you can using a ruler.
The follow-up task was:
Draw 6 different angles in your books. How are they different? When are they used?
Where do you think you could find these angles at home?
Uarda made the following comments on this unit:
I think the program worked well. I used the small group work again and immersed them in different contexts wherever I could. The planning was probably slightly quicker as I didn’t need to spend time with the explicitly teaching section as such, but more so on thinking about questions to ask to find generalisations of their findings and more [on] the context and content I wanted to teach.
I gave them a standard angles test and the only area they struggled in was accurately measuring the angles using a protractor.
Uarda’s approach shows several features of the Teaching for Abstraction model: She
started with several familiar contexts that incorporated the ideas she wanted to teach and used
discussion to draw out underlying generalisations. The follow-up tasks definitely tested
children’s understanding of the abstract ideas that had been discussed. However, one feature
of Teaching for Abstraction did not seem to be present: the search for underlying similarities
between the contexts studied. The concepts students learned were common to all the contexts
studied; but there was no sign that Uarda had addressed this point in the same way as, for
example, is done in the angles unit distributed by the New South Wales Department of
Education and Training (2003), which is based on our earlier experiments.
Discussion
We discuss the results in terms of the four components of the Integrated Model of
Teacher Professional Development (Figure 1).
The Domain of Practice: Implementation of the Teaching for Abstraction model
The two lessons certainly incorporated major elements of the Teaching for
Abstraction model. Most obvious was the emphasis on exploring a variety of contexts where
a concept arises (Phase 1 of the model). Both lessons were the result of careful planning,
firstly to clearly identify a focus concept or generalisation and secondly to select scenarios
that embodied this abstraction and would be familiar to the students. However, although
students did indeed seem to be quite familiar with all the contexts chosen, in the second
lesson calculator difficulties meant that several students could not operate fluently within the
discount context.
Similarity recognition (Phase 2) was also present. In the first lesson, students showed
a strong tendency to focus on superficial similarities, and it was difficult for Uarda to bring
students’ attention to mathematical similarities. However, in the second lesson, the question
“What surprised you?” did seem to focus students’ attention on a generalisation that was
implicit in the two scenarios investigated⎯in this case, the result of recognising a difference
rather than a similarity.
Neither lesson proceeded very far with Reification (Phase 3), where the underlying
structure could have been laid bare, explained, and formalised. The attempt to use Dienes
blocks to explain place value in the first lesson did not seem to relate well to the similarities
27
proper exploration of the target generalisation that could have extended it from the specific
context of discounts to the general context of abstract percentages.
Phase 4 of the model, Application, was deliberately avoided in the first lesson but did
occur in the second lesson (see Figure 5, Items 3 and 4). However, as Uarda noted, it would
have been better to give more time to elucidating the percentage generalisation before
attempting to apply it.
The Domain of Consequence: Student outcomes
The assessment of student outcomes for the first lesson suggested that most students
had achieved the narrow objective of ordering one- and two-place decimals. However,
understanding was not deep enough to allow many students to extend this knowledge to
decimals with more than two places or containing zeros after the decimal point. We attribute
this finding to shortcomings in the Similarity and Reification phases of the lesson.
The second lesson did not appear to be so successful in terms of student learning, but
the results of the cognitive closure exercise showed that many students had learnt the target
generalisation.
The two lessons had some other positive outcomes. The realistic nature of the
activities in the first lesson appeared to engage students more than usual, and many students
appreciated the challenging nature of the second lesson. Throughout, there was clear evidence
that students were responding well to the chance to think for themselves and were learning
some significant ideas.
The Personal Domain: Teacher learning
Uarda emphasised right from the first meeting her belief in the importance of
embedding mathematics in realistic, familiar contexts. However, the idea of using more than
one context for each concept was clearly new to her, and in the initial discussion sessions the
authors had to repeatedly stress the importance of similarity recognition in the Teaching for
Abstraction model. Consequently, she put a lot of thought and effort into the process of
identifying and selecting appropriate contexts for the two trial lessons and used the same
principle in her follow-up lesson on angles. Our observations showed that she was skilled in
managing a classroom so that students could work on several contexts in one lesson. We
conclude that Uarda had successively learned to implement the Familiarity phase of the
Uarda also attempted to implement the Similarity phase in that she challenged
students to identify similarities in, and make generalisations from the exploratory activities
they had just carried out. However, she did not clearly distinguish superficial and
mathematical similarities and did not probe for explanations or forge meaningful links to
students’ existing knowledge. For a similar reason, Uarda did not effectively address the
Reification phase in either lesson. The little evidence we have from her follow-up lesson
confirms that she had formed no clear concept of the content and purpose of these two
phases.
Uarda tended to adopt a didactic mode by presenting her own explanations or
procedures. For example, neither the use of Dienes blocks in the first lesson nor the use of
calculators in the second lesson had been discussed in the lesson planning sessions. These
were honest attempts to address known student difficulties, but they only served to disrupt the
structure of the Teaching for Abstraction lesson. In this respect, Uarda’s modifications were
similar to the way teachers in earlier studies had subverted the model by returning to a more
familiar lesson structure (White & Mitchelmore, 2010).
For time reasons, it was not possible to judge how Uarda would have treated the
Application phase.
The External Domain: Collaborative lesson planning
The collaborative lesson planning went according to plan, although it would certainly
have been more effective had all the teachers been able to participate to the extent that Uarda
did. There is no doubt that she had ownership of the plan for her lessons.
However, it is now clear that the professional development we provided for Uarda and
her colleagues did not stress strongly enough the significance of the crucial steps of similarity
recognition and reification. It is clear in hindsight that the teachers needed to spend more time
reflecting on mathematical similarities⎯how to distinguish them from superficial
similarities, how to draw them out through careful questioning, how to derive adequate
explanations, how to link students’ learning to their previous knowledge, and how to reify
29 Conclusions
To answer our research questions, then, it appears that collaborative lesson
development of the type we provided did not lead to faithful implementation of the Teaching
for Abstraction model. In particular, there were serious difficulties in implementing the
Similarityand Reification phases of the model. As a consequence, although students gained
from the use of familiar contexts and the challenge of reaching their own conclusions, it
seems that they did not reach the desired depth of understanding.
Because most modern curriculum innovations stress the importance of linking abstract
concepts to familiar situations, it appears to be relatively easy for teachers to learn the
Familiarity phases of the Teaching for Abstraction model. However, the Similarity and
Reification phases are unique to the model, and are therefore likely to be completely novel to
teachers. As Sullivan, Clarke, & Clarke (2009) found in a similar context, teachers may need
a lot of help in developing the new skills required to implement these two phases effectively.
We conclude once again that the type of one-off intervention that was the subject of
the present study is unlikely to achieve the desired effects. More time is needed for teachers
to experiment with the new lesson structure and to reflect on the results in the classroom. A
successful professional development would need to allow teachers to experience more
examples of Teaching for Abstraction than the two we were able to provide in this study.
They would then be better able to recognise the underlying structure of the model, reify it
into a set of principles to be followed, and apply their understanding to the design of new
lessons. In other words, we probably need to teach teachers Teaching for Abstraction by
abstraction.
Acknowledgements
The study reported in this paper was supported by a grant from the National Centre of
Science, Information and Communication Technology, and Mathematics Education for Rural
and Regional Australia (SiMERR).
References
Clarke, D., & Hollingsworth, H. (2002). Elaborating a model