LOGIKA MATEMATIKA
Logika matematika mempunyai peranan mendasar dalam perkembangan teknologi computer. Karena logika digunakan dalam berbagai aspek di bidang computer seperti pemrograman, ersitektur computer, basisdata dan sebagainya. Nah coba kamu tentukan keterkaitan antara logika matematika dengan pemrograman computer.
Logika merupakan ilmu yang mempelajari aturan-aturan penalaran (pemikiran logis) baik dalam bidang matematika, sains, hokum dan bidang lainnya.
Logika berhubungan dengan pernyataan. Oleh karena itu, dalam logika hanya terdapat dua kemungkinan kebenaran, yaitu benar atau salah.
Dalam pengoperasian computer hanya dikenal du kondisi yang analog dengan logika, yaitu ada atau tidak adanya aliran listrik. Kondisi ini dapat diartikan dalam bahasa logika sebagai kondisi “True” atau “False”.
Masih ingatkah kamu akan bilangan biner? Sistem bilangan inilah yang digunakan dalam setiap instruksi pada computer. Instruksi ini pada dasarnya merupakan serangkaian kombinasi logis.
Dalam bahasan berikut, kita akan mempelajari logika dimulai dengan pengertian tentang pernyataan, bentuk-bentuk logika sama dengan metode-metode penalaran atau pemikiran logis.
A. PERNYATAAN, BUKAN PERNYATAAN, NILAI KEBENARAN, DAN KALIMAT TERBUKA. 1. Pernyatan dan Bukan Pernyataan
Kalimat merupakan rangkaian kata-kata yang disusun sedemikian rupa sehingga memiliki arti yang utuh. Kalimat itu sendiri dikelompokkan menjadi 4 (empat) kelompok, yaitu : kalimat pernyataan, kalimat Tanya, kalimat perintah, dan kalimat seru.
Dalam matematika, kalimat yang penting adalah kalimat pernyataan (deklaratif). Kalimat seperti ini memiliki cirri khusus, yaitu kita dapat menentukan kalimat itu sebagai kalimat yang hanya benar saja atau sebagai kalimat yang salah saja. Sebagai contoh :
a. Sembilan adalah bilangan ganjil
b. Sin 300 sama dengan 1 3 2
c. Ibu kota Indonesia adalah Yogyakarta.
d. Pada segitiga siku-siku berlaku kuadrat sisi miring sama dngan jumlah kuadrat sisi-sisi yang lain.
Kalimat (a), (b), (c), (d) pada contoh di atas merupakan pernyataan, mengapa?
Pada kalimat (a) dan (d) kita dapat menentukan bahwa kalimat-kalimat tersebut adalah benar dan kalimat (b) dan (c) adalah kalimat yang bernilai salah.
Dari penjelasan di sata, kita peroleh definisi sebagai berikut :
Perhatikan contoh berikut : a. x + 5 = 17
b. p adalah bilangan prima c. Ani adalah gadis yang cantik
d. Jarak antara Jakarta dan Surabaya adalah dekat.
Kalimat (a), (b), (c) dan (d) bukan pernyataan. Pada kalimat-kalimat tersebut kita tidak dapat menentukan papakah kalimat itu benar atau salah. Untuk lebih jelasnya perhatikan penjelasan berikut ini.
Kalimat “x + 5 = 17” adalah bukan pernyataan karena bila x diganti dengan 12, maka 12 + 5 = 17 menjadi pernyataan yang benar, tetapi bila x diganti dengan sembarang bilangan real yang
Pernyataan adalah kalimat tertutup yang hanya benar atau salah saja, tetapi tidak sekaligus kedua-duanya
tidak sama dengan 12, maka kalimat tersebut bernilai salah. Jadi kalimat tersebut bias bernilai benar atau bernilai salah tergantung dari nilai x. Jadi x + 5 = 17 bukanlah pernyataan.
Kalimat “p adalah bilangan prima” merupakan bukan pernyataan karena bila p diganti dengan 0, maka pernyataan “0 adalah bilangan prima” bernilai salah, tetapi bila p diganti dengan 3, maka pernyataan “3 adalah bilangan prima” bernilai benar.
Kalimat “Ani adalah gadis cantik” adalah relative, cantik menurut si A belum tentu cantik menurut si B. Jadi kalimat “Ani adalah gadis cantik” bukan pernyataan.
Demikian pula hanya untuk kalimat “jarak antara Jakarta dan Surabaya adalah dekat” adalah bukan pernyataan. Karena dekat itu relative. Jarak antara Jakarta dan Surabaya dekat apabila dibandingkan dengan jarak antara Jakarta dan Kairo sehingga menjadi pernyataan yang benar, tetapi bila dibandingkan dengan jarak antara Jakarta dan Bandung maka menjadi pernyataan yang salah.
Dari penjelasan di atas, maka diperoleh definisi sebagai berikut.
Soal Latihan
Manakah dari kalimat-kalimat berikut yang merupakan pernyataan? tentukan nilai kebenarannya. 1. Sin2 300 + cos2 300 = 1
2. 2x – 6 = 18 3. 54 habis dibagi 3
4. Persegi adalah persegi panjang yang mempunyai panjang dan lebar sama 5. 100 : 5 = 20
6. Jumlah sudut dalam segitiga adalah 3600
7. Rumus luas persegi panjang adalah panjang dikalikan lebarnya. 8. Menara itu sangat tinggi
9. 2adalah bilangan rasional
10. Bilangan asli merupakan himpunan bagian dari bilangan bulat 11. Sekarang menunjukkan jam 09.00
12. Pelajar yang malas tidak suka belajar
Suatu kalimat merupakan bukan pernyataan jika kalimat tersebut tidak dapat ditentukan benar atau salahnya atau menggantung pengertian relative.
13. Kota besar menyerap tenaga kerja dari pedesaan
14. Keliling segitiga merupakan jumlah panjang ketiga sisi-sisinya 15. Udara di Kota Bandung sejuk sekali
Manakah dari kalimat-kalimat berikut yang merupakan kalimat terbuka? Tentukan penyelesaian dari himpunan penyelesaiannya!
16. Satu jam sama dengan 360 detik
17. x menit sama dengan 3 4jam 18. 2x2 – 7x – 15 = 0, x anggota Real
19. 2k +1 merupakan bilangan ganjil untuk k anggota bilangan cacah 20. 2k merupakan bilangan genap untuk k anggoata bilangan cacah 21. Untuk setiap bilangan riil x berlaku x < x2
22. cos x < 1 untuk 00 x 900 23. Ada bilangan prima yang genap 24. x2 < 3 – 2x, x anggota bilangan real 25. Satu windu sama dengan p hari
B. INGKARAN atau NEGASI
Dalam kehidupan sehari-hari kita sering menyangkal atau mengingkari sesuatu. Untuk mengingkari atau menyangkal sesuatu kita seringkali menggunakan kata “tidak”, “tidak benar” atau “bukan”. Misalnya ada seorang teman kamu mengatakan bahwa “Paus bernafas dengan insang”. Karena kamu mengetahui bahwa pernyataan temanmu itu salah, maka kamu menyangkal pernyataan tersebut dengan mengatakan
1. Tidak benar bahwa paus bernafas dengan insang, atau 2. Paus tidak bernafas dengan insang, atau
3. Paus bernafas bukan dengan insang, atau 4. Paus bernafas dengan paru-paru.
Keempat pernyataan baru diatas yang diperoleh dari menyangkal pernyataan awal disebut negasi. Negasi atau ingkaran dari pernyataan p ditulis p.
Nilai kebenaran dari suatu ingkaran selalu berlawanan dengan pernyataan semula. Jika “p” benar, maka ” p ” salah dan jika “p” salah maka “ p ” benar. Perhatikan table kebenaran berikut!
Tabel 1.1 Tabel kebenaran Negasi p p
B S S B
Catatan:
Metamatematika atau metalogika merupakan cabang dari logika yang berkaitan dengan kombinasi dan aplikasi symbol matematika. Metalogika juga berkaitan dalam penelusuran penalaran (pembuktian) teorema-teorema yang ada pada matematika
Metalogika ini sendiri terdiri dari beberapa prinsip dasar yang pada umumnya berkaitan dengan bukti-bukti dari ketetapan dalam merumuskan suatu teorema. Metalogika berkembang pada sekitar tahun 1800-an seiring dengan banyaknya usaha yang dilakukan metematikawan dalam merumuskan suatu teorema. Teorema itu sendiri diperoleh sebagai akibat dari aksioma yang tidak memerlukan pembuktian tersendiri.
Karena memiliki tingkat kesulitan yang tinggi, dalam merumuskan suatu teorema diperlukan usaha yang lama dan teliti sedemikian sehingga metematika pada saaat itu dipandang sebagai suatu buku cerita atau novel. Sampai pada akhirnya Whitehead dan Russel menerbitkan buku berjudul “Principia Mathematica”sekitar tahun 1925. sebagai contoh, ratusan halaman diperlukan untuk memperoleh suatu pernyataan sederhana seperti 1 + 1 = 2
C. PERNYATAAN MAJEMUK
Dua atau lebih pernyataan dapat digabungkan sehingga membentuk pernyataan baru yang disebut pernyataan majemuk. Penggabungan tersebut menggunakan kata hubung logika seperti dan ( ), atau ( ), jika …,maka …( ), serta …jika dan hanya jika …( )
Ada 4 jenis pernyataan majemuk, yaitu: 1. Konjungsi
2. Disjungsi 3. Implikasi 4. Biimplikasi
Suatu pernyataan dapt bernilai benar atau salah, sehingga ada dua kemungkinan nilai untuk setiap satu pernyataa, yaitu benar (B) atau salah (S). Oleh karena itu, untuk gabungan dua pernyataan p dan q (pernyataan majemuk) mempunyai komposisi nilai kebenaran seperti pada table berikut :
Table 1.2 Komposisi Pernyataan p q B B B S S B S S
Dengan kata lain suatu pernyataan majemuk tidak diharuskan memiliki hubungan antara komponen-komponennya. Hal itu merupakan sifat yang mendasar di dalam logika matematika.
1. KONJUNGSI
Konjungsi adalah pernyataan majemuk yang menggunakan kata hubung “dan” dilambangkan dengan “ ”. Konjungsi pernyataan p dan pernyataan q adalah
Suatu konjungsi akan mempunyai nilai benar, jika kedua pernyataannya benar. Tetapi jika salah satu atau kedua-duanya bernilai salah, maka konjungsi itu bernilai salah.
Tabel 1.3 Nilai Kebenaran p q
p q p q B B B B S S S B S S S S Contoh :
Tentukan nilai kebenaran dari konjungsi berikut :
a. P : Tan 300 = 1 3 2 (benar) q : 24 = 16 (benar) (p q) : tan 300 = 1 3 2 dan 2 4 = 16 bernilai benar
b. p : Surabaya ibukota provinsi Jawa Timur (benar) q : 7 adalah bilangan genap (salah)
(p q) : Surabaya ibukota provinsi Jawa Timur dan 7 adalah bilangan genap bernilai salah c. p : 225 habis dibagi 4 (salah)
q : 3 x 7 = 16 (salah)
(p q) : 225 habis dibagi 4 dan 3 x 7 = 16 bernilai salah
Catatan :
Pada konjungsi kata logika “dan” dapat diganti dengan “tetapi”, “walaupun”, dan “meskipun”.
2. DISJUNGSI
Disjungsi adalah pernyataan majemuk yang menggunakan kata hubung “atau” dan dilambangkan dengan “ ”. Disjungsi pernyataan p dan pernyataan q dinotasikan sebagai berikut :
Suatu konjungsi akan mempunyai nilai kebenaran salah jika kedua pernyataannya bernilai salah. Tetapi jika salah satu atyau kedua-duanya bernilai benar, maka disjungsi itu bernilai benar. Perhatikan table kebenaran untuk disjungsi berikut :
Tabel. 1.4 Nilai Kebenaran pv q
p q p v q B B B B S B S B B S S S Contoh :
Tentukan nilai kebenaran dari disjungsi berikut :
a. Semua bilangan prima adalah ganjil atau semua grafik fungsi kuadrat memotong sumbu x b. Ada bilangan asli yang terbesar atau jumlah sudut-sudut dalam segitiga adalah 1800 c. Semua persegi mempunyai sisi sama panjang atau besar sudut pusat lingkaran sama
dengan dua kali sudut keliling Jawab :
a. p : semua bilangan prima ganjil, berarti pernyataan bernilai salah
q : semua grafik fungsi kuadrat memotong sumbu x, pernyataan bernilai salah jadi p v q bernilai salah
b. p : ada bilangan asli yang terbesar , berarti pernyataan bernilai salah
q : jumlah sudut sudut dalam segitiga adalah 1800 , pernyataan bernilai benar jadi p v q bernilai benar
c. p : semua persegi mempunyai sisi sama panjang, pernyataan bernilai benar
q : besar sudut pusat lingkaran sama denngan dua kali sudut keliling, pernyataan bernilai benar
jadi p v q bernilai benar
3. IMPLIKASI
Implikasi atau pernyataan bersyarat adalah pernyataan majemuk dari pernyataan p dan pernyataan q yang berbentuk :
p disebut anteseden (sebab) dan q disebut konsekuen (akibat atau konklusi). Jadi, suatu implikasi menyatakan hubungan sebab-akibat walaupun pada dasarnya nilai kebenaran suatu pernyataan majemuk tiddak diharuskan ada hubungan antara komponen-komponen pembentuknya. Perhatikan table kebenaran berikut :
Tabel 1.5 Nilai kebenaran Implikasi
p q q q
B B B
B S S
S B B
S S B
Dari table diatas dapat kita lihat pada baris ke-2. Suatu implikasi bernilai salah bila anteseden bernilai benar dan konsekuennya bernilai salah. Jika anteseden bernilai salah , maka
p q dibaca : a. jika p, maka q b. bila p, maka q c. p hanya jika q d. q jika p
e. p syarat cukup bagi q f. q syarat perlu bagi p
nilai kebenaran dari implikasi itu bernilai benar. Jika konsekuennya bernilai benar, maka nilai kebenaran dari suatu implikasi bernilai benar.
Contoh :
Tentukan nilai kebenaran dari implikasi berikut:
a. Jika ada grafik fungsi kuadrat yang berpotongan dengan sumbu x, maka 16 bilsngsn genap b. Jika (ab)2 = a2b2, maka Lampung terletak di pulau Jawa
c. Jika 3log 9 = 3, maka 3 adalah bilangan genap
d. Jika Kudus ibukota provinsi Jawa Tengah, maka Semarang terletak di Jawa Tengah Jawab :
a. p : ada grafik fungsi kuadrat yang berpotongan dengan sumbu x, pernyataan bernilai benar q : 16 adalah bilangan genap, pernyataan bernilai benar
jadi p q bernilai benar
b. p : (ab)2 = a2b2 , pernyataan bernilai benar
q : Lampung terletak di pulau Jawa, pernyataan bernilai salah jadi p q bernilai salah
c. p : 2log 9 = 3 , pernyataan bernilai salah q : 3 adalah bilangan genap, pernyataan ssalah jadi p q bernilai benar
d. p : Kudus ibukota Jawa Tengah, pernyataan bernilai salah q : Semarang terletak di Jawa Tengah, pernyataan bernilai benar jadi p q bernilai benar
4. BIIMPLIKASI
Biimplikasi atau implikasi dua arah adalah pernyataan majemuk dari pernyataan p dan pernyataan q yang berbentuk
pq atau (pq)(qp) dibaca :
a. p jika dan hanya jika q
b. p syarat perlu dan cukup bagi q c. q syarat perlu dan cukup bagi p d. p jika q dan q jika p
Suatu bilangan bernilai benar bila kedua pernyataanya mempunyai nilai kebenaran yang sama. Perhatikan table kebenaran berikut :
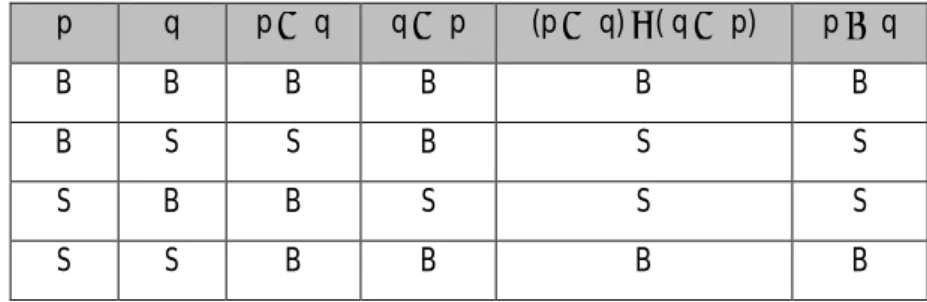
Tabel 1.6 Nilai Kebenaran Biimplikasi
p q p q q p (p q) ( q p) p q B B B B B B B S S B S S S B B S S S S S B B B B Contoh :
Tentukan nilai kebenaran dari biimplikasi berikut :
a. Surabaya ibukota provinsi Jawa Timur jika dan hanya jika Jakarta ibukota Negara Indonesia b. 1 + 1 = 3 jika dan hanya jika 2 x 2 = 5
c. Arema adalah klub sepakbola dari Malang dan hanya jika 22 = 8 Jawab :
a. p : Surabaya ibukota provinsi Jawa Timur, pernyataan bernilai benar q : Jakarta ibukota Negara Indonesia, pernyataan bernilai benar jadi p q bernilai benar
b. p : 1+1 = 3 , pernyataan bernilai salah q : 2 x 2 = 5 , pernyataan bernilai salah jadi p q bernilai benar
c. p : Arema adalah klub sepakbola dari Malang, pernyataan bernilai benar q : 22 = 8 , pernyataan bernilai salah
jadi p q bernilai salah
SOAL LATIHAN
Untuk soal no 1-2 tentukan nilai kebenaran dari (p q) untuk pernyataan-pernyataan berikut : 1. p : 2log 5 . 5 log 32 = 5
q : 8log 2 =1 2
2. p : Persamaan kuadrat yang akar-akarnya ½ dan 3 adalah 2x2 – 7x + 3 = 0 q : Nilai minimum dari f(x) = -2 sin x adalah -2
Untuk soal no 3-4 tentukan nilai kebenaran dari (pvq) untuk pernyataan-pernyataan berikut: 3. p : x2 + 5x +10 = 0 mempunyai dua akar real yang berlainan
q : Grafik fungsi kuadrat f(x) = x2 +4x +10 tidak memotong sumbu x
4. p : untuk m > 9
4, persamaan x
2
+ 3x + m = 0 mempunyai dua akar real yang berlainan
q : jumlah kuadrat akar-akar persamaan 8x2 – 6x + 1 = 0 adalah 5 10
Untuk soal no 5 – 6 tentukan nilai kebenaran dari (p q) untuk pernyataan-pernyataan berikut : 5. p : 23. 25 = 215
q : 2 2 + 32 = 5 2
6. p : grafik fungsi kuadrat f(x) = x2 – 3x + 2 memotong sumbu x di titik (1,0) dan (2,0) q : Daerah hasil fungsi kuadrat f(x) = x2 – 6x + 4 adalah
y y 5
Untuk soal no 7 – 8 tentukan nilai kebenaran dari (p q ) untuk pernyataan-pernyataan berikut. 7. p : grafik fungsi kuadrat f(x) = x2 + 3x +10 terletak di bawah sumbu x
q : grafik fungsi kuadart f(x) = -x2 + 4x – 10 terletak di atas sumbu x 8. p : log 15 + log 5 = log 20
q : log 15 – log 5 = log 3
Tentukan nilai x agar bentuk implikasi berikut benar. 9. Jika 2log (x – 1) < 1, maka x2 – 4x + 3 < 0
10. x 2 > 1 atau x > 6
Tentukan nilai x agar bentuk biimplikasi berikut benar. 11. x2 – 4x – 5 = 0 jika dan hanya jika x2 + x = 0
EKUIVALENSI, TAUTOLOGI, KONTRADIKSI, DAN KONJUNGSI 1. Ekuivalensi
Sampai dengan saat ini, kita telah mengetahui bahwa nilai kebenaran pernyataan majemuk merupakan fungsi dari nilai kebenaran pernyataan-pernyataan penyusunnya. Dalam bahasan berikut, kita akan mendefinisikan dua pernyataan majemuk yang ekuivalen.
Perhatikan table berikut ini :
Tabel 1.7 Tabel penyataan yang ekuivalen
p q p
q p v q p qB B S S B B
B S S B S S
S B B S B B
S S B B B B
Perhatikan bahwa nilai kebenaran dari pernyataan majemuk p v q dan p q adalah sama. Dengan demikian kita peroleh definisi berikut :
Berikut adalah beberapa ekuivalensi yang penting untuk diketahui. 1. Hukum Komutatif a. p v q q v p b. p q q p 2. Hukum Asosiatif a. p (q r) (p q) r b. p v (q v r) (p v q) v r 3. Hukum Distributif a. p (q v r) (p q) v (p r) b. p v (q r) (p v q) (p v r) 4. Hukum De Morgan a. (p q) p v
q b. (p v q) p
qDua pernyataan majemuk A dan B dikatakan ekuivalen jika memiliki nilai kebenaran yang sama dan dinotasikan dengan AB
5. Bentuk ekuivalensi lainnya : a. (p) p b. pq p v q c. pq qp d. p q (pq) (qp) e. (pq) p
qBerdasarkan nilai kebenarannya, suatu pernyataan majemuk dapat dibagi menjadi tiga macam, yaitu : tautology, kontradiksi dan kontingensi
2. Tautologi
Suatu pernyataan majemuk merupakan tautology, jika nilai kebenarannya selalu benar. Contoh :
Tabel 1.8 Tautologi
p p p v p
B S B
S B B
Selalu benar (tautologi) 3. Kontradiksi
Suatu pernyataan majemuk merupakan kontradiksi, jika nilai kebenarannya selalu salah. Contoh :
Tabel 1.9 Kontradiksi
p p p p
B S S
S B S
Selalu salah (kontradiksi)
4. Kontingensi
Suatu pernyataan majemuk merupakan kontingensi, jika nilai kebenarannya memuat benar dan salah.
Contoh :
Tabel 1.10 Kontingensi
p p p p
S B B
Memuat benar dan salah (kontingensi)
Soal Latihan
Untuk soal nomor 1 – 6, tunjukkan dengan menggunakan table kebenaran bahwa pernyataan berikut benar.
1. p v q q v q 4. p q (p q) (q p) 2. p v (q v r) (q v p) v r 5. p q p v q
3. p (q v r) (p q) v (p r) 6. p q q p
Untuk soal nomor 7 – 12, tentukan mana diantara pernyataan berikut yang termasuk tautologi, kontradiksi atau kontingensi.
7.
p (p q)
q 10. p v
(p q) (p r)
8. p v (p q) 11. (p q) (p v q ) 9. (p q) v (p q ) 12.
p (p q)
qE. Invers, Konvers, dan Kontraposisi Perhatikan implikasi berikut :
Jika MAlang ibukota Jawa Timur, maka Medan ada di pulau Sumatra Implikasi di atas bernilai benar.
Dari bentuk implikasi di atas, dapat dinyatakan menjadi pernyataan baru, diantaranya : a. Jika Malang bukan ibukota Jawa Timur, maka Medan bukan di pulau Sumatra b. Jika Medan berada di pulau Sumatra, maka Malang ibukota Jawa Timur c. Jika Medan bukan di pulau Sumatra, maka Malang bukan ibukota Jawa Timur. Misalnya pernyataan-pernyataan penyusun dari implikasidi atas dinyatakan sebagai
p : Malang ibukota Jawa Timur q : Medan ada di pulau Sumatra
maka pernyataan (a) – (c) dapat dinyatakan sebagai : a. p q
b. q p c. q p
Bentuk-bentuk di atas berturut-turut disebut invers, konvers, dan kontraposisi dari suatu implikasi p q. Dengan demikiann dari suatu implikasi kita dapat mengubahnya menjadi pernyataan baru yaitu konvers, invers, dan kontraposisi.
Contoh :
Nyatakan konvers, invers, dan kontraposisi dari pernyataan implikasi berikut :
“ Jika persamaan kuadrat mempunyai diskriminan sama dengan nol, maka akar-akarnya kembar” Jawab :
Misal
p : Persamaan kuadrat mempunyai diskriminan sama dengan nol q : Persamaan kuadrat mempunyai akar-akar kembar
a. Konvers : Jika persamaan kuadrat mempunyai akar-akar kembar, maka diskriminannya sama dengan nol
b. Invers : Jika persamaan kuadrat diskriminannya tidak sama dengan nol, maka persamaan kuadrat tidak mempunyai akar-akar kembar
c. Kontraposisi : Jika persamaan kuadrat tidak mempunyai akar-akar kembar, maka diskriminannya tidak sama dengan nol.
Soal Latihan
Untuk soal nomor 1 – 6, tentukan konvers, invers, dan kontraposisinya. 1. p (q v p ) 4. (p q) (q v p) 2 (p q) r 5.
q (q p) p 3. (p q) (p q) 6.
(p q) p
qUntuk soal nomor 7 – 10, tentukan konvers, invers, dan kontraposisinya dari pernyataan berikut : 7. Jika suatu bilangan adalah genap, maka bilangan itu tidak habis dibagi 3
8. Jika kuadrat suatu bilangan adalah positif, maka bilangan itu adalah genap 9. Jika ABC sama sisi, maka ABC sama kaki
10. Jika Kiki rajin belajar, maka ia akan lulus ujian 1. p q inversnya adalah p q 2. p q konversnya adalah q p
F. Pernyataan Berkuantor 1. Kuantor Universal ( Umum )
Perhatikan kalimat terbuka berikut ini! x2 + x + 1 > 0
Untuk menyatakan kalimat terbuka di atas menjadi sebuah pernyataan, terlebih dahulu kita tentukan penyelesaiannya. Dalam hal ini, penyelesaian dari x2 + x + 1 > 0 adalah x bilangan real. Denagn kata lain, jika kita membatasi daerah asal x sebagai bilangan real, maka x2 + x + 1 > 0 bernilai benar. Dengan demikian penyelesaian dari x2 + x + 1 > 0sama halnya dengan pernyataan :
Untuk setiap x bilangan real berlaku x2 + x + 1 > 0
Perrnyataan di atas tersebut pernyataan berkuantor universal (umum). Dalam hal ini, kata
setiap atau semua sebagai kuantor universal.
Secara umum, suatu kalimat terbuka p(x) dapat dinyatakan sebagai pernyataan dengan cara menambahkan kuantor universal sebelum kalimat terbuka tersebut dengan penyelesaian dari p(x) dibatasi pada pembicaraan semesta S, yaitu
2. Kuantor Eksistensial
Perhatikan kalimat terbuka berikut ini. x + 3 = 7
Penyelesaian dari x + 3 = 7 adalah x = 4. Dengan kata lain, jika kita mengganti x dengan 4, maka 4 +3 = 7 bernilai benar.
Analog dengan penjelasan di atas, jika kita membatasi daerah asal dari x sebagai bilangan real, maka terdapat x, yaitu x = 4 yang memenuhi x + 3 = 7 bernilai benar, atau dengan kata lain :
Terdapat x bilangan real sehingga x + 3 = 7
Pernyataan di atas merupakan pernyataan berkuantor ekstensial dengan kata terdapat atau ada atau beberapa sebagai kuantor eksistensial.
Secara umum, misalnya p(x) merupakan kalimat terbuka, maka penyelesaian dari p(x) dapat dinyatakan sebagai :
x S, p(x)
Dibaca : untuk setiap x anggota S berlaku p(x)
x S, p(x)
3. Ingkaran dari Pernyataan Berkuantor
Dalam bahasan sebelumnya, kita telah mempelajari ingkaran dari suatu pernyataan, yaitu : a. Ingkaran dari pernyataan p adalah p
b. Jika p bernilai benar, maka p bernilai salah c. Jika p bernilai salah, maka p bernilai benar
Aturan-aturan di atas juga berlaku untuk pernyataan berkuantor. Untuk lebih jelasnya perhatikan contoh berikut :
Contoh :
Diketahui pernyataan berkuantor universal p : Setiap makhluk hidup pasti akan mati. Tentukan ingkaran dan nilai kebenarannya. Jawab :
Pernyataan p merupakan pernyataan yang bernilai benar.
Dengan demikian, ingkaran dari p haruslah mengandung arti sebagai berikut : Ada makhluk hidup yang tidak akan mati.
Jadi, jelas bahwa p bernilai salah.
Dari contoh di atas, terlihat bahwa ingkaran dari pernyataan berkuantor universal adalah pernyataan berkuantor eksistensial. Secara matematis ditulis sebagai :
( x, p (x) ) x, p(x)
Dibaca : Ingkaran dari setiap x berlaku p(x) ekuivalen dengan ada x yang bukan p(x).
Soal Latihan
Untuk soal nomor 1 – 4, nyatakan pernyataan-pernyataan berikut dengan menggunakan kuantor universal atau eksistensial.
1. Setiap haji adalah muslim 2. Semua manusia adalah fana 3. Ada tumbuhan yang tidak berdaun
4. Tidak semua anak pandai diterima di sekolah favorit.
Untuk soal nomor 5 – 8, nyatakan dalam notasi kuantor yang tepat dari pernyataan yang diberikan, serta nyatakan juga negasinya.
5. Setiap ilmuwan terpelajar
6. Setiap orang yang jujur adalah bahagia 7. Tidak ada manusia yang fana
Untuk soal nomor 9 – 10, tentukan nilai kebenaran tiap pernyataan berikut untuk nilai x, dan y anggota bilangan bulat.
9. x, y, x2 + y2 + 2 0 10. x, y, 3x – y 4
6. PENARIKAN KESIMPULAN
Dalam kehidupan sehari-hari kita sering menghadapi berbagai persoalan dan kita harus menentukan keputusan yang tepat untuk menyelesaikan persoalan tersebut. Sebagai contoh, seorang hakim yang memutuskan perkara di pengadilan sangat berat tanggung jawabnya, tidak hanya bertanggung jawab kepada Negara dan bangsa, tetapi juga harus bertanggung jawab kepada Tuhan kelak di kemudian hari atas keputusan yang diambilnya.
Dalam logika matematika, penarikan kesimpulan dilakukan berdasarkan premis-premis penyusunnya sampai denngan diperoleh suatu kesimpulan (konklusi). Misalnya, premis-premis tersebut p1, p2, p3, …,pn dan kesimpulan yang diperoleh adalah q. Penarikan kesimpulan dapat
dilakukan berdasarkan konjungsi dari premis-premisny. P1 p2 p3 …pn yang menghasilkan
kesimpulan q. Secara umum :
Penarikan kesimpulan di atas dikatakan sah atau valid, jika konklusi q merupakan konsekuen dari premis-premisnya. Ertinya premis-premisnya benar, maka q benar, yaitu :
(p1 p2 … pn) q
Merupakan tautologi. Keabsahan penarikan kesimpulan di atas dapat diperiksa dengan menggunakan table kebenaran dari (p1 p2 … pn ) q.
Berikut akan kita pelajari beberapa metode penarikan kesimpulan, diantaranya modus ponens, modus tolens, dan silogisme.
p1 p2 . . pn kesimpulan : q
1. Modus Ponens
Penarikan kesimpulan dengan modus ponens dilakukan berdasarkan premis-premisnya yang berbentuk :
Modus ponens di atas dapat juga dinyatakan dalam bentuk implikasi berikut :
(pq)p q
Untuk menguji keabsahannya dapat dilakukan dengan menggunakan table kebenaran untuk
(pq)p q
, yang merupakan implikasi tautologi. Tabel 1.11 Nilai Kebenaran dan Modus Ponens
p q p q (p q) q (pq)p
qB B B B B
B S S S B
S B B B B
S S B S B
Terbukti bahwa (pq)p
qmerupakan implikasi tautology Contoh :Tentukan kesimpulan dari pernyataan-pernyataan berikut ini. 1. P1 : Jika Adi rajin belajar, maka ia akan naik kelas
P2 : Adi rajin belajar
2. P1 : Jika x bilangan real, maka x 0 P2 : x bilang real
Jawaban :
1. P1 : Jika Adi rajin belajar, maka ia akan naik kelas P2 : Adi rajin belajar
Kesimpulan : Adi naik kelas
2. P1 : Jika x bilangan real, maka x 0 P2 : x bilang real
Kesimpulan : x 0 Premis 1 : p q Premis 2 : p Kesimpulan : q
2. Modus Tolens
Penarikan kesimpulan modus Tolens dilakukan premis-premisnya yang berbentuk p q dan q yang menghasilkan konklusi p. Secara matematis dinyatakan sebagai :
Modus Tolens di atas dapat dinyatakan dalam bentuk implikasi yaitu :
(p q) q
pUntuk menguji keabsahannya dapat dilakukan dengan menggunakan table kebenaran dari
(p q) q
pTabel 1.12 Nilai Kebenaran dari Modus Tolens
p q p q
p q (p q) q
(p q) q
pB B B S S S B
B S S S B S B
S B B B S S B
S S B B B B B
Karena pernyataan
(p q) q
p merupakan tautology (pernyataan yang selalul benar), maka kesimpulan itu benar dan sah.Contoh :
Tentukan konklusi dari premis-premis berikut.
1. P1 : Jika ia seorang pemimpin, maka tindakannya terpuji P2 : Tindakannya tidak terpuji
2. P1 : Jika hewan adalah mamalia, maka ia bernafas dengan paru-paru P2 : Ikan bernafas tidak dengan paru-paru
Jawaban :
1. P1 : Jika ia seorang pemimpin, maka tindakannya terpuji P2 : Tindakannya tidak terpuji
Kesimpulan : Ia bukan seorang pemimpin Premis 1 : p q
Premis 2 : q Kesimpulan :
p2. P1 : Jika hewan adalah mamalia, maka ia bernafas dengan paru-paru P2 : Ikan bernafas tidak dengan paru-paru
Kesimpulan : Ikan bukan hewan mamalia
3. Silogisme
Penarikan kesimpulan dengan silogisme dilakukan berdasarkan premis-premisnya yang berbentuk p q dan q r yang menghasilkan kesimpulan p r. Secara matematis dinyatakan sebagai :
Jika dinyatakan dengan bentuk implikasi, maka pernyataan di atas dinyatakan sebagai
(p q) (q r)
(p q)Untuk menguji keabsahannya dapat dilakukan dengan menggunakan table kebenaran dari
(p q) (q r)
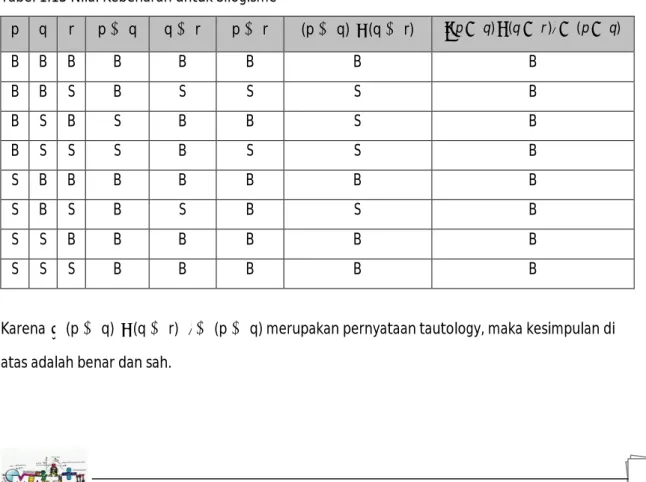
(p q)Tabel 1.13 Nilai Kebenaran untuk Silogisme
p q r p q q r p r (p q) (q r) (pq) ( qr)
(pq) B B B B B B B B B B S B S S S B B S B S B B S B B S S S B S S B S B B B B B B B S B S B S B S B S S B B B B B B S S S B B B B BKarena
(p q) (q r)
(p q) merupakan pernyataan tautology, maka kesimpulan di atas adalah benar dan sah.Premis 1 : p q Premis 2 : q r Kesimpulan : p r
Contoh :
Premis 1 : Jika kita sabar, maka kita disayang Tuhan Premis 2 : Jika kita disayang Tuhan, maka kita akan bahagia Kesimpulan : Jika kita sabar, maka kita akan bahagia.
Soal Latihan
Untuk soal nomor 1 – 5, tentukan sah atau tidak tiap argumen berikut. 1. P1 : Jika hari hujan, maka Adi membawa payung
P2 : Hari ini hujan
Kesimpulan : Adi membawa paying
2. P1 : Jika Aryo pemain basket, maka ia berpostur tinggi P2 : Aryo pemain basket
Kesimpulan : Aryo berpostur tinggi
3. P1 : Jika f(-x) = - f(x) untuk semua x R, maka f(s) fungsi ganjil P2 : f(x) fungsi linier
Kesimpulan : f(x) bukan fungsi ganjil
4. P1 : Jika Nanda seorang pramugari, maka ia berparas cantik P2 : Jika Nanda berparas cantik, maka ia disenangi banyak orang.
Kesimpulan : Jika Nanda seorang pramugari, maka ia disenangi banyak orang 5. P1: Jika x bilangan real, maka x2 0
P2 : x2 < 0
Kesimpulan : x bukan bilangan real.
Untuk soal nomor 6 – 10, periksalah keabsahan argumentasi yang diberikan. 6. P1 : p q 8. P1 : q q 10. P1 : p q P2 : q P2 : q r P2 : q v r p r p P3 : p r 7. P1 : p v q 9. P1 : p q P2 : p q P2 : p q
UJI KOMPETENSI
LOGIKA MATEMATIKA
A. Pilihlah jawaban yang benar
1. Kalimat-kalimat berikut merupakan pernyataan kecuali.... a. a2 – b2 = (a – b)(a + b)
b. 3 + 18 = 21 c. x + 3 = 9
d. Semua bilangan ganjil habis dibagi 3
e. Kota Yogyakarta pernah menjadi ibukota Republik Indonesia
2. Negasi dari pernyataan :”Semua tamu undangan berdiri saat pengantin tiba adalah ” a. Tidak semua tamu undangan duduk saat pengantin tiba
b. Tidak benar ada tamu undangan yang tidak berdiri saat pengantin tiba c. Semua tamu undangan duduk saat pengantin tiba
d. Tidak ada tamu yang duduk saat pengantin tiba
e. Ada tamu undangan yang tidak berdiri saat pengantin tiba
3. Diketahui p adalah pernyataan ”ia kaya” dan q adalah pernyataan ” ia kikir”. Pernyataan p q adalah
a. ia kaya atau kikir b. Ia kaya tetapi kikir c. Ia tidak kaya dan kikir d. Ia kaya atau tidak kikir e. Ia kaya walaupun tidak kikir
4. Pernyataan-pernyataan berikut yang bernilai benar adalah a. (m – n)2 = m2 + 2mn + n2 b. 3 + 8 = 16 – 7 c. Sin 300 = 1 2 atau 5324 d. Sin 300 = 1 2dan cos 60 0 = 1 3 2 e. a – b = b – a
5. Jika pernyataan p benar dan pernyataan q bernilai salah, maka pernyataan berikut yang benar adalah
b. p v q e. q p c. p q 6. p q
p q p v q p q (pvq) (p q) B B S S B S … B S S B B S … S B B S B S … S S B B S B …Nilai kebenaran yang tepat diisikan pada kolom (p v q) (p q) adalah
a. BBBS d. SSSB
b. SSBB e. SBBB
c. SBBS
7. Pernyataan (p v q) p bernilai benar jika a. p benar atau q benar
b. p benar dan q salah c. p salah dan q benar d. p salah dan q salah e. p salah atau q benar
8. Pernyataan berikut ekuivalen dengan “jika p benar, maka q salah “adalah a. p benar atau q salah
b. Jika q salah, maka p benar c. jika p salah, maka q benar d. jika q benar, maka p salah e. jika q benar, maka p benar
9. Perhatikan kalimat ”jika ia berusaha, maka ia berhasil”. Kontraposisinya adalah a. jika ia tidak berusaha, maka ia tidak berhasil
b. jika ia berusaha, maka ia berhasil
c. jika ia tidak berhasil, maka ia tidak berusaha d. ia tidak berusaha, tetapi ia berhasil
e. ia tidak berusaha, tetapi ia tidak berhasil
10. Negasi dari pernyataan “semua siswa uang lulus SMU ingin masuk perguruan tinggi” adalah a. tiada siswa yang lulus SMU ingin masuk perguruan tinggi
c. ada siswa yang lulus SMU tidak ingin masuk perguruan tinggi d. ada siswa yang lulus SMU ingin masuk perguruan tinggi
e. tidak semua siswa yang lulus SMU tidak ingin masuk perguruan tinggi 11. Konvers dari pernyataan ”jika ia sakit, maka tidak masuk sekolah” adalah
a. ia tidak masuk sekolah jika ia sakit b. ia sakit, jika ia tidak masuk sekolah c. jika ia masuk sekolah, maka ia tidak sakit d. jika ia tidak sakit, maka ia masuk sekolah e. jika ia tidak sakit, maka ia tidak masuk sekolah
12. Kontraposisi dari pernyataan :jika matahari terbit, maka semua ayam jantan berkokok” adalah a. jika beberapa ayam jantan tidak berkokok, maka matahari tidak terbit
b. jika beberapa ayam jantan berkokok, maka matahari tidak terbit c. jika beberapa ayam jantan berkokok, maka matahari terbit
d. jika matahari tidak terbit, maka beberapa ayam jantan tidak berkokok e. jika matahari terbit
13. Diantara pernyataan di bawah ini yang bukan kalimat terbuka adalah … a. 2a 10
b. 3x x
c. x2 x 5
d. Jika hari ini hujan maka Rudi tidak berangkat sekolah e. Ibu kota RI adalah Semarang
14. Negasi dari kalimat ”Semua siswa senang ketika guru tidak datang” adalah... I.Semua siswa tidak senang ketika guru tidak datang.
II.Tidak ada yang senang ketika guru tidak datang. III.Ada yang senang ketika guru datang.
IV.Ada siswa yang tidak senang ketika guru datang. V.Tidak ada siswa yang tidak senang ketika guru datang.
15. Negasi dari pernyataan ”Jika bulan ini turun hujan maka panen padi tahun ini akan melimpah ” adalah ..
a. Jika bulan ini tidak turun hujan maka panen padi tahun ini tidak melimpah b. Jika bulan ini tidak turun hujan maka panen padi tahun ini akan melimpah c. Bulan ini turun hujan tetapi panen padi tahun ini tidak melimpah
d. Bulan ini turun hujan dan panen padi tahun ini akan melimpah e. Bulan turun hujan dan panen padi tahun ini melimpah
16. Ingkaran pernyataan ”Jika harga bahan pokok turun maka semua orang senang.” adalah ... a. Harga bahan pokok turun dan semua orang senang.
b. Harga bahan pokok turun dan ada orang tidak senang.
c. Jika harga bahan pokok tidak turun maka semua orang tidak senang. d. Harga bahan pokok tidak turun dan semua orang tidak senang. e. Harga bahan pokok turun dan semua orang akan senang. 17. Ingkaran dari
p q
r adalah...A. (p~ ) ~q r D. ~p~q r B.
p ~ q
~r E.
~ p q
r C. p q ~ r18. Konvers pernyataan ”Jika sungai itu dalam maka sungai itu banyak ikannya.” adalah... a. Jika sungai itu tidak dalam maka sungai itu tidak banyak ikannya.
b. Jika sungai itu tidak banyak ikannya maka sungai itu tidak dalam. c. Jika sungai banyak ikannya maka sungai itu dalam.
d. Jika sungai itu tidak dalam maka sungai itu banyak ikannya. e. Sungai itu dalam tetapi sungai itu tidak banyak ikannya.
19. Invers pernyataan ”Jika bulan diatas laut maka laut pasang” adalah ... a. Jika bulan tidak diatas laut maka laut pasang.
b. Jika bulan tidak diatas laut maka laut tidak pasang. c. Jika laut pasang maka bulan diatas laut.
d. Jika laut tidak pasang maka bulan tidak diatas laut. e. Jika bulan diatas laut maka laut tidak pasang.
20. Kontraposisi pernyataan ”Jika tidak ada pejabat korupsi maka pembangunan berjalan lancar.” adalah ...
a. Jika tidak ada pejabat korupsi maka pembangunan tidak berjalan lancar. b. Jika ada pejabat korupsi maka pembangunan berjalan lancar.
c. Jika pembangunan berjalan lancar maka tidak ada pejabat korupsi. e. Jika ada pejabat korupsi maka pembangunan tidak berjalan lancar. e. Jika pembangunan tidak berjalan lancar maka ada pejabat korupsi.
21. Kontraposisi pernyataan ”Jika semua penjahat tertangkap maka guru negara dalam keadaan aman” adalah...
a. Jika negara dalam keadaan aman maka semua penjahat tertangkap. b. Jika negara tidak dalam keadaan aman maka semua penjahat tertangkap. c. Jika negara tidak dalam keadaan aman ada penjahat yang tidak tertangkap.
d. Jika ada penjahat yang tidak tertangakap maka guru negara tidak dalam keadaan aman. e. Jika ada penjahat yang tidak tertangkap maka negara dalam keadaan aman.
22. Invers dari penyataan
p~q
padalah ... a. p
p~q
b. ~ p
p q
c.
~ p q
p d.
~p q
~p e.
p~q
~p23. Premis I : ”Jika Rudi jual motor maka ia berangkat sekolah naik kendaraan umum”. Premis II : ”Rudi berangkat sekolah tidak naik kendaraan umum”.
Kesimpulan dari argumen diatas adalah... a. Rudi jual motor.
b. Rudi berangkat sekolah tidak naik kendaraan umum. c. Rudi berangkat sekolah naik motor.
d. Rudi tidak jual motor.
e. Rudi jual motor dan naik kendaraan umum.
24. Premis I : ”Jika Yuli rajin menabung maka ia orang yang hemat.” Premis II : ”Yuli rajin menabung.”
Kesimpulannya adalah ..
a. Yuli rajin menabung tetapi bukan orang yang hemat. b. Yuli bukan orang hemat.
c. Yuli kadang-kadang hemat d. Yuli rajin menabung. e. Yuli orang hemat
25. Premis I : ”Jika Romi rajin belajar maka ia pandai.” Premis II : ”Jika Romi pandai maka ia akan naik kelas.” Kesimpulannya adalah...
a. Jika Romi pandai maka ia naik kelas. b. Jika Romi rajin belajar maka ia pandai. c. Jika Romi rajin belajar maka ia naik kelas.
d. Jika Romi tidak rajin belajar maka ia tidak naik kelas. e. Jika Romi rajin belajar maka ia tidak naik kelas.
a. BBBB b. BBBS c. BBSS d. BSSS e. SBBB
27. Pernyataan ~p ~qekivalen dengan... a. qp
b. ~ {pq) c. ~ qp
d. p ~q
e. q~p
28. Kontraposisi dari pernyataan majemuk p → ( p V ~q ) adalah …. a. ( p V ~q ) → ~p
b. (~p Λ q ) → ~p c. ( p V ~q ) → p d. (~p V q ) → ~p e. ( p Λ ~q ) → ~p
29. Invers dari pernyataan p → ( p Λ q ) a. (~p Λ ~q ) → ~p b. (~p V ~q ) → ~p c. ~p → (~p Λ ~q ) d. ~p → (~p Λ q ) e. ~p → (~p V ~q ) 30. Diketahui pernyataan :
I. Jika hari panas, maka Ani memakai topi
II. Ani tidak memakai topi atau ia memakai payung III. Ani tidak memakai payung
Kesimpulan yang sah adalah …. a. Hari panas
b. Hari tidak panas c. Ani memakai topi
d. Hari panas dan Ani memakai topi e. Hari tidak panas dan Ani memakai topi