ANALISA KESTABILAN PERSAMAAN GERAK ROKET TIPE RKX-200 LAPAN DAN SIMULASINYA

(1)

Mohammad Rifa’i, Subchan, Ph.D, DR. Erna Apriliani, M.si

Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Teknologi Sepuluh Nopember Surabaya

Jl. Arief Rahman Hakim, Surabaya 60111

E-mail:

subchan@matematika.its.ac.id

,

april@matematika.its.ac.id

Abstrak – Roket kendali merupakan wahana terbang yang digunakan dalam berbagai misi tertentu, salah satunya adalah sebagai sistem pertahanan wilayah atau negara. Secara umum, roket kendali mempunyai enam derajat kebebasan yang terdiri dari tiga gerak translasi dan tiga gerak rotasi yang memungkinkan roket bergerak tidak stabil. Sistem persamaan gerak roket merupakan model persamaan nonlinear. Untuk itu, dibutuhkan suatu hampiran persamaan nonlinear dengan bentuk linear, yaitu proses linearisasi. Pada tugas akhir ini, dibahas tentang proses linearisasi sistem persamaan gerak roket. Kemudian, dilakukan analisa kestabilan sistem persamaan gerak roket menggunakan kriteria kestabilan Ruth- Hurwitz. Selanjutnya, dilakukan uji kestabilan sistem dari berbagai output serta mengambil data parameter terbang pada roket tipe RKX-200 LAPAN yang dianalisa dari beberapa kondisi kecepatan. Hasil dari penelitian tugas akhir ini diketahui bahwa sistem persamaan gerak roket pada kecepatan mach 0.2, mach 0.5, mach 1.0 dikatakan sistem telah stabil. Sedangkan pada analisa kecepatan diatas kecepatan mach 1.0 diketahui bahwa sistem persamaan gerak roket diketahui tidak stabil.

Kata Kunci--kriteria kestabilan Routh-Hurwitz, linearisasi, persamaan nonlinear, roket RKX-200 LAPAN.

I. PENDAHULUAN

Roket merupakan salah satu teknologi yang penting untuk dikembangkan, utamanya teknologi bidang kendali roket. Banyak negara yang mengembangkan teknologi tersebut untuk kepentingan kemajuan negaranya, termasuk Indonesia. Sebagai negara yang berkembang, Indonesia sangat membutuhkan teknologi ALUSISTA yang lengkap untuk menunjang kemajuan dan kemandirian negara. Salah satunya, adalah roket kendali.

Roket kendali merupakan wahana terbang yang dapat digunakan pada berbagai misi tertentu, misalnya untuk kepentingan ilmiah dan pertahanan keamanan suatu negara. Roket kendali yang dibahas dalam hal ini adalah roket RKX-200 LAPAN. Roket ini didesain dengan menggunakan dua stage (fase), yaitu boosting dan sustaining. Fase boosting adalah fase yang dimulai sejak awal peluncuran roket sampai ketinggian tertentu. Setelah itu roket mengalami separasi (pemisahan) dan motor roket akan dinyalakan. Pada saat

motor roket menyala fase inilah yang dinamakan fase sustaining. Dalam fase sustaining, roket akan dikendalikan untuk mencapai target atau sasaran tertentu [3]. Pada roket kendali terdapat gaya dorong, sistem penargetan, dan sistem pengendalian. Sistem kendali roket dapat bekerja dengan baik, apabila semua subsistem mampu bersinergi secara maksimal. Sehingga mampu mencapai hasil yang diharapkan.

Secara umum, roket memiliki enam derajat kebebasan gerak (six freedom of degree) yang terdiri dari tiga gerak translasi dan tiga gerak rotasi. Sehingga memungkinkan roket bergerak tidak stabil. Untuk itu, diperlukan sistem persamaan gerak roket yang stabil. Sistem persamaan gerak roket merupakan persamaan nonlinear tiga dimensi yang rumit dan kompleks. Dalam analisa lebih lanjut diperlukan proses hampiran persamaan nonlinear dengan bentuk linear yaitu proses linearisasi Persamaan gerak roket terdiri dari dua bagian, yaitu gerak longitudinal dan gerak lateral-directional [5]. Pada gerak longitudinal ini terdapat dua gerak translasi dan satu gerak rotasi. Sedangkan pada gerak lateral directional terdapat dua gerak rotasi dan satu gerak translasi. Gerakan roket ini ditentukan oleh sirip yang berada pada tail (ekor roket), meliputi elevator, rudder dan aileron. Sirip-sirip inilah yang nantinya mengontrol pergerakan suatu roket.

Pada tugas akhir ini, dibahas tentang linearisasi persamaan nonlinear gerak roket serta analisa kestabilan sistem persamaan gerak roket pada fase sustaining menggunakan kriteria kestabilan Routh-Hurwitz. Kemudian dilakukan uji kestabilan dari sistem persamaan gerak roket. Parameter yang digunakan dalam uji kestabilan ini, adalah parameter roket RKX-200 LAPAN yang dianalisa pada kondisi kecepatan terbang yang bervariasi.

II. TINJAUAN PUSTAKA

A. Geometri Roket RKX-200 LAPAN

Roket RKX-200 LAPAN merupakan roket kendali yang mempunyai diameter 200 mm. RKX-200 LAPAN ini merupakan salah satu roket yang disiapkan untuk menjadi guided missile (peluru kendali). Roket RKX-200 LAPAN mempunyai empat tail fin, yang masing-masing terdiri dari

ANALISA KESTABILAN PERSAMAAN GERAK ROKET

(2)

dua tail fin vertikal dan horizontal yang berfungsi sebagai sirip kendali. Sirip kendali roket ada tiga jenis, yaitu elevator, rudder dan aileron. Kontrol elevator merupakan kontrol yang mengatur gerakan naik turun hidung roket. Tail yang bekerja pada kontorl elevator adalah tail fin horizontal. Kontrol rudder merupakan kontrol yang dapat membelokkan hidung roket ke kanan dan ke kiri. Tail yang bekerja pada kontrol rudder adalah tail fin vertikal. Sedangkan kontrol aileron merupakan kontrol yang mengatur gerak roll (memutar) roket.

Berikut ini adalah gambaran umum bentuk RKX-200 LAPAN [4]

0

Gambar 1. Bentuk roket RKX-200 LAPAN [4]

B. Model Persamaan Gerak Roket

Persamaan gerak roket merupakan model persamaan nonlinear. Jika diasumsikan roket sebagai benda tegar, maka roket mempunyai enam derajat kebebasan. Berdasarkan hukum kedua Newton, persamaan gerak roket dapat dibagi menjadi dua, yaitu persamaan gaya dan persamaan momen.

) (mV dt d m F (1) ) (H dt d 



₍₂₎

Kemudian dengan mentrasnformasi persamaan gaya dan momen dalam acuan koordinat sumbu bumi, persamaan gerak roket secara umum dapat dituliskan sebagai berikut

)

cos

(

)

sin

cos

(

)

sin

(









g

uq

vp

w

m

F

g

pw

ur

v

m

F

vr

qw

u

m

F

z y x























(3) qr I I I pq p I r I N I I pr r p I q I M I I qr pq r I p I L xz xx yy xz zz zz xx xz yy yy zz xz xx                ) ( ) ( ) ( ) ( ) ( 2 2      (4) Untuk membantu penyelesaian persamaan (3) dan (4) diperlukan persamaan kecepatan anguler yang ditransformasi dari koordinat sumbu bumi ke koordinat sumbu badan.

φ

θ

ψ

φ

θ

r

φ

θ

ψ

φ

θ

q

θ

ψ

φ

p

cos

sin

cos

sin

















(5)

III. HASIL DAN PEMBAHASAN

A. Lineariasi

Persamaan nonlinear gerak roket termasuk persamaan yang rumit, sehingga perlu dilakukan penyederhanaan untuk kepentingan analisa. Dalam hal ini, persamaan nonlinear akan dilinearisasi menggunakan teori gangguan kecil dititik kesetimbangannya. Teori gangguan kecil ini mengasumsikan bahwa gerak roket terdiri dari pergeseran kecil dari kondisi terbang stabil. Dengan kata lain, semua pvariabel dari persamaan gerak roket diganti dengan nilai kesetimbangan ditambah dengan gangguan.

Ketika gangguan dari kondisi rata-rata dianggap sangat kecil, maka berlaku sebagai berikut [2]:

a. perkalian (product) antar gangguan dianggap nol.

b. sinus dari sudut gangguan dianggap sama dengan sudut gangguan, sedangkan cosinus dari sudut gangguan dianggap sama dengan satu.

Sehingga persamaan (3)-(5) berubah menjadi

] 0 0 0 0 0 cos [              m u w q q w v r r v g x F  w p p w u r r u v m y F            0 0 0 0 [ 

cos cos sin sin ]

0 0 0 0 φ Δφ g θ φ Δθ θ g   u q q u v p p v w m z F            0 0 0 0 [ 

cos sin sin cos ]

0 0 0 0 φ φ g θ φ θ θ g    

(6) ) )( ( ₀ ₀ _zz _yy xz xx p I r q r r q I I I L           

Ixz(p0qq0p) ) ( 2 ) )( (p0 r r0 p I I I p0 p r0 r q I M yy     xx zz  xz      ) )( ( ₀ 0 yy xx xz zz r I p p q q p I I I N           

Ixz(q0rr0q) (7) 0 0 sin cos          p 0 0 0 0

0sin  cos cos sin

    

 q

0(cos0cos0sin0sin0) 0 0 0

0 sin cos cos

cos      

    

 r

0(cos0sin0sin0cos0) ₍₈₎

Persamaan (6)-(7) merupakan persamaan gerak roket terlinearisasi dengan menghilangkan persamaan pada kondisi awal setimbang (trim). Pada kasus tertentu perlu dipertimbangkan kondisi penerbangan sederhana, misalnya pkondisi terbang lurus, symetric, flying with wings level,

terbang setimbang atau ideal [1]. Hal ini mengakibatkan

0 0 0 0 0 0 0 0 0 0 0 v  p q r p q r  

_

_



.

(3)

] sin [ ] cos [ ] cos [ 0 0 0 0 0 0 0                              g q u w m F g p w r u v m F g q w u m F z y x    (9) p I r I N q I M r I p I L xz zz yy xz xx                  

F

(10) 0 0 cos sin                     r q I q p yy (11) Persamaan (9) dan (10) merupakan persamaan gerak untuk perubahan kecil disekitar nilai kesetimbangannya atau disebut persamaan gangguan dari gaya dan momen.

Gangguan dalam analisa gerak roket sangat berpengaruh pada gaya dan momen roket. Gangguan-gangguan ini secara tidak langsung ditransformasi ke dalam bentuk fungsi gangguan sebagai berikut [3]

) , , , , ( ) , , , , ( ) , , , , ( ) , , , , ( ) , , , ( ) , , ( 6 5 4 3 2 1 a r e a r e z r y e x r p v f N q w w u f M r p v f L q w w u f F r p v f F w u f F



                                        

Fungsi gangguan tersebut dideretkan menggunakan ekspansi Deret Taylor seperti berikut :

e e z F q q z F w w z F w w z F u u z F z F r r y F r r y F p p y F v v y F y F e e x F w w x F u u x F x F                                                            a a N r r N r r N p p N v v N N e e M q q M w w M w w M u u M M a a L r r L r r L p p L v v L L                                                                      

Sehingga diperoleh persamaan diferensial orde pertama gerak roket sebagai berikut :

e e xw xu F g F F u     _   cos ₀ p w r u r F p F v F v yr yp yv           0 0  r r y F g   _   0 cos q u q F w F w F u F w zq w z zw zu           0   

_e e z F g   _   0 sin ₍₁₂₎ r r xx xz r p v _I r L I r L p L v L p         _   

a a L     e e q w w u u M w M w M q M M q                r r zz xz r p v _I p N I r N p N v N r              

N _a a     (13) Kemudian, dari data terbang aerodinamika tidak semua parameter terbang berpengaruh signifikan. Parameter yang rdiabaikan adalah yr yp w z zq F F F F , _, , [2].

Dengan menggunakan sumbu kestabilan (keseimbangan) roket, w₀dapat dianggap nol. Sedangkan



₀ sama dengan sudut jalur terbang



₀ jika sudut serang



₀ diasumsikan no

l. Sehingga persamaan gerak roket menjadi berikut :

e e x xw xu u F w g F F u             0 0 u F u g r F r r y yv               e e z zw zu u F w u q F F w       _   0  a a r r p p L r L r L L L p _     _   _   w F M M u F M M q zw w w zu w u       ( _ ) ( _ )

M M u q w q  ( ) 0  e e z F w M e M_  _  ( _ ) a a r r N N r N p N N r                    

(14)

dengan : q

p

B. Pembentukan Matriks State Space

Persamaan (14) dapat dibentuk menjadi matriks state space yang dibagi menjadi dua bagian, yaitu persamaan longitudinal dan persamaan lateral-directional. Adapun martiks state space-nya adalah sebagai berikut :

(4)

 

_e e z w e e z e x q w zw xw u zu xu F M M F F q w u g M u M F F M F F q w u                                                                                     0 ) ( 0 0 0 1 ~ 0 0 ~ 0 ~ 0      dengan : ~ ( ) zu w u u M M F M   _

~ ( ) zw w w w M M F M   

~ ( ) 0 u M M M w q q   

Dari matriks state space diatas, terlihat bahwa variabel keadaannya terdiri dari kecepatan linear u, kecepatan linear w, laju sudut angguk q, sudut angguk . input dari sistem tersebut adalah defleksi sirip elevator

e



.

Sedangkan Output yang diharapkan adalah sebagai berikut

:

Tabel 1

. Output persamaan longitudinal

No Output Matriks Output

1. u



1 0 0 0



2. w



0 1 0 0



3. q



0 0 1 0



4. 



0 0 0 1



b.matriks state space persamaan lateral-directional

                                                                                                     a r a a r r y r r p p yv N L r N L u F r p u g N L N L N L F r p              0 0 0 0 0 0 0 1 1 0 0 0 0     dengan : ( ) v v xx xz v _I N L I L  

( ) v v zz xz v _I L N I N  

( ) p p xx xz p _I N L I L  

( ) p p zz xz p _I L N I N  

( ) r r xx xz r _I N L I L  

( ) r r zz xz r _I L N I N  

( ) a a xx xz a L N I I L_  _  _

( ) a N a L zz I xz I a N_  _  _

) ( r r xx xz r L N I I L_  _  _

( ) r r N L zz I xz I r N_  _  _

0 u L L v   

N Nvu0

Pada matriks state space di atas, terlihat bahwa yang menjadi variabel state adalah sideslip angles



,laju sudut yawp, laju sudut rollr, serta sudut yaw



. Input dari sistem tersebut adalah defleksi sirip rudder

r

 dan aileron



_a. Sedangkan Output yang diharapkan adalah sebagai berikut :

Tabel 2. Output persamaan lateral-directional No Output Matriks Output

1. 





1 0 0 0



2. p



0 1 0 0



3. r



0 0 1 0



4. 





0 0 0 1



C. Analisa Kestabilan Persamaan Gerak Roket

Hal pertama yang harus dilakukan untuk menganalisa kestabilan suatu sistem adalah mencari nilai eigen pada masing-masing persamaan gerak roket.

a. kestabilan pada gerak longitudinal Matriks A dari gerak longitudinal adalah

                  0 0 0 1 ~0 0 0 ~ 0 ~ g M u M F x F M F F A q w zw w u zu xu

dengan menggunakan rumus det(



IA)0diperoleh persamaan karakteristik berikut :

) ~ ( 3 4 xu zw q F F M      ) ~ ~ ~ ( 2 0 xu q xu zw xw zu w zw qF M u F M F F F F M      ) ~ ~ ~ ~ ~ ( 0 0 xw zu q u xw u w xu q zw xuF M F M u F F M M F u gM F     

 ( ~  ~ )0 u zw w zuM F M F g

maka

menjadi bentuk umum persamaan polinomial orde

4 sebagai berikut :

0 4 3 2 2 3 1 4 0 a a a a  a     dengan : 1 0  a

( ~ ) 1 Mq Fzw Fxu a    

(~ ~ ~ ) 0 2 MqFzw Mwu FxuMq FxuFzw FxwFzu a     

) ~ ~ ~ ~ ~ ( 0 0 3 FxuFzwMq FxuMwu FxwFzuMq MuFxwu gMu a     

) ~ ~ ( 4 g FzuMw FzwMu a  

Selanjutnya untuk mendapatkan akar-akar karakteristik (nilai eigen ) dari polinomial derajat 4 tersebut, kemudian

(5)

digunakan kriteria kestabilan Routh-Hurwitz untuk menentukan kestabilannya.

Tabel 3. Routh-Hurwitz pada gerak longitudinal

0 0 0 0 0 0 4 3 2 1 3 1 4 2 0 0 1 2 3 4 b b b b a a a a a      dengan , 1 3 0 2 1 1 _a a a a a b  

a b  2

, 1 1 2 3 1 3 _b a b a b b  

4 2 4 a b b  

Menurut kriteria Routh-Hurwitz sistem dikatakan stabil, jika semua suku-suku pada kolom pertama bernilai sama yaitu positif atau negatif semua. Sehingga, sistem pada persamaan gerak longitudinal dikatakan stabil menurut kriteria kestabilan Routh-Hurwitz, apabila memenuhi : 1. (~   )0 xu zw q F F M 2. (~ 2 )( ) ( 2 ~ )( ~ ) 0 zw q w xu zw xu zu zw q F F F F F M u F M M      ] ~ 2 ) ~ [( 2 ) ( ~ 0 zw q xu xu q zw xw u _F M F F M F g u F M      3. u zw w zuM F M F ~  ~ 4. [( (~ ) ~ ~ )] 0 xu q xw zu w xu q zw M F M u F M F F F     ] ~ ) ~ ~ ( ) ~ ~ ( [ 0 0 xw zu q u u w q zw xu F M M u F F M M u gM F      ) ~ )( ~ ~ ( xu zw q u zw w zwM F M M F F F g     ) ~ 2 ] ~ ) ~ ~ ( ) ~ ~ ( [ 0 0 xu zw q u u q zu xw w q zw xu F F M M g u M M F F u M M F F        

b. kestabilan pada gerak lateral-directional Matriks A dari gerak lateral-directional adalah

                        0 0 0 0 0 1 1 0 0 u g r N r L p N p L β N β L yv F A

diperoleh persamaan karakteristik sebagai berikut :

) ( 3 4 yv p r L F N   



2(L N L N F N F L N_) p yv r yv p r r p           

( ) 0     L u g N L N L N L F N L F p p p r yv r p yv               ( ) 0 0        r rN L N L u g  

Kemudian dengan menggunakan kriteria kestabilan Routh-Hurwithz seperti dijelaskan pada bagian sebelumnya, sistem persamaan gerak lateral-directional dikatakan stabil apabila memenuhi : 1. (      )0 yv p r L F N 2. ( 2 )( ) ( 2 )( ) p r r p yv yv r p N N F F N N N L L  _          ] 2 ) [( 2 ) ( 0 r yv p yv p r p _N F L F L N u g N L            _ 3. r rN L N L _  _  4. [L (N F ) L N F N N_] r yv p r yv r p           ) ( 2 ] ) ( ) ( [ ) )( ( 0 0 yv p r p p p r r p yv yv p r r r F L N N L u g N L N L N L F F L N N L N L u g                                ] ) ( ) ( [ 0   _u L N g N L N L N L yv F p p p r r p            

D. Uji Kestabilan Sistem

Uji kestabilan dalam tugas akhir ini menitikberatkan pada uji titik terbang yang ditentukan. Titik yang dimaksud disini adalah kecepatan roket untuk tipe roket RKX-200 LAPAN.

Kecepatan yang dianalisa antara lain pada mach 0.2, mach 0.5, mach 1.0, mach 1.1 mach 1.3, mach 1.5. Berikut ini adalah contoh grafik simulasi yang menggambarkan suatu kestabilan atau ketidakstabilan.

 Gerak longitudinal dengan output kecepatan linear sumbu-x 0 5 10 15 20 25 30 35 -5 -4 -3 -2 -1 0 Respon Sistem Waktu (detik) Kece pa ta n Li nea r Sum bu-x mach 0.2 mach 0.5 mach 1.0

Gambar 1. Grafik kecepatan linear sumbu-x pada mach 0.2, mach 0.5, mach 1.0

(6)

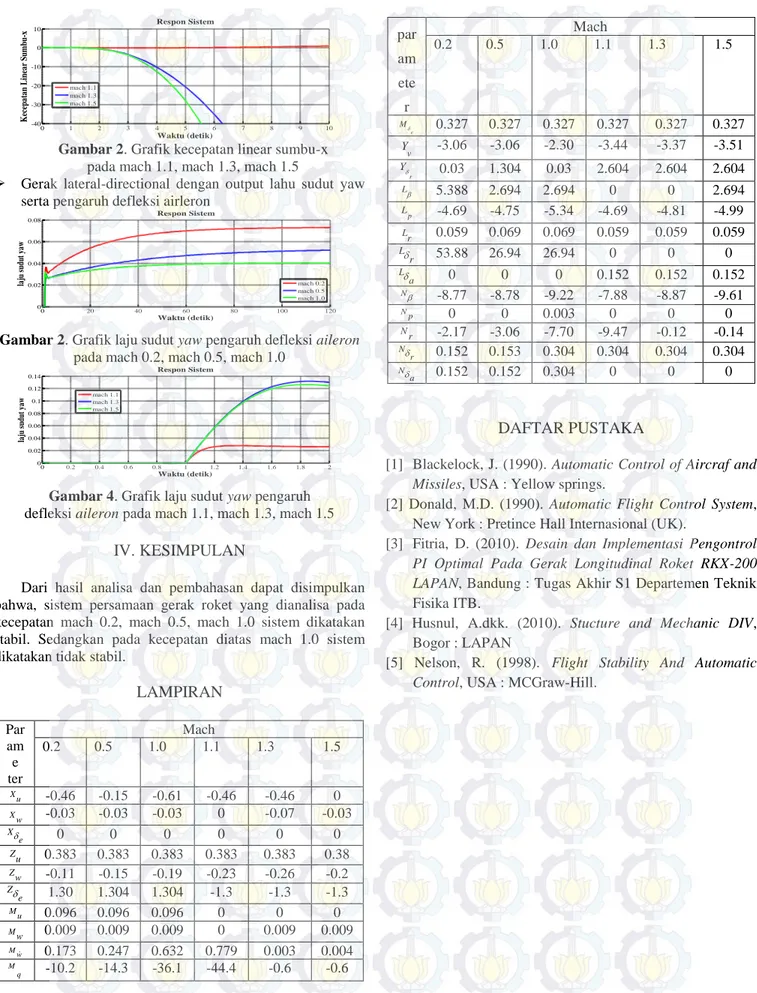
0 1 2 3 4 5 6 7 8 9 10 -40 -30 -20 -10 0 10 Respon Sistem Waktu (detik) Kece pa ta n Li nea r Sum bu-x mach 1.1 mach 1.3 mach 1.5

Gambar 2. Grafik kecepatan linear sumbu-x pada mach 1.1, mach 1.3, mach 1.5

 Gerak lateral-directional dengan output lahu sudut yaw serta pengaruh defleksi airleron

0 20 40 60 80 100 120 0 0.02 0.04 0.06 0.08 Respon Sistem Waktu (detik) la ju sudu t ya w mach 0.2 mach 0.5 mach 1.0

Gambar 2. Grafik laju sudut yaw pengaruh defleksi aileron pada mach 0.2, mach 0.5, mach 1.0

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 Respon Sistem Waktu (detik) la ju sudu t ya w mach 1.1mach 1.3 mach 1.5

Gambar 4. Grafik laju sudut yaw pengaruh defleksi aileron pada mach 1.1, mach 1.3, mach 1.5

IV. KESIMPULAN

Dari hasil analisa dan pembahasan dapat disimpulkan bahwa, sistem persamaan gerak roket yang dianalisa pada kecepatan mach 0.2, mach 0.5, mach 1.0 sistem dikatakan stabil. Sedangkan pada kecepatan diatas mach 1.0 sistem dikatakan tidak stabil.

LAMPIRAN

Par am e ter Mach 0.2 0.5 1.0 1.1 1.3 1.5 u X _-0.46 _-0.15 _-0.61 _-0.46 _-0.46 ₀ w X -0.03 -0.03 -0.03 0 -0.07 -0.03 e X_ ₀ ₀ ₀ ₀ ₀ ₀ u Z _0.383 _0.383 _0.383 _0.383 _0.383 _0.38 w Z _-0.11 _-0.15 _-0.19 _-0.23 _-0.26 _-0.2 e Z_ _1.30 _1.304 _1.304 _-1.3 _-1.3 _-1.3 u M _0.096 _0.096 _0.096 ₀ ₀ ₀ w M 0.009 0.009 0.009 0 0.009 0.009 w M_ _0.173 _0.247 _0.632 _0.779 _0.003 _0.004 q M _-10.2 _-14.3 _-36.1 _-44.4 _-0.6 _-0.6 par am ete r Mach 0.2 0.5 1.0 1.1 1.3 1.5 e M_ _0.327 _0.327 _0.327 _0.327 _0.327 _0.327 v Y -3.06 -3.06 -2.30 -3.44 -3.37 -3.51 r Y_ _0.03 _1.304 _0.03 _2.604 _2.604 _2.604  L _5.388 _2.694 _2.694 ₀ ₀ _2.694 p L _-4.69 _-4.75 _-5.34 _-4.69 _-4.81 _-4.99 r L 0.059 0.069 0.069 0.059 0.059 0.059 r L_ _53.88 _26.94 _26.94 ₀ ₀ ₀ a L_ ₀ ₀ ₀ _0.152 _0.152 _0.152  N _-8.77 _-8.78 _-9.22 _-7.88 _-8.87 _-9.61 p N ₀ ₀ _0.003 ₀ ₀ ₀ r N _-2.17 _-3.06 _-7.70 _-9.47 _-0.12 _-0.14 r N_ _0.152 _0.153 _0.304 _0.304 _0.304 _0.304 a N_ _0.152 _0.152 _0.304 ₀ ₀ ₀

DAFTAR PUSTAKA

[1] Blackelock, J. (1990). Automatic Control of Aircraf and Missiles, USA : Yellow springs.

[2] Donald, M.D. (1990). Automatic Flight Control System, New York : Pretince Hall Internasional (UK).

[3] Fitria, D. (2010). Desain dan Implementasi Pengontrol PI Optimal Pada Gerak Longitudinal Roket RKX-200 LAPAN, Bandung : Tugas Akhir S1 Departemen Teknik Fisika ITB.

[4] Husnul, A.dkk. (2010). Stucture and Mechanic DIV, Bogor : LAPAN

[5] Nelson, R. (1998). Flight Stability And Automatic Control, USA : MCGraw-Hill.