Double-edged population monotonicity of Walrasian
equilibrium—a note on the nature of competition
a ,* 1 ,b
Murat R. Sertel , Muhamet Yıldız
aDepartment of Economics, Bogazic¸i University, Bebek, 80815 Istanbul, Turkey˘ ~ b
Graduate School of Business, Stanford University, Stanford, USA
Received 22 January 1997; received in revised form 30 September 1997; accepted 3 April 1998
Abstract
We show that extending an economy by admitting new agents of an incumbent type has a double-edged effect on the Walrasian utilities of the original agents so long as substitution effect dominates income effect on the average (i.e. the inner product of price change and the change in aggregate demand is nonpositive) for the original economy at the Walrasian prices of the original and the extended economies: agents of the entrants’ type are if anything hurt, and some others are if anything better off. We also show that, if aggregate demand in the subeconomy consisting of incumbent agents whose type is not replenished satisfies the generalized axiom of revealed preferences at these prices, then the converse is also true, so that the double-edged monotonicity in question is then characterized by the mentioned domination of substitution over income effect.
1999 Elsevier Science B.V. All rights reserved.
Keywords: Walrasian equilibrium; Double-edged population monotonicity
JEL classification: D41; D511
1. Introduction
For some economic solution concepts, population solidarity of the solution (i.e. the quality of all incumbent agents’ welfare moving in the same direction under such a solution as new agents join) is too coarse a notion, for under these solutions some types
*Corresponding author. Tel.: and fax:190-212-277-5336.
E-mail address: [email protected] (M.R. Sertel) 1
˘ This paper was written when this author was a graduate student at the Department of Economics, Bogazic¸i
¨ ~
University, and a researcher at the Mathematics Division of TUBITAK-Marmara Research Center. 0165-4896 / 99 / $ – see front matter 1999 Elsevier Science B.V. All rights reserved.
2
of agents will gain and some will lose by the adjunction of new agents of certain types. In fact, a central aspect of the nature of competition under an economic solution concept concerns the matter of precisely which types gain and which types lose as new agents of various types join: the entrants’ (potential) rivals under a given solution concept should be hurt by such an entry, while those who benefit from increased rivalry among these agents might typically be their main (potential) partners in trade.
For instance, in two-sided matching, we know that the men-optimal matching improves (if anything) for the men and worsens (if anything) for the women when new women join (Gale and Sotomayor, 1985). We would say that men (resp., women) are
3
mutual rivals of each other and partners with women (resp., men) under this solution . As another example, when a new oligopolist joins a Cournotian industry, the incumbents (the entrant’s rivals) will if anything lose, while their customers (entrant’s trade partners) if anything gain. Then again, in economies with public goods, ignoring the effect in the private goods sector, the adjunction of new agents tends to facilitate the finance of the production of public goods and generally has a beneficial effect on all incumbents’ welfare, who are thus all partners, although counter-examples to this trend prevail when the public goods are not normal (Sertel and Yıldız, 1998). And, of course, in division problems where the cake grows only concavely in total input by agents, Shapley-wise division renders all agents mutual rivals (Mo and Gong, 1989).
What our brief tour of economic allocation problems (matching, oligopoly, public-good production and finance, division) under their salient or canonical solutions (Gale–Shapley, Cournot, Lindahl, Shapley) suggests is that solution concepts will impart certain relations of rivalry and partnership. The question of ‘‘population monotonicity’’ is really quite narrow in an economic world, concerning itself only with cases where all agents are classified as mutual rivals, and ‘‘population solidarity’’ is only a bit broader, asking for all agents to fall into a single class: all mutual rivals or all mutual partners. With a general research horizon perhaps more befitting of the economic
2
There is a sizeable literature concerned with the population monotonicity of various game theoretic, bargaining and economic solution concepts. (For a survey we would refer our readers to Thomson, 1995). While many central such solution concepts are population-monotonic, many are not. For example, while
¨ Shapley value is population-monotonic for concave games (Sprumont, 1990), the nucleolus is not (Sonmez, 1994). While the Kalai–Smorodinsky bargaining solution is population-monotonic, the Nash bargaining solution is not (Thomson, 1995). [When we apply bargaining solution concepts to the bargaining problems determined by economies, the Nash bargaining solution renders a population-monotonic allocation rule for single-commodity economies (Chun and Thomson, 1988), although this fails for economies with more than one commodity.] Then again, for economies the egalitarian-equivalent solution is monotonic (Thomson, 1995), but the Walrasian solution from equal split is not (Chichilnisky and Thomson, 1987). As to the Walrasian solution pure and simple, Thomson (1995) shows that it fails population monotonicity, as our present paper will amply corroborate. Finally, even population solidarity is so strong a condition that, although the core correspondence admits of a refinement which satisfies population solidarity (Moulin, 1990a), there is no Pareto-optimal and envy-free allocation rule satisfying this solidarity condition (Moulin, 1990b) [Then again, Alkan (1994) shows that a local form of population monotonicity (construed for single-agent expansions and contractions of population) is compatible with both Pareto-optimality and envy-freeness.]
3
nature of the subject, one might instead aim to classify solution concepts according to
4
the rivalry and partnership relation which they induce.
A modest first step in such a program should regard the central economic solution concept of L. Walras and investigate the rivalry and partnership relation it imparts, and this is our aim here. Precisely, we aim to explore the domain of the conjecture that the Walrasian solution sets agents of the same type in rivalry. We feel that our conjecture is shared by the man in the street, and so we regard it as a ‘‘folk conjecture.’’
What would the man in the street expect from the entry of a new economic agent in a pure trade economy? We are neither professionals nor in any sense amateurs of social psychology, but we would reckon that the man in the street—at least in the streets which we trod—would expect the entry of a new agent in a private-good economy to affect incumbent agents differentially, benefiting some and hurting others. Normally, agents of the entrant’s type (or of sufficiently similar types) should be hurt, and if the solution is in the core, some agents should then furthermore benefit from the entry; in fact, one should expect to find benefiting agents among those who trade most intensively with the type of agent who enters.
What we prove here is that the correctness of this folk conjecture is closely related to two classical conditions on the aggregate demand: (1) a pointwise version of the gross substitution hypothesis, namely that substitution effect dominates income effect, i.e., the inner product of the change in aggregate demand with the change in the price vector is nonpositive, and (2) the generalized axiom of revealed preferences (GARP), i.e., the requirement that aggregate demand is consistent with the maximization of a locally-insatiable utility function.
The first part of our main result here (Theorem 1) parallels the folk conjecture above
5
and, so, constitutes a folk theorem: We show that, extending an economy by the adhesion of further agents of any particular incumbent type, so long as substitution effect dominates income effect for the original economy at the old and new Walrasian prices, the incumbent agents of the entrants’ type are hurt while some others benefit. Furthermore, we show that as long as the aggregate demand in the subeconomy consisting of the agents whose types are not replenished satisfies the GARP, the converse is also true, i.e., the validity of our folk conjecture implies that substitution effect dominates income effect for the original economy at the old and new Walrasian prices. For economies whose agents are of just two types, of course, this determines exactly when our folk conjecture holds (Corollary 1). In order to complete the picture, we further show that, given any economy where aggregate demand fails the ‘‘strict’’ GARP (with strict inequalities), we can extend the economy (by admitting further agents of a single type) so as to obtain a new economy for which we can construct a
counter-4
Note that rivalry and partnership relations need not be equivalence relations (themselves classifying the agents): an agentamay beb’s rival whilebisa’s partner. A primary question to settle for an exploration of this rich terrain would ask when rivalry and partnership are symmetric and when they are transitive relations. 5
¯
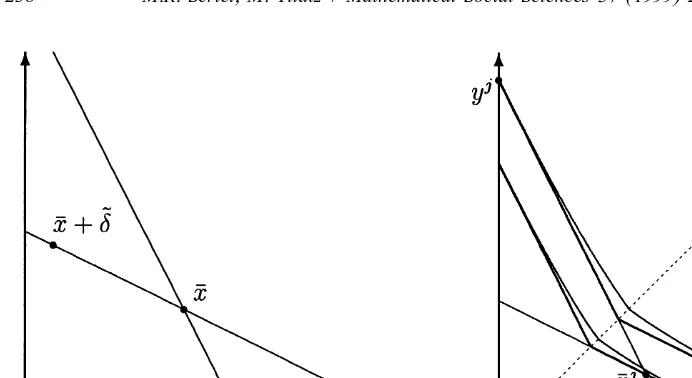
Fig. 1. An illustration of Proposition 2. In (a), we have an economy with aggregate initial endowment x,
˜ ˜
exhibiting aggregate excess demanddanddat prices p and p, respectively. In (b) we construct an agent j with
j j j j ˜
˜ ˜
¯ ¯ ¯
initial endowment x who demands y 5x -d and yj5x -d/ 2 at prices p and p, respectively. The kinked line segments are the indifference curves for utility function U (in the proof). We then perturb U to some strictly
j j
˜
quasi-concave utility function whose indifference curves are tangent to those of U at y and y .
example where our folk conjecture holds but substitution effect fails to dominate income effect (Proposition 2 Fig. 1).
Along the way we also show two useful results: Taking any economy and extending it by admitting new agents of a single incumbent type, we show that substitution effect dominates income effect for the original economy at the Walrasian prices if and only if each incumbent agent of the entrants’ type could afford at the original price what he demands at the new price, and substitution effect dominates income effect for the
extended economy at the Walrasian prices if and only if, at the new price, the rest of the
original economy can collectively afford their original aggregate demand.
Before we proceed to establish these in formal detail, there are a couple of points to remark. For one, in the central doctrine of Economics the Walrasian solution epitomizes
competition. This clearly is not in the sense that it renders all agents mutual rivals. It is,
however, in the sense that it renders agents mutual rivals if they are of the same type. The fact that the Walrasian solution is in the core then implies also that on the whole an agent should see agents of some other type(s) as partners. It is natural to ask what other
6
solution concepts for economies, games, etc. are competitive in this sense. Second, referring to the man in the street, it has to be remarked that there is a clear intuitive basis justifying our (folk) conjecture in a context of imperfect competition, as we note in a Cournotian example above and discuss in Section 5 below. This could very well constitute a folk basis of the folk conjecture. But here we pursue this conjecture in
6
7
perfect competition, and in a salient class of economies the conjecture turns out to be
true there as well. This is perhaps the less ‘‘folksy’’ part of our conjecture and the ‘‘egghead’’ content of our theorem.
2. Basic definitions
We will denote Nfor the set of all positive integers,R(resp., R1) for the set of all
k k
(resp., nonnegative) real numbers,R for k-dimensional Euclidean space andR1 for the
k
nonnegative cone in R.
m
Let M5h1, . . . ,mjbe the set of private goods for some m[N, and denote X5R1. A function u: X→Ris said to be locally insatiable iff, given any x[X, for every open
neighborhood V(x) of x, there exists some y[V(x) such that u( y).u(x). We denote 8
for the set of all quasi-concave, continuous and locally insatiable functions u: X→R. By an (n-person) economy we mean any function ´: N→T, for some finite N,N, where
Note that D( p, ´) is always nonempty since u is continuous, in fact singleton since ui i i i i i
¯
is strictly quasi-concave. Given any agent´ 5(u , x ), since u is locally insatiable, we
i i
utility functions are locally insatiable, the Walrasian allocation x of ( p, x)[W(´) is in the core of economy ´, in other words, there is no nonempty coalition N9#N which
i i
the generalized axiom of revealed preferences (GARP) at prices p, p9[3iff we do not
have
i i i i
¯ ¯
p9 ?
O
(D( p,´)2x )#0 and p?O
(D( p9,´)2x ),0. (1)i[N i[N
In this definition we restrict the well-known generalized axiom of revealed preferences to the data sets consisting of two data (namely, two consumption bundles demanded in
7
two budget sets); and we know that a data set satisfies the GARP iff it is consistent with maximization of a locally insatiable utility function. (For more on this, see, e.g., Afriat, 1967). Since our agents have locally insatiable utility functions, it follows that, given any economy consisting of agents of a single type, its aggregate demand satisfies the GARP at any two prices.
i
For any agent ´ of an economy ´[%, we say that substitution effect dominates
i income effect at prices p, p9[3 for´ iff
i i
( p2p9)?(D( p,´)2D( p9,´))#0. (2)
Given an economy´: N→T, we say that substitution effect dominates income effect on the average at prices p, p9[3 for´ iff
income effect at prices p and p9for each agent´ (i[N ) then, clearly, substitution effect
dominates income effect on the average at prices p and p9 for ´.
8
Remark. Monotonicity of aggregate (excess) demand, requiring inequality (3 ) at each
p, p9[3, is a strong condition. In particular, it implies the uniqueness of Walrasian
i equilibrium. (See, e.g., Mas-Colell, 1991). Nevertheless, given any agent ´ with a quasi-linear utility function u [8 of the form
i
which imply inequality (2 ). To formulate one such condition, take any p, p9[3 with
i i we had (nonpositively) compensated him against the price change.] Our condition is that
ˆx1.0. (4)
[In other words, our condition stipulates that an agent who is not hurt by a price change
ˆ
to, say, p9( p9[3) ends up with a positive amount x of the‘‘numeraire’’ when given
1 m
ˆ
the endowment x[R1 determined by the tangency of her initial indifference curve with the new price vector p9.] To see that this condition guarantees inequality (2 ), note that,
ˆ ˆ
since u is also quasi-linear with first coordinatei ‘‘numeraire’’, x1.0 and u (x )i #
i i
ˆ
u (D( pi 9,´)) imply that the differenced 5D( p9,´)2x is zero in each coordinate other than that of the‘‘numeraire’’. Thus,
8
i i i
where the last equation is due simply to the fact that p15p151 by definition. On the
other hand, since u is quasi-concave, the classical Substitution Theorem implies thati
i ˆ
( p2p9)?(D( p,´)2x )#0. (6)
Together with (5 ), this gives us (2 ), and completes the proof.
˜ ˆ
of which new agents join to extend ´ to ´, and N is the set of agents in the original
ˆ ˜
economy´who have this type t. The agents of any other type remain the same in´as in
´].
ˆ
Throughout the paper, we assume that N±[, i.e., the newcomers are of an incumbent
ˆ ˜
type. When N5N, all the agents in economies´and´are of the same type, hence the Walrasian solution leaves economies unchanged, thus our results trivially hold. We
ˆ
therefore assume that N±N from here on.
3. The main result
Our main result is Theorem 1, which states that extending an economy by admitting a new agent of an incumbent type has a double-edged effect on the Walrasian utilities of the original agents so long as substitution effect dominates income effect for the original economy (´) on the average at the Walrasian prices of the original and the extended economies: agents of the new agent’s type are if anything hurt, and some others are if anything now better off. What is more, this double-edged effect occurs only when substitution effect dominates income effect, as long as the aggregate demand of subeconomy ´N \Nˆ (consisting of the agents of the other types in the original economy)
˜
satisfies the GARP at the Walrasian prices p and p of the original and the extended economies. (In Proposition 2 we further show that this qualification is always necessary in the sense that, whenever it fails, we can embed ´N \Nˆ into an economy for which we can construct a counter-example.)
In the previous section we presented a standard model of an exchange economy with divisible goods, which allowed us to use a relatively simple notation. Our proofs in this section, however, employ only the following three properties of that model:
9
• By definition of a Walrasian equilibrium, markets clear:
• Utility functions are locally insatiable. Hence, in individuals’ optimization problems budget constraints are always binding:
• Identical agents are equally treated:
i i j j i j ˜ ˜ ˜
¯ ¯
(u , x )5(u , x )⇒[x 5x ] (i, j[N ). (11)
Our first result is Proposition 1, which tells us exactly when it is the case that the incumbent agents of the entrants’ type can afford their new Walrasian demand at the original Walrasian prices:
j j ˆ
˜ ¯
Proposition 1. The budget inequality p?(x 2x )#0 holds for each j[N iff substitution effect dominates income effect on the average for economy ´at the Walrasian prices p
˜
[The first equation follows by (7), the next terms are obtained by rearrangements of terms, the penultimate equation then following by use of (8) and (10) for each i[N. The
Theorem 1. If substitution effect dominates income effect on average for economy´at
subeconomy ´uN \Nˆ satisfies the GARP at prices p and p, then the converse of this
statement is also true.
ˆ
Proof. Take any i[N. By Proposition 1, if substitution effect dominates income effect
i i i i
coalition N blocks the Walrasian allocation x, contradicting the fact that x is in the core
j j j j ˆ
i[N but substitution effect fails to dominate income effect at the Walrasian prices p and
˜ ˜
u is locally insatiable, this implies that p?(x2x )$0; for otherwise, x would not be
˜
optimal at price p. Together with the material balances Eq. (7), this implies that
i i
˜ ¯
p?
O
(x 2x )#0. (14)ˆ i[N•N
Now assume that substitution effect fails to dominate income effect at the Walrasian
i i
By definition (1), inequalities (14) and (15) reveal that the aggregate demand of
˜
subeconomy´uN \Nˆ fails the GARP at the prices p and p; and this completes the proof.j
The second statement in our Theorem tells us how necessary our sufficiency condition
10
in the first statement is. In particular, when there are only two incumbent types, since the rest of the economy (i.e., ´uN \Nˆ) consists of the agents of only one type, hence satisfies the GARP, it tells us that our sufficiency condition indeed was necessary. Therefore, our Theorem has the following corollary, which characterizes double-edgedness with substitution effect dominating income effect for economies of just two types.
10
Corollary 1. Assume that u´(N )u52. Then, we have inequalities
iff substitution effect dominates income effect on the average at p and p for economy´.
The question is again How necessary is our sufficiency condition? The second statement in our Theorem provides an answer: if the rest of the economy is ‘‘coherent enough’’ to be represented by a single agent (i.e., if their aggregate demand satisfies the GARP at the Walrasian prices), then indeed, it is necessary. What is left unanswered there is How tight is this answer? In the following we will answer this question: We will show that, if aggregate demand of an economy ´9: N9→T fails the GARP at any two
11 ˜
prices p and p[3with strict inequalities in (GARP), then by allowing new agents of
˜ ˜
respectively, the agents of replenished type t are hurt by extension from´to´under the Walrasian solution, yet the substitution effect does not dominate income effect at prices
˜
are aggregate demands of economy e9 at prices p and p, respectively. For any two
˜
Proof. Throughout the proof, we will use the notation in the statement of our
j j k k j
¯ ¯
Proposition. We will construct (u , x )5(u , x )[T in such a way that agent e ’s excess
demand at price p will balance the aggregate excess demand of economy´9 at price p
j j 12
˜ ¯
(i.e., y 2x 5 2d), his excess demand at price p will balance half the excess demand
11
If one of the inequalities is not strict, then it is not possible to construct an example with a strictly quasi-concave utility function.
12 k j j k
˜ ˜ ˜
j j 1˜
Since Property 3 is a direct consequence of 1 and 2, this will leave to prove only 4. But this will be a direct consequence of Proposition 1 and inequality (18), which we will derive in a moment; and this will complete the proof.
Let us first set
where max picks the largest entry in each coordinate, hence both y ;x 2d and
j j 1˜ j j Since d is aggregate excess demand of e9 at p and the utility functions are locally
j j j j
˜p, respectively. Consider the function U : X→R which sets
j j
is not strictly quasiconcave (although it is quasiconcave). We can, however, construct a
j j j j j j j
˜ ˜
utility function u [8 such that u ( y )5U( y ) and u (y )5U(y ), and moreover, the j j
˜
indifference surfaces of these two function are tangent to each other at both y and y .
j
This actually completes the proof. [Check that one such u [8 is defined by setting
j
(if anything) gain from such entry, and for economies of only two types, this would further imply that the rest of the economy would benefit from the entry. This provides the focus of Proposition 3, below, where we characterize the case where the entry of new agents of a certain incumbent type on the whole benefits the incumbent agents of the other types, i.e., these incumbent agents can collectively buy at the new Walrasian
˜
price p what they demand at the Walrasian price p of the original economy ´. Note that our Proposition 3 and Proposition 1 are complementary: while Proposition 1 assures us that incumbent agents of entrants’ type can afford their new demand at the original Walrasian prices iff substitution effect dominates income effect for the original
economy´on the average, Proposition 3 tells us that the incumbent agents whose types are not replenished can afford as a group their original demand at the new Walrasian
˜
prices iff substitution effect dominates income effect now for the extended economy´on the average.
Proposition 3. The aggregate budget inequality
i i holds iff substitution effect dominates income effect on the average for economy´at the
˜ Walrasian prices p and p.
Proof. By the material balances Eq. (8), we have
i i i i
Now take any j[N. Since all the newcomers are of type´( j ) (exhibiting identical net demands), together with material balances Eq. (7), Eq. (21) gives
ˆ uNu
i i i i
˜ ¯ ]] ˜ ˜ ˜
p?
O
(x 2x )5 ( p2p )?O
(D( p, e )2x ), (24)˜
ˆ uN•Nu ˜ i[N•N i[N
so,
i i i i
˜ ¯ ˜ ˜ ˜
p?
O
(x 2x )#0⇔( p2p )?O
(D( p, e )2x )#0. jˆ ˜
i[N•N i[N
4. Examples of where the substitution effect fails to dominate income effect
In this section we present two examples in order to exhibit how the domination of substitution effect and hence our double-edged population monotonicity of Theorem 1 can fail in very regular economies. We first present Example 1, where a new agent of type t0 is admitted in extending a two-type economy ´: N→ht9, t0j, but now, in exact opposition to the double-edged population monotonicity of Theorem 1, incumbents of
˜
type t0 gain while those of type t9 lose in passing from ´ to ´ under the Walrasian solution.
Before we present Example 1, we record Lemma 1, which gives us a key to generating Walrasian equilibria of economies from Walrasian equilibria of certain ‘‘summary’’ economies with just one (‘‘representative’’) agent of each type. First we present the notation we use in our Lemma.
21
Notation. Take any economy ´: N→T. For each i[N, define N(i )5´ h´(i )j, so that
hN(i )ui[Njis a partition of N and i|j⇔N(i )5N( j ) defines an equivalence relation on N. Taking i][N(i ) as a representative of N(i ) at each i[N, we denote N]5hiui] [Nj for the set of ‘‘representatives’’. We define the (one-to-one) ‘‘summary’’ economy´]: N]→T
i i i i i i
] ¯] ¯] ¯] ] ]
by setting ´](i )] 5(u , x ) at each i] ] [N(i ), where x] 5uN(i )ux and u (x)] ] 5u (x /uN(i )u) at
m
each x[R1.
Lemma 1. Given any economy´: N→T and any allocation x of economy ´for which i j
agents of the same type receive the same consumption bundle (i.e. x5x at each i, j[N with ´(i )5´( j )), we have
( p; x)[W(e)⇔( p; x)] [W(´]),
i i i
] ] ]
¯
where x]5hx] ji[Nis an allocation of the summary economy ]´such that x] 5uN(i)] ux at
]
each i] ][N.
Proof. Take any allocation x as hypothesized. Clearly, x is an allocation of] ´], for oi[N
] ]
i i i i i i
] ] ¯ ¯] ¯]
x5oi[NuN(i )ux5oi[Nx5oi[Nx 5oi[NuN(i )ux 5oi[Nx . Taking any i[N, we have
i i m i
] ] ¯]
D( p,´])5argmaxhu (x)ux] [R1, p?(x2x )] #0j x
i m i
]] ¯
5argmax
H S D
u ux[R1, p?(x2uN(i )ux )#0J
uN(i )u
x x
i m i
]] ]] ¯
5argmax
H S D
u uN(i )u ux[R1, p?S
uN(i )u2xD J
#0i m i i
¯
5uN(i )uargmaxhu (x)ux[R1, p?(x2x )#0j5uN(i )uD( p,´).
i i
Now, ( p, x)[W(´) iff D( p, ´)5x at each i[N; and the latter is true iff D( p, i i i
] ] ]
´)5uN(i )ux5x at each i[N, i.e. ( p; x)[W(´), as is to be shown Fig. 2.j
] ] ] ] ] ] ]
1
Example 1. Let m52 and consider the economy´:h1, 2j→T with´(1)5t95(u , (0, 5))
2 1 2
and ´(2)5t05 (u , (5, 0)) where u (x)5minh4x , x1 2j and u (x)5minhx , 4x1 2j at each
2
x[R1. The unique Walrasian equilibrium of´ is ( p; x)5((1, 1); ((1, 4), (4,1))). If an agent of type t0 enters the economy, then the unique Walrasian equilibrium in the new
7 2 8 14 7 14 7
˜ ˜ ˜ ] ] ] ] ] ] ]
economy ´ will be (p; x )5((1, 2); (( ,3 3), (3, 6), (3 , 6))). At the Walrasian allocation of´, the first agent enjoys a utility level of 4, but at the Walrasian allocation
8 14
˜ ] ] ˜
of ´only a utility level of 3. Agent 2’s utility increases from 4 at W(´) to 3 at W(´) with the entry of a new agent of his own type.
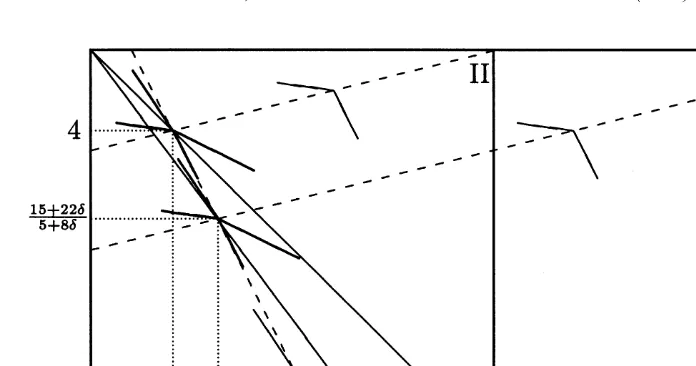
In Example 2, substitution effect fails to dominate income effect to an arbitrarily small extent in a net of two-good economies in whose limit the two goods are perfect substitutes and the gross substitution condition is satisfied. In each economy of the net, of course, agents whose type is replenished gain and the other agents lose under the
Fig. 3. The Edgeworth boxes for economies in Example 2 for a typicald.
Walrasian solution, although the limiting economy exhibits our double-edged population monotonicity of Theorem 1 (See Fig. 3).
Example 2. Let m52 and consider the net of economiesh´d:h1, 2j→Tjd[( 0,1 / 2 ) with
1 1 2 2 1
9 99
´ 5d td5(u , (0, 5)) andd ´ 5d td5(u , (5, 0)) where u (x) mind d h3((11d)x11x ),(12 2 2
d)x11x211014dj and u (x)d 5minh(528d)((112d)x11x ), (52 18d) ((122d)x11
2 1 2 1 2
x2)jat each x[R1. Asd→0, clearly, (u ) and (u ) converge to u and u , respectively,d d
1 2 2
where both u and u represent the same preference relation and u (x)55(x11x ) at2 2
each x[R1. Compute that, for everyd[(0, 1 / 2), W(´d)5h((1, 1); ((1, 4), (4, 1)))j as ˜
in the previous example. Now consider the net of economies h´d:h1, 2, 3j→Tjd[( 0,1 / 2 )
1 2 3
˜ 9 ˜ ˜ 99 ˜
with ´ 5d t andd ´ 5´ 5d d t . For everyd d[(0, 1 / 2), compute that economy ´d has a
d d d
˜ ˜
unique Walrasian equilibrium (p ; 1 /(518d)x ) where p 5(1, (514d) /(519d)) and
d
˜x 5((1018d, 15122d), (20136d, 519d), (20136d, 519d)). Note, for eachd[(0, 1 / 2), that Agent 1 is worse off at the Walrasian allocation of the extended economy
while Agent 2 is better off.
5. Closing remarks
solution concept for) a perfectly competitive environment, such as a large (possibly
13
atomless) economy where no agent is able to affect the prices; and for such environments, we cannot directly advance the sort of concrete economic reasoning we just presented. Instead, we may have to invoke some imperfectly competitive environ-ments which approach a perfectly competitive environment. Proceeding along such a route, our double-edged population monotonicity of the Walrasian solution requires the solution to be monotonic not (only) for these imperfectly competitive environments but (also) for the limit; and this may explain why a natural conjecture of ‘‘the competitive solution setting agents of the same type in rivalry’’ is characterized (at least for the economies consisting of two types) by a pointwise version of a strong condition like monotonicity of aggregate demand (i.e., gross substitution hypothesis), namely substitu-tion effect dominating income effect. One might wonder whether there is a natural
14
habitat where this condition is valid. In particular, the ‘‘double-edged’’ nature of the population effect is one familiar in the world of matching, as we noted in the Introduction, where preferences are quasi-linear and (4) is satisfied. Thus, in such a matching context the ‘‘double-edgedness’’ of the population effect would also have followed from an analysis such as ours. The special structure of matching is, of course, missing in our present study, and such a structure would need to be invoked in order to relate our present analysis unequivocally to the matching world.
Acknowledgements
´
We thank Herve Moulin, an anonymous editor and two anonymous referees for their comments, which improved this paper substantially. This paper was presented at the European Workshop on General Equilibrium Theory, 2–3 June 1995, Barcelona, and the Econometric Society European Meeting, 26–31, August 1997, Toulouse. We also thank the participants of these conferences for comments.
13
By an atomless economy we mean a ‘‘general economy’’ where each incumbent agent has infinitely many copies. By a type distribution we mean a probability distribution on the type space T. Given any economy´:
21
N→T, the type distributionm´: T→[0, 1] of´is defined by settingm´(t)5u´ (t)u/uNuat each t[T. Again
given any economy´:h1, 2, . . . ,nj→T, we can construct an atomless economya´: [0, n)→T with type
distributionm´by settinga´(a)5´(a11) at each a[[0, n), where.picks the integer part of its argument. (For technical details see, e.g., Kannai (1970) or Hildenbrand, 1974). Since the type distributionm´contains all the necessary information for the Walrasian prices of economy´(and, of course, ofa´), our analysis in this paper straightforwardly generalizes to the set of such atomless economies. Finally, we note that, given an
ˆ ˜
economy´: N→T with u´(N )u$2, an economy´ is an extension of´by some incumbent type t[T iff
ˆ ˆ ˆ ˆ ˆ
m´˜(t )$m´(t ).0 andm´˜(t)5m´(t)(12m´˜(t )) /(12m´(t )) for each type t[T \htj(i.e., by entry of agents of an
ˆ ˆ
incumbent type t, the weight of type t is increased and the weights of other types are scaled down proportionately so that the weights of all types sum up to 1).
14
References
Afriat, S., 1967. The construction of utility functions from expenditure data. International Economic Review 8, 67–77.
Alkan, A., 1994. Monotonicity and envy-free assignments. Economic Theory 4, 605–616.
Chichilnisky, G., Thomson, W., 1987. The Walrasian mechanism from equal division is not monotonic with respect to variations in the number of consumers. Journal of Public Economics 31, 119–124.
Chun, Y., Thomson, W., 1988. Monotonicity properties of bargaining solutions when applied to economics. Mathematical Social Sciences 15, 11–27.
Gale, D., Sotomayor, M., 1985. Some remarks on the stable matching problem. Discrete Mathematical Monthly 11, 223–232.
Hildenbrand, W., 1974. Core and Equilibria of a Large Economy. Princeton University Press, Princeton, NJ, USA.
Kannai, Y., 1970. Continuity properties of the core of a market. Econometrica 38 (6), 795–815.
Mas-Colell, A., 1991. On the uniqueness of equilibrium once again. In: Barnett, W. et al. (Eds.), Equilibrium Theory and Applications, Proceedings of the Sixth International Symposium in Economic Theory and Econometrics. Cambridge University Press, pp. 275–296.
Mo, J., Gong, J., 1989. Second order conditions in coalition game theory. Mimeo, Academia Sinica. Moulin, H., 1990a. Cores and large cores when population varies. International Journal of Game Theory 19,
219–232.
Moulin, H., 1990b. Fair division under joint ownership: recent results and open questions. Social Choice and Welfare 7, 149–170.
Sertel, M.R., Yıldız, M. 1998. The Lindahl solution with changing population and resources. In: Moulin, H., Sprumont, Y. (Eds.) Mathematical Social Sciences, 35(2); Special Issue on Axiomatics of Resource Allocation.
Shapley, L.S., 1962. Complements and substitutes in the optimal assignment problem. Naval Research Logistic Quarterly 9, 45–48.
¨
Sonmez, T., 1994. Population monotonicity on a class of public goods problems. Mimeo, University of Rochester.
Sprumont, Y., 1990. Population monotonic schemes for cooperative games with transferable utility. Games and Economic Behavior 2, 378–394.