Untitled Document

(1)

i

MATEMATIKA EKONOMI

SOPAR M.H

�

=

−

�

(

�

+

–�

�

(2)

ii

(3)

i

SETANGGI TIMUR

Buku Matematika Ekonomi ini disusun sedemikian rupa untuk dapat digunakan di seluruh rumpun Ekonomi , baik jurusan Studi Pembangunan , Akuntansi , Manajemen Bisnis , Manajemen Keuangan , manajemen Sumber Daya Manusia , maupun Manajemen Rumah Sakit .

Buku Matematika Ekonomi bukanlah buku Matematika Dasar tetapi lebih condong ke Matematika Terapan Lanjutan , yaitu Tingkat Madya , maupun Studi lebih lanjut (advanced ) , tetapi disajikan sedemikian rupa untuk dapat digunakan di Strata S-1 .

Karena buku ini pegangan lanjutan , bukan dasar , maka penulis menganggap seluruh pembaca , seperti mahasiswa dianggaap sudah menguasai seluruh materi matematika di SMA , dengan demikian penyajiannya tidak sederhana namun tidak begitu kompleks.

Buku Matematika Ekonomi ini disusun sesuai perkembangan ekonomi era kini , yang menampilkan seluruh bagian yang berhubungan dengan Riset- riset Ekonomi baik Ekonomi makro maupun Ekonomimikro , apalagi ekonomimikro menjadi prasyarat mengambil mata kuliah ekonomimakro , demikian pula matematika ekonomi menjadi prasyarat mata kuliah Statistik . Sekalipun prasyarat terakhir agak rancu , sebab antara matematika ekonomi dan statistik hampir tidak berhubungan , sekalipun statistik yang dimaksud Statistik Ilmu Sosial . Yang lebih tepat matematika ekonomi dan statistik ilmu sosial sebagai prasyarat mata kuliah Ekonometrik , atau Risearch Design , sesuai tuntutan perkembangan ilmu ekonomi era modern .

Akhirnya penulis ucapkan terimakasih pada sidang pembaca yang telah menggunakan buku ini , dan dengan terbuka menerima saran sidang pembaca untuk revisi .

Banda Aceh, Desember 2004.

Hormat Penulis

(4)

ii

DAFTAR ISI

=

−

1+1

−1 +1

+

,

k  konstanta ,(hasil ini disebut IAD ) ,ini memang dikarang-karang saja agar hasilnya kembali ke fungsi Primitif,

Y = axn + k ,

Perbedaannya hanya konstanta, k .

Fungsi primitif yang di-defferensial memberikan fungsi Turunan, dan fungsi Turunan yang diintegrasi kembali ke fungsi Primitif.

Tapi fungsi ,

Y = axn + k ,

Jika di-defferensial maka member hasil

Y = naxn-1 pula , sebab d(k) = 0.

2. Integral Substitusi

Diberikan sebuah fungsi

Y = 3x (x2 + 1).

Jika sekarang ingin dicari integral dari fungsi di atas, yaitu

∫3x (x

2

+ 1) dx , maka dilakukan pemisalan , u = x2 + 1 d

du = d(x2 + 1) = d(x2) + d(1) du = 2x dx + 0 dx = 2x dx du = 2x dx ( X 3/2 )

3

2 = 3

(7)

2

3. Integral Separatis (Integral Sepihak)

Jika persoalan yang sama seperti di atas ingin di-integralkan dengan integral separatis, yaitu

∫3x (x

2

+ 1) dx , apakah hasilnya sama ? Karena fungsi di atas adalah fungsi perkalian dua fungsi, maka

(8)

3 4. Differensial Fungsi Dua Variabel

Apa yang dilakukan dengan IAD , Integral Substitusi , Integral Separatis adalah penyelesaian dengan fungsi satu variabel x .

Sekarang, jika kedua variabel x dan y disatukan dalam sebuah fungsi, sebutlah z = f (x,y) , dalam sebuah ruang tiga dimensi ,

Ingin dicari differensial dari sebuah fungsi lebih dari satu variabel , sebutlah

W = W(x,y,z,…) dalam n dimensi.

Diberikan sebuah fungsi dua variabel

Z= Z(x,y) = 2xy + x2– y2 Z = 2xy + x2– y2 d dZ = d(2xy + x2–y2 )

Untuk menemukan fungsi turunannya diasumsikan fungsi tersebut hanya satu variabel, ceteris paribus , variabel yang lain diasumsikan konstan , demikian dilakukan seterusnya sampai seluruh variabel terdefferensial.

Untuk maksud ini diadakan sebuah notasi differensial partial ( sebagian-sebagian ) , yaitu z/x , dan z/y , yang dibaca do-zet-do-ex ,untuk membedakan dari dy/dx , de-ye-de-ex.

Tentu , z/x , berarti differensial z terhadap x , ceteris paribus , dan z/y , differensial z terhadap y , ceteris paribusi .

Jikalau dilaksanakan diperoleh ,

Z = 2xy + x2– y2 

z/x = 2y + 2x (y diasumsikan kontanta) Y

Z

X

(X,Y)

Z

(9)

4 z/y = 2x – 2y (x diasumsikan konstanta.)

Asumsi yang bahasa inggrisnya “assume” hanyalah penyederhanaan persoalan agar differensial

fungsi satu variable dapat digunakan untuk fungsi n variable.

Tetapi jika keduanya dijumlahkan , yaitu z terhadap x dan z terhadap y , diperoleh differensial Total z , atau

dZ = z/x dx + z/y dy

dZ = (2y + 2x ) dx + (2x – 2y) dy

Differensial Parsial satu variable terha dap x

(10)

5

BAB II

ALJABAR MATRIK

1. Definisi Matrik

Matrik adalah sekumpulan data berbentuk segi- empat . Dalam operasinya berlaku hukum Aljabar perkalian dan Penjumlahan.

Pengurangan adalah negatif dari Penjumlahan , sedang Pembagian adalah balikan ( invers) dari Perkalian.

Data matrik disebut element ( anggota) , atau entry(masuk) , dan diikat dengan notasi „ kurung

-siku „ atau „ tanda- kurung.‟

Diberikan sebuah matrik sebagai berikut ,

0 2 3

3 4 5 , disebut matrik ordo 2 x 3 ,

dengan elemen 2 baris , dan 3 kolom. Generalisasi matrik ,

11 12 … 1

Tiap elemen dijumlahkan dengan elemen matrik lain yang seletak.

0 2

(11)

6

10 19 19 37 2 2

Dua buah matrik dapat dikalikan , jika kolom matrik pertama sama dengan jumlah baris matrik kedua.

Matrik dikalikan , dengan cara mengalikan semua baris matrik pertama keseluruh kolom matrik kedua, sampai selesai.

A . B  B . A (Hk.Komutatif ) A . ( B + C ) = A .B + A . C (Hk.Distributif ) A . ( B . C ) = (A .B ) . C (Hk.Assosiatif )

4. Matrik Nol

Adalah matrik yang seluruh entry-nya nol.

5. Matrik Identitas

Adalah matrik yang diagonal utamanya 1 , dan yang lainnya 0. I . A = A . I

3 =

1 0 0 0 1 0 0 0 1

6. Matrik Transpose

Dua buah matrik saling Transpose jika baris matrik pertama ditukar dengan kolom matrik kedua , dan sebaliknya.

= 2 4

0 3 =

2 0 4 3 ; A

T_

matrik transpose

7. Skalar

= 2 0

0 2 = 2 = , k = 2 adalah scalar matrik A.

8. Vektor

Vektor adalah matrik dengan satu baris atau satu kolom.

1 2 ,

(12)

7 9. Invers Matrik

Invers matrik adalah balikan dari sebuah matrik.

A . A-1 = A-1.A = I ; A-1 invers matrik

Berlaku hukum Komutatif , perkalian sebuah matrik dan invers- nya menghasilkan matrik identitas.

Akibat dari sifat ini :

I . A = A . I = A ( matrik diri sendiri.)

10.Determinan Matrik

Diberikan = , maka

Determinan matrik A = ad – bc −1 ₌ 1

. , matrik adjoint A (sekawan A)  adj. A ;

≡

. = −

−

(13)

8

BAB III

PENERAPAN DALAM EKONOMI

1. Sistim Persamaan Linier (Pangkat Satu) dengan Tiga Peubah (Variabel)

Contoh : Tentukan harga dan kuantitas keseimbangan untuk tiga barang substitusi. Penyelesaian :

Qd1 = 23 – 5P1+ P2 +P3 ; Qs1 = –8 + 6P1

Qd2 = 15 + P1–3P2 + 2P3 ; Qs2 = –11 + 3P2

Qd3 = 19 + P1+ 2P2– 4P3 ; Qs3 = –5 + 3P3 , d = demand ;s = supply,

( P = price = harga, Q = kuantitas = jumlah.) Qd1 = Qs1 ( pasar keseimbangan) Qd2 = Qs2

23 – 5P1 + P2 +P3 = –8+6P1 15 + P1–3P2 + 2P3 = –11+ 3P2

31 –11P1+ P2 + P3 = 0 ...(1) 26 + P1–6P2 + 2P3= 0 ………(2)

Qd3 = Qs3

19 + P1+ 2P2–4P3 = –5 + 3P3

24 + P1 + 2P2–7P3= 0 ……..(3)

(a) & (3) :

31 –11P1+ P2 + P3 = 0 (x2) 62– 22P1 + 2P2 + 2P3 = 0

24 + P1 + 2P2–7P3 = 0 24 + P1 + 2P2–7P3 = 0 –

38–23P1+ 9P3= 0 ……….(4)

(2) & (3) :

26 + P1–6P2 + 2P3 = 0 26 + P1–6P2 + 2P3 = 0

24 + P1 + 2P2–7P3 = 0 (x3) 72 + 3P1 + 6P2–21P3 = 0 +

98 + 4P1–19P3= 0 ……… (5)

(4) & (5) :

98 + 4P1–19P3 = 0 (x9) 882 + 36P1–171P3 = 0

38–23P1+ 9P3 = 0 (x19) 772–432P1 + 171P3 = 0 +

P1 = 4

Substitusi P1 ke (5) : Substitusi P3 ke (3) :

98 + 4(4)–19P3 = 0 24 + 4 + 2P2–7(6) = 0

P3 = 6 P2 = 7

Untuk memperoleh kuantitas Qd1, Qd2, Qd3 , Qs1, Qs2, dan Qs3 , substitusi P1,P2,

dan P3 ke masing- masing persamaan tersebut.

(14)

9 2. Persamaan Kuadrat (Pangkat Dua)

Contoh : Fungsi laba (keuntungan ) untuk dua perusahaan yang berbeda masing=masing adalah 1 = –Q2 + 7Q –42

1 = –Q2 + 16Q –38

Jika persamaan kuadrat ax2 + bx + c =0 diselesaikan , maka ada dua penyelesaian ,yaitu

1,2

=

− ± 2₋₄

2

,

2

−

₄

≥

₀

_.

a) Pada tingkat output berapa perusahaan pertama akan mendapatkan laba nol ? b) Pada tingkat output yang mana perusahaan kedua akan mendapatkan laba Rp.25,

? Penyelesaian :

a) – Q2 + 7Q –42 = 0 ; a = –1, b = 17 , c = –42, diperoleh

1,2 =

−17 ± 172₋₄₋₁ ₍₋₄₂₎

2(−1) = 14,3

b) – Q2 + 16Q –38 = 25

– Q2 + 16Q –63 = 0 ; a = –1, b = 16 , c = –63, diperoleh

1,2 =

−16 ± 162₋₄₋₁ ₍₋₆₃₎

2(−1) = 9,7

3. Konsep Marginal (MP) ,Rerata (AP), Total (TP)

TP

A

B

C AP MP

C B

A

Input X

Input X Total output

(15)

10 TC = TC(Q) = Total Cost (Biaya)

TR = TR(Q) = Total Revenue (Penerimaan)

Marginal Cost = MC = dTC/dQ ; Marginal Revenue = MR = dTR/dQ

TR = PQ ; P Price

Average Cost = AC = TC/Q

Contoh :

Tentukan Marginal , rerata , dan fungsi total cost berikut . Hitung fungsi pada Q = 3 , Q = 5.

Penyelesaian :

TC = 3Q2 + 7Q + 12

(1) MC = dTQ/dQ = 6Q + 7 (Konsep Marginal adalah kosep differensial) Untuk Q = 3 , MC = 6(3) + 7 = 25

Q = 5 , MC = 37

(2) AC = TC/Q = (3Q2 + 7Q + 12)/Q (rerata ,membagi fungsi dengan Q) = 3Q + 7 + 12/Q

Untuk Q = 3 , AC = 20 Q = 5 , AC = 24,4

Contoh :

Sebuah perusahaan mempunyai fungsi permintaan 22 –0,5Q –P = 0 dan

AC = 1/3Q2–8,5Q + 50 + 90/Q Tentukan output maksimum. Penyelesaian :

22 –0,5Q –P = 0 P = 22 –0,5Q

TR = (22 –0,5Q )Q = 22 –0,5Q2 TR maksimum , jika MR = 0 MR = dTR/dQ = 22 –Q = 0

Q = 22 Laba =  = TR –TC

TC = AC x Q = (1/3Q2–8,5Q + 50 + 90/Q)

TC = 1/3Q3–8,5Q2 + 50Q + 90

TR = 22 –0,5Q2 –

 = TR –TC = –1/3Q3 +8Q2–28Q – 90  Maksimum , jika d/dQ = 0

(16)

11

Q = 14 , Q = 2

Pada Q =14 , diperoleh  = 171,33

4. Metode Gauss Untuk Menyelesaikan Persamaan Linier

Metode Eliminasi Gauss untukk penyelesaian persamaan linier semata- mata dengan menerapkan operasi baris berulang- ulang sampai matrik koeifisien sebuah matrik berubah menjadi matrik identitas.

Algoritma :

1. Perhatikan elemen diagonal utama

2. Ubah elemen a11 matrik koeifisien menjadi 1

3. Dengan operasi baris rubah semua elemen lain dalam kolom pertama menjadi nol (0)

4. Ubah elemen a22 menjadi 1

5. Dengan operasi baris rubah semua elemen lain dalam kolom kedua menjadi nol (0)

6. Ulangi langkah di atas sampai selesai

Contoh :

Tentukan penyelesaian sistim persamaan 2x1 + 12x2 = 40

8x1 + 4x2 = 28

Penyelesaian :

Rubah sistim persamaan menjadi ke bentuk matrik

2 12

1. Perhatikan elemen diagonal utama

2. Baris pertama dikali dengan ½ , diperoleh

12

2.bKalikan baris pertama dengan 8 , diperoleh

(X ½)

(17)

12 �₈ 48 1

2 =

160 28

2.c Baris kedua dikurang baris pertama , diperoleh

6

3.b Baris kedua dikali dengan 6 , diperoleh

6

3.c Baris pertama dikurang baris kedua , diperoleh

0

Ekspansi Laplace dari determinan ordo 3 x 3 dinyatakan sebagai berikut

(18)

13 adalah minor , yaitu , determinan dari sub matrik 2 x 2 setelah menghapus baris –i dan kolom ke- j .

Jadi , = 22 23

32 33

−1 + adalah tanda matrik kofaktor . Karena (-1) dipangkat ganjil adalah negative , maka tanda matrik kofaktor , dibuat sbb ,

+ − +

− + −

+ − +

, berganti-ganti tanda .

Contoh :

=

12 7 0 5 8 3 6 7 0

= 13 13 + 23 23 + 33 33 , Dipilih kolom ketiga , karena berisi banyak elemen nol ,

=−126

6. Kaidah Crammer Untuk Penyelesaian Matrik

Kaidah Crammer , dinyatakan sebagai :

=

adalah determinan matrik koeifisien.

adalah determinan , di mana kolom ke-i matrik koeifisien diganti dengan matrik konstanta.

Contoh :

Carilah x1 , dan x2 dari sistim persamaan linier

6x1 + 5x2 = 49

3x1 + 4x2 = 32

Penyelesaian :

6 5 3 4

1 2 =

49 32

= 6 5

3 4 = 9

(19)

14

(20)

15

Menggunakan Operator Leibnitz :

=

�(� )

Output baja memerlukan input antara batu- bara , bijih , besi , listrik , dll. Output baja adalah permintaan akhir.

Permintaan total X untuk produk , i , sama dengan jumlah semua input antara ditambah permintaan akhir , b .

Pengguna akhir adalah konsumen , investor , pemerintah , dan eksportir .

Jika , aij , adalah koeifisien teknis yang menyatakan harga input , i , yang diperlukan untuk

memproduksi produk baja, j ,seharga satu rupiah , maka permintaan total produk , i , dinyatakan sebagai ,

A disebut matrik koeifisien teknis. Jadi,

X – AX = B ( I – A)X = B

(21)

16 Untuk perekonomian tiga sector , diperoleh :

1 input, yang merupakan nilai tambah perusahaan. Jumlah vertikal elemen-elemen dalam kolom j dalam model tersebut sama dengan satu : biaya input untuk memproduksi sebuah unit komoditi atau memproduksi komoditi seharga satu rupiah.

Contoh :

Diketahui Tabel Permintaan Transaksi Antarindustri di bawah ini dalam jutaan Rupiah. Tentukan Matrik Koeifisien Teknis .

Sektor Asal

Sektor Tujuan Permintaan

Akhir

Perhatikan jumlah Produksi Bruto masing- masing input sama dengan Permintaan Total masing-masing input .

Koeifisien teknis aij menyatakan jumlah unit atau rupiah , i , yang diperlukan untuk

memproduksi satu unit atau satu rupiah produk , j,.

Jadi a11 persentase baja dalam satu rupiah baja , a21  persentase besi dalam satu rupiah baja ,

dan a31 persentase mobil dalam satu rupiah baja .

Untuk mencari koeifisien teknis tersebut bagikan setiap elemen dalam masing – masing kolom dengan nilai produksi bruto yang terletak di bagian bawah kolom dengan mengeluarkan nilai tambah .

Penyelesaian :

(22)

17

Diketahui Tabel Permintaan Transaksi antar industry di bawah ini : a. Tentukan matrik koeifisien teknis

b. Cocokkan jawaban yang diperoleh

Sektor asal Sektor tujuan Permintaan

(23)

18 Contoh :

Anggaplah bahwa nilai tambah (value added) dari soal di atas seluruhnya terdiri Input primer tenaga kerja .

c. Berapa banyak tenaga kerja diperlukan untuk mencapai permintaan akhir ?

d. Jika jumlah tenaga kerja yang tersedia dalam perekonomian adalah 100 , apakah komposisi dari bauran output (output mix) tersebut mungkin (feasible) ?

e. Cocokkan ketelitian koeifisien teknis Penyelesaian :

c. Bagilah masing- masing nilai tambah dengan produksi bruto . Diperoleh , ₁ = 30/40 = 0,214 ; ₂= 50/150 = 0,333 ; ₃= 20/130 = 0,154 .

Jumlah tenaga kerja yang diperlukan untuk permintaan akhir sama dengan koeifisien teknis tenaga kerja dikali dengan permintaan akhir , karena tenaga kerja juga digunakan untuk memproduksi produk-produk antara . Jadi , diperoleh :

= 0,214 0,333 0,54 140 150 130

= 99,93

d. Karena 99,93 < 100 , maka komposisi di atas layak .

e. Karena setiap rupiah output harus dihitung dalam satuan input , maka koeifisien teknis diperiksa dengan menjumlahkan seluruh koeifisien teknis yang jumlahnya sama dengan satu .

1 2 3

1 0,143 0,4 0,077

2 0,357 0,067 0,615

3 0,286 0,2 0,154

Nilai tambah (tenaga kerja)

0,24 0,333 0,154

1 1 1

10.Akar dan Vektor Karakteristik (Nilai Eigen ,Vektor Eigen )

Akar karakteristik suatu matrik digunakan untuk memeriksa kedefinitan tanpa definisi defferensial ( derevatif.)

(24)

19 AV = cV , di mana V adalah vector  0 dan c adalah scalar yang memenuhi persamaan di atas .

Mungkinkah AV = cV ? , di mana A matrik persegi Anxn dan c sbuah scalar (konstanta ) ?

Tentu ordo V ruas kiri sama dengan ordo V ruas kanan . Dan V sudah pasti vector kolom , sebab Anxn tak dapat dikalikan dengan vector baris .

Kalau demikian jawabnya , persamaan di atas dapat terjadi.

Di sini c disebut akar karakteristik atau ( eigen value) , dan V disebut vector karakteristik atau ( eigen vector ) .

Persamaan di atas dapat dinyatakan sebagai , AV = cIV (I  identitas )

Untuk memperoleh penyelesaian tunggal , dilakukan Normalisasi , dengan syarat element vi dari

V , memenuhi  vi2 = 1 , atau

(25)

20 Contoh :

Diketahui ,

= −6 3 3 −6

Penyelesaian :

− = −6− 3

3 −6− = 0

(−6− ) −6− − 3.3 = 0

( c + 9 )( c + 3 ) = 0 c1 = –9 c2 = –3

Kedua c negative , maka A definit negatif. ( A –cI )V = 0

−₃6 ₋3₆ 1 2 = 0 3v1 + 3v2 = 0  v1 = –v2

Dari Normalisasi :  vi2 = 1

v12 + v22 = 1

(–v22) + v22 = 1  v22 + v22 = 1

 2v22 = 1  v2 =  ½ 2

Jadi,

� =

1 2 2

−1₂ 2 ,sebagai eigenvector .

11.Linier Programming : Metode Simpleks

Metode Simpleks atau algoritma simpleks digunakan untuk menyelesaikan Sistim Pertidaksamaan Linier yang berisi sangat banyak variable linier menggunakan grafik .

Contoh :

Maksimumkan fungsi laba berikut ,

 = 5x1 + 3x2 ( fungsi objektif / sasaran ) , dengan

Kendala

6x1 + 2x2 36 2x1 + 4x2 28

5x1 + 5x2 40 x1, x2 0

(26)

21 Algoritma :

1. TABEL SIMPLEKS AWAL

i. Ubah pertidaksamaan menjadi persamaan dengan menaambah variable slack, diperoleh

6x1 + 2x2 + s1 = 36

5x1 + 5x2 + s2 = 40

2x1 + 4x2 + s3 = 28

Penambahan variable slaxk ,s memungkinkan penulisan pertidaksamaan menjadi persamaan .

ii. Bentuk matrik persamaan

6 2 5 5

2 4

1 2 1 2 3

= 36 40 28

Identitas 3x3

iii. Buat table simpleks awal :

Tuliskan vektor kolom variabel di atas matrik koeifisien . Tuliskan koeifisien fungsi objektif di bawah matrik koeifisien , dengan member tanda negatif ( indikator) ,

 = 5x1 + 3x2 + 0s1+ 0s2+ 0s3 = 0.

Elemen kolom konstanta dituliskan sama dengan nol (0) , yaitu fungsi objektif di titik asal ( 0,0 ) ,

 = 5.0 + 3.0 = 0 , di mana x1 = x2 = 0

Tabel simpleks awal :

x1 x1 s1 s2 s3 Konstanta

(X 1/6) 6 2 1 0 0 36

5 5 0 1 0 40

2 4 0 0 1 28

–5 –3 0 0 0 0 (Fungsi ob

jektif awal ) Indikator

(27)

22 i. Kolom Pivot :

Tentukan nilai absolute terbesar dari indikator negatif . Karena nilai absolute −5 = 5, maka –5 merupakan indikator yang pertama dipilih . Karena –5 terletak pada kolom pertama , maka x1 masuk ke dalam basis , dan

kolom x1 menjadi kolom Pivot , ditandai dengan tanda

panah .

ii. Baris Pivot :

Bagi elemen konstanta dengan kolom Pivot ,diperoleh 36/6 < 40/5 < 28/2 .

Pembagian terkecil , dengan mengabaikan hasil lebih kecil atau sama dengan nol (  0 ) , {0, -1/2 , . . . }, menentukan variabel yang mrninggalkan basis .

Karena 36/6 terkecil , baris pertama adalah baris Pivot . Karena s1 mempunyai koeifisien 1 pada baris Pivot , maka

s1 keluar dari basis.

Perpotongan baris Pivot dan kolom Pivot , merupakan elemen Pivot . Jadi , 6 adalah elemen Pivot.

3. Pivoting

i. Kalikan baris Pivot dengan balikan elemen Pivot , diperoleh

Tabel Kedua

1 1/3 1/6 0 0 6

5 5 0 1 0 40

2 4 0 0 1 28

–5 –3 0 0 0 0

ii. Reduksi seluruh elemen kolom Pivot menjadi nol (0) , kecuali elemen baris pivot , diperoleh :

( baris 2 ) dikurang ( 5x baris 1) , ( baris 3 ) dikurang ( 2x baris 1), ( baris 4 ) dikurang ( 5x baris 1),

(28)

23

1 1/3 1/6 0 0 6

0 10/3 –5/6 1 0 10

0 10/3 –1/3 0 1 16

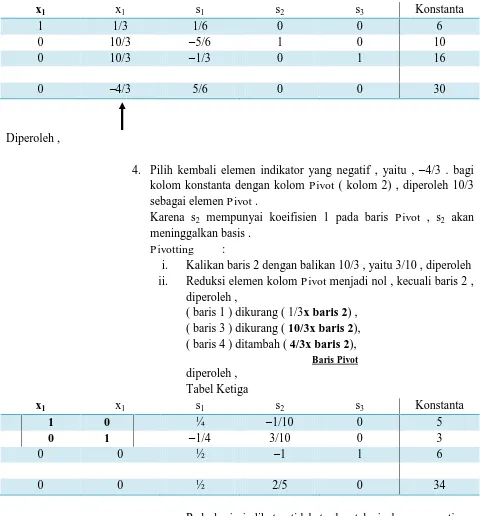
0 –4/3 5/6 0 0 30

Diperoleh ,

4. Pilih kembali elemen indikator yang negatif , yaitu , –4/3 . bagi kolom konstanta dengan kolom Pivot ( kolom 2) , diperoleh 10/3 sebagai elemen Pivot .

Karena s2 mempunyai koeifisien 1 pada baris Pivot , s2 akan

meninggalkan basis . Pivotting :

i. Kalikan baris 2 dengan balikan 10/3 , yaitu 3/10 , diperoleh ii. Reduksi elemen kolom Pivot menjadi nol , kecuali baris 2 ,

diperoleh ,

( baris 1 ) dikurang ( 1/3x baris 2) , ( baris 3 ) dikurang ( 10/3x baris 2), ( baris 4 ) ditambah ( 4/3x baris 2), Baris Pivot diperoleh ,

Tabel Ketiga

1 0 ¼ –1/10 0 5

0 1 –1/4 3/10 0 3

0 0 ½ –1 1 6

0 0 ½ 2/5 0 34

Pada baris indikator tidak terdapat lagi elemen negative , maka penyelesaian sudah optimum .

Elemen pada kolom konstanta menunjukkan ,

1

(29)

24 12.Investasi ,Biaya Total , dan Biaya Marginal

Investasi bersih didefinisikan sebagai tingkat perubahan dalam formasi saham modal (capital stock ) K selama waktu , t .

Pembentukan modal sepanjang waktu , diperoleh

I(t) = dK(t) / dt = K(t) .

Pembentukan modal merupakan integral yang berkenanan dengan waktu investasi bersih .

I(t) = dK(t) / dt

I(t) dt = dK(t) ∫

∫I(t) dt = ∫dK(t)

= K(t) + c

c = K0 = saham modal awal K0 .

Biaya marginal adalah perubahan dalam biaya total akibat perubahan incremental (tambahan ) dalam output , MC = dTC / dQ , dan hanya biaya Variabel yang berubah bersamaan dengan tingkat output ,

MC = dTC / dQ

MC dQ = dTC ∫

∫MC dQ = TC = VC + c

C = FC (Fixed Cost ) = biaya awal . VC (Variabel Cost )

Contoh :

Diberikan Investasi bersih , I(t) = 140 t3/4 dan saham awal pada t = 0 adalah 150 . Diperoleh ,

K = ∫I(t) dt = ∫140 t

3/4

dt

= 1403

4+1

3

4+1+

= 1407 4

7

4+

= 80 7/4+ , c = K0 = 150

= 80 7/4+ 150 .

Contoh :

Diketahui , MC = dTC / dQ = 32 + 18 Q –12Q2 , FC = 43

(30)

25 Penyelesaian :

TC = ∫(32 + 18 Q –12Q

2

)dQ = 32Q + 9Q2–4Q3 + c = VC + c Pada , Q = 0 , TC = FC= 43

TC = 32Q + 9Q2–4Q3+ 43

AC = TC/ Q = 32 + 9Q –4Q2 + 43 / Q VC = 32Q + 9Q2–4Q3

13.Nilai Sekarang dari Arus Kas

Nilai sekarang dari sejumlah uang yang diterima di masa mendatang , bila dimajemukkan secara kontinu , ditunjukkan oleh

P = Se

-n . Oleh karena itu , nilai sekarang dari suatu arus penghasilan yang akan datang ( uang yang diterima setiap tahun selama n tahun ) , ditunjukkan oleh integral

= − = − = −1 −

0 0

0

=− − ₀ = − − − − (0)

= − − −1 = 1− − ; r  tingkat bunga majemuk.

(31)

26

BAB IV

PERSAMAAN DIFF ERENSIAL 1. Definisi

Jenjang atau orde suatu persamaan differensial adalah jenjang atau orde dari turunan tertinggi yang terdapat di dalam persamaan . Derajat (degree) suatu persamaan differensial ditunjukkan oleh pangkat tertinggi dari turunan jenjang tertinggi dalam persamaan differensial .

Contoh :

dy / dx = 2x + 6 . Jenjang pertama , derajat pertama .

4−5 5 = 0 . Jenjang pertama , derajat empat .

2

2+

3

+ 2 = 0 Jenjang kedua , derajat pertama .

2 2

7

+ 3₃

5

= 75 . Jenjang tiga , derajat lima .

2. Rumus Umum Persamaan Differensial Linier Jenjang Satu

dy / dt + vy = z , v , z , konstanta , atau fungsi waktu .

3. Penyelesaian Umum Persamaan Differensial Linier Jenjang Satu

= − ( + ) , A  konstanta sembarang .

* ( Penyelesaian Umum ini akan diuraikan setelah pasal Persamaan Differensial Eksak .)

Penyelesaian berisi dua bagian :

− _{, disebut fungsi pelengkap ( komplementer ) ; y}_c_, − _{,disebut integral khusus (particular ),y}_p_. yc , penyimpangan dari keseimbangan .

yp , keseimbangan antar waktu ( level ekuilibrium .)

Untuk y(t) dinamis stabil : y(t) = yp ; yc = 0 .

Contoh :

Selesaikan dy / dt + 4y = 12 Penyelesaian :

v = 4 , z = 12 .

(32)

27

4. Persamaan Differensial Eksak

Diketahui persamaan fungsi dua variabel F( y,t ) , di mana : M = F / y dan N = F / t , differensial totalnya :

dF( y,t ) = F / y dy + F / t dt.

Jika , disamakan dengan nol , diperoleh

Mdy + Ndt = 0 , ( disebut Persamaan Differensia Eksak. )

2. Buat integralPartial yang terdiri dari

M = F / y , dan Z(t) , untuk mencari fungsi primitive F(y,t) . 3. Differensial F(y,t) terhadap t

(33)

28

5. Kaidah-kaidah Faktor Pengintegralan

Persamaan jenjang pertama non – linier dapat diselesaikan dengan persamaan differensial eksak menggunakan faktor pengintegralan .

Assumsikan, M / t N / y

Dengan demikian faktor pengintegralannya , 1/ ₌ ln ₌

Jadi , penyelesaiannya :

5yt dy + (5y2 + 8t ) dt = 0 (kedua ruas dikali faktor pengintegralan , t . demikian persaman diffe-

Ingat IAD :

Jika , d(ln t ) = 1/t dt , maka ∫1/t dt = ln t.

Juga ingat HukumEksponen dan Logaritma: Misalkan : ln ₌ _{__ ln}

(kedua ruas dilogaritmakan ) , diperoleh

Ln t ln e = ln x

Ln t .1 = ln x  ln t = ln x  x = t ,

(34)

29 rensialeksak dapat diselesaiakan .

6. Pemisahan Variabel

Merubah persamaan differensial eksak

M dy + N dt = 0 , menjadi

M(y) dy + N(t) dt = 0 , tanpa faktor pengintegralan . Contoh :

dy / dt = y2 t Penyelesaiannya :

dy / dt = y2t ( X (dt/ y2) )

dy / y2 = t dt

(1 /y2) dy = t dt ∫

−2 ₌

− −1₊ 1 =

1 2

2₊ 2

t2 + 1/y + c3 = 0 (X 2y)

t2y + 2 + c3y= 0

y = –2 / (t2 + c4)

*Penyelesaian Umum Persamaan Differensial Linier Jenjang Satu

Berikut ini diturunkan Penyelesaian Umum Persamaan Differensial Linier Jenjang Satu

dy / dt + uy = w dirubah ke persamaan homogen , menjadi

dy + (uy – w ) dt = 0 , persamaan homogen mempunyai faktor integrasi

e

udt  eksponen (  udt ) , yang diperoleh dari penyelesaian umum persamaan homogen .

Misalkan I merupakan faktor integrasi , sehingga persamaan di atas , menjadi

(35)

30 M fungsi I saja , u = u(t) , w = w(t) , maka N yang berisi I dan u , w , harus fungsi dalam t saja .

Test eksak

M / t = N / y

M / t = I / t

N / y = Iu

karena I fungsi satu variable dalam t . Jadi ,

I / t = Iu  =

=

______________ ∫

=

= +  = . = , A = ec

Dari pada menggunakan , lebih baik menggunakan untuk memudahkan perhi tungan .

Kalau faktor integrasi ini dikalikan ke persamaan

I dy + I (uy –w) dt = 0 , diperoleh

+ − = 0

� � = � = .� = .

� � =� ( − = .

Jadi , M / t = N / y .

I / t = Iu = dI / dt

Ingat IAD :

(36)

31 Sekarang ,

i. Persamaan terakhir diintegrasi partial terhadap y untuk mencari y . Misalkan :

� , = +Ψ =

Jadi : (t) merupakan penyelesaian suku kedua ,

− , dan d(k) = 0 , F(y,t) fungsi primitif .

� , = +Ψ =

ii. Untuk mencari (t) , persamaan ini dideferensial partial terhadap t , diperoleh

�� = .� � +Ψ′ =

+Ψ′ =

Tapi �� = = ( − )

Maka , dengan identitas , diperoleh

Ψ′ ₌₋

iii. Sekarang untuk mencari (t) , maka

Ψ′ ₌₋ _{, diintegrasi , diperoleh}

Ψ =−

iv. Substitusi ke bentuk I , diperoleh

− =

= +

(37)

32 7. Persamaan Bernuolli

Persamaan Bernoulli adalah persamaan differensialnon-linier berbentuk

dy / dt = ay = byn , a , b , konstanta atau fungsi t , n  0 , n  1 .

Dengan memisalkan = 1− , diperoleh Persamaan DifferensialLinier

dw / dt + (1–n) aw = (1–n) b

yang dapat diselesaikan dengan memisalkan v = (1–n) a dan z =(1–n) b . Contoh :

Persamaan Bernoulli , dy / dt – y = ty2 (Persamaan y dalam t .) Penyelesaian :

dy / dt – y = ty2 , jika dibandingkan dengan Persamaan Umum Bernoulli ,

dy / dt + ay = byn , diperoleh a = –1 , n = 2 , b = t . Dirubah ke Persamaan Linier

dw / dt + (1–n) aw = (1–n) b ( Persamaan w dalam t .) dw / dt + (1–2) (–w) = –1 t

dw / dt + w) = t diperoleh Persamaan Differensial Linier Jenjang Satu  v = t , z = –t

Maka penyelesaiannya adalah ,

= − 1 ( + –t 1 ) = − ( + –t )

= − − + 1

Kembali ke pemisalan Bernoulli , diperoleh

= 1− = 1−2 = 1/

Jadi penyelesaiannya dalam y , adalah

= ( − − + 1)−1

(38)

33

BAB V

PERSAMAAN DIFF ERENSI (SELISIH)

1. Definisi

Persamaan differensi menyatakan hubungan antara suatu variabel tak bebas dan variabel bebas bersenjang ( lagged independent variabel ) yang berubah pada interval waktu diskrit (putus – putus ) .

Berbeda dengan Persamaan differensial yang tergantung pada interval waktu kontinu ( berlanjut .)

Jenjang atau orde persamaan differensi ditentukan oleh banyaknya priode selang terbesar. Jenjang pertama menyatakan suatu kesenjangan waktu ( time lag ) dalam satu priode ; jenjang kedua , dalam dua priode , dan seterusnya .

Perubahan dalam y karena t berubah dan t ke (t + 1) disebut differensi pertama dari y , yaitu ,

∆y / ∆t = ∆yt = yt+1 –yt ,

Operator ∆ menggantikan operator d / dt untuk mengukur perubahan kontinu dalam persamaan differensial .

Contoh :

It = a ( Yt –1 – Yt –2 ) jenjang 2

Qs = a + bP t –1 jenjang 1

yt+3 –9yt+2 + 2yt+1 + 6yt = 8 jenjang 3

∆yt = 5yt jenjang 1

Contoh :

Diketahui y awal y0 , dalam persamaan differensi

yt+1 = b y3

Untuk t = 0,1,2,3, dan seterusnya , diperoleh

y1 = by0

y2 = b y1 = b (by0) = b2y0

yt = bty0

2. Rumus Umum Persamaan Differensi Linier Jenjang Satu

yt = by t –1 + a , a , b konstanta

3. Rumus Umum Penyelesian Persamaan Differensi Linier Jenjang Satu

(39)

34 yt = y0 + at jika b = 1 **)

Penurunan untuk *) :

yt = by t –1 + a

y1 = by0 + a

y2 = by1 + a = b(by0 + a ) = b2y0 + ab + a

y3 = by2 + a = b(b2y0 + ab + a) + a = b3y0 + ab2 + ab + a

y4 = by3 + a = b(b3y0 + ab2 + ab + a) = b4y0 + ab3 + ab2 + ab + a

= 0+ −1+ −2+ −3+ + + 3+ 2+ +

= −1 0+ + + 2+ 3+ + +

3 ₊ 2₊ ₊

= 0 + + 2+ 3+ + +

3₊ 2₊ ₊

= 0+ 1

+ 1₂+ 1₃+ + + 2+ + 1 + = 0+

1

1−0

1−1 +

1

1−0

1−1 +

= 0−₁₋ +₁₋ , untuk b  1 ( jika b =1 , tidak

terdefinisi .)

Penurunan untuk **) :

yt = by t –1 + a , Untuk b = 1, maka

yt = y t –1 + a

y1 = y0 + a

y2 = y1 + a = (y0 + a ) + a = y0 + 2a

y3 = y2 + a = (y0 + 2a ) + a = y0 + 3a

yt = y0 + at

(40)

35 Contoh :

Diketahui persamaan differensi

yt = –7y t –1 + 16 dan y0 = 5

Penyelesaian :

b = –7 , a = 16 ,

maka , = (−7) 5− 16

1+7 + 16

1+7= 3(−7) + 2

4. Model Cobweb

Untuk komoditi hasil pertanian , yang ditanam setahun sebelum dipasarkan , penawaran saat ini tergantung pada harga tahun yang lalu .

Jika ,

Qdt = c + bPt dan Qst = g + hP t –1

Dalam keseimbangan ,

Qdt = Qst

Jadi , = ₋1 + −

Karena b < 0 dan h > 0 ( Karena b koeifisien permintaan selalu negatif , h koeifisien penawaran selalu positif , maka menurut penyelesaian Persamaan DifferensiLinier jenjang satu ,

≠1 < 0 , maka , diperoleh penyelesaian persamaan differensiberikut „

= 0 −

−

− + − − ,

Jika dalam keseimbangan : Pt = P t –1 ( karena berada di satu titik potong yang sama .)

Dengan demikian Pe = Pt = P t –1 (Pe harga ekuilibrium ) , sehingga diperoleh

Pe =

− −

Jadi :

= 0 − / +

Karena itu h / b < 0 , dan lintasan waktu beralun .

Jika : > , / > 0 , lintasan waktu Pt meledak .

Jika : = , / = −1 , lintasan waktu beralun seragam

Jika : < , / < 1 , lintasan waktu Pekonvergen , dan Pt mendekati .

(41)

36

MISCELANOUS PROBLEM ( SOAL CAMPURAN )

1. Tentukanlah keseimbangan harga dan kuantitas untuk dua barang komplementer , celana ( S) dan jaket (J) , dengan menggunakan metode eliminasi

(1) QdS = 410 –5PS–2PJ

QsS = –60 + 3PS

(2) QdJ = 295 –PS–3PJ

QsJ = –120 + 2PJ

2. Sebuah perusahaan elektronika memproduksi TV (T) dan streo (S) . Kurva transformasi ( transformation curves) , juga disebut kurva kemungkinan produksi ( production possibility curve ) , yang menunjukkan kombinasi berbeda untuk setiap barang yang yang dapat diproduksi perusahaan dengan menggunakan semua sumber dayanya secara efisien , dinyatakan dengan persamaan

S2 + 3S + 5T = 130 . Tentukan :

(a) Jumlah maksimal stereo yang dapat diproduksi oleh perusahaan , (b) Jumlah maksimal TV ,

(c) Jumlah maksimal stereo jika 18 TV diproduksi , dan (d) Jumlah maksimal TV jika 7 stereo diproduksi

(e) Gambar grafik kurva transformasi untuk perusahaan tersebut

3. Cari fungsi –fungsi MR yang berhubungan dengan fungsi penawaran berikut . Hitung fungsi tersebut pada Q = 4 , Q = 10 .

P = Q2 + 2Q + 1

4. Gunakan Metode Gauss untuk menyelesaikan sistim persamaan linier

6x1 + 2x2 + 5x3 = 73

7x1– 3x2 + x3 = –1

4x1 + 8x2– x3 = –9

5. Dengan ekspansi Laplace tentukan determinan dari matrik berikut

=

2 4 1 5 3 2 5 1 1

3 2 4

(42)

37 6. Syarat jenjang pertama optimisasi berkendala adalah :

TC / x = 16x –y +  = 0 TC / y = 16y –x +  = 0 TC /  = x + y –42 = 0 ,

Gunakan Kaidah Crammer untuk mencari x , dan y .

7. Gunakan determinan Jacobian untuk menentukan ketergantungan fungsi dalam sistim persamaan :

y1 = x12–3x2 + 5

y2 = x14–6x12x2 + 9 x22

8. Optimumkan fungsi berikut , dengan menggunakan determinan Hessian untuk syarat jenjang kedua .

y = 3x12–5x1–x1x2 + 6x22–4x2 + 2x2x3 + 4x32 + 2x3– 3x1x3

9. Tentukan permintaan total untuk industry 1, 2 , dan 3 , apabila diketahui matrik koeifisien teknis A dan vektor permintaan akhir B berikut :

Output industry

1 2 3

=

0,4 0,3 0,1 0,2 0,2 0,3 0,2 0,4 0,2

1 2 3

input industry = 140 220 18

10. Gunakan eigenvalue untuk memaksimumkan laba ,

=

4 6 3 0 2 5 0 1 3

11. Gunakan metode Simpleksuntuk memaksimumkan laba ,

 = 3 y1 + 4y2 , dengan

kendala

2,5 y1 + y2 20 y1 + 2y2 16

3 y1 + 3y2 30 y1 , y2  0

12. Diketahui MC = 16e0,4Q , dan FC = 100 . Cari TC

(43)

38 Cari K .

14. Nilai sekarang dari Rp.100 yang dibayarkan tiap- tiap tahun selama 3 tahun apabila suku bunga 5 % dimajemukkan secara kontinu adalah ?

15. Selesaikan persamaan differensial eksak berikut : ( 4y + 8t2 ) dy + ( 16yt –3) dt =0

16. Selesaikan persamaan differensialnon linier , Bernoulli berikut :

dy / dt + y = ty3

17. Selesaikan persamaan differensi ( selisih ) dari

yt = 6y t –1

18. Untuk Qdt = 180 –0,75Pt , dan

Qst = –30 + 0,3P t –1 ,

P0 = 0 .

Tentukan :

(44)

39

DAFTAR PUSTAKA

Alpha C.Chiang.1993.Dasar-Dasar Matematika Untuk Ekonomi.Jilid I,II.Erlangga.Jakarta.

Dowling E.1995.Matematika Untuk Ekonomi.Erlangga.Jakarta.

Murray R.Spiegel.1981.Advanced Calculus.McGraw-Hill International Book Company. Singapore.

Piskunov.N.Differential and Integral Calculus.Vol I.Mir Publisher Moscow.

(45)

40 CURICULUMVITAE

Identitas :

Nama : Sopar M.H.

Lahir : 19 Pebruari 1967 di Balik Papan , Kalimantan Timur Pendidikan :

1. SD NEGERI 060922 MEDAN SUNGGAL 2. SMP BUDI BERSUBSIDI SUNGGAL , MEDAN

3. SMPP NEGERI 24 , MEDAN SUNGGAL /IPA /TAMAT 1986

4. IKIP NEGERI MEDAN / SARJANA PENDIDIKAN MATEMATIKA/ TAMAT 1991

5. UNSYIAH BANDA ACEH /MAGISTER SAINS EKONOMI / TAMAT 2005

6. UNPAD BANDUNG / PROGRAM DOKTOR SAINS EKONOMI / MASUK 2005

Pekerjaan :

Dosen PNS KOOPERTIS WIL. I SUMUT-NAD Pengalaman :

1. Dosen MATEMATIKA ASTRONOMI , MATEMATIKA TEHNIK , MATEMATIKA EKONOMI Akademi Maritim Belawan (AMB) ,Medan , Tahun 2001 – 2005 .

2. Dosen MATEMATIKA EKONOMI , EKONOMIMIKRO , EKONOMI MAKRO di Universitas HKBP NOMMENSEN , UHN Medan , 2012 – sekarang .

Jabatan :

Sekretaris PPL (Program Pengalaman Lapangan ) FKIP HKBP NOMMENSEN MEDAN .

Riset :

Simulasi Gauss Seidel- Reformasi Pajak Indonesia .2003.

Computable General Equilibrium.Pemanasan Global Indonesia.2005.

Untitled Document

MATEMATIKA EKONOMI

SOPAR M.H

�

�

=

−

�

(

�

+

–�

�

�

Contents

=

+

,

=

,

−

4

≥

0

.

=

=

P = Se

e

₄

₀

_.