Polinomial karakteristik matrik dalam aljabar mark-plus Artikel Maryatun

MAKS-PLUS

Maryatun, Siswanto, dan Santoso Budi Wiyono Program Studi Matematika FMIPA UNS

Abstrak. _{Polinomial dalam aljabar maks-plus dapat dinotasikan sebagai}p(z) =⊕m r=0cr

⊗zjr dengan c

r, jr ∈ R. Bilangan jr disebut degree (derajat) dari p(z) dan m+ 1 disebut length (panjang). Penelitian ini bertujuan untuk mengkaji ulang polinomial karakteristik dari suatu matriks, sudut terbesar (the greatest corner) dari polinomial karakteristik dan polinomial karakteristik dari matriks khusus dalam aljabar maks-plus. Selanjutnya diberikan contoh untuk polinomial karakteristik matriks, sudut terbesar, dan matriks khusus. Hasil penelitian ini, yaitu suatu polinomial karakteristik suatu matriks, sudut terbesar dengan menggunakan nilai eigen dan polinomial karakteristik dari matriks khusus, yaitu polinomial karakteristik dari matriks diagonal dominan dan matriks atas

T ={0,−∞}.

Kata kunci_{: polinomial karakteristik, sudut terbesar, matriks khusus, matriks diagonal} dominan, matriks atasT ={0,−∞}.

1. Pendahuluan

Aljabar maks-plus merupakan himpunan bilangan R_{maks =} R_{∪ {−∞} yang}

dilengkapi dengan dua operasi biner yakni operasi ”maksimum” dan operasi ”plus”

(Bacelli et al. [2]). Aljabar maks-plus banyak diterapkan untuk menyelesaikan

persoalan di bidang teori graf, kombinatorik, teori sistem, teori antrian, dan

pro-ses stokastik. Polinomial maks-plus terdapat dalam aljabar maks-plus. Polinomial

maks-plus dapat dinyatakan dalam bentuk p(z) = ⊕m

r=0cr ⊗zjr dengan cr, jr ∈ R.

Bilangan jr disebut degree (derajat) dari p(z) dan m+ 1 disebut length (panjang)

(Butkovic [3]).

Pemfaktoran polinomial maks-plus berbeda dengan pemfaktoran pada

alja-bar konvensional (Butkovic [3]). Menurut Anton [1], jika A adalah suatu matriks

berukuran n×n maka nilai eigen λ dapat diperoleh dengan mencari akar-akar

da-ri persamaan det(λI − A) = 0. Persamaan tersebut disebut sebagai persamaan

karakteristik dari A. Schutter [8] dan Farlow [6] menunjukkan bagaimana cara

me-nentukan persamaan karakteristik dalam aljabar maks-plus. Dalam hal ini penulis

ingin membahas tentang polinomial karakteristik matriks dalam aljabar maks-plus.

Penelitian ini bertujuan untuk mengkaji ulang polinomial karakteristik dalam

aljabar maks-plus. Selanjutnya, dicari sudut terbesar dari polinomial karakteristrik

menggunakan nilai eigen terbesar. Kemudian, dicari polinomial karakteristik dari

matriks khusus, yaitu polinomial karakteristik dari matriks diagonal dominan dan

2. POLINOMIAL KARAKTERISTIK MAKS-PLUS

Menurut Butcovic [3], bentuk dari polinomial karakteristik didefinisikan

seba-gai berikut.

Definisi 2.1. JikaA = (aij)∈R n×n

maka polinomial karakteristik maks-plus adalah

χA(x) = maper(A⊕x⊗I)

= maper        

a11⊕x a12 · · · a1n

a21 a22⊕x · · · a2n

..

. ... ...

an1 an2 · · · ann⊕x

       

= xn⊕δ1⊗xn−1⊕. . .⊕δn−1⊗x⊕δn

dapat ditulis χA(x) = Σ⊕_k=0,...,nδn−k⊗xk dengan δ0 = 0.

Contoh 2.1. Dari Butcovic dan Murfit [4]. Diberikan suatu matriksA =



   

1 3 2

0 4 1

2 5 0

     ,

dengan menggunakan Definisi 2.1 dapat diperoleh

χA(x) = maper



   

1⊕x 3 2

0 4⊕x 1

2 5 0⊕x

     ,

sehingga didapatkan polinomial karakteristik matriks A adalah

χA(x) = (1⊕x)⊗(4⊕x)⊗(0⊕x)⊕3⊗1⊗2⊕2⊗0⊗5⊕

3⊗0⊗(0⊗x)⊕(1⊕x)⊗1⊗5⊕2⊗(4⊕x)⊗2

= x3⊕4⊗x2⊕6⊗x⊕8.

Jadi, polinomial karakteristik dari matriksAadalahχA(x) =x3⊕4⊗x2⊕6⊗x⊕8.

Contoh 2.2. Dari Jafari dan Hosseinyazdi [7] dan Cuninghame-Green [5].

Diberik-an suatu matriks B =



   

2 1 4

1 0 1

2 2 1



   

polinomial karakteristik dari matriks B adalah

χB(x) = maper



   

2⊕x 1 4

1 0⊕x 1

2 2 1⊕x



   

= (2⊕x)⊗(0⊕x)⊗(1⊕x)⊕1⊗1⊗2⊕4⊗1⊗2

⊕1⊗1⊗(1⊕x)⊕(2⊕x)⊗1⊗2⊕4⊗(0⊕x)⊗2

= x3⊕2⊗x2⊕6⊗x⊕7.

Jadi, polinomial karakteristik dari matriks B adalahχB(x) = x3⊕2⊗x2⊕6⊗x⊕7.

Teorema 2.2. Jika A = (aij) ∈ R n×n

, maka δk = ∑⊕_B∈Pk₍A₎maper(B) untuk k =

1, . . . , n, dengan Pk(A) adalah himpunan submatriks utama A dengan orde k.

Bukti.

Koefisien δk merupakan koefisien dari xn−k di χA(x) dan karena itu bobot

maksi-mum dari semua permutasi adalah n−k dari x, dan k adalah konstanta dari baris

dan kolom yang berbeda dari submatriks A dengan menghapus baris dan kolomx.

Kolom x hanya muncul dari diagonal yang sesuai submatriks utama. Oleh karena

itu, dengan mudah menemukan δn =maper(A) dan δ1 =maks(a11, . . . , ann).

Teorema 2.3. Jika A = (aij) ∈ R n×n

, maka χA(x) = xn jika dan hanya jika DA

asiklik.

Bukti.

JikaDAasiklik, maka semua bobot permutasi yang berhubungan dengan submatriks

utama Aadalah ε dan dengan demikian semuaδk=ε. JikaDA mengandungcycle,

misalnya (i1, , ik, i1) untuk beberapak ∈N, makamaper(A(i1, . . . , ik))> ε, sehingga

δk > ε.

3. SUDUT TERBESAR (THE GREATEST CORNER) POLINOMIAL

KARAKTERISTIK MAKS-PLUS

Menurut Butcovic [3], definisi sudut tebesar (the greatest corner) sebagai

Definisi 3.1. Sudut terbesar dalam polinomial maks-plusp(z) = ⊕m

r=0cr⊗zjr,m >0

adalah maksr=0,...,m−1c_jrm−−cjmr.

Definisi 3.2. Jikap(x) = χA(x)dengan A= (aij)∈R n×n

maka m=n, jr =r, dan

cr =δn−r untuk r= 0,1, . . . , n dengan cm =δ0 = 0. Oleh karena itu, sudut terbesar

dari χA(x) adalah maksr=0,...,n−1δ n

−r

n−r atau ekuivalen dengan maksk=1,...,n δk

k.

Contoh 3.1. Diberikan matriksA=



   

8 4 3

2 6 1

1 2 5



   

. Akan dicari sudut terbesar dari

χA(x).

Berdasarkan matriks A, diperoleh polinomial karakteristik dari matriks A sesuai

dengan Definisi 2.1 adalahχA(x) =x3⊕8⊗x2⊕14⊗x⊕19. Sehingga didapatkan

δ0 = 0, δ1 = 8, δ2 = 14, δ3 = 19. Dari polinomial karakteristik tersebut, dicari sudut

terbesar dari χA(x) dengan Definisi 3.2 yaitu

maksr=0,...,n−1

δn−r

n−r = maks{

δ3−0 3−0,

δ3−1 3−1,

δ3−2 3−2}

= maks{19

3 , 14

2 , 8 1}

= maks{19

3 ,7,8} = 8.

Didapatkan sudut terbesar dari χA(x) adalah 8.

Teorema 3.3. Jika A= (aij)∈R n×n

maka sudut terbesar dari χA(x) adalah λ(A).

Contoh 3.2. Diberikan matriksA=



   

8 4 3

2 6 1

1 2 5



   

. Akan dicari besarnya nilai eigen

dalam matriks. Berdasarkan matriks A, didapatkan graf berarah seperti gambar

[image:5.595.209.413.146.300.2]

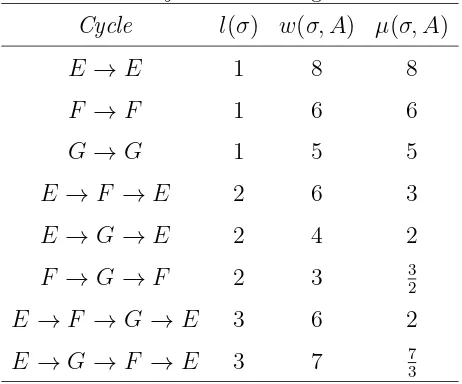
Gambar 1. Graf berbobot berarah

Berdasarkan gambar 1 diperoleh cycle dasar seperti pada tabel 1.

Tabel 1. Cycle dasar dari gambar 1

Cycle l(σ) w(σ, A) µ(σ, A)

E →E 1 8 8

F →F 1 6 6

G→G 1 5 5

E →F →E 2 6 3

E →G →E 2 4 2

F →G →F 2 3 3₂

E →F →G→E 3 6 2

E →G →F →E 3 7 7

3

Berdasarkan tabel, didapatkan λ(A) =maksσµ(σ, A) = maks{8,6,5,3,2,3₂,2,7₃}

= 8 yang berarti bahwa nilai eigen adalah 8. Pada Contoh 3.1, didapatkan sudut

terbesar dariχA(x) adalah 8, sehingga dapat disimpulkan bahwa sudut terbesar dari

χA(x) sama dengan nilai eigen. Hal ini terbukti dari Teorema 3.3, didapatkan sudut

terbesar dari χA(x) = 8.

4. POLINOMIAL KARAKTERISTIK DARI MATRIKS KHUSUS

4.1. Matriks Diagonal Dominan.

Definisi 4.1. Matriks diagonal dominan adalah matriks bujur sangkar yang meme-nuhi |aii|>∑n

[image:5.595.195.426.374.566.2]

Teorema 4.2. Jika A = (aij) ∈ R n×n

diagonal dominan, maka semua submatriks

pokok dari A dan semua koefisien dari polinomial karakteristik maks-plus dapat

di-temukan dengan rumus δk = ai1i1 +ai2i2 +. . .+aikik, untuk k = 1, . . . , n dengan

ai1i1 > ai2i2 > . . . > ainin.

Contoh 4.1. Dari Teorema 4.2. Diberikan contoh suatu matriks diagonal dominan

A=



   

5 0 0

2 4 0

0 0 3



   

, dengan menggunakan Definisi 2.1 didapatkan

χA(x) = maper



   

5⊕x 0 0

2 4⊕x 0

0 0 3⊕x



   

sehingga didapatkan

χA(x) = (5⊕x)⊗(4⊕x)⊗(3⊕x)⊕0⊗0⊗0⊕0⊗2⊗0⊕

0⊗2⊗(3⊕x)⊕(5⊕x)⊗0⊗0⊕0⊗(4⊕x)⊗0

= x3⊕5⊗x2⊕9⊗x⊕12.

Berdasarkan Teorema 4.2 didapatkan polinomial karakteristik dari matriks diagonal

dominan A sebagai berikut.

δk =ai1i1 +ai2i2 +. . .+aikik,

δ0 = 0, δ1 = 5, δ2 = 5 + 4 = 9, dan δ3 = 5 + 4 + 3 = 12. Sehingga berdasarkan

Definisi 2.1, diperoleh polinomial karaketristik

χA(x) = Σ⊕k=0,...,nδn−k⊗xk

= x3⊕5⊗x2⊕9⊗x⊕12.

Jadi polinomial karakteristik dari matriks diagonal dominan A adalah

4.2. Matriks Atas T ={0,−∞}.

Definisi 4.3. Matriks atas T = {0,−∞} adalah matriks bujur sangkar dengan anggota matriks tersebut {0,−∞}. Matriks A = (aij) ∈ Tn×n dengan δk = 0 atau

δk =−∞, untuk setiap k = 1, . . . , n.

Contoh 4.2. Diberikan contoh matriks atas T ={0,−∞}, yaitu

T =



   

0 0 −∞

−∞ −∞ 0

0 −∞ −∞



    ,

dengan menggunakan Definisi 2.1 didapatkan polinomial karakteristik dari matriks

T yaitu

χT(x) = (0⊕x)⊗(−∞ ⊕x)⊗(−∞ ⊕x)⊕0⊗0⊗0⊕ −∞ ⊗ −∞ ⊗ −∞ ⊕

0⊗ −∞ ⊗(−∞ ⊕x)⊕(0⊕x)⊗0⊗ −∞ ⊕ −∞ ⊗(−∞ ⊕x)⊗0

= x3⊕x2⊕x⊕0.

Jadi, polinomial karakteristk dari matriks atas T adalah

χT(x) =x3 ⊕x2 ⊕x⊕0.

5. KESIMPULAN

(1) Polinomial karakteristik maks-plus dari matriks A dapat diperoleh dengan

χA(x) adalah

xn⊕δ1⊗xn−1⊕. . .⊕δn−1⊗x⊕δn atau Σ⊕k=0,...,nδn−k⊗xk, dengan δ0 = 0.

(2) Sudut terbesar (the greatest corner) dari χA(x) dapat dicari dengan rumus

maksr=0,...,n−1δ n

−r

n−r atau ekuivalen dengan maksk=1,...,n δk

k. Adanya

kesama-an nilai sudut terbesar dari polinomial karakteristik maks-plus dengkesama-an nilai

eigen.

(3) Terdapat dua matriks khusus dalam aljabar maks-plus, yaitu sebagai berikut.

(a) Matriks Diagonal Dominan

Menurut Teorema 4.2 matriks diagonal dominan adalah matriks bujur

Misalkan A=



      

a11 a12 · · · a1n

a21 a22 · · · a2n

... ... ... ...

an1 an2 · · · ann.



      

Untuk mencari koefisien dari polinomial karakteristik matriks tersebut

adalahδk=ai1i1+ai2i2+. . .+aikik, untuk k = 1, . . . , n, dengan ai1i1 >

ai2i2 >. . .>ainin. Sehingga dihasilkan polinomial karakteristik dengan

menggunakan Definisi 2.1 dan sesuai Teorema 4.2 didapatkan

χA(x) = Σ⊕k=0,...,nδn−k⊗xk,

denganδ0 = 0.

(b) Matriks AtasT ={0,−∞}

Matriks atasT ={0,−∞}adalah matriks bujur sangkar dengan

anggo-ta matriks tersebut {0,−∞}. Matriks A= (aij)∈Tn×n dengan δk = 0

atau δk =−∞, untuk setiap k = 1, . . . , n.

DAFTAR PUSTAKA

[1] Anton, H.,Aljabar Linear Elementer, Edisi Kelima, terjemahan, Erlangga, Jakarta, 1997. [2] Baccelli, F., G. Cohen, G. J. Olsder, and P. Quadrat,Synchronization and Linearity, John

Wiley and Sons, New York, 2001.

[3] Butkovic, P.,Max-Linear Systems: Theory and Algorithms, Springer Monographs in Mathe-matics, Springer-Verlag London Ltd., London, 2010.

[4] Butkovic, P. and L. Murfitt,Calculating Essential Terms of a Characteristic Maxpolinomial. Central European Journal of Operations Research. 8 (2000), no. 3, pp. 237-247.

[5] Cuninghame-Green, R. A.,The Characteristic Maxpolynomial of a Matrix. Mathematical Ana-lysis and Application 95 (1983), pp. 110-116.

[6] Farlow, Kasie G., Max-Plus Algebra, Master’s thesis, Virginia Polytechnic Institute and State University, Virginia, 2009.

[7] Jafari, H. and M. Hosseinyazdi,Characteristic Max-Polynomial of a Triangular and Certain Strictly Double R-astic Matrices. Applied Science and Technology 8 (2012), no.1, pp. 47-56. [8] Schutter, B. D., Max-Algebraic System Theory for Discrete Event Systems, Ph. D. thesis,