Hendra Gunawan. 2 Oktober 2013

(1)

MA1101 MATEMATIKA 1A MA1101 MATEMATIKA 1A

Hendra Gunawan

Semester I, 2013/2014 Semester I, 2013/2014

2 Oktober 2013

(2)

Apa yang Telah Dipelajari pada Bab 2 Apa yang Telah Dipelajari pada Bab 2

2.1 Dua Masalah Satu Tema 2.2 Turunan

2.3 Aturan Turunan

2.4 Turunan Fungsi Trigonometri 2 5 Aturan Rantai

2.5 Aturan Rantai

2.6 Notasi Leibniz dan Turunan Tingkat Tinggi 2 7 Turunan Implisit

2.7 Turunan Implisit

2.8 Laju yang Berkaitan

2 9 Dif i l d H i

2.9 Diferensial dan Hampiran

10/02/2013 (c) Hendra Gunawan 2

(3)

BAB 3. PENGGUNAAN TURUNAN

MA1101 MATEMATIKA 1A

BAB 3. PENGGUNAAN TURUNAN

(4)

Sasaran Kuliah Hari Ini Sasaran Kuliah Hari Ini

3 1 Maksimum dan Minimum 3.1 Maksimum dan Minimum

Menentukan nilai maksimum dan minimum dari suatu fungsi yang diberikan

dari suatu fungsi yang diberikan.

3.2 Kemonotonan dan Kecekungan

Menentukan selang kemonotonan (dan titik ekstrim), serta selang kecekungan dan titik) g g belok, dari suatu fungsi yang diberikan.

(5)

3.1 MAKSIMUM DAN MINIMUM

Menentukan nilai maksimum dan minimum dari suatu fungsi yang diberikan.

(6)

Maksimum dan Minimum Maksimum dan Minimum

Misalkan f : I → R dan c є I. (Pada umumnya, I me‐

rupakan suatu selang di R) rupakan suatu selang di R).

Nilai f(c) disebut nilai maksimum apabila f(c) ≥ f(x) untuk setiap x є I.

Nilai f(c) disebut nilai minimum apabila f(c) ≤ f(x) untuk setiap x є I.

Nilai maksimum atau minimum disebut nilai ekstrim Nilai maksimum atau minimum disebut nilai ekstrim.

4

Contoh 1. Misalkan f(x) = x², y

x є [ 1 2] Nilai maksimumnya x є [‐1,2]. Nilai maksimumnya adalah 4 [= f(2)], sedangkan nilai minimumnya adalah 0

‐1 0 2 x

nilai minimumnya adalah 0 [= f(0)]. Perhatikan grafiknya.

(7)

Teorema Eksistensi Nilai Ekstrim Teorema Eksistensi Nilai Ekstrim

Jika f kontinu pada [a b] maka f akan mencapai Jika f kontinu pada [a,b], maka f akan mencapai nilai maksimum dan minimum pada [a,b].

Catatan. Teorema ini mengatakan bahwa

kekontinuan merupakan syarat cukup untuk kekontinuan merupakan syarat cukup untuk

eksistensi nilai ekstrim (maksimum dan minimum).

Sbg contoh fungsi pada Contoh 1 merupakan Sbg contoh, fungsi pada Contoh 1 merupakan fungsi yang kontinu pada [‐1,2], shg mempunyai nilai maksimum dan minimum pada [‐1 2]

nilai maksimum dan minimum pada [ 1,2].

(8)

Contoh Contoh

2. Fungsi yang tidak kontinu mungkin saja mem‐

2. Fungsi yang tidak kontinu mungkin saja mem punyai nilai ekstrim. Sebagai contoh, fungsi yang didefinisikan sebagai berikut:

f(x) = ‐1, jika x = 0,

jik 0 1

= x, jika 0 < x < 1,

= 2, jika x = 1,

mempunyai nilai maksimum 2 [= f(1)] dan nilai minimum ‐1 [= f(0)] Gambar grafiknya!

minimum 1 [ f(0)]. Gambar grafiknya!

(9)

Contoh Contoh

3. Namun demikian, ketakkontinuan tidak 3. Namun demikian, ketakkontinuan tidak menjamin eksistensi nilai ekstrim. Sebagai contoh, fungsi

1

g(x) = ½, jika x = 0 atau 1,

1

= x, jika 0 < x < 1,

1 0

tidak mempunyai nilai ekstrim, baik maksimum maupun minimum.

(10)

Teorema Lokasi Titik Ekstrim Teorema Lokasi Titik Ekstrim

Misalkan daerah asal f adalah selang I yang memuat titik c Jika f(c) adalah nilai ekstrim maka c haruslah titik c. Jika f(c) adalah nilai ekstrim, maka c haruslah merupakan titik kritis, yakni c merupakan

(i) titik ujung selang I,

( ) j g g

atau (ii) titik stasioner f, yakni f ’(c) = 0,

atau (iii) titik singular f, yakni f ’(c) tidak ada.

Catatan. Teorema ini mengatakan bahwa nilai ekstrim hanya mungkin tercapai di titik kritis, karena itu

teorema ini dikenal pula sebagai Teorema Titik Kritis.

Untuk menentukan nilai ekstrim suatu fungsi, teorema

ini menganjurkan utk mencari titik‐titik kritisnya dulu.

(11)

Contoh Contoh

4. Fungsi. u gs f(x) = xf( ) ², x є [‐1,2], , є [ , ], ^y ⁴ mencapai nilai maksimum 4

di x = 2 (titik ujung kanan)

d l d

dan nilai minimum 0 di x = 0 (titik stasioner).

5 F i f( ) | | [ 1 2]

‐1 0 2 x

5. Fungsi f(x) = |x|, x є [‐1,2], mencapai nilai maksimum 2

di x = 2 (titik ujung kanan) ²

y

di x 2 (titik ujung kanan) dan nilai minimum 0 di x = 0

(titik singular). ^‐1 ⁰ ² ^x

(12)

Contoh 6. Tentukan nilai maksimum dan minimum

( ) ³ ²

fungsi f(x) = ‐2x³ + 3x² + 1 pada [‐1,2].

Jawab: Turunan ff adalah f ’(x) = ‐6xf ( ) ²+ 6x = 6x(1 – x).( ) Jadi titik stasionernya adalah 0 dan 1, sedangkan titik singularnya tidak ada. Dengan demikian terdapat

(

empat titik kritis, yakni ‐1, 0, 1, dan 2 (dua titik ujung selang dan dua titik stasioner).

M t T Ek i t i Nil i Ek t i d T

Menurut Teorema Eksistensi Nilai Ekstrim dan Teorema Lokasi Titik Ekstrim, f mencapai nilai ekstrim di titik kritis tsb Sekarang bandingkan nilai f di titik‐titik kritis tsb:

tsb. Sekarang bandingkan nilai f di titik titik kritis tsb:

f(‐1) = 6, f(0) = 1, f(1) = 2, f(2) = ‐3.

Jadi f mencapai nilai maksimum 6 di x = ‐1 (titik ujung

kiri) dan nilai minimum ‐3 di x = 2 (titik ujung kanan).

(13)

Latihan Latihan

1 Tentukan nilai ekstrim fungsi f(x) = x³– 12x 1. Tentukan nilai ekstrim fungsi f(x) = x 12x pada [‐3,3].

2 Tentukan titik titik kritis fungsi 2. Tentukan titik‐titik kritis fungsi

g(x)= 50x – x²/2, jika 0 ≤ x ≤ 20,

= 60x – x², jika 20 < x ≤ 60.

Tentukan nilai maksimum dan minimumnya Tentukan nilai maksimum dan minimumnya.

[Ingat baik‐baik fungsi ini; nanti akan ketemu lagi!]

(14)

3.2 KEMONOTONAN & KECEKUNGAN

Menentukan selang kemonotonan (dan titik ekstrim), serta selang kecekungan dan titik belok, dari suatu fungsi yang diberikan

(15)

Kemonotonan Kemonotonan

Fungsi f dikatakan naik pada selang I apabila Fungsi f dikatakan naik pada selang I apabila untuk setiap x, y є I dengan x < y berlaku

f(x) < f(y) f(x) < f(y).

Fungsi f dikatakan turun pada selang I apabila

k i I d b l k

untuk setiap x, y є I dengan x < y berlaku f(x) > f(y).

Fungsi naik atau turun pada selang I dikatakan monoton padap I.

(16)

Teorema Kemonotonan Fungsi Teorema Kemonotonan Fungsi

Misalkan f kontinu dan mempunyai turunan Misalkan f kontinu dan mempunyai turunan pada I. Jika f ’(x) > 0 untuk setiap x є I, maka f naik pada I Jika f ’(x) < 0 untuk setiap x є I f naik pada I. Jika f (x) < 0 untuk setiap x є I, maka f turun pada I.

Catatan Pada Catatan. Pada gambar di

samping, titik

c

p g,

c merupakan titik minimum.

c x

(17)

Contoh 1 Contoh 1

Diketahui f(x) = x³ – 12x. Kita hitung turunannya:

Diketahui f(x) x 12x. Kita hitung turunannya:

f ’(x) = 3x² – 12 = 3(x – 2)(x + 2).

Periksa tanda f ’(x) pada garis bilangan real:

‐2 2

+ + + – – – + + +

Menurut Teorema Kemonotonan, fungsi f naik pada (‐∞,‐2) dan juga pada (2,∞); dan f turun

(18)

Kecekungan Kecekungan

Misalkan f mempunyai turunan Misalkan f mempunyai turunan pada I = (a,b).

Jika f ’ naik pada I maka grafik cekung ke atas

Jika f naik pada I, maka grafik fungsi f cekung ke atas pada I.

g

Jika f ’ turun pada I, maka grafik

fungsig ff cekung ke bawah padag p I. cekung ke bawahcekung ke bawah

(19)

Teorema Kecekungan Fungsi Teorema Kecekungan Fungsi

Misalkan f mempunyai turunan kedua pada I. Jika f ’’(x) > 0 untuk setiap x є I,

maka grafik fungsi f cekung ke atas pada I.

Jika f ’’(x) < 0 untuk setiap x є I, maka grafik fungsi f cekung ke bawah pada I.

Penjelasan. Jika f ’’(x) > 0, maka

f ’(x) naik Jadi f cekung ke atas cekung ke atas

f’’(x) > 0

f (x) naik. Jadi f cekung ke atas.

Jika f ’’(x) < 0, maka f ’(x) turun.

Jadi f cekung ke bawah.

cekung ke atas

f’’( )

f g

f’’(x) < 0

(20)

Contoh 2 Contoh 2

Diketahui f(x) = x³ – 12x. Maka, f ’(x) = 3x²– 12 dan f ’’(x) = 6x. Periksa tanda f ’’(x):

– – – + + +

Menurut Teorema Kecekungan grafik fungsi f

0

– – – + + +

Menurut Teorema Kecekungan, grafik fungsi f cekung ke atas pada (0,∞) dan cekung ke

bawah pada (‐∞,0).

bawah pada ( ,0).

Catatan. Titik x = 0 merupakan titik infleksi (titik belok) grafik fungsi f. Di titik ini, grafik (t t be o ) g a u gs f t t , g a

fungsi f mengalami perubahan kecekungan.

(21)

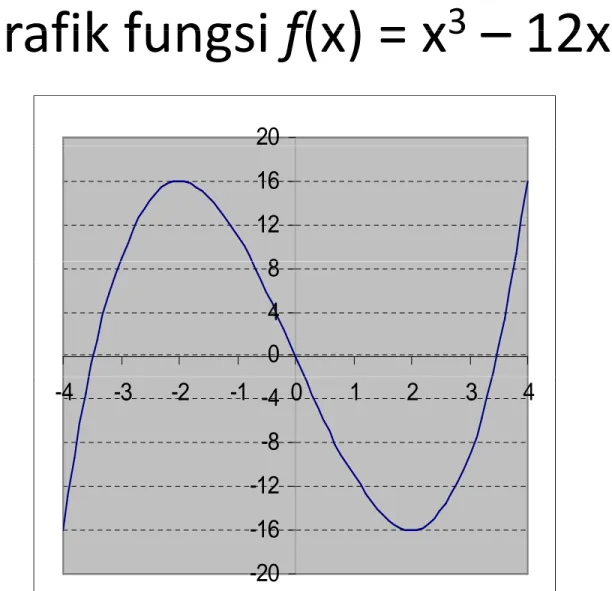
Grafik fungsi f(x) = x

³

12x Grafik fungsi f(x) = x

³

– 12x.

20

8 12 16

0 4 8

-12 -8

-4 -3 -2 -1 -4 0 1 2 3 4

-20 -16 12

(22)

Latihan Latihan

1. Tentukan pada selang mana grafik fungsi f(x) =

3 2 ² 1 ik t t T t k l

x³ – 2x² + x + 1 naik atau turun. Tentukan pula pada selang mana ia cekung ke atas atau cekung ke bawah serta titik belok nya bila ada

ke bawah, serta titik belok‐nya, bila ada.

2. Air dituangkan ke dalam tangki berbentuk kerucut terbalik dengan laju 8 dm³/menit kerucut terbalik dengan laju 8 dm³/menit.

Jika tinggi tangki tersebut adalah 24 dm dan jari‐jari permukaan atasnya 12 dm nyatakan jari‐jari permukaan atasnya 12 dm, nyatakan tinggi air (h) sebagai fungsi dari waktu (t).

Selidiki kemonotonan dan kecekungan grafik Selidiki kemonotonan dan kecekungan grafik fungsi h(t).