ANALISIS ENERGI DAN FUNGSI GELOMBANG POTENSIAL NON SENTRAL ROSEN MORSE PLUS HULTHEN, ROSEN MORSE, DAN COULOMB MENGGUNAKAN POLINOMIAL ROMANOVSKI

commit to user

POTENSIAL NON SENTRAL ROSEN MORSE PLUS HULTHEN, ROSEN MORSE, DAN COULOMB

MENGGUNAKAN POLINOMIAL ROMANOVSKI

TESIS

Untuk Memenuhi Sebagian Persyaratan untuk Mencapai Derajat Magister

Program Studi Ilmu Fisika

Oleh

CECILIA YANUARIEF S911108003

PROGRAM PASCASARJANA UNIVERSITAS SEBELAS MARET

SURAKARTA 2012

commit to user

ii

SENTRAL ROSEN MORSE PLUS HULTHEN, ROSEN MORSE, DAN COULOMB MENGGUNAKAN POLINOMIAL ROMANOVSKI

TESIS Oleh Cecilia Yanuarief

S911108003

Komisi Nama Tanda Tangan Tanggal

Pembimbing

Pembimbing I. Dra. Suparmi, M.A., Ph.D ... 16 Oktober 2012 NIP. 19520915 197603 2 001

Pembimbing II. Drs. Cari, M.Sc., M.A., Ph.D ... 16 Oktober 2012 NIP : 19610306 198503 1 002

Telah dinyatakan memenuhi syarat Pada tanggal 16 Oktober 2012 Ketua Program Studi Ilmu Fisika

Program Pascasarjana UNS

Drs.Cari, M.Sc., M.A., Ph.D NIP : 19610306 198503 1 002

commit to user

iii

SENTRAL ROSEN MORSE PLUS HULTHEN, ROSEN MORSE, DAN COULOMB MENGGUNAKAN POLINOMIAL ROMANOVSKI

TESIS

Oleh Cecilia Yanuarief

S911108003

Tim Penguji

Jabatan Nama Tanda

Tangan Tanggal Ketua Drs. Harjana, M.Si., Ph.D NIP.19590725 198601 1 002 ... … November 2012 Sekretaris

Dr. Agus Supriyanto, S.Si.,M.Si

NIP.19690826 199903 1 001 ... … November 2012 Anggota

Penguji

Dra. Suparmi, M.A., Ph.D

NIP. 19520915 197603 2 001 ... … November 2012 Drs. Cari, M.Sc., M.A., Ph.D

NIP . 19610306 198503 1 002 ... … November 2012

Telah dipertahankan di depan penguji Dinyatakan memenuhi syarat Pada tanggal … November 2012

Direktur Program Pascasarjana UNS Ketua Program Studi Ilmu Fisika

Prof. Dr. Ir. Ahmad Yunus, M.S NIP. 19610717198601 1 001

Drs. Cari, M.Sc., M.A., Ph.D NIP : 19610306 198503 1 002

commit to user

iv Saya menyatakan dengan sebenarnya bahwa:

1. Tesis yang berjudul “ANALISIS ENERGI DAN FUNGSI GELOMBANG POTENSIAL NON SENTRAL ROSEN MORSE PLUS HULTHEN, ROSEN MORSE, DAN COULOMB MENGGUNAKAN POLINOMIAL ROMANOVSKI” ini adalah karya penelitian saya sendiri, tidak terdapat karya ilmiah yang pernah diajukan oleh orang lain untuk memperoleh gelar akademik, serta tidak terdapat karya atau pendapat yang pernah ditulis atau diterbitkan oleh orang lain kecuali secara tertulis digunakan sebagai acuan dalam naskah dan disbutkan dalam sumber acuan serta daftar pustaka. Apabila dikemudian hari terbukti pernyataan saya ini tidak benar, maka saya bersedia menerima sanksi sesuai ketentuan peraturan perundang-undangan (Permendiknas No. 17, Tahun 2010)

2. Publikasi sebagian atau keseluruhan dari isi tesis ini pada jurnal atau forum ilmiah lain harus seijin dan menyertakan tim pembimbing sebagai author dan PPs-UNS sebagai institusinya. Apabila dalam waktu sekurang-kurangnya satu semester (enam bulan sejak pengesahan tesis) saya tidak melakukan publikasi dari sebagian atau keseluruhan tesis ini, maka PPs-UNS berhak mempublikasikannya pada jurnal ilmiah yang diterbitkan oleh Prodi Ilmu Fisika PPs-UNS. Apabila saya melakukan pelanggaran dari ketentuan publikasi ini, maka saya bersedia mendapatkan sanksi akademik yang berlaku.

Surakarta, 30 Oktober 2012 Mahasiswa

Cecilia Yanuarief S911108003

commit to user

v

MOTTO DAN PERSEMBAHAN

Semua orang percaya kalau hidup tidak akan selalu seperti ini.. Karena mereka paham apapun yang dilakukan harus bisa membawa manfaat.. Jangan mengeluhkan dunia.. Karena sesungguhnya suatu saat semua pasti akan berubah.. Tapi, semua bergantung pada arah kita melangkah dan doa yang kita

munajatkan.. Jangan TAKUT!!

Torehan tinta emasku ini aku persembahkan untuk :

1. Allah SWT yang telah memberiku kesempatan dan rizki,

2. Kedua orang tuaku yang telah memberiku kasih sayang dan dukungan, 3. ”Vegy“ yang selalu setia mengantarku kemanapun aku pergi.

commit to user

vi

Potensial Non Sentral Rosen Morse Plus Hulthen, Rosen Morse, dan Coulomb Menggunakan Polinomial Romanovski”. Tesis: Program Pascasarjana Ilmu

Fisika Universitas Sebelas Maret Surakarta. Pembimbing: (1). Dra. Suparmi, M.A., Ph.D (2). Drs. Cari, M.Sc., M.A., Ph.D

ABSTRAK

Penelitian ini bertujuan untuk menentukan nilai energi dan fungsi gelombang untuk potensial non sentral Rosen Morse plus Hulthen, Rosen Morse, dan Coulomb.

Potensial non sentral Rosen Morse plus Hulthen, Rosen Morse, dan Coulomb merupakan potensial yang variabelnya terpisahkan. Fungsi gelombang polar dan radial untuk potensial non sentral Rosen Morse plus Hulthen, dan Rosen Morse, diselesaikan menggunakan metode polinomial Romanovski sedangkan fungsi gelombang radial potensial non sentral Rosen Morse plus Coulomb diselesaikan dengan metode yang lebih umum, yaitu NU. Penyelesaian persamaan Schrödinger dengan polinomial Romanovski dilakukan dengan cara mereduksi persamaan differensial orde 2 menjadi persamaan differensial tipe hypergeometry perantara melalui substitusi variabel yang sesuai dengan parameter Romanovski. Dari persamaan hypergeometry perantara yang diperoleh, penentuan persamaan tingkat energi dan fungsi gelombang ditentukan dengan mensubstitusi permisalan fungsi gelombang Romanovski kedalam persamaan hypergeometry perantara dan menjabarkannya sehingga diperoleh persamaan differensial Romanovski.

Tingkat energi yang diperoleh merupakan fungsi tertutup sedangkan fungsi gelombang baik radial maupun polar dinyatakan dalam bentuk persamaan polinomial Romanovski. Spektrum energi dan fungsi gelombang bagian radial dan polar serta grafik probabilitas divisualisasikan dengan pemrograman komputer yang berbasis Matlab. Visualisasi fungsi gelombang radial yang terbentuk mendiskripsikan nilai probabilitas ditemukannya partikel, sedangkan Visualisasi fungsi gelombang polar yang terbentuk mendiskripsikan momentum sudut spin suatu elektron yang berada dalam pengaruh potensial sistem.

commit to user

vii

Non Central Rosen Morse plus Hulthen, Rosen Morse, and Coulomb Potential With Romanovski Polynomial”. Thesis: Program Pascasarjana Ilmu Fisika

Universitas Sebelas Maret Surakarta. Advisor: (1). Dra. Suparmi, M.A., Ph.D (2). Drs. Cari, M.Sc., M.A., Ph.D

ABSTRACT

This research is aimed to determine energy levels and wave functions for non central Rosen Morse potential plus Hulthen, Rosen Morse, and Coulomb.

Non central Rosen Morse potential plus Hulthen, Rosen Morse, and Coulomb are the potensial which separated variable. Polar and radial wave functions of non central Rosen Morse potential plus Hulthen, and Rosen Morse solved by Romanovski polynomial method and radial wave functions of non central Rosen Morse potential plus Coulomb potential solved by NU. To solve the Schrödinger equation with Romanovski polinomial has reduced the two order differential equation to be intermediatery hypergeometry differential equation with substituting of variable which appropriate to Romanovski’s parameter. From intermediatery hypergeometry differential equation which given, the energy levels and wave function are determine with subtituting Romanovski’s wave function like into the intermediatery hypergeometry differential equation and derivating until be obtained the Romanovski’s differensial equation. From its Romanovski’s hypergeometry equation would determine the energy levels and wave function.

Energy levels which obtained make up closed function and the wave functions, consist of radial and polar part, have showed by Romanovski polinomial form. Energy spectrum, wave functions and probability graph have visualized with Matlab. Visualization of radial wave functions which obtained are descripting the probability value to found a particle, whereas, Visualization of radial wave functions which obtained are descripting the spin-angular momentum of electron which under system potential effect.

commit to user

viii

Puji syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan tesis dengan judul, “Analisis Energi dan Fungsi Gelombang Potensial Non Sentral Rosen Morse Plus Hulthen, Rosen Morse, dan Coulomb Menggunakan Polinomial Romanovski” ini. Penyusunan tesis ini bertujuan untuk memenuhi sebagian persyaratan guna memperoleh gelar Magister pada Program Studi Ilmu Fisika Program Pascasarjana Universitas Sebelas Maret Surakarta.

Penulis menyadari bahwa tanpa bantuan dari berbagai pihak, tesis ini tidak akan terwujud. Oleh karena itu, penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Bapak Prof. Dr. Ir. Ahmad Yunus, M.S, selaku Direktur Program Pascasarjana Universitas Sebelas Maret Surakarta.

2. Bapak Drs. Cari, M.Sc., M.A., Ph.D, selaku Ketua Program Studi Ilmu Fisika Pascasarjana Universitas Sebelas Maret Surakarta, sekaligus sebagai Pembimbing II yang telah banyak memberikan banyak bimbingan dan arahan serta motivasi kepada penulis sehingga mampu menyelesaikan tesis ini. 3. Ibu Dra. Suparmi, M.A., Ph.D, selaku pembimbing I yang telah dengan sabar

membimbing dan mengajari penulis, serta memberikan semangat kepada penulis untuk dapat menyelesaikan tesis ini.

4. Bapak/Ibu Dosen Program Studi Ilmu Fisika Pascasarjana Universitas Sebelas Maret Surakarta yang telah memberikan banyak ilmu tentang fisika.

commit to user

ix

Penelitian ini didanai oleh Program Hibah Penelitian Tim Pascasarjana (HPTP) Universitas Sebelas Maret tahun 2012 dengan nomer kontrak 2345/UN27.16/PN/2012.

Surakarta, 2012 Penulis

commit to user x Halaman HALAMAN JUDUL ... i HALAMAN PERSETUJUAN ... ii

HALAMAN PENGESAHAN ...iii

SURAT PERNYATAAN... iv

MOTTO DAN PERSEMBAHAN ... v

ABSTRAK ... vi

KATA PENGANTAR ...viii

DAFTAR ISI ... x

DAFTAR GAMBAR ... xi

DAFTAR TABEL ...xiii

DAFTAR SIMBOL...xvi

BAB I PENDAHULUAN A. Latar Belakang Masalah... 1

B. Identifikasi Masalah... 4

C. Batasan Masalah... 4

D. Rumusan Masalah... 5

E. Tujuan Penelitian... 5

commit to user

xi

A. Definisi Persamaan Schrödinger... 7

B. Persamaan Schrödinger untuk Koordinat 3 Dimensi... 11

C. Persamaan Schrödinger untuk Koordinat Bola... 14

D. Penyelesaian Fungsi Gelombang dan Energi Dengan Fungsi Hypergeometry... 19

E. Penyelesaian Fungsi Gelombang dan Energi Dengan Polinomial Romanovski... 29

F. Penyelesaian Fungsi Gelombang dan Energi Dengan Metode NU... 31

G. Potensial Hulthen... 35

H. Potensial Rosen Morse... 36

I. Potensial Coulomb... 38

J. Potensial Non Sentral Rosen Morse... 38

BAB III METODE PENELITIAN A. Lokasi dan Waktu Penelitian... 40

B. Objek Penelitian... 40

C. Instrumentasi Penelitian... 40

D. Prosedur Penelitian... 41

1. Langkah Kerja...41

commit to user

xii

A. Pendahuluan... 46

B. Penyelesaian Bagian Polar Potensial Non Sentral Rosen Morse plus Hulthen... 47

C. Penyelesaian Bagian Radial Potensial Non Sentral Rosen Morse plus Hulthen... 71

D. Penyelesaian Bagian Radial Potensial Non Sentral Rosen Morse plus Rosen Morse... 94

E. Penyelesaian Bagian Radial Potensial Non Sentral Rosen Morse plus Coulomb... 118

BAB V KESIMPULAN DAN SARAN A. Kesimpulan... 133

B. Saran... 134

DAFTAR PUSTAKA... 135

commit to user

xiii

Gambar (2.1). Potensial Kotak... 12 Gambar (2.2). Potensial Rosen Morse dan Spektrumnya... 37 Gambar (4.1). Perbandingan Perubahan Fungsi Gelombang Polar Terhadap

Perubahan Nilai 𝜇... 66 Gambar (4.2). Perbandingan Perubahan Fungsi Gelombang Polar Terhadap

Perubahan Nilai 𝜈... 67 Gambar (4.3). Perbandingan Perubahan Fungsi Gelombang Polar Terhadap

Perubahan Nilai 𝜈 dan 𝜇... 69 Gambar (4.4). Grafik Tingkat Energi Potensial Non Sentral Rosen Morse

plus Hulthen... 86 Gambar (4.5). Visualisasi Fungsi Gelombang Radial Potensial Non Sentral

Rosen Morse plus Hulthen... 91 Gambar (4.6). Grafik Probabilitas Potensial Non Sentral Rosen Morse plus

Hulthen…………... 92 Gambar (4.7). Grafik Tingkat Energi Potensial Non Sentral Rosen Morse plus

Rosen Morse... 111 Gambar (4.8). Visualisasi Fungsi Gelombang Radial Potensial Non Sentral

Rosen Morse plus Rosen Morse……….. 116 Gambar (4.9).Grafik Probabilitas Potensial Non Sentral Rosen Morse plus

Hulthen... 100 Gambar (4.10). Grafik Tingkat Energi Potensial Non Sentral Rosen Morse plus

commit to user

xiv

Rosen Morse plus Coulomb... 130 Gambar (4.12). Grafik Probabilitas Potensial Non Sentral Rosen Morse plus

commit to user

xv

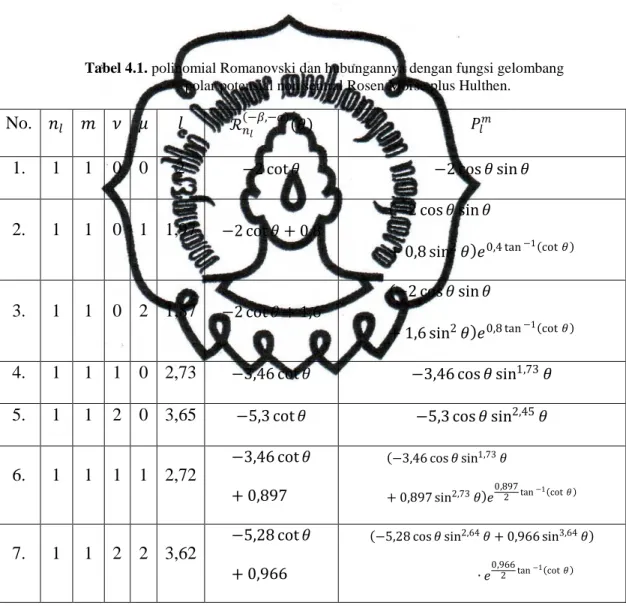
Tabel 4.1. Polinomial Romanovski dan Hubungannya Dengan Fungsi Gelombang Polar Potensial Non Sentral Rosen Morse plus Hulthen... 64 Tabel 4.2. Polinomial Romanovski dan Hubungannya Dengan Fungsi

Gelombang Radial Potensial Non Sentral Rosen Morse plus Hulthen... 89 Tabel 4.3. Polinomial Romanovski dan Hubungannya Dengan Fungsi

Gelombang Radial Potensial Non Sentral Rosen Morse plus Rosen Morse... 115 Tabel 4.4. Fungsi Gelombang Radial Potensial Non Sentral Rosen Morse plus

commit to user xvi 𝑚𝑒 = massa elektron, 9,1 × 10−31kg, ℎ = konstanta Planck, 6,626 × 10−34_Js , ℏ = ℎ 2𝜋 = 1,05 × 10 −34_Js, 𝜔 = kecepatan sudut, Ψ = fungsi gelombang, 𝑘 = bilangan gelombang, 𝑝 = momentum, 𝜆 = 2𝜋 𝑘 = panjang gelombang, 𝜐 = 2𝜋 𝜔 = frekuensi, 𝐾 = energi kinetik, 𝑉 = energi potensial,

𝑛 = bilangan kuantum utama, 𝑙 = bilangan kuantum orbital, 𝑚 = bilangan kuantum magnetik, 𝑛_𝑟 = bilangan kuantum radial,

commit to user

PENDAHULUAN

A. Latar Belakang

Mekanika kuantum sudah lama dikenal sebagai “ilmu dasar” bagi penelaahan gejala dan sifat berbagai sistem mikroskopik. Pemanfaatannya tidak hanya berhasil memperluas dan memperdalam pemahaman peristiwa alami di dalam laboratorium, tetapi juga menghasilkan kemajuan teknologi secara luas, dan mempengaruhi kualitas serta corak hidup manusia secara tidak langsung. Perkembangan mekanika kuantum berakar dari konsep dasar teori kuantum yang meliputi dugaan-dugaan baik secara diskrit maupun ketidakteraturan. Teori kuantum terbukti mampu menjelaskan fenomena kuantum dari sistem makroskopik seperti superkonduktivitas dan superfluiditas yang memiliki potensi aplikasi penting. Dalam proses pembelajaran fisika kuantum khususnya mekanika kuantum selalu melibatkan persamaan-persamaan yang rumit dan penyelesaiannya membutuhkan analisa dan pemikiran yang tinggi. Contoh masalah yang cukup rumit adalah penyelesaian fungsi gelombang dari persamaan Schrödinger.

Persamaan Schrödinger diperoleh mulai dari fungsi gelombang partikel yang bergerak bebas. Perluasan persamaan Schrödinger untuk kasus khusus partikel bebas ke kasus umum dengan sebuah partikel yang mengalami gaya sembarang yang berubah terhadap ruang dan waktu merupakan suatu

commit to user

membuktikan bahwa perluasan itu benar. Yang bisa dilakukan hanyalah mengambil postulat bahwa persamaan Schrödinger berlaku untuk berbagai situasi fisis dan membandingkan hasilnya dengan hasil eksperimen. Jika hasilnya cocok, postulatnya harus dibuang dan pendekatan lain harus dijajaki. Dengan kata lain, persamaan Schrödinger tidak bisa diturunkan dari prinsip pertama, tetapi persamaan Schrödinger itu sendirilah yang merupakan prinsip pertama. Persamaan Schrödinger telah menghasilkan ramalan yang sangat tepat mengenai hasil eksperimen yang diperoleh dan harus diakui bahwa persamaan Schrödinger menyatakan suatu postulat yang berhasil mengenai aspek tertentu dari dunia fisis. Perlu diketahui bahwa persamaan Schrödinger bukanlah penambahan banyak postulat yang diperlukan untuk memberikan cara kerja alam fisis, karena hukum kedua Newton mengenai gerak yang dalam mekanika klasik dipandang sebagai postulat dapat diturunkan dari persamaan Schrödinger.

Penelitian tentang penyelesaian fungsi gelombang pada persamaan Schrödinger merupakan penelitian yang sangat penting dalam ilmu fisika modern. Berbagai metode penyelesaian persamaan Schrödinger untuk gerak partikel bermuatan pada potensial-potensial sentral dan non sentral dengan suatu potensial vektor atau suatu potensial skalar terpisahkan telah dikembangkan (Ikot, 2011). Berbagai metode yang telah dikembangkan tersebut diantaranya adalah metode Supersymmetry, metode shape invariant

commit to user

Romanovski (Cari, 2012).

Penelitian ini menitikberatkan pada penyelesaian fungsi gelombang dan energi persamaan Schrödinger dari suatu elektron yang bergerak di dalam potensial kombinasi antara dua potensial non-sentral menggunakan polinomial Romanovski. Pada tahun 1884 Sir E. J. Routh merumuskan metode ini dan pada tahun 1929 dikembangkan kembali oleh V. I. Romanovski yang kemudian dikenal dalam beberapa literatur matematika sebagai polinomial “Romanovski”. Polinomial Romanovski merupakan bagian dari penyelesaian eksak untuk beberapa kasus biasa dan supersymetry mekaniaka kuantum (Cari, 2012). Secara umum, tepatnya persamaan Schrödinger memegang peranan spesial karena banyak member peran dalam menjelaskan fenomena mikroskopik serta menjadi tokoh kunci dalam ilmu fisika. Polinomial Romanovski dan polinomial Jacobi memiliki hubungan yang cukup erat, yaitu, polinomial Romanovski merupakan bentuk kompleks dari polinomial Jacobi tetapi pada kenyataannya substitusi faktor kompleks pada polinomial Jacobi tidak selalu menghasilkan polinomial Romanovski. Polinomial Romanovski dapat diturunkan sebagai solusi polinomial dari ODE.

Pembahasan polinomial Romanovski tidak begitu meluas dalam berbagai aplikasi, tetapi dalam beberapa tahun terakhir ini metode ini cukup popular dalam pemecahan kasus-kasus mekanika kuantum, seperti pada contoh diskripsi spektrum atom hidrogen pada potensial Coulomb (Yanuarief, 2012), atau gerak partikel pada potensial Hulthen atau Rosen Morse.

commit to user

Berdasarkan uraian dari latar belakang di atas, maka dapat dituliskan perumusan masalah sebagai berikut :

1. Bagaimana cara agar proses pembelajaran fisika kuantum khususnya mekanika kuantum dapat diselesaikan dengan persamaan-persamaan yang relatif lebih sederhana?

2. Sejauh mana konsep mekanika kuantum dapat menjelaskan berbagai fenomena mikroskopik di alam semesta?

3. Seberapa luas cakupan konsep persamaan Schrödinger dalam aplikasi mendiskripsikan gerak partikel pada beberapa potensial?

4. Bagaimana penyelesaian fungsi gelombang dan energi persamaan Schrödinger untuk potensial non sentral dilakukan?

5. Bagaimana cara mengaplikasikan polinomial Romanovski untuk menyelesaikan persamaan Schrödinger?

6. Sebesar apa peran polinomial Romanovski sebagai metode popular dalam penyelesaian persamaan Schrödinger?

C. Batasan Masalah

Penelitian ini dibatasi dalam lingkup :

1. Penyelesaian fungsi gelombang dan energi persamaan Schrödinger untuk potensial non sentral,

commit to user

Hulthen, non sentral Rosen Morse plus Rosen Morse, dan non sentral Rosen Morse plus Coulomb,

3. Metode analitik untuk menjabarkan potensial non sentral Rosen Morse plus Hulthen dan potensial non sentral Rosen Morse plus Rosen Morse adalah menggunakan metode polinomial Romanovski.

4. Metode analitik untuk menjabarkan potensial non sentral Rosen Morse plus Coulomb adalah menggunakan kombinasi metode NU dan polinomial Romanovski.

D. Rumusan Masalah

1. Bagaimana analisis energi dan fungsi gelombang potensial non sentral Rosen Morse plus Hulthen?

2. Bagaimana analisis energi dan fungsi gelombang potensial non sentral Rosen Morse plus Rosen Morse?

3. Bagaimana analisis energi dan fungsi gelombang potensial non sentral Rosen Morse plus Coulomb?

E. Tujuan Penelitian

Tujuan yang ingin dicapai dalam penelitian ini adalah :

1. Mendeskripskan hasil analisis energi dan fungsi gelombang potensial non sentral Rosen Morse plus Hulthen.

commit to user

sentral Rosen Morse plus Rosen Morse.

3. Mendiskripsikan hasil analisis energi dan fungsi gelombang potensial non sentral Rosen Morse plus Coulomb.

F. Manfaat Penelitian 1. Bagi Peneliti :

a. Mengembangkan kemampuan peneliti dalam penguasaan tekhnik penyelesaian fungsi gelombang dan energi persamaan Schrödinger untuk berbagai potensial,

b. Mengembangkan kemampuan peneliti dalam penguasaan bahasa Matlab, c. Mengembangkan kemampuan logika berfikir dalam penyusunan alur

program komputasi. 2. Bagi Pembaca :

a. Visualisasi grafik yang dihasilkan dapat mempemudah pemahaman tentang mekanika kuantum.

b. Sebagai sumber informasi tambahan dalam komputasi sehingga dapat memberikan kontribusi bagi ilmu pengetahuan.

commit to user

BAB II KAJIAN TEORI

A. Definisi Persamaan Schrödinger

Baik hukum Newton, persamaan Maxwell, maupun persamaan Schrödinger tidak dapat diturunkan dari seperangkat asas dasar, namun pemecahan yang diperoleh darinya ternyata sesuai dengan pengamatan percobaan. Persamaan Schrödinger hanya dapat dipecahkan secara eksak untuk beberapa potensial sederhana tertentu; yang paling sederhana adalah potensial konstan dan potensial osilator harmonik. Kedua kasus sederhana ini memang tidak “fisis”, dalam artian bahwa pemecahannya tidak dapat diperiksa kebenarannya dengan percobaan. Namun demikian, kasus sederhana ini cukup bermanfaat dalam memberikan gambaran tentang teknik umum pemecahan persamaan Schrödinger.

Untuk merumuskan persamaan Schrödinger yang sampai saat ini dipergunakan untuk memecahkan persoalan fisika kuantum, berbagai pertimbangan haruslah diperhatikan karena diketahui bahwa tidak adanya hasil percobaan yang dapat dijadikan sebagai bahan perbandingan. Beberapa pertimbangan itu diantaranya:

1. Tidak boleh melanggar hukum kekekalan energi. Meskipun mengorbankan sebagian besar kerangka fisik klasik, hukum kekekalan energi adalah salah satu asas yang tetap berlaku.

commit to user

𝐾 + 𝑉 = 𝐸 (2.1)

dengan 𝐾 = energi kinetik, 𝑉 = energi potensial, 𝐸 = energi total (jumlah energi kinetik dan energi potensial)

Karena kajian fisika kuantum dibatasi oleh keadaan relativistik, maka, 𝐾 =1

2𝑚𝑒𝑣

2 ₌ 𝑝2

2𝑚𝑒 (2.2)

dengan 𝑚_𝑒 = massa partikel elementer

2. Bentuk persamaan differensial apapun yang ditulis, haruslah taat asas terhadap hipotesis deBroglie. Jika pemecahan persamaan matematika bagi suatu partikel dengan momentum 𝑝, maka pemecahan yang didapat harus berbentuk sebuah fungsi gelombang dengan panjang gelombang 𝜆 yang nilainya sama dengan ℎ

𝑝, dan dengan mendefinisikan 𝑝 = ℏ𝑘 maka nilai energi kinetik pada persamaan (2.2) menjadi, 𝐾 = 𝑝2 2𝑚𝑒 = ℏ𝑘 2 2𝑚𝑒 = ℏ2 2𝑚𝑒𝑘 2 _(2.3) dengan ℏ = ℎ

2𝜋 , ℎ = konstanta plank, 𝑘 = bilangan gelombang

3. Persamaan yang dihasilkan diharapkan dapat memberikan informasi tentang probabilitas untuk menemukan partikelnya, misalnya, probabilitas tersebut berubah secara tidak kontinu, karena ini partikelnya berarti bahwa partikelnya menghilang secara tiba-tiba dari satu titik dan muncul kembali pada titik lainnya. Sehingga disyaratkan bahwa fungsinya harus bernilai tunggal, tidak boleh ada dua atau lebih probabilitas untuk menemukan partikel di satu titik

commit to user

yang sama. Kemudian juga harus bersifat linier, agar gelombangnya memiliki sifat superposisi yang diharapkan sebagai milik gelombang yang berperilaku baik.

Dengan memeilih bernalar dalam urutan terbalik, akan ditinjau terlebih dahulu pemecahan dari persamaan yang sedang dicari. Dengan rujukan awal beberapa fungsi gelombang,

1. Gelombang berjalan:

𝑦 𝑥, 𝑡 = 𝐴 sin 𝑘𝑥 − ω𝑡 (2.4)

2. Gelombang elektromagnet (GEM):

𝐸 𝑥, 𝑡 = 𝐸₀sin 𝑘𝑥 − ωt (2.5a)

𝐵 𝑥, 𝑡 = 𝐵0sin 𝑘𝑥 − ωt (2.5b)

dengan 𝑦 𝑥, 𝑡 , 𝐸 𝑥, 𝑡 dan 𝐵 𝑥, 𝑡 = simpangan; 𝐴, 𝐸0 dan 𝐵0 = amplitudo, 𝑘 = bilangan gelombang, 𝑥 = posisi, ω = kecepatan sudut, 𝑡 = waktu.

Oleh karena itu, dipostulatkan bahwa gelombang deBroglie partikel bebas Ψ 𝑥, 𝑡 memiliki bentuk matematis yang juga serupa dengan persamaan (2.4) dan (2.5), yaitu bentuk dasar sebuah gelombang dengan amplitudo yang merambat dalam arah 𝑥 positif, memiliki panjang gelombang 𝜆 =2𝜋

𝑘 dan frekuensi 𝜈 = 2𝜋

𝜔. Dengan mengabaikan ketergantungan pada waktu Ψ 𝑥, 𝑡 = 0 , maka dapat dituliskan persamaan gelombang deBroglie partikel bebas sebagai,

commit to user

Persamaan differensial, yang pemecahannya adalah Ψ 𝑥, 𝑡 dapat mengandung turunan terhadap 𝑥 atau 𝑡, tetapi haruslah hanya bergantung pada orde satu dari Ψ dan turunan-turunannya, sehingga suku seperti Ψ2 _atau ∂Ψ

∂𝑡 2

tidak boleh muncul. Persamaan haruslah mengandung potensial 𝑉, jika 𝑉 berorde satu, maka agar taat asas dengan kekekalan energi persamaan (2.1), 𝐾 harus juga berorde satu. Dengan merujuk pada persamaan (2.3), maka satu-satunya cara untuk memperoleh suku yang mengandung 𝑘2 adalah dengan mendifferensialkan dua kali persamaan (2.6), yaitu,

d2

dx2Ψ 𝑥 = −𝑘 2_Ψ

0sin 𝑘𝑥 = −𝑘2Ψ 𝑥 (2.7)

dengan mensubstitusi persamaan (2.3) ke persamaan (2.7) maka didapatkan, d2

dx2Ψ 𝑥 = − 2𝑚𝑒

ℏ2 𝐾Ψ 𝑥 (2.8)

dan dengan mensubstitusi persamaan (2.1) ke persamaan (2.8) maka didapatkan, d2 dx2Ψ 𝑥 = − 2𝑚𝑒 ℏ2 𝐸 − 𝑉 Ψ 𝑥 d2 dx2Ψ 𝑥 = 2𝑚𝑒 ℏ2 𝑉Ψ 𝑥 − 2𝑚𝑒 ℏ2 𝐸Ψ 𝑥 (2.9)

kemudian kedua ruas dari persamaan (2.9) dikalikan dengan − ℏ2

2𝑚𝑒 , menjadi,

− ℏ2 2𝑚𝑒

d2

dx2Ψ 𝑥 + 𝑉Ψ 𝑥 = 𝐸Ψ 𝑥 (2.10)

Perlu ditekankan bahwa yang dilakukan bukanlah suatu penurunan, tetapi adalah membentuk suatu persamaan differensial yang memiliki sifat-sifat:

commit to user

2. linier dan bernilai tunggal,

3. memberikan pemecahan partikel bebas yang sesuai dengan sebuah gelombang deBroglie tunggal.

Persamaan lain dapat dibentuk dengan sifat-sifat yang sama, namun hanya persamaan (2.10) yang lolos pengujian ketat tersebut sebagai yang sesuai dengan hasil-hasil percobaan dalam berbagai situasi fisis. Persamaan (2.10) merupakan persamaan Schrödinger bebas waktu (stasioner) satu dimensi. Meskipun gelombang nyata selain bergantung pada koordinat ruang dan juga pada waktu, dan bahwa alam bukanlah berdimensi satu, melainkan tiga, maka berbagai pemecahan persamaan (2.10) untuk berbagai koordinat dalam kasus-kasus fisika kuantum dapat dilakukan dengan model-model matematika yang sudah ada. (Krane, 171-173).

B. Persamaan Schrödinger untuk koordinat 3 Dimensi

Pada sistem koordinat 3 dimensi, misal pada contoh kasus suatu partikel yang terkurung didalam potensial kotak berukuran 𝑎 × 𝑏 × 𝑐 (gambar 2.1)

commit to user

Gambar (2.1). Potensial Kotak

maka di setiap dinding kotak memiliki energi potensial yang sangat besar, 𝑉 → ∞, sedangkan energi potensial didalam kotak bernilai 0. Oleh karena partikel bergerak bebas memiliki probabilitas dalam arah 3 dimensi, maka berlaku operator nabla sebagai divergensi dari gradient Ψ 𝑥, 𝑦, 𝑧 atau laplacian Ψ 𝑥, 𝑦, 𝑧 untuk operasi differensial (Arfken, 49-54) pada suku pertama persamaan (2.10), yaitu, ∇2₌ ∂2 ∂x2+ ∂2 ∂y2+ ∂2 ∂z2 (2.11)

maka persamaan (2.10) untuk kasus potensial kotak dapat ditulis menjadi, − ℏ2

2𝑚∇

2_{Ψ 𝑥, 𝑦, 𝑧 = 𝐸Ψ 𝑥, 𝑦, 𝑧 (2.12)}

dengan mensubstitusi persamaan (2.11) ke persamaan (2.12), maka dapat dituliskan, − ℏ2 2𝑚 ∂2Ψ 𝑥,𝑦,𝑧 ∂x2 + ∂2Ψ 𝑥,𝑦,𝑧 ∂y2 + ∂2Ψ 𝑥,𝑦,𝑧 ∂z2 = 𝐸Ψ 𝑥, 𝑦, 𝑧 (2.13) b a c 𝑥 𝑦 𝑧

commit to user

Persamaan (2.13) tersebut diselesaikan dengan metode sparasi variabel dengan menguraikan,

Ψ 𝑥, 𝑦, 𝑧 = 𝑋 𝑥 𝑌 𝑦 𝑍 𝑧 (2.14)

dengan,

𝑋 𝑥 : bagian fungsi gelombang fungsi 𝑥, 𝑌 𝑦 : bagian fungsi gelombang fungsi 𝑦, 𝑍 𝑧 : bagian fungsi gelombang fungsi 𝑧,

kemudian persamaan (2.14) disubstitusi ke persamaan (2.13), maka menjadi,

− ℏ2 2𝑚 ∂2 ∂x2𝑋 𝑥 𝑌 𝑦 𝑍 𝑧 + ∂2 ∂y2𝑋 𝑥 𝑌 𝑦 𝑍 𝑧 + ∂2 ∂z2𝑋 𝑥 𝑌 𝑦 𝑍 𝑧 = 𝐸𝑋 𝑥 𝑌 𝑦 𝑍 𝑧 − ℏ2 2𝑚 𝑌 𝑦 𝑍 𝑧 d2 dx2𝑋 𝑥 + 𝑋 𝑥 𝑍 𝑧 d2 dy2𝑌 𝑦 + 𝑋 𝑥 𝑌 𝑦 d2 dz2𝑍 𝑧 = 𝐸𝑋 𝑥 𝑌 𝑦 𝑍 𝑧 (2.15)

Jika kedua ruas dari persamaan (2.15) dibagi dengan 𝑋 𝑥 𝑌 𝑦 𝑍 𝑧 , maka persamaan (2.15) menjadi, − ℏ2 2𝑚 1 𝑋 𝑥 d2 dx2𝑋 𝑥 + 1 𝑌 𝑦 d2 dy2𝑌 𝑦 + 1 𝑍 𝑧 d2 dz2𝑍 𝑧 = 𝐸 (2.16)

dengan 𝐸 merupakan energi total untuk sistem 3 dimensi, dimana,

𝐸 = 𝐸_𝑥+ 𝐸_𝑦 + 𝐸_𝑧 (2.17)

commit to user − ℏ2 2𝑚𝑒 1 𝑋 𝑥 d2 dx2𝑋 𝑥 − ℏ2 2𝑚𝑒 1 𝑌 𝑦 d2 dy2𝑌 𝑦 − ℏ2 2𝑚𝑒 1 𝑍 𝑧 d2 dz2𝑍 𝑧 = 𝐸𝑥 + 𝐸𝑦 + 𝐸𝑧 (2.18) Dari bentuk persamaan (2.18), terlihat bahwa masing-masing suku telah mewakili satu fungsi gelombang, sehingga persamaan tersebut dapat direduksi menjadi,

−_2𝑚ℏ2 𝑒 d2 dx2𝑋 𝑥 = 𝐸𝑥𝑋 𝑥 (2.19a) −_2𝑚ℏ2 𝑒 d2 dy2𝑌 𝑦 = 𝐸𝑦𝑌 𝑦 (2.19b) − ℏ2 2𝑚_𝑒 d2 dz2𝑍 𝑧 = 𝐸𝑧𝑍 𝑧 (2.19c)

Persamaan (2.19) tersebut tidak lain merupakan persamaan Schrödinger untuk partikel dalam potensial satu dimensi.

C. Persamaan Schrödinger Untuk Koordinat Bola

Beberapa potensial yang digunakan bersama pada persamaan Schrödinger merupakan potensial sentral dan merupakan fungsi dari jarak antara suatu partikel terhadap beberapa titik yang dijadikan acuan/pusat. Pada sistem koordinat bola, suatu titik pada ruang didefinisikan sebagai jarak r dari sebuah titik tersebut terhadap pusat sistem koordinat dengan arah dua sudut, yaitu zenithal 𝜃 dan

azimuthal 𝜙. Oleh karena itu, dapat ditentukan secara spesifik posisi dari suatu

titik tunggal dalam sistem tiga dimensi menggunakan triplets 𝑟, 𝜃, 𝜙 tersebut. Untuk menentukan letak atau posisi dalam koordinat bola untuk setiap titik, jangkauan dari setiap titik tersebut harus dibatasi. Secara umum ditentukan yaitu

commit to user

𝑟 ≥ 0, 0 ≤ 𝜃 ≤ 𝜋, dan 0 ≤ 𝜙 ≤ 2𝜋. Pada bagian tersebut, seseorang dapat mengajukan sebuah pertanyaan tentang “mengapa” diperlukan sistem koordinat bola dalam proses penyelesaian persamaan Schrödinger untuk suatu partikel dalam fungsi potensial. Untuk potensial-potensial fisika, sekaligus menjadi sebuah jawaban, persamaan Schrödinger dalam sistem koordinat bola dapat di selesaikan dengan menggunakan pemisahan (sparasi) fungsi gelombang 3 dimensi menjadi fungsi gelombang yang berdiri sendiri (independen), yaitu : Ψ 𝑟, 𝜃, 𝜙 = 𝑅 𝑟 Υ 𝜃, 𝜙 .

Pergerakan suatu molekul berputar atau pada suatu elektron yang bergerak mengelilingi suatu inti atom dapat lebih baik didiskripsikan dalam koordinat bola dengan hanya mereduksi dalam koordinat tunggal atau 1 dimensi.

Sebagai contoh, pada potensial Coulomb yang merepresentasikan suatu interaksi elektromagnetik antara sebuah elektron dan sebuah proton yang dapat dituliskan : V 𝑥, 𝑦, 𝑧 = − 𝑒′2

𝑥2_+𝑦2_+𝑧2 dalam koordinat kartesian, dimana 𝑒 ′₌

𝑒

4𝜋𝜀0, 𝑒 merupakan muatan elementer dan 𝜀0 merupakan permitivitas ruang hampa. Persamaan tersebut tidak begitu saja dapat digunakan untuk menyelesaikan persamaaan Schrödinger dengan potensial V 𝑥, 𝑦, 𝑧 karena potensial yang digunakan pada persamaan Schrödinger tidak dipisahkan dalam koordinat kartesian. Transformasi ke dalam koordinat bola dari koordinat kartesian akan mempermudah penyelesaian persamaan Schrödinger karena pada

commit to user

kasus ini, potensial V 𝑥, 𝑦, 𝑧 dapat di ubah menjadi V 𝑟 = −𝑒′2

𝑟 yang hanya mengandung fungsi 𝑟. Untuk transformasi tersebut, digunakan konversi 𝑟 = 𝑥2_{+ 𝑦}2_{+ 𝑧}2_{. Selanjutnya, variabel-variabel 𝑥, 𝑦, 𝑧 pada koordinat kartesian}

dapat dihubungkan ke dalam variabel-variabel 𝑟, 𝜃, 𝜙 pada koordinat bola, dengan hubungan :

𝑥 = 𝑟 sin 𝜃 cos 𝜙 𝑦 = 𝑟 sin 𝜃 sin 𝜙 𝑧 = 𝑟 cos 𝜃 (2.20) Dengan devinisi ∇2 untuk koordinat bola,

∇2= 1 𝑟2 𝜕 𝜕𝑥 𝑟 2 𝜕 𝜕𝑟 + 1 𝑟2_{sin 𝜃} 𝜕 𝜕𝜃 sin 𝜃 𝜕 𝜕𝜃 + 1 𝑟2_sin2_𝜃 𝜕2 𝜕𝜙2 (2.21)

Sehingga persamaan Schrödinger dapat dituliskan sebagai berikut, −_2𝑚ℏ2 _𝑟12 𝜕 𝜕𝑥 𝑟 2 𝜕 𝜕𝑟 + 1 𝑟2_{sin 𝜃} 𝜕 𝜕𝜃 sin 𝜃 𝜕 𝜕𝜃 + 1 𝑟2_sin2_𝜃 𝜕2 𝜕𝜙2 + 𝑉 𝑟 Ψ 𝑟, 𝜃, 𝜙 = 𝐸Ψ 𝑟, 𝜃, 𝜙 (2.22)

Potensial yang digunakan adalah potensial sentral karena hanya dipengaruhi oleh jarak 𝑟 dari pusat koordinat dengan solusi pemisahan variabel pada persamaan Schrödinger,

Ψ 𝑟, 𝜃, 𝜙 = 𝑅 𝑟 Υ 𝜃, 𝜙 (2.23)

Menggunakan persamaan (2.23) tersebut, maka persamaan (2.22) dapat dituliskan: 1 𝑅 𝑟 𝑑 𝑑𝑟 𝑟 2 𝑑𝑅 𝑟 𝑑𝑟 + 2𝑚𝑒𝑟2 ℏ2 𝐸 − 𝑉 𝑟 = − 1 Υ 𝜃,𝜙 1 sin 𝜃 𝜕 𝜕𝜃 sin 𝜃 𝜕Υ 𝜃,𝜙 𝜕𝜃 + 1 sin2𝜃 𝜕2Υ 𝜃,𝜙 𝜕𝜙2 (2.24)

commit to user

Kedua ruas dari persamaan (2.24) memiliki variabel-variabel yang berbeda namun keduanya dapat disebandingkan hanya jika keduanya memiliki nilai konstanta sebesar 𝜆. Oleh karena itu, persamaan (2.24) dapat dibagi menjadi persamaan-persamaan: 1 𝑟2 𝑑 𝑑𝑟 𝑟 2 𝑑𝑅 𝑟 𝑑𝑟 + 2𝑚𝑒 ℏ2 𝐸 − 𝑉 𝑟 − 𝜆 𝑟2 𝑅 𝑟 = 0 (2.25) 1 sin 𝜃 𝜕 𝜕𝜃 sin 𝜃 𝜕Υ 𝜃,𝜙 𝜕𝜃 + 1 sin2_𝜃 𝜕2_{Υ 𝜃,𝜙} 𝜕𝜙2 + 𝜆Υ 𝜃, 𝜙 = 0 (2.26)

Dari persamaan (2.25) dan (2.26), tiap persamaan telah mewakili masing-masing variabel yang terpisahkan, yaitu variabel radial pada persamaan (2.25) dan variabel sudut pada persamaan (2.26). Penyelesaian bagian sudut dari persamaan (2.26) dapat langsung diselesaikan karena bagian ini tidak terdapat sebuah potensial ataupun energi sehingga dapat dilanjutkan kembali untuk memisahkan variabel dengan mengasumsikan fungsi sudut Υ 𝜃, 𝜙 = Θ 𝜃 Φ 𝜙 . Sehingga persamaan (2.26) memiliki bentuk penyelesaian,

1 sin 𝜃 𝑑 𝑑𝜃 sin 𝜃 𝑑Θ 𝜃 𝑑𝜃 + 𝜆 − 𝑚2 sin2𝜃 Θ 𝜃 = 0 (2.27) 1 Φ 𝜙 𝑑2Φ 𝜙 𝑑𝜙2 = −𝑚 2 _(2.28)

Dengan 𝑚 harus bernilai positif atau bulat negatif, 𝑚 = 0, ±1, ±2, … Konstanta 𝑚 merupakan bilangan kuantum magnetik. Jika kembali pada persamaan yang lebih rumit yang dipengaruhi oleh variabel 𝜃, persamaan (2.27) dapat ditulis kembali dengan mengubah variabel cos 𝜃 = 𝜔.

𝑑 𝑑𝜔 1 − 𝜔 2 𝑑𝑃 𝜔 𝑑𝜔 + 𝜆 − 𝑚2 1−𝜔2 𝑃 𝜔 = 0 (2.29)

commit to user

Dengan 𝑃 𝜔 merupakan polinomial Legendre. Umumnya, persamaan (2.29) memiliki dua penyelesaian independen yang bernilai tak terhingga untuk 𝜔 = ±1. Meskipun demikian, fungsi gelombang yang memenuhi untuk kondisi khusus persamaan (2.29) bernilai terhingga. Akan tetapi, jika konstanta 𝜆 didefinisikan sebagai,

𝜆 = 𝑙 𝑙 + 1 (2.30)

Dengan 𝑙 dinyatakan sebagai bilangan kuantum orbital yang memiliki nilai,

𝑙 = 0, 1, 2, 3, … (2.31)

Untuk nilai-nilai 𝑙 tersebut, maka solusi 𝑃 𝜔 dapat bernilai terhingga untuk semua nilai-nilai 𝜔. Pada definisi fungsi Legendre asosiasi, magnitude dari bilangan kuantum magnetik 𝑚 haruslah terbatas pada nilai-nilai yang lebih kecil atau sama dengan 𝑙 karena polinomial-polinomial Legendre merupakan polinomial-polinomial fungsi 𝑙,

𝑚 = 0, 1, 2, 3, … ≤ 𝑙 (2.32)

Di sisi lain, terdapat nilai 2𝑙 + 1 yang dipenuhi nilai-nilai untuk 𝑚, −𝑙 ≤ 𝑚 ≤ 𝑙. Mensubstitusi persamaan (2.30) ke persamaan (2.25) menunjukkan bahwa fungsi gelombang radial 𝑅 𝑟 dan eigenvalue 𝐸 dari persamaan Schrödinger bergantung pada bilangan kuantum orbital 𝑙 dan dipenuhi oleh persamaan,

𝑑2𝑅 𝑟 𝑑𝑟2

+

2 𝑟 𝑑𝑅 𝑟 𝑑𝑟

+

2𝑚_𝑒 ℏ2

𝐸 − 𝑉 𝑟 −

ℏ2𝑙 𝑙+1 2𝑚_𝑒𝑟2

𝑅 𝑟 = 0

(2.33)

Persamaan (2.33) dapat digambarkan sebagai suatu persamaan differensial biasa dengan koefisien variabel dan dapat diselesaikan dengan metode-metode standar.

commit to user

D. Penyelesaian Fungsi Gelombang dan Energi Dengan Fungsi Hypergeometry Persamaan Schrödinger untuk sistem partikel yang dipengaruhi oleh potensial yang mana energi potensialnya merupakan fungsi posisi biasanya diselesaikan dengan cara mereduksi persamaan Schrödinger menjadi persamaan differensial orde dua fungsi khusus seperti fungsi hypergeometry dengan substitusi variabel yang sesuai. Jika persamaan hypergeometry telah diperoleh, maka tingkat-tingkat energi dan fungsi gelombang akan diperoleh dengan mudah. Variabel baru yang disubstitusikan biasanya diperoleh dengan cara coba-coba, namun sekali dapat menemukan variabel baru untuk suatu sistem, variabel baru untuk sistem yang lain dapat ditentukan dengan menebak yang lebih logis dan terarah.

Persamaan differensial orde dua fungsi hypergeometry yang diusulkan oleh Gauβ dinyatakan sebagai,

𝑧 1 − 𝑧 𝑑2𝜙

𝑑𝑧2 + 𝑐 − 𝑎 + 𝑏 + 1 𝑧 𝑑𝜙

𝑑𝑟 − 𝑎𝑏𝜙 = 0 (2.34)

persamaan (2.34) mempunyai dua buah titik reguler singular yaitu di titik 𝑧 = 0 dan 𝑧 = 1, karena penyelesaian di titik 𝑧 = 0 lebih sederhana dari pada penyelesaian di titik 𝑧 = 1, maka mula-mula dipilih penyelesaian fungsi gelombang 𝜙 di sekitar titik 𝑧 = 0 dengan bentuk deret di sekitar titik 𝑧 = 0, yaitu,

𝜙 = 𝑧𝑠 𝑦𝑛𝑧𝑛 (2.35)

commit to user −𝑎𝑏 𝑦_𝑛𝑧𝑛+𝑠 ~ 𝑛=0 = −𝑎𝑏 𝑦₀𝑧𝑠_{+ 𝑦} 1𝑧𝑠+1+ 𝑦2𝑧𝑠+2+ 𝑦3𝑧𝑠+3+ ⋯ 𝑐 − 𝑎 + 𝑏 + 1 𝑧 𝑑 𝑑𝑧 𝑦𝑛𝑧 𝑛+𝑠 ~ 𝑛=0 = 𝑐 − 𝑎 + 𝑏 + 1 𝑧 𝑠𝑦0𝑧𝑠−1+ 𝑠 + 1 𝑦1𝑧𝑠 + 𝑠 + 2 𝑦2𝑧𝑠+1 + 𝑠 + 3 𝑦₃𝑧𝑠+2+ ⋯ 𝑧 1 − 𝑧 𝑑 2 𝑑𝑧2 𝑦𝑛𝑧𝑛+𝑠 ~ 𝑛=0 = 𝑧 1 − 𝑧 𝑠 − 1 𝑠𝑦₀𝑧𝑠−2+ 𝑠 𝑠 + 1 𝑦₁𝑧𝑠−1+ 𝑠 + 1 𝑠 + 2 𝑦₂𝑧𝑠 + ⋯ 0 = 𝑧𝑠−1 _𝑐𝑠𝑦 0+ 𝑠 𝑠 − 1 𝑦0 + 𝑧𝑠 −𝑎𝑏𝑦0+ 𝑐 𝑠 + 1 𝑦1 − 𝑎 + 𝑏 + 1 𝑠𝑦0+ 𝑠+1𝑠𝑦1−𝑠𝑠−1𝑦0 +𝑧𝑠+1 −𝑎𝑏𝑦1 + 𝑐 𝑠 + 2 𝑦2− 𝑎 + 𝑏 + 1 𝑠 + 1 𝑦1+ 𝑠 + 2 𝑠 + 1 𝑦2− 𝑠+1𝑠𝑦1 +… (2.36)

Persamaan (2.36) merupakan persamaan identitas sehingga koefisien dari masing-masing suku z pangkat tertentu harus di-nol-kan , yaitu,

Untuk 𝑧𝑠−1,

𝑐𝑠𝑦0+ 𝑠 𝑠 − 1 𝑦0 = 0, 𝑠𝑦0 𝑐 + 𝑠 − 1 = 0, 𝑦0 ≠ 0 (2.37)

persamaan (2.37) merupakan “index equation” yang memberikan harga,

𝑠 = 0 atau 𝑠 = 1 − 𝑐 (2.38a)

Untuk 𝑧𝑠,

−𝑎𝑏𝑦0+ 𝑐 𝑠 + 1 𝑦1− 𝑎 + 𝑏 + 1 𝑠𝑦0 + 𝑠 + 1 𝑠𝑦1− 𝑠 𝑠 − 1 𝑦0 = 0

commit to user

−𝑎𝑏 − 𝑎 + 𝑏 + 1 𝑠 − 𝑠 𝑠 − 1 𝑦0+ 𝑐 𝑠 + 1 + 𝑠 + 1 𝑠 𝑦1 = 0

sehingga diperoleh hubungan, 𝑦₁ = 𝑠2+ 𝑎+𝑏 𝑠+𝑎𝑏 𝑠+1 𝑠+𝑐 𝑦0 atau 𝑦1 = 𝑠+𝑎 𝑠+𝑏 𝑠+1 𝑠+𝑐 𝑦0 (2.38b) Untuk 𝑧𝑠+1_, −𝑎𝑏𝑐₁+ 𝑐 𝑠 + 2 𝑦₂ − 𝑎 + 𝑏 + 1 𝑠 + 1 𝑦₁+ 𝑠 + 2 𝑠 + 1 𝑦₂− 𝑠+1𝑠𝑦1=0 −𝑎𝑏 − 𝑠 + 1 𝑠 − 𝑎 + 𝑏 + 1 𝑠 + 1 𝑦1+ 𝑐 𝑠 + 2 + 𝑠 + 2 𝑠 + 1 𝑦2 = 0

sehingga diperoleh hubungan,

𝑦2 = 𝑠 + 1 𝑠 + 𝑎 + 𝑏 + 1 𝑠 + 1 + 𝑎𝑏 𝑐 𝑠 + 2 + 𝑠 + 2 𝑠 + 1 𝑦1 𝑦₂ = 𝑠 2_{+ 𝑠 + 𝑎 + 𝑏 + 1 𝑠 + 1 + 𝑎𝑏} 𝑠 + 2 𝑠 + 𝑐 + 1 𝑦1 𝑦₂ = 𝑠+1+𝑎 𝑠+1+𝑏 𝑠+2 𝑠+𝑐+1 𝑦1 (2.39a)

dengan menghubungkan persamaan (2.38b) ke persamaan (2.39a), maka diperoleh,

𝑦₂ = 𝑠+𝑎 𝑠+𝑏 𝑠+1 𝑠+𝑐

𝑠+1+𝑎 𝑠+1+𝑏

𝑠+2 𝑠+𝑐+1 𝑦0 (2.39b)

Setelah itu, persamaan (2.39b) dapat dinyatakan dalam bentuk umum, yaitu, 𝑦𝑛 =

𝑠+𝑎 𝑠+𝑏 𝑠+1+𝑎 𝑠+1+𝑏 𝑠+1 𝑠+𝑐 𝑠+2 𝑠+𝑐+1

… 𝑠+ 𝑛−1 +𝑎 𝑠+ 𝑛−1 +𝑏

… 𝑠+𝑛 𝑠+𝑐+ 𝑛−1 𝑦0 (2.40)

commit to user 𝑠 = 0, 𝑦_𝑛 = 𝑎 𝑏 1 + 𝑎 1 + 𝑏 1 𝑐 2 𝑐 + 1 … 𝑛 − 1 + 𝑎 𝑛 − 1 + 𝑏 … 𝑛 𝑐 + 𝑛 − 1 𝑦0 𝑦_𝑛 = 𝑎 𝑎+1 𝑏 𝑏+1 𝑐 𝑐+1 … 𝑎+𝑛−1 𝑏+𝑛−1 … 𝑛 𝑐+𝑛−1 ∙𝑛! 𝑦0 (2.41)

maka akan didapatkan bentuk penyelesaian persamaan differensial hypergeometry persamaan (2.34), yaitu, 2𝐹1 𝑎, 𝑏, 𝑐; 𝑧 = 𝜙 = 𝑎 𝑛 𝑏 𝑛 1 𝑛 𝑐 𝑛 𝑧 𝑛 ₌ 𝑎 𝑛 𝑏 𝑛 𝑛! 𝑐 𝑛 𝑧 𝑛 _(2.42) dimana 𝑎𝑛 = 𝑎 𝑎 + 1 𝑎 + 2 𝑎 + 3 … 𝑎 + 𝑛 − 1

agar penyelesaian (2.42) mempunyai nilai, maka penyebut tidak boleh bernilai nol, maka 𝑐 ≠ −𝑛, dimana 𝑛 = 0,1,2,3 …

Jika, 𝑎 = −𝑛 atau 𝑏 = −𝑛 (2.43)

maka bentuk penyelesaian yang berupa deret menjadi terputus sehingga diperoleh penyelesaian yang berhingga yaitu polinomial pangkat 𝑛. Dari kondisi yang dinyatakan pada persamaan (2.43) dapat diperoleh tingkat energi sistem.

Persamaan (2.34) dapat digunakan untuk menganalisis fungsi gelombang dan spektrum energi suatu sistem yang dipengaruhi oleh potensial tertentu. Salah satu contoh potensial yang mempengaruhi sistem yang dapat diselesaikan yaitu potensial Gendehshtein II yang memiliki potensial efektif,

𝑉𝑒𝑓𝑓 = − ℏ2 2𝑚𝑒 2𝑢(𝑡+1 2) cosh 𝑥 sinh2_𝑥 − 𝑢2+𝑡(𝑡+1) sinh2_𝑥 (2.44)

commit to user −_2𝑚ℏ2 𝑒 d2_χ dx2+ ℏ2 2𝑚_𝑒 𝑢2_{+𝑡 𝑡+1} sinh2_𝑥 − ℏ2 2𝑚_𝑒 2𝑢 𝑡+1 2 cosh 𝑥 sinh2_𝑥 χ = 𝐸χ (2.45)

persamaan (2.45) dapat diubah menjadi persamaan differensial orde dua fungsi hypergeometry dengan cara melakukan substitusi variabel, yaitu,

cosh 𝑥 = 1 − 2𝑧 maka sinh 𝑥 = 2 𝑧 𝑧 − 1 (2.46) dari persamaan (2.46), diperoleh,

𝑧 = 1 − cosh 𝑥 2 𝑑𝑧 𝑑𝑥 = − 1 2sinh 𝑥 = − 𝑧 𝑧 − 1 𝑑 𝑑𝑥 = − 𝑧 𝑧 − 1 𝑑 𝑑𝑧 𝑑 𝑑𝑥 𝑑 𝑑𝑥= 𝑑2 𝑑𝑥2 = − 𝑧 𝑧 − 1 𝑑 𝑑𝑧 − 𝑧 𝑧 − 1 𝑑 𝑑𝑧 𝑑2 𝑑𝑥2 = 𝑧 𝑧 − 1 1 2 1 𝑧 𝑧 − 1 2𝑧 − 1 𝑑 𝑑𝑧+ 𝑧 𝑧 − 1 𝑑2 𝑑𝑧2 𝑑2 𝑑𝑥2 = 1 2 2𝑧 − 1 𝑑 𝑑𝑧+ 𝑧 𝑧 − 1 𝑑2 𝑑𝑧2 𝑑2 𝑑𝑥2 = 𝑧 𝑧 − 1 d2 dz2+ 𝑧 − 1 2 d dz (2.47)

dengan mensubstitusi persamaan (2.46) dan (2.47) ke persamaan (2.45), maka dapat dituliskan, 𝑧 1 − 𝑧 𝑑2χ 𝑑𝑧2+ 𝑧 − 1 2 𝑑χ 𝑑𝑟 − 𝑢2+𝑡 𝑡+1 4𝑧 𝑧−1 − 2𝑢 𝑡 + 1 2 1−2𝑧 4𝑧 𝑧−1 χ=− 2𝑚𝑒 ℏ2 𝐸χ (2.48) jika dimisalkan 2𝑚𝑒 ℏ2 𝐸 = −𝑘 2

commit to user

maka persamaan (2.48) dapat ditulis kembali menjadi,

𝑧 1 − 𝑧 𝑑2χ 𝑑𝑧2+ 1 2− 𝑧 𝑑χ 𝑑𝑟 + 𝑘 2₋ 𝑡+ 1 2 −𝑢 2 −1 4 4𝑧 − 𝑡+1 2 +𝑢 2 −1 4 4 𝑧−1 χ= 0 (2.49)

Persamaan differensial orde dua pada persamaan (2.49) yang dibentuk dari hasil substitusi variabel merupakan persamaan hypergeometry perantara. Persamaan ini mempunyai 2 buah titik regular singular di titik 𝑧 = 0 dan 𝑧 = 1,

Untuk titik 𝑧 = 0, persamaan (2.49) memiliki penyelesaian,

𝑧 1 − 𝑧 𝑑2χ 𝑑𝑧2+ 1 2− 𝑧 𝑑χ 𝑑𝑟 − 𝑡+1 2 −𝑢 2 −1 4 4𝑧 χ= 0 (2.50)

karena suku-suku _{𝑧 1−𝑧} 𝑘2 dan

𝑡+1 2 +𝑢

2 −1

4

4𝑧 𝑧−1 2 diabaikan terhadap suku 𝑡+1 2 −𝑢 2 −1 4 4𝑧2 _1−𝑧 untuk 𝑧 mendekati nol, serta bentuk persamaan (2.50) merupakan bentuk persamaan hypergeometry seperti pada persamaan (2.34) maka persamaan (2.50) diselesaikan dengan fungsi gelombang χ yang sesuai seperti bentuk persamaan (2.35) yaitu,

χ = zs ∞n=0cn𝑧𝑛 (2.51)

kemudian persamaan (2.51) disubstitusi ke persamaan (2.50), dan diperoleh,

𝑧 1 − 𝑧 𝑑2 𝑑𝑧2 𝑐𝑛𝑧 𝑛+𝑠 ~ 𝑛=0 + 1 2− 𝑧 𝑑 𝑑𝑧 𝑐𝑛𝑧 𝑛+𝑠 ~ 𝑛=0 − 𝑡+1 2 −𝑢 2 −1 4 4𝑧 𝑐𝑛𝑧 𝑛+𝑠 ~ 𝑛=0 = 0 (2.52)

kemudian masing-masing suku dari persamaan (2.52) diuraikan secara terpisah, yaitu:

commit to user − 𝑡+ 1 2 −𝑢 2 −1₄ 4𝑧 𝑐𝑛𝑧 𝑛+𝑠 ~ 𝑛=0 = − 𝑡+1₂ −𝑢 2 −1₄ 4𝑧 𝑐0𝑧 𝑠_{+ 𝑐} 1𝑧𝑠+1+ 𝑐2𝑧𝑠+2+ 𝑐3𝑧𝑠+3+ ⋯ (2.53a) 1 2− 𝑧 𝑑 𝑑𝑧 𝑐𝑛𝑧 𝑛 +𝑠 ~ 𝑛=0 = 1 2− 𝑧 𝑠𝑐0𝑧 𝑠−1_{+ 𝑠 + 1 𝑐} 1𝑧𝑠+ 𝑠 + 2 𝑐2𝑧𝑠+1+ 𝑠 + 3 𝑐3𝑧𝑠+2+ … (2.53b) 𝑧 1 − 𝑧 𝑑2 𝑑 𝑧2 ~𝑛=0𝑐𝑛𝑧𝑛+𝑠 = 𝑧 1 − 𝑧 𝑠 − 1 𝑠𝑐0𝑧𝑠−2+ 𝑠 𝑠 + 1 𝑐1𝑧𝑠−1+ 𝑠 + 1 𝑠 + 2𝑐2𝑧𝑠+… (2.53c)

kemudian dari uraian pada persamaan (2.53a), (2.53b), dan (2.53c) dijumlahkan sesuai hubungan pada persamaan (2.52) dan dikelompokan berdasarkan variabel 𝑧 pangkat tertentu, yaitu,

0 = 𝑧𝑠−1 ₋ 𝑡+ 1 2 −𝑢 2 −1 4 4 𝑐0+ 1 2𝑠𝑐0+ 𝑠 − 1 𝑠𝑐0 + 𝑧 𝑠 ₋ 𝑡+ 1 2 −𝑢 2 −1 4 4 𝑐1+ 1 2 𝑠 + 1 𝑐1− 𝑠𝑐0+ ⋯ + ⋯ (2.54) dari persamaan (2.54), suku dengan variabel 𝑧 pangkat terendah harus di-nol-kan, yaitu, − 𝑡 +1_{2 − 𝑢} 2 −1₄ 4 + 1 2𝑠 + 𝑠 − 1 𝑠 𝑐0= 0, 𝑐0≠ 0 − 𝑡 +1_{2 − 𝑢} 2 −1₄ 4 + 1 2𝑠 + 𝑠 − 1 𝑠 = 0 𝑠2−1 2𝑠 − 𝑡 +1_{2 − 𝑢} 2 −1₄ 4 = 0

commit to user 4𝑠2− 2𝑠 − 𝑡 +1 2 − 𝑢 2 −1 4 = 0 𝑡 +1 2 − 𝑢 2 −1 4= 2𝑠 2𝑠 − 1 (2.55)

dari persamaan (2.55), jika dimisalkan nilai 𝑠 untuk 𝑧 menuju 0 adalah 𝛼, maka, 𝛼 =−𝑡+𝑢

2 (2.56)

sehingga diperoleh penyelesaian pendekatan disekitar titik 𝑧 = 0 yang dinyatakan sebagai,

χ ~ zα (2.57)

Untuk titik 𝑧 = 1, persamaan (2.49) memiliki penyelesaian,

𝑧 1 − 𝑧 𝑑2χ 𝑑𝑧2+ 1 2− 𝑧 𝑑χ 𝑑𝑟 − 𝑡+1 2 +𝑢 2 −1 4 4 𝑧−1 χ= 0 (2.58) karena suku-suku 𝑘2 𝑧 1−𝑧 dan 𝑡+1 2 −𝑢 2 −1 4

4𝑧2 _1−𝑧 diabaikan terhadap suku 𝑡+1 2 +𝑢 2 −1 4 4𝑧 𝑧−1 2 untuk𝑧 = 1

dan analog dengan persamaan (2.50), penyelesaian pendekatannya dapat dituliskan sebagai,

χ ~ 1 − z 𝛽 (2.59)

dengan parameter yang disubstitusi dinyatakan sebagai,

𝑡 +1 2 + 𝑢 2 −1 4= 2𝛽 2𝛽 − 1 , 𝛽 = −𝑡−𝑢 2 (2.60)

commit to user

Penyelesaian umum dari persamaan (2.49) merupakan kombinasi dari penyelesaian yang diperoleh disekitar titik 𝑧 = 0 dan di 𝑧 = 1 dan dikalikan dengan suatu fungsi baru yang dapat ditulis sebagai,

χ = 𝑧𝛼 1 − 𝑧 𝛽_{𝑓 𝑧 (2.61)}

Kemudian untuk menyelesaikan persamaan (2.49), dihitung terlebih dahulu turunan pertama dan kedua dari persamaan (2.61), yaitu,

𝑑χ 𝑑𝑧 = 𝛼𝑧 𝛼−1 _{1 − 𝑧} 𝛽_{𝑓 𝑧 − 𝑧}𝛼_{𝛽 1 − 𝑧} 𝛽−1_{𝑓 𝑧 + 𝑧}𝛼 _{1 − 𝑧} 𝛽_{𝑓′ 𝑧 (2.62a)} 𝑑2χ 𝑑𝑧2 = 𝛼 − 1 𝛼𝑧 𝛼 −2 _{1 − 𝑧} 𝛽_{𝑓 𝑧 − 𝛼𝑧}𝛼−1_{𝛽 1 − 𝑧} 𝛽−1_{𝑓 𝑧 + 𝛼𝑧}𝛼−1 _{1 −} 𝑧𝛽𝑓′𝑧−𝛼𝑧𝛼−1𝛽1−𝑧𝛽−1𝑓𝑧+𝑧𝛼𝛽−1𝛽1−𝑧𝛽−2𝑓𝑧−𝑧𝛼𝛽1−𝑧𝛽−1𝑓′𝑧+𝛼𝑧𝛼−11− 𝑧𝛽𝑓′𝑧−𝑧𝛼𝛽1−𝑧𝛽−1𝑓′𝑧+𝑧𝛼1−𝑧𝛽𝑓′′𝑧 (2.62b)

bila persamaan (2.56), (2.60), (2.61), (2.62a), dan (2.62b) dimasukkan ke dalam persamaan (2.49), maka diperoleh persamaan,

𝑧 1 − 𝑧 𝑑2𝑓 𝑧 𝑑𝑧2 + 2𝛼 + 1 2 − 2𝛼 + 2𝛽 + 1 𝑧 𝑑𝑓 𝑧 𝑑𝑟 + 𝛼 + 𝛽 2_−𝑘2 _{𝑓 𝑧 =} 0 (2.63)

bentuk persamaan (2.63) merupakan bentuk persamaan differensial orde dua fungsi hypergeometry. Dengan mengaplikasikan kondisi pada persamaan (2.43) pada persamaan (2.63), maka diperoleh,

𝛼 + 𝛽 + 𝑘 = −𝑛 atau 𝛼 + 𝛽 − 𝑘 = −𝑛 (2.64)

commit to user −𝑡 + 𝑢 2 + −𝑡 − 𝑢 2 + − 2𝑚𝑒 ℏ2 𝐸= −𝑛 −2𝑚𝑒 ℏ2 𝐸 = −𝑛 − −𝑡 −2𝑚𝑒 ℏ2 𝐸 = 𝑡 − 𝑛

maka diperoleh spektrum energi, yaitu,

𝐸𝑛 = − ℏ2

2𝑚_𝑒 𝑡 − 𝑛

2 _(2.65)

Kemudian dengan membandingkan persamaan (2.34) dengan persamaan (2.63), serta hubungan persamaan (2.43) dan (2.64), maka dapat dinyatakan hubungan, 𝑎 = 𝛼 + 𝛽 + 𝑘, 𝑏 = 𝛼 + 𝛽 − 𝑘, dan 𝑐 = 2𝛼 +1

2 (2.66) dengan menjumlahkan persamaan (2.56) dan (2.60), yaitu

𝛼 + 𝛽 =−𝑡 + 𝑢

2 +

−𝑡 − 𝑢 2

𝛼 + 𝛽 = −𝑡 (2.67)

maka persamaan (2.66) dapat ditulis kembali menjadi, 𝑎 = −𝑡 + 𝑘, 𝑏 = −𝑡 − 𝑘, dan 𝑐 = −𝑡 + 𝑢 +1

2 (2.68)

Sehingga, dari persamaan (2.42), (2.46) dan (2.68), diperoleh penyelesaian yang merupakan fungsi hypergeometry, yaitu,

2𝐹1 −𝑡 + 𝑘, −𝑡 − 𝑘, −𝑡 + 𝑢 + 1 2; 1−cosh 𝑥 2 = −𝑡+𝑘 𝑛 −𝑡−𝑘 𝑛 𝑛 ! −𝑡+𝑢+1 2 𝑛 1−cosh 𝑥 2 𝑛 (2.69)

commit to user

Dengan mensubstitusi persamaan (2.46), (2.57), (2.60), dan (2.69) ke persamaan (2.61), maka didapatkan, 𝜒_𝑛 = 1−cosh 𝑥 2 −𝑡+𝑘 _{1+cosh 𝑥} 2 −𝑡−𝑘 −𝑡+𝑘 𝑛 −𝑡−𝑘 𝑛 𝑛 ! −𝑡+𝑢+1 2 𝑛 1−cosh 𝑥 2 𝑛 (2.70)

Persamaan (2.70) menunjukan penyelesaian umum fungsi gelombang potensial Gendensthein II, dengan fungsi gelombang tingkat dasar 𝑛 = 0 :

𝜒0 = 1−cosh 𝑥 2 −𝑡+𝑘 _{1+cosh 𝑥} 2 −𝑡−𝑘 (2.71) (Suparmi, 162-165)

E. Penyelesaian Fungsi Gelombang dan Energi Dengan Polinomial Romanovski Dari bentuk umum persamaan hypergeometry,

𝜍 𝑥 𝑑2𝑦𝑛 𝑥 𝑑𝑥2 + 𝜏 𝑥 𝑑𝑦𝑛 𝑥 𝑑𝑥 + 𝜆𝑛𝑦𝑛 𝑥 = 0 (2.72) Dengan, 𝜍 𝑥 = 𝑎𝑥2_{+ 𝑏𝑥 + 𝑐; 𝜏 = 𝑑𝑥 + 𝑒 dan 𝜆} 𝑛 = − 𝑛 𝑛 − 1 + 2𝑛 1 − 𝑝 (2.73) Jika persamaan (2.73) disubstitusikan ke persamaan (2.72), maka dapat dituliskan, 𝑎𝑥2_{+ 𝑏𝑥 + 𝑐} 𝑑2𝑦𝑛 𝑥 𝑑𝑥2 + 𝑑𝑥 + 𝑒 𝑑𝑦𝑛 𝑥 𝑑𝑥 − 𝑛 𝑛 − 1 + 2𝑛 1 − 𝑝 𝑦𝑛 𝑥 = 0 (2.74) Dengan parameter Romanovski :

commit to user

𝑎 = 1, 𝑏 = 0, 𝑐 = 1, 𝑑 = 2 1 − 𝑝 , dan 𝑒 = 𝑞, 𝑝 > 0, 𝑦_𝑛 𝑥 =𝐷_𝑛 𝑝,𝑞 𝑥 ,

𝑝 = −𝛽 > 𝑛 (2.75)

sehingga persamaan (2.74) dapat ditulis kembali menjadi,

1 + 𝑥2 𝑑2𝐷𝑛 𝑝 ,𝑞 𝑥 𝑑𝑥2 + 2𝑥 1 − 𝑝 + 𝑞 𝑑𝐷_𝑛 𝑝 ,𝑞 𝑥 𝑑𝑥 − 𝑛 𝑛 − 1 + 2𝑛 1 − 𝑝 𝐷𝑛 𝑝,𝑞 _{𝑥 =} 0 (2.76)

Persamaan (2.76) merupakan persamaan differensial orde 2 polinomial Romanovski dengan 𝐷_𝑛 𝑝,𝑞 𝑥 adalah polinomial Romanovski. Persamaan (2.76) memiliki bentuk yang sama dengan persamaan (2.34). Persamaan Schrödinger untuk potensial shape invariant dapat direduksi menjadi persamaan differensial orde dua yang dinyatakan dalam bentuk persamaan (2.76) dengan melakukan substritusi variabel yang sesuai. Metode yang digunakan untuk menjabarkan persamaan (2.76) sama seperti metode yang digunakan pada penjabaran persamaan hypergeometry, persamaan (2.34), tetapi dengan penyelesaian fungsi gelombang persamaan Schrödinger, seperti penyelesaian fungsi gelombang pada persamaan (2.62), untuk polinomial Romanovski, yaitu,

𝑋𝑛 = 1 + 𝑥2 − 𝑝 2𝑒 𝑞 2𝑡𝑎𝑛 −1 _𝑥 𝐷_𝑛 𝑝,𝑞 𝑥 (2.77) dengan, 𝐷_𝑛 𝑝,𝑞 𝑥 = 1 𝑤 𝑥 𝑑𝑛 𝑑𝑥𝑛 1 + 𝑥 2 𝑛_{𝑤(𝑥) (2.78)}

𝑤 𝑥 merupakan faktor bobot yang dapat ditentukan dengan menggunakan persamaan differensial Pearson, yaitu,

commit to user

𝑑

𝑑𝑥 𝜍 𝑥 𝑤 𝑥 = 𝜏 𝑥 𝑤(𝑥) (2.79)

dengan mensubstitusi persamaan (2.67) ke persamaan (2.71), maka diperoleh,

𝑤 𝑥 = exp⁡ 𝑑 − 2𝑎 𝑥 + (𝑒 − 𝑏) 𝑎𝑥2_{+ 𝑏𝑥 + 𝑐} 𝑑𝑥 𝑤 𝑥 = exp 2 1 − 𝑝 − 2 𝑥 + 𝑞 1 + 𝑥2 𝑑𝑥 = exp −2𝑝𝑥 + 𝑞 1 + 𝑥2 𝑑𝑥 𝑤 𝑥 = 𝑒𝑥𝑝 −𝑝 𝑙𝑛 1 + 𝑥2 + 𝑞 𝑡𝑎𝑛−1_𝑥 𝑤 𝑥 = 1 + 𝑥2 −𝑝 𝑒𝑞 𝑡𝑎𝑛−1 𝑥 = 1 + 𝑥2 𝛽 𝑒−𝛼 𝑡𝑎𝑛−1 𝑥 (2.80)

F. Penyelesaian Fungsi Gelombang dan Energi Dengan Metode NU

Metode NU didasari pada persamaan diferensial hypergeometry orde 2. Untuk suatu potensial yang ditentukan, persamaan Schrödinger dalam koordinat bola direduksi kedalam suatu persamaan umum hypergeometrik dengan suatu transformasi koordinat 𝑟 → 𝑠 dan kemudian diselesaikan secara sistematis dengan penyelesaian khusus. Persamaan utama ditunjukan dalam bentuk dibawah ini : 𝜓′′ 𝑠 +𝜏 𝑠

𝜍 𝑠 𝜓

′ _{𝑠 +} 𝜍 𝑠

𝜍2 _𝑠 𝜓 𝑠 = 0 (2.81)

dimana 𝜍 𝑠 dan 𝜍 𝑠 merupakan polinomial orde 2, 𝜏 𝑠 adalah polinomial orde 1, dan 𝜓 𝑠 merupakan suatu fungsi dari hypergeometry.

Dengan mendefinisikan 𝜓 𝑠 = 𝜙 𝑠 𝑦 𝑠 dan memilih suatu fungsi 𝜙 𝑠 yang tepat, persamaan (2.81) direduksi menjadi suatu bentuk:

𝑦′′ 𝑠 + 2𝜙′ 𝑠 𝜙 𝑠 + 𝜏 𝑠 𝜍 𝑠 𝑦 ′ _{𝑠 +} 𝜙′′ 𝑠 𝜙 𝑠 + 𝜙′ 𝑠 𝜙 𝑠 𝜏 𝑠 𝜍 𝑠 + 𝜍 𝑠 𝜍2 _𝑠 𝑦 𝑠 = 0 (2.82)

commit to user

dari koefisien 𝑦′ _{𝑠 diperoleh bentuk,}

2𝜙′ 𝑠 𝜙 𝑠 + 𝜏 𝑠 𝜍 𝑠 = 𝜏 𝑠 𝜍 𝑠 (2.83)

dan dari persamaan (2.83), diperoleh bentuk, 𝜙′ 𝑠 𝜙 𝑠 = 𝜋 𝑠 𝜍 𝑠 (2.84) dengan, 𝜋 𝑠 =1 2 𝜏 𝑠 − 𝜏 𝑠 (2.85) 𝜏 𝑠 = 𝜏 𝑠 + 2𝜋 𝑠 (2.86)

parameter baru ð 𝑠 adalah polinomial orde 1. Kemudian, faktor 𝜙′′ 𝑠 𝜙 𝑠 yang muncul pada koefisien 𝑦 𝑠 dari persamaan (2.82) dijabarkan dalam bentuk, 𝜙′′ 𝑠 𝜙 𝑠 = 𝜙′ 𝑠 𝜙 𝑠 ′ + 𝜙′ 𝑠 𝜙 𝑠 2 = 𝜋 𝑠 𝜍 𝑠 ′ + 𝜋 𝑠 𝜍 𝑠 2 (2.87)

kemudian, koefisien 𝑦 𝑠 diubah kedalam bentuk yang lebih cocok dengan mengambil kesebandingan yang ditunjukan dari persamaan (2.84),

𝜙′′ 𝑠 𝜙 𝑠 + 𝜙′ 𝑠 𝜙 𝑠 𝜏 𝑠 𝜍 𝑠 + 𝜍 𝑠 𝜍2 _𝑠 = 𝜍 𝑠 𝜍2 _𝑠

(2.88) dimana, 𝜍 𝑠 = 𝜍 𝑠 + 𝜋2 _{𝑠 + 𝜋 𝑠 𝜍 𝑠 − 𝜍′ 𝑠 + 𝜋′ 𝑠 𝜍 𝑠}

_(2.89) Dengan mensubstitusi ruas kanan dari persamaan (2.83) dan (2.88) ke persamaan (2.82), maka diperoleh persamaan hypergeometry,

𝑦′′ 𝑠 +𝜏 𝑠 𝜍 𝑠 𝑦

′ _{𝑠 +} 𝜍 𝑠

commit to user

Sebagai konsekuensi dari transformasi yang dibahas diatas, bentuk fungsi persamaan (2.81) terlindung oleh langkah-langkah sistematis. Jika polinomial 𝜍 𝑠 pada persamaan (2.90) dapat diubah dalam fungsi 𝜍 𝑠 , dengan hubungan,

𝜍 𝑠 = 𝜆𝜍 𝑠 (2.91)

dengan 𝜆 adalah konstanta, maka persamaan (2.92) dapat direduksi menjadi,

𝜍 𝑠 𝑦′′ 𝑠 + 𝜏 𝑠 𝑦′ _{𝑠 + 𝜆𝑦 𝑠 = 0 (2.92)}

Untuk menentukan polinomial 𝜋 𝑠 , persamaan (2.89) dibandingkan dengan persamaan (2.91) dan kemudian suatu persamaan kuadrat untuk 𝜋 𝑠 dituliskan sebagai berikut,

𝜋2 _{𝑠 + 𝜏 𝑠 − 𝜍′ 𝑠 𝜋 𝑠 + 𝜍 𝑠 − 𝑘𝜍 𝑠 = 0 (2.93)}

𝑘 = 𝜆 − 𝜋′ 𝑠 (2.94)

Penyelesaian persamaan (2.93) adalah,

𝜋 𝑠 =𝜍′ 𝑠 −𝜏 𝑠 2 ± 𝜍′ 𝑠 −𝜏 𝑠 2 2 − 𝜍 𝑠 + 𝑘𝜍 𝑠 (2.95)

Agar dapat menyatakan penyelesaian yang sesuai dengan tanda positif dan negatif pada persamaan (2.95), maka parameter 𝑘 didalam tanda akar haruslah eksplisit. Untuk memenuhinya, suku-suku yang berada didalam tanda akar harus memiliki bentuk polinomial kuadrat. Dari penyelesaian umum persamaan (2.92) dengan representasi 𝜐₁ 𝑠 = 𝑦′ _{𝑠 ,}

𝜍 𝑠 𝜐₁′′ _{𝑠 + 𝜏}

1 𝑠 𝜐1′ 𝑠 + 𝜇1𝜐1 𝑠 = 0 (2.96)

dimana 𝜏1 𝑠 = 𝜏 𝑠 + 𝜍′ 𝑠 dan 𝜇1 = 𝜆 + 𝜏′ 𝑠 . 𝜏1 𝑠 merupakan polinomial

commit to user

bergantung pada variabel s. Ini menunjukan bahwa persamaan (2.96) adalah persamaan tipe Hypergeometrik. Dengan mensubstitusi 𝜐₂ 𝑠 = 𝑦′′ 𝑠 sebagai representasi baru, maka suku ke-2 pada persamaan (2.92) menjadi,

𝜍 𝑠 𝜐2′′ 𝑠 + 𝜏2 𝑠 𝜐2′ 𝑠 + 𝜇2𝜐2 𝑠 = 0 (2.97)

dengan,

𝜏2 𝑠 =𝜏1 𝑠 +𝜍′ 𝑠 = 𝜏 𝑠 + 2𝜍′ 𝑠 (2.98)

𝜇2 = 𝜇1+ 𝜏1′ 𝑠 = 𝜆 + 2𝜏′ 𝑠 +𝜍′′ 𝑠 (2.99) Dengan cara yang sama, suatu persamaan tipe hypergeometry dapat dibentuk dengan susunan penyelesaian-penyelesaian khusus dari persamaan (2.92) dengan mendefinisikan 𝜐_𝑛 𝑠 =𝑦 𝑛 𝑠 ;

𝜍 𝑠 𝜐𝑛′′ 𝑠 + 𝜏𝑛 𝑠 𝜐𝑛′ 𝑠 + 𝜇𝑛𝜐𝑛 𝑠 = 0 (2.100) dan hubungan rekursi umum untuk 𝜏𝑛 𝑠 dan 𝜇𝑛 yaitu,

𝜏_𝑛 𝑠 =𝜏 𝑠 + 𝑛𝜍′ 𝑠 (2.101)

𝜇_𝑛 = 𝜆 +𝑛𝜏′ 𝑠 +𝑛 𝑛−1

2 𝜍′′ 𝑠 (2.102)

Saat 𝜇_𝑛 = 0, maka persamaan (2.102) menjadi,

𝜆_𝑛 = −𝑛𝜏′ 𝑠 −𝑛 𝑛−1

2 𝜍′′ 𝑠 , 𝑛 = 0,1,2, … (2.103)

dan kemudian persamaan (2.100) memiliki penyelesaian khusus dengan bentuk 𝑦 𝑠 = 𝑦𝑛 𝑠 yang merupakan suatu polinomial orde n. Untuk menentukan solusi

eigen nilai metode NU, maka hubungan antara 𝜆 dan 𝜆_𝑛 harus dibentuk sesuai persamaan (2.94) dan (2.103). 𝑦_𝑛 𝑠 adalah suatu fungsi tipe hypergeometry dengan penyelesaian polinomial diberikan dalam bentuk formula Rodrigues,

commit to user

𝑦_𝑛 𝑠 = 𝐵𝑛 𝜌 𝑠

𝑑𝑛

𝑑𝑠𝑛 𝜍𝑛 𝑠 𝜌 𝑠 (2.104)

dengan 𝐵𝑛 adalah konstanta normalisasi dengan faktor bobot 𝜌 𝑠 harus memenuhi kondisi,

𝑑

𝑑𝑠 𝜍 𝑠 𝜌 𝑠 = 𝜏 𝑠 𝜌 𝑠 (2.105)

Kemudian dengan mengkombinasi nilai 𝜙 𝑠 dan formula rodrigues pada persamaan (2.104) akan diperoleh eigen fungsi (fungsi gelombang) 𝑋 𝑟 , dengan hubungan,

𝑋 𝑟 = 𝜙 𝑠 𝑦_𝑛 𝑠 (2.106)

(Nikiforov, A.V. & Uvarov, V.B, 1-8)

G. Potensial Hulthen

Potensial Hulthen memiliki persamaan:

𝑉 𝑟 = −ℏ2 2𝑚 𝑉0𝑒 −𝑟 𝑎 1−𝑒 −𝑟 𝑎 (2.107a) atau, 𝑉 𝑟 = −ℏ2 2𝑚 𝑉0 𝑒 𝑟 𝑎₋₁ (2.107b)

Dengan ℏ adalah konstanta planck dan 𝑚 merupakan adalah massa partikel elementer. Sehingga, berdasarkan variabelnya, potensial Hulthen dapat dinyatakan sebagai, 𝑉 𝑟 ≈ − 𝑉0 𝑒 𝑟 𝑎−1 (2.108)

commit to user

dengan 𝑉₀ dan 𝑎 merupakan kekuatan dan parameter jarak. Potensial Hulthen memiliki gaya atraktif Coulomb untuk 𝑟 yang relatif sangat kecil terhadap 𝑎, 𝑟 ≪ 𝑎. Jika variabel radial 𝑟 relatif sangat kecil terhadap 𝑎, suku eksponensial akan diekspansikan ke deret Taylor, yaitu:

𝑒 𝑟 𝑎 = 1 +𝑟 𝑎+ 1 2! 𝑟 𝑎 2 + 1 3! 𝑟 𝑎 3 + ⋯ (2.109)

Suku-suku pada orde yang lebih tinggi dari persamaan (2.109) dapat diabaikan dan hanya mengambil dua suku pertama. Sehingga, persamaan (2.109) dapat ditulis kembali menjadi,

𝑒𝑎𝑟 ≈ 1 +𝑟

𝑎 (2.110)

Jika persamaan (2.110) tersebut disubstitusi ke persamaan (2.109), maka persamaan (2.109) dapat dituliskan menjadi,

𝑉 𝑟 ≈ − 𝑉0 1 +_{𝑎 − 1}𝑟 𝑉 𝑟 ≈ −𝑉0𝑎

𝑟 (2.111)

Dari persamaan (2.111), maka dapat disimpulkan untuk nilai 𝑟 ≪ 𝑎, potensial Hulthen memiliki bentuk interaksi potensial Coulomb.

H. Potensial Rosen Morse

Potensial Rosen Morse memungkinkan terjadinya interaksi quark dalam pembahasan dinamika quark-gluon QCD. Potensial ini mereproduksi daerah perantara potensial pengungkungan linier (berhubungan dengan interaksi multi

commit to user

gluon) sebagai ketentuan kalkulasi-kalkulasi pola geometris molekul-molekul QCD pada sifat hadron (Compean, 2006).

Gambar (2.2). Potensial Rosen Morse dan Spektrumnya

Secara independent, persamaan potensial Rosen Morse adalah, 𝑉 𝑟 = ℏ2

2𝑚

𝑎 𝑎+1

sin2𝑟 − 2𝑏 cot 𝑟 (2.112)

Dengan ℏ adalah konstanta planck, 𝑚 merupakan adalah massa partikel elementer, 𝑎 dan 𝑏 adalah konstanta.

Jika 𝑟 → 𝑖𝑟, 𝑏 → 𝑖𝑏 maka persamaan (2.112) dapat ditulis kembali menjadi,

𝑉 𝑟 = ℏ 2 2𝑚 𝑎 𝑎 + 1 sin𝑖𝑟 2− 2𝑖𝑏 cot𝑖𝑟 = ℏ2 2𝑚 𝑎 𝑎 + 1 𝑖 sinh𝑟 2− 2𝑖𝑏 −𝑖 coth𝑟 𝑉 𝑟 = ℏ2 2𝑚 − 𝑎 𝑎+1 sinh2r − 2𝑏 coth𝑟 (2.113)

Persamaan (2.113) diatas merupakan persamaan potensial Eckart. Hal ini berarti bahwa potensial Rosen Morse merupakan bentuk compleks dari potensial Eckart.

commit to user

I. Potensial Coulomb

Potensial Coulomb yang menghubungkan suatu elektron dengan muatan – 𝑒 berputar dalam medan elektrostatik Coulomb inti atom. Jika inti atom merupakan proton yang bermuatan 𝑒, permasalahan yang muncul adalah pada atom hidrogen dalam sistem fisika yang sebenarnya dimana terletak dalam sistem tiga dimensi. Sehingga, atom hidrogen tersusun atas sebuah elektron yang berputar dalam sistem koordinat bola terhubung dalam atraksi lemah Coulomb dengan proton. Kedua sistem partikel ini dapat dikonversi kedalam satu sistem partikel dengan mempertimbangkan gerak elektron yang relatif terhadap proton yang berada di pusat massa dari dua partikel tersebut sesuai dengan prinsip mekanika klasik. Pada kerangka tersebut, massa elektron dapat substitusi oleh sebuah partikel dengan massa tereduksi dan bergerak relatif terhadap proton. Persamaan potensial Coulomb adalah:

𝑉 𝑟 =−𝑒2

𝑟 (2.114)

dengan 𝑒 adalah muatan elektron.

J. Potensial Non Sentral Rosen Morse

Potensial non sentral Rosen Morse merupakan potensial Rosen Morse yang variabelnya bergantung pada fungsi radial dan polar. Sehingga pada penyelesaian fungsi gelombang dan energi pada persamaan Schrödinger, potensial

commit to user

non sentral Rosen Morse memiliki variabel yang terpisahkan. Potensial non sentral Rosen Morse memiliki bentuk persamaan,

𝑉 𝑟, 𝜃 = ℏ2 2𝑚 𝑟2

𝜈 𝜈 +1

sin2_𝜃 − 2𝜇 cot 𝜃 (2.115)

Dengan ℏ adalah konstanta planck, 𝑚 merupakan adalah massa partikel elementer, 𝜈 dan 𝜇 adalah konstanta.

Dari uraian diatas, maka dapat disimpulkan bahwa penyelesaian fungsi gelombang dan energi untuk persamaan Schrödinger dapat diselesaikan dengan persamaan hypergeometry dengan melakukan substitusi variabel yang cocok sehingga penyelesaian persamaan Schrödinger dapat diselesaikan secara mudah dengan menggunakan fungsi gelombang pendekatannya. Dalam penelitin ini, akan dilakukan penyelesaian fungsi gelombang dan energi untuk potensial shape invariant dengan menggunakan polinomial Romanovski. Potensial yang dipilih adalah kombinasi antara potensial non sentral Rosen Morse plus Hulthen, potensial non sentral Rosen Morse plus Rosen Morse, dan potensial non sentral Rosen Morse plus Coulomb.

commit to user

METODOLOGI PENELITIAN

A. Lokasi dan Waktu Penelitian

Waktu penelitian selama 8 bulan mulai dari bulan Januari sampai Oktober 2012 dan penelitian dilakukan di Ruang Prodi Ilmu Fisika, PPs, Universitas Sebelas Maret.

B. Objek Penelitian

Objek dalam penelitian ini adalah kombinasi dari dua persamaan potensial efektif yang shape invariant, yaitu :

a. Non sentral Rosen Morse plus Hulthen b. Non sentral Rosen Morse plus Rosen Morse c. Non sentral Rosen Morse plus Coulomb

C. Instrumentasi Penelitian

Instrumentasi penelitian yang digunakan :

1. Satu unit notebook AMD Athlon X2, 3 Gb memory 2. Perangkat lunak (Software) “Matlab 2010” :