METODE SKYLINE UNTUK MENYIMPAN MATRIKS KEKAKUAN P ADA PERSOALAN ELEMEN HINGGA. Mike Susmikanti., Utaja.., Arya'

(1)

METODE SKYLINE

UNTUK MENYIMPAN MATRIKS KEKAKUAN P ADA PERSOALAN ELEMEN HINGGA

Mike Susmikanti., Utaja.., Arya'

ABSTRAK

METODE SKYLINE UNTUK MENYIMPAN MATRIKS KEKAKUAN PADA PERSOALAN ELEMEN HINGGA. Penyelesaian persoalan teknik atau fisika dengan menggunakan Metode Elemen Hingga, akan menghasilkan rnatriks simetri dan spars dengan ukuran yang besar. Agar proses penyelesaian dan penyimpanan dapat dilakukan dengan cepat, diperlukan metode yang sesuai. Makalah ini menguraikan metode skyline yang dapat menyimpan dan memproses peyelesaian matriks seperti keadaan tersebut di atas secara efisien. Dengan metode skyline, jumlah koefisien matriks kekakuan yang diproses jauh lebih sedikit dibandingkan dengan jumlah koefisien semula. Hal ini berakibat banyaknya memori untuk penyimpanan lebih sedikit dan proses penyelesaiannya lebih cepat.

ABSTRACT

SKYLINE METHOD TO STORE STIFFNESS MATRICES ON FINITE ELEMENT PROBLEMS. Solutions to technique or physics problems using finite element method will produce big symmetric and sparce matrices. For the final solution, the finishing and storing process need the correct methods. This paper explains the skyline method which can store and will process the solutions matrices more efficiently. The number of coefficients of stiffness matrices to be processes using the skyline method decreases. This method causes more efficient memory usage and faster processing.

PENDAHULUAN

Penyelesaian suatu persoalan tehnik menggunakan Metode Elemen Hingga

memberikan beberapa sifat koefisien matriks, diantaranya matriks simetri clan menyebar (spars). Matriks spars adalah matriks dengan koefisien tidak nol yang mengumpul dekat dengan diagonal utama clan koefisien bemilai nol yang letaknya jauh daTi diagonal utama (banded) [1]. Pada penyelesaian perhitungan menggunakan metode elemen hingga akan dijumpai operasi matriks dengan matriks berukuran besar.

Proses penyelesaian metode elemen hingga yang digunakan pada paket program

seperti NISA II clan ANSYS tidak dapat dilacak lagi (Black Box). Diharapkan dengan

.Pusat Pengembangan Teknologi Informasi dan Komputasi -BATAN ..Pusat Pengembangan Perangkat Nuklir -BAT AN

(2)

Risalah Lokakarya Komputasi dalam Sains clan Teknologi Nuklir XN, Juli 2003 (171-181)

metode skyline ini, persoalan teknik yang diselesaikan dengan elemen hingga dapat dilakukan secara ringkas daD cepat.

Adapun proses penyimpanan koefisien matriks dalam metode skyline dimulai dengan menyimpan banyaknya koefisien matriks pada setiap kolom, mulai daTi baris yang nilainya bukan Dol, sampai dengan diagonal utama. Selanjutnya menyimpan banyaknya koefisien matriks sampai dengan diagonal utama untuk suatu kolom tertentu. Untuk membatasi proses pengulangan (loop) dilakukan proses menyimpan banyaknya koefisien matriks pada setiap baris mulai diagonal utama sampai dengan kolom yang berisi bukan koefisien nolo Metode ini dipakai di dalam program berbasis elemen hingga yang dikembangkan di P2PN [2].

Diharapkan dengan metode skyline ini jumlah koefisien matriks yang disimpan akan lebih sedikit dibandingkan dengan jumlah koefisien semula daD proses penyelesaiannya akan menjadi lebih ringkas daD cepat.

TEORI

Penyelesaian dengan metode elemen hingga, dilakukan dengan membagi benda menjadi sejumlah elemen yang dinamakan elemen hingga. Akibat pembagian

semacam ini maka distribusi perpindahan turnt didiskritisasi menjadi sub-sub daerah yang sesuai. Sehingga elemen-elemen basil pembagian lebih mudah ditinjau dibandingkan dengan peninjauan seluruh benda. Misalkan suatu lempeng diidealisasi sebagai benda dua dimensi. Dalam hal ini dipilih pembagian elemen yang masing-masing berbentuk segitiga seperti dalam Gambar 1 berikut. Masing-masing node basil pembagian elemen diberi nomor 1 sampai dengan 15.

Gambar 1. Pembagian elemen dan penomoran node

Pemberian nomor node seperti pada Gambar-l akan menghasilkan matriks kekakuan (stiffness matrix) dengan posisi koefisien matriks seperti pada Gambar-2 berikut. Pada Gambar I terlihat bahwa nomor node terkecil yang paling dekat dengan node I adalah node I, dengan demikian letak koefisien matriks pada kolom pertama

(3)

Metode Skyline untuk Menyimpan Matriks Kekakuan pada Persoalan Elemen Hingga (Mike Susmikanti, Utaja, Arya)

akan dimulai daTi baris satu sampai dengan diagonal utama. Untuk nomor node terkecil yang dekat dengan node 2 yaitu node 1, sehingga letak koefisien matriks pada kolom dua dimulai pada baris dua sampai diagonal utama. Berikutnya nomor node terkecil yang paling dekat dengan node 3 adalah node 2, sehingga pada kolom tiga letak koefisien matriks dimulai pada baris dua. Demikian seterusnya untuk node 4 clan node 5, nomor node terkecil yang dekat dengan node 4 clan node 5 adalah node I, sehingga letak koefisien matrik pada kolom empat clan lima dimulai daTi baris 1. Ketentuan ini berlaku sarna untuk setiap posisi koefisien matriks pada matriks kekakuan.

Pada matriks kekakuan terdapat tiga macam koefisien matriks yaitu koefisien bernilai bukan nol, koefisien bernilai nol clan koefisien embedded. Koefisien embedded merupakan koefisien bernilai nol yang diapit oleh koefisien bernilai tidak nol clan dianggap tidak nol dikarenakan nantinya akan diproses. Pada metoda skyline yang akan diproses adalah koefisien bernilai bukan nol berarti termasuk koefisien embedded. Koefisien embedded dalam matriks kekakuan secara cepat dapat terlihat dengan memperhatikan tidak adanya hubungan antara masing-masing node. Misalnya untuk node 2, tidak terhubung dengan node 4, sehingga posisi pada baris 2 kolom 4 terdapat koefisien embedded. Demikian pula antara node 3 clan node 4 tidak terhubung, berarti posisi pada baris tiga kolom empat akan terdapat koefisien

embedded

Gambar 2. Posisi koefisien matriks kekakuan

Pada matriks di atas tampak bahwa banyak koefisien nol yang letaknya berjauhan dengan diagonal utama clan koefisien tidak nol yang letaknya mengumpul

dekat diagonal utama. Matriks tersebut merupakan matriks banded. Penyimpanan dengan metode skyline akan efisien karena mengabaikan koefisien nol yang jauh daTi diagonal utama.

(4)

Risalah Lokakarya Komputasi dalam Sains dan Teknologi Nuklir XIV, Juli 2003

METODE

Langkah-langkah pada metode skyline dilakukan sebagai berikut :

1. Menentukan banyaknya koefisien matrik pada setiap kolom mulai pada baris yang berisi nilai bukan not sampai dengan diagonal utama. Nilai ini dinyatakan dengan variabel JSTK(i).

2. Menentukan banyaknya koefisien matriks sampai dengan diagonal utama pada baris atau kolom ke i (termasuk koefisien matriks pada kolom/baris sebelumnya. Nilai tersebut dinyatakan dengan variabel JDIAG(i)

3. Menentukan banyaknya koefisien matriks pada setiap baris mulai daTi diagonal utama sampai dengan kolom dengan nilai koefisien bukan not (termasuk pula koefisien matriks bemilai not yang diapit oleh koefisien matriks bemilai tidak not). Nilainya dinyatakan dengan variabel ISTK(i). 4. Nilai JSTK(i) dan JDIAG(i) mempunyai hubungan [2] :

illIAG(i) = ~ JSTK(i) ₍₁₎

Posisi matriks M(ij) di mana

5

~i

POSISI = illIAG(j) -(j-i) ₍₂₎

Variabel ISTK(i) dipakai untuk membatasi LOOP pada penyelesaian matriks.

6.

BASIL DAN BAHASAN

Dan Gambar 1 terlihat bahwa terdapat 15 simpul dengan penomoran seperti terlihat pada gambar. Dalam persoalan distribusi suhu, setiap node memiliki satu derajat kebebasan. Diperoleh matriks kekakuan dengan ukuran 15 x 15 seperti pada Gambar 2. Terlihat bahwa koefisien matriks tidak nol, banyak mengumpul dekat dengan diagonal utama clan koefisien nol menyebar jauh daTi diagonal utama.

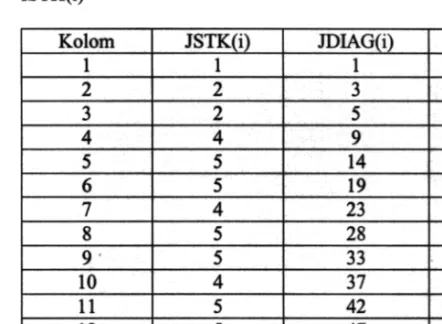
Tabel berikut menyatakan nilai masing-masing variabel JSTK(i), illIAG(i) clan ISTK(i) yang pengisiannya dibahas di bawah ini.

(5)

Metode Skyline untuk Menyirnpan Matriks Kekakuan pada Persoalan Elemen Hingga (Mike Susmikanti, Utaja, Arya)

Tabel Hubungan kolom masing-masing dengan variabel JSTK(i), illIAG(i) clan ISTK(i)

Kolom

_JSTK(i) _JDIAG(i)

1 3

5

9 14 19

23

28 33 37 42 47 51 56 61 ISTK(i) 5 5 4

5

4

5

4

5

5 4 3

2

3

4 5 6 7 8 9 . 10 11 12 13 14 15

2

4

5

5 4

5

4 5 5 4 5

5

Banyaknya koefisien matriks pada masing-masing kolom sampai dengan diagonal utama disimpan dalam kolom atau variabel JSTK(i) seperti pada Tabel-l tersebut di atas. Contohnya untuk kolom 1, variabel JSTK(1) bernilai 1 sedangkan untuk kolom 2 variabel JSTK(2) bernilai 2, demikian seterusnya.

Nilai-nilai pada kolom JDIAG(i) menyatakan banyaknya semua koefisien matriks sampai dengan diagonal utama pada baris atau kolom ke-i ( termasuk koefisien matriks daTi baris/kolom sebe1umnya ). Dalam hal ini untuk kolom 3 atau baris 3, diperoleh JDIAG(3) bernilai 5 yaitu banyaknya semua koefisien matriks daTi kolom 1,2 clan 3 sampai dengan diagonal utama (1+2+2), sesuai dengan persamaan (I). Sedangkan untuk kolom 4 atau baris 4, JDIAG(4) bernilai 9 yaitu banyaknya semua koefisien matriks daTi kolom I, 2, 3 clan 4 sampai dengan diagonal utama (I +2+2+4). Termasuk koefisien matrik bernilai nol didalamnya yang diapit oleh koefisien matrik bernilai tidak nol (embedded).

Selanjutnya nilai-nilai pada kolom ISTK(i) diisi dengan banyaknya koefisien matrik pada setiap baris mulai daTi diagonal utama sampai dengan kolom dengan nilai koefisien bukan nol (termasuk koefisien nol yang diapit oleh koefisien bukan nol). Sebagai contoh, pada kolom I nilai ISTK(I) mempunyai koefisien matriks berjumlah

5 pada baris pertama. Pada kolom 2, nilai ISTK(2) mempunyai koefisien matriks berjumlah 5 pada baris 2.

(6)

Risalah Lokakarya Kornputasi dalam Sains dan Teknologi Nuklir XIV. Juli 2003

Berikut ini beberapa contoh posisi matriks sesuai dengan persamaan (2) dengan nilai JDIAG(i) diambil daTi Tabel-l;

Posisi m(l,l) = JDIAG(l) -( 1 -1 ) = 1 -0 = 1

Berarti nilai koefisien matriks kekakuan m(l, 1) akan disimpan di kotak nomor 1. Posisi m(1,2) = JDIAG(2) -(2 -1 ) = 3 -1 = 2 (disimpan di kotak nomor 2)

Posisi m(1,3) = JDIAG(3) -( 3 -1 ) = 5 -2 = 3 (tidak disimpan). Adapun syarat disimpan jika dipenuhi :

J -I ~ JSTK(J) -1

Pada posisi m( 1,3), karena 3 -1 tidak 1ebih kecil atau sarna dengan 2 -1, berarti syarat penyimpanan tidak dipenuhi. Se1ain itu pula nilai koefisien matriks pada posisi m(1,3) bemilai no1.

Kotak nomor 3 akan digantikan dengan nilai koefisien matriks pada posisi m(2,2) berikut;

Posisi m(2,2) = JDIAG(2) -(2 -2) = 3 -0 = 3 (disimpan di kotaknomor 3) Posisi m(2,3) = JDIAG(3) -( 3 -2 ) = 5 -1 = 4 (disimpan di kotak nomor 4) Posisi m(3,3) = JDIAG(3) -( 3 -3 ) = 5 -0 = 5 (disimpan di kotak nomor 5) Posisi m(1,4) = JDIAG(4) -(4 -1) = 9 -3 = 6 (disimpan di kotaknomor 6) Posisi m(2,4) = JDIAG(4) -(4 -2 ) = 9 -2 = 7 (disimpan dikotak nomor 7) Posisi m(3,4) = JDIAG(4) -(4 -3) = 9 -1 = 8 (disimpan dikotaknomor 8)

Posisi m(4,4) = JDIAG(4) -( 4 -4 ) = 9 -0 = 9 (disimpan dikotak nomor 9), demikian seterusnya. Nilai koefisien matriks m(2,4) daD m(3,4) walaupun bemilai Dol tetap disimpan karena nilai tersebut termasuk koefisien matrik yang diapit oleh nilai koefisien yang bemilai tidak Dol (embedded).

Posisi matriks kekakuan dua dimensi ini, saat ini telah berubah menjadi matrik satu dimensi, yang selanjutnya akan digunakan untuk menentukan distribusi

perpindahan.

Variabel ISTK(i) dipakai untuk membatasi LOOP yang akan diper1ukan pada saat penyelesaian matriks da1am menentukan distribusi perpindahan tiap node.

Dari Tabel-1, diperoleh jumlah kotak yang diperlukan untuk penyimpanan seluruh koefisien matriks kekakuan berjumlah 61. Terlihat pada nilai JDIAG(15) = 61.

Pemberian nomor node seperti pada Gambar 1, apabila diubah menurut susunan seperti pada Gambar 3 akan menghasilkan matriks kekakuan dengan posisi koefisien matriks seperti pada Gambar 4.

Pada Gambar 3 terlihat bahwa nomor node terkecil yang paling dekat dengan node 1 adalah node 1, sehingga letak koefisien matriks pada kolom satu akan dimulai daTi baris satu sampai dengan diagonal utarna. Hal ini tampak pada Gambar 4. Untuk node terkecil yang dekat dengan node 2 adalah node 1, sehingga letak koefisien matriks pada kolom dua dimulai pada baris dua sampai diagonal utama. Berikutnya node terkecil yang paling dekat dengan node 3 adalah node 2, sehingga pada kolom tiga letak koefisien matriks dimulai pada baris dua. Demikian pula untuk node 4, node

(7)

terkecil yang terdekat dengan node 4 adalah node 3, berarti letak koefisien rnatrik pada kolom 4 dimulai pada bans tiga. Untuk nomor node terkecil yang paling dekat dengan nomor node 5 adalah nomor node 4, sehingga letak koefisien matriks pada kolom lima dimulai daTi bans empat. Sedangkan untuk nomor node 6 yang terdekat adalah nomor node 1,berarti letak koefisien matriks pada kolom 6 dimulai pada baris 1. Hal ini berlaku sarna untuk semua kolom pada matriks kekakuan tersebut dibawah ini.

Penentuan posisi koefisien embedded seperti dijelaskan sebelumnya dalam matriks kekakuan diperoleh dengan memperhatikan tidak terdapatnya hubungan antara masing-rnasing node. Misalnya untuk nomor node 2 tidak terhubung dengan nomor node 4, sehingga posisi pada bans dua kolom empat terdapat koefisien embedded (Gambar 4). Demikian pula antara nomor node 3 clan nomor node 4 tidak terhubung, berarti posisi pada baris tiga kolom empat akan terdapat koefisien embedded. Pada posisi matriks kekakuan untuk bans tiga kolom 5 dijumpai koefisien embedded dikarenakan antara nomor node 3 clan node 5 tidak terhubung. Demikian selanjutnya untuk pengisian posisi koefisien matriks yang embedded yang lain berlaku serupa.

Gambar 3. Pembagian elemen clan penomoran node dengan bentuk susunan lain

I 2

~

6

~

12 13 14 15

~:=~==~t:=i

=:+-~

~

--

_{.'K~_""nrd} ~ nrd,"'9_"""'(-) .'Koefisien'"

~

Gambar 4 Posisi koefisien matriks kekakuan sesuai dengan penomoran node pada

~

Gambar 3

(8)

Risalah wkakarya Komputasi dalam Sains clan Teknologi Nuklir XIV, Juli 2003

Dengan metode skyline, susunan nomor node seperti pada Gambar-3 dengan matriks kekakuan yang tampak pada Gambar-4, diperoleh nilai-nilai JSTK(I), JDIAG(I) clan ISTK(I) yang ditampilkan pada Tabel 2.

Tabel2. Hubungan kolom masing-masing dengan variabel JSTK(i), illIAG(i) clan ISTK(i) sesuai dengan penomoran node pada Gambar 3

Kolom 1 2

3

4

5

6 7

8

9 10 11 12 13 14 15 JSTK(I) 1

2

6 7 7

7

6

7

m~G(!2-~

ISTK(I)

7

7 7

7

6

7

6

5

4

3

2 1 3 5 7 9 15 22 29 36 43 49 56 63 70 77

Dan Tabel 2, diperoleh jumlah kotak yang diperlukan untuk penyimpanan seluruh koefisien matriks kekakuan berjumlah 77. (JDIAG(15) = 77).

Terlihat bahwa jumlah kotak yang diperlukan untuk penempatan nomor node seperti pada Gambar 1 dibandingkan dengan Gambar 3, temyata lebih efisien penempatannya seperti pada Gambar 1 dengan jumlah kotak yang diperlukan hanya berjumlah 66.

KESIMPULAN

Dengan metode skyline, jumlah koefisien matriks yang disimpan temyata lebih sedikit dibandingkan dengan jumlah koefisien semula dan proses penyelesaiannya akan menjadi lebih ringkas dan cepat. Selain itu metode skyline cocok digunakan untuk memproses penyelesaian matriks simetri dan spars dengan ukuran yang besar.

(9)

DAFTARPUSTAKA

ROBERT D. COOK, "Concepts and Applications of Finite Element Analysis' John Wiley & Sons, Inc. (1974)

2.

UTAJA, "Metode RCM untuk Mencegah Timbulnya Matrib dengan Banded Tidak Beraturan pada Metode Elemen Hingga", Prosiding Lokakarya Komputasi dalam Sains clan Teknologi Nuklir X, Jakarta (1999)

3 FRANK L. STASA, "Applied Finite Element Analysis for Engineers", CBS College Publishing (1985)

(10)

Risalah Lokakarya Komputasi dalam Sains dan Teknologi Nuklir XN, Juli 2003

DISKUSI

RUSTAMA

1. Penomoran node dalam arah yang berbeda menghasilkan jumlah koefisien matriks yang dihasilkan berbeda. Apakah ada "rules" untuk menetapkan arah penomoran yang paling optimal?

2. Apakah jumlah koefisien matriks yang banyak pada metode skyline dengan yang lebih sedikit, menunjukkan yang banyak itu lebih teliti?

MIKE SUSMIKANTI

1. Tidak acta suatu ketentuan yang pasti untuk menetapkan arab penomoran node yang paling optimal, tetapi berdasarkan pengalaman diusahakan bahwa nomOI node yang besar tidak diletakkan berdekatan dengan nomer node yang kecil. Sebenarnya acta suatu makalah yang ingin dikemukakan oleh bapak Vtaja, mengenai cara khusus untuk penomoran node tersebut.

2. Dalam matrik kekakuan sebenarnya yang perlu diperhatikan adalah nilai-nilai koefisien matriksnya yang kemungkinan memberikan ill condition (kondisi buruk) yang berpengaruh pacta proses penyelesaian nilai perpindahan .Pemecahan persoalan ini dapat diselesaikan secara numerik dengan LV dekomposisi.

RULIY ANTI P ARDEWI

1. Yang menentukan matriks ukuran besar apakah dengan mengetahui jum1ah node saja atau juga melihat derajat kebebasan?

2. Bagaimana mengetahui bahwa suatu persoalan elemen hingga untuk perhitungan matriknya dapat diselesaikan dengan metode skyline.

(11)

Metode Skyline untuk Menyirnpan Matriks Kekakuan pada Persoalan Elemen Hingga (Mike Susmikanti, Utaja, Arya)

MIKE SUSMIKANTI

1. Untuk mengetahui sebelumnya, apakah suatu matriks kekakuan mempunyai ukuran yang besar tidak hanya dipengaruhi oleh faktor, banyaknya node tetapi juga oleh faktor derajat kebebasan atau arah pergerakan yang dialami benda tersebut.

2. Perhitungan matriks dalam persoalan elemen hingga dapat diselesaikan dengan metode skyline apabila matriks tersebut berukuran besar, menyebar, banded dan simetri.

DAFTAR RIWAYAT HIDUP

.S2 Magister Manajemen, STIE IGI Pengalaman KeIja :

6.

.StafPengolahan Data-Biro Bina Program BATAN

.Kasubbid Statistik -Pusat Pengembangan Informatika BAT AN .Pranata Komputer -P2TIK BAT AN

Organisasi Profesional : -7

lRl