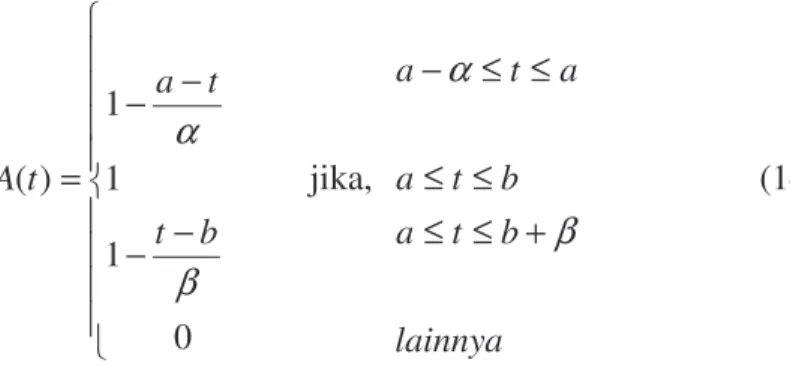BAB 2 LANDASAN TEORI

BAB 2

LANDASAN TEORI

2.1 Analytic Hierarchy Process

Metode Analytic Hierarchy Process (AHP) dikembangkan oleh Prof. Thomas Lorie Saaty dari Wharston Business school untuk mencari ranking atau urutan prioritas dari berbagai alternatif dalam pemecahan suatu permasalahan. Dalam kehidupan sehari-hari, seseorang senantiasa dihadapkan untuk melakukan pilihan dari berbagai alternatif. Disini diperlukan penentuan prioritas dan uji konsistensi terhadap pilihan-pilihan yang telah dilakukan. Dalam situasi yang kompleks, pengambilan keputusan tidak dipengaruhi oleh satu faktor saja melainkan multifaktor dan mencakup berbagai jenjang maupun kepentingan.

Pada dasarnya AHP adalah suatu teori umum tentang pengukuran yang digunakan untuk menemukan skala rasio baik dari perbandingan berpasangan yang diskrit maupun kontinu. Perbandingan-perbandingan ini dapat diambil dari ukuran aktual atau skala dasar yang mencerminkan kekuatan perasaan dan preferensi relatif. AHP memiliki perhatian khusus tentang penyimpangan dari konsistensi, pengukuran dan ketergantungan di dalam dan di luar kelompok elemen strukturalnya.

Analytic Hierrchy Process (AHP) mempunyai landasan aksiomatik yang terdiri dari: 1. Resiprocal Comparison, yang mengandung arti bahwa matriks

perbandingan berpasangan yang terbentuk harus bersifat berkebalikan. Misalnya, jika A adalah k kali lebih penting daripada B maka B adalah 1/k kali lebih penting dari A.

2. Homogenity, yang mengandung arti kesamaan dalam melakukan perbandingan. Misalnya, tidak dimungkinkan membandingkan jeruk dengan bola tenis dalam hal rasa, akan tetapi lebih relevan jika membandingkan dalam hal berat.

3. Dependence, yang berarti setiap jenjang (level) mempunyai kaitan (complete hierarchy) walaupun mungkin saja terjadi hubungan yang tidak sempurna (incomplete hierarchy).

4. Expectation, yang artinya menonjolkan penilaian yang bersifat ekspektasi dan preferensi dari pengambilan keputusan. Penilaian dapat merupakan data kuantitatif maupun yang bersifat kualitatif. Dalam menyelesaikan persoalan dengan metode Analytic Hierarchy Process (AHP) ada beberapa prinsip dasar yang harus dipahami antara lain:

1. Decomposition;

2. Comparative judgment; 3. Synthesis of Priority; 4. Logical Consistency. 1. Decomposition

Pengertian decomposition adalah memecahkan atau membagi problema yang utuh menjadi unsur-unsurnya ke dalam bentuk hierarki proses pengambilan keputusan, dimana setiap unsur atau elemen saling berhubungan. Untuk mendapatkan hasil yang akurat, pemecahan dilakukan terhadap unsur-unsur sampai tidak mungkin dilakukan pemecahan lebih lanjut, sehingga didapatkan beberapa tingkatan dari persoalan yang hendak dipecahkan. Struktur hirarki keputusan tersebut dapat dikategorikan sebagai complete dan incomplete. Suatu hirarki keputusan disebut complete jika semua elemen pada suatu tingkat memiliki hubungan terhadap semua elemen yang ada pada tingkat berikutnya, sementara hirarki keputusan incomplete kebalikan dari hirarki yang complete.

Comparative Judgment dilakukan dengan membuat penilaian tentang kepentingan relatif dua elemen pada suatu tingkat tertentu dalam kaitannya dengan tingkatan diatasnya. Penilaian ini merupakan inti dari AHP karena akan berpengaruh terhadap urutaan prioritas dari elemen-elemenya. Hasil dari penilaian ini lebih mudah disajikan dalam bentuk matriks pairwise comparisons yaitu matriks perbandingan berpasangan memuat tingkat preferensi beberapa alternatif untuk tiap kriteria. Skala preferensi yang digunakan yaitu skala 1 yang menunjukkan tingkat yang paling rendah (equal importance) sampai dengan skala 9 yang menunjukkan tingkatan yang paling tinggi (erxtreme importance).

3. Synthesis of Priority

Synthesis of Priority dilakukan dengan menggunakan egine vector method untuk mendapatkan bobot relatif bagi unsur-unsur pengambilan keputusan.

4. Logical Consistency

Logical Consistency merupakan karakteristik penting AHP. Hal ini dicapai dengan mengagregasikan seluruh eigenvector yang diperoleh dari berbagai tingkatan hirarki dan selanjutnya diperoleh suatu vector composite tertimbang yang menghasilkan urutan pengambilan keputusan.

2.1.1 Proses Penentuan Prioritas dengan Metode AHP

Tahapan-tahapan pengambilan keputusan dalam metode AHP pada dasarnya meliputi:

1. Mendefinisikan masalah dan menentukan solusi yang diinginkan 2. Membuat struktur hirarki yang diawali dengan tujuan umum,

dilanjutkan dengan kriteria-kriteria, sub kriteria dan alternatif-alternatif pilihan yang ingin di ranking

3. Membentuk matriks perbandingan berpasangan yang menggambarkan kontribusi relatif atau pengaruh setiap elemen terhadap masing-masing tujuan atau kriteria yang setingkat diatasnya. Perbandingan dilakukan berdasarkan pilihan atau

“judgment” dari pembuat keputusan dengan menilai tingkat kepentingan suatu elemen dibandingkan elemen lainnya

4. Menormalkan data yaitu dengan membagi nilai dari setiap elemen di dalam matriks yang berpasangan dengan nilai total dari setiap kolom

5. Menghitung nilai eigen vector dan menguji konsistensinya, jika tidak konsisten pengambil data (preferensi) perlu diulangi. Nilai eigen vector yang dimaksud adalah nilai eigen vector maximum yang diperoleh dengan menggunakan matlab maupun manual

6. Mengulangi langkah 3,4, dan 5 untuk seluruh tingkat hirarki

7. Menghitung eigen vector dari setiap matriks perbandingan berpasangan. Nilai eigen vector merupakan bobot setiap elemen. Langkah ini mensintesis pilihan dan penentuan prioritas elemen-elemen pada tingkat hirarki terendah sampai pencapaian tujuan 8. Menguji konsistensi hirarki. Jika tidak memenuhi dengan

CR<0,100 maka penilaian harus diulang kembali.

2.1.2 Penyusunan Prioritas

Menentukan susunan prioritas elemen adalah dengan menyusun perbandingan berpasangan yaitu membandingkan dalam bentuk berpasangan seluruh elemen untuk setiap sub hirarki. Perbandingan tersebut ditransformasikan dalam bentuk matriks. Contoh, terdapat n objek yang dinotasikan dengan (A1, A2,...,An) yang akan dinilai

berdasarkan pada nilai tingkat kepentingannya antara lain Ai dan Aj dipresentasikan

Tabel 2.1 Matriks Perbandingan Berpasangan

A1 A2 . . . An

A1 a₁₁ a₁₂ . . . a_1n

A2 a₂₁ a₂₂ . . . a_2n

An a_m1 a_m2 a_nn

Membuat matriks perbandingan berpasangan memerlukan besaran-besaran yang mampu mencerminkan perbedaan antara faktor satu dengan faktor lainnya. Untuk menilai perbandingan tingkat kepentingan satu elemen terhadap elemen lainnya digunakan skala 1 sampai 9. Pendekatan AHP menggunakan skala Saaty mulai dari bobot 1 sampai 9, seperti terlihat pada tabel berikut ini.

Tabel 2.2 Skala Saaty Tingkat

kepentingan

Definisi

1 Sama pentingnya dibanding yang lain

3 Moderat (cukup) pentingnya dibanding yang lain 5 Kuat pentingnya dibanding yang lain

7 Sangat kuat pentingnya dibanding yang lain 9 Ekstrim pentingnya dibanding yang lain 2,4,6,8 Nilai diantara dua nilai yang berdekatan

Resiprokal Jika elemen i memiliki salah satu angka diatas ketika dibandingkan elemen j, maka j memiliki kebalikannya ketika dibanding elemen i

Model AHP didasarkan pada pairwise comparison matrix, dimana elemen-elemen pada matriks tersebut merupakan judgment dari decision maker. Seorang decision maker akan memberikan penilaian, mempersepsikan, ataupun memperkirakan kemungkinan dari sesuatu hal/peristiwa yang dihadapi. Matriks tersebut terdapat pada setiap level of hierarchy dari suatu struktur model AHP yang membagi habis suatu persoalan.

Berikut ini contoh suatu Pairwise Comparison Matrix pada suatu level of Hierarchy, yaitu. i j k i 1 8 2 1 A= j 2 1 4 k 1 4 1 8 1

Membacanya atau membandingkannya, dari kiri ke kanan.

Jika i dibandingkan dengan j, maka jvery strong importance dari pada i dengan nilai judgment sebesar 4. Dengan demikian pada baris 1 kolom 2 diisi dengan kebalikan dari 4 yaitu 1 4. Artinya,

i dibanding j→ j lebih penting dari i

jika i dibandingkan dengan k, maka i extreme importance daripada k dengan nilai judgment sebesar 8. Jadi baris 1 kolom 3 diisi dengan 8, dan seterusnya.

2.1.3 Eigen value dan Eigenvector

Definisi. Jika A adalah matriks n n× maka vektor tak nol x di dalam _ℜn _dinamakan

eigen vector dari A jika Ax kelipatan skalar x, yakni :

Ax=

λ

x

Skalar

λ

dinamakan eigenvalue dari A dan x dikatakan eigenvector yang bersesuaian dengan

λ

. untuk mencari eigenvalue dari matriks A yang berukuran n n× maka dapat ditulis pada persamaan berikut :

Ax=

λ

x

atau secara ekivalen (λI A− ) 0=

Agar

λ

menjadi eigen value, maka harus ada pemecahan tak nol dari persamaan ini. Akan tetapi, persamaan diatas akan mempunyai pemecahan tak nol jika dan hanya jika:

det (λI A− ) 0=

Ini dinamakan persamaan karakteristik A, skalar yang memenuhi persamaan ini adalah eigen value dari A.

Bila diketahui bahwa nilai perbandingan elemen Ai terhadap elemen Aj adalah

ij

a , maka secara teoritis matriks tersebut berciri positif berkebalikan, yakni aij =1 aij. Bobot yang dicari dinyatakan dalam vektor w=( , , ,..., )w w w_{1 2 3} wn . Nilai wn menyatakan bobot kriteria An terhadap keseluruhan set kriteria pada sub sistem

tersebut.

Jika aij mewakili derajat kepentingan i terhadap faktor j dan ajk manyatakan kepentingan dari faktor j terhadap faktor k, maka agar keputusan menjadi konsisten, kepentingan i terhadap faktor k harus sama dengan .a aij jk atau jika .a aij jk =aik untuk semua i,j,k maka matriks tersebut konsisten.

Untuk suatu matriks konsisten dengan faktor w, maka elemen

a

ij dapat ditulis

i ij j

w

a

w

=

_;

_∀

_{i j}

_,

₌

_{1, 2,3,...,}

_n

₍₁₎

Akan diperoleh hubungan persamaan berikut: 0 0

. _j = _{ij j} − _i =

ij w atau a w w

a (2)

Jadi matriks konsisten adalah:

. i . j i ij jk ik j k k w w w a a a w w w = = = (3)

Seperti yang diuraikan diatas, maka untuk pairwise comparison matrix diuraikan seperti berikut ini:

1

1

j ji i i ij j

w

a

w

w

a

w

=

=

=

₍₄₎

Dari persamaan di atas dapat dilihat bahwa . i 1 ji j w a w = ; ∀i j, =1, 2,3,...,n (5)

Dengan demikian untuk pairwise comparison matrix yang konsisten menjadi:

1 1 . . n ij ij j ij a w n w = = ; ∀i j, =1, 2,3,...,n (6) 1 . n ij ij ij j a w nw = = ; ∀i j, =1, 2,3,...,n (7) Persamaan di atas ekivalen dengan bentuk persamaan matriks di bawah ini:

.

.

A w n w

=

(8)

Dalam teori matriks, formulasi ini diekspresikan bahwa w adalah eigenvector dari matriks A dengan eigen value n. Perlu diketahui bahwa n merupakan dimensi matriks itu sendiri. Dalam bentuk persamaan matriks dapat ditulis sebagai berikut:

1 1 1 1 1 1 2 2 2 2 2 2 1 2 . n n n n w w w w w w w w w w A n w w w w w w w w = = (9)

Pada prakteknya, tidak dapat dijamin bahwa : ik ij jk

a

a

a

=

(10)

Salah satu faktor penyebabnya yaitu karena unsur manusia (responden) tidak selalu dapat konsisten mutlak (absolte consistent) dalam mengekpresikan preferensinya terhadap elemen-elemen yang dibandingkan. Dengan kata lain, judgment yang diberikan tidak untuk setiap elemen persoalan pada suatu level hierarchy dapat saja inconsistent.

2.1.3 Uji Konsistensi Indeks dan Rasio

Dalam teori matriks dapat diketahui kesalahan kecil pada koefisien akan menyebabkan penyimpangan kecil pada eigenvalue. Dengan mengkombinasikan apa yang telah diuraikan sebelumnya, jika diagonal utama dari matriks A bernilai satu dan jika A konsisten maka penyimpangan kecil dari aijakan tetap menunjukkan eigenvalue terbesar

λ

maks, nilainya akan mendekati n dan eigenvalue sisanya akan mendekati nol. Penyimpangan dari konsistensi dinyatakan dengan indeks konsistensi dengan persamaan: ( ) ( 1) maks n CI n

λ

− = − (11)

Di mana: CI = Rasio penyimpangan (deviasi) konsistensi (consistency index) maks

λ

= eigenvalue maksimum n = ukuran matriks

Apabila CI bernilai nol, berarti matriks konsisten, batas ketidakkonsistensi (inconsistency) yang ditetapkan Saaty diukur dengan menggunakan Rasio Konsistensi (CR), yakni perbandingan indeks konsistensi dengan nilai random indeks (RI) yang diperlihatkan seperti tabel 2.3. Nilai ini bergantung pada ordo matriks n. Dengan demikian, Rasio Konsistensi dapat dirumuskan :

CI CR

RI

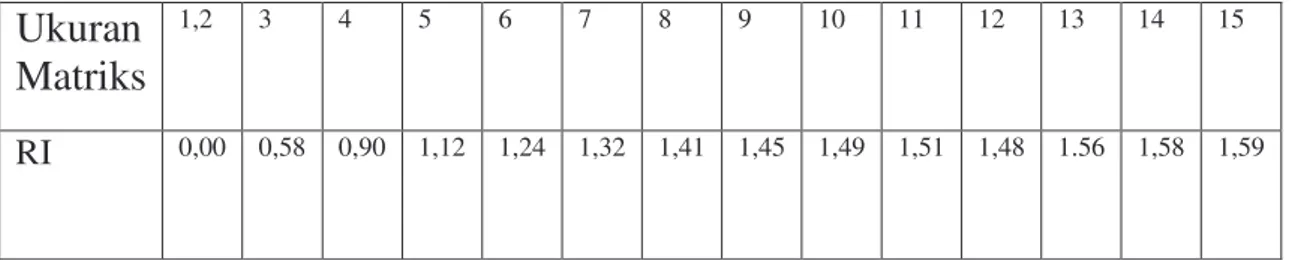
Tabel 2.3 Nilai Indeks Random (RI)

Ukuran

Matriks

1,2 3 4 5 6 7 8 9 10 11 12 13 14 15

RI 0,00 0,58 0,90 1,12 1,24 1,32 1,41 1,45 1,49 1,51 1,48 1.56 1,58 1,59

2.2 Teori Himpunan Fuzzy

Himpunan A dikatakan crisp jika sebarang anggota-anggota yang ada pada himpunan A tersebut dikenakan suatu fungsi, akan bernilai 1 yakni jika a∈A maka fungsi a=1. Namun jika a∉A, maka nilai fungsi yang dikenakan pada a adalah 0. Nilai fungsi yang dikenakan pada sebarang anggota himpunan A dikatakan sebagai nilai keangotaan. Jadi pada himpunan crisp, hanya mempunyai 2 nilai keanggotaan yaitu 0 atau 1. Tetapi pada himpunan fuzzy, nilai keanggotaan dari anggota-anggota nya tidak hanya 1 dan 0 saja. Tapi berada pada interval tertutup [0,1]. Dengan kata lain himpunan A dikatakan fuzzy selama fungsi

µ

:A→

[ ]

0,1.

Misalkan diketahui klasifikasi sebagai berikut : MUDA umur < 35 tahun SETENGAH BAYA 35 ≤ umur ≤ 55 tahun TUA umur > 55 tahun,

dengan menggunakan pendekatan crisp, amatlah tidak adil untuk menetapkan nilai SETENGAH BAYA. Pendekatan ini bisa saja dilakukan untuk hal-hal yang bersifat diskontinu. Misalkan klasifikasi untuk umur 55 dan 56 sangat jauh berbeda, umur 55 tahun termasuk SETENGAH BAYA, sedangkan umur 56 tahun sudah termasuk tua. Demikian pula untuk kategori MUDA dan TUA. Orang yang berumur 34 tahun dikatakan MUDA, sedangkan orang yang berumur 35 tahun sudah TIDAK MUDA lagi. Orang yang berumur 55 tahun termasuk SETENGAH BAYA, orang yang berumur 55 tahun lebih 1 hari sudah TIDAK SETENGAH BAYA lagi. Dengan demikian pendekatan crisp ini sangat tidak cocok diterapkan pada hal-hal yang bersifat kontinu, seperti umur. Selain itu, untuk menunjukkan suatu umur pasti

termasuk SETENGAH BAYA atau tidak termasuk SETENGAH BAYA, dan menunjukkan suatu nilai kebenaran 0 atau 1, dapat digunakan nilai pecahan, dan menunjukkan 1 atau nilai yang dekat 1 untuk umur 45 tahun, kemudian perlahan menurun menuju ke 0 untuk umur dibawah 35 tahun dan diatas 55 tahun.

2.3 Fungsi Keanggotaan Fuzzy

Sebuah himpunan fuzzy A dari bilangan riil ℜ didefinisikan oleh fungsi keanggotaannya (dinotasikan oleh A)

A : ℜ → [ 0,1 ]

Jika x∈ℜ maka A(x) dikatakan sebagai derajat keanggotaan x dalam A. Himpunan fuzzy dalam ℜ disebut normal jika terdapat x∈ℜ sehingga A(x) =1.

Himpunan fuzzy dalam ℜ disebut convex jika A adalah unimodal (sebagai sebuah fungsi). Bilangan fuzzy A adalah himpunan fuzzy dari bilangan riil dengan normal, (fuzzy) convex dan fungsi keanggotaan yang kontinu dari penyokong yang terbatas.

2.3.1 Bilangan Fuzzy Triangular

Sebuah himpunan fuzzy A disebut bilangan fuzzy triangular dengan nilai tengah a, sebelah kiri

α

> 0, dan sebelah kanan β > 0.

Fungsi keanggotaannya adalah sebagai berikut :

− − − − = 0 1 1 ) (

β

α

a t t a t A jika, lainnnya a t a a t a

β

α

+ ≤ ≤ ≤ ≤ − (13)

Penyokong A adalah ( a−

α

,b+

β

). Bilangan fuzzy triangular dengan nilai tengah a dilihat sebagai nilai kwantitas fuzzy.

1

“x dekat terhadap a “ atau “x hampir sama dengan a “.

Gambar 2.1 Bilangan Fuzzy Triangular Contoh 2.2 :

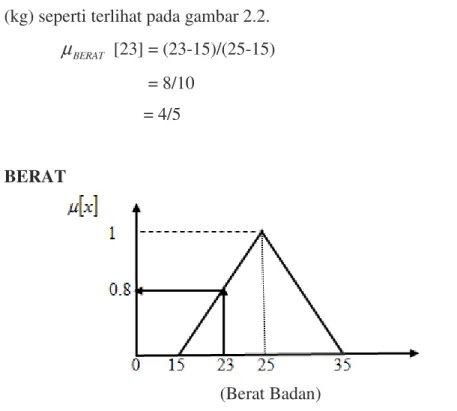
Fungsi keanggotaan triangular untuk himpunan BERAT pada variabel berat badan (kg) seperti terlihat pada gambar 2.2.

BERAT

µ

[23] = (23-15)/(25-15) = 8/10 = 4/5 BERAT (Berat Badan)

Gambar 2.2 Himpunan fuzzy : BERAT (kurva triangular)

2.3.2 Bilangan Fuzzy Trapezoidal

Sebuah himpunan fuzzy A disebut bilangan fuzzy trapezoidal dengan interval toleransi [ a, ], sebelah kiri b

α

dan kanan

β

.

− − − − = 0 1 1 1 ) (

β

α

b t t a t A jika, lainnya b t a b t a a t a

β

α

+ ≤ ≤ ≤ ≤ ≤ ≤ − (14)

Penyokong A adalah ( a−

α

,b+

β

). Bilangan fuzzy trapezoidal dapat dilihat sebagai kwantitas fuzzy.

“ x mendekati pada interval [ a, ] “ b

α

−

a a b b+

β

Gambar 2.3 Bilangan Fuzzy Trapezoidal Contoh 2.3 :

Fungsi keanggotaan trapezoidal untuk himpunan BERAT pada variabel berat badan (kg) terlihat seperti gambar 2.4.

BERAT

µ

[23] = (35-32)/(35-27) = 3/8 BERAT (Berat badan)

2.4 Himpunan Penyokong ( Support Set )

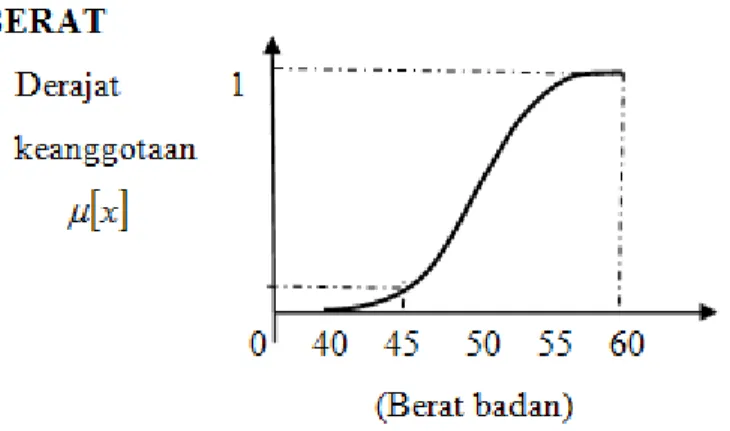
Terkadang bagian tidak nol dari suatu himpunan fuzzy tidak ditampilkan dalam domain. Sebagai contoh, domain untuk BERAT adalah 15 kg hingga 35 kg, namun kurva yang ada dimulai dari 17 kg hingga 33 kg (gambar 2.5). Daerah ini disebut dengan himpunan penyokong (support set). Hal ini penting untuk menginterpretasikan dan mengatur daerah fuzzy yang dinamis.

BERAT

Gambar 2.5 Support set untuk himpunan fuzzy BERAT 2.5 Nilai Alfa – Cut

Salah satu teknik yang erat hubungannya dengan himpunan penyokong adalah himpunan level-alfa (

α

-cut). Level-alfa ini merupakan nilai ambang batas domain yang didasarkan pada nilai keanggotaan untuk tiap-tiap domain. Himpunan ini berisi semua nilai domain yang merupakan bagian dari himpunan fuzzy dengan nilai keanggotaan lebih besar atau sama dengan

α

.

α

- cut lemah dapat dinyatakan sebagai :

µ

_A

( )

x ≥

α

α

-cut kuat dapat dinyatakan sebagai :

µ

_A

( )

x >

α

2.6 Operasi – operasi Pada Himpunan Fuzzy

Seperti halnya himpunan biasa, ada beberapa operasi yang didefinisikan secara khusus untuk mengkombinasi dan memodifikasi himpunan fuzzy. Berikut ini beberapa operasi logika fuzzy yang didefinisikan oleh Zadeh :

Interseksi :

µ

_A∩_B =min

(

µ

_A

[ ] [ ]

x,

µ

_B y

)

(15)

Union :

µ

_A∪_B =max

(

µ

_A

[ ] [ ]

x,

µ

_B y

)

(16)

Komplemen :

µ

_A'=1−

µ

_A

[ ]

x (17)

Karena himpunan fuzzy tidak dapat dibagi dengan tepat, seperti halnya pada himpunan crisp, maka operasi-operasi ini diaplikasikan pada tingkat keanggotaan. Suatu elemen dikatakan menjadi anggota himpunan fuzzy jika :

1. Berada pada domain himpunan tersebut. 2. Nilai kebenaran keanggotaannya 0≥

3. Berada diatas

α

- cut yang berlaku 2.6.1 Interseksi Himpunan Fuzzy

Pada himpunan crisp, interseksi antara dua himpunan berisi elemen-elemen yang berada pada kedua himpunan. Hal ini ekivalen dengan operasi aritmatik atau logika AND. Pada logika fuzzy konvensional, operator AND diperlihatkan dengan derajat keanggotaan minimal antar kedua himpunan. Berikut adalah aturan dasar Zadeh untuk interseksi fuzzy, daerah diantara dua himpunan ditentukan oleh aplikasi operasi tersebut.

[ ] [ ]

(

_A x _B y

)

B A

µ

µ

µ

∩ =min ,

2.6.2 Union Himpunan Fuzzy

Union dari dua himpunan dibentuk dengan menggunakan operator OR. Pada logika fuzzy konvensional, operator OR diperlihatkan dengan derajat keanggotaan minimal antar kedua himpunan. Operator fuzzy OR jarang sekali digunakan dalam pemodelan sistem, karena operasi OR pada dasarnya dapat dibentuk sebagai gabungan dari 2 proposisi fuzzy. Sebagai contoh : If x is A OR y is B then z is C Dapat dibentuk : If x is A then z is C If y is B then z is C

Pada kedua kasus, kekuatan nilai keanggotaan antara konsekuen z dan daerah Fuzzy C oleh max

(

µ

_A

[ ] [ ]

x,

µ

_B y

)

. Seperti halnya pada operator AND, dapat juga memvisualisasikan proses ini sebagai peng-OR-an bit pada vector Boolean yang merepresentasikan kebenaran dari ekspresi himpunan karakteristik untuk tiap-tiap kategori.Untuk membangun himpunan fuzzy menggunakan union dari dua himpunan berikut digunakan aturan Zadeh dasar untuk union Fuzzy, ditentukan oleh operasi sebagai berikut :

[ ] [ ]

(

_A x _B y

)

B A

µ

µ

µ

∪ =max , (18) 2.6.3 Komplemen (Negasi)

Komplemen atau negasi suatu himpunan A berisi semua elemen yang tidak berada di A dan direpresentasikan dengan :

[ ]

x

A

A

µ

µ

'=1− (19)

Pada logika fuzzy, komplemen dihasilkan dengan cara menginversikan fungsi kebenaran untuk tiap-tiap titik pada himpunan fuzzy tersebut.

2.7 Perhitungan Dasar Logika fuzzy 2.7.1 Fuzzyfikasi

Fuzzyfikasi dalah suatu proses pengubahan nilai tegas/real yang ada ke dalam fungsi keanggotaan fuzzy.

2.7.2 Defuzzyfikasi

Merupakan proses pemetaan himpunan fuzzy ke himpunan tegas (crips). Proses ini merupakan kebalikan dari proses fuzzyfikasi

Proses defuzzyfikasi diekspresikan sebagai berikut : Z = defuzzidier (Z)

Dimana :

Z = Hasil penalaran fuzzy Z = keluaran fuzzy logic Defuzzier = Operasi defuzzie