de Bordeaux 17(2005), 13–23
Binary quadratic forms and Eichler orders
parMontserrat ALSINA
R´esum´e. Pour tout ordre d’Eichler O(D, N) de niveau N dans une alg`ebre de quaternions ind´efinie de discriminantD, il existe un groupe Fuchsien Γ(D, N)⊆SL(2,R) et une courbe de Shimura
X(D, N). Nous associons `aO(D, N) un ensembleH(O(D, N)) de formes quadratiques binaires ayant des coefficients semi-entiers quadratiques et developpons une classification des formes quadra-tiques primitives deH(O(D, N)) pour rapport `a Γ(D, N). En par-ticulier nous retrouvons la classification des formes quadratiques primitives et enti`eres de SL(2,Z). Un domaine fondamental ex-plicite pour Γ(D, N) permet de caract´eriser les Γ(D, N) formes r´eduites.
Abstract. For any Eichler orderO(D, N) of levelN in an in-definite quaternion algebra of discriminantD there is a Fuchsian group Γ(D, N) ⊆ SL(2,R) and a Shimura curve X(D, N). We associate toO(D, N) a setH(O(D, N)) of binary quadratic forms which have semi-integer quadratic coefficients, and we develop a classification theory, with respect to Γ(D, N), for primitive forms contained in H(O(D, N)). In particular, the classification the-ory of primitive integral binary quadratic forms by SL(2,Z) is recovered. Explicit fundamental domains for Γ(D, N) allow the characterization of the Γ(D, N)-reduced forms.
1. Preliminars
LetH =a,bQbe the quaternionQ-algebra of basis{1, i, j, ij}, satisfying
i2 = a, j2 =b, ji =−ij, a, b ∈Q∗. Assume H is an indefinite quaternion algebra, that is, H ⊗QR ≃ M(2,R). Then the discriminant DH of H is
the product of an even number of different primesDH =p1· · ·p2r≥1 and
we can assumea >0. Actually, a discriminantD determines a quaternion algebra H such thatDH = D up to isomorphism. Let us denote by n(ω)
the reduced norm ofω ∈H.
Fix any embedding Φ : H ֒→ M(2,R). For simplicity we can keep in mind the embedding given at the following lemma.
Lemma 1.1. LetH =a,bQbe an indefinite quaternion algebra witha >0. An embeddingΦ :H ֒→M(2,R) is obtained by:
Φ(x+yi+zj+tij) =
x+y√a z+t√a b(z−t√a) x−y√a
.
Given N ≥ 1, gcd(D, N) = 1, let us consider an Eichler order of level
N, that is aZ-module of rank 4, subring ofH, intersection of two maximal orders. By Eichler’s results it is unique up to conjugation and we denote it byO(D, N).
Consider Γ(D, N) := Φ({ω ∈ O(D, N)∗|n(ω)>0})⊆SL(2,R) a group of quaternion transformations. This group acts on the upper complex half plane H = {x+ιy ∈ C | y > 0}. We denote by X(D, N) the canonical model of the Shimura curve defined by the quotient Γ(D, N)\H, cf. [Shi67], [AAB01].
For anyγ = a b c d
∈GL(2,R) we denote byP(γ) the set of fixed points inCof the transformation defined by γ(z) = az+bcz+d.
Let us denote by E(H, F) the set of embeddings of a quadratic field F
into the quaternion algebraH. Assume there is an embeddingϕ∈ E(H, F). Then, all the quaternion transformations in Φ(ϕ(F∗))⊂GL(2,R) have the same set of fixed points, which we denote byP(ϕ). In the case thatF is an imaginary quadratic field it yields to complex multiplication points, since P(ϕ)∩ H is just a point,z(ϕ).
Now, we take in account the arithmetic of the orders. Let us consider the set of optimal embeddings of quadratic orders Λ into quaternion orders O,
E∗(O,Λ) :={ϕ| ϕ: Λ֒→ O, ϕ(F)∩ O=ϕ(Λ)}.
Any groupG≤Nor(O) acts onE∗(O,Λ), and we can consider the quo-tient E∗(O,Λ)/G. Put ν(O,Λ;G) := ♯E∗(O,Λ)/G. We will also use the notation ν(D, N, d, m;G) for an Eichler order O(D, N) ⊆ H of level N
and the quadratic order of conductorm in F = Q(√d), which we denote Λ(d, m).
Since further class numbers in this paper will be related to this one, we include next theorem (cf. [Eic55]). It provides the well-known relation between the class numbers of local and global embeddings, and collects the formulas for the class number of local embeddings given in [Ogg83] and [Vig80] in the caseG=O∗. Consider ψp the multiplicative function given by ψp(pk) = pk(1 + 1p), ψp(a) = 1 if p ∤ a. Put h(d, m) the ideal class
number of the quadratic order Λ(d, m).
and gcd(m, D) = 1. Then,
ν(D, N, d, m;O∗) =h(d, m) Y
p|DN
νp(D, N, d, m;O∗).
The local class numbers of embeddings νp(D, N, d, m;O∗), for the primes
p|DN, are given by
(i) If p|D, then νp(D, N, d, m;O∗) = 1−DF p
.
(ii) If pkN, then νp(D, N, d, m;O∗) is equal to 1 +DF p
if p∤m, and equal to 2 if p|m.
(iii) Assume N =pru1, withp∤u1, r ≥2. Put m=pku2, p∤u2.
(a) If r ≥ 2k+ 2, then νp(D, N, d, m;O∗) is equal to 2ψp(m) if
DF p
= 1, and equal to 0 otherwise.
(b) If r = 2k+ 1, then νp(D, N, d, m;O∗) is equal to 2ψp(m) if
DF p
= 1, equal to pk if
DF
p
= 0, and equal to0 if
DF
p
= −1.
(c) If r= 2k, then νp(D, N, d, m;O∗) =pk−1
p+ 1 +DF p
.
(d) If r ≤2k−1, then νp(D, N, d, m;O∗) is equal to pk/2 +pk/2−1
if k is even, and equal to 2pk−1/2 if k is odd.
2. Classification theory of binary forms associated to quaternions
Givenα= a b c d
∈M(2,R), we putfα(x, y) :=cx2+ (d−a)xy−by2. It is called the binary quadratic form associated toα.
For a binary quadratic formf(x, y) :=Ax2+Bxy+Cy2= (A, B, C), we
consider the associated matrix A(f) = B/2A B/2C , and the determinants det1(f) = detA(f) and det2(f) = 22detA(f) =−(B2−4AC). Denote by P(f) the set of solutions in C of Az2+Bz+C = 0. If f is (positive or negative) definite, then P(f)∩ His just a point which we denote by τ(f).
The proof of the following lemma is straightforward. Lemma 2.1. Let α ∈M(2,R).
(i) For all λ, µ∈Q, we have fλα=λfα and fα+µId=fα; in particular, P(fλα+µId) =P(fα).
(ii) z∈Cis a fixed point of α if and only if z∈ P(fα), that is, P(fα) = P(α).
(iii) Let γ ∈GL(2,R). Then A(fγ−1αγ) = (detγ−1)γtA(fα)γ; in
particu-lar, if γ ∈SL(2,R), z∈ P(fα) if and only if γ−1(z)∈ P(fγ−1αγ).
Given a quaternion algebraH denote by H0 the pure quaternions. By
using lemma 2.1 it is enough to consider the binary forms associated to pure quaternions:
H(a, b) ={fΦ(ω) :ω∈H0}, H(O) ={fΦ(ω):ω∈ O ∩H0}.
Definition 2.3. LetO be an order in a quaternion algebra H. We define the denominatormOofOas the minimal positive integer such thatmO·O ⊆ Z[1, i, j, ij]. Then the ideal (mO) is the conductor of O inZ[1, i, j, ij].
Properties for these binary forms are collected in the following proposi-tion, easy to be verified.
Proposition 2.4. Consider an indefinite quaternion algebra H = a,bQ, and an order O ⊆H. Fix the embedding Φas in lemma 1.1. Then:
(i) There is a bijective mapping H0 → H(a, b) defined by ω 7→ fΦ(ω).
Moreover det1(fΦ(ω)) = n(ω).
(ii) H(a, b) ={(b(λ2+λ3√a), λ1√a,−λ2+λ3√a)|λ1, λ2, λ3 ∈Q}
={(bβ′, α,−β)|α, β ∈Q(√a),tr(α) = 0}.
(iii) the binary quadratic forms of H(O) have coefficients in Zhm1 O,
√ ai
Given a quaternion orderO and a quadratic order Λ, put H(O,Λ) :={f ∈ H(O) : det1(f) =−DΛ}.
Remark that an imaginary quadratic order yields to consider definite bi-nary quadratic forms, and a real quadratic order yields to indefinite bibi-nary forms.
Givenω∈ O∩H0, considerFω =Q( √
d),d=−n(ω). Thenϕω( √
d) =ω
defines an embedding ϕω ∈ E(H, Fω). By considering Λω := ϕ−ω1(O)∩ Fω, we have ϕω ∈ E∗(O,Λω). Therefore, by construction, it is clear that P(fΦ(ω)) =P(Φ(ω)) =P(ϕω). In particular, if we deal with quaternions of
positive norm, we obtain definite binary forms, imaginary quadratic fields and a unique solutionτ(fΦ(ω)) =z(ϕω)∈ H. The points corresponding to
these binary quadratic forms are in fact the complex multiplication points. Theorem 4.53 in [AB04] states a bijective mappingffrom the setE(O,Λ) of embeddings of a quadratic order Λ into a quaternion order O onto the setH(Z+ 2O,Λ) of binary quadratic forms associated to the ordersZ+ 2O and Λ. By using optimal embeddings, a definition of primitivity for the forms in H(Z+ 2O,Λ) was introduced. We denote by H∗(Z+ 2O,Λ) the corresponding subset of (O,Λ)-primitive binary forms. Then equivalence of embeddings yields to equivalence of forms.
Fix O = O(D, N), Λ = Λ(d, m) and G = O∗. We use the notation h(D, N, d, m) :=♯H∗(Z+ 2O(D, N),Λ(d, m))/Γ
O∗. Thus, h(D, N, d, m) = ν(D, N, d, m;O∗), which can be computed explicitly by Eichler results (cf. theorem 1.2).
3. Generalized reduced binary forms
Fix an Eichler order O(D, N) in an indefinite quaternion algebra H. Consider the associated group Γ(D, N) and the Shimura curve X(D, N).
For a quadratic order Λ(d, m), consider the set H∗(Z+ 2O(2p, N),Λ) of binary quadratic forms. As above, for a definite binary quadratic form
f =Ax2+Bxy+Cy2, denote by τ(f) the solution of Az2+Bz+C = 0 inH.
Definition 3.1. Fix a fundamental domain D(D, N) for Γ(D, N) in H. Make a choice about the boundary in such a way that every point in H is equivalent to a unique point of D(D, N). A binary form f ∈ H∗(Z+ 2O(D, N),Λ) is called Γ(D, N)-reduced form ifτ(f)∈ D(D, N).
Theorem 3.2. The number of positive definite Γ(D, N)-reduced forms in H∗(Z+ 2O(D, N),Λ(d, m))is finite and equal to h(D, N, d, m).
Proof. We can assume d < 0, in order H∗(Z + 2O(D, N),Λ(d, m)) consists on definite binary forms. By lemma 2.1 (iii), we have that Γ(D, N)-equivalence of forms yields to Γ(D, N)-equivalence of points. Note thatτ(f) =τ(−f), but f is not Γ(D, N)-equivalent to −f. Thus, in each class of Γ(D, N)-equivalence of forms there is a unique reduced binary form. ConsiderG={ω∈ O∗ |n(ω)>0}in order to get Φ(G) = Γ(D, N). The groupGhas index 2 inO∗and the number of classes of Γ(D, N)-equivalence inH∗(Z+ 2O(D, N),Λ(d, m)) is 2 h(D, N, d, m). In that set, positive and negative definite forms were included, thus the number of classes of positive
definite forms is exactly h(D, N, d, m).
4. Non-ramified and small ramified cases
Definition 4.1. LetHbe a quaternion algebra of discriminantD. We say that H is nonramified if D = 1, that is H ≃ M(2,Q). We say H is small ramified if D = pq; in this case, we say it is of type A if D = 2p, p ≡ 3 mod 4, and we say it is of type B ifDH =pq,q≡1 mod 4 and
p q
Proposition 4.2. ForH =p,qQ,p, q primes, exactly one of the following statements holds:
(i) H is nonramified.
(ii) H is small ramified of type A. (iii) H is small ramified of type B.
We are going to specialize above results for reduced binary forms for each one of these cases.
4.1. Nonramified case. Consider H = M(2,Q) and take the Eichler order
O0(1, N) := cN da b|a, b, c, d∈Z .
Then Γ(1, N) = Γ0(N) and the curveX(1, N) is the modular curveX0(N).
To unify results with the ramified case, it is also interesting to work with the Eichler order O(1, N) := Zh1,j+ij2 , N(−j+ij)2 ,1−2ii in the nonramified quaternion algebra1,Q−1.
Proposition 4.3. Consider the Eichler order O = O0(1, N) ⊆ M(2,Q)
and the quadratic order Λ = Λ(d, m). Then:
(i) H∗(Z+ 2O,Λ)≃ {f = (N a, b, c)|a, b, c∈Z,det2(f) =−D
Λ}.
(ii) The (O,Λ)-primitivity condition isgcd(a, b, c) = 1.
(iii) If d < 0, the number of Γ0(N)-reduced positive definite primitive
binary quadratic forms in H∗(Z+ 2O,Λ)is equal to h(1, N, d, m). For N = 1, the well-known theory on reduced integer binary quadratic forms is recovered. In particular, the class number of SL(2,Z)-equivalence ish(d, m).
ForN >1, a general theory of reduced binary forms is obtained. ForN
equal to a prime, let us fix the symmetrical fundamental domain D(1, N) =
z∈ H | |Re(z)| ≤1/2, z−Nk
> N1, k∈Z,0<|k| ≤ N−21
given at [AB04]; a detailed construction can be found in [Als00]. Then a positive definite binary form f = (N a, b, c), a >0, is Γ0(N)-reduced if
and only if |b| ≤ N a and |τ(f) − Nk| > N1 for k ∈ Z, 0 < |k| ≤ N2−1. Figure 4.1 shows the 46 points corresponding to reduced binary forms in H∗(Z+ 2O0(1,23),Λ) for DΛ = 7,11,19,23,28,43,56,67,76,83,88,91,92,
Note that for these symmetrical domains it is easy to implement an algorithm to decide if a form in this set is reduced or not, by using isometric circles.
Figure 4.1. The points τ(f) for some f reduced binary forms corresponding to quadratic orders Λ(d, m) in a fun-damental domain forX(1,23).
4.2. Small ramified case of type A. Let us considerHA(p) :=
p,−1
Q
and the Eichler order OA(2p, N) := Z h
1, i, N j,1+i+j+ij2 i, for N | p−21, N
square-free. The elements in the group ΓA(2p, N) areγ = 12
α β
−β′ α′
such that α, β ∈ Z[√p], α ≡ β ≡ α√p mod 2, detγ = 1, N|tr(β)−β√−βp′
. We denote byXA(2p, N) the Shimura curve of type A defined by ΓA(2p, N).
Proposition 4.4. Consider the Eichler orderOA(2p, N) and the quadratic order Λ = Λ(d, m).
(i) The set H(Z+ 2OA(2p, N),Λ)of binary forms is equal to
{f = (a+b√p,2c√p, a−b√p) : a, b, c∈Z, a≡b≡c mod 2, N |(a+b), det1(f) =−DΛ}.
(ii) The (OA(2p, N),Λ)-primitivity condition for these binary quadratic
forms is gcd c+b2 ,a+b2N, b
= 1.
(iii) If d <0, the number of ΓA(2p, N)-reduced positive definite primitive
binary forms in H∗(Z+ 2OA(2p, N),Λ)is equal to h(2p, N, d, m).
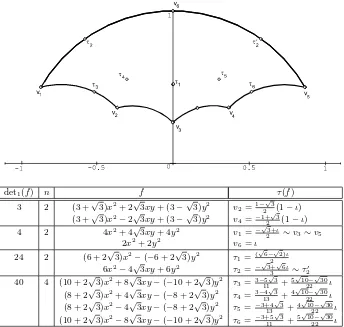
For example, consider the fundamental domain D(6,1) for the Shimura curve XA(6,1) in the Poincar´e half plane defined by the hyperbolic
polygon of vertices {v1, v2, v3, v4, v5, v6} at figure 4.2 (cf. [AB04]). The
table contains the corresponding reduced binary quadratic forms f ∈ H∗(Z+ 2OA(6,1),Λ(d,1)) and the associated points τ(f) for det1(f) =
4,3,24,40, that isd=−1,−3,−6,−10. Since the vertices are elliptic points of order 2 or 3, they are the associated points to forms of determinant 4 or 3, respectively. We putn=h(6,1, d,1) the number of such reduced forms for each determinant.
4.3. Small ramified case of type B. Consider HB(p, q) :=
p,q
Q
and the Eichler order OB(pq, N) := Z
h
1, N i,1+j2 ,i+ij2 i, where N|q−41, N
square-free and gcd(N, p) = 1. Then the group of quaternion transfor-mations is
ΓB(pq, N) = n
γ= 12qβα β′α′
: α, β∈Z[√p], α≡β mod 2, N | α−α2′√−β+βp ′, detγ = 1o.
Figure 4.2. Reduced binary forms in a fundamental
do-(ii) The (OB(pq, N),Λ)-primitivity condition for these binary quadratic
forms in (i) isgcd a, b,c2N−b
= 1.
(iii) If d <0, the number of ΓB(pq, N)-reduced positive definite primitive
binary forms in H∗(Z+ 2OB(pq, N),Λ) is equal toh(pq, N, d, m).
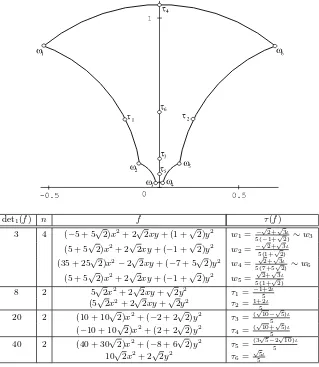
In figure 4.3 we show a fundamental domain for ΓB(10,1) given by the
hyperbolic polygon of vertices{w1, w2, w3, w4, w5, w6}. All the vertices are
Figure 4.3. Reduced binary forms in a fundamental do-main forXB(10,1).
det1(f) n f τ(f)
3 4 (−5 + 5 √
2)x2+ 2√2xy+ (1 +√2)y2 w1= − √
2+√3ι 5(−1+√2)∼w3 (5 + 5√2)x2+ 2√2xy+ (−1 +
√
2)y2 w2= − √
2+√3ι 5(1+√2) (35 + 25√2)x2−2√2xy+ (−7 + 5
√
2)y2 w4= √
2+√3ι 5(7+5√2)∼w6 (5 + 5√2)x2+ 2√2xy+ (−1 +
√
2)y2 w5= √
2+√3ι 5(1+√2) 8 2 5√2x2+ 2√2xy+√2y2 τ1= −1+25 ι
(5√2x2+ 2√2xy+√2y2 τ2= 1+25ι 20 2 (10 + 10√2)x2+ (−2 + 2
√
2)y2 τ3= ( √
10−√5)ι 5 (−10 + 10
√
2)x2+ (2 + 2√2)y2 τ4= ( √
10+√5)ι 5 40 2 (40 + 30√2)x2+ (−8 + 6
√
2)y2 τ5= (3 √
5−2√10)ι 5 10√2x2+ 2√2y2 τ6=
√ 5ι 5
forms of determinant 3. We also represent the points corresponding to reduced binary quadratic formsf with det1(f) = 40, which correspond to
References
[AAB01] M. Alsina, A. Arenas, P. Bayer (eds.),Corbes de Shimura i aplicacions. STNB, Barcelona, 2001.
[AB04] M. Alsina, P. Bayer,Quaternion orders, quadratic forms and Shimura curves. CRM Monograph Series, vol.22, American Mathematical Society, Providence, RI, 2004.
[Als00] M. Alsina,Dominios fundamentales modulares. Rev. R. Acad. Cienc. Exact. Fis. Nat.
94(2000), no. 3, 309–322.
[Eic55] M. Eichler,Zur Zahlentheorie der Quaternionen-Algebren. J. reine angew. Math.195
(1955), 127–151.
[Ogg83] A. P. Ogg,Real points on Shimura curves. Arithmetic and geometry, Vol. I, Progr. Math., vol.35, Birkh¨auser Boston, Boston, MA, 1983, pp. 277–307.
[Shi67] G. Shimura,Construction of class fields and zeta functions of algebraic curves. Annals of Math.85(1967), 58–159.
[Vig80] M.F. Vigneras, Arithm´etique des alg`ebres de quaternions. Lecture Notes in Math., no.800, Springer, 1980.
MontserratAlsina
Dept. Matem`atica Aplicada III EUPM