M02164

(1)

INNOMA (Innovation on Mathematics) with Curves and

Surfaces for Enrichment Mathematics Curriculum

H A Parhusip*

Mathematics Department , Science and Mathematics Faculty Universitas Kristen Satya Wacana, Salatiga ,Jawa Tengah Indonesia

*_{hanna.arini@staff.uksw.edu}

Abstract. Innovation on mathematics with curves and surfaces are shown here to give enrichment in mathematics curriculum. The innovation relates to present mathematics into objects instead of presenting formulas directly. The enrichment here means that students may learn more than the standard curriculum for particular topics. The simple circle equation sphere are used to deliver ideas of innovation and enrichment yielding some new mathematical expressions leading to enrichment of studying circle and sphere in schools. In a topic from undergraduate mathematics, the parametric representation of circle and sphere are then implemented for modifying a hypocycloid curve into modified curves and surfaces. The derivative of each curve or surface is also illustrated. The visualizations are done with MATLAB. Other innovations with algebraic surfaces are introduced using SURFER such that the visualizations are done without writing a code. The resulting curves and surfaces are then used to be curve stitching designs (can be used in schools), batik motifs (can be a mathematical project), mathematical ornaments and motifs for several kinds of souvenirs (bags, t-shirt, glass) for promoting mathematics.

Key words : circle, sphere, hypocycloid, curve stitching algebraic surfaces.

1.Introduction

Mathematics is mainly considered to be collection of formulas. Therefore mathematical symbols are frequently introduced firstly in learning and teaching mathematics traditionally leading to negative attitude of public images about the essence of mathematics (only numbers and formulas). On the other hand mathematics is thought meaningful for wide areas. This is not known in basic level of education. As a result, students gradually understand mathematics with lots of formulas rather than its applications.

(2)

software since mathematical operators and expression have geometrical meanings. In this paper, mathematical operators and expression will be introduced through curves and surfaces.

There have been several software are developed such as Geogebra, Maple, MATLAB where geometrical mathematics expression are easily visualized. Other software such as Cinderella and Surfer are more challenging to present more dynamic physical operator and algebraic surfaces respectively. The available software influences the development on teaching, learning and exploring mathematics and applied science.

This paper is expected to inspire educators and researchers in schools and undergraduate mathematics particularly to have their own enrichment in routine materials of teaching (curriculum based) into a growing study such that the essence of research can be adjusted automatically by students. Some examples of these explorations are shown to be innovation of some mathematical lessons in schools and undergraduate mathematics.

.

2. Background for Creating Innovation

Several ideas for popularizing mathematics have been addressed by many groups in mathematics and educations (Ahuja, 1996). The research of innovations here have been developed with curves and surfaces meaning the known equations are explored, e.g. mapped with complex functions, extended into 3 dimensional equations, using well known sequences and ratio, i.e. Fibonacci and Golden Ratio (GR) for creating Fibonacci curves and surfaces Fibonacci (Parhusip,2016). Some motifs were obtained and tried to find the similarity in natures such as flowers and animals where sacred geometry was studied (Suryaningsih et.al.,2013). Hypocycloid curve and its derivative were explored into 3 dimensional with many different values of parameters where new curves and surfaces were collected to be possible mathematical ornaments, accessories and designs for souvenirs (Purwoto,2014)(Parhusip,2015) and exhibited for popularizing mathematics Some designs have been used as designs in batik (called BATIMA) and for new curves stitching designs. The background to start an innovation in mathematics is shown here as examples for a further individual learning.

2.1 Innovation on Circle

Before we do an innovation, one has already standard equations e.g. an equation for a circle, a ball in 3 dimensional. For instance,

x

2



y

2



r

2is a circle with a radius r and a center O on origin of coordinate system. This equation is known in junior/senior schools. Similar expression is obtained in undergraduate mathematics such as an astroid is formulated by

x

2/3



y

2/3



r

2/3. In number

theory, the expression

x

p



y

p



r

p is studied for positive integers x,y,r where p > 2, p integers.

Consider

x

p



y

p



r

p and p=4, we take

r



z

1/2such that the equation becomes

2 4 4

y

z

x





(1)

It was proven that x, y, z all nonzero and relatively prime integers (Boston,2003) , the Eq. (1) has no solution. Note that in number theory we seek positive triple (x,y,z) satisfying Eq.(1). It is known as Fermat Last Theorem, that this expression has no positive integer solutions stated since 1637 and proven formally in 1995 by Wiley. We see that the number theory focuses on a point containing positive integer (x,y,r) for

x

p



y

p



r

p. In geometry, one has more pay attention on its geometrical interpretation. An innovation is started.

2.2 Geometrical innovation in a modified circle equation

In this paper, we create an innovation in circle by observing values of p for a positive fixed value of r where several innovations are encountered. For a given r, we may write :

p p p

r

y

x





_(2.a)

(3)



p

r

x



cos

2/ ,

y



r

sin

2/p



.

_(2.b)

Substituting the expression Eq.(2.b) into

y

p



r

p



x

p , i.e.

y

p



r

p





r

cos

2/p





p



r

p



1



cos

2





.

For 1<p < 2, we have

cos

2/p



and

sin

2/p



in unusual exponent. Let us study for p=1.1, one yields :





2/1.1





1.8182 /

2

cos

1.1

2





p . Similarly





1.8182 /

2

sin

1.1

2





c



p

.

Let us denote



cos





1.8182



u

. As we know



1



cos





1

for all values of



. Illustrations of





2/1.1

cos



and



sin





2/1.1 are depicted in Fig.1.

Figure 1. Illustration



cos





2/1.1 and



sin





2/1.1.

Figure 2. Illustration



cos





2/ and



sin





2/.

For p



, we have

cos

2/p



and

sin

2/p



_{are depicted in Fig.2. These studies are very rare coming}

to any education levels that we come to a fact finding a negative to a rational and an irrational power.

We get that

cos

2/p



and

sin

2/p



_{are nonzero for} k  k

2 3

2   , for

k









(

k



1

)



, for 

Z

k respectively and both are not real numbers. Computer defines as not real numbers meaning the values are complex. In Geogebra, we get signs ‘?’ . In MATLAB , we have complex values. Some values of

cos

2/p



and

sin

2/p



for

0







2



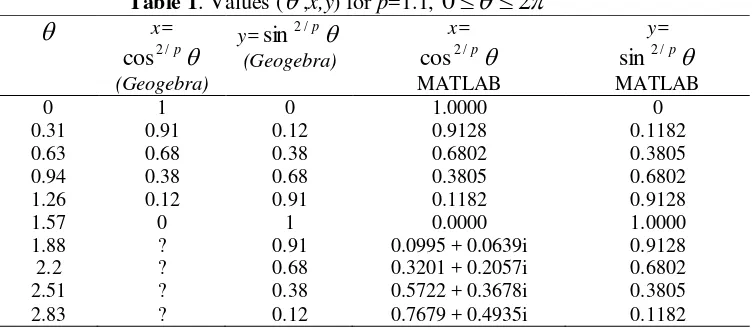
are listed in Table 1. Let us list the values (x,y) for

p=1.1 shown in Table 1. The same profiles will be similar for

x



r

cos

2/p



,

y



r

sin

2/p



with

p=1.1 since r simply represents the amplitude of x and y.

Table 1. Values (



,x,y) for p=1.1,

0







2





x=



p / 2

cos

(Geogebra)

y=

sin

2/p



(Geogebra) x=



p / 2

cos

MATLAB y=



p / 2

sin

MATLAB 0 0.31 0.63 0.94 1.26 1.57 1.88 2.2 2.51 2.83 1 0.91 0.68 0.38 0.12 0 ? ? ? ? 0 0.12 0.38 0.68 0.91 1 0.91 0.68 0.38 0.12 1.0000 0.9128 0.6802 0.3805 0.1182 0.0000 0.0995 + 0.0639i 0.3201 + 0.2057i 0.5722 + 0.3678i 0.7679 + 0.4935i

(4)

π 3.46 3.77 4.08 4.4 4.71 5.03 5.34 5.65 5.97 6.28 ? ? ? ? ? 0 0.12 0.38 0.68 0.91 1 0 ? ? ? ? ? ? ? ? ? 0

0.8413 + 0.5406i 0.7679 + 0.4935i 0.5722 + 0.3678i 0.3201 + 0.2057i 0.0995 + 0.0639i

0 0.1182 0.3805 0.6802 0.9128 1.0000 0.0000 0.0995 + 0.0639i 0.3201 + 0.2057i 0.5722 + 0.3678i 0.7679 + 0.4935i 0.8413 + 0.5406i 0.7679 + 0.4935i 0.5722 + 0.3678i 0.3201 + 0.2057i 0.0995 + 0.0639i

0

2.3 Geometrical interpretation of

x

p



y

p



r

p

An interesting geometrical part of Eq.(2) is the family curves obtained by

p



5

, the real part

of each point (x,y) behaves similarly. One suggests that for

p



5

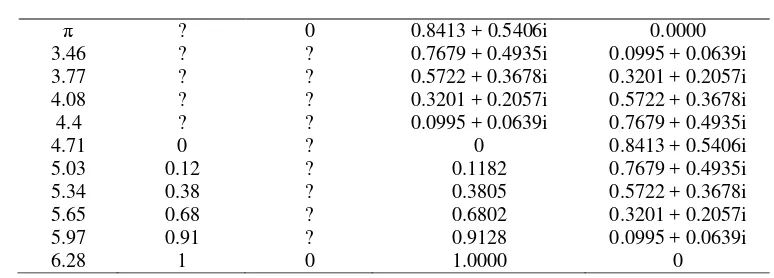
, the geometric visualization of the solution is in one family of curves. This is illustrated in Fig. 3-4. Figure 3 describes all geometric visualization of Eq.(2) for p=1 ,2,3,4. Some different curves appear on this figure. We deduce that there exists no similarity pattern in these curves. On the other hand, Fig. 3 depicts some similar curves for p=5,6,7,8 . The additional observations lead to the same geometrical phenomenon for p=9,10,11,12 as shown in Fig. 4. The family of curves is called weak kite in this paper.

Figure 3. Geometrical visualization of Eq.(1) for p=1,2,3,and 4.

Figure 4. Geometrical visualization of Eq.(1) for

p=5,6,7,and 8 (the real part of (x,y)). and for

p=9,10,11,and 12. All curves are called weak kites.

All curves above drive to a general question, such as which values of p leading to similar curves. Since a special p=2/3 has been known as an asteroid in calculus, one may research for any other fractional numbers in the form k/3 for any natural number of k with k >2. One may predict that for

p=k/3 with k5, Eq.(1) creates a family of curves, the same attitudes for arbitrary integer values of

5



p

. By extending the domain of the axes, we have still a close curve. By increasing the value of p, i.e. p=13/3, 14/3, 15/3, 16/3, a family of weak kites appears since all curves behave the same as in Fig. 4. Again, the values of p are varied in the form k/3 similarities are observed as depicted in Fig.5. The observations lead to patterns of weak kites for p started from 13/3 up to 33/3. Processing up to

p=100/3, similar patterns are obtained. Note that the solutions of

z

₁p



z

₂p



r

p can be complex

numbers. Therefore the real part solutions of

z

₁p



z

₂p



r

p are concluded to be family of weak kites

for p=k/3 with k



13,14,...



. One may prove formally which is not shown here. As mentioned above that the interest in this paper is the geometrical phenomenon of (Re z1,Re z2) satisfying_.

p p p

r

z

(5)

p=1,1/2 /, 1/3 and ¼

p=1/3,2/3/, 3/3 and 4/3

p=5/3, p=6/3, p=7/3 and p=8/3.

p=9/3, p=10/3, p=11/3 and 4=12/3.

a weak circle for p=4 or 12/3.

p=13/3,14/3 , 15/3,16/3 p=17/3,18/3 ,19/3,20/3. p=21/3,22/3 ,23/3,24/3.

Figure 5. Real solutions of

x

p



y

p



r

p

3. Innovation on Surfaces

3.1 Modified ball equation

Some well known curve and surface such as a circle and a ball are presented in Cartesian

coordinates, polar coordinates and parametric coordinates. The equation

x

p



y

p



r

p

(

x

,

y

)



R

2 describes a circle in Cartesian coordinate for p=2. In particular, an astroid can be obtained for p=2/3. Rectangular representation of astroid is

x

2/3



y

2/3



r

2/3and its parametric is in the form



3

cos

r

x



and 3

sin

r

y  . The second studied geometrical surface is a generalization of ball, i.e.

p p p p

r

z

y

x





_. ₍₃₎

This equation gives us a ball with a center O and its radius r for p=2. Furthermore, one may extend the Eq. (3) to be a 3 dimensional astroid by using spherical coordinates, i.e.

,

cos

;

sin

;

cos

sin

3



3





3



3





3







y

z

x

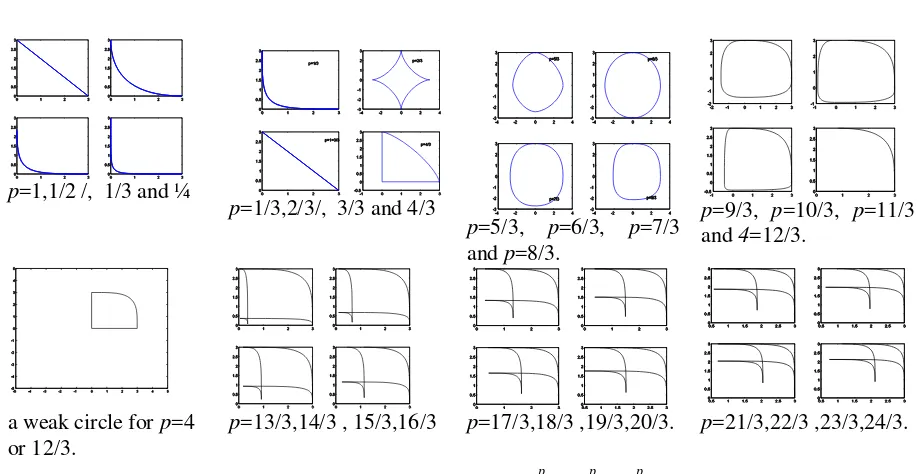
02; 0 _. ₍₄₎

and the geometrical illustration is shown in Fig. 6.

Figure 6. Ilustration of 3 dimensional astroid using spherical coordinates.

As in 2 dimensional case, one may express Eq.(3) into parametric equations, i.e.

















p p p p p

z

y

x



sin

2/

cos

2/

;



sin

2/

sin

2/

;



cos

2/

;

₀







2



;

₀









. (5). Since 3 dimensional astroid can be defined, one generalizes Eq.(3) into Eq.(5) and try to find the appeared geometrical phenomena for different values of p . Thus, the surfaces given by Eq.(5) will be the real parts of solutions

;

3 2 1

p p p p

r

z









3

3 2

1

,

z

,

z

C

(6)

3.2 Innovation from modified hypocycloid curve

The third type innovation done in this paper is a generalization of 2 dimensional hypocycloid curve into 3 dimensional surfaces, i.e. (Purwoto, et.al, 2014)





cos cos

 

sin ;

sin





x





b b a b b a

x _

                    





sin sin

 

sin ;

sin





y





b b a b b a

y _

                    





cos



z

. (6)

where

;

2 2

sin

r

x

y

r











and a, b are real numbers. Originally, a and b denote radius of 2

different circles, a > b. In this case, a and b are freely chosen. Another innovation is done by replacing the minus signs in the Eq.(6) to be positive. The innovation can still be created by presenting of each derivative to create the new curves (from x_{ } ,y  ) and surfaces. This paper provides some

similar patterns in curves and surfaces for the generalization defined above.

3.3 Innovation from Algebraic Surfaces

According to the equations used to create surfaces, algebraic surfaces are surfaces created from polynomials of three variables, e.g. ellipsoid, sphere classified as quadric surfaces. Other classifications are quartic surfaces, Caley cubic, Barth Sextic, and many more. One may refer to Wikipedia for other variation of algebraic surfaces. There is an available software called SURFER to visualize those algebraic surfaces such that a user simply writes an algebraic equation to create a surface without writing a code. The used of SURFER is not only for presenting algebraic surfaces for education but also for architecture and art (). The examples for some algebraic surfaces using SURFER will be shown.

Among all surfaces, the mathematical studies usually involve several types of curvatures on curves and surfaces. In this paper, the curvatures are not discussed since the main focus is about innovating curves and surfaces. Finally, the next chapter shows innovation results for 3 classifications above, i.e. innovation on curves and surfaces from circle- sphere equations, modified hypocycloid and algebraic surfaces.

4 Innovation Results

4.1 Innovation Surfaces of Generalized Ball Equations

Note that the derivatives of the equations may create other curve and surfaces. In 3 dimensional case (see Eq.5), we may have some possible triple to visualize the surfaces due to the

derivatives, i.e.

 

x_;



 x _;



 x _;

 

y _;



 y_;



 y_;



 

 

z z

; and





z _{. Since} 



z _{=0 ,the number of possible}

surfaces are

C

₃8=56 . Furthermore, the second derivatives may be created.

Since p=2/3 has led to a known geometry (astroid), we try for p=k/3, k=1, 2,…,20. One

observes for p=12,…,20 the surfaces have the same families. The collections of surfaces are called

(7)

Figure 7. A family of parking surfaces for p=13/3,14//3,15/3/16/3 (from left to right) Note that the 2 dimensional projections have the same images as shown in Figure 5.

Finally some surfaces are found by varying the values of p. Started with astroid in 3 dimensional (p=2/3) and vary for p=2/k, k=4, 5, 6, 7, 8, 9, one observes geometrical patterns as depicted in Fig. 8. Weak astroids are observed for p=2/3, 2/5, 2/7 and 2/9 with diminishing surfaces area. Generally, one may have weak astroids for p=2/(2n+1), for n is natural number.

Figure 8. Visualization of



Re

,

Re

,

Re



;

3 3 2

1

z

C

z



rR_,_p_{=2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 2/9 (from}

left to right).

As we notice, The real solutions 1 2 3

;

p p p p

r

z





_{have closed astroid surfaces with}

decreasing area of surfaces for p=2/3, p/5, p/7. On the other hand the open surfaces are found for

p=2/4, 2/6, 2/8. One may increase the value of denominator and we have the area of surfaces tends to

zero for all p. Some variations of parameters have been observed in the results of surfaces where the value of

p





/

k

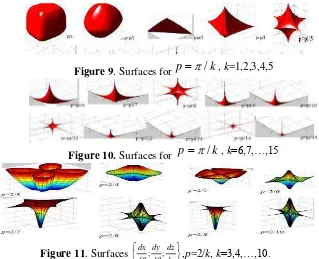
, k=1,2,3,…,15.

For irrational numbers of p some interesting patterns of surfaces are found. One observes that

families of surfaces are started from

p





/

5

. Closed surfaces called weak astroid are obtained for

5

/





p

,

p





/

8

,

p





/

11

and

p





/

14

with each area is diminishing. Otherwise, for

6

/





p

,

p





/

7

,

...,

p





/

13

, the open surfaces are shown with similar pattern in Fig. 9-10. _By

studying the surfaces created by the derivatives, open surfaces are obtained for p=2/k, k is an odd number and closed surfaces for p=2/t where t is an even number (see Fig. 11). As above, the area of surfaces are decreasing for increasing values of k and t. These surfaces are possible to be some mathematical ornaments or for other purposes such as motifs for batik.

Figure 9. Surfaces for

p





/

k

, k=1,2,3,4,5

Figure 10. Surfaces for

p





/

k

, k=6,7,…,15

Figure 11. Surfaces

   

 

 

 d

dz d dy d dx

;

; ,p=2/k, k=3,4,…,10.

(8)

As mention previous sections, various curves and surfaces have been obtained. The obtained designs can be 2 dimensional and 3 dimensional. This paper focuses on presenting the 2 dimensional designs for curve stitching that can be used for students to be material for innovation on mathematics. Originally curve stitching has been designed with creating line or parabola into different kinds of motifs. This research has obtained many curves from a modification of hypocycloid curve into kind of polygons called Connected Pseudo Polygon (CPP). Several designs of CPP for curve stitching are displayed in Fig.11-12.

a=1, p=24, q=12, dan b=2 , n=50 (the

number of points). a_{(the number of points).}=457, p=35, q=33, b=-(p/q), n=50 a=1, _{(the number of points).}p=24, q=12, b=2, n=50

Figure 11. Modified Hypocycloid curve

             b b a b b a

x( ) ( )cos cos ; 

            b b a b b a

y( ) ( )sin sin .

Derivative of modified hypocycloid curve;a=20, p=800,

q=-500, b=1.6 , n=25 (the number of points)

a=20, p=250, q=-20, b=12.5 ,

n=25 (the number of points). p=450;q=-10;a=20;b =-(p/q); n=13 (the number of points).

p=450;q=10;a=20;b =-(p/q); n=13 (the number of points). Repeated by Fibonacci sequence.

Figure 12. Modified hypocycloid curve :

            b b a b b a

x ( )cos cos ( )sin sin  .

           b b a b b a y

The designs of curve stitching strongly depend on the order of arranging the material. Thus the designs require numbering on each vertex. Finally by following the numbers, the curve stitching can be made. The examples are shown in Fig.13. Furthermore, if one requires a particular size, the code can provide the minimum one dimensional material.

Figure 13. Curve stitching based on modified hypocycloid curve.

4.3 Results of surfaces innovations

Several mathematical ornaments and art are created based on the modified hypocycloid and weak balls obtained in Section 3. Figure 14 and Fig.15 illustrate 2 pairs of designs and the related products made by at least 11 home industries for all products. In this paper, the results from 4 home industries are displayed. Figure 16 illustrates designs and the related products called BATIMA (as one of Indonesian innovations in 2016) and puzzles with the same designs. Thus the same designs can be used for several purposes. There are also designs can be used for an architecture for a building in future.

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -2 -1.5 -1 -0.5 0 0.5 1 1.5

-500-400-300-200-100 0 100200 300400 500 -500 -400 -300 -200 -100 0 100 200 300 400 500

-3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 -3 -2 -1 0 1 2 3

-80 -60 -40 -20 0 20 40 60 80 -80 -60 -40 -20 0 20 40 60 80

-50-40-30-20-10 0 10 20 3040 50 -50 -40 -30 -20 -10 0 10 20 30 40 50

-150 -100 -50 0 50 100 150 -150 -100 -50 0 50 100 150

(9)

Second derivative of hypocycloid for

p=1;q=4;a=1;b=-(p/q) 

 

 

 

 d

dz d dy d dx

;

; p=1;q=4; a=1;

b=-(p/q)

   

 

z d dy d dx

, ,



 p=1;q=4;a=1;b=-(p/q)

Figure 14. Design and its surface of Derivative of hypocycloid

’

Derivative of hypocycloid for

p=1;q=6; a=1;b=-(p/q) (second pair, right)

p p p

p _y _z _r

x    _forp/7 The second derivative of hypocycloid for

a=1;p=1;q=4;b=p/q.

Figure 15. Design and its surface of modified hypocycloid and weak balls

Figure 16. Designs and the related products (puzzle and batik (BATIMA))

4.4 Innovation on Algebraic Surfaces

A sphere is one of algebraic surfaces in quadric surfaces. The other quadric surfaces are, Cone, ellipsoid, paraboloid. The algebraic surfaces are governed by polynomial surfaces. A new development for creating algebraic surfaces is a software called surfer (found by Imaginary research group from Germany). This software can be easily used to visualize without doing programming as above. Several surfaces are displayed here as examples. Figure18 can be models for Christmas ornaments called Santa Xmas Ornaments, and Xmas-hats are also created. Additionally, the designs can also be used to be batik motifs.

Figure 18.Santa Xmas-Ornaments by an algebraic surface, i.e:

(10)

Figure 19. Xmas-hats from algebraic surfaces as combination of several 3 and 5 spheres with 1 ellipsoid.

Conclusion

Creations curves and surfaces as innovations on mathematics are discussed to provide enrichment of mathematics curriculum. The exponent in the circle equation is changed to be any real number leading to find the complex sets of solutions and the related geometrical solutions. This approach is extended to a sphere where the geometrical surfaces as real parts of the solutions. The spherical coordinates are used to express the modified hypocycloid curve into new surfaces including the derivatives to give visualisation between the equation and its derivative.

The results are classified into 3 types of innovations. The first is an innovation on extending circle and sphere into higher exponent in the equations yielding to enrichment of curves and surfaces into weak kites and weak balls respectively. The modified hypocycloid curves are the second innovation finally collected to be designs for curve stitching and the surfaces employed to be batik motifs, puzzles and mathematical ornaments. The designs are also used for several designs on souvenirs. The batik creation called BATIMA has been selected as one of 108 Indonesian innovations in 2016 by BIC (Business Innovation Center).

The algebraic surfaces as the third innovation have also been used to be surfaces innovation through SURFER where the expression can be typed directly to create the surfaces. The Xmas Ornaments and Xmas-hats are shown here to be examples of the surfaces.

Remark

The approach in this paper very rare met with reputable and modern journals since the innovation means that the creation beyond the standard related topics. Therefore, author has very limited references.

Acknowledgment

Special thank to Dr. Bianca Violet from Imaginary Mathematisches Forschungsinstitut Oberwolfach,Germany who has inspired me to use SURFER for creating algebraic surfaces.

References

[1] Ahuja O P 1996. Let’s Popularize Mathematics, The Mathematics Educator , Vol. l , No. 1. 82-98.

[2] Piggott J 2007 The nature of mathematical enrichment: a case study of Implementation, Educate, Vol.7, No.2, pp. 30-45,University of Cambridge, Faculty of Education.

[3] Diković L 2009 Applications GeoGebra into teaching some topics of Mathematics at the College Level, Computer Science and Information Systems , 6(2), 191-203.

[4] Parhusip H A 2014 Arts revealed in calculus and its extension. International Journal of Statistics and Mathematics, 1(3): 002-009, Premier-Publisher.

(11)

[6] Parhusip H A 2010 Learning Complex Function And Its Visualization With Matlab, South East Asian Conference On Mathematics And Its Applications Proceedings Institut Teknologi Sepuluh Nopember, Surabaya , ISBN 978 – 979 – 96152 – 5 – 1,pp.373-384.

[7] Parhusip H A and Sulistyono 2009 Pemetaan

















z

w

1

dan hasil pemetaannya, Prosiding,

Seminar Nasional Matematika dan Pendidikan Matematika,FMIPA UNY 5 Des 2009, ISBN : 978-979-16353-3-2,T-16, hal. 1127-1138 (Indonesian).

[8] Purwoto Parhusip H A, Mahatma T 2014 Perluasan Kurva Parametrik Hypocycloid Dimensi Menjadi 3 Dimensi Dengan Sistem Koordinat Bola, prosiding Seminar Nasional UNNES,8 Nov 2014, ISBN 978-602-1034-06-4; hal.326-336 (Indonesian).

[9] Hartkopf A and Matt A D 2013 SURFER in Math Art, Education and Science Communication Proceedings of Bridges: Mathematics, Music, Art, Architecture, Culture.

[10] Suryaningsih V Parhusip H A, Mahatma T 2013 Kurva Parametrik dan Transformasinya untuk Pembentukan Motif Dekoratif, Prosiding, Seminar Nasional Matematika dan Pendidikan Matematika UNY,9 Nov, ISBN:978-979-16353-9-4,hal. MT – 249-258.

[11] Parhusip H A 2016 Sains dan Matematika untuk Art untuk Technoeducation, Science Festival , organized by LK-FSM, UKSW, 26 Feb 2016, di gedung GKJ Salatiga. DOI: 10.13140/RG.2.1.4388.8402

[12] Parhusip H A 2014 Arts revealed in Calculus and Its Extension International Journal of Statistics and Mathematics, 1(3): 002-009, Premier-Publisher, available online on :

(12)

International Conference on Mathematics :

Education, Theory, and Application (ICMETA) 2016

Department of Mathematics

Faculty of Mathematics and Natural Sciences

6

th

& 7

th

December 2016, Hotel ALILA

(13)

SCHEDULE-ICMETA, DECEMBER 6-7, 2016 1 Ballroom Hotel Alila

08.00 - 08.10 ’ Opening of Master of Ceremony

08.10 - 08.20 ’

Samsuri Sutarna, M.Sn

Lecturer of Institute Seni Indonesia-Surakarta Central Java

Traditional Dance Performance : Tari Klana Topeng

08.20 - 08.40 ’ Vox Magistra FKIP UNS

a. Singing Traditional

b. Singing National

Anthem (audiences)

WELCOME SPEECH

08.40 - 08.50

’ Dr. Dewi Retno Sari Saputro, M.Kom. Chair of ICMETA

08.50 - 09.00 ’ Prof. Ari Handono Ramelan,

M.Sc.(Hons),Ph.D.

Dean of FMIPA

09.00 - 09.10 ’ Prof. Dr. Ravik Karsidi, M.S. Rector of Universitas Sebelas

Maret

09.10 - 09.25 5’ Coffee Break Lobby Ballroom Hotel Alila

Keynote Session - Ballroom Hotel Alila

Prof. Drs. Tri Atmojo K, M,Sc. Ph.D.

Department of Mathematics, Faculty of

Mathematics and Natural Sciences

Universitas Sebelas Maret, Indonesia

Moderator

09.25 - 10.10 ’ Prof. Dr. Edy Tri Baskoro, M.Sc.

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bandung Institute of Technology , Indonesia

Keynote Speaker I

10.10 - 10.55 ’ Dr. Darfiana Nur, M.Sc.

Statistical Science in the School of Computer Science, Engineering and Mathematics, Flinders University, Australia

Keynote Speaker II

10.55 - 11.10 5’ Panel Discussion and Q & A Session

Putranto Hadi Utomo, M.Si.

(14)

SCHEDULE-ICMETA, DECEMBER 6-7, 2016 2 Science, University of Malaya, Malaysia

12.40 -12.55 ’ Panel Discussion and Q & A Session

12.55 -13.40 45’ Lunch Lobby Ballroom Hotel Alila

Paper Presentation Parallel Session 1

13.40 - 15.00 ’ Mathematics Education Room Meeting Hotel Alila

a. Room 1 5 papers

b. Room 2 5 papers

c. Room 3 5 papers

Combinatorics

a. Room 4 5 papers

b. Room 5 5 papers

Statistics

a. Room 6 5 papers

b. Room 7 5 papers

Applied Mathematics

a. Room 8 5 papers

b. Room 9 5 papers

c. Room 10 5 papers

15.00 - 15.30 ’ Coffee Break Room Meeting Hotel Alila

Paper Presentation Parallel Session 2

15.30 - 16.45 ’ Mathematics Education Room Meeting Hotel Alila

a. Room 1 4 papers

b. Room 2 5 papers

c. Room 3 5 papers

Combinatorics

a. Room 4 6 papers

b. Room 5 5 papers

Statistics

a. Room 6 5 papers

b. Room 7 5 papers

Applied Mathematics

a. Room 8 4 papers

b. Room 9 4 papers

c. Room 10 4 papers

(15)

SCHEDULE-ICMETA, DECEMBER 6-7, 2016 3 2nd_{Day Opening}

Ballroom Hotel Alila

08.00 - 08.15 ’ Opening of Master of Ceremony

08.15 - 08.30 20’ Coffee Break Lobby Ball Room

Hotel Alila

Keynote Session Ballroom Hotel Alila Dra. Mania Roswitha, M.Si.

Moderator

08.30 - 09.25 ’ Dr. Hanna Arini Parhusip

Department of Mathematics, Faculty of Science and Mathematics, UKSW, Salatiga Indonesia

Keynote Speaker V

09.25-10.10 ’ Prof. Dr. Kenjiro T. Miura

Realistic Modeling Laboratory, Department of Mechanical Engineering, Shizuoka University, Japan

Keynote Speaker VI

10.10-10.25 ’ Panel Discussion and Q & A Session

Keynote Session-Ballroom Hotel Alila

Drs. Isnandar Slamet, M.Sc., Ph.D.

Department of Statisticss, Faculty of

Moderator

10.25 - 11.10 ’ Dr. Sutanto, DEA

Department of Mathematics, Faculty of Mathematics and Natural Sciences Universitas Sebelas Maret, Indonesia

Keynote Speaker VII

11.10 - 11.55 ’ Dr. Benoît Liquet

Laboratory of Mathematics and Their

Applications, Université de Pau et des Pays de l'Adou, France

Keynote Speaker VIII

(16)

SCHEDULE-ICMETA, DECEMBER 6-7, 2016 4

Room Meeting Hotel Alila

b. Room 2 5 papers

c. Room 3 5 papers

Combinatorics

Room 4 5 papers

Statistics

a. Room 5 5 papers

b. Room 6 5 papers

Room Algebra & Analysis

Room 7 5 papers

a. Room 8 5 papers

b. Room 9 5 papers

c. Room 10 5 papers

15.00 - 15.30 ’ Coffee Break

Paper Presentation Parallel Session 4

15.30 - 16.30

’

Mathematics Education Room Meeting Hotel Alila

a. Room 1 4 papers

b. Room 2 5 papers

c. Room 3 4 papers

Combinatorics

Room 4 5 papers

Statistics

a. Room 5 4 papers

b. Room 6 4 papers

Room Algebra & Analysis

Room 7 3 papers

a. Room 8 4 papers

b. Room 9 5 papers

c. Room 10 4 papers

(17)

(18)

Secretariat ICMETA 2016 :

2nd floor, A Building

Department of Mathematics, Faculty of Mathematics and Natural Sciences SebelasMaret University

Ir. Sutami 36 A Solo, Central Java, Indonesia

No : 021/ICMETA/2016

Subject :Invitation as Keynote Speaker for the ICMETA

Dear Dr Hanna Arini Parhusip