Transformasi fourier diskrit dan aplikasinya pada kompresi citra digital.

viii ABSTRAK

Tulisan ini membahas tentang Transformasi Fourier Diskrit (TFD) yang merupakan implementasi dari transformasi Fourier. Transformasi Fourier Diskrit mentransformasikan suatu fungsi pada domain ruang/waktu ke domain frekuensi. Transformasi Fourier Diskrit dapat digunakan dalam pemrosesan sinyal atau citra, seperti penyaringan sinyal, dekomposisi spektral, dan kompresi sinyal atau citra. Pada bagian akhir tulisan ini akan dibahas mengenai aplikasi transformasi Fourier diskrit pada kompresi citra digital, khususnya citra beraras keabu-abuan. Dalam bidang matematika, transformasi Fourier Diskrit mentransformasikan suatu vektor menjadi vektor yang lebih sederhana dan apabila diinverskan kembali vektor hasilnya serupa dengan vektor aslinya.

Suatu nilai ambang batas mempunyai pengaruh besar dalam pemampatan data menggunakan transformasi Fourier Diskrit. Nilai ambang batas ini akan menentukan nilai-nilai frekuensi yang harus dianggap nol. Apabila nilai ambang batas semakin kecil (mendekati nol), maka hasil pemampatannya serupa dengan data aslinya.

ix ABSTRACT

This thesis discusses the Discrete Fourier transform (DFT), which is an implementation of the Fourier transform. Discrete Fourier Transform to transform a function on the domain space/time domain to the domain frequency. Discrete Fourier transform can be used in signal or image processing, such as signal filtering, spectral decomposition, and signal or data compression. In the final section of this thesis will discuss the application of the Discrete Fourier transform on the digital image compression, especially grayscale image. In mathematics, the Discrete Fourier transform to transform a vector into a vector that is more simple and if it is inversed back, it will have similar properties as the original one.

A threshold value is significance to the data compression using Discrete Fourier transform. This threshold value will determine the frequency values that should be considered zero. If the threshold is getting smaller (close to zero), then the compression have similar properties as the original one.

i

TRANSFORMASI FOURIER DISKRIT

DAN APLIKASINYA PADA KOMPRESI CITRA DIGITAL

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains Program Studi Matematika

Oleh:

Ayu Sri Wulandari

NIM: 103114004

PROGRAM STUDI MATEMATIKA

JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

DISCRETE FOURIER TRANSFORM

AND ITS APPLICATION IN IMAGE DIGITAL COMPRESSION

Thesis

Presented As a Partial Fulfillment of the Requirements

to Obtain the Sarjana Sains Degree in Mathematics

By:

Ayu Sri Wulandari

Student Number: 103114004

MATHEMATICS STUDY PROGRAM,

DEPARTMENT OF MATHEMATICS

FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

SKRIPSI

TRANSFORMASI FOURIER DISKRIT

DAN APLIKASII\TYA PADA KOMPRESI CITRA DIGITAL

'.Y:d"

-\

Disusun oleh:

.*dftffiH"e

1$ffi3

';.,' ,r!

NI%$ffi114004

O

r;-.\

:-effiS

*a

-A,

Telah

fsetujui oleh: , _^11

I

Pembimbing

*t'be"'oocd

ffif

( Dr.rer.nat. Herrj, Pribawanto S. ₎ Tanggal 26 Januan2}ll

SKRIPSI

TRANSFORMASI FOURIER DISKRIT

DAN APLIKASINYA PADA KOMPRESI CITRA DIGITAL

Dipersiapkan dan ditulis oleh:

Ayu Sri Wulandari

NIM: 103114004

Telah dipertahankan di depan Panitia Penguji pada tangg al 29 J anuai 201 5

dan dinyatakan memenuhi syarat.

SUSUNAN PANITIA PENGUJI Nama Lengkap

Ketua

: k. Ig. Aris Dwiatmoko, M.Sc. Sekretaris : Y. G. Hartono, Ph.D.

Anggota

: Dr.rer.nat.Herry Pribawanto S.

t{rdutun

*,

&rl

,fu-rt"L

-Yogyakarta,

2Z

Februari 2015

Fakultas Sains dan Teknologi Universitas Sanata Dharma Dekan

f"#tX

\'. '-cvc.xo

1V

PERTTYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini

tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustak4 sebagaimana layaknya karya ilmiah.

Yogyakarta, 26 J anuari 201 5

Penulis

w

I

//'

vi

HALAMAN PERSEMBAHAN

“Don’t limit yourself, many people limit themselves to what

they think they can do. You can go as far as your mind lets

you. What you believe, remember, you can achieve.”

MARY KAY ASH

-Skripsi ini penulis persembahkan kepada:

Tuhan Yesus Kristus dan Bunda Maria,

Bapak Stefanus Wagiyo (alm) dan Ibu Ch. Sri Nursilowati,

Kakak-kakak tersayang (Indah, Aris, Daniel),

serta sahabat-sahabat yang selalu berada di sisi saya.

LEMBAR PER}IYATAAN PERSETUJUAN

PUBLIKASI KARYA

ILMIAII

T]NTUK KEPENTINGAN AKADEMIS

Saya yang bertanda tangan di bawah ini, mahasiswi Universitas Sanata Dharma: Nama

NIM

: Ayu Sri Wulandari : 10 3114004

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:

Transformasi Fourier Dislcrit dan Aplikasinya pada Kompresi Citra Digital

Beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma unutk menyimpan, mengalihkan

ke

dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media

lain untuk kepentingan akademis tanpa perlu meminta

ijin dari

saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat dengan sebenarnya. Dibuat di Yogyakarta

Pada tanggal: 26 Januari 20 I 5

Yang menyatakan

W1

J -tr- t r'l

T

t-12

(Ayu Sri Wulandari)

viii ABSTRAK

Tulisan ini membahas tentang Transformasi Fourier Diskrit (TFD) yang merupakan implementasi dari transformasi Fourier. Transformasi Fourier Diskrit mentransformasikan suatu fungsi pada domain ruang/waktu ke domain frekuensi. Transformasi Fourier Diskrit dapat digunakan dalam pemrosesan sinyal atau citra, seperti penyaringan sinyal, dekomposisi spektral, dan kompresi sinyal atau citra. Pada bagian akhir tulisan ini akan dibahas mengenai aplikasi transformasi Fourier diskrit pada kompresi citra digital, khususnya citra beraras keabu-abuan. Dalam bidang matematika, transformasi Fourier Diskrit mentransformasikan suatu vektor menjadi vektor yang lebih sederhana dan apabila diinverskan kembali vektor hasilnya serupa dengan vektor aslinya.

Suatu nilai ambang batas mempunyai pengaruh besar dalam pemampatan data menggunakan transformasi Fourier Diskrit. Nilai ambang batas ini akan menentukan nilai-nilai frekuensi yang harus dianggap nol. Apabila nilai ambang batas semakin kecil (mendekati nol), maka hasil pemampatannya serupa dengan data aslinya.

ix ABSTRACT

This thesis discusses the Discrete Fourier transform (DFT), which is an implementation of the Fourier transform. Discrete Fourier Transform to transform a function on the domain space/time domain to the domain frequency. Discrete Fourier transform can be used in signal or image processing, such as signal filtering, spectral decomposition, and signal or data compression. In the final section of this thesis will discuss the application of the Discrete Fourier transform on the digital image compression, especially grayscale image. In mathematics, the Discrete Fourier transform to transform a vector into a vector that is more simple and if it is inversed back, it will have similar properties as the original one.

A threshold value is significance to the data compression using Discrete Fourier transform. This threshold value will determine the frequency values that should be considered zero. If the threshold is getting smaller (close to zero), then the compression have similar properties as the original one.

x

KATA PENGANTAR

Puji dan Syukur penulis haturkan kepada Tuhan Yesus atas segala cinta kasih-Nya yang melimpah sehingga penulis dapat menyelesaikan skripsi untuk memenuhi tugas akhir dalam menempuh gelar Sarjana (S1) di Universitas Sanata Dharma dengan lancar dan baik.

Selama penulisan skripsi ini, penulis menyadari bahwa banyak pihak yang telah berperan besar dalam bimbingan, dukungan dan bantuannya bagi penulis untuk menyelesaikan skripsi ini. Oleh karena itu, penulis ingin mengucapkan terimakasih yang sebesar-besarnya kepada:

1. Tuhan Yesus Kristus atas berkat dan penyertaan-Nya selama proses penulisan skripsi ini sehingga penulis dapat menyelesaikan skripsi ini dengan baik. 2. Bapak Dr.rer.nat. Herry Pribawanto, M.Si., selaku dosen pembimbing skripsi

yang telah membimbing, mendampingi, dan memberikan masukan kepada penulis selama proses penulisan skripsi ini.

3. Bapak Y.G. Hartono, Ph.D., selaku Ketua Program Studi Matematika dan dosen pembimbing skripsi yang telah membimbing, mendampingi, dan memberikan masukan kepada penulis selama proses penulisan skripsi ini. 4. Ibu Paulina H. Prima Rosa, S.Si., M.Sc., selaku Dekan Fakultas Sains dan

Teknologi Universitas Sanata Dharma Yogyakarta.

5. Bapak Ir. Ign. Aris Dwiatmoko, M.Sc., selaku Dosen Pembimbing Akademik 6. Bapak, Ibu, dan Romo, dosen program studi Matematika yang senantiasa

xi

7. Bapak Z. Tukija dan para staf sekretariat Fakultas Sains dan Teknologi lainnya yang telah banyak membantu dalam proses administrasi.

8. Perpustakaan USD yang telah membantu menyediakan bahan dan fasilitas selama proses penulisan skripsi ini.

9. Bapak Stephanus Wagiyo (alm) dan Ibu Ch. Sri Nursilowati, selaku orang tua penulis, kakak-kakakku tersayang Indah, Daniel dan Aris dan segenap keluarga atas segala doa dan dukungannya kepada penulis.

10. Sahabat-sahabat terdekatku, Happy adik almamaterku, dan teman-teman prodi Matematika terkhusus angkatan 2010: Arga, Celly, Astri, Agnes, Dini, Leny, Marsel, Pandu, Yosi, Roy, Ratri, Tika, Yohan, Sari; atas doa, semangat dan kebersamaan yang diberikan kepada penulis.

11. Semua pihak yang tidak dapat disebutkan satu per satu yang telah membantu dalam penyusunan skripsi ini.

Penulis menyadari bahwa masih ada kekurangan dalam penulisan skripsi ini. Oleh karena itu, penulis mengharapkan kritik dan saran yang membangun demi kesempurnaan skripsi ini.

Yogyakarta, 26 Januari 2015

xii DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN... iii

HALAMAN PENGESAHAN... iv

HALAMAN PERNYATAAN KEASLIAN TULISAN... v

HALAMAN PERSEMBAHAN... vi

ABSTRAK... viii

ABSTRACT... ix

KATA PENGANTAR... x

DAFTAR ISI... xii

DAFTAR TABEL... xv

DAFTAR GAMBAR... xvi

BAB I PENDAHULUAN... 1

1.1. Latar Belakang... 1

1.2. Perumusan Masalah... 11

1.3. Pembatasan Masalah... 11

1.4. Tujuan Penelitian... 11

1.5. Manfaat Penulisan... 12

1.6. Metode Penulisan... 12

1.7. Sistematika Penulisan... 12

BAB II LANDASAN TEORI... 14

2.1. Aljabar Fungsi... 14

2.1.1. Periode Fungsi... 14

xiii

2.1.3. Turunan Fungsi... 16

2.1.4. Fungsi Mulus... 17

2.1.5. Bilangan Kompleks... 18

2.1.6. Konjugat Kompleks... 18

2.1.7. Fungsi Eksponensial Kompleks... 19

2.2. Aljabar Matriks... 20

2.2.1. Matriks Identitas... 20

2.2.2. Invers Matriks... 20

2.2.3. Matriks Simetris... 22

2.2.4. Matriks Uniter... 22

2.2.5. Ruang Hasilkali Dalam dan Norma... 23

2.2.6. Ortogonalitas... 26

BAB III TRANSFORMASI FOURIER DISKRIT... 27

3.1. Deret Fourier... 27

3.2. Transformasi Fourier... 37

3.2.1. Sifat-sifat Dasar Transformasi Fourier... 41

3.3. Transformasi Fourier Diskrit... 48

3.3.1. Definisi Transformasi Fourier Diskrit... 49

3.3.2. Sifat-sifat Dasar Transformasi Fourier Diskrit... 68

3.3.3. Transformasi Fourier Diskrit 2 Dimensi... 74

3.3.4. Transformasi Fourier Diskrit pada Kompresi Sinyal... 84

BAB IV APLIKASI TRANSFORMASI FOURIER DISKRIT... 88

4.1. Citra Diskrit... 88

4.2. Citra Beraras Keabu-abuan... 88

xiv

BAB V PENUTUP... 96

5.1. Kesimpulan... 96

5.2. Saran... 97

DAFTAR PUSTAKA... 98

xv

DAFTAR TABEL

Tabel 3.1... 57

Tabel 3.2... 58

Tabel 4.1... 93

xvi

DAFTAR GAMBAR

Gambar 1.1... 2

Gambar 1.2... 2

Gambar 1.3... 3

Gambar 1.4... 4

Gambar 1.5... 5

Gambar 1.6... 6

Gambar 1.7... 8

Gambar 1.8... 8

Gambar 1.9... 9

Gambar 1.10... 9

Gambar 1.11... 10

Gambar 1.12... 10

Gambar 2.1... 16

Gambar 2.2... 18

Gambar 3.1... 40

Gambar 3.2... 48

Gambar 3.3... 49

Gambar 3.4... 58

Gambar 3.5... 59

Gambar 3.6... 75

Gambar 3.7... 85

Gambar 3.8... 86

xvii

Gambar 4.2... 90

Gambar 4.3... 91

Gambar 4.4... 92

Gambar 4.5... 94

BAB I

PENDAHULUAN

1.1.Latar Belakang Masalah

Citra merupakan suatu kombinasi antara titik-titik, garis, bidang dan warna untuk menciptakan sebuah tiruan dari obyek nyata. Citra dapat difungsikan sebagai suatu simbol untuk menyampaikan pesan antar manusia. Dalam kehidupan sehari-hari, citra hanya tampak dalam bentuk dua dimensi dan tiga dimensi. Citra dalam wujud dua dimensi dapat berupa suatu citra digital, sedangkan citra dalam wujud tiga dimensi dapat berupa patung atau ukiran. Citra digital merupakan gambar tiruan dari suatu obyek nyata yang diciptakan oleh perangkat optik seperti kamera, akan tetapi ukuran resolusi dari citra digital sangat besar sehingga akan berdampak dalam penyimpanan dan proses pengiriman gambar. Oleh karena itu, untuk menyelesaikan masalah tersebut perlu dilakukan minimisasi ukuran resolusi yang dikenal dengan kompresi.

waktu dalam pertukaran ataupun pengirimannya. Berikut beberapa contoh citra asli dan hasil kompresinya:

Gambar 1.1. Citra asli berukuran 77,9 kilobyte (kiri). Citra terkompresi berukuran 19,11 kilobyte (kanan).

(Sumber:https://old.ntchosting.com/multimedia/jpg-image-file-format.html)

Gambar 1.2. Citra asli (kiri) dan citra terkompresi (kanan).

(Sumber: http://petapixel.com/2009/12/22/why-higher-iso-leads-to-larger-file-sizes)

Berdasarkan kandungan informasi pada citra hasil kompresi, pemampatan/kompresi dikelompokkan menjadi dua, yaitu pemampatan tanpa kehilangan (lossless compression) dan pemampatan berkehilangan (lossy compression).

apabila berkas citra digital berukuran 256x256 berwarna polos (setiap pixel berwarna sama) dan tiap pixelnya berukuran 4 byte, tanpa pemadatan, berkas harus disimpan berukuran 4 kali 256x256, sama dengan 262144 byte. _{Namun, dengan pemadatan, maka data yang perlu}

disimpan hanya data satu warna tersebut. Jadi, data yang perlu disimpan hanyalah 4 byte ditambah beberapa byte untuk menandakan pengulangan pixel yang sama.

Gambar 1.3. Ilustrasi Lossless Compression JPEG 2000. Gambar asli (atas);

Gambar terkompresi 1 berukuran 4990 kilobyte (kiri bawah); Gambar terkompresi 2 berukuran 4184 kilobyte (kanan bawah).

(Sumber: http://www.steves-digicams.com/knowledge-center/whatever-happened-to-jpeg2000.html)

menghasilkan ratio kompresi yang lebih besar daripada metode lossless. Misal terdapat citra digital asli berukuran 12,249 byte, kemudian dilakukan kompresi dengan JPEG kualitas 30 dan ukurannya menjadi 1,869 byte berarti citra digital tersebut 85% lebih kecil dan ratio kompresinya 15%. Contoh format gambar yang teknik kompresinya menggunakan lossy compression adalah JPEG.

Gambar 1.4. Ilustrasi Lossy Compression. Gambar asli berukuran 12 kilobyte

(kiri); Gambar terkompresi 85% berukuran 1,8 kilobyte (tengah); Gambar terkompresi 96% berukuran 0.56 kilobyte (kanan).

(Sumber:https://onramps.instructure.com/courses/1196409/pages/compressio n-algorithms)

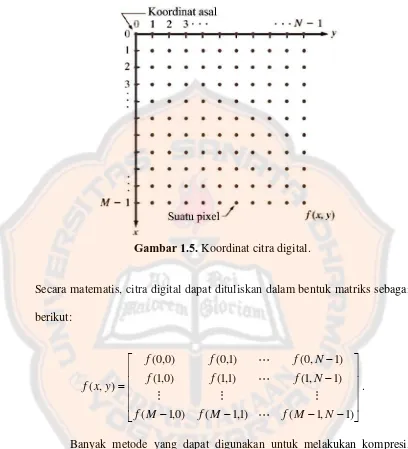
Dari sudut pandang matematis, citra digital merupakan suatu array

Gambar 1.5. Koordinat citra digital.

Secara matematis, citra digital dapat dituliskan dalam bentuk matriks sebagai berikut:

. ) 1 , 1 ( )

1 , 1 ( ) 0 , 1 (

) 1 , 1 ( )

1 , 1 ( )

0 , 1 (

) 1 , 0 ( )

1 , 0 ( )

0 , 0 ( )

, (

   

 

   

 

  



 



N M f M

f M

f

N f f

f

N f f

f

y x f



 



 

Banyak metode yang dapat digunakan untuk melakukan kompresi, antara lain metode Huffman, RLE (Run Length Encoding), metode Shannon-Fano, kompresi citra berbasis transformasi, dan sebagainya. Dalam bidang matematika, salah satu teori yang dapat diterapkan untuk melakukan kompresi citra berbasis transformasi adalah Transformasi Fourier Diskrit.

awal munculnya analisis Fourier. Terdapat dua masalah lain yang menjadi akar dari munculnya analisis Fourier. Masalah pertama adalah cara untuk mendeskripsikan getaran yang diciptakan oleh senar yang bergetar bila kedua ujungnya diikat dengan kencang. Masalah ini mengarah pada persamaan gelombang, seperti yang telah dirumuskan oleh matematikawan Jean

d’Alembert, Leonhard Euler, Daniel Bernoulli, dan Joseph-Louis Lagrange. Matematikawan Bernoulli memberikan penyelesaian berbentuk deret trigonometri

... 2 cos 2 sin cos

sin  

 A x at B x at y

dengan x adalah koordinat spasial dan t adalah variabel waktu. Penyelesaian yang diberikan oleh Bernoulli ini menyerupai bentuk kontinyu dari deret Fourier. Sedangkan, Euler dan Lagrange menDiskritisasi masalah getaran tersebut dengan menggambarkan bahwa senar tersebut terdiri dari partikel-partikel yang terbatas dan partikel-partikel-partikel-partikel tersebut saling terhubung (Gambar 1.6).

Penyelesaian dari masalah Diskritisasi tersebut ialah dengan mencari sampel-sampel dari fungsi yang menggambarkan pergerakan senar tersebut. Lagrange memberikan penyelesaian berbentuk jumlahan fungsi sinus dari berbagai frekuensi yang beragam. Penyelesaiannya ini merupakan dasar transformasi sinus Fourier Diskrit. Masalah kedua yaitu, menentukan orbit dari benda-benda langit. Euler, Lagrange dan Alexis Claude Clairaut membuat pemikiran dasar di mana data yang diambil dari pengamatan diaproksimasi dengan kombinasi linear dari fungsi periodik. Perhitungan koefisien dalam ekspansi trigonometri ini mengarah ke perhitungan yang kemudian akan disebut dengan transformasi Fourier Diskrit.

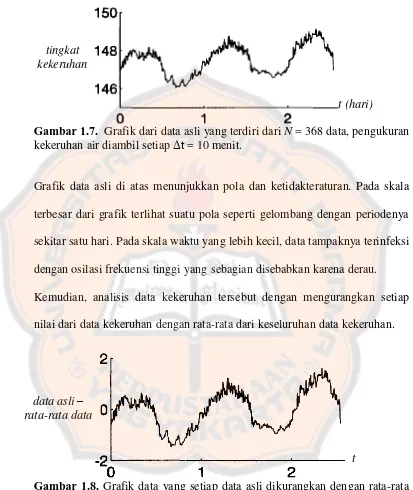
Gambar 1.7. Grafik dari data asli yang terdiri dari N = 368 data, pengukuran kekeruhan air diambil setiap Δt = 10 menit.

Grafik data asli di atas menunjukkan pola dan ketidakteraturan. Pada skala terbesar dari grafik terlihat suatu pola seperti gelombang dengan periodenya sekitar satu hari. Pada skala waktu yang lebih kecil, data tampaknya terinfeksi dengan osilasi frekuensi tinggi yang sebagian disebabkan karena derau. Kemudian, analisis data kekeruhan tersebut dengan mengurangkan setiap nilai dari data kekeruhan dengan rata-rata dari keseluruhan data kekeruhan.

Gambar 1.8. Grafik data yang setiap data asli dikurangkan dengan rata-rata

datanya.

Nilai data yang muncul sebagai fluktuasi nilai rata-rata dari nol. Dengan kumpulan data yang disesuaikan, dari data tersebut dapat diperoleh dekomposisi spektral/frekuensinya dengan menggunakan konsep dari transformasi Fourier Diskrit. Hasilnya dapat dilihat pada Gambar 1.9.

tingkat kekeruhan

t (hari)

t data asli –

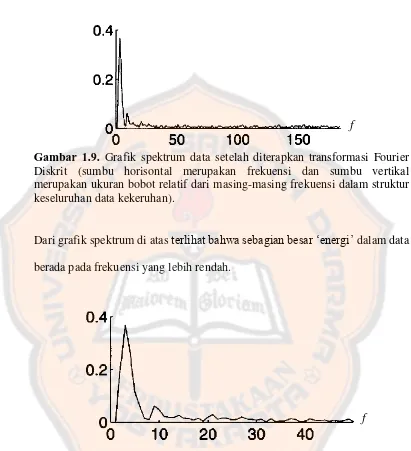
Gambar 1.9. Grafik spektrum data setelah diterapkan transformasi Fourier Diskrit (sumbu horisontal merupakan frekuensi dan sumbu vertikal merupakan ukuran bobot relatif dari masing-masing frekuensi dalam struktur keseluruhan data kekeruhan).

Dari grafik spektrum di atas terlihat bahwa sebagian besar ‘energi’ dalam data berada pada frekuensi yang lebih rendah.

Gambar 1.10. Perbesaran dari grafik spektrum data pada frekuensi rendah.

Dari gambar 1.7 dapat dilihat bahwa dari data asli muncul ‘derau’. ‘Derau’ yang muncul karena kontribusi semua frekuensi tinggi dalam spektrum,

sehingga untuk mengatasi ‘derau’ tersebut dilakukan penyaringan. Istilah dari

penyaringan dapat digambarkan dengan sederhana, yaitu menghilangkan semua frekuensi yang tinggi pada spektrum di atas frekuensi yang dipilih.

f

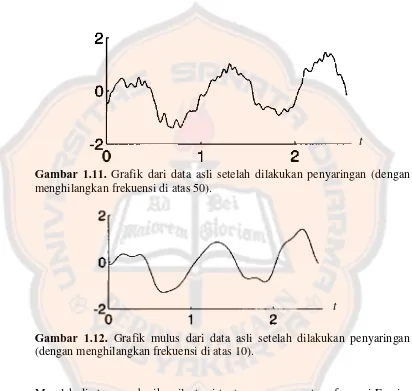
Spektrum baru yang terbentuk direkonstruksi dengan invers dari transformasi Fourier Diskrit, sehingga dapat dihasilkan data yang grafiknya lebih mulus dari data aslinya.

Gambar 1.11. Grafik dari data asli setelah dilakukan penyaringan (dengan menghilangkan frekuensi di atas 50).

Gambar 1.12. Grafik mulus dari data asli setelah dilakukan penyaringan (dengan menghilangkan frekuensi di atas 10).

Masalah di atas memberikan ilustrasi tentang penerapan transformasi Fourier Diskrit dalam dekomposisi spektral dan penyaringan sinyal.

Dalam tulisan ini, penerapan transformasi Fourier Diskrit yang akan dibahas ialah penerapan transformasi Fourier Diskrit dalam pemrosesan citra, khususnya dalam kompresi pada citra digital

t

1.2.Perumusan Masalah

Pokok permasalahan yang akan dibahas dalam tulisan ini dirumuskan sebagai berikut.

1. Apa yang dimaksud dengan Transformasi Fourier Diskrit dan bagaimana landasan teoritisnya?

2. Bagaimana penerapan Transformasi Fourier Diskrit pada kompresi citra digital?

3. Bagaimana algoritma dan pemrograman MATLAB untuk kompresi citra digital dengan Transformasi Fourier Diskrit?

1.3.Pembatasan Masalah

Penulis akan membatasi beberapa hal untuk uraian masalah yang akan dibahas, yaitu:

1. Fungsi domain spasial pada citra digital yang akan dibahas dalam tulisan ini merupakan fungsi yang periodik.

2. Tulisan ini hanya akan membahas penerapan transformasi Fourier Diskrit 2D.

3. Penerapan transformasi Fourier Diskrit 2D hanya dibatasi pada citra digital beraras keabu-abuan.

1.4.Tujuan Penulisan

sebagai pemenuhan tugas akhir dalam program studi Matematika Universitas Sanata Dharma.

1.5.Manfaat Penulisan

Manfaat penulisan ini adalah memperoleh pengetahuan mengenai konsep transformasi Fourier Diskrit dan penerapannya dalam kompresi citra digital. Selain itu, dapat juga dibuat algoritma dan pemrograman MATLAB sehingga proses komputasi lebih efektif dan efisien.

1.6.Metode Penulisan

Metode yang digunakan penulis adalah metode studi pustaka, yaitu dengan mempelajari buku-buku yang berkaitan dengan pengolahan citra, sinyal, transformasi Fourier Diskrit dan penerapannya dalam kompresi citra.

1.7.Sistematika Penulisan

2.2. Aljabar Matriks

BAB III TRANSFORMASI FOURIER DISKRIT 3.1. Deret Fourier

3.2. Transformasi Fourier

3.3. Transformasi Fourier Diskrit

BAB IV APLIKASI TRANSFORMASI FOURIER DISKRIT BAB V PENUTUP

5.1. Kesimpulan 5.2. Saran

BAB II

LANDASAN TEORI

2.1.Aljabar Fungsi

2.1.1. Periode Fungsi

Definisi 2.1

Suatu fungsi f dikatakan periodik jika terdapat suatu bilangan positif

p sedemikian sehingga



x p



f

 

x f  

untuk semua bilangan riil x di dalam daerah asal f . Bilangan p

tersebut disebut periode f . Contoh 2.1

Fungsi f

 

x sinx mempunyai periode 2 , sebab













 





 

2 sin cos 2

cos sin

2 sin 2

x x

x x

f

 

 



x sin

 ,xℝ .

2.1.2. Kekontinyuan Fungsi

Definisi 2.2

Fungsi f

 

x dikatakan kontinyu di suatu titik c, jika f

 

c terdefinisi dan

 

x f

 

c f

c

x 

Definisi 2.3

Suatu fungsi f dikatakan kontinyu pada interval [a,b] jika fungsi tersebut kontinyu di semua titik pada interval

 

a,b dan jika

 

a f x f

a

x  

) (

lim dan f x f

 

b

b

x 

) (

lim .

Fungsi f dikatakan kontinyu sepotong-sepotong pada [a,b] jika interval tersebut dapat dibagi menjadi subinterval berhingga dan pada setiap subinterval tersebut f kontinyu.

Contoh 2.2

Misal,



 



  

  

 

  

 

 

  



. 2 1

untuk

5 1 1 ln 1

, 1 0

untuk ln

, 0 1

-untuk 2 1 2

) (

x x

x

x x

x

x x

x f

Gambar 2.1. Grafik dari fungsi sepotong-sepotong f

 

x pada interval



1,2



.

2.1.3. Turunan Fungsi

Definisi 2.4

Turunan suatu fungsi f adalah fungsi lain f' (dibaca “ f aksen”) yang nilainya di sebarang bilangan x adalah

 



  

h x f h x f x

f

h

  

0 lim '

asalkan limit ini ada dan bukan atau . Contoh 2.3

Jika f

 

x x3 7x, maka

 



  

















h

x x h x h xh h x x

h

x x h x h

x h

x f h x f x

f

h h h

7 7

7 3

3 lim

7 7

lim lim '

3 3

2 2

3 0

3 3

0 0

       

     

  

[image:35.595.100.509.99.719.2]









. 7 3 7 3 3 lim 7 3 3 lim 7 3 3 lim 2 2 2 0 2 2 0 3 2 2 0                  x h xh x h h xh x h h h h xh h x h h h

2.1.4. Fungsi Mulus

Definisi 2.5

Suatu fungsi f dikatakan mulus pada suatu interval

 

a,b jika f dan '

f kontinyu pada interval tersebut. Contoh 2.4 Misal,



 



                    , 2 1 untuk 5 1 1 ln 1 , 1 0 untuk ln , 0 1 -untuk 2 1 2 ) ( 2 2 x x x x x x x x x g dan



 

 



                    . 2 1 untuk 1 1 ln 1 2 , 1 0 untuk ln 2 , 0 1 -untuk 2 1 ) ( ' x x x x x x x x x x g



1,0



,



0,1



dan



1,2



dan fungsi turunan g'

 

x juga kontinyu

sepotong-sepotong pada setiap subinterval tersebut.

Gambar 2.2. Grafik dari fungsi mulus sepotong-sepotong g

 

x (kiri) dan g'

 

x (kanan) pada interval



1,2



.

2.1.5. Bilangan Kompleks

Definisi 2.6

Jika z xiy menyatakan sembarang bilangan kompleks, maka

 

z

xRe merupakan bagian riil dari zdan y Im

 

z merupakan bagian imajiner dari z . Re

 

z dan Im

 

z merupakan bilangan riil.

2.1.6. Konjugat Kompleks

Definisi 2.7

Untuk setiap bilangan kompleks z xiy, maka bilangan kompleks y

i x z 

[image:37.595.101.510.193.611.2]

Contoh 2.5

Misal, z3i5, maka konjugat kompleksnya adalah 5

3 i z  .

2.1.7. Fungsi Eksponensial Kompleks

Definisi 2.8

Untuk bilangan kompleks z xiydidefinisikan



y i y



e

ez  x cos  sin . Jika diambil ziy, yℝ, maka

y i y e

ez  iy cos  sin , untuk yℝ, yang dikenal juga dengan nama rumus Euler.

Lemma 2.1

Untuk semua x,yℝ berlaku 1. eix2eix,

2. eix 1,

3. eix eix, 4. eixeiy eixy, 5. eix/eiy eixy, 6.

 

eix ieix

dx d

2.2.Aljabar Matriks

2.2.1. Matriks Identitas

Definisi 2.9

Matriks persegi yang elemen diagonal utamanya bernilai 1 dan elemen lainnya 0 disebut sebagai matriks identitas. Matriks identitas dinotasikan dengan I ,

             1 0 0 0 1 0 0 0 1        I .

2.2.2. Invers Matriks

Definisi 2.10

Jika A merupakan matriks persegi, dan jika ada suatu matriks A1

dengan ukuran matriks yang sama dengan A sedemikian sehingga

I A A

AA1 1  , maka A disebut sebagai matriks nonsingular (atau

invertible), dan A1 disebut invers dari A. Contoh 2.6

Misal _

        3 1 5 2

A dan _

       2 1 5 3 1

A , maka

I

AA _ 

                      1 0 0 1 2 1 5 3 3 1 5 2 1 , I A

A _ 

                      1 0 0 1 3 1 5 2 2 1 5 3 1 .

Teorema 2.1

Jika A adalah matriks invertible, dan jika B dan C merupakan invers dari A, maka BC; yang berarti, suatu matriks invertible

mempunyai invers tunggal. Bukti:

Karena B adalah invers dari A, kita punya BAI. Kemudian, kalikan kedua ruas dengan C, sehingga diperoleh

 

 

BAC C.

IC C BA

 

Karena C juga merupakan invers dari A, kita punya ACI. Sehingga, ruas kiri dari persamaan di atas dapat ditulis kembali sebagai

 

BACB

 

AC BI  B,

ini mengakibatkan BC. Teorema 2.2

Jika A dan B matriks invertible dengan ukuran matriks yang sama, maka AB invertible dan

 

1 _ 1 1

A B

AB .

Bukti:

2.2.3. Matriks Simetris

Definisi 2.11

Matriks persegi A disebut matriks simetris jika

A AT  .

Secara aljabar, suatu matriks A

 

a_ij simetris jika dan hanya jika

   

Aij  A ji (atau aij aji).

Contoh 2.7

Misal, _

  



 



5 3

9 2

A , maka _

  

   

5 9

3 2 T

A .

2.2.4. Matriks Uniter

Definisi 2.12

Jika A merupakan matriks dengan elemen-elemennya berupa bilangan kompleks (matriks kompleks), maka transpose konjugat dari

A, dinotasikan dengan A*, didefinisikan oleh T

A A*  . Contoh 2.8

Misal, _

  

 

   

i i i i A

2 3 2

0 1

, maka transpose konjugat dari A ialah

  

 

  

 

    

i i i

i A

A T

0

2 3

2 1

*

Definisi 2.13

Matriks kompleks persegi A dikatakan uniter jika *

1

A

A  atau atau A*AI.

2.2.5. Ruang Hasilkali Dalam dan Norma

Definisi 2.14

Hasilkali dalam pada ruang vektor V adalah suatu operasi pada V yang memetakan setiap pasang vektor-vektor x dan y di dalam V dengan sebuah bilangan riil x,y yang memenuhi syarat berikut:

i. x,x 0 dengan x,x 0 jika hanya jika x0. ii. x,y  y,x untuk semua x,yV .

iii. xy,z  x,z  y,z untuk semua x,y,zV dan semua skalar  dan .

Suatu ruang vektor V yang dilengkapi dengan hasilkali dalam disebut ruang hasilkali dalam.

Definisi 2.15

Jika diberikan vektor

   

 

   

 



n

x x x



2 1

x dan

   

 

   

 



n

y y y



2 1

y , maka hasilkali dalam





. , 1 2 2 1 1 2 1 2 1



                    n i i i n n n n T y x y x y x y x y y y x x x    y x y x Contoh 2.9 Jika        3 1

x dan _

      5 2 y ,

maka hasilkali dalam dari x dengan y pada ruang vektor ℝ2 adalah





2 15 13

5 2 3

1 _  

       x y y

x, T .

Definisi 2.16

Jika diberikan matriks

           mn m n a a a a A      1 1 11 dan            mn m n b b b b B      1 1 11 ,

maka hasilkali dalam dari A dan B pada ruang vektor ℝ × adalah





   n j ij ij m i b a B A 1 1 , . Contoh 2.10 Jika        3 2 4 1

A dan _

      0 2 7 1 B ,

. 33 0 4 28 1 0 2

7 1 3 2

4 1

                 

B A,

Definisi 2.17

Hasil kali dalam dari dua buah vektor x



x1,,xn



dan



y1,,yn





y dengan xi,yi ℂ pada ruang vektor ℂ adalah





 n

i i iy

x

1 ,y

x .

Definisi 2.18

Hasilkali dalam dari dua fungsi f dan g di dalam ruang fungsi bernilai kompleks yang didefinisikan dalam interval

 

a,b adalah

   



 b

a

dx x g x f g

f, .

Definisi 2.19

Suatu ruang vektor V dikatakan ruang linear bernorma jika untuk setiap vektor vV dikaitkan dengan suatu bilangan riil v yang disebut norma dari v yang memenuhi:

1. v 0 dengan v 0 jika dan hanya jika v0, 2. v   v untuk setiap skalar  ,

Definisi 2.20

Jika V suatu ruang hasilkali dalam, maka persamaan v

v,

v  untuk semua vV , mendefinisikan suatu norma pada V .

Contoh 2.11

Jika _

     

3 1

x , maka x  x,x  19  10.

2.2.6. Ortogonalitas

Definisi 2.21

Dua vektor x dan ydi ℝ dikatakan ortogonal jika dan hanya jika 0



y

x, .

Contoh 2.12

Vektor-vektor



1,2,2,4



1

v dan v₂ 



2,1,4,2



merupakan dua vektor yang ortogonal di ℝ4, sebab

 

2 2 1 2

 

4 4 2 2 2 8 8 0 1

2

1v               

v .

Contoh 2.13

Fungsi f

 

t sint dan g

 

t cost ortogonal di ruang fungsi









 

   

 

  

 









  



-R f x dx f

L2 2

| ,

:

, sebab

   

 

cos

 

2 0.

4 1 2

sin 2 1 cos

sin

,    

 









 

 



t dt

t dt

t t g

BAB III

TRANSFORMASI FOURIER DISKRIT

Pada bab ini, terdapat tiga subbab yang akan dibahas untuk memahami transformasi Fourier Diskrit, yaitu:

 Deret Fourier

 Transformasi Fourier

 Transformasi Fourier Diskrit

3.1.Deret Fourier

Deret Fourier menguraikan suatu sinyal pada



,



ke dalam komponen-komponen yang bergetar dengan frekuensi-frekuensi berupa bilangan bulat. Berikut akan dibahas mengenai definisi dari deret Fourier dalam bentuk kompleks dan riil.

Definisi 3.1

Misal f merupakan suatu fungsi yang bersifat periodik dengan periode



A ℝ.

Maka deret Fourier yang berasosiasi dengan f merupakan deret trigonometri





 

k

A kx i ke c x

f( )~ 2 (3.1)

dengan







 2

2

2 ) ( 1

A A

dx e

x f A

Simbol ~ berarti bahwa deret Fourier berasosiasi dengan fungsi f . Untuk membuat (3.1) lebih kuat, yaitu nilai ruas kiri dan kanannya sama di setiap titik, maka akan ditunjukkan bahwa nilai koefisien ck benar dan hal

tersebut bergantung pada sifat ortogonalitas. Untuk menyatakan sifat ortogonalitas digunakan notasi yang disebut sebagai modular Kronecker delta.

Definisi 3.2

Misalkan k bilangan bulat, kita definisikan ˆ_N

 

k dengan

 

  

 



lainnya.

0

, kelipatan atau

0 jika 1

ˆ_N k k k N



Contoh 3.1

Jika diketahui N = 4 dan k = {-3, 0, 1,8}, maka modular Kronecker delta bernilai ˆ₄

 

3 0,ˆ₄

 

0 1,ˆ₄

 

1 0,danˆ₄

 

8 1.

Teorema 3.1 (Ortogonalitas dari Fungsi Eksponensial Kompleks)

Misal j dan k bilangan bulat. Maka fungsi eksponensial kompleks ei2kx A

memenuhi





 _{ }

2

2

) ( 2

2

A A

k j A dx e

ei jx A ikx A  .

Bukti:

 Bila j–k = 0 ( j = k), maka



(jk)1

Akan dibuktikan:





 _

2

2

2 2

A A

A dx e

 



A A A A

x dx dx e dx e dx e e A A A A A A A A A A x k j A i A kx i A jx i               









2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 0 2 2

2  

 Bila j–k  0 ( jk), maka



(jk)0

Akan dibuktikan:



  _ 2 2 0 2 2 A A dx e

ei jx A ikx A

 

































2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 cos 2 1 2 sin 2 1 2 sin 2 cos 2 sin 2 cos 2 2 2 2 2 A A A A A A A A A A A A A A x k j A x A k j i x k j A x A k j dx x k j A i dx x k j A dx x k j A i x k j A dx e dx e

ei jx A i kx A i A j kx





























































































0 cos cos 2 cos cos sin sin 2 2 cos 2 sin 2 2 cos 2 2 sin 2 0 2 0 0 2 2 2 2 2 2 2 2 2 2 2 2                                                _           _            _            _                                   k j k j x k j A i k j k j i k j k j x k j A x k j A i x k j A x k j A x k j A x k j A i x k j A x k j A A A A A A A A A               

Ortogonalitas pada kasus kontinyu juga dapat dipandang sebagai ortogonalitas dari vektor-vektor dalam suatu ruang fungsi yang didefinisikan dalam interval I. Di dalam ruang vektor L2



A 2,A 2



fungsi-fungsi bernilai kompleks pada interval



A 2,A 2



, fungsi-fungsi

A kx i k

e x) 2 ( 

ω _, kℤ

   

). ( , 2 2 2 2 2 2 k j A dx e e dx x x A A A A A kx i A jx i k j k j    





      ω ω ω ω

Untuk mencari koefisien c_k, diasumsikan bahwa fungsi f dengan periode A merupakan jumlahan dari deret Fourier, sehingga

. )

(



2

    j A jx i je c x f 

Kedua ruas persamaan ini dikalikan dengan

 

1 Aei2kx A dan asumsikan pengintegralan suku demi suku terhadap



A 2,A 2



diperbolehkan,

      k k j A x k j i j j A x k j i j j A kx i c dx e A c dx e c A dx e x f A A A A A A A                





 



             2 2 2 2 2 2 2 2 2 1 1 ) ( 1

Dengan sifat ortogonalitas, 1 Adikali integral bernilai nol kecuali saat j k. Satu-satunya suku yang tersisa dalam deret di ruas kanan bila jk ialah

. ) ( 1 2 2 2



   A A dx e x f A

c_k i kx A

Contoh 3.2

 

           . 0 jk 1 0 jk 1 x x x f  

Tentukan deret Fourier dari f .

Diketahui:  2 A

, maka A2.

Maka koefisien dari deret Fouriernya adalah

 

                                    









k i e k i k i k i e k i e k i e dx e dx e dx e dx e x f A c ik ik x k i x k i x ik x k i x k i A x k i k A A               1 1 2 1 2 1 2 1 2 1 2 1 1 0 0 0 0 2 2 2          k i e k i ik  2 2 2 1

 

 







 



_                   genap. jika 0 ganjil jika 2 cos 1 1 1 k k k i k k i k e i i i k i

e ik ik _

     

Sehingga deret Fourier dari f adalah





  . 1

2

2 2 2 1 2

2





          n x n i k A kx i k e n i e

c   

Definisi 3.3

Misal f _{adalah fungsi bernilai riil dengan periode} A. Maka deret Fourier yang berasosiasi dengan f merupakan deret trigonometri

 





                  1 1 0 2 sin 2 cos 2 ~ k k k k A kx b A kx a a x

f   ,

dengan

 

, 2 2 2 0



  A A dx x f A a (3.2)

 



        2 2 2 cos 2 A A dx A kx x f A

a_k  (3.3)

untuk k = 1, 2, ..., dan

 



        2 2 2 sin 2 A A dx A kx x f A

b_k  (3.4)

untuk k = 1, 2, ... Contoh 3.3 Misal,

 

       lainnya. 0 , 1 0 jika 1 x x f

Hitung deret Fourier dari f pada interval 2x2.

Diketahui: 2 2 

A

, maka A4.

Maka koefisien deret Fouriernya adalah

 

 

2 1 2 1 1 2 1 4 2 1 0 1 0 2 2

0 







 

Untuk k1

 





k k kx k dx kx dx x k x f

ak _

 

 

 sin 2

2 sin 1 2 cos 2 1 4 2 cos 4 2 1 0 1 0 2 2                      





 ,

ketika k genap, sin



k 2



0 maka ak 0, sedangkan ketika k 2n1 ganjil, sin



k 2

  

 1n, sehingga kita peroleh

 





, 2 1, 0,1,... 1

2

1 _{  }

 

 k n n

n a

n

k  .

 











cos 2 1



, 1 1 2 cos 2 cos 1 2 sin 2 1 4 2 sin 4 2 1 0 1 0 2 2                            





 k k k k k kx k dx kx dx x k x f b_k         













                         3 4 1 , 3 4 ketika 1 2 1 , 2 4 ketika 1 4 1 , 1 4 ketika 0 , 4 ketika m b m k m b m k m b m k b m k k k k k   

dengan m0,1,....

Jadi, deret Fourier dari f adalah

 





                   1 1 0 4 2 sin 4 2 cos 2 k k k k kx b kx a a x

f  

Jika f merupakan suatu fungsi bernilai riil, bentuk riil dari deret Fourier dapat diturunkan dari bentuk kompleksnya dan sebaliknya. Pertama, uraikan bentuk kompleks deret Fourier ke dalam suku-suku positif dan negatif:

 









          1 1 2 0 0 2 2 ~ k k A kx i k A kx i k k A kx i

ke c e c e c e

c x

f   







       1 1 2 0 2 k k A kx i k A kx i

ke c c e

c   . (3.5)

Jika f merupakan fungsi bernilai riil, maka c_k c_k karena

 

 

k

A kx i A kx i

k f x e dx c

A dx e x f A c A A A A   





    2 2 2 2 2 2 1

1 _{ }

.

Oleh karena itu, (3.5) menjadi

 





      1 2 1 2 0 ~ k A kx i k k A kx i

ke c e

c c

x

f   .

Karena zz2Re

 

z untuk setiap zℂ, persamaan ini dapat ditulis sebagai

 

      



 1 2 0 2Re

~ k A kx i ke c c x

f  . (3.6)

Hubungan antara ck dan



ak,bk



dapat diturunkan dengan menggunakan rumus Euler, sehingga diperoleh:

 

 

2 1

1 0 ₀

                            





   2 2 2 2 2 sin 2 cos ) ( 1 ) ( 1 2 A A A A dx A kx i A kx x f A dx e x f A

c_k i kx A

 











, untuk 1. 2 1 2 1 2 2 1 2 sin ) ( 2 cos ) ( 1 2 2 2 2          _        _                       





  k ib a ib a A A b A i a A A dx A kx x f i dx A kx x f A k k k k k k A A A A  

Dengan menggunakan persamaan (3.6), kita peroleh

 

, 2 sin 2 cos 2 2 sin 2 cos 2 2 cos 2 sin 2 sin 2 cos Re 2 2 sin 2 cos 2 Re 2 2 Re 2 ~ 1 1 0 1 0 1 0 1 0 1 2 0













                                                                                                                                          k k k k k k k k k k k k k k k k A kx i k A kx b A kx a a A kx b A kx a a A kx b A kx a i A kx b A kx a a A kx i A kx ib a a e c c x f           

yang merupakan bentuk riil dari deret Fourier f .

Definisi 3.4

 Limit kiri dan kanan dari f di titik x didefinisikan sebagai berikut. Limit kiri : f



x



f



x h



h 



 _

0 lim

0 .

Limit kanan: f



x



f



x h



h 



 _

0 lim

0 .

 Fungsi f dikatakan terdiferensial kiri dan kanan di x jika limitnya ada:







  

h

x f h x f x

f

h

  

 _

0 lim 0

' dan







  

h x f h x f x

f

h

  

 _

0 lim 0

' .

Teorema 3.2. (Kekonvergenan Deret Fourier)

Misal f merupakan fungsi yang periodik dan kontinyu sepotong-sepotong. Jika x adalah titik di mana f terdiferensial kiri dan kanan (tetapi tidak kontinyu). maka deret Fourier dari f di x konvergen ke



 



2

0 0  

 f x x

f

.

Bukti:

Bukti dapat dilihat pada buku Albert Boggess: A First Course in Wavelets with Fourier Analysis, hal.70, tahun 2001 .

Pada subbab selanjutnya akan dibahas mengenai transformasi Fourier.

3.2.Transformasi Fourier

interval waktu yang tak berhingga ke dalam suatu komponen dengan frekuensi , di mana  merupakan bilangan riil atau kompleks.

Definisi 3.5

Diberikan fungsi f _{terdefinisi dalam interval (-},) dan mempunyai sifat,

 







 

dx x

f , (3.7)

maka fˆ dengan

 





 

 



 f x e dx

fˆ  i2x , (3.8)

fˆ _disebut Transformasi Fourier dari f dan

 





 

 

   

d e f x

f ˆ i2 x

, (3.9)

disebut sebagai invers Transformasi Fourier fˆ ( dan i 1 merupakan satuan imajiner).

Contoh 3.4

Diberikan fungsi f

 

x ex . Tunjukkan fungsi tersebut memenuhi (3.7).

Diketahui:

   

 

 

0 ,

0 ,

x x

x x

x , maka

 

   

  



 

0 ,

0 ,

x e

x e e

x f

x x x

.

                                    









2 ) 1 0 ( ) 0 1 ( ) ( )

( 0 0

0 0 0 0 e e e e e e dx e dx e dx e dx e x x x x x x

Selain fungsi pada Contoh 3.4, terdapat fungsi-fungsi lainnya yang mempunyai sifat tersebut, misal, fungsi kepadatan peluang, fungsi probabilitas kontinyu, dan sebagainya.

Dari sifat fungsi f , maka fungsi fˆ juga memenuhi (3.7), berarti fˆ terdefinisi dengan baik pada (-,).

 

 

 

 

ˆ ˆ 2 2





          dx e x f f dx e x f f x i x i      

 





 

integral untuk segitiga n ketaksamaa sifat 2 2





          dx e x f dx e x f x i x i    

 

 .



2 1



    



x i e dx x

f 

domain spasial jika x merupakan koordinat spasial, atau dalam domain waktu jika f adalah fungsi yang bergantung pada waktu spasial.

Contoh 3.5

Misal, f

 

x 1 pada interval  x. Maka transformasi Fourier dari f

adalah

 





 

 



 f x e dx fˆ  i2x































2sin 2



sin



2



.

2 1

2 sin 2

cos 2

sin 2

cos 2

1 2 1 2

1

2 2

2 2

2 2

2 2

2 2

2 2

   

 

  

 

 

 

 

   



  

  

 

 

 

 



 

   

   





i i

i i

i

e e

i e i dx e

i i

x i x

i

[image:59.595.100.516.189.713.2]

Selanjutnya akan dibahas mengenai sifat-sifat dasar dari transformasi Fourier.

3.2.1.Sifat-sifat Dasar Transformasi Fourier

Untuk membahas sifat-sifat dasar transformasi Fourier akan digunakan notasi alternatif

ℱ

 

f

 

  fˆ

 

 ,

dengan ℱ menyatakan transformasi Fourier dari f . Operator Fourier ℱ dianggap sebagai pemetaan yang domain dan rangenya merupakan ruang fungsi bernilai kompleks yang didefinisikan pada garis bilangan riil. Input dari ℱ adalah sebuah fungsi, katakanlah f , dan menghasilkan output berupa fungsi lain, ℱ

 

f  fˆ .

Sedangkan, invers dari transformasi Fourier menggunakan notasi operator sebagai berikut

ℱ−1

 

_fˆ

 

_x  _f

 

_{x .} Teorema 3.3

Misalkan f dan g merupakan fungsi terdiferensial yang terdefinisi pada garis bilangan riil dengan f

 

x 0 untuk x yang semakin membesar

 

_ 



 _



 0

lim f x

x .

1. Transformasi Fourier dan inversnya bersifat linear, artinya untuk sebarang konstanta c

ℱ−1

 

_fˆ_gˆ _ℱ−1

 

_fˆ _+ℱ−1

 

_gˆ _{dan ℱ}−1

 

_cfˆ _cℱ−1

 

_fˆ _. 2. Transformasi Fourier dari suatu hasilkali f dengan xn diberikan oleh

ℱ



 



 

n n n n

d d i x

f x



  _ℱ

  

f  .

3. Invers transformasi Fourier dari suatu hasilkali f dengan n diberikan oleh

ℱ−1



 



   

n n n n

dx d i x f   

 ˆ _ℱ−1

 

_fˆ

 

_{x .} 4. Transformasi Fourier dari suatu turunan ke-n diberikan oleh

ℱ

 

 n

  



n i

f   2 ℱ

  

f 

( f n menyatakan turunan ke-n dari f ).

5. Invers transformasi Fourier dari suatu turunan ke-n diberikan oleh

ℱ−1

 

 n

  



n x i x

fˆ   2 ℱ−1

 

fˆ

 

x . 6. Transformasi Fourier dari suatu translasi diberikan oleh

ℱ









 

i a e a

x

f     ℱ

  

f  . 7. Transformasi Fourier dari suatu rescaling diberikan oleh

ℱ



 



 

b bx

f  1ℱ

 



    