CATATAN KULIAH RISET OPERASIONAL

Pertemuan minggu pertama (2 x 50 menit)

Pemrograman Bulat Linear (Integer Linear Programming

- ILP)

Tujuan Instruksional Umum : Mahasiswa dapat menggunakan algoritma yang ada pada metode pemrograman bulat untuk mendapatkan solusi optimal permasalahan pemrograman linier, sehingga diharapkan dapat membuat program aplikasinya.

Tujuan Instruksional Khusus :

1. Mahasiswa mengerti pentingnya penggunaan pemrograman bulat. 2. Mahasiswa dapat memahami algoritma metode Branch and Bound.

Apa itu Pemrograman Bulat

Metode simpleks (OR1) solusi optimal mungkin tidak integer.

Bayangkan misalnya jika kita tertarik untuk menentukan solusi optimal dari satu lini perakitan televisi, yang memproduksi beberapa tipe televisi.

Mengganggu batasan

ILP

Metode Branch and bound

Algoritma:

Asumsikan permasalahan maksimisasi. Berikan z sebagai batas bawah solusi optimum ILP.

1. Fathoming/Bounding. Pilih LPi sebagai subproblem untuk dibulatkan.

Selesaikan untuk LPi dan usahakan fathom.

Fathom dipenuhi jika salah satu kondisi ini dipenuhi:

1. subproblem menghasilkan solusi integer layak permasalahan ILP.

2. subproblem tidak dapat menghasilkan solusi yang lebih baik dari solusi batas bawah terbaik yang ada (z) permasalahan ILP yang ada.

a. Jika LPi fathomed, perbaharui batas bawah z jika solusi ILP lebih baik.

Jika tidak, pilih subproblem yang baru dan ulangi ulangi langkah 1. jika Pembulatan matematis ?

semua subproblem sudah diselidiki, stop. Solusi optimum ILP adalah z batas bawah terakhir, jika ada. Jika tidak ada :

b. Jika LPi belum fathomed, teruskan ke langkah 2.

2. Branching (pencabangan). Pilih satu variabel xj yang nilai optimumnya tidak

memenuhi batasan integer. Hilangkan daerah

 

x*j xj 

 

x*j 1, (dimana [A]

menunjukkan integer terbesar sedemikian shg  A) dengan membuat dua subproblem LP yang sesuai dengan 2 pembatas mutually exclusive :

 

* j j x x  dan xj 

 

x*j 1 Kembali ke langkah 1. Contoh : Maks z5x14x2 Sub to : eger dan x x x x x x int 0 , 45 6 10 5 2 1 2 1 2 1     

Dengan simpleks, solusi optimal untuk kasus tersebut ditunjukkan tabel berikut:

VB X1 X2 S1 S2 NK

Z 0 0 5/2 ¼ 23.75

X2 0 1 5/2 -1/4 1.25

X1 1 0 -3/2 ¼ 3.75

Batasan integer untuk varaibek x1 dan x2 tidak dipenuhi, dimana nilai optimal

masing-masing secara berturut-turut adalah 3.75 dan 1.25. Solusi ini kita sebut sebagai LP0.

Penyelesaian dengan ILP :

1. Branching : pilih x1, maka batasan baru x1  3 dan x1  3+1 (atau x1  4). Pilih

batasan x1 3 (ini akan menjadi LP1), maka model matematik menjadi :

Maks z5x14x2 Sub to : 45 6 10 5 2 1 2 1     x x x x 3 1 x 0 , ₂ 1 x  x

Selesaikan dengan simpleks, maka didapat tabel optimal:

VB X1 X2 S1 S2 S3 NK

Z 0 0 4 0 1 23

X2 0 1 1 1 -1 2

S2 1 0 0 0 -4 3

X1 0 0 0 0 1 3

2. solusinya memenuhi batasan integer (x1 = 3, x2 = 2 dan z = 23), sehingga

dikatakan LP1 sudah fathomed. Solusi ini adalah batas bawah.

2. Branching : Pilih batasan x1  4, maka model matematik menjadi :

Maks z5x14x2 Sub to : _{10 6} 5 ₄₅ 2 1 2 1     x x x x 4 1 x 0 , ₂ 1 x  x

Selesaikan dengan dual simpleks, maka didapat tabel optimal:

VB X1 X2 S1 S2 S3 NK

Z 0 0 0 2/3 5/3 23.333

S1 0 1 1 -1/6 -2/3 1/6

X2 1 0 0 1/6 5/3 5/6

X1 0 0 0 0 -1 4

3. solusinya belum memenuhi batasan integer (x1 = 4, x2 = 5/6 dan z = 23.333),

sehingga harus dibuat pencabangan.

Dari LP2, terbentuk cabang x2  1 dan x2  0, demikian seterusnya sampai semua

cabang-cabangnya sudah ditelusuri.

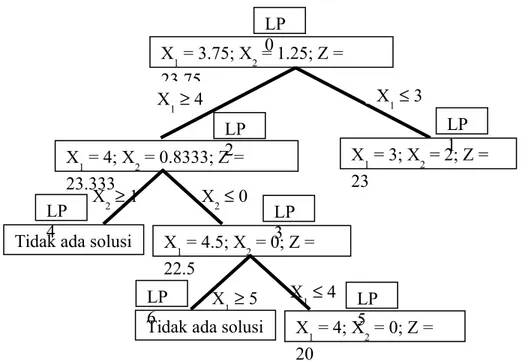
Secara lengkap, cabang-cabang penyelesaian dari LP0 dengan memilih X1 untuk memulai

pencabangan LP1 dan seterusnya ditunjukkan oleh gambar 1 di bawah: Maka solusi optimal ILP adalah solusi LP1.

Gambar 1. Pohon penyelesaian ILP

Pertemuan minggu kedua (2 x 50 menit)

Metode Cutting-Plane

Tujuan Instruksional Khusus :

Mahasiswa dapat memahami algoritma metode Cutting-Plane dengan pure dan mixed integer.

Perhatikan tabel simpleks berikut:

VB X1 ... Xi ... Xm W1 ... Wj ... Wn NK Z 0 ... 0 ... 0 c₁ ... cj ... c_n ₀ X1 1 ... 0 ... 0 ₁1 ... ₁j ... ₁n ₀ .. . ... ... ... ... ... ... ... ... Xi 0 ... 1 ... 0 1_i ... _ij ... _in _i .. . ... ... ... ... ... ... ... Xm 0 ... 0 ... 1 1_m ... _mj ... _mn _m Pure Integer

Digunakan jika semua variabel keputusan harus integer. Algoritma Pure integer :

Input : solusi optimal primal simpleks.

X₁ 4 X₁ 5 X₂ 0 X₂ 1 X₁ = 4; X₂ = 0.8333; Z = 23.333 X₁ = 3.75; X₂ = 1.25; Z = 23.75 X 1 = 3; X2 = 2; Z = 23 X₁ = 4; X₂ = 0; Z = 20 X₁ = 4.5; X₂ = 0; Z = 22.5

Tidak ada solusi

Tidak ada solusi LP 0 LP 1 LP 3 LP 2 LP 4 LP 5 LP 6 X₁ 3 X₁ 4

1. Tentukan baris sumber baris variabel keputusan yang akan dibulatkan. Jika lebih dari satu, boleh dipilih sembarang.

j n j j i i i w x



   1   _{, i tidak integer.}

2. buat ke dalam bentuk fractional cut penambahan kendala baru.



   n j i j ij i f w f S 1 atau 



  n j i j ij i f w f S 1 VB X1 ... Xi ... Xm W1 ... Wj ... Wn Si NK Z 0 ... 0 ... 0 c₁ ... cj ... c_n 0 ₀ X1 1 ... 0 ... 0 ₁1 ... ₁j ... ₁n 0 ₀ .. . ... ... ... ... ... ... ... ... ... Xi 0 ... 1 ... 0 1_i ... _ij ... _in 0 _i .. . ... ... ... ... ... ... ... ... Xm 0 ... 0 ... 1 1_m ... _mj ... _mn 0 _m Si 0 ... 0 ... 0 -fi1 ... -fij ... -fin 1 -fi

3. selesaikan dengan dual simpleks. Contoh Kasus : Maks z7x19x2 Sub to : 35 7 6 3 2 1 2 1      x x x x 2 1, x

x _{positif dan bulat.}

Solusi optimalnya dengan simpleks adalah :

VB X1 X2 S1 S2 NK

Z 0 0 28/11 15/11 63

X2 0 1 7/22 1/22 7/2

X1 1 0 -1/22 3/22 9/2

1. Ambil baris X2 sebagai baris sumber :

2 7 22 1 22 7 _{1 2} 2 s  s  x _atau



0 722

 

1 0 122

 

2 3 12



2  s   s   x

2 1 22 1 22 7 2 1 3 s  s  s

Dan tabel simpleksnya adalah :

VB X1 X2 S1 S2 S3 NK

Z 0 0 28/11 15/11 0 63

X2 0 1 7/22 1/22 0 7/2

X1 1 0 -1/22 3/22 0 9/2

S3 0 0 -7/22 -1/22 1 -1/2

3. Dengan dual simpleks, solusi optimalnya adalah :

VB X1 X2 S1 S2 S3 NK Z 0 0 0 1 8 59 X2 0 1 0 0 1 3 X1 1 0 0 1/7 -1/7 7 4 4 S1 0 0 1 1/7 -22/7 7 4 1

Solusi belum bulat, sehingga baris sumber dan fractional cut baru harus dibentuk. 1. X1 sebagai baris sumber :

7 4 4 7 1 7 1 _{2 3} 1 s  s  x _atau



0 17



2



1 67

 

2 4 47



1  s    s   x

2. Maka fractional cutnya adalah :

7 4 7 6 7 1 3 2 4  s  s  s

Dan tabel simpleksnya adalah :

VB X1 X2 S1 S2 S3 S4 NK Z 0 0 0 1 8 0 59 X2 0 1 0 0 1 0 3 X1 1 0 0 1/7 -1/7 0 7 4 4 S3 0 0 1 1/7 -22/7 0 7 4 1 S4 0 0 0 -1/7 -6/7 1 -4/7

3. Dengan dual simpleks, solusi optimalnya adalah :

Z 0 0 0 0 2 7 55

X2 0 1 0 0 1 0 3

X1 1 0 0 0 -1 1 4

S1 0 0 1 0 -4 1 1

S2 0 0 0 1 6 -7 4

Maka solusi optimal ILPnya adalah : X1 = 4, X2 = 3 dan Z = 55. Mixed Integer

Digunakan jika tidak semua variabel keputusan harus integer. Algoritma mixed integer :

1. Tentukan baris sumber dengan memilih salah satu varaibel yang akan dibulatkan dari tabel optimal simpleks :

 

_



       n j j j k k n j k j j k k k w f w x 1 1    

supaya xk integer, maka xk 

 



k atau xk 

 



k 1harus dipenuhi, dengan demikian :



  n j k j j kw f 1 



   n j k j j kw f 1 1 

2. definisikan J himpunan subscript j dimana _kj 0

_J_{= himpunan subscript j dimana} _kj 0

k J J j j kw  f



   _dan k J J j j k k k _{w f} f f _ 1



_{ } 3. mixed cut : k J J j j k k k J J j j k k w _f f w f s            





  _    1

4. Masukkan ke tabel simpleks sebelumnya dan selesaikan dengan dual simpleks. Maks z7x19x2 Sub to : 35 7 6 3 2 1 2 1      x x x x 2 1, x x _positif x1 bulat.

VB X1 X2 S1 S2 NK

Z 0 0 28/11 15/11 63

X2 0 1 7/22 1/22 7/2

X1 1 0 -1/22 3/22 9/2

 Baris sumber (baris x1, karena hanya x1 yang akan dibulatkan) :

          2 1 4 22 3 22 1 2 1 1 s s x  3   J , J  4 , 2 1 1 f  Mixed cut :

2

1

22

1

1

2

1

2

1

22

3

1 2 3







































 



























S

s

S

atau 2 1 22 3 22 1 2 1 3 S  S  S  Tabel simpleks : VB X1 X2 S1 S2 S3 NK Z 0 0 28/11 15/11 0 63 X2 0 1 7/22 1/22 0 7/2 X1 1 0 -1/22 3/22 0 9/2 S3 0 0 -1/22 -3/22 1 -1/2  Solusi optimalnya : VB X1 X2 S1 S2 S3 NK Z 0 0 23/11 0 10 58 X2 0 1 10/33 0 -1/3 10/3 X1 1 0 -1/11 0 1 4 S2 0 0 1/3 1 -22/3 11/3

Pertemuan minggu Ketiga (2 x 50 menit)

Model Jaringan

Tujuan Instruksional Umum : Mahasiswa dapat menggunakan algoritma yang ada pada model jaringan untuk mendapatkan solusi optimal permasalahan pemrograman linier, sehingga diharapkan dapat membuat program aplikasinya.

Tujuan Instruksional Khusus :

1. Mahasiswa dapat memahami dan menggunakan algoritma minimum spanning tree.

2. Mahasiswa dapat memahami dan menggunakan algoritma rute terpendek.

Apa itu Model Jaringan?

Perhatikan situasi berikut:

1. Disain jaringan pipa gas alam yang menghubungkan Arun Aceh dengan tangki penampungan Pertamina di salah satu kota dengan tujuan minimisasi biaya

pemasangan pipa.

2. penentuan rute terpendek yang menghubungkan dua kota pada jaringan jalan yang sudah ada.

3. penentuan kapasitas maksimum tahunan (dalam ton) jaringan pipa coal slurry yang menghubungkan pertambangan dengan daerah pusat pembangkit energi. 4. penentuan jadwal aliran biaya-minimum dari pertambangan ke kilang pemurnia

dan akhirnya ke pusat pendistribusian minyak.

Jaringan adalah himpunan simpul yang dihubungkan oleh garis atau kurva. Notasi standar jaringan G : G = (N,A).

Predecessor adalah aktivitas yang mendahului suatu aktivitas tertentu. Successor adalah aktivitas yang mengikuti suatu aktivitas tertentu.

Algoritma Minimum Spanning Tree.

 Asumsikan himpunan C sebagai himpunan simpul yang terhubung dan C

sebagai himpunan simpul yang tidak terhubung.

 Solusi Awal : C = { } dan C beranggotakan semua simpul.

 Pilih sembarang simpul sebagai titik awal, maka C sekarang memiliki satu anggota dan C berkurang satu.

 Hubungkan simpul itu dengan simpul terdekat. C bertambah satu dan C

berkurang satu.

 Hubungkan salah satu dari kedua simpul yang ada pada C dengan simpul terdekat, maka C bertambah satu lagi dan C berkurang satu.

 Demikian seterusnya sampai C ={ } dan setiap simpul sudah terhubung. Contoh :

Seorang petugas lapangan di The National Park Service setiap hari harus berkendaraan menggunakan mobil untuk memantau empat lokasi yang ada di taman. Setiap area harus dia kunjungi sekali, berangkat dari dan berakhir di pintu masuk. Area-area tersebut beserta jarak jalan yang sudah dibangun ( dalam mil) antara satu area dengan area lainnya ditunjukkan tabel di bawah. Tanda strip (-) menunjukkan bahwa kedua area tidak dihubungkan dengan jalan raya yang bisa dilalui mobil.

Masuk Raksasa Point Meadow Pintu Masuk - 7.1 19.5 19.1 25.7 Air Terjun 7.1 - 8.3 16.2 13.2 Batu Raksasa 19.5 8.3 - 18.1 5.2 Sunset Point 19.1 16.2 18.1 - 17.2 The Meadow 25.7 13.2 5.2 17.2 -Penyelesaian :

Jaringan dari kasus di atas adalah:

 Solusi Awal : C = { PM} C = {AT, BR, SP, TM}

 Iterasi 1 : C = {PM, AT} C = {BR, SP, TM}, Total jarak = 7.1  Iterasi 2 : C = {PM, AT, BR} C ={SP, TM}, Total jarak = 15.4  Iterasi 3 : C = {PM, AT, BR, TM} C = { SP}, Total jarak = 20.6

 Iterasi 4 : C = {PM, AT, BR, TM, SP} C ={ }, Total jarak = 36.8 Solusi Optimum :

Rute Terpendek.

Acyclic

Jaringan asiklik kalau tidak memuat loop. Algoritma :

 Berikan uj = jarak terpendek dari simpul 1 ke simpul j, maka u1 = 0.

 Hitung uj untuk j=2, 3, ... secara rekursif dengan rumus berikut:

PM AT BR SP TM 5.2 19.2 7.1 16.2 8.3 13.2 17.2 19.5 25.7 18.1 PM AT BR SP TM 5.2 7.1 16.2 8.3



i ij



i j u d

u min 

ui = jarak terpendek ui ke simpul yang langsung mendahului.

dij = jarak antara simpul j dengan semua predecessor i.

Contoh :

Tentukan rute terpendek!!! Penyelesaian : Simpu l j Perhitungan uj Label 1 2 3 4 5 6 7 u1 = 0 u2 = u1 +d12 = 0+2 = 2, dari 1 u3 = u1 +d13 = 0+4 = 4, dari 1 u4 = min {u1 +d14 , u2 +d24 , u3 +d34 }= min {0+10, 2+11, 4+3} = 7, dari 3

u5 = min { u2 +d25 , u4 +d45 }= min {2+5, 7+8} = 7, dari 2

u6 = min {u3 +d36 , u4 +d46 }= min {4+1, 7+1} = 5, dari 3

u7 = min {u5 +d57 , u6 +d67 }= min {7+6, 5+9} = 13, dari 5

[0, -] [2, 1] [4, 1] [7, 3] [7, 2] [5, 3] [13, 5]

Pertemuan minggu Keempat (2 x 50 menit)

Teori Keputusan

Tujuan Instruksional Umum : Mahasiswa dapat menjelaskan jenis-jenis pengambilan keputusan berdasarkan sifat datanya dan menggunakan kriteria pengambilan keputusan sehingga diharapkan dapat membuat program aplikasinya.

Tujuan Instruksional Khusus :

1. Mahasiswa dapat menggunakan kriteria Laplace untuk pengambilan keputusan.

5 1 1 10 8 4 2 6 3 5 7 4 3 2 7 6 9 11

2. Mahasiswa dapat menggunakan kriteria minimaks dan maksimin untuk pengambilan keputusan.

3. Mahasiswa dapat menggunakan kriteria Savage regret untuk pengambilan keputusan.

4. Mahasiswa dapat menggunakan kriteria Hurwicz untuk pengambilan keputusan.

Pengertian Metode Keputusan Tidak Pasti

Data yang digunakan dalam pengambilan keputusan bersifat tidak pasti dan ketidakpastian tersebut tidak dapat dihitung dalam bentuk peluang.

Lawan (opponen) pengambil keputusan adalah alam.

Kriteria Laplace

Setiap kriteria keputusan dianggap mempunyai peluang yang sama untuk terjadi.

Contoh Diberikan tabel perolehan dalam bentuk biaya berikut :

Suplai level Kategori customer 1 2 3 4 a1 5 10 18 25 a2 8 7 8 23 a3 21 18 12 21 a4 30 22 19 15 Penyelesaian : E{a1} = (1/4)(5+10+18+25) = 14.5 E{a2} = (1/4)(8+7+8+23) =

11.5

E{a3} = (1/4)(21+18+12+21) = 18.0 E{a4} = (1/4)(30+22+19+15) = 21.5

Kriteria Minimaks dan Maksimin

Biasanya digunakan oleh pengambil keputusan yang bersifat pesimis. Memilih yang terbaik dari antara yang terburuk.

Minimaks tabel perolehan dalam bentuk biaya (kerugian). Maksimin tabel perolehan dalam bentuk keuntungan.

Contoh Diberikan tabel perolehan dalam bentuk biaya berikut :

Suplai level Kategori customer 1 2 3 4 a1 5 10 18 25 a2 8 7 8 23 a3 21 18 12 21 a4 30 22 19 15 Penyelesaian :

Suplai level 1 2 3 4 a1 5 10 18 25 25 a2 8 7 8 23 23 a3 21 18 12 21

21

a4 30 22 19 15 30

Jika tabel di atas dianggap perolehan dalam bentuk keuntungan, maka penyelesaiannya adalah:

Suplai level

Kategori customer Minimum

1 2 3 4

a1 5 10 18 25 5

a2 8 7 8 23 7

a3 21 18 12 21 12

a4 30 22 19 15

15

Kriteria Savage Regret

Perbaikan dari Minimaks dan Maksimin

Contoh : Diberikan tabel perolehan dalam bentuk biaya berikut: Suplai level Kategori customer Maksimum 1 2 a1 5 100 100 a2 50 100 100 a3 90 85

90

a4 60 90

90

Dengan Savage regret

Bentuk tabel savage regret, lalu gunakan kriteria minimaks.

Suplai level Kategori customer Maksimum 1 2 a1 0 15

15

a2 45 15 45 a3 85 0 85 a4 55 5 55

Kriteria Hurwicz

Contoh Diberikan tabel perolehan dalam bentuk biaya berikut. Misalkan  = 0.4. Kategori customer

Minimaks

Maksimin

Minimaks

Suplai level 1 2 3 4 a1 5 10 18 25 a2 8 7 8 23 a3 21 18 12 21 a4 30 22 19 15 Penyelesaian : Suplai level

Kategori customer Maksimum Minimum

1 2 3 4 a1 5 10 18 25 25 5 a2 8 7 8 23 23 7 a3 21 18 12 21 21 12 a4 30 22 19 15 30 15 E{a1} = (0.4*5)+(0.6*25) = 17 E{a2} = (0.4*7)(0.6*23) =

16.6

E{a3} = (0.4*12)(0.6*21) = 17.4 E{a4} = (0.4*15)(0.6*30) = 24