PENENTUAN DAN PENJADWALAN PEKERJA FULL-TIME DAN PEKERJA PART-TIME DENGAN KENDALA LIBUR HARI KERJA DAN LIBUR AKHIR PEKAN

(1)

HARI KERJA DAN LIBUR AKHIR PEKAN

Oleh:

YUDI ARISANDI

G54102045

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(2)

HARI KERJA DAN LIBUR AKHIR PEKAN

YUDI ARISANDI

G54102045

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(3)

Off-weekend Constraints. Supervised by FARIDA HANUM and DONNY CITRA LESMANA. A company operates seven days a week that consist of five weekdays and two days in weekend. The number of workers that needed in weekdays is assumed to be constant every day. This assumption also holds for the number of workers in weekend. However they can differ each other. Full-time workers get priority to fulfill the need of workers. Assuming that every full-time worker gets two days off per week (some of them are weekend off), the lack of workers needed are fulfilled by hiring part-time workers. In this paper, we study the number of full-time and part-time workers needed by the company for the whole period as well as their work schedules.

(4)

Kendala Libur Hari Kerja dan Libur Akhir Pekan. Dibimbing oleh FARIDA HANUM dan

DONNY CITRA LESMANA.

Suatu perusahaan beroperasi tujuh hari dalam seminggu, yaitu lima hari kerja dan dua hari akhir pekan. Banyaknya pekerja yang dibutuhkan pada setiap hari kerja diasumsikan sama setiap harinya. Demikian juga, banyaknya pekerja yang dibutuhkan pada hari akhir pekan, adalah sama setiap harinya, tetapi boleh berbeda dengan banyaknya pekerja yang dibutuhkan di hari kerja. Pada awalnya, pekerja yang dibutuhkan perusahaan hanyalah pekerja full-time. Setiap pekerja full-time diberikan dua hari libur setiap pekannya yang di antaranya adalah sejumlah libur akhir pekan. Akibatnya terkadang perusahaan membutuhkan pekerja tambahan untuk memenuhi kebutuhan pekerja pada hari-hari yang kekurangan pekerja. Untuk itu perusahaan juga mempekerjakan pekerja part-time. Dalam tulisan ini dibahas tentang formula dalam menentukan banyaknya pekerja full-time dan pekerja part-time yang dibutuhkan perusahaan beserta penjadwalan kerjanya.

(5)

HARI KERJA DAN LIBUR AKHIR PEKAN

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

YUDI ARISANDI

G54102045

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

(6)

NRP : G54102045

Menyetujui:

Mengetahui:

Tanggal Lulus :

Pembimbing I,

Dra. Farida Hanum, M.Si.

NIP 131 956 709

Pembimbing II,

Donny Citra Lesmana, M.Fin.Math

NIP 132 311 927

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP 131 578 806

(7)

Puji syukur penulis panjatkan ke hadirat Allah SWT atas limpahan rahmat dan karunia-Nya penulis dapat menyelesaikan penulisan karya ilmiah ini. Tak lupa shalawat serta salam tercurah selalu kepada Nabi Muhammad SAW.

Skripsi yang berjudul Penentuan dan Penjadwalan Pekerja Full-time dan Part-time dengan Kendala Libur Hari Kerja dan Libur Akhir Pekan ini merupakan salah satu syarat untuk mendapatkan gelar Sarjana Sains.

Penyusunan skripsi ini tidak lepas dari bantuan dari berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Allah SWT, atas segala rahmat dan izin-Nya 2. Nabi Muhammad SAW

3. Ibu Dra. Farida Hanum, M.Si. selaku dosen pembimbing I, Bapak Donny Citra Lesmana, M.Fin.Math selaku pembimbing II, dan Bapak Dr. Toni Bakhtiar, M.Sc. selaku dosen penguji. Terima kasih atas ilmu, bimbingan, saran, motivasi, dan masukannya.

4. Kedua orang tua, papa, mama. Kakak adik tersayang, Ses, Didit dan Putri. Terima kasih atas doa dan dukungannya.

5. Semua saudara sekeluarga besar dan teman-teman di Lampung.

6. Teman-teman seperjuangan di Matematika 39, Rizal, Yana, Ungkap, Agus, Rian, Andri, Aden, Riswan, Ikhe, Wenny, Dina, Ade, Elis, Desi, Rani, Nita, Lia, Tami, Ari, Arif, Kabul, Febi, Fitrah, Amin, Lutfi, Mere, Mega, Erit, Irwan, Indra, Nur, Tieka, Avi, Rodih. Terima Kasih untuk semua kerjasama, keceriaan dan kisah-kisah yang telah ada.

7. Sahabat-sahabat penulis. Ikhe dan Ambar (semua akan kembali seperti yang dulu. Tetapi tidak dengan persahabatan). Terima kasih untuk semua kebaikan, kebersamaan, bantuan, keceriaan dan motivasinya.

8. Ochi, Dwinita, Vey dan Fifit, terima kasih atas semua kisahnya. 9. Matematika 40, 41 dan 42 yang tidak mungkin disebutkan satu per satu.

10. Anak Kc-Math, Andri, Yana, Riswan, Agus, Aden, dan Ungkap. Terima kasih atas keceriaan yang singkat namun membekas di hati. Anak-anak Kos Gizi Abadi, Asep, Prima, Imam, Didin, Isal, Anton, Randy, Mas Fajar, Mas Risang, Dodo, Rian, Esa, dll. 11. Rina, terima kasih atas keceriaan dan bantuannya selama ini.

12. Diah, Aji dan Mahnur, atas kesediannya menjadi pembahas di seminar penulis. 13. Prima, atas kebersamaan, segala bantuannya selama ini dan pinjaman komputernya. 14. Semua yang sudah memberi warna, cahaya, tawa dan air mata.

Semua yang telah menggoreskan hitam dan putih.

Semua yang telah menaburkan duri, menancapkan luka dan memberi api. 15. Semua pihak yang sudah membantu penulis menyelesaikan skripsi ini. Semoga skripsi ini dapat memberikan manfaat bagi penulis dan pembaca.

Bogor, Januari 2008

(8)

kedua dari empat bersaudara, anak dari pasangan Junaidi Alwi dan Juhaini yang beralamat di Jalan Perintis Raya, Sukarame, Bandar Lampung.

Tahun 2002, penulis lulus dari SMUN 9 Bandar Lampung dan pada tahun yang sama diterima di IPB melalui jalur SPMB. Penulis memilih Program Studi Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama mengikuti kegiatan perkuliahan, penulis pernah aktif menjadi anggota himpunan profesi mahasiswa matematika yang dikenal dengan nama GUMATIKA dalam Departemen Kaderisasi pada masa kepengurusan 2003/2004. Selain itu penulis juga pernah aktif sebagai anggota kepanitiaan di beberapa kegiatan kemahasiswaan di lingkar kampus.

(9)

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... ix I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Tujuan ... 1 II LANDASAN TEORI ... 1 III PEMBAHASAN 3.1 Masalah Penentuan Pekerja Full-time... 3

3.2 Masalah Penentuan Pekerja Full-time dan Dua Jenis Pekerja Part-time ... 4

3.3 Contoh Permasalahan ... 14

3.4 Algoritme Pembangkit Jadwal ... 17

3.5 Algoritme Modifikasi untuk Penjadwalan Libur Hari Kerja... 18

3.6 Algoritme untuk Perusahaan yang Memulai Usaha pada Hari Minggu... 23

IV SIMPULAN DAN SARAN 4.1 Simpulan ... 30

4.2 Saran ... 30

DAFTAR PUSTAKA ... 30

LAMPIRAN ... 31

(10)

1

Nilai P (ue ud )

+ +

= + untuk beberapa kasus nilai F jika be<bd... 8

2

Nilai P (ue ud ) + + = + untuk beberapa kasus nilai F jika be=bd... 8

3

Nilai P (ue ud ) + + = + untuk beberapa kasus nilai F jika be>bd... 11

4 Penjadwalan pekerja untuk Contoh 4 dengan hari Senin sebagai awal usaha ... 19

5 Penjadwalan pekerja untuk Contoh 5 dengan hari Senin sebagai awal usaha ... 20

6 Penjadwalan pekerja yang telah dimodifikasi untuk Contoh 4 dengan hari Senin sebagai awal usaha ... 21

7 Penjadwalan pekerja yang telah dimodifikasi untuk Contoh 5 dengan hari Senin sebagai awal usaha ... 22

8 Penjadwalan pekerja untuk Contoh 4 dengan hari Minggu sebagai awal usaha... 24

9 Penjadwalan pekerja untuk Contoh 5 dengan hari Minggu sebagai awal usaha... 25

10 Penjadwalan pekerja yang telah dimodifikasi untuk Contoh 4 dengan hari Minggu sebagai awal usaha ... 28

11 Penjadwalan pekerja yang telah dimodifikasi untuk Contoh 5 dengan hari Minggu sebagai awal usaha ... 29

DAFTAR GAMBAR

Halaman 1 Grafik u_d dan u_e dengan D=8, 12, E= dan 0, 4θ = ... 6

2 Grafik ud dan ue seperti Gambar 1 ... 6

3 Grafik C(F) jika P seperti pada Gambar 2 dengan G=7 ... 6

4 Grafik C(F) jika g≥2E+5D ... 7 5 Grafik C(F) jika b_e<b_d ... 8 6 Grafik C(F) jika b_e=b_d ... 9 7 Grafik C(F) jika b_e≤b_d ... 9 8 Grafik C(F) jika be>bd ... 11 9 Grafik C(F) jika g≥2(1−θ)(be−bd)... 11 10 Grafik C(F) jika g<2(1−θ)(b_e−b_d)... 12 viii

(11)

1 Penurunan Persamaan (3.2.11) ... 32

2 Fungsi C(F) pada Persamaan (3.2.11) minimum pada F=bg ... 32

3 Bukti pertaksamaan C₁

( ) ( )

_{⎣ ⎦}⎢ ⎥bg <C₂ ⎡ ⎤_{⎢ ⎥}bg pada Persamaan (3.2.12) ekuivalen dengan

(

bg−⎢ ⎥⎣ ⎦bg

) (

cp+ ⎢ ⎥⎡ ⎤bg −bg

)

cp<cf ... 33

4 Fungsi C(F) pada Persamaan (3.2.13) minimum pada F= ... 33 b_t 5 Bukti pertaksamaan C₄

( )

⎣ ⎦⎢ ⎥bt <C₃

( )

⎡ ⎤⎢ ⎥bt pada Persamaan (3.2.14) ekuivalen dengan

(

)

f t t p c b b c −⎢ ⎥_{⎣ ⎦} < ... 34 6 Penurunan Persamaan (3.2.15) ... 34

7 Fungsi C(F) pada Persamaan (3.2.15) minimum pada F=b_g ... 35

8 Penurunan Persamaan (3.2.17) ... 36

9 Fungsi C(F) pada Persamaan (3.2.17) minimum pada F=b_g atau F=b_h ... 37

10 Bukti pertaksamaan C₁

( )

⎣ ⎦⎢ ⎥bd <C₆

( )

⎡ ⎤⎢ ⎥bd pada Persamaan (3.2.18) ekuivalen dengan

(

b_d −⎢ ⎥_{⎣ ⎦}b_d

)

c_p<⎡_⎣5c_f −2(1−θ)c_p⎤_⎦/(3 2 )+ θ ... 38

11 Bukti pertaksamaan C₆

( )

⎣ ⎦⎢ ⎥bh <C₅

( )

⎡ ⎤⎢ ⎥bh pada Persamaan (3.2.19) ekuivalen dengan

(

b_h−_{⎣ ⎦}⎢ ⎥b_h

)

c_p+

(

⎡ ⎤_{⎢ ⎥}b_h −b_h

)

c_p<5c_f / 2(1−θ)... 39

12 Fungsi C(F) pada Persamaan (3.2.20) minimum pada F=b_d atau F= ... 40 b_e 13 Bukti pertaksamaan C4

( )

⎣ ⎦⎢ ⎥be <C7

( )

⎡ ⎤⎢ ⎥be pada Persamaan (3.2.21) ekuivalen dengan (5D−5⎣ ⎦ ⎢ ⎥⎢ ⎥ ⎡ ⎤bd − bd )cp<5cf / 2(1−θ) ... 41

14 Bukti pertaksamaan C7

( )

⎣ ⎦⎢ ⎥be <C3

( )

⎡ ⎤⎢ ⎥be pada Persamaan (3.2.22) ekuivalen dengan 5 / 2(1 ) e e f p b −⎢ ⎥_{⎣ ⎦}b < c −θ c ... 41

15 Workstretch yang dihasilkan dari algoritme pembangkit jadwal dan modifikasinya untuk Contoh 4 ... 42

(12)

1.1 Latar Belakang

Masalah penjadwalan pekerja merupakan salah satu masalah yang sudah sepantasnya selalu menjadi perhatian oleh sebuah perusahaan, apalagi masalah tersebut sangat berkaitan dengan efisiensi kinerja dan sumber daya pekerja yang digunakan oleh perusahaan.

Secara garis besar, masalah penjadwalan pekerja dapat diklasifikasikan menjadi tiga jenis, yaitu days-off, shift, dan tour scheduling problems. Days-off scheduling problem ialah masalah menentukan hari kerja dan waktu istirahat pekerja dalam suatu interval waktu tertentu. Shift scheduling problem terjadi bila dalam days-off scheduling problem harus ditentukan waktu awal kerja, lamanya shift, interval dan waktu awal istirahat pekerja. Bila days-off schedule dan shift schedule harus ditentukan dalam suatu pola, maka masalahnya menjadi masalah menentukan rute penjadwalan atau tour scheduling problems.

Dalam karya ilmiah ini, pekerja dibedakan menjadi dua jenis, yaitu pekerja full-time dan pekerja part-time. Karena masalah seperti pada karya ilmiah ini terjadi pada perusahaan yang beroperasi setiap hari,

maka setiap pekerja full-time akan diberikan sejumlah hari libur, yaitu libur hari kerja dan libur akhir pekan.

Dalam karya ilmiah ini akan dipelajari cara menentukan banyaknya pekerja, baik pekerja full-time maupun pekerja part-time, yang dibutuhkan suatu perusahaan dalam jangka waktu tertentu dengan memenuhi kendala kebutuhan pekerja setiap harinya dan kendala hari libur. Juga akan dipelajari cara menjadwalkerjakan para pekerja tersebut.

Karya ilmiah ini merupakan rekonstruksi jurnal yang berjudul Sizing and sheduling a full-time and part-full-time workforce with off-day and off-weekend constraints, yang ditulis oleh Hamilton Emmons dan Du-Shean Fuh pada Annals of Operation Research, vol. 70 halaman 473-492 tahun 1998.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah menentukan kombinasi pemakaian pekerja full-time dan part-full-time yang akan dipekerjakan oleh suatu perusahaan, beserta penjadwalan hari kerja masing-masing pekerja, dengan memenuhi kendala libur hari kerja dan libur hari akhir pekan, sehingga biaya yang dikeluarkan dapat ditekan seminimal mungkin.

II LANDASAN TEORI

Definisi 1. Fungsi Sesepenggal

Fungsi sesepenggal (piecewise function) adalah fungsi yang terdefinisi oleh rumus yang berlainan sesuai dengan daerah asalnya.

(Stewart, 2001)

Contoh1.

Contoh-contoh piecewise function: 1. ( ) 1, 1, 2 1. x x f x x x − ≤ ⎧ = ⎨ ₊ _> ⎩ 2. ( ) 1, 0 < z 1, 2, 1 < z 2. f z = ⎨⎧ ≤ ≤ ⎩

3. Fungsi nilai mutlak

, 0, ( ) , 0. x x f z x x x ≥ ⎧ = _{= ⎨} − < ⎩

4. Fungsi bilangan bulat terbesar

⎢ ⎥

_{⎣ ⎦}

x

=

Bilangan bulat terbesar yang lebih kecil atau sama dengan x. Misalkan 1≤ < , maka x 4 1, 1 2, ( ) 2, 2 3, 3, 3 4. x f x x x x ⎧ ≤ < ⎪⎪ ⎪⎪ ⎢ ⎥ =_{⎣ ⎦}=⎨ ≤ < ⎪⎪ ⎪ ≤ < ⎪⎩

⎡ ⎤

_{⎢ ⎥}

x

=

Bilangan bulat terkecil yang lebih besar atau sama dengan x. Misalkan 1< ≤ , maka x 4 2, 1 2, ( ) 3, 2 3, 4, 3 4. x f x x x x ⎧ < ≤ ⎪⎪ ⎪⎪ ⎡ ⎤ =_{⎢ ⎥}=⎨ < ≤ ⎪⎪ ⎪ < ≤ ⎪⎩

(13)

Definisi 2. Fungsi Naik dan Fungsi Turun Misalkan f(x)=y,

• Fungsi f disebut fungsi naik pada selang I, jika f(x1) < f(x2), bilamana x1

< x2 di I.

• Fungsi f disebut fungsi turun pada selang I, jika f(x1) > f(x2), bilamana x1

< x2 di I.

(Stewart, 2001)

Definisi 3. Modulo

Jika sebuah bilangan bulat a yang taknol membagi selisih bilangan bulat b dan c, maka b dikatakan kongruen ke c modulo a, dinotasikan

(mod )

b≡c a , atau dapat ditulis dengan mod

b=c a. Jika b c− tidak habis dibagi a, maka a tidak kongruen ke c mod a, yang ditulis

(mod )

b≡c a , atau dapat ditulis dengan mod

b=c a.

(Niven et al., 1991)

III PEMBAHASAN

Suatu perusahaan beroperasi setiap hari, lima hari kerja yaitu hari Senin sampai dengan hari Jum’at, dan dua hari akhir pekan, hari Sabtu dan hari Minggu. Dalam membangun usahanya selama B pekan, perusahaan mempekerjakan F pekerja full-time. Akan tetapi terkadang perusahaan juga mempekerjakan pekerja part-time sebagai tambahan pekerja full-time. Penambahan pekerja part-time ini dilakukan untuk memenuhi kebutuhan pekerja pada waktu tertentu, sehingga ketidakefektifan pekerja dapat dihindari dan pemakaian biaya dapat ditekan sekecil mungkin.

Pada setiap hari kerja, diputuskan bahwa perusahaan membutuhkan D pekerja full-time dari F pekerja full-time, yang bekerja dan E pekerja full-time dari F pekerja full-time, yang bekerja pada hari akhir pekan. Selama B pekan pengoperasian, setiap pekerja full-time memiliki dua hari libur tiap pekannya dan libur A akhir pekan dari B akhir pekan seluruhnya. Dengan kendala hari libur tersebut, maka akan ditentukan banyaknya pekerja full-time dan pekerja part-time yang dibutuhkan perusahaan selama B pekan pengoperasian, dengan biaya yang minimum, beserta penjadwalan kerjanya.

Dalam karya ilmiah ini, dipergunakan aturan shift tunggal (single shift) dari sejumlah pekerja.

Definisi 4. Shift

Shift adalah pola kerja harian yang terdiri atas sejumlah waktu kerja yang beruntun dari seorang pekerja.

(Brusco & Jacobs, 1995)

Dalam permasalahan ini akan digunakan beberapa asumsi, yaitu:

1. Perusahaan beroperasi 8 jam setiap hari, lima hari kerja dan dua hari akhir pekan. 2. Banyaknya pekerja pada hari kerja boleh

lebih besar, sama dengan, atau lebih kecil daripada banyaknya pekerja pada hari akhir pekan.

3. Perusahaan hanya mempunyai satu shift setiap harinya, yang lamanya adalah 8 jam. 4. Karena kendala hari libur yang menyatakan

setiap pekerja full-time libur 2 hari setiap pekannya, maka setiap pekerja full-time bekerja 5 hari setiap pekannya selama B pekan.

5. Setiap pekerja, baik pekerja full-time maupun pekerja part-time dapat ditempatkan pada hari mana saja sesuai kebutuhan, dan

6. Faktor-faktor tak terduga yang dapat menghambat jalannya pekerjaan seperti sakit, libur nasional, dan sebab lainnya diabaikan.

Pada awalnya, diketahui bahwa setiap pekerja memiliki satu shift setiap harinya. Akan tetapi karena adanya penentuan dua hari libur setiap pekannya untuk setiap pekerja, maka untuk mempermudah pembahasan, selanjutnya shift yang dimiliki setiap pekerja tersebut dibedakan menjadi dua, yaitu shift yang dipakai pekerja untuk bekerja disebut shift kerja dan shift yang dipakai pekerja untuk libur disebut shift libur. Dengan demikian pemakaian “shift” dapat digantikan dengan “hari”.

(14)

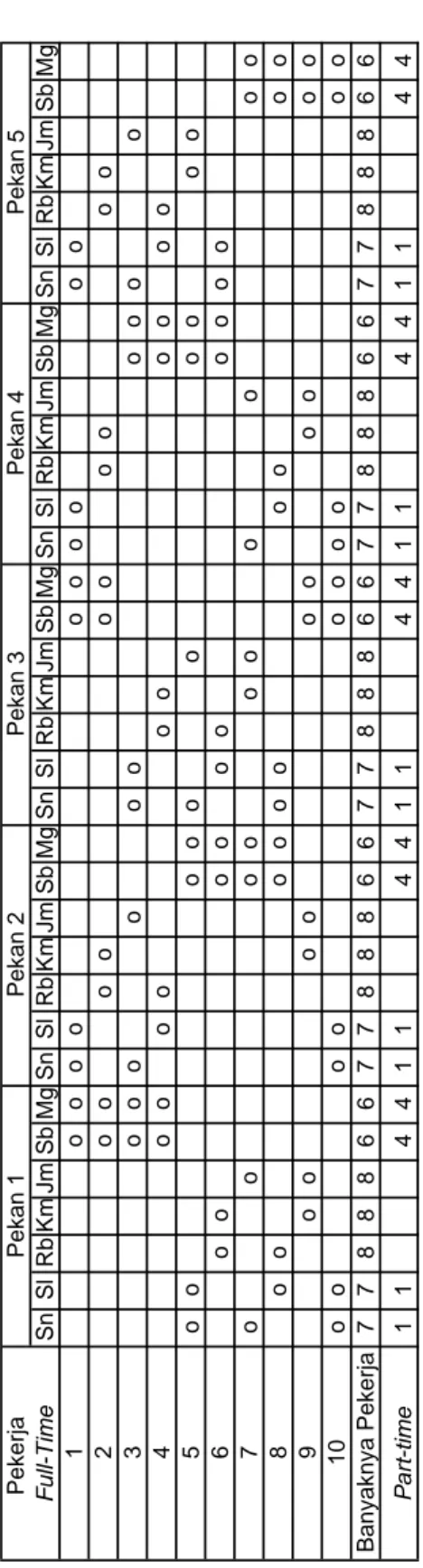
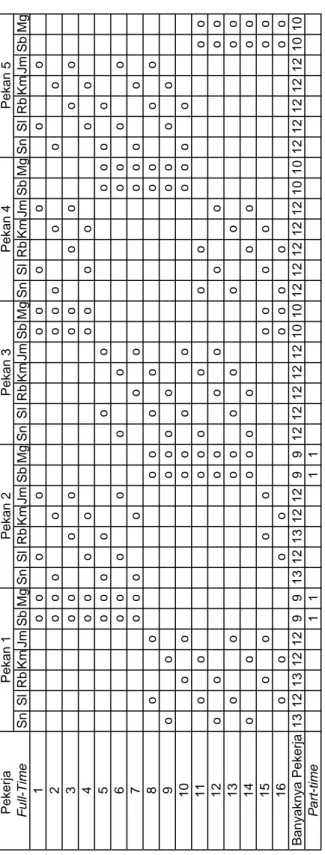
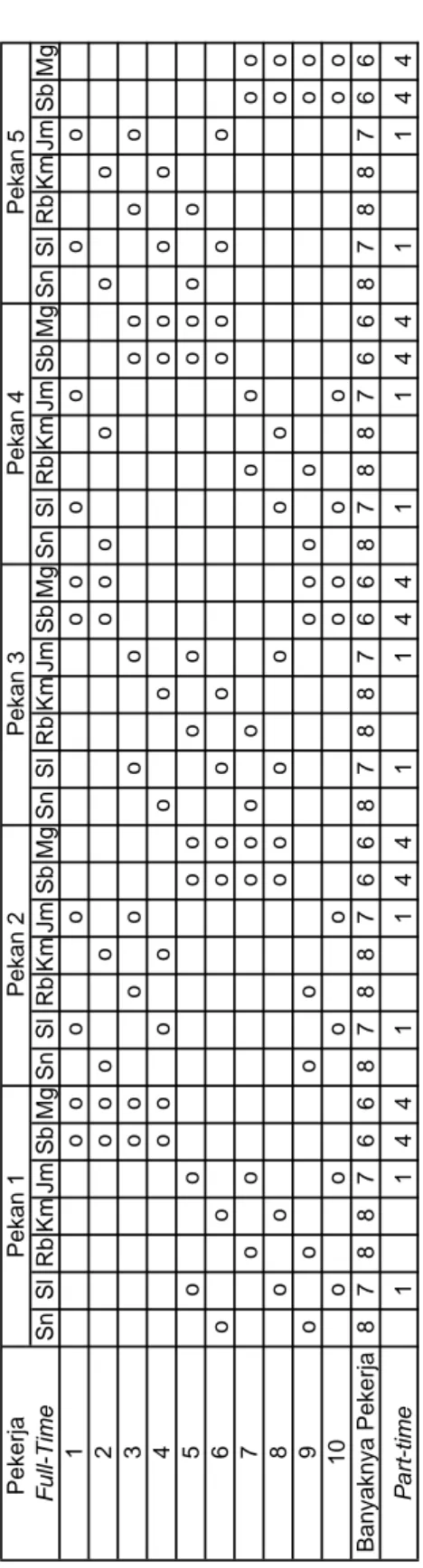
Untuk lebih memahami penggunaan istilah shift, diberikan ilustrasi di bawah ini:

Ilustrasi 1

Pekerja Sn Sl Rb Km Jm Sb Mg

a o o

b o o

Tabel di atas menggambarkan jadwal kerja Pekerja a dan Pekerja b selama satu pekan. Shift kerja digambarkan dengan kotak kosong. Sedangkan kotak yang berisi “o” adalah shift libur pekerja yang bersangkutan. Jadi dari tabel di atas, Pekerja a memiliki shift libur pada akhir pekan atau dapat juga diartikan Pekerja a mempunyai hari libur akhir pekan pada pekan tersebut. Sedangkan Pekerja b mempunyai hari libur pada hari Senin dan Kamis.

Dalam pembahasan ini, akan dibahas cara menentukan rumusan dalam menentukan banyaknya pekerja full-time yang diperlukan perusahaan selama B pekan dan banyaknya pekerja part-time jika dibutuhkan, dengan biaya yang minimum. Juga akan dibahas cara menjadwalkerjakan pekerja-pekerja tersebut. Untuk mempermudah pemahaman, diberikan contoh-contoh kasus yang bersesuaian.

Permasalahan seperti ini juga sering dihadapi oleh perusahaan yang bekerja tanpa henti, 24 jam setiap hari. Perusahaan tersebut tentunya memiliki lebih dari satu shift setiap harinya yang tidak saling berpotongan (overlap). Dengan demikian, penjadwalan pekerja seperti pada karya ilmiah ini dapat dilakukan pada setiap shift secara terpisah.

Untuk selanjutnya pembahasan masalah penentuan dan penjadwalan pekerja full-time dan pekerja part-time akan dibagi menjadi dua, yaitu pembahasan masalah penentuan pekerja full-time tanpa pekerja part-time dan pembahasan masalah penentuan pekerja full-time dan pekerja part-full-time, beserta penjadwalan kerjanya.

3.1 Masalah Penentuan Pekerja

Full-time

Dalam subbab ini dimisalkan perusahaan memutuskan untuk tidak menggunakan pekerja part-time dan banyaknya pekerja full-time yang diperlukan perusahaan selama B pekan adalah sebanyak W pekerja.

Selanjutnya diketahui bahwa terdapat 2( - )B A hari akhir pekan yang dipakai bekerja oleh setiap pekerja. Karena setiap pekerja mempunyai 1 shift setiap harinya, maka terdapat 2 (W B−A) shift kerja di akhir pekan. Juga diketahui bahwa terdapat 2B hari akhir pekan seluruhnya. Karena disyaratkan terdapat E pekerja yang bekerja di setiap hari akhir pekan dan setiap pekerja mempunyai 1 shift setiap harinya, maka terdapat 2BE shift kerja yang disyaratkan di akhir pekan.

2W B( −A) shift kerja di akhir pekan tersebut harus meng-cover 2BE shift kerja yang disyaratkan di akhir pekan. Karena dalam subbab ini hanya menggunakan pekerja full-time tanpa menggunakan pekerja part-full-time, maka diasumsikan 2 (W B−A)≥2BE. Jadi BE W B A ≥ − . Misalkan , e BE b B A = − maka W≥b_e. (3.1.1) Di pihak lain, karena setiap pekerja bekerja 5 hari setiap pekan, dan 1 hari kerja pekerja adalah 1 shift maka total banyaknya shift kerja dari W pekerja selama B pekan adalah 5WB. 5WB shift kerja tersebut harus meng-cover B(2E+5D) shift kerja yang disyaratkan seluruhnya. Karena dalam subbab ini hanya menggunakan pekerja full-time tanpa menggunakan pekerja part-time, maka diasumsikan 5WB≥B(2E+5 ) D . Jadi 2 5 5 E D W≥ + . Misalkan 2 5 5 t E D b = + , maka W≥ . (3.1.2) bt

Karena dari Persamaan (3.1.1), W≥b_e dan dari Persamaan (3.1.2), W≥bt, maka banyaknya pekerja full-time yang dibutuhkan perusahaan adalah

(15)

Misalkan cf adalah biaya pekerja

full-time per orang per hari. Karena setiap pekerja bekerja 5 hari setiap pekan, maka banyaknya biaya yang dikeluarkan perusahaan untuk mempekerjakan W pekerja full-time selama B pekan adalah

( ) 5 f. C W = BWc

Contoh 2.

Untuk menjalankan usahanya selama 5 pekan (B=5), sebuah perusahaan mempekerjakan pekerja full-time tanpa pekerja part-time. Setiap pekerja mempunyai 2 hari libur tiap pekannya, termasuk di dalamnya libur 2 akhir pekan (A=2) dari 5 akhir pekan yang tersedia. Perusahaan memutuskan bahwa dari seluruh pekerja yang dimiliki, harus terdapat 8 pekerja yang bekerja pada setiap hari kerja (D=8), dan 10 pekerja pada setiap hari akhir pekan (E=10). Diputuskan juga bahwa biaya pekerja per orang per hari sebesar 7 satuan (cf=7).

Dengan menggunakan Persamaan (3.1.1), ditentukan (5)(10) 50 16, 67 ( ) (5 2) 3 e BE b B A = = = = − −

dan dengan menggunakan Persamaan (3.1.2), ditentukan (2 5 ) (2)(10) (5)(8) 12. 5 5 t E D b = + = + =

Jadi dari Persamaan (3.1.3), dapat ditentukan banyaknya pekerja full-time yang harus dipekerjakan perusahaan selama 5 pekan, yaitu:

{

}

{

}

{

}

max , max 16, 67 , 12 max 17,12 17. e t W = ⎡ ⎤ ⎡ ⎤_{⎢ ⎥ ⎢ ⎥}b b = ⎡_⎢ ⎤ ⎡ ⎤_{⎥ ⎢ ⎥} = =

Biaya yang dikeluarkan perusahaan untuk membayar seluruh pekerja adalah

( ) 5 (17) (5)(5)(17)(7) 2975 satuan. f C W BWc C = = =

Jadi selama 5 pekan beroperasi, perusahaan harus mempekerjakan sebanyak 17 pekerja full-time, dengan biaya pekerja seluruhnya sebesar 2975 satuan.

3.2 Masalah Penentuan Pekerja Full-time dan Dua Jenis Pekerja Part-time

Selain menggunakan pekerja full-time, terkadang perusahaan juga memerlukan pekerja part-time. Pekerja part-time terdiri atas dua jenis, yaitu limited part-time dengan jumlah yang terbatas tetapi biaya lebih kecil daripada biaya pekerja full-time, dan pekerja unlimited part-time, dengan jumlah yang tidak dibatasi tetapi biaya yang lebih besar daripada biaya pekerja full-time. Jika dimisalkan

biaya pekerja - per orang per hari, biaya pekerja - per orang per hari, dan

biaya pekerja - per orang per hari,

f p

p

c full time c limited part time

c unlimited part time =

= =

maka diketahui bahwa cp <cf <cp.

Kemudian didefinisikan

banyaknya pekerja - yang tersedia selama pekan,

= perbandingan antara banyaknya akhir pekan tiap pekerja yang dapat dipakai libur,

dengan banyaknya akhir pekan seluruhnya

=

G limited part time B

A B θ

=

; karena dan 0 maka 0 1,

banyaknya pekerja - yang dibutuhkan setiap hari kerja, = banyaknya pekerja - yang

dibutuhkan setiap hari akhir pekan, = rata-rata banyaknya pek

A B B D full time E full time g θ < ≠ < < = erja tiap pekan selama pekan

= ,

limited part

time se B

G B

sehingga akan ditentukan

banyaknya pekerja - yang

dibutuhkan perusahaan selama pekan, dan

F full time

B =

= banyaknya pekerja - yang dibutuhkan perusahaan selama pekan.

P part time

B

Banyaknya pekerja part-time ditentukan oleh banyaknya shift kerja pekerja full-time yang tidak ter-cover. Jadi dalam menentukan pekerja part-time, terlebih dahulu diasumsikan bahwa pekerja yang bekerja pada perusahaan hanyalah pekerja full-time.

Akibat dari kendala hari libur yang telah diuraikan di atas, maka diketahui bahwa total ada sebanyak 2AF shift libur di akhir pekan. Hal ini berarti ada 2(B-A)F shift kerja di akhir pekan. Karena disyaratkan terdapat 2BE shift

(16)

kerja di akhir pekan seluruhnya, maka didefinisikan

[

]

2 2( ) 2 (1 ) . (3.2.1) e u BE B A F B E θ F = − − = − −

Jika ue bernilai positif, maka ue disebut

weekend underage, yaitu terdapat shift kerja pekerja full-time pada akhir pekan yang tidak ter-cover. Namun jika ue bernilai

negatif, maka ue disebut weekend overage,

yaitu terdapat kelebihan shift kerja pekerja full-time pada akhir pekan. Dengan mendefinisikan

max{0, }, x+ = x didefinisikan

= banyaknya pekerja - yang diperlukan di akhir pekan selama pekan, dan

(- ) = banyaknya kelebihan pekerja pada akhir pekan.

e e u part time B u full time + +

Karena setiap pekerja mempunyai hari libur 2 hari tiap pekannya, maka terdapat 2BF shift libur pekerja selama B pekan dan 2AF di antaranya adalah hari akhir pekan. Hal ini berarti bahwa ada 2( - ) B A F shift libur pekerja pada hari kerja. Karena perusahaan mensyaratkan hanya D pekerja full-time yang bekerja pada setiap hari kerja, maka disyaratkan terdapat 5BD shift kerja pada hari kerja seluruhnya.

Selanjutnya dengan mendefinisikan 5BF adalah banyaknya shift pada hari kerja seluruhnya, maka didefinisikan

[

]

[

]

5 5 2( ) 5 (3 2 ) . (3.2.2) d u BD BF B A F B D θ F = − − − = − +

Jika ud bernilai positif, maka ud disebut

weekday underage, yaitu terdapat shift kerja pekerja full-time pada hari kerja yang tidak ter-cover. Namun jika ud bernilai negatif,

maka ud disebut weekday overage, yaitu

terdapat kelebihan shift kerja pekerja full-time pada hari kerja. Dengan penotasian seperti sebelumnya, didefinisikan

= banyaknya pada hari kerja yang disusun oleh kelebihan pekerja - pada akhir pekan, ditambah pekerja - jika ada, dan

d

u shift

full time

part time

+

(- ) = banyaknya kelebihan pekerja pada hari kerja.

d

u + full time

Dengan ue dan ud yang telah didefinisikan

di atas, selanjutnya akan ditentukan P=P F( ), yaitu total banyaknya pekerja part-time yang dibutuhkan perusahaan.

• Jika u_e> dan 0 u_d > maka 0 P=u_e+u_d. • Jika ue< dan 0 ud> , maka kelebihan 0

pekerja pada akhir pekan dapat digunakan untuk meng-cover kebutuhan pekerja pada hari kerja. Jadi P=(ue+ud)+.

• Jika ue> dan 0 ud < , maka 0 P=ue.

• Jika u_e< dan 0 u_d < , maka perusahaan 0 tidak memerlukan pekerja part-time. Jadi

0 P= .

Pernyataan-pernyataan di atas dapat dikombinasikan menjadi sebuah rumusan untuk menentukan besarnya P, yaitu

( e d ) (3.2.3) P= u +u + +

Dimisalkan C(F) adalah biaya F pekerja full-time ditambah minimum pekerja part-time selama B pekan. Karena biaya pekerja limited part-time lebih kecil daripada biaya pekerja unlimited part-time, pemakaian pekerja limited part-time lebih diprioritaskan daripada pemakaian pekerja unlimited part-time. Selagi masih tersedia pekerja limited part-time, pekerja part-time yang digunakan perusahaan sebagai tambahan pekerja full-time adalah pekerja limited part-time. Jika masih kurang, barulah perusahaan mempekerjakan pekerja unlimited time. Jika pekerja limited time tidak tersedia (G=0), maka pekerja part-time yang digunakan perusahaan sebagai tambahan pekerja full-time adalah pekerja unlimited part-time. Jadi

. , , ( ), > , ( )( ) (3.2.4) ( ) 5 = 5 p p p p p p f f c c P P G c G c P G P G c P c P G C F BFc BFc ⎧⎪ ⎨ ⎪⎩ + ≤ + ₊ ₋ + + − − =

Dengan menyubstitusi Persamaan (3.2.3) ke Persamaan (3.2.4) maka didapat

. (3.2.5) ( ) 5 _f p( e _d ) ( p p) ( e _d ) C F BFc c u u c c ⎡⎢_⎣u u G⎤⎥_⎦ + + + + + = + + + − + −

(17)

e

u dan u adalah fungsi linear dari F. d

Karena kemiringan u dan e u terhadap F d

adalah negatif, maka u_e dan u_d adalah fungsi turun. Selanjutnya ditentukan: { : 0} /(1 ), dan (3.2.6) { : 0} 5 /(3 2 ). (3.2.7) e e d d b F u E b F u D θ θ = = = − = = = +

Nilai b dan e b akan membagi daerah asal d

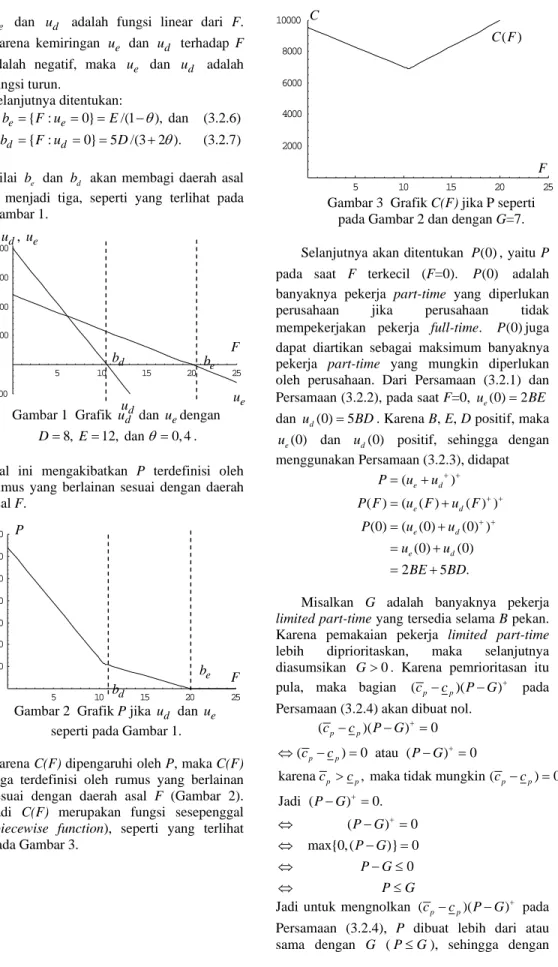
F menjadi tiga, seperti yang terlihat pada Gambar 1. 5 10 15 20 25 -100 100 200 300 400

Gambar 1 Grafik ud dan uedengan

8, 12, dan 0, 4 D= E= θ = .

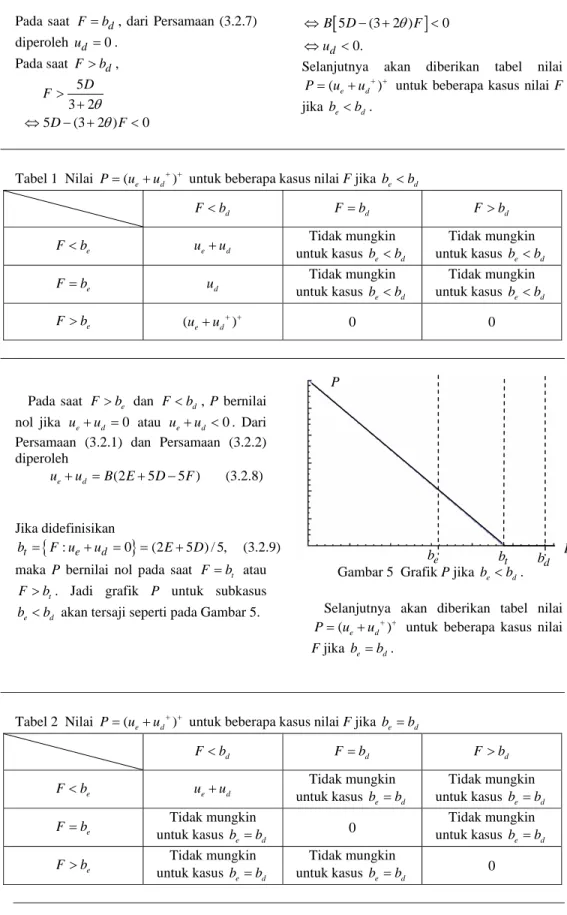
Hal ini mengakibatkan P terdefinisi oleh rumus yang berlainan sesuai dengan daerah asal F. 5 10 15 20 25 100 200 300 400 500 600 700

Gambar 2 Grafik P jika u_d dan u_e seperti pada Gambar 1.

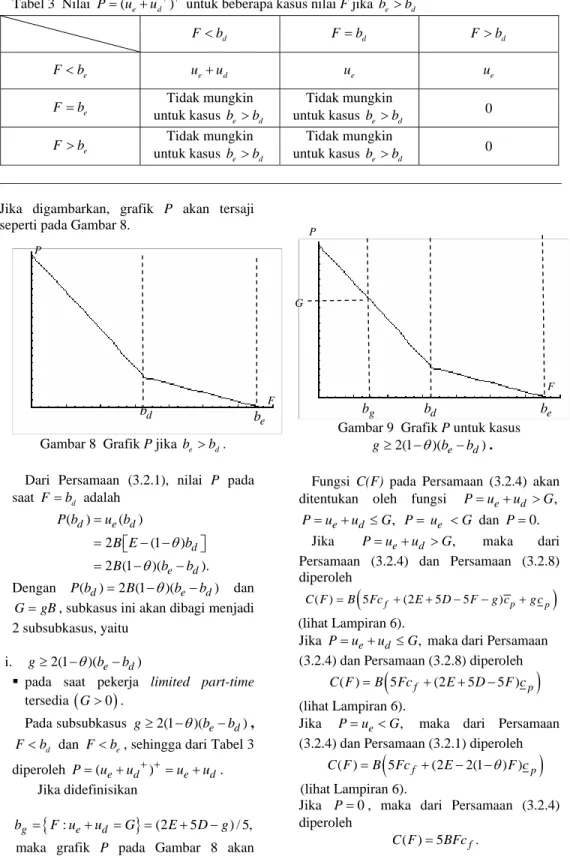
Karena C(F) dipengaruhi oleh P, maka C(F) juga terdefinisi oleh rumus yang berlainan sesuai dengan daerah asal F (Gambar 2). Jadi C(F) merupakan fungsi sesepenggal (piecewise function), seperti yang terlihat pada Gambar 3. 5 10 15 20 25 2000 4000 6000 8000 10000

Gambar 3 Grafik C(F) jika P seperti pada Gambar 2 dan dengan G=7.

Selanjutnya akan ditentukan (0)P , yaitu P pada saat F terkecil (F=0). (0)P adalah banyaknya pekerja part-time yang diperlukan perusahaan jika perusahaan tidak mempekerjakan pekerja full-time. P(0)juga dapat diartikan sebagai maksimum banyaknya pekerja part-time yang mungkin diperlukan oleh perusahaan. Dari Persamaan (3.2.1) dan Persamaan (3.2.2), pada saat F=0, ue(0)=2BE dan ud(0)=5BD. Karena B, E, D positif, maka

(0)

e

u dan ud(0) positif, sehingga dengan menggunakan Persamaan (3.2.3), didapat

( ) ( ) ( ( ) ( ) ) (0) ( (0) (0) ) (0) (0) 2 5 . e d e d e d e d P u u P F u F u F P u u u u BE BD + + + + + + = + = + = + = + = +

Misalkan G adalah banyaknya pekerja limited part-time yang tersedia selama B pekan. Karena pemakaian pekerja limited part-time lebih diprioritaskan, maka selanjutnya diasumsikan G> . Karena pemrioritasan itu 0 pula, maka bagian (cp cp)(P G)

+

− − pada

Persamaan (3.2.4) akan dibuat nol. ( )( ) 0

( ) 0 atau ( ) 0

karena , maka tidak mungkin ( ) 0. Jadi ( ) 0. ( ) 0 max{0, ( )} 0 0 p p p p p p p p c c P G c c P G c c c c P G P G P G P G + + + + − − = ⇔ − = − = > − = − = ⇔ − = ⇔ − = ⇔ − ≤ ⇔ P≤G

Jadi untuk mengnolkan (cp cp)(P G)

+

− − pada

Persamaan (3.2.4), P dibuat lebih dari atau sama dengan G ( P≤ ), sehingga dengan G

e u d u e b F , d e u u F P C ( ) C F F e b d b d b

(18)

(0) (2 5 )

P=P =B E+ D dan G=gB, didapat beberapa kasus

Kasus 1. g≥2E+5D

Akibat dari (cp cp)(P G)

+

− − pada

Persamaan (3.2.4) bernilai nol, Persamaan (3.2.4) menjadi ( ) 5 5 ( ) . f p f p e d C F BFc c P BFc c u u + + = + = + +

Dengan F yang cukup kecil, ue dan ud yang

didefinisikan oleh Persamaan (3.2.1) dan (3.2.2) bernilai positif, sehingga

2 2( ) ( ) 5 (5 2( ) ) (2 5 5 ). e d BE B A F u u BD BF B A F B E D F + + ⎛ − − + ⎞ + _{= ⎜} _⎟ − − − ⎝ ⎠ = + − Jadi ( ) 5 ( (2 5 5 )) 5 ( ) (2 5 ). f p f p p C F BFc c B E D F B c c F Bc E D = + + − = − + + Karena cf >cp, C(F) mempunyai

kemiringan yang positif, yaitu 5 (B c_f −c_p) seperti yang ditunjukkan pada Gambar 4.

Gambar 4 Grafik C(F) jika 2g≥ E+5D. Jadi minimum pekerja full-time yang diperlukan perusahaan untuk meminimumkan biaya adalah

0. F=

Kondisi seperti ini mengindikasikan bahwa untuk memenuhi kebutuhan pekerja setiap harinya, perusahaan hanya mempekerjakan pekerja limited part-time tanpa pekerja full-time. Hal yang seperti ini bukan suatu perencanaan yang diharapkan.

Kasus 2. g<2E+5D

Berdasarkan nilai b , e b dan ketersediaan d

pekerja limited part-time, Kasus 2 akan dibagi menjadi beberapa subkasus dan subsubkasus sebagai berikut:

a) be≤bd

 pada saat pekerja limited part-time tersedia

(

G>0

)

.

 pada saat pekerja limited part-time tidak tersedia

(

G=0

)

.

b) be> bd

i. g≥2(1−θ)(b_e−b_d)

 pada saat pekerja limited part-time tersedia

(

G>0

)

.

ii. g<2(1−θ)(be−bd)

(

G>0

)

.

 pada saat pekerja limited part-time tidak tersedia

(

G=0

)

.

Selanjutnya akan dilakukan peninjauan kepada masing-masing subkasus sebagai berikut

a) be≤bd

 pada saat pekerja limited part-time tersedia

(

G>0

)

. Pada saat F< , be

[

]

1 (1 ) 0 2 (1 ) 0 0. e E F E F B E F u θ θ θ < − ⇔ − − > ⇔ − − > ⇔ >

Pada saat F= , dari Persamaan (3.2.6) be

diperoleh u_e = 0. Pada saat F> , b_e

[

]

1 (1 ) 0 2 (1 ) 0 0. e E F E F B E F u θ θ θ > − ⇔ − − < ⇔ − − < ⇔ < Pada saat F<b_d,

[

]

5 3 2 5 (3 2 ) 0 5 (3 2 ) 0 0. d D F D F B D F u θ θ θ < + ⇔ − + > ⇔ − + > ⇔ > C _{C F}_{( )} F

(19)

Pada saat F=bd, dari Persamaan (3.2.7) diperoleh ud = . 0 Pada saat F>b_d, 5 3 2 5 (3 2 ) 0 D F D F θ θ > + ⇔ − + <

[

5 (3 2 )

]

0 0. d B D F u θ ⇔ − + < ⇔ <

Selanjutnya akan diberikan tabel nilai ( e d )

P= u +u+ + untuk beberapa kasus nilai F jika be<bd.

Tabel 1 Nilai P (ue ud )

+ +

= + untuk beberapa kasus nilai F jika be<bd d Fbd e F b (ue ud ) + + + 0 0

Pada saat F> dan be F<bd, P bernilai

nol jika ue+ud = atau 0 ue+ud < . Dari 0

Persamaan (3.2.1) dan Persamaan (3.2.2) diperoleh (2 5 5 ) (3.2.8) e d u +u =B E+ D− F Jika didefinisikan

{

: 0

}

(2 5 ) / 5, (3.2.9) t e d b = F u +u = = E+ D

maka P bernilai nol pada saat F= atau bt t

F> . Jadi grafik P untuk subkasus b

e d

b <b akan tersaji seperti pada Gambar 5.

Gambar 5 Grafik P jika be<bd.

Selanjutnya akan diberikan tabel nilai ( e d )

P= u +u + + untuk beberapa kasus nilai F jika be= . bd

+ +

= + untuk beberapa kasus nilai F jika be=bd d Fbd e F< b ue+ud Tidak mungkin untuk kasus be= bd Tidak mungkin untuk kasus be=bd e F= b Tidak mungkin untuk kasus be=bd

0 _{untuk kasus}Tidak mungkin

e d b =b e F> b Tidak mungkin untuk kasus be=bd Tidak mungkin untuk kasus be= bd 0 d b e b b_t P F

(20)

sehingga grafik P tersaji seperti Gambar 6.

Gambar 6 Grafik P jika be=bd.

Jadi pada subkasus be≤bd,

( _e _d ) _e _d. P= u +u + +=u +u

Pemakaian pekerja limited part-time di samping pekerja full-time terjadi jika terdapat pekerja limited part-time (G>0) dan P≤ , sedangkan jika P GG > , maka perusahaan menggunakan pekerja limited part-time dan unlimited part-time sebagai tambahan pekerja full-time.

Jika G> , maka dengan 0 mendefinisikan

{

:

}

(2 5 ) / 5, (3.2.10) g e d b F u u G E D g = + = = + −

maka grafik P akan menjadi seperti pada Gambar 7,

Gambar 7 Grafik P jika be≤bd.

sehingga C(F) pada Persamaan (3.2.4) akan ditentukan oleh fungsi P=u_e+u_d >G,

,

e d

P=u +u ≤G dan P=ue+ud = 0.

Jika P=ue+ud > , maka dari G

Persamaan (3.2.4) dan Persamaan (3.2.8) diperoleh

(

)

( ) 5 _f (2 5 5 ) _p _p C F =B Fc + E+ D− F−g c +gc

(lihat Lampiran 1).

Jika P=u_e+u_d ≤ , maka dari Persamaan G (3.2.4) dan Persamaan (3.2.8) diperoleh

(

)

( ) 5 f (2 5 - 5 ) p

C F =B Fc + E+ D F c

(lihat Lampiran 1).

Jika 0,P=u_e+u_d = maka dari Persamaan (3.2.4) diperoleh ( ) 5 _f C F = BFc (lihat Lampiran 1). Jadi 5 (2 5 5 ) , 0 , ( ) 5 (2 5 - 5 ) , , (3.2.11) 5 , . p p g f g t p f t f Fc E D F g c gc F b C F B Fc E D F c b F b Fc b F ⎧ ⎪ ⎪ ⎨ ⎪ ⎪⎩ < < + + − − + ≤ ≤ = + + ≤

C(F) mempunyai dua break point, yaitu

g b dan bt. Misalkan

(

)

1 2 3 ( ) 5 (2 5 5 ) , ( ) (5 (2 5 5 ) ), ( ) 5 , p f p f p f C F B Fc E D F g c gc C F B Fc E D F c C F BFc = + + − − + = + + − = maka 1 2 3 ( ), 0 , ( ) ( ), , ( ), . g g t t C F F b C F C F b F b C F b F ≤ ≤ ⎧ ⎪ =⎨ < ≤ ⎪ _< ⎩

Karena c_p<c_f <c_p, maka C(F) akan minimum pada F=b_g (lihat Lampiran 2).

e d b =b t b P F P t b g b G

(21)

Karena F adalah banyaknya pekerja full-time yang dibutuhkan perusahaan, F haruslah bilangan bulat. Jika F=bg

bukan bilangan bulat, maka F bernilai

g

b ⎢ ⎥

⎣ ⎦ atau ⎡ ⎤⎢ ⎥ bergantung pada biaya bg

pekerja yang paling kecil yang dihasilkan dari keduanya.

Nilai F= ⎣ ⎦ terdapat pada selang ⎢ ⎥bg

0,bg

⎡ ⎤

⎣ ⎦ , sehingga biaya yang dikeluarkan perusahaan untuk mempekerjakan ⎢ ⎥⎣ ⎦ bg

pekerja full-time adalah C1

( )

⎢ ⎥⎣ ⎦ . bg

Sedangkan F= ⎢ ⎥ terdapat pada selang ⎡ ⎤bg

(b b , sehingga biaya yang dikeluarkan g, ]t

perusahaan untuk mempekerjakan ⎡ ⎤⎢ ⎥ bg

pekerja full-time adalah C2

( )

⎡ ⎤⎢ ⎥ . Jadi bg

jika F=bg bukan bilangan bulat maka

( ) ( )

1 2 1 2 , , , . (3.2.12)

{

g g g g g g b C b C b b C b C b F ⎢ ⎥ ⎢ ⎥ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ ⎢ ⎥ ⎡ ⎤ ⎢ ⎥ ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ ⎢ ⎥ < ≥ = Pertaksamaan C1

( ) ( )

⎢ ⎥⎣ ⎦bg <C2 ⎡ ⎤⎢ ⎥bg pada

Persamaan (3.2.12) ekuivalen dengan

(

bg−⎣ ⎦⎢ ⎥bg

) (

cp+ ⎡ ⎤⎢ ⎥bg −bg

)

cp<cf

(lihat Lampiran 3).

(

G=0

)

.

Jika pekerja limited part-time tidak tersedia (G=0), maka g= dan 0 cp= . 0 Persamaan (3.2.10) menjadi

(2 5 ) / 5,

t

F=b = E+ D sehingga Persamaan (3.2.11) menjadi 5 +(2 5 -5 ) , 0 , 5 , . ( )

{

f p t f t Fc E D F c F b B Fc b F C F + ≤ ≤ < = (3.2.13) Misalkan 4 3 ( ) (5 (2 5 5 ) ), dan ( ) 5 , f p f C F B Fc E D F c C F BFc = + + − = maka 4 3 ( ) 0 , ( ) ( ) . t t C F F b C F C F b F ≤ ≤ ⎧ = ⎨ _< ⎩

Fungsi C(F) akan minimum pada F= b_t (lihat Lampiran 4).

Jika F= bukan bilangan bulat, maka F bt

bernilai ⎢ ⎥⎣ ⎦ atau bt ⎡ ⎤⎢ ⎥ bergantung pada bt

biaya pekerja yang paling kecil yang dihasilkan dari keduanya.

Nilai F= ⎢ ⎥⎣ ⎦ terdapat pada selang bt

[ ]

0,bt ,

sehingga biaya yang dikeluarkan perusahaan untuk mempekerjakan ⎢ ⎥⎣ ⎦ pekerja full-time bt

adalah C4

( )

⎢ ⎥⎣ ⎦ . bt F= ⎡ ⎤⎢ ⎥ terdapat pada bt

selang ( , )bt ∞ , sehingga biaya yang

dikeluarkan perusahaan untuk mempekerjakan ⎡ ⎤⎢ ⎥ pekerja full-time adalah bt

( )

3 t

C ⎡ ⎤_{⎢ ⎥ . Jadi jika}b F= bukan bilangan bt

bulat maka 4 3 4 3 , ( ) ( ), (3.2.14) , ( ) ( ). t t t t t t b C b C b F b C b C b ⎧⎢ ⎥ ⎢ ⎥ < ⎡ ⎤ ⎪⎣ ⎦ ⎣ ⎦ ⎢ ⎥ = ⎨_{⎡ ⎤} _{⎢ ⎥} _≥ _{⎡ ⎤} ⎪⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎩ P ertaksamaan C₄

( )

⎣ ⎦⎢ ⎥bt <C₃

( )

⎡ ⎤⎢ ⎥bt pada

Persamaan (3.2.14) ekuivalen dengan

(

)

f t t p c b b c −⎢ ⎥_{⎣ ⎦} < (lihat Lampiran 5). b) be >bd

Dengan menggunakan ue dan ud yang

telah ditentukan pada awal kasus 2a), maka diberikan tabel nilai P (ue ud )

+ +

= + untuk

(22)

+ +

= + untuk beberapa kasus nilai F jika be> bd d Fbd e F bd Tidak mungkin untuk kasus be> bd 0 e F> b Tidak mungkin untuk kasus be>bd Tidak mungkin untuk kasus be> bd 0

Jika digambarkan, grafik P akan tersaji seperti pada Gambar 8.

Gambar 8 Grafik P jika be> . bd

Dari Persamaan (3.2.1), nilai P pada saat F=bd adalah ( ) ( ) 2 (1 ) 2 (1 )( ). d e d d e d P b u b B E b B b b θ θ = = ⎡_⎣ − − ⎤_⎦ = − − Dengan P b( _d)=2 (1B −θ)(b_e−b_d) dan

G=gB, subkasus ini akan dibagi menjadi 2 subsubkasus, yaitu

i. g≥2(1−θ)(b_e−b_d)

(

G>0

)

.

Pada subsubkasus g≥2(1−θ)(be−bd),

d

F<b dan F< , sehingga dari Tabel 3 be

diperoleh P=(u_e+u_d+ +) =u_e+u_d. Jika didefinisikan

{

:

}

(2 5 ) / 5,

g e d

b = F u +u =G = E+ D−g maka grafik P pada Gambar 8 akan menjadi seperti yang terlihat pada Gambar 9.

Gambar 9 Grafik P untuk kasus 2(1 )( e d) g≥ −θ b −b .

Fungsi C(F) pada Persamaan (3.2.4) akan ditentukan oleh fungsi P=u_e+u_d >G,

,

e d

P=u +u ≤G P= ue < dan G P= 0.

Jika P=ue+ud >G, maka dari Persamaan (3.2.4) dan Persamaan (3.2.8) diperoleh

(

)

( ) 5 _f (2 5 5 ) _p _p C F =B Fc + E+ D− F−g c +gc

(lihat Lampiran 6).

Jika P=u_e+u_d ≤G, maka dari Persamaan (3.2.4) dan Persamaan (3.2.8) diperoleh

(

)

( ) 5 _f (2 5 5 ) _p

C F =B Fc + E+ D− F c

(lihat Lampiran 6).

Jika ,P=u_e<G maka dari Persamaan (3.2.4) dan Persamaan (3.2.1) diperoleh

(

)

( ) 5 _f (2 2(1 ) ) _p

C F =B Fc + E− −θ F c

(lihat Lampiran 6).

Jika P= , maka dari Persamaan (3.2.4) 0 diperoleh

( ) 5 _f.

C F = BFc

(lihat Lampiran 6), sehingga didapat

d b b_e g b F P G d b e b P F

(23)

5 (2 5 5 ) , 0 , 5 (2 5 5 ) , , ( ) . 5 (2 2(1 ) ) , , 5 , p p g f g p f d e p f d f Fc E D F g c gc F b Fc E D F c b F b C F B Fc E F c b F b Fc θ + + − − + ≤ ≤ + + − < ≤ = + − − < ≤ (3.2.15) be F. ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ <

C(F) mempunyai tiga break point, yaitu

g b , bd dan be. Misalkan

(

)

(

)

(

)

1 2 5 3 ( ) 5 (2 5 5 ) , ( ) 5 (2 5 5 ) , ( ) 5 (2 2(1 ) ) , ( ) 5 , p f p f p f p f C F B Fc E D F g gc C F B Fc E D F c C F B Fc E F c C F BFc c θ = + + − − + = + + − = + − − = maka 1 2 5 3 0 , ( ) ( ) ( ) ( ) ( ) g g d d e e F b C F b F b C F C F C F b F b C F b F ≤ ≤ ⎧ ⎪ _{< ≤} ⎪ = ⎨ _{< ≤} ⎪ ⎪ _< ⎩

Fungsi C(F) akan minimum pada F=b_g (lihat Lampiran 7). Jika F=bg bukan

bilangan bulat maka nilai F ditentukan oleh Persamaan (3.2.12).

ii. g<2(1−θ)(be−bd)

(

G>0

)

.

Pada subsubkasus g<2(1−θ)(b_e−b_d), d

F>b dan F< , sehingga dari Tabel 3 be

diperoleh P=(ue+ud+ +) =ue. Jika didefinisikan

{

:

}

(2 ) / 2(1 ) (3.2.16)

h e

b = F u =G = E−g −θ

maka grafik P pada Gambar 8 akan menjadi seperti yang terlihat pada Gambar 10.

Gambar 10 Grafik P untuk kasus 2(1 )( _e _d)

g< −θ b −b .

C(F) pada Persamaan (3.2.4) akan ditentukan

olehP=ue+ud >G,P=ue>G, e

P=u ≤ dan G P= 0.

Jika P=u_e+u_d >G, maka dari Persamaan (3.2.4) dan Persamaan (3.2.8) diperoleh

(

)

( ) 5 _f (2 5 5 ) _p _p C F =B Fc + E+ D− F−g c +gc (lihat Lampiran 8).

Jika ,P=ue>G maka dari Persamaan

(3.2.4) dan Persamaan (3.2.1) diperoleh

(

)

( ) 5 _f (2 2(1 ) ) _p _p C F =B Fc + E− −θ F−g c +gc (lihat Lampiran 8).

Jika ,P=u_e≤G maka dari Persamaan (3.2.4) dan Persamaan (3.2.1) diperoleh

(

)

( ) 5 _f (2 2(1 ) ) _p

C F =B Fc + E− −θ F c

(lihat Lampiran 8).

Jika P= , maka dari Persamaan (3.2.4) 0 diperoleh ( ) 5 _f. C F = BFc (lihat Lampiran 8), sehingga didapat d b bh b_e F P G

(24)

5 (2 5 5 ) , 0 , 5 (2 2(1 ) ) , , ( ) (3.2.17) 5 (2 2(1 ) ) , , 5 , . p p f d p p f d h e p f h e f Fc E D F g c gc F b Fc E F g c gc b F b C F B Fc E F c b F b Fc b F θ θ ⎧ ⎪ ⎪⎪ ⎨ ⎪ ⎪ ⎪⎩ + + − − + ≤ ≤ + − − − + < ≤ = ₊ ₋ ₋ _{< ≤} <

C(F) mempunyai 3 break point, yaitu, bd, h b dan b_e. Misalkan

(

)

(

)

(

)

1 6 5 3 ( ) 5 (2 5 5 ) , ( ) 5 (2 2(1 ) ) , ( ) 5 (2 2(1 ) ) , ( ) 5 , p f p f p p f p f C F B Fc E D F g c gc C F B Fc E F g c g c C F B Fc E F c C F BFc θ θ = + + − − + = + − − − + = + − − = maka 1 6 5 3 ( ), 0 , ( ), , ( ) ( ), , ( ), , d d h h e e C F F b C F b F b C F C F b F b C F b F ≤ ≤ ⎧ ⎪ _{< ≤} ⎪ = ⎨ _{< ≤} ⎪ ⎪ < ⎩

Fungsi C(F) akan minimum pada F=b_d atau F=b_h (lihat Lampiran 9).

Jika F=bd bukan bilangan bulat,

maka F bernilai ⎢ ⎥⎣ ⎦ atau bd ⎡ ⎤⎢ ⎥ bd

bergantung pada biaya pekerja yang paling kecil yang dihasilkan dari keduanya.

Nilai F= ⎢ ⎥⎣ ⎦ terdapat pada selang bd

[

0,bd

]

, sehingga biaya yang dikeluarkan

perusahaan untuk mempekerjakan ⎢ ⎥⎣ ⎦ bd

(

⎢ ⎥⎣ ⎦ . bd

)

Sedangkan F= ⎡ ⎤⎢ ⎥ terdapat pada selang bd

(b bd, h], sehingga biaya yang dikeluarkan perusahaan untuk mempekerjakan ⎡ ⎤⎢ ⎥ bd

(

⎡ ⎤⎢ ⎥ . Jadi bd

)

jika F=bd bukan bilangan bulat maka

1 6 1 6 , ( ) ( ), (3.2.18) , ( ) ( ). d d d d d d b C b C b F b C b C b ⎧⎢ ⎥ ⎢ ⎥ < ⎡ ⎤ ⎪⎣ ⎦ ⎣ ⎦ ⎢ ⎥ = ⎨_{⎡ ⎤} _{⎢ ⎥} _≥ _{⎡ ⎤} ⎪⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎩ Pertaksamaan C₁

( )

⎣ ⎦⎢ ⎥bd <C₆

( )

⎡ ⎤⎢ ⎥bd pada

Persamaan (3.2.18) dapat ditulis sebagai

(

b_d−_{⎣ ⎦}⎢ ⎥b_d

)

c_p<⎡_⎣5c_f −2(1−θ)c_p⎤_⎦/(3 2 )+ θ

(lihat Lampiran 10).

Jika F= bukan bilangan bulat, maka F bh

bernilai ⎢ ⎥⎣ ⎦ atau bh ⎡ ⎤⎢ ⎥ bergantung pada bh

biaya pekerja yang paling kecil yang ditimbulkan dari keduanya.

Nilai F= ⎢ ⎥⎣ ⎦ terdapat pada selang bh

(

b b , sehingga biaya yang dikeluarkan d, h

]

perusahaan untuk mempekerjakan ⎢ ⎥⎣ ⎦ bh

(

⎢ ⎥⎣ ⎦ . bh

)

Sedangkan F= ⎡ ⎤⎢ ⎥ terdapat pada selang bh

( ,b b , sehingga biaya yang dikeluarkan h e] perusahaan untuk mempekerjakan ⎡ ⎤⎢ ⎥ bh

(

⎡ ⎤⎢ ⎥ . Jadi jika bh

)

h

F= bukan bilangan bulat maka b

6 5 6 5 , ( ) ( ), (3.2.19) , ( ) ( ). h h h h h h b C b C b F b C b C b ⎧⎢ ⎥ ⎢ ⎥ < ⎡ ⎤ ⎪⎣ ⎦ ⎣ ⎦ ⎢ ⎥ = ⎨_{⎡ ⎤} _{⎢ ⎥} _≥ _{⎡ ⎤} ⎪⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎩ Pertaksamaan C6

( )

⎣ ⎦⎢ ⎥bh <C5

( )

⎡ ⎤⎢ ⎥bh pada

(

bh−⎣ ⎦⎢ ⎥bh

)

cp+

(

⎡ ⎤⎢ ⎥bh −bh

)

cp<5cf / 2(1−θ)

(

G=0

)

.

Jika pekerja limited part-time tidak tersedia (G=0) maka g= dan 0 c_p= . Persamaan 0 (3.2.16) menjadi

/(1 )

e

F=b =E −θ , sehingga Persamaan (3.2.17) menjadi

(25)

5 (2 5 5 ) , 0 , ( ) 5 (2 2(1 ) ) , , (3.2.20) 5 , . f p d f p d e f e Fc E D F c F b C F B Fc E F c b F b Fc b F θ < < ⎧ + + − ≤ ≤ ⎪⎪ = ⎨ + − − ≤ ⎪ ⎪⎩ Misalkan 4 7 3 ( ) (5 +(2 5 - 5 ) ), ( )= (5 +(2 2(1 ) ) ) dan ( ) 5 , f p f p f C F B Fc E D F c C F B Fc E F c C F BFc θ = + − − = maka 4 7 3 ( ), 0 , ( ), , ( ) ( ), . d d e e C F F b C F b F b C F B C F b F ≤ ≤ ⎧ ⎪ _< _≤ = ⎨ ⎪ _< ⎩

Fungsi C(F) akan minimum pada F=bd

atau F= (lihat Lampiran 12) b_e

Jika F=bd bukan bilangan bulat, maka

F bernilai ⎢ ⎥⎣ ⎦ atau bd ⎡ ⎤⎢ ⎥ bergantung pada bd

Nilai F= ⎢ ⎥⎣ ⎦ terdapat pada selang bd

[

0,bd

]

perusahaan untuk mempekerjakan ⎢ ⎥⎣ ⎦ bd

(

⎢ ⎥⎣ ⎦ , bd

)

sedangkan F= ⎡ ⎤⎢ ⎥ terdapat pada selang bd

(b bd, e], sehingga biaya yang dikeluarkan perusahaan untuk mempekerjakan ⎡ ⎤⎢ ⎥ bd

(

⎡ ⎤⎢ ⎥ . Jadi jika bd

)

d

F=b bukan bilangan bulat, maka

4 7 4 7 , ( ) ( ), (3.2.21) , ( ) ( ). d d d d d d b C b C b F b C b C b ⎧⎢ ⎥ ⎢ ⎥ < ⎡ ⎤ ⎪⎣ ⎦ ⎣ ⎦ ⎢ ⎥ = ⎨_{⎡ ⎤} _{⎢ ⎥} _≥ _{⎡ ⎤} ⎪⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎩ Pertaksamaan C4

( )

⎣ ⎦⎢ ⎥be <C7

( )

⎡ ⎤⎢ ⎥be pada

(

b_d−_{⎣ ⎦}⎢ ⎥b_d

)

c_p <⎡_⎣5c_f −2(1−θ)c_p⎤_⎦/(3 2 )+ θ

Jika F= bukan bilangan bulat, maka be

F bernilai ⎢ ⎥⎣ ⎦ atau be ⎡ ⎤⎢ ⎥ bergantung pada be

Nilai F= ⎢ ⎥⎣ ⎦ terdapat pada selang be

(

b bd, e

]

perusahaan untuk mempekerjakan ⎢ ⎥⎣ ⎦ be

(

⎢ ⎥⎣ ⎦ , be

)

sedangkan F= ⎡ ⎤⎢ ⎥ terdapat pada selang be

( , )be ∞ , sehingga biaya yang dikeluarkan

perusahaan untuk mempekerjakan ⎡ ⎤⎢ ⎥ be

(

⎡ ⎤⎢ ⎥ . Jadi jika be

)

e

F= bukan bilangan bulat maka b

7 3 7 3 , ( ) ( ), (3.2.22) , ( ) ( ). e e e e e e b C b C b F b C b C b ⎧⎢ ⎥ ⎢ ⎥ < ⎡ ⎤ ⎪⎣ ⎦ ⎣ ⎦ ⎢ ⎥ = ⎨_{⎡ ⎤} _{⎢ ⎥} _≥ _{⎡ ⎤} ⎪⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎩ Pertaksamaan C7

( )

⎣ ⎦⎢ ⎥be <C3

( )

⎡ ⎤⎢ ⎥be pada

5 / 2(1 )

e e f p

b −⎢ ⎥_{⎣ ⎦}b < c −θ c

3.3 Contoh Permasalahan

3.3.1 Pemakaian Pekerja Full-time dan Kedua Jenis Pekerja Part-time

Dari pembahasan kasus-kasus di atas, diperoleh bahwa jika perusahaan menggunakan pekerja limited part-time dan unlimited part-time, maka banyaknya pekerja full-time yang dibutuhkan perusahaan adalah sebagai berikut

1. Jika b_e≤b_d, atau b_e>b_d dan 2(1 )( _e _d)

g≥ −θ b −b , maka

(2 5 ) / 5

g

F=b = E+ D−g .

Jika F bukan bilangan bulat, maka F bernilai ⎢ ⎥⎣ ⎦ atau bg ⎡ ⎤⎢ ⎥ yang bg

ditentukan oleh Persamaan (3.2.12).

2. Jika be>bd dan g<2(1−θ)(be−bd), maka , (2 ) 2(1 ) 5 /(3 2 ), 5 2(1 ) , 5 2(1 ) .

{

d f p p h f E g b D c c b c c F θ θ θ θ − − = + ≥ − = < − =

Jika F bukan bilangan bulat, maka F ditentukan oleh Persamaan (3.2.18) dan Persamaan (3.2.19).

(26)

Contoh 3.

Misalkan sebuah perusahaan beroperasi tujuh hari dalam sepekan selama 5 pekan (B=5). Perusahaan mempekerjakan pekerja full-time yang masing-masing diberikan hari libur sebanyak 2 hari per pekan termasuk di dalamnya libur 2 akhir pekan (A=2) dari 5 akhir pekan seluruhnya. Perusahaan membutuhkan 8 pekerja full-time pada setiap hari kerja (D=8), dan 10 pekerja pada tiap akhir pekan (E=10). Biaya pekerja full-time,

7

f

c = satuan per pekerja per hari. Selain mempekerjakan pekerja full-time, perusahaan juga memutuskan untuk mempekerjakan pekerja limited time dan unlimited part-time dengan biaya berturut-turut adalah 5 satuan

(

c_p=5

)

dan 9 satuan

(

c_p=9

)

per pekerja per hari. Juga ditentukan bahwa banyaknya pekerja limited part-time yang tersedia adalah 8 pekerja (G=8). Selanjutnya akan ditentukan banyaknya pekerja full-time dan part-time yang akan dipekerjakan perusahaan, serta biaya yang dikeluarkan untuk mempekerjakan pekerja-pekerja tersebut.

Dari data yang ada, dapat didefinisikan 8 1, 6 5 G g B = = = dan 2 0, 4 5 A B θ = = = . Dengan menggunakan Persamaan (3.2.6) dan Persamaan (3.2.7) ditentukan 10 10 16, 67 dan (1 ) (1 0, 4) 0, 6 e E b θ = = = = − − 5 (5)(8) 40 10, 53. (3 2 ) (3 2(0, 4)) 3,8 d D b θ = = = = + + karena be>bd, g=1, 6<2 1

(

−θ

)

(

be−bd

)

7, 37 = , dan 5c_f =35>2(1−θ)c_p=10,8, maka dari Point 2 pada Subsubbab 3.3.1 diperoleh F=bd =10, 53.

Karena F bukan bilangan bulat, maka nilai F akan ditentukan dengan menggunakan Persamaan (3.2.18). Karena

(

)

5 2(1 ) 4, 77 6,37 3 2 f p d d p c c b b c θ θ − − −⎢ ⎥_{⎣ ⎦} = < = + maka 10 d F=⎢ ⎥_{⎣ ⎦}b = .

Jadi nilai F sekarang adalah 10, artinya banyaknya pekerja full-time yang dibutuhkan perusahaan adalah sebanyak 10 pekerja.

Selanjutnya dengan F=10ditentukan

2 2( ) (2)(5)(10) 2(5 2)(10) 100 60 40 e u = BE− B−A F = − − = − = dan

(

)

(

)

5 5 2( ) (5)(5)(8) (5)(5)(10) 2(5 2)(10) 200 190 10. d u = BD− BF− B−A F = − − − = − =

Karena 0u_e > dan u_d > , maka 0 50

e d

P=u +u = . Karena pekerja limited part-time yang tersedia adalah 8 pekerja, maka 50 pekerja part-time tersebut terdiri atas 8 pekerja limited part-time dan 42 pekerja unlimited part-time.

Dari Persamaan (3.2.17) dengan 10 F=⎢ ⎥_{⎣ ⎦}_bd = diperoleh

(

)

( ) 5 (2 5 5 ) (5)(10)(7) ((2)(10) (5)(8) (10) 5 (5)(10) 1, 6)9 (1, 6)(5) 2546 satuan. f p p C F B Fc E D F g c gc C = + + − − + + + − ⎛ ⎞ = ⎜ ₋ ₊ ⎟ ⎝ ⎠ =

Jadi selama 5 pekan beroperasi, perusahaan harus mempekerjakan 10 pekerja full-time, 8 pekerja limited part-time dan 42 pekerja unlimited part-time dengan 40 pekerja part-time yang bekerja pada akhir pekan dan sisanya bekerja pada hari kerja. Biaya minimum yang harus dikeluarkan dalam mempekerjakan pekerja-pekerja tersebut adalah sebesar 2546 satuan.

3.3.2 Pekerja Full-time dan Pekerja Limited Part-time

Dari pembahasan kasus-kasus di atas, diperoleh bahwa jika perusahaan menggunakan pekerja limited part-time selain pekerja full-time, maka banyaknya pekerja full-time yang dibutuhkan perusahaan adalah sebagai berikut

1. Jika b_e≤b_d, atau b_e>b_d dan 2(1 )( e d) g≥ −θ b −b , maka (2 5 ) / 5 g F=b = E+ D−g . 2. Jika be>bd dan g<2(1−θ)(be−bd), maka (2 ) / 2(1 ). h F=b = E−g −θ Jika F bukan bilangan bulat, maka F bernilai F⎡ ⎤_{⎢ ⎥ dan bukan bernilai F}⎢ ⎥_{⎣ ⎦ , karena}