DINAMIKA DAN INTERAKSI SOLITON DNA MODEL PEYRARD-BISHOP-DAUXOIS DENGAN APROKSIMASI POTENSIAL MORSE ORDE LIMA IZZATU YAZIDAH

DINAMIKA DAN INTERAKSI SOLITON DNA

MODEL PEYRARD-BISHOP-DAUXOIS DENGAN

APROKSIMASI POTENSIAL MORSE ORDE LIMA

IZZATU YAZIDAH

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2012

Izzatu Yazidah. Dinamika dan Interaksi Soliton DNA Model

Peyrard-Bishop-Dauxois dengan Aproksimasi Potensial Morse Orde Lima.

Dibimbing

oleh

: Dr. Husin Alatas, S. Si, M. Si.

Abstrak

DNA model PBD (perpanjangan dari model Peyrard-Bishop) merupakan model DNA yang menggambarkan denaturasi (replikasi) DNA. Tulisan ini menjelaskan makna fisis dari solusi numerik DNA model PBD dengan aproksimasi potensial morse hingga orde lima dalam efek gangguan pada dinamika gelombang soliton DNA. Dengan menggunakan metode finite-difference yang dibantu metode interpolasi Lagrange diperoleh solusi numerik dinamika soliton DNA model PBD yang diberikan gangguan pada solusi stabilnya. Pengaruh gangguan dengan mengalikan nilai (1+ɛ) pada solusi stabilnya dapat terlihat pada peristiwa undulasi (dimana terjadi penyempitan soliton dan kenaikan amplitudo), sedangkan gangguan beda fase (θ=0,π/2 dan π) tidak memberikan pengaruh yang cukup signifikan terhadap kondisi selanjutnya.

Kata kunci: DNA model PBD, metode finite-difference, interpolasi Lagrange, potensial morse, soliton.

PERNYATAAN

Dengan ini saya menyatakan bahwa skripsi yang berjudul

Dinamika dan

Interaksi Soliton DNA Model Peyrard-Bishop-Dauxois dengan Aproksimasi

Potensial Morse Orde Lima

adalah benar-benar hasil karya saya sendiri dibawah

bimbingan Dr. Husin Alatas. S.Si, M.Si, dan belum pernah digunakan sebagai

karya ilmiah pada perguruan tinggi atau lembaga manapun. Sumber informasi

yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan

dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar

Pustaka di bagian akhir skripsi ini.

Bogor, Agustus 2012

Judul : Dinamika dan Interaksi Soliton DNA Model Peyrard-Bishop-Dauxois

dengan Aproksimasi Potensial Morse Orde Lima

Nama : Izzatu Yazidah

NRP : G74070035

Menyetujui,

Pembimbing

Dr. Husin Alatas, S.Si, M.Si

NIP : 19710604 199802 1 001

Mengetahui,

Ketua Departemen Fisika FMIPA IPB

Dr. Akhiruddin Maddu, M.Si

NIP : 19710604 199802 1 001

DINAMIKA DAN INTERAKSI SOLITON DNA MODEL

PEYRARD-BISHOP-DAUXOIS DENGAN APROKSIMASI

POTENSIAL MORSE ORDE LIMA

Oleh:

IZZATU YAZIDAH

NRP. G74070035

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada

Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2012

i

KATA PENGANTAR

Puji dan syukur penulis panjatkan kehadirat Allah SWT karena atas

limpahan rahmat dan hidayah-Nya penulis dapat menyelesaikan penulisan laporan

tugas akhir dengan judul ”

Dinamika dan Interaksi Soliton DNA Model

Peyrard-Bishop-Dauxois dengan Aproksimasi Potensial Morse Orde Lima

”

.

Shalawat serta salam tidak lupa dipanjatkan kepada Nabi besar Muhammad SAW

beserta para pengikutnya hingga akhir masa kelak.

Laporan penelitian tugas akhir yang dilakukan oleh penulis ini disusun

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas

Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor. Penulis

mengucapkan terima kasih kepada pihak-pihak yang telah membantu dalam

penyelesaian penulisan laporan tugas akhir ini, yaitu kepada dosen pembimbing,

dosen penguji, editor, keluarga besar di rumah serta teman-teman yang tidak dapat

dituliskan satu persatu.

Penulis menyadari bahwa usulan penelitian ini jauh dari sempurna, oleh

karena itu, saran dan kritik yang bersifat membangun sangat diperlukan bagi

penulis. Semoga laporan tugas akhir ini bermanfaat bagi semuanya.

Bogor, Agustus 2012

ii

UCAPAN TERIMA KASIH

Pada kesempatan ini, penulis ingin mengucapkan terima kasih kepada

seluruh pihak yang telah membantu dalam penyelesaian penelitian serta laporan

tugas akhir yang dilakukan:

1.

Bapak Dr. Husin Alatas - selaku dosen pembimbing akademik serta

pembimbing tugas akhir yang telah banyak memberikan bimbingan,

masukan, dan semangat kepada penulis.

2.

Bapak Dr. Irmansyah dan Ibu Mersi Kurniati, M.Si – selaku dosen penguji

yang telah memberikan masukan dan semangat kepada penulis.

3.

Bapak M.N Indro, M.Sc – selaku editor yang telah memberikan masukan

mengenai tatacara penulisan laporan tugas akhir serta memberikan

semangat kepada penulis.

4.

Bapak Dr. Laksmana Tri Handoko dan tim GFTK LIPI FISIKA yang telah

memberikan kesempatan kepada penulis untuk belajar mengenai

komputasi di GFTK, LIPI Puspiptek Serpong, Tangerang.

5.

Keluarga besar H. Ahmad Suhaily – Papa, (Alm.) Mama, Cindy, Rully,

Ahsan dan Ela - yang telah memberi dorongan kepada penulis baik secara

materi maupun spiritual.

6.

Laskar SA Palembang dan Big Families H. Syawal.

7.

Direktur, Kasubdit serta staff di Direktorat Panas Bumi, Ditjen EBTKE,

Kementrian ESDM RI atas bantuan selama ini



.

8.

Switenia Wana Putri dan Dede Hermanudin – selaku rekan satu team dan

seperjuangan dalam melakukan penelitian DNA PBD ini. Terima kasih

banyak atas bantuan dan kebersamaan kita selama ini ^^.

9.

Dita Rahayu B. – Teman, Sahabat, Saudara penulis selama berada di IPB,

Bogor. Terima kasih banyak atas sukaduka, kebersamaan, keceriaan dan

bantuan selama ini ^^~.

10. Teman-teman penghuni Lab Fisika Teori dan Komputasi, Ka Fabian, Ka

Teguh, Ka Mardhani, Ka Andre, Ka Chandra K, Firman, Maman, Hema.

11. Teman-teman Fisika 44 Dede Y, Hilal, Leli, Balgies, Neneng, Ayul, Wita,

Mbah, dll serta teman-teman dari Dept. Fisika IPB Bambang, Bagus, Epa,

Anggi, Nisa, Mbak Ais, Mbak Wenny, Mas Ian, Bu Grace, Pak Firman,

Mang Jun serta lainnya yang tidak dapat dituliskan satu persatu.

12. Teman-teman kosan RZ, GMSK, 348Nation, Pioner WI, Doetha serta adik

kelas di IPB angkatan 46,47 dan 48 yang tidak dapat dituliskan satu

persatu.

13. Teman-teman admin dan member di komunitas Korea: KPOPDRAMALv,

SungJoonID, SunghyunLv, dan ANJELL Indo, serta Wedding Channel –

Mediaworks Indonesia.

iii

DAFTAR RIWAYAT HIDUP

Penulis lahir di Bekasi pada 08 April 1989, anak ketiga dari

tiga bersaudara pasangan H. Ahmad Suhaily dan Hj.Lulu

Lutfiah, Dsy. (Alm). Pendidikan penulis dimulai pada tahun

1994 di TK Parkit Darma Wanita Tambun, tahun 1995 di

SD Negeri Mekarsari 01 Tambun, tahun 2001 di SLTP

Negeri 2 Tambun Selatan, tahun 2004 di SMA Negeri 1

Tambun Selatan dan tahun 2007 di Institut Pertanian Bogor

melalui jalur USMI.

Selama di IPB, penulis aktif di Organisasi Mahasiswa Daerah (OMDA)

Bekasi - KEMSI sebagai anggota pada tahun 2007-2008 dan Bendahara 2 pada

tahun 2008-2009, Himpunan Mahasiswa Fisika (HIMAFI) sebagai Ketua Divisi

Infokom pada tahun 2009 serta ikut aktif dalam berbagai kepanitian besar di

kampus sebagai divisi acara, pdd, humas dan konsumsi. Selain itu penulis juga

mengajar sebagai asisten praktikum Fisika Dasar untuk mahasiswa TPB pada

tahun 2008-2011 serta asisten praktikum Eksperimen Fisika 2 pada tahun 2011.

iv

DAFTAR ISI

Halaman

DAFTAR GAMBAR ...………

v

DAFTAR LAMPIRAN………

vi

BAB 1 PENDAHULUAN ...

1

1.1 Latar Belakang ...

1

1.2 Tujuan Penelitian ...

1

1.3 Perumusan Masalah ...

1

1.4 Hipotesis ...

1

BAB 2 TINJAUAN PUSTAKA ...

2

2.1 Replikasi DNA ………....……

2

2.2 Model DNA PBD ………....……

2

BAB 3 METODE PENELITIAN ...

6

3.1 Waktu dan Tempat Penelitian ...

6

3.2 Peralatan ...

6

3.3 Metode Penelitian ...

6

3.3.1 Studi Pustaka ...

6

3.3.2 Penguasaan

Software

dan Persamaan Matematis ...

6

3.3.3 Pembuatan dan Pengujian Program ...

6

3.3.3.1 Aplikasi Metode

Finite Difference

Dalam

Program ……….

6

3.3.3.2 Aplikasi Interpolasi Lagrange Dalam Program..

8

BAB 4 HASIL DAN PEMBAHASAN ...

9

4.1 Simulasi Perambatan Soliton pada Kondisi Stabil ...

9

4.2 Simulasi Perambatan Soliton Akibat Gangguan pada Amplitudo 10

4.3 Simulasi Interaksi Dua Soliton ...

11

BAB 5 SIMPULAN ...

13

SARAN ...

14

DAFTAR PUSTAKA ...

14

v

DAFTAR GAMBAR

Halaman

Gambar 1. Tiga cara teoritis replikasi DNA …...

2

Gambar 2. Representasi grafis model pegas sederhana untuk rantai DNA ....

3

Gambar 3. Perkiraan untuk turunan dari

f (x)

di P dengan menggunakan

Forward, Backward

, dan

Central Difference

………...

6

Gambar 4. Karakteristik solusi persamaan NLS soliton DNA model PBD

hingga orde lima stabil ……….

9

(a) profil soliton DNA dalam tiga dimensi ………...

9

(b) plot hubungan y

n

(pm) terhadap nl (pm), dimana grafik

berwarna merah menunjukkan grafik pada saat T

awal

, dan grafik

biru menunjukkan grafik pada saat T

akhir

……….

9

Gambar 5. Karakteristik solusi persamaan NLS soliton DNA model PBD

hingga orde lima Perturbasi I ………...………

10

(a) profil soliton DNA dalam tiga dimensi ………...

10

(b) plot hubungan y

n

(pm) terhadap nl (pm), dimana grafik

berwarna merah menunjukkan grafik pada saat T

awal

, grafik biru

menunjukkan grafik pada saat T

akhir

, dan grafik hijau

menunjukkan saat terjadinya undulasi ……….

10

Gambar 6. Karakteristik solusi persamaan NLS soliton DNA model PBD

hingga orde lima Perturbasi II ………...………...

11

(a) profil soliton DNA dalam tiga dimensi ………..

10

(b) plot hubungan y

n

(pm) terhadap nl (pm), dimana grafik

berwarna merah menunjukkan grafik pada saat T

awal

, dan grafik

biru menunjukkan grafik pada saat T

akhir

………..

11

Gambar 7. Karakteristik solusi persamaan NLS soliton DNA model PBD

hingga orde lima Perturbasi III plot hubungan y

n

(pm) terhadap

nl (pm), dimana grafik berwarna merah menunjukkan grafik

pada saat T

awal

, dan grafik biru menunjukkan grafik pada saat

T

akhir

………...

12

(a) profil soliton DNA dalam tiga dimensi untuk θ = 0 ………..

12

(b) profil soliton DNA dalam tiga dimensi untuk θ =

𝜋

2

……...

12

(c) profil soliton DNA dalam tiga dimensi untuk θ = π ……...

12

vi

DAFTAR LAMPIRAN

Halaman

Lampiran A

. Program Simulasi Perambatan Soliton pada Kondisi Stabil ….

17

Lampiran B

. Program Simulasi Perambatan Soliton Akibat Gangguan pada

Amplitudo ……… 20

Lampiran C

. Program Simulasi Interaksi Dua Soliton ……….……...

23

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Asam deoksiribonukleat atau yang lebih dikenal DNA (Deoxyribo Nucleic Acid), adalah sejenis asam nukleat yang tergolong biomolekul utama penyusun berat kering setiap organisme. Struktur heliks ganda DNA mengalami dinamika yang sangat kompleks seperti transkripsi, translasi dan mutasi. Dinamika DNA sendiri telah dipelajari dengan hirarki-hirarki yang berbeda dari model struktural batang elastik yang sederhana sampai ke nonlinier kisi heliks diskrit1-4. Dinamika nonlinier telah berhasil digunakan untuk menjelaskan denaturasi DNA5. Masih banyak spekulasi pada kemungkinan peran nonlinier (Kinks atau soliton) dalam masalah interaksi protein-DNA, regulasi transkripsi, interaksi jarak jauh dari protein-protein, dan konfirmasi gelombang yang diproduksi oleh karsinogen.1

Model nonlinear juga mendukung eksitasi koheren yang muncul dalam banyak bidang ilmu pengetahuan dirintis sejak penemuan oleh Fermi, Pasta dan Ulam6. Penemuan Fermi, Pasta dan Ulam tersebut mendorong banyak ilmuwan menggunakan model nonlinier dalam studi sistem yang kompleks7, diantaranya model nonlinear yang mulai masuk ke dalam fisika DNA. Englander et al.8 pada tahun 1980, memodelkan dinamika DNA dengan persamaan sinus-Gordon. Sejak saat itu, banyak pekerjaan yang dikhususkan untuk eksitasi nonlinier dalam DNA, baik dari sudut pandang mekanika dinamik dan statistik. Di antara bagian kerja tersebut, terutama model yang sukses yakni model dinamika DNA yang diajukan pertama kali oleh Peyrard-Bishop (PB)5,9, dan dikembangkan oleh Dauxois10-14 dengan potensial morse berperan menggambarkan ikatan hidrogen antar nukleotida dalam strand

(rantai) yang berbeda. Model Peyrard-Bishop-Dauxois selanjutnya disebut

sebagai model PBD yang akan menjadi fokus dalam penelitian ini.

Dinamika DNA model PBD dapat didekati dengan gelombang soliton,

karena soliton merupakan solusi persamaan diferensial nonlinear, yang memiliki energi total berhingga, terlokalisasi dalam ruang, bersifat stabil, dan tidak menyebar. Profil sebaran rapat energinya menyerupai gundukan yang terpusat dalam rentang ruang berhingga. Setiap gelombang soliton dicirikan oleh sifat tidak berubahnya topologi yang menunjukkan sifat kestabilannya.15

1.2 Tujuan Penelitian

Di dalam penelitian ini akan dicari bagaimanakah solusi numerik menggunakan metode beda higga ( finite-difference). Kemudian melakukan simulasi terhadap berbagai macam efek gangguan dan menjelaskan arti fisis dari hasil yang diperoleh.

1.3

Perumusan Masalah

Sampai saat ini, penelitian yang dilaporkan di berbagai literatur masih terbatas pada model DNA PBD semi-diskrit. Pada model ini di asumsikan bahwa untai DNA merupakan sistem kontinu. Padahal kenyataannya DNA merupakan sistem diskrit. Dinamika DNA untuk model semi-diskrit sendiri telah dikaji secara analitik hingga orde ke lima. Dan pada penelitian ini, akan ditinjau pemecahan bagaimana solusi numerik dan simulasi yang dihasilkan pada persamaan soliton DNA model PBD orde ke lima saat diberi gangguan?.

1.4 Hipotesis

Solusi numerik persamaan soliton DNA model PBD yang diberi gangguan akan memberikan hasil yang berbeda dengan solusi eksak tanpa diberi gangguan.

BAB 2

TINJAUAN PUSTAKA

2.1 Replikasi DNA

DNA atau asam deoksiribonukleat merupakan polimer yang terdiri atas tiga komponen utama, yaitu gugus fosfat, gula deoksiribosa, dan basa nitrogen19. Salah satu fungsi pokok DNA adalah menyimpan informasi genetik dan dengan tepat dapat meneruskan informasi tersebut dari tetua kepada keturunannya, dari generasi ke generasi. Fungsi ini merupakan fungsi genotipik, yang dilaksanakan melalui replikasi.

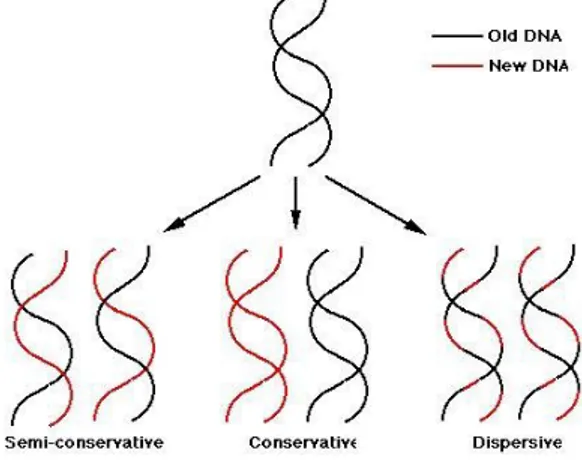
Ada tiga cara teoretis replikasi DNA yang pernah diusulkan, yaitu semikonservatif, konservatif, dan dispersif (lihat Gambar 1). Pada replikasi semikonservatif tangga berpilin mengalami pembukaan terlebih dahulu sehingga kedua untai polinukleotida akan saling terpisah, namun masing-masing untai ini tetap dipertahankan dan akan bertindak sebagai cetakan (template) bagi pembentukan untai polinukleotida baru. Pada replikasi konservatif seluruh tangga berpilin DNA awal tetap dipertahankan dan akan mengarahkan pembentukan tangga berpilin baru. Pada replikasi dispersif kedua untai polinukleotida mengalami fragmentasi di sejumlah tempat. Fragmen-fragmen polinukleotida yang terbentuk akan menjadi cetakan bagi fragmen nukleotida baru sehingga fragmen lama dan baru akan dijumpai berselang-seling di dalam tangga berpilin yang baru.

Di antara ketiga cara replikasi DNA yang diusulkan tersebut, hanya cara semikonservatif yang dapat dibuktikan kebenarannya melalui percobaan yang dikenal dengan nama sentrifugasi seimbang dalam tingkat kerapatan atau

equilibrium density-gradient centrifugation. Percobaan ini dilaporkan hasilnya pada tahun 1958 oleh M.S. Meselson dan F.W. Stahl.19

Gambar 1. Tiga cara teoritis replikasi DNA.19

2.2 Solusi Model DNA PBD

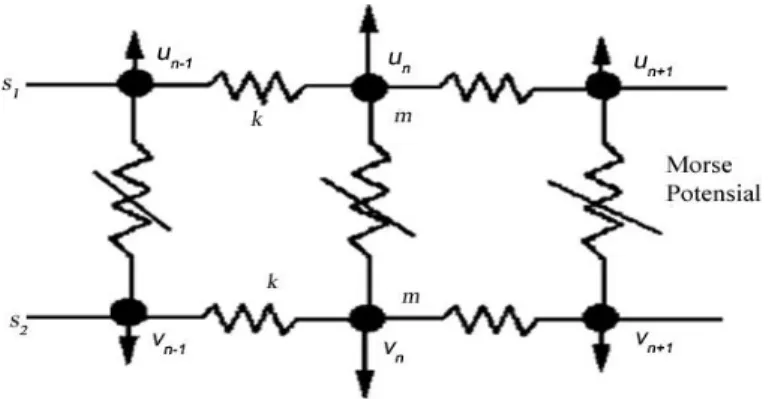
Model yang digunakan untuk mendeskripsikan dinamika molekul DNA pada penelitian ini adalah model Peyrard-Bishop-Dauxois. Bentuk B-DNA dalam model Watson-Crick merupakan helix ganda, yang terdiri atas dua alur yang digabungkan melalui ikatan hidrogen (alur s1 dan s2) seperti terlihat pada Gambar 2. Salah satu alur dapat diasumsikan sebagai sebuah massa umum

m untuk semua nukleotida yang memiliki nilai sama untuk konstanta kopling k untuk interaksi longitudinalnya5,14. Struktur helicoidal dari rantai DNA menunjukkan bahwa nukleotida dari alur yang berbeda menjadi cukup dekat sehingga alur-alur tersebut dapat berinteraksi. Ini berarti bahwa suatu nukleotida n disalah satu alur berinteraksi dengan kedua nukleotida (n+h) dan (n-h) pada alur lainnya.

2 2

Gambar 2. Representasi grafis model pegas sederhana untuk rantai DNA.10

Nukleotida mengalami gerak transversal un dan vn dari posisi kesetimbangan di sepanjang arah ikatan hidrogen. Energi nukleotida tersebut direpresentasikan melalui Hamiltonian untuk rantai DNA 10, 11,13

𝐻 = 𝑚 2 𝑢 2_{+ 𝑣} 2 ₊𝑘 2 𝑢𝑛− 𝑢𝑛 −1 2₊ 𝑣𝑛−𝑣𝑛−12+𝐾2𝑢𝑛−𝑣𝑛+𝑕2+𝑢𝑛−𝑣𝑛 −𝑕2+𝐷[𝑒^ −𝑎(𝑢_𝑛−𝑣_𝑛 ) −1]2 ………….…...….. (1)

Dimana k adalah konstanta harmonik

helicoid untuk untai yang sama; K adalah konstanta harmonik helicoid untuk untai yang berbeda; H adalah Hamiltonian potensial morse yang mendekati potensial ikatan hidrogen; D adalah kedalaman potensial morse; dan a adalah jarak antar nukleotida pada rantai yang berbeda.

Dari Persamaan (1) akan lebih mudah untuk menggambarkan gerakan dua alurnya dengan membuat transformasi ke koordinat pusat massa yang mewakili gerak ke dalam dan gerakan keluar untuk

gerakan transversal, yaitu

𝑥𝑛 = 𝑢𝑛+𝑣𝑛

2 , 𝑦𝑛 = 𝑢𝑛−𝑣𝑛

2 ………... (2) Dengan menyubstitusi Persamaan (2) ke Persamaan (1) maka akan diperoleh persamaan dinamis yang menggambarkan gelombang linear dan gelombang nonlinier. 𝑚𝑥 𝑛 = 𝑘 𝑥𝑛+1+ 𝑥𝑛−1− 2𝑥𝑛 + 𝐾 𝑥𝑛 +𝑕+ 𝑥𝑛−𝑕 − 2𝑥𝑛 …... (3) dan 𝑚𝑦 = 𝑘 𝑦𝑛+1+ 𝑦𝑛−1−2𝑦𝑛 − 𝐾 𝑦𝑛+𝑕+ 𝑦𝑛−𝑕 + 2𝑦𝑛 + 2 2𝑎𝐷[𝑒^(−𝑎 2 𝑦_𝑛 ) − 1] 𝑒^(−𝑎 2 𝑦_𝑛 ) ..…………. (4) Seperti dijelaskan dalam beberapa artikel10,11,13,16-18 dapat diterapkan transformasi

𝑦𝑛 = 𝜀1/2Φ𝑛 atau Φ𝑛 = 𝑦_𝑛

𝜀1/2 …... (5)

Dimana faktor skala 0 < ɛ << 1 membolehkan kita untuk mengembangkan potensial Morse menjadi ekspansi Taylor orde lima dengan menyesuaian pada Hamiltonian sehingga didapatkan persamaan gerak untuk Φ𝑛

Φ𝑛 = 𝑘 𝑚 Φ𝑛+1+Φ𝑛−1−2Φ𝑛 − 𝐾 𝑚 Φ𝑛+𝑕 +Φ𝑛−𝑕 + 2Φ𝑛 − 𝜔𝑔2 Φ𝑛+∝ 𝜀1/2Φ𝑛2+ 𝛽εΦ𝑛3+ γ𝜀3/2Φ𝑛4 ………..…...…. (6) dimana 𝜔𝑔2= 4𝑎2𝐷 𝑚 , 𝛼 = − 3𝑎 2, 𝛽 = 7𝑎2 3 dan 𝛾 = −5𝑎3 2 2 ...………... (7) Kita asumsikan pemecahan Persamaan (7) menggunakan pendekatan semi-diskrit

sehingga solusi Φ𝑛 diberikan sebagai berikut:

Φ𝑛 = 𝐹1 𝜀𝑛𝑙, 𝜀𝑡 𝑒𝑖𝜃𝑛 + 𝑐. 𝑐 +

𝜀1/2 _𝐹

0 𝜀𝑛𝑙, 𝜀𝑡 +

𝐹2𝜀𝑛𝑙,𝜀𝑡𝑒𝑖2𝜃𝑛+𝑐.𝑐+𝑂𝜀 ..(8) dimana 𝜃 ≡ 𝜃𝑛 = 𝑛𝑞𝑙 − 𝜔𝑡 ……….... (9) dengan parameter l, ω dan q=2π/λ dimana

l merupakan jarak antara dua nukleotida

tetangga pada rantai yang sama, q adalah bilangan gelombang soliton DNA, ω adalah frekuensi optik dari getaran pendekatan linear dan c.c adalah istilah

conjugate-compleks dari fungsi F1dan F2.

Untuk kasus semi-diskrit kita mengambil batas 𝑛𝑙 → 𝑧 untuk fungsi 𝐹𝑖 sehingga secara umum menghasilkan pendekatan : 𝐹𝑖 𝜀 𝑛 ± 𝑕 𝑙, ɛ𝑡 → 𝐹𝑖 𝑍, 𝑇 ± 𝜀𝑕𝑙 𝐹𝑍 𝑍, 𝑇 + 1 2𝜀 2_𝑕2_𝑙2 _𝐹 𝑍𝑍 𝑍, 𝑇 ...(10) Dimana variabel kontinu z dan t telah disubtitusi 𝑧 = 𝑍/𝜀, dan 𝑡 = 𝑇/𝜀. Subtitusi Persamaan (8) kedalam Persamaan (6) dan dengan mengumpulkan

exp(i0) didapatkan bentuk hubungan dari

ɛ1/2: 𝐹0= 𝜇 𝐹1 2…………...…... (11) dengan 𝜇 = −2𝛼 1 + 4𝐾 𝑚 𝜔_𝑔2 −1 ...….. (12) Selanjutnya dari hubungan harmonik exp(2i𝜃𝑛) kita dapat mengeluarkan

ɛ0sehingga mengikuti relasi untuk 𝐹2 : 𝐹2= 𝛿 𝐹12 …………...…..…... (13) dengan

𝛿 = 𝑚𝜔𝑔2𝛼

2 𝑘 cos 2𝑞𝑙 −1 −𝐾 cos 2𝑞𝑕𝑙 +1 +𝑚(4𝜔2_−𝜔

𝑔2) (14) Berdasarkan hubungan Persamaan (11) dan (13) kita dapat mengikuti kondisi konsisten yang berasal dari ɛ3/2 dengan aturan exp(i𝜃𝑛):

α(μ² + 2δ²) + 6β(μ + δ) + 6γ = 0 ….... (15) Akhirnya dari hubungan harmonik exp(i𝜃𝑛) kita akan memperoleh persamaan : 𝜀2 𝜕2𝐹1 𝜕𝑇2 − 2𝑖ɛ𝜔 𝜕𝐹₁ 𝜕𝑇 − 𝜔²𝐹1 = 𝑘 𝑚[2𝐹1(cos 𝑞𝑙 − 1) + 2𝑖ɛ𝑙𝐹1𝑍sin 𝑞𝑙 + ɛ 2_𝑙2_𝐹 1𝑍𝑍 cos 𝑞𝑙] − 𝐾 𝑚[2𝐹1(cos 𝑞𝑙𝑕 − 1) + 2𝑖ɛ𝑙𝑕𝐹1𝑍sin 𝑞𝑙𝑕 + ɛ2_𝑙2_𝑕2_𝐹 1𝑍𝑍cos 𝑞𝑙𝑕] − 𝜔𝑔2{𝐹1+ ɛ[2𝛼 𝜇 + 𝛿 + 3𝛽]|𝐹1|²𝐹1+ ɛ² 3𝛽 𝜇2_{+ 2𝜇𝛿 + 2𝛿}2 _{+ 4𝛾 3𝜇 +} 4𝛿 |𝐹1|4𝐹1} ………... (16)

kemudian diperoleh hubungan dispersi sebagai berikut: 𝜔2₌2𝑘 𝑚 1 − cos 𝑞𝑙 + 2𝐾 𝑚 cos 𝑞𝑕𝑙 + 1+𝜔𝑔2 ……….…... (17) kemudian kita menerapkan transformasi koordinat baru 𝑆 = 𝑍 − 𝑉𝑔𝑇, 𝜏 =

𝜀𝑇 dengan Vgmerupakan kecepatan group

dari nukleotida sehingga Persamaan (16) menjadi : 𝑉_𝑔− 𝑙 𝑚𝜔(𝑘 sin 𝑞𝑙 − 𝐾𝑕 sin 𝑞𝑙𝑕) 𝜕𝐹1 𝜕𝑆 = 𝑖𝜔𝑔2 2𝜔[2𝛼 𝜇 + 𝛿 + 3𝛽]|𝐹1|²𝐹1 ….….. (18) untuk orde ɛ, sedangkan untuk orde ɛ² :

1 2𝜔 𝑉𝑔² − 𝑙2 𝑚(𝑘 cos 𝑞𝑙 − 𝐾𝑕 2_{cos 𝑞𝑙𝑕)} 𝜕2𝐹1 𝜕𝑆2 − 𝑖 𝜕 𝐹1 𝜕𝑇 = − 𝜔𝑔2 2𝜔[3𝛽 𝜇 2_{+ 2𝜇𝛿 + 2𝛿}2 ₊ 4𝛾 3𝜇 + 4𝛿 ]|𝐹1|4𝐹1 ……..… (19) Dari hubungan dispersi yang

diberikan oleh Persamaan (17) kita dapat menemukan hubungan kecepatan grup dari nukleotida dengan menetapkan

𝑉𝑔 = 𝑑𝜔/𝑑𝑞 sehingga diberikan :

𝑉𝑔 = 𝑙

𝜔𝑚 𝑘 sin 𝑞𝑙 − 𝐾𝑕 sin 𝑞𝑙𝑕 ... (20) dengan mudah dapat dilihat kecepatan grup pada Persamaan (20) menghilangkan

sisi kanan dari Persamaan (18) sehingga dari Persamaan (15) akan didapatkan:

2α(μ+ δ) + 3β = 0 …………... (21) dengan pemecahan secara simultan untuk kondisi Persamaan (15) dan (20) untuk μ dan δ :

𝜇 = −𝛽 ± 10𝛽²−8𝛼𝛾

2𝛼 ………... (22a)

𝛿 = −2𝛽 ± 10𝛽²−8𝛼𝛾

2𝛼 ………... (22b) dimana α, β, dan γ telah diberikan pada Persamaan (7) sehingga untuk Persamaan (22) mudah dibuktikan selalu real pada

10𝛽² − 8𝛼𝛾 =220 𝑎2

9 > 0.

Dari penjumlahan Persamaan (22) dengan Persamaan (12) dan (14) dapat ditentukan nilai konstanta pegas k dan K dengan memasukan nilai parameter m, a,

D, q, l dan h melalui hubungan berikut :

𝐾 = −1 4𝑚𝜔𝑔 2 _{(1 +}2𝛼 𝜇) ……... (23) 𝑘 =𝑚 𝜔𝑔 2 𝛼 𝛿−3 +4𝐾[𝑐𝑜 𝑠2𝑞𝑙𝑕 −2(cos 𝑞𝑙𝑕 +1)] 4(cos 𝑞𝑙 −1)² ... (24)

sebagai ilustrasi, kita menganggap nilai parameter sebagai berikut16 :

l = 3.4 x 10−10

m, m = 5.1 x 10−25

kg, h = 5,

a = 0.9 x1010_𝑚−1_{, D = 9.6 x 10}−21_{J …. (25)} Akhirnya jelas bahwa Persamaan (19) tidak ada apa-apa tetapi persamaan NLS

Kuintik dapat dituliskan dengan sederhana menjadi : 𝑖𝜕𝐹1 𝜕𝜏 + 𝑃 𝜕²𝐹1 𝜕𝑆 ² + 𝑅 𝐹1 4_𝐹 1= 0 …...… (26) dengan koefisien dispersi dan koefisien

nonlinear : 𝑃 =_2𝜔1 _𝑚𝑙2 𝑘 cos 𝑞𝑙 − 𝐾 𝑕2_{cos 𝑞𝑕𝑙 −} 𝑉𝑔2 ………..…….… (27) 𝑅 = −𝜔𝑔2 2𝜔 3𝛽 𝜇 2_{+ 2𝜇𝛿 + 2𝛿}2 ₊ 4𝛾3𝜇+4𝛿 ………..……... (28) Agar Persamaan (26) dapat diselesaikan maka diberikan persamaan anzats

(tebakan) dari persamaan NLS kuintik

𝐹1 𝑆, 𝜏 = 𝑓 𝑆 − 𝑢𝑒𝜏 exp⁡[𝑖𝜎 𝑆 − 𝑢𝑐𝜏 ] (29) dengan F1 merupakan fungsi dari S dan 𝜏, Sedangkan ζ merupakan frekuensi gelombang soliton DNA berperan sebagai

varibel bebas dan 𝑓 𝑆 − 𝑢𝑒𝜏 merupakan fungsi real.

Masukan Persamaan (29) kedalam Persamaan (26) maka akan didapatkan bagian imajiner dengan hubungan:

𝜎 =𝑢𝑒

2𝑃 ………... (30) Sementara hasil bagian real mengikuti persamaan diferensial biasa :

𝑓′′ − 𝐴𝑓 + 𝐵𝑓5= 0 ………... (31) dimana: 𝐴 = 𝑢𝑒²−2𝑢𝑐𝑢𝑒 4𝑃² , 𝐵 = 𝑅 𝑃 ……….... (32) Dengan memindahkan koordinat (S-𝑢𝑒𝜏) dan mengalikan Persamaan (31) dengan 𝑓′ sebagai integral pertama maka akan didapatkan solusi sederhana:

𝑓 𝑆 − 𝑢𝑒𝜏 = ( 3𝐴

𝐵)

1/4_sech1/2_{[2 𝐴 𝑆 −} 𝑢𝑒𝜏] ... (33) Terakhir dengan menggabungkan Persamaan (8), (29), (30), (32) dan (33) serta mengembalikan Z  ɛnl dapat dituliskan hubungan persamaan kuintik

NLS DNA model PBD semi diskrit sebagai berikut:

𝑦𝑛 𝑡 = 2𝜀1/2Ʌ sech1/2 2ɛ 𝐴 𝑛𝑙 − 𝑉𝑒𝑡 cos 𝛩𝑛𝑙 − 𝛺𝑡 + Ʌɛ1/2 sech1/2 2ɛ 𝐴 𝑛𝑙 − 𝑉𝑒𝑡

𝜇

2+ 𝛿 cos 2 𝛩𝑛𝑙 − 𝛺𝑡 + 𝑂(ɛ) ……….. (34) 5

dengan : Ʌ = 3(𝑢𝑒2− 𝑢𝑒𝑢𝑐) 4𝑃𝑅 1/4 ... (35) 𝑉𝑒 = 𝑉𝑔 + ɛ𝑢𝑒 ... (36) 𝛩 = 𝑞 + ɛ𝑢𝑒 2𝑃 ... (37) 𝛺 = 𝜔 +ɛ𝑢𝑒 2𝑃 (𝑉𝑔+𝜀𝑢𝑐)... (38)

BAB 3

METODE PENELITIAN

3.1 Waktu dan Tempat Penelitian

Penelitian ini dilakukan di Laboratorium Fisika Teori dan Komputasi Departemen Fisika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor mulai bulan Februari 2011 sampai bulan Februari 2012.

3.2 Peralatan

Peralatan yang digunakan adalah alat tulis, PC, laptop, software Matlab versi 2008b, software Microsoft Office 2007

dan beberapa sumber literatur dari jurnal-jurnal ilmiah, buku dan internet.

3.3 Metode Penelitian

3.3.1 Studi Pustaka

Studi pustaka dilakukan untuk memahami dan mempelajari konsep dasar dari persamaan soliton DNA model PBD.

3.3.2 Penguasaan

Software

dan

Persamaan Matematis

Penguasaan software Matlab 2008b

dilakukan agar lebih memahami dasar-dasar pemrograman Matlab. Persamaan matematis sendiri dilakukan untuk mempermudah saat pembuatan algoritma program simulasi soliton DNA model PDB.

3.3.3 Pembuatan dan Pengujian

Program

Pembuatan dan pengujian program dengan bahasa pemrograman Matlab

diperlukan untuk mendapatkan solusi numerik DNA model PBD. Pemecahan solusi numerik sendiri didapatkan melalui simulasi terhadap berbagai macam efek gangguan yang diberikan sehingga akan menggambarkan karakteristik DNA model PBD.

Sintaks program simulasi dibuat dengan bantuan software Matlab 2008b

dan menggunakan metode numerik:

finite-difference dan interpolasi Lagrange.

3.3.3.1 Aplikasi Metode

Finite

Difference

Dalam Program

Teknik-teknik pada Finite Difference

didasarkan pada pendekatan mengganti persamaan Differensial dengan persamaan Finite Difference. Pendekatan

Finite Difference ini dalam bentuk aljabar dan solusinya terkait dengan titik kisi. Skema dari Finite Difference :

Persamaan Differensial  memperkirakan turunan numerik 

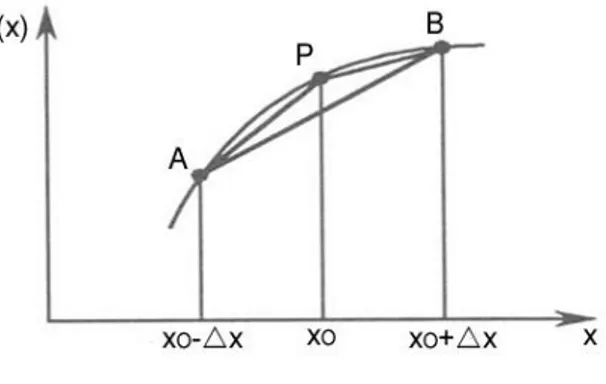
persamaan Finite Difference. Diberikan sebuah fungsi f(x) yang ditunjukkan pada Gambar 3. Kita dapat memperkirakan turunan, kemiringan atau garis singgung P dengan melihat kemiringan busur PB, PA atau AB. Dengan melihat kemiringan busur dapat diperoleh persamaan untuk masing-masing Forward-Difference, Backward-Difference, atau Central-Difference.

Gambar 3. Perkiraan untuk turunan dari fungsi f(x) di P dengan menggunakan Forward, Backward, dan Central Difference. 20

Pendekatan yang digunakan untuk memperoleh persamaan Finite Difference

adalah deret Taylor :

𝑓 𝑥0+ ∆𝑥 = 𝑓 𝑥0 + ∆𝑥 𝑓′ 𝑥0 + 1 2! ∆𝑥 2_𝑓′′ _𝑥 0 + 1 3! ∆𝑥 3_𝑓′′′ _𝑥 0 + 𝑂(∆𝑥)4_{……….……(39)} dan 𝑓 𝑥0− ∆𝑥 = 𝑓 𝑥0 − ∆𝑥 𝑓′ 𝑥0 + 1 2! ∆𝑥 2_𝑓′′ _𝑥 0 − 1 3! ∆𝑥 3_𝑓′′′ _𝑥 0 + 𝑂(∆𝑥)4_{……….(40)} dimana 𝑂(∆𝑥)4 merupakan error yang disebabkan oleh deret yang dipotong. Dengan mengurangi Persamaan (39) dan (40), kita akan memperoleh :

𝑓 𝑥0+ ∆𝑥 − 𝑓 𝑥0− ∆𝑥 =

2∆𝑥 𝑓′ 𝑥0 ...…. (41) yang dapat dituliskan kembali menjadi berikut yang merupakan persamaan

Central-Difference :

𝑓′ _𝑥 0 =

𝑓 𝑥0+∆𝑥 −𝑓 𝑥0−∆𝑥

2∆𝑥 ……… (42) Persamaan Forward-Difference dan

Backward-Difference dapat diperoleh dengan mengatur Persamaan (39) dan (40) sehingga :

Untuk persamaan Forward-Difference

𝑓′ _𝑥 0 =

𝑓 𝑥0+∆𝑥 −𝑓 𝑥0

∆𝑥 …………. (43) dan untuk persamaan Backward-Difference

𝑓′ 𝑥0 =

𝑓 𝑥₀ −𝑓 𝑥0−∆𝑥

∆𝑥 …………. (44) Kita dapat menemukan pemotongan kesalahan untuk kedua persamaan dalam bentuk ∆𝑥. Setelah menambahkan Persamaan (43) dan (44) maka didapatkan

𝑓 𝑥0+ ∆𝑥 + 𝑓 𝑥0− ∆𝑥 = 2𝑓 𝑥0 +

∆𝑥 2_𝑓′′ _𝑥

0 ………... (45) Kemudian akan diperoleh :

𝑓′′ _𝑥 0 =

𝑓 𝑥0+∆𝑥 − 2𝑓 𝑥0 + 𝑓 𝑥0−∆𝑥

∆𝑥 2 …. (46)

Orde yang lebih tinggi untuk pendekatan

Finite Difference dapat diperoleh dengan mengambil banyak batas dalam ekspansi deret Taylor20. Metode ini digunakan untuk membantu dalam menentukan solusi numerik dari persamaan NLS (26) sebelumnya, yang dapat dituliskan kembali 𝑖𝜕𝐹1 𝜕𝜏 + 𝑃 𝜕²𝐹1 𝜕𝑆 ² + 𝑅 𝐹1 4_𝐹 1= 0 .. (26) persamaan tersebut dapat diselesaikan dengan melakukan pendekatan numerik beda hingga untuk masing-masing turunan parsial, sehingga akan diperoleh persamaan 𝑖𝐹 𝑥𝑖,𝑡𝑖+1 − 𝐹 𝑥𝑖,𝑡𝑖+1 ∆𝑡 + 𝑃 𝐹 𝑥_𝑖+1,𝑡_𝑖 −2 𝐹 𝑥𝑖,𝑡𝑖 +𝐹 𝑥𝑖−1,𝑡𝑖 ∆𝑥² + 𝑅 𝐹1 4_𝐹 1= 0 ... (47) Kemudian akan diperoleh persamaan selanjutnya yang akan diubah ke dalam bahasa pemrograman MATLAB. 𝐹 𝑥𝑖, 𝑡𝑖+1 = 2𝑖 ∆𝑡 ∆𝑥2𝑃 𝑓 𝑥𝑖+1, 𝑡𝑖 − 2 𝑓 𝑥𝑖, 𝑡𝑖 + 𝑓 𝑥𝑖−1, 𝑡𝑖 + 𝑅 𝐹1 4𝐹1𝐹 𝑥𝑖, 𝑡𝑖+1 (48) . 7

3.3.3.2

Aplikasi

Interpolasi

Lagrange Dalam Program

Interpolasi Lagrange diterapkan untuk mendapatkan fungsi polinomial P(x) berderajat tertentu yang melewati sejumlah titik data. Misalnya, kita ingin mendapatkan fungsi polinomial berderajat satu yang melewati dua buah titik yaitu (x0, y0) dan (x1, y1). Langkah pertama yang kita lakukan adalah mendefinisikan fungsi berikut

𝐿0 𝑥 = 𝑥 −𝑥1 𝑥0−𝑥1 ... (49a) dan 𝐿1 𝑥 = 𝑥 −𝑥0 𝑥1−𝑥0 ……… (49b)

kemudian definisikan fungsi polinomial sebagai berikut:

𝑃 𝑥 = 𝐿0 𝑥 𝑦0+ 𝐿1(𝑥)𝑦1… (50) Substitusi Persamaan (49a) dan (49b) ke Persamaan (50), maka akan didapat: 𝑃 𝑥 = 𝑥 −𝑥1 𝑥₀−𝑥₁𝑦0+ 𝑥−𝑥_𝑜 𝑥₁−𝑥₀𝑦1 …. (51) dan ketika 𝑥 = 𝑥0 𝑃 𝑥0 = 𝑥0−𝑥1 𝑥0−𝑥1𝑦0+ 𝑥0−𝑥𝑜 𝑥1−𝑥0𝑦1= 𝑦0 (52a)

dan pada saat 𝑥 = 𝑥1

𝑃 𝑥1 = 𝑥1−𝑥1

𝑥0−𝑥1𝑦0+

𝑥1−𝑥𝑜

𝑥1−𝑥0𝑦1= 𝑦1 (52b)

Dari persamaan tersebut dapat disimpulkan bahwa Persamaan (51) benar-benar melewati titik (𝑥𝑜, 𝑦𝑜) dan (𝑥1, 𝑦1).21

Persamaan (50) dinamakan interpolasi Lagrange derajat 1. Nama interpolasi ini diambil dari nama penemunya, yaitu Joseph Louis Lagrange yang berkebangsaan Perancis. Bentuk umum interpolasi Lagrange derajat ≤ n untuk (n+1) titik berbeda adalah:

𝑃 𝑥 = 𝑛𝑖=0𝑎𝑖𝐿𝑖 𝑥 = 𝑎0𝐿0 𝑥 + 𝑎1𝐿1 𝑥 + ⋯ + 𝑎𝑛𝐿𝑛 ... (53) 𝑎𝑖 = 𝑦𝑖 , 𝑖 = 0, 1, 2, … , 𝑛 dan 𝐿𝑖 𝑥 = 𝑥−𝑥𝑗 𝑥_𝑖−𝑥_𝑗 = 𝑛 𝑗 =0 𝑗 ≠𝑖 𝑥−𝑥0 𝑥−𝑥1 … 𝑥−𝑥𝑖−1 𝑥−𝑥𝑖+1 … 𝑥−𝑥𝑛 (𝑥_𝑖−𝑥) 𝑥_𝑖−𝑥_𝑖 … 𝑥𝑖−𝑥𝑖−1 𝑥𝑖−𝑥𝑖+1 …(𝑥𝑖−𝑥𝑛) (54)

Mudah dibuktikan bahwa:

𝐿𝑖 𝑥𝑗 = 1 , 𝑖 = 𝑗_{0 , 𝑖 ≠ 𝑗}

dan polinom interpolasi P(x) melalui setiap titik data.22

Jika terdapat N data yang terdiri dari titik-titik 𝑥0, 𝑥1, 𝑥2, 𝑥3, dan seterusnya,

dan jarak antara titik satu dengan lainnya adalah h, maka Persamaan (53) dapat ditulis untuk tiga titik terdekat (𝑥0, 𝑥1, 𝑥2, 𝑥3): 𝑃 𝑥 = 𝑥 − 𝑥1 (𝑥 − 𝑥2) 𝑥0− 𝑥1 (𝑥0− 𝑥2) 𝑦0+ 𝑥 − 𝑥0 (𝑥 − 𝑥2) 𝑥1− 𝑥0 (𝑥1− 𝑥2) 𝑦1+ 𝑥 − 𝑥0 (𝑥 − 𝑥1) 𝑥2− 𝑥0 (𝑥2− 𝑥1) 𝑦2 = −2𝑕 (−3𝑕) −𝑕 (−2𝑕) 𝑦0+ −𝑕 (−3𝑕) 𝑕(−𝑕) 𝑦1+ −𝑕 (−2𝑕) 2𝑕 (𝑕) 𝑦2 = 3𝑦0− 3𝑦1+ 𝑦2 ... (55) Persamaan-persamaan matematis yang telah diubah kedalam bentuk persamaan finite-difference dan interpolasi Lagrange diubah kedalam bahasa pemrograman MATLAB

[Lampiran A-C]. Program simulasi soliton DNA model PBD ini akan ditampilkan dalam bentuk grafik tiga

N h h h h h x x0 x1 x2 x3 N 8 8

dimensi yang merupakan hasil solusi numerik soliton DNA model PBD ini. Solusi numerik yang diperoleh kemudian dianalisa dengan melihat tingkat kestabilan serta karakteristik dari dinamika DNA model PDB yang telah diberi gangguan serta mengetahui bahwa program yang telah dibuat sudah benar.

BAB 4

HASIL DAN PEMBAHASAN

4.1 Simulasi Perambatan Soliton

pada Kondisi Stabil

Hasil-hasil analisis numerik dari DNA model PBD dengan karakteristik solusi hingga orde-5 akan dibahas pada bagian ini. Parameter numerik yang digunakan adalah parameter yang sudah

ada di literatur sehingga akan difokuskan pada hasil numerik pada tiga keadaan yakni keadaan stabil (tanpa gangguan), dengan gangguan serta interaksi dua buah solusi soliton. Dengan menggunakan metode finite-difference dan interpolasi Lagrange sebagai syarat batas terkait maka akan diperoleh solusi numeriknya dalam bentuk grafik tiga dimensi dan dua dimensi.

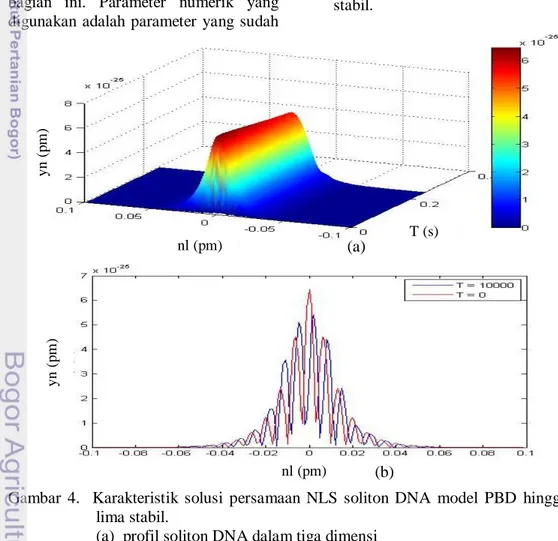
Keadaan pertama yakni pada stabil (tanpa gangguan) dapat terlihat pada Gambar 4 bahwa pada keadaan ini karakteristik stabil sejak waktu awal (T=1) hingga waktu akhirnya. Dari gambar terlihat bahwa solusi yang diperoleh untuk keadaan stabil (tanpa gangguan) yakni bentuk dari profil soliton dengan amplitudo yang cukup stabil.

Gambar 4. Karakteristik solusi persamaan NLS soliton DNA model PBD hingga orde lima stabil.

(a) profil soliton DNA dalam tiga dimensi

(b) plot hubungan yn (pm) terhadap nl (pm), dimana grafik berwarna merah

menunjukkan grafik pada saat Tawal, dan grafik biru menunjukkan grafik

pada saat Takhir

.

9 (a) (b) yn (p m ) nl (pm) nl (pm) T (s) yn (p m )

4.2 Simulasi Perambatan Soliton

Akibat Gangguan pada Amplitudo

Keadaan kedua yakni karakteristik solusi hingga orde-5 yang diberi gangguan. Gangguan yang diberikan yakni terhadap amplitudonya dengan mengalikan persamaan stabil 𝐹1 𝑆, 𝜏

dengan suatu nilai 1 + 𝜀 . Untuk keadaan ini nilai ɛ yang digunakan adalah 0.5. Penjelasan mengenai perubahan yang terjadi saat keadaan stabil dengan keadaan saat diberikan gangguan dapat dilihat pada Gambar 5 dan 6 sebagai berikut ini:

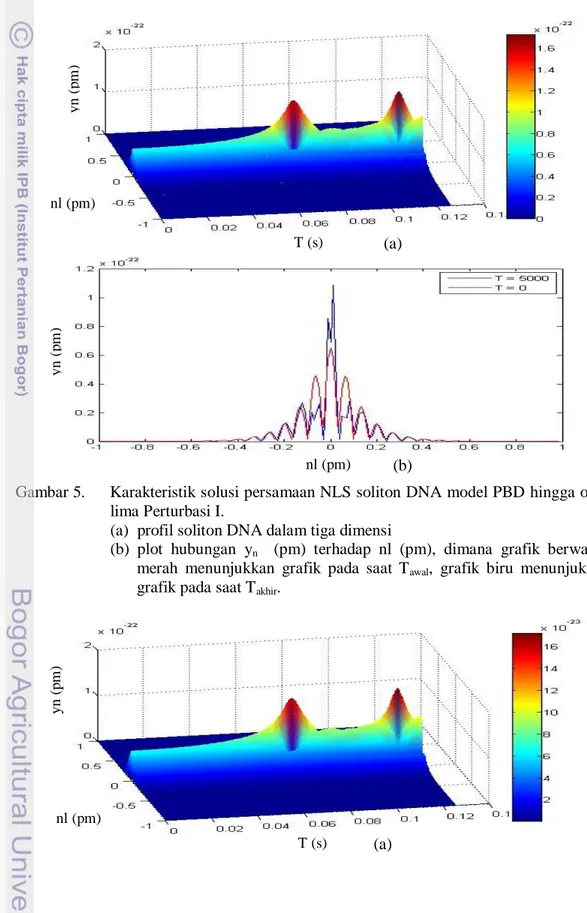
Gambar 5. Karakteristik solusi persamaan NLS soliton DNA model PBD hingga orde lima Perturbasi I.

(a) profil soliton DNA dalam tiga dimensi

(b) plot hubungan yn (pm) terhadap nl (pm), dimana grafik berwarna

merah menunjukkan grafik pada saat Tawal, grafik biru menunjukkan

grafik pada saat Takhir.

(a) (a) 10 (b) nl (pm) T (s) nl (pm) yn (p m ) nl (pm) T (s) yn (p m ) yn (p m )

Gambar 6. Karakteristik solusi persamaan NLS soliton DNA model PBD hingga orde lima Perturbasi II

(a) profil soliton DNA dalam tiga dimensi

(b) plot hubungan yn (pm) terhadap nl (pm), dimana grafik berwarna merah

menunjukkan grafik pada saat Tawal, dan grafik biru menunjukkan

grafik pada saat Takhir

Dari kedua gambar diatas terlihat perbedaan antara solusi stabil (tanpa gangguan) dengan solusi yang diberi gangguan. Pada soliton DNA yang diberi gangguan terbentuk undulasi. Pada saat undulasi terjadi penyempitan yang diiringi dengan kenaikan amplitudonya. Gambar 5 dan 6 menunjukkan bahwa amplitudo untuk solusi gangguan lebih tinggi dibandingan dengan solusi stabil sehingga menunjukkan bahwa gangguan yang diberikan pada anzatz mempengaruhi amplitudo dari soliton. Perubahan profil pada soliton itu sendiri juga terjadi, hal ini terlihat dengan perubahan amplitudo yang terjadi serta soliton yang mengalami dispersi lebih besar dari keadaan stabilnya. Hal ini dapat berarti gangguan yang diberikan juga mempengaruhi hubungan dispersi pada persamaan Hamiltoniannya.

Pada kasus ini terdapat dua keadaan yakni solusi perturbasi I dengan nilai

1 + 𝜀 yang dikalikan hanya pada satu parameter sedangkan pada solusi perturbasi II terdapat dua parameter yang dikalikan dengan 1 + 𝜀 . Dari Gambar 5 dan 6 dapat terlihat bahwa undulasi pada solusi II tampak lebih lebar daripada solusi I namun nilai amplitudo undulasi pada solusi II lebih kecil dari solusi I. Undulasi pada keadaan solusi perturbasi

ini mengakibatkan pengurangan jumlah nukleotida dalam proses denaturasi. Dalam hal ini, nukleotida pada solusi II berkurang lebih sedikit jika dibandingan dengan jumlah nukleotida pada solusi I.

Hasil numerik yang dapat dijelaskan dari solusi perturbasi I dan II yakni terjadi peristiwa undulasi pada keduanya. Peristiwa undulasi terjadi ketika soliton mengalami penyempitan karena efek nonlinier mengalami ketidakstabilan yang lebih dominan daripada efek dispersinya. Pada peristiwa ini terjadi pengurangan jumlah eksitasi nukleotida yang terlibat dalam proses denaturasi dimana nukleotida yang awalnya meregang menjadi terhalangi akibat efek nonlinier ini.

4.3 Simulasi Interaksi Dua Buah

Soliton

Bagian ini membahas mengenai simulasi dari interaksi dua buah soliton dimana persamaan yang digunakan adalah 𝐹1 𝑆, 𝜏 = ( 3𝐴 𝐵) 1/4_sech1/2 _{2 𝐴 𝑆 −} 𝑢𝑒𝜏 exp⁡[𝑖𝜃] ………... (56) (b) 11 yn (p m ) nl (pm)

Dengan membuat variasi pada nilai beda fase (θ) yakni degan nilai θ = 0, θ = 𝜋

2,

dan θ = π) didapatkan hasil simulasinya yang ditunjukkan pada Gambar 7 berikut

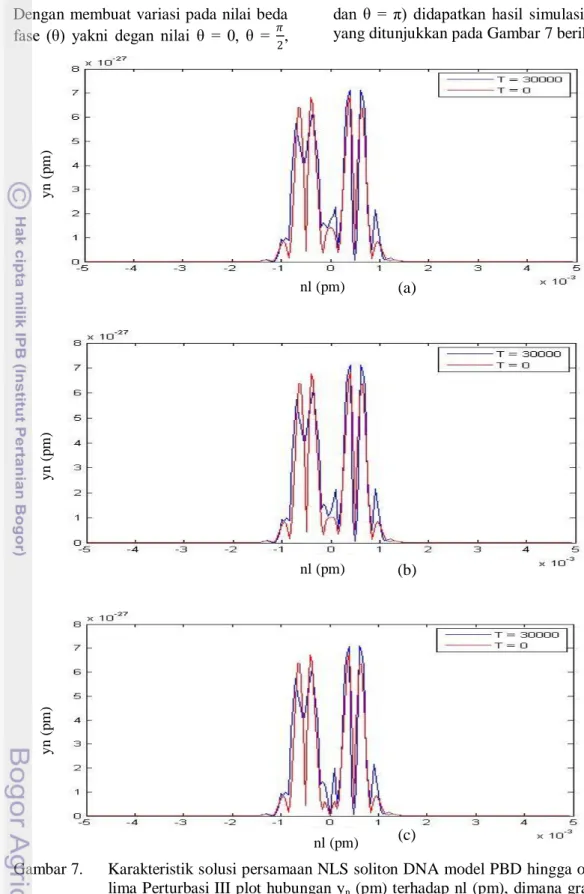
Gambar 7. Karakteristik solusi persamaan NLS soliton DNA model PBD hingga orde lima Perturbasi III plot hubungan yn (pm) terhadap nl (pm), dimana grafik

berwarna merah menunjukkan grafik pada saat Tawal, dan grafik biru

menunjukkan grafik pada saat Takhir

(a) profil soliton DNA dalam tiga dimensi untuk θ = 0 (b) profil soliton DNA dalam tiga dimensi untuk θ = π/2 (c) profil soliton DNA dalam tiga dimensi untuk θ = π

12 (a) (b) (c) yn (p m ) nl (pm) yn (p m ) nl (pm) yn (p m ) nl (pm)

Untuk kondisi x= 0.0005 pm dan θ = 0, artinya, jarak antara soliton satu dengan yang lain adalah 0.0005 pm dengan beda fase 0. Pada gangguan ini tampak pada gambar 7, kedua soliton yang awalnya terpisah dengan jarak 0.0005 menjalar dengan bentuk dan kecepatan yang sama, kemudian kedua soliton semakin mendekat namun masih dalam kondisi yang sama (tetap stabil).

Untuk kondisi interaksi dua soliton pada θ = 𝜋

2 dan θ = π terlihat bahwa hasil yang diperoleh sama seperti pasa kondisi θ = 0 yakni pada awalnya terbentuk dua buah soliton yang terpisah dengan jarak 0.0005 pm dengan amplitudo dan kecepatan yang sama namun sampai akhir kondisi ini tetap sama dan tidak ada perubahan yang signifikan. Hal ini berarti beda fase tidak memberikan pengaruh yang cukup signifikan terhadap kondisi selanjutnya. Terlihat pula bahwa soliton mengalami undulasi, kenaikan dan penurunan amplitudo, serta dispersi yang semakin meningkat.

BAB 5

SIMPULAN

Pada penelitian sebelumnya15, telah diperoleh solusi analitik untuk persamaan NLS kubik DNA model PBD. Model PBD merupakan model yang menggambarkan denaturasi DNA. Penelitian ini dilakukan untuk mencari solusi numerik persamaan NLS kubik DNA model PBD dengan menggunakan metode finite-difference dengan interpolasi Lagrange. Hasil yang diperoleh dari solusi numerik yang dilakukan adalah bagaimana profil dari dinamika DNA saat terjadi proses denaturasi dimana DNA mengalami dinamika yang cukup stabil dari proses awal hingga akhirnya. Keadaan DNA model PBD yang ditinjau pada penelitian ini yakni keadaan stabil (tanpa gangguan), diberi gangguan serta interaksi dua buah solusi soliton. Dengan

menggunakan metode finite-difference

dan interpolasi Lagrange sebagai syarat batas terkait maka akan diperoleh solusi numeriknya dalam bentuk grafik tiga dimensi dan dua dimensi.

Pada keadaan stabil (tanpa gangguan) terlihat bentuk dari profil soliton dengan amplitudo yang cukup stabil serta gambaran umum proses replikasi (denaturasi) DNA yang bergerak dominan ke arah un. Keadaan

kedua yakni karakteristik solusi hingga orde lima yang diberi gangguan. Gangguan yang diberikan yakni terhadap amplitudonya dengan mengalikan persamaan stabil 𝐹1 𝑆, 𝜏 dengan suatu nilai 1 + 𝜀 . Kondisi ini menunjukkan bahwa amplitudo untuk solusi gangguan lebih tinggi dibandingan dengan solusi stabil sehingga menunjukkan bahwa gangguan yang diberikan pada anzatz mempengaruhi amplitudo dari soliton. Perubahan profil pada soliton itu sendiri juga terjadi, yakni pada perubahan amplitudo serta dispersi lebih besar dari keadaan stabilnya. Saat diberi gangguan terlihat pula di gambar bahwa terdapat undulasi. Peristiwa undulasi terjadi ketika soliton mengalami penyempitan karena efek nonlinier mengalami ketidakstabilan yang lebih dominan daripada efek dispersinya. Pada peristiwa ini terjadi pengurangan jumlah eksitasi nukleotida yang terlibat dalam proses denaturasi dimana nukleotida yang awalnya meregang menjadi terhalangi akibat efek nonlinier ini.

Pada interaksi dua soliton dengan jarak x telah ditinjau kasus tiga kondisi fase awal yaitu dengan membuat variasi pada beda fase diantara kedua soliton, yaitu pada saat θ = 0, 𝜋

2 , dan π. Interaksi dua soliton pada jarak x dapat diartikan sebagai proses denaturasinya, dimana nukleotida terlokalisasi dalam dua ruang. Untuk kondisi x= 0.0005 pm dan θ = 0, artinya, jarak antara soliton satu dengan yang lain adalah 0.0005 pm dengan beda fase 0. Pada gangguan ini terlihat bahwa kedua soliton yang awalnya terpisah dengan jarak 0.0005 menjalar dengan

bentuk dan kecepatan yang sama, kemudian kedua soliton semakin mendekat namun masih dalam kondisi yang sama (tetap stabil). Begitupula untuk kondisi interaksi dua soliton pada θ = 𝜋

2 dan θ = π yakni pada awalnya terbentuk dua buah soliton yang terpisah dengan jarak 0.0005 pm dengan amplitudo dan kecepatan yang sama namun sampai akhir kondisi ini tetap sama dan tidak ada perubahan yang signifikan. Hal ini berarti beda fase tidak memberikan pengaruh yang cukup signifikan terhadap kondisi selanjutnya. Terlihat pula bahwa soliton mengalami undulasi, kenaikan dan penurunan amplitudo, serta dispersi yang semakin meningkat.

SARAN

Untuk pengembangan selanjutnya, ada beberapa hal yang perlu dilakukan. Metode numerik yang digunakan sebaiknya yang mempunyai tingkat akurasi yang tinggi dan mengekpansi potensial morse hingga orde yang lebih tinggi agar perhitungan solusi dapat lebih cepat dan hasilnya akurat (mendekati keadaan sebenarnya). Selain itu penelitian ini dapat dikembangkan dengan mengamati DNA model lainnya atau dapat pula meninjau untuk gerak

longitudinal atau gerak torsional untuk DNA model PBD.

DAFTAR PUSTAKA

1. Yakushevich, L.V. (1998).

Nonlinear Physics of DNA. Wiley Series in Nonlinear Science, John Wiley, Chichester.

2. Christiansen, P. L., Lomdahl, P.S. & Muto, V. (1990). On a Toda lattice model with a transversal degree of freedom. Nonlinearity 4, 477-501. 3. Muto, V., Scott A.C., Christiansen

P.L. (1989). Microwave and thermal

generation of solitons in DNA. J. de Phys. 50 (C3), 217-222.

4. Ichikawa, Y. H., Konno K, Wadati M. (1981). Nonlinear transverse oscillation of elastic beams under tension. J. Phys. Soc. 50, 1799. 5. Peyrard, M. and Bishop, A.R.

(1989). Statistical mechanics of a nonlinear model for DNA denaturation. Phys. Rev. Lett. 62, 2755-2758.

6. E. Fermi, J. R. Pasta and S. Ulam, Los Alamos Report LA-UR-1940 (1955); reprinted in Collected Papers of Enrico Fermi, edited by E. Segr¶e, University of Chicago, Chicago (1965).

7. A. C. Scott. (1999). Nonlinear Science. Oxford University, Oxford. 8. Englander, S.W., Kalenbach, N.R.,

Heeger, A.J., Krumhansl, J.A. and Litwin, S. (1980). Nature of the open state in long polynucleotide double helices: possibility of soliton excitations. Proc. Natl. Acad. Sci. USA 77, 7222-7226.

9. T. Dauxois, M. Peyrard, and A. R. Bishop. (1993). Entropy-driven DNA denaturation. Phys. Rev. E 47, R44.

10. Dauxois, T. (1991). Dynamics of breathers modes in a nonlinear “helocoidal” model of DNA. Phys. Lett. A-159, 390-395.

11. Dauxois, T. and Peyrard, M. (1991). Dynamics of Breather Modes in a Nonlinear Helicoidal Model of DNA. Lecture Notes in Physics 393, Dijon, p.79.

12. Zdravković, S. and Satarić, M.V. (2001). „Impact of viscosity on DNA dynamics‟, Phys. Scripta 64, 612-615.

13. Satarić, M.V. and Tuszyński, J.A. (2002). Impact of regulatory proteins on the nonlinear dynamics of DNA.

The American Physics Society. 65, 1-10.

15

14. Zdravković, S., Tuszyński, J.A. and Satarić, M.V. (2004). Peyrard-Bishop-Dauxois model of DNA dynamics and impact of viscosity. J. Comput. Theor. Nanosci.1, 171-179. 15. Hermanudin, D. (2011). Efek osilasi

anharmonik pada soliton Deoxyribo Nucleic Acid Peyrard-Bishop-Dauxois [Skripsi]. Bogor: Departemen Fisika-FMIPA, IPB. 16. Alatas, Husin dan Hermanudin,

Dede. (2011). Quintic DNA-Breather in Peyrard-Bishop-Dauxois Model with Fifth Order Approximation Morse Potential [Jurnal]. Bogor: Departemen Fisika-FMIPA, IPB. 17. Remoissenet, M. (1986).

Low-amplitude breather and envelope solitons in quasi-one dimentional physical models. Phys. Rev. B-33, 2386-2392.

18. Zdravković, S. and Satarić, M.V. (2001). Impact of viscosity on DNA dynamics. Phys. Scripta 64, 612-615. 19. Anonim. BAB IV. REPLIKASI DNA. Edublogs. Februari 2010. Web. 28

Februari 2011.

<http://biomol.edublogs.org/files/201

0/02/BAB-IV-REPLIKASI-DNA.pdf>.

20. A. Thom an C. J. Apelt. (1961).

Field Computations in Engineering and Physics. London: D. Van Nostrand.

21. Supriyanto. (2007). Komputasi untuk Sains dan Teknik. Jakarta: Universitas Indonesia.

22. Munir, R. (2006). Metode numerik. Bandung: Informatika.

17

Lampiran A

Program Simulasi Perambatan Soliton pada Kondisi Stabil

clear all

clc

% ## DEFINISI NILAI PARAMETER ## %Parameter Awal M = 10000; N = 200; dx = 0.001; dt = 2.5000e-005; r = dt/dx^2; t0 = -N/2*dt; x0 = -N/2*dx; %Parameter Masukan k=5.370; K=1.146; l=3.4e-13; m=5.1e-23; h=5; a=0.9e-9 D = 9.6e-21; Ue=10^5; Uc=0; e1=0.0001; lamda=10*l; q=(2*pi)/lamda; ql=0.85*pi; tau=0; phi=0.001; psi=0.002; epsilon=0.5;

% ## DEFINISI NILAI KOEFISIEN ##

Wg = 2*a*sqrt(D/m); alfa =(-3*a)/sqrt(2); beta = (7*(a^2))/3;

gamma =(-5*(a^3))/(2*sqrt(2));

% ## DEFINISI HUBUNGAN DISPERSI ##

W = sqrt((Wg^2) + (2/m)*(k*(1-cos(q*l)) + (K*(cos(q*l*h)+1))));

% ## DEFINISI HUB. F1 dgn F0 dan F2

miu = -2*alfa/(1+(4*K)/(m*Wg.^2));

delta = (m*(Wg.^2) * alfa)/((m*((4*W^2)-(Wg^2))) + (2*((k*(cos(2*q*l)-1)/m) - (K*(cos(2*h*q*l)+1)))));

% ## DEFINISI KECEPATAN GRUP

18

% ## DEFINISI KOEF. DISPERSI (P) DAN KOEF.NON LINIER (R)

P = (1/(2*W))*((l^2/m)*((k*cos(q*l))- (K*(h^2)*(cos(q*l*h))))-Vg^2); R = (-Wg^2/(2*W))*((3*beta*(miu^2+(2*miu*delta)+(2*(delta^2))))+(4*gamma *((3*miu)+(4*delta)))); sigma=10^10; A=sigma/P; B=R; Ag=((3*(Ue^2-(Ue*Uc)))/(4*P*R))^0.25; Ve=Vg+(e1*Ue); Q=q*((e1*Ue)/(2*P)); ohm=W+(((e1*Ue)/(2*P))*(Vg+(e1*Uc))); O=0; % ## RUNNING PROGRAM ## F=zeros(N,M); yn=zeros(N,M); for i=1:N x(i,1)=x0+(i-1)*dx; F(i,1)=((3/P)^0.25*psi)*((sech(2*x(i,1)/phi))^0.5); end for j=1:M for i=3:N-1 if i==3 F(i-1,j)=3*F(i,j)-3*F(i+1,j)+F(i+3,j); end if i==N-1 F(i+1,j)=3*F(i,j)-3*F(i-1,j)+F(i-3,j); end if j==1 F(i,j+1)=1i*((r*phi^2*(F(i+1,j)-2*(F(i,j))+F(i-1,j)))+ (psi^6*dt*((conj(F(i,j))^2)*(F(i,j)^3))))+F(i,j); else F(i,j+1)=2*1i*((r*phi^2*(F(i+1,j)-2*(F(i,j))+F(i-1,j)))+(psi^6*dt*((conj(F(i,j))^2)*(F(i,j)^3))))+F(i,j-1); end t(j)=(j-1)*dt; yn(i,j)= (2*(e1^0.5)*(psi*F(i,j)/(sqrt(R/sigma)))*((cos((sigma*tau)+theta(i ,j)))+ (((e1^0.5)*(psi*F(i,j)/(sqrt(R/sigma))))*((miu/2)+(delta*cos(2*((s igma*tau)+theta(i,j)))))))); end j end surf(t,x,abs(yn(:,1:M))) view(0,90); colorbar shading interp

19 xlabel ('T (s)'); ylabel ('nl (pm)'); zlabel ('yn (pm)'); figure plot(x,abs(yn(:,1))); figure plot(x,abs(yn(:,M)));

20

Lampiran B

Program Simulasi Perambatan Soliton Akibat Gangguan pada Amplitudo

clear all

clc

% ## DEFINISI NILAI PARAMETER ## %Parameter Awal M = 10000; N = 200; dx = 0.001; dt = 2.5000e-005; r = dt/dx^2; t0 = -N/2*dt; x0 = -N/2*dx; %Parameter Masukan k=5.370; K=1.146; l=3.4e-13; m=5.1e-23; h=5; a=0.9e-9 D = 9.6e-21; Ue=10^5; Uc=0; e1=0.0001; lamda=10*l; q=(2*pi)/lamda; ql=0.85*pi; tau=0; phi=0.1; psi=0.2; epsilon=0.25;

% ## DEFINISI NILAI KOEFISIEN ##

Wg = 2*a*sqrt(D/m); alfa =(-3*a)/sqrt(2); beta = (7*(a^2))/3;

gamma =(-5*(a^3))/(2*sqrt(2));

% ## DEFINISI HUBUNGAN DISPERSI ##

W = sqrt((Wg^2) + (2/m)*(k*(1-cos(q*l)) + (K*(cos(q*l*h)+1))));

% ## DEFINISI HUB. F1 dgn F0 dan F2

miu = -2*alfa/(1+(4*K)/(m*Wg.^2));

delta = (m*(Wg.^2) * alfa)/((m*((4*W^2)-(Wg^2))) + (2*((k*(cos(2*q*l)-1)/m) - (K*(cos(2*h*q*l)+1)))));

% ## DEFINISI KECEPATAN GRUP

21

% ## DEFINISI KOEF. DISPERSI (P) DAN KOEF.NON LINIER (R)

P = (1/(2*W))*((l^2/m)*((k*cos(q*l))- (K*(h^2)*(cos(q*l*h))))-Vg^2); R = (-Wg^2/(2*W))*((3*beta*(miu^2+(2*miu*delta)+(2*(delta^2))))+(4*gamma *((3*miu)+(4*delta)))); sigma=10^10; A=sigma/P; B=R; Ag=((3*(Ue^2-(Ue*Uc)))/(4*P*R))^0.25; Ve=Vg+(e1*Ue); Q=q*((e1*Ue)/(2*P)); ohm=W+(((e1*Ue)/(2*P))*(Vg+(e1*Uc))); O=0; % ## RUNNING PROGRAM ## F=zeros(N,M); yn=zeros(N,M); for i=1:N x(i,1)=x0+(i-1)*dx; % Solusi Perturbasi I F(i,1)=(((3/P)^0.25)*psi)*((sech(2*x(i,1)/phi))^0.025)* (1+epsilon); % Solusi Perturbasi II %F(i,1)=(((3/P)^0.25)*psi)*((sech(2*(1+epsilon)*x(i,1)/phi))^0 .025)*(1+epsilon); end for j=1:M for i=3:N-1 if i==3 F(i-1,j)=3*F(i,j)-3*F(i+1,j)+F(i+3,j); end if i==N-1 F(i+1,j)=3*F(i,j)-3*F(i-1,j)+F(i-3,j); end if j==1 F(i,j+1)=1i*((r*phi^2*(F(i+1,j)-2*(F(i,j))+F(i-1,j)))+ (psi^6*dt*((conj(F(i,j))^2)*(F(i,j)^3))))+F(i,j); else F(i,j+1)=2*1i*((r*phi^2*(F(i+1,j)-2*(F(i,j))+F(i-1,j)))+(psi^6*dt*((conj(F(i,j))^2)*(F(i,j)^3))))+F(i,j-1); end t(j)=(j-1)*dt; yn(i,j)= (2*(e1^0.5)*(psi*F(i,j)/(sqrt(R/sigma)))*((cos((sigma*tau)+theta(i ,j)))+ (((e1^0.5)*(psi*F(i,j)/(sqrt(R/sigma))))*((miu/2)+(delta*cos(2*((s igma*tau)+theta(i,j)))))))); end j end

22 surf(t,x,abs(yn(:,1:M))) view(0,90); colorbar shading interp xlabel ('T (s)'); ylabel ('nl (pm)'); zlabel ('yn (pm)'); figure plot(x,abs(yn(:,1))); figure plot(x,abs(yn(:,M)));

23

Lampiran C

Program Simulasi Interaksi Dua Soliton

clear all

clc

% ## DEFINISI NILAI PARAMETER ## %Parameter Awal M = 10000; N = 200; dx = 0.001; dt = 2.5000e-005; r = dt/dx^2; t0 = -N/2*dt; x0 = -N/2*dx; %Parameter Masukan k=5.370; K=1.146; l=3.4e-13; m=5.1e-23; h=5; a=0.9e-9 D = 9.6e-21; Ue=10^5; Uc=0; e1=0.0001; lamda=10*l; q=(2*pi)/lamda; ql=0.85*pi; tau=0; phi=0.000015; psi=0.000025; epsilon=1;

% ## DEFINISI NILAI KOEFISIEN ##

Wg = 2*a*sqrt(D/m); alfa =(-3*a)/sqrt(2); beta = (7*(a^2))/3;

gamma =(-5*(a^3))/(2*sqrt(2));

% ## DEFINISI HUBUNGAN DISPERSI ##

W = sqrt((Wg^2) + (2/m)*(k*(1-cos(q*l)) + (K*(cos(q*l*h)+1))));

% ## DEFINISI HUB. F1 dgn F0 dan F2

miu = -2*alfa/(1+(4*K)/(m*Wg.^2));

delta = (m*(Wg.^2) * alfa)/((m*((4*W^2)-(Wg^2))) + (2*((k*(cos(2*q*l)-1)/m) - (K*(cos(2*h*q*l)+1)))));

% ## DEFINISI KECEPATAN GRUP

24

% ## DEFINISI KOEF. DISPERSI (P) DAN KOEF.NON LINIER (R)

P = (1/(2*W))*((l^2/m)*((k*cos(q*l))- (K*(h^2)*(cos(q*l*h))))-Vg^2); R = (-Wg^2/(2*W))*((3*beta*(miu^2+(2*miu*delta)+(2*(delta^2))))+(4*gamma *((3*miu)+(4*delta)))); sigma=10^10; A=sigma/P; B=R; Ag=((3*(Ue^2-(Ue*Uc)))/(4*P*R))^0.25; Ve=Vg+(e1*Ue); Q=q*((e1*Ue)/(2*P)); ohm=W+(((e1*Ue)/(2*P))*(Vg+(e1*Uc))); O=0; % ## RUNNING PROGRAM ## F=zeros(N,M); yn=zeros(N,M); for i=1:N x(i,1)=x0+(i-1)*dx;

% Interaksi 2 soliton dengan θ=0

F(i,1)=(((3/P)^0.25)*psi)*((sech((x(i,1)+0.055)/phi))+ (sech((x(i,1)-0.015)/phi))*(exp(1i*(0))));

% Interaksi 2 soliton dengan θ=π

%F(i,1)=(((3/P)^0.25)*psi)*((sech((x(i,1)+0.055)/phi))+

(sech((x(i,1)-0.015)/phi))*(exp(1i*(pi)))); % Interaksi 2 soliton dengan θ=π/2

%F(i,1)=(((3/P)^0.25)*psi)*((sech((x(i,1)+0.055)/phi))+ (sech((x(i,1)-0.015)/phi))*(exp(1i*(pi/2)))); end for j=1:M for i=3:N-1 if i==3 F(i-1,j)=3*F(i,j)-3*F(i+1,j)+F(i+3,j); end if i==N-1 F(i+1,j)=3*F(i,j)-3*F(i-1,j)+F(i-3,j); end if j==1 F(i,j+1)=1i*((r*phi^2*(F(i+1,j)-2*(F(i,j))+F(i-1,j)))+ (psi^6*dt*((conj(F(i,j))^2)*(F(i,j)^3))))+F(i,j); else F(i,j+1)=2*1i*((r*phi^2*(F(i+1,j)-2*(F(i,j))+F(i-1,j)))+(psi^6*dt*((conj(F(i,j))^2)*(F(i,j)^3))))+F(i,j-1); end t(j)=(j-1)*dt; yn(i,j)= (2*(e1^0.5)*(psi*F(i,j)/(sqrt(R/sigma)))*((cos((sigma*tau)+theta(i ,j)))+ (((e1^0.5)*(psi*F(i,j)/(sqrt(R/sigma))))*((miu/2)+(delta*cos(2*((s igma*tau)+theta(i,j)))))))); end j

25 end surf(t,x,abs(yn(:,1:M))) view(0,90); colorbar shading interp xlabel ('T (s)'); ylabel ('nl (pm)'); zlabel ('yn (pm)'); figure plot(x,abs(yn(:,1))); figure plot(x,abs(yn(:,M)));