Pemodelan Transmisi Video Pada Jaringan Wireless Local Area Network

BAB 2

TINJAUAN PUSTAKA

2.1. Pemodelan

Tantangan dalam jaringan telekomunikasi adalah bagaimana untuk merancang sistem dengan biaya yang rendah dengan tetap memenuhi kualitas yang diharapkan. Pada jaringan telekomunikasi, aliran dan antrian trafik adalah subyek penelitian yang penting dalam penilaian kinerja jaringan. Pendekatan model dan simulasi pada aliran dan antrian trafik ini menjadi metodologi yang utama dalam penelitian perancangan jaringan dan pengkajian kinerja jaringan.

Dalam menganalisis jaringan yang menghindarkan biaya besar melalui pembangunan langsung, diperlukan sebuah model untuk mengambarkan jaringan yang ada. Model yang ada secara umum terdiri dari elemen seperti yang ditunjukkan pada Gambar 2.1.

Gambar 2.1 Elemen model sistem jaringan [6]

Model direpresentasikan dengan rumusan matematika diturunkan dengan menggunakan pengetahuan menyeluruh tentang trafik. Model yang diperoleh kemudian dibandingkan dengan data yang diukur dari eksperimen. Jika terjadi ketidakcocokan, model dapat dimodifikasi dan proses iteratif diulang lagi.

Model yang baik harus memiliki persyaratan sebagai berikut [6]:

1. Model dapat mengambarkan perilaku komponen jaringan.

2. Model harus dapat diproses, dibuktkan dan parameter-parameter model dapat diperoleh dari pengambilan atau pengamatan data.

3. Model harus dapat diaplikasikan dalam pengukuran.

Model memerlukan metode statistik. Kedatangan permintaan digambarkan sebagai proses stokastik, interval waktu antar permintaan dapat digambarkan dengan distribusi peluang.

Trafik (Permintaan)

Struktur (hardware)

Strategi (Software) Pengguna

Stokastik

Alternatif dari sebuah model matematika adalah sebuah model simulasi atau model fisik. Kesulitan dari model simulasi adalah karena model simulasi tidak menggambarkan secara umum, setiap kasus harus disimulasikan. Tesis ini memilih model matematis untuk dibandingkan dengan hasil eksperimen.

2.2. Pemodelan Trafik Video

Menurut Richardson (2002), pengkodean frame video standar menggunakan tiga jenis frame: frame I, frame P, dan frame B. Frame I (Intra-coded) dikodekan secara independen dan diterjemahkan dengan sendirinya. Frame P (predictive-coded) dikodekan menggunakan prediksi hasil urutan video dari frame I sebelumnya atau frame P. Frame B (Bi-directionally predictive coded) dikodekan menggunakan prediksi dari frame I atau P sebelumnya.

Format MPEG-1 mengharuskan setiap frame berukuran sama dengan mengatur tingkat kompresi yang dilakukan pada tiap frame. Selain itu, dilakukan juga kompresi pada setiap perbedaan yang terjadi antara dua frame. Metode ini dikenal dengan interframe compression. Struktur IBP dari format MPEG-1 dan MPEG-2

tidak memungkinkan sebuah video untuk diproses sebelum GOP secara lengkap diterima. Ini menjadikan format MPEG-1 dan MPEG-2 tidak cocok digunakan untuk

streaming di Internet. Proses transfer data di Internet yang menggunakan paket-paket, memungkinkan paket yang dikirim untuk diterima secara tidak berurutan. Keterlambatan penerimaan salah satu paket yang berisi frame IBP dapat menjadikan

MPEG-4 kemudian hadir untuk mengatasi masalah di atas. Secara umum, urutan seluruh video dapat didekomposisi menjadi unit-unit lebih kecil yang kemudian dikodekan bersama-sama, yang disebut GOP (Group of Pictures). GOP

adalah gabungan dari Frame I, Frame P, dan Frame B. Gambar 2.2 menunjukkan contoh sebuah GOP. Pola GOP ditandai oleh dua parameter, G (N, M): jarak frame I-I (N), dan jarak frame (M) I-I-P. Misalnya G (12, 3): group video ini terdiri dari satu jenis frame I, tiga jenis frame P, dan delapan frame B. Kedua frame yang menandai awal GOP berikutnya. Selain itu, tanda panah menunjukkan bahwa frame B dan frame P diterjemahkan tergantung pada proses frame I atau P sebelumnya.

Gambar 2.2 Contoh mpeg group of picture (n=12 dan m=3) [26]

Tesis ini menggunakan jenis frame I dan P dengan urutan GOP IPP. Hal ini dilakukan agar proses pengkodean dan pendekodean berlangsung lebih cepat.

2.2.1. Model trafik decodable frame rate

Q= N

− + − ... (2.1)

Dengan Ndec adalah penjumlahan dari Ndec-1 dan Ndec-P, yaitu jumlah frame I

dan frame P yang dapat didekodekan.

Sebuah frame dianggap decodable ketika semua data dalam setiap frame diterima. Namun frame hanya dianggap decodable jika, dan hanya jika semua frame di mana itu tergantung pada juga decodable. Dalam kasus terburuk, seluruh GOP

dapat dianggap tidak decodable karena codec video frame I yang salah, karena semua lainnya frame dalam GOP tergantung langsung atau tidak langsung pada frame I.

Tabel 2.1 menunjukkan parameter Frame Rate decodable agar lebih mudah dalam perhitungan.

Tabel 2.1 Adopsi notasi

Notasi Keterangan rumus

Ntotal –I

N total –P

Jumlah total frame tiap tipe

N dec –I

N dec –p

Junlah frame decodable tiap tipe

Ndec Total Jumlah frame decodable aliran video

NGop Total Jumlah GOP aliran video

CI , CP Rata-rata Jumlah paket transport data tiap tipe

P Packet lose rate

1. Jumlah frame decodable yang diharapkan (Ndec- I)

Dalam GOP, frame I decodable jika semua paket milik frame I dikirimkan dan diterima dalam keadaan utuh atau tidak terjadi kehilangan data. Oleh karena itu, probabilitas bahwa frame I decodable sesuai dengan persamaan (2.2)

S(I) = − ... (2.2)

Sehingga total decodable benar yang dharapkan dari frame I untuk seluruh video adalah sesuai dengan persamaan (2.3)

Ndec-I = − ∗ _� ... (2.3)

2. Jumlah decodable dari frame P (Ndec-P)

Dalam GOP, frame P adalah decodable hanya jika frame I sebelumnya atau frame P adalah decodable dan semua paket yang termasuk ke dalam frame P yang decodable. Dalam GOP, ada NP P frame, dan probabilitas frame P yang decodable

adalah sebagai berikut:

S(P1) = − ∗ − p = − +Cp ... (2.4)

S(P2) = − ∗ − p∗ − p = − + Cp ... (2.5)

S(PNp) = − ∗ − ∗ p= − +Np+Cp ... (2.6)

Dengan demikian jumlah proses atau hasil benar yang diharapkan dari decodable frame P untuk seluruh video adalah sesuai dengan persamaan (2.7)

Agar dapat menganalisis model decodable frame rate, nilai faktor loss rate

pada saat video ditransmisikan harus diketahui. Penentuan nilai faktor loss rate

diperoleh dari hasil eksperimen berdasarkan pada perubahan keadaan dari urutan paket ketika video yang ditransmisikan.

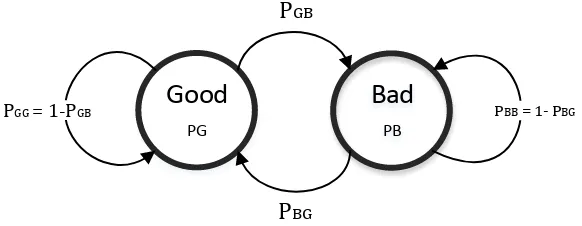
Gambar 2.3 mengilustrasikan perubahan keadaan ketika video ditransmisikan. Bila terjadi perubahan keadaan dari urutan paket atau tidak sesuai dengan urutan

paket yang dikirimkan maka dikatakan “Bad” atau disebut probabilitas . Perubahan

urutan paket menjadi Bad diakibatkan oleh hilangnya paket ketika dikirimkan. Bila urutan paket yang diterima sesuai dengan yang dikirimkan maka dikatakan “Good” atau disebut probabilitas _�. Perubahan dari keadaan Good menjadi Bad disebut dengan _� . Sedangkan perubahan dari keadaan Bad menjadi Good disebut dengan _�. Probabilitas steady state dari masing – masing keadaan Good dan Bad

dinyatakan oleh persamaan (2.8) dan (2.9) [8].

Good

PG

Bad

PB PGB

PGG = 1-PGB PBB = 1- PBG

PBG

Gambar 2.3 Diagram transisi keadaan

state dari masing – masing keadaan Good dan Bad dinyatakan oleh persamaan (2.8) dan (2.9) [8].

�� = ��

��+ �� ... (2.8)

� = ��

��+ �� ... (2.9)

Nilai rata – rata Packet loss rate dapat diperoleh dengan menggunakan persamaan (2.10):

= ��� + � ... (2.10)

adalah packet loss rate dari lapisan transport. Packet loss rate pada lapisan medium (Pdecodable) diperoleh sebagai hasil pangkat packet loss rate pada

lapisan transport dengan jumlah retransmisi maksimum yang diizinkan pada lapisan medium (N). Sehingga diperoleh:

= ( ) ... (2.11)

Namun, pada jaringan wireless tidak ada retransmisi pada broadcasting dan

multicasting, sehingga packet loss dari lapisan network sama dengan packet loss dari lapisan aplikasi. Packet loss yang dirasakan pada lapisan aplikasi diberikan oleh persamaan (2.12):

= ∑ − − _{= −}

Karena media transmisi video pada percobaan ini menggunakan jaringan 802.11, maka nilai packet loss rate dipengaruhi oleh probabilitas dari keberhasilan

transmisi pada jaringan 802.11 yang diberikan oleh persamaan (2.13):

= � −�_{− −�}− ... (2.13)

Dengan adalah jumlah user, dan � adalah stationary probability dalam percobaan ini merupakan nilai probabilitas packet loss untuk model Decodable

Frame Rate � = ).

Nilai packet loss rate merupakan probabilitas dari kegagalan transmisi dari jaringan 802.11 = yang diberikan oleh persamaan (2.14):

= − ... (2.14)

2.2.2. Model trafik two state markov

Berbeda dengan penelitian yang dilakukan oleh Zhao et al dengan judul

“MPEG-4 Video Transmission over Wireless Networks A Link Level Performance

Study” yang memodelkan lapisan aplikasi dengan mengirimkan frame video dengan sekaligus, model two-sta te markov mendekati situasi nyata di mana frame video di lapisan aplikasi terfragmentasi dan dikirim ke dalam beberapa paket, seperti yang ditunjukkan pada Gambar 2.4(a) [5]. Frame I terpecah menjadi x paket dan frame P

terpecah menjadi y paket. Diasumsikan terdapat dua keadaan, keadaan user

state markov chain seperti pada Gambar 2.4(b). Probabilitas mengirimkan paket frame I dan frame P dilambangkan masing-masing sebagai k dan h. Selain keadaan mengirimkan kedua jenis paket, lapisan aplikasi juga memiliki keadaan idle, dimana tidak ada paket yang dikirim. Namun karena paket yang dikirim oleh lapisan aplikasi disimpan dalam lapisan buffer medium access (MAC) sebelum proses transmisi terjadi, maka keadaan idle diabaikan.

Sebagai akibatnya, probabilitas k adalah persentase pengiriman paket I dalam satu GOP dan probabilitas h adalah

(a). Video generation and transmission (b). Video transmission model

Gambar 2.4 Aplication layer model [5]

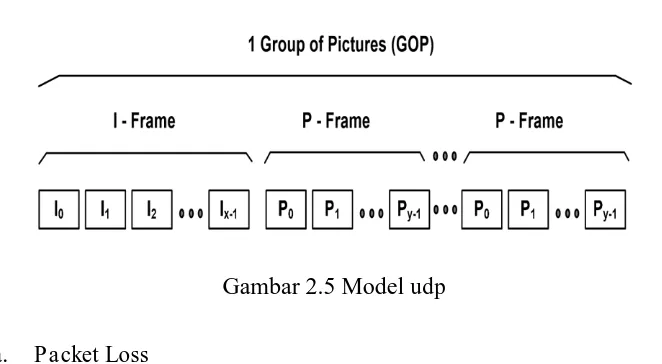
Persentase pengiriman paket P dalam satu GOP. Probabilitas mengirimkan paket berurutan dilambangkan sebagai (1 - p) dan (1 - r). Dengan asumsi protokol yang digunakan adalah UDP, dari x paket frame I, hanya 1 paket di ikuti oleh paket

P, demikian juga setelah pengiriman paket y, hanya 1 paket diikuti oleh paket I. Oleh

karenanya, p =1/x dan r =1/y. Probabilitas steady state dari model two-state markov

ditunjukkan pada Gambar 2.5, dengan persamaan sebagai berikut:

�� = ₊ ... (2.15)

� = ₊ ... (2.16)

Probabilitas kesalahan ( ) dapat dihitung sesuai dengan kenyataan bahwa kesalahan terjadi ketika sebuah penerima menerima paket yang bukan paket I atau paket P, sehingga nila ( ) dinyatakan dengan persamaan (2.17)

= − − ℎ ∗ ��+ � ... (2.17)

Gambar 2.5 Model udp

a. Packet Loss

Pada jaringan 802.11, user mendeteksi saluran dan mengirimkan paket jika kanal dalam keadaan idle untuk jangka waktu Distributed Inter Frame Space (DIFS). Jika kanal dalam keadaan sibuk, user menunda transmisi pada rentang back off

Probabilitas proses transmisi yang mengalami tabrakan dapat diekspresikan sesuai dengan persamaan (2.18):

= − − � − _{... (2.18)}

Sementara Probabilitas bahwa user berhasil mengirimkan paket dinyatakan dengan persamaan (2.19):

= � −�_{− −�}− ... (2.19)

Jika laju kedatangan rata-rata setiap user adalah λ, maka probabilitas user

mengirimkan paket dapat dinyatakan sebagai π = λ/n, dimana n adalah jumlah user.

Sehingga Persamaan 2.19 dapat ditulis kembali sesuai dengan persamaan (2.20):

= _{− − /}− / − ... (2.20)

Jika kita diasumsikan setiap packet error dianggap sebagai packet loss, maka total paket loss dapat diproyeksikan dengan menggunakan persamaan (2.17) dan (2.19), probabilitas kesalahan (PE) menjadi:

= ( − . � − ℎ. ) ∗ ��+ � ... (2.21)

Packet loss dapat dihitung dengan persamaan (2.22):

� = ⁄ . . + � . � + − ⁄ . . ... (2.22)

b. Packet Delay

Dengan mempertimbangkan dua komponen utama delay: Delay di buffer dan

delay akses medium.Waktu tunggu dalam buffer user dimodelkan dengan

menggunakan sistem antrian M/G/1. Model ini juga digunakan dalam [10]. Waktu tunggu dalam buffer simpul user diberikan oleh:

= ⁄_{− ⁄} ... (2.23)

Delay akses medium didefinisikan sebagai berikut:

= − ₋+ + ₋ − − � + + − ... (2.22)

Dimana Pcoll adalah probabilitas terjadinya tabrakan, Ptr adalah probabilitas

setidaknya satu simpul melakukan transmisi, Psuc adalah probabilitas keberhasilan, Ts

adalah lama waktu bila trasmisi berhasil, Tc adalah lama waktu bila proses tabrakan

terjadi dan α adalah slot waktu.

2.3. Pemodelan Jaringan 802.11 dengan Model Bianchi

tabrakan dan proses transmisi yang sukses, berpindah dari satu tahapan ketahapan selanjutnya.

Model ini mengadopsi skala waktu diskrit dan integer. Pada skala waktu t dan t+1 cocok untuk memulai 2 buah slot waktu yang berurutan. Setiap pengurangan

station akan menghitung waktu mundur pada saat dimulai waktu slot. Pengurangan waktu mundur akan berhenti ketika saluran dalam keadaan sibuk dengan interval waktu t dan t+1, dan akan lebih dari waktu slot untuk 802.11, karena sudah termasuk waktu pengiriman paket dan proses tabrakan.

Jika P adalah probabilitas didalam waktu slot, setidaknya salah satu N-1

station tersisa untuk mentransmisikan juga, maka P ditulis [11]:

Ptr = 1 – ( − � − ... (2.25)

Probabilitas saluran akses � dari node fungsi waktu mundur pada level m dan nilai aggapan minimum dari jendela Wmin serta probabilitas tabrakan P

Π= ∑₌ �, = ₋, = _{− +} − ₋ ... (2.26)

Π=

+ + ∑ ₌− ... (2.27)

Sehingga nilai saturasi throughput dapat dihitung

Ƭ = [ _[ ]

]

Ƭ = �

Dimana:

Ptr: Probability of at least one transmission in slot time

a. Ps:Probability of successful transmission during a random time slot

b. L:Average packet payload size

c. Tid:Duration of the idle period

d. tACK:ACK transmission time

e. tH:Header transmission time

f. tL:Payload transmission time

Ps = � −� −

− −� ... (2.29)

Ts = th + tL + SIFS+σ + tACK + DIFS + σ ... (2.30)

Tc = th + tL + DIFS + σ ... (2.31)

2.4. Parameter Kinerja Trafik Jaringan

Pengujian sistem bertujuan untuk mengetahui kemampuan jaringan WLAN sebagai media video streaming serta untuk mengetahui kualitas video yang diterima pada sisi client. Pengujian dilakukan menggunakan editor netbean untuk piranti lunak

Parameter kinerja yang digunakan dalam mengukur kinerja jaringan WLAN adalah decodable frame rate. Decodable frame rate adalah perbandingan antara jumlah frame decodable dengan jumlah frame yang dikirimkan oleh sumber video, atau dinyatakan dengan rumus:

=

� �� �+ � �� � ... (2.32)

2.5. Analisis Statistik

Analisis Korelasi adalah metode statistika yang digunakan untuk menentukan kuatnya atau derajat hubungan linier antara dua variabel atau lebih. Semakin nyata hubungan linear, maka semakin kuat atau tinggi derajat hubungan garis lurus antara kedua variabel atau lebih. Ukuran untuk derajat hubungan garis lurus ini dinamakan koefisien korelasi. Untuk menunjukkan besarnya keeratan hubungan antara dua variabel acak yang masing-masing memiliki skala pengukuran minimal interval dan berdistribusi bivariat, digunakan koefisien korelasi yang dirumuskan sebagai berikut [12]:

=_{√[ ∑ − ∑}.∑ −∑ .∑_{][ ∑y − ∑ ]} ... (2.33)

Dimana:

a. Koefisien korelasi yang dirumuskan seperti itu disebut koefisien korelasi Pearson atau koefisien korelasi product moment.

c. Tanda + menunjukkan pasangan X dan Y dengan arah yang sama,

sedangkan tanda − menunjukkan pasangan X dan Y dengan arah yang

berlawanan.

d. yang besarnya semakin mendekati 1 menunjukkan hubungan X dan Y cenderung sangat erat. Jika mendekati 0 hubungan X dan Y cenderung kurang kuat.

e. = 0 menunjukkan tidak terdapat hubungan antara X dan Y

Analisis Regresi adalah metode statistika yang digunakan untuk menentukan kemungkinan bentuk hubungan antara dua atau lebih variabel bebas (X) dengan variabel terikat (Y). Tujuan pokok penentuan metode ini adalah untuk meramalkan atau memperkirakan nilai dari satu variabel (Y) dalam hubungannya dengan variabel yang lain (X).

Analisis regresi sederhana adalah proses mengestimasi sebuah fungsi hubungan antara variable dependen (Y) dengan variabel independen (X). Dalam suatu persamaan regresi besarnya nilai variable dependen adalah tergantung pada nilai variable lainnya. Model persamaan regresi linear sederhana:

Y = α + βX + ε (model populasi) ... (2.34)

Y = a + bX + e (model sampel) ... (2.35)

pengaruh X terhadap Y, secara grafik menunjukkan slope (kemiringan garis regresi). Jika data hasil observasi terhadap sampel acak berukuran n telah tersedia, maka untuk mendapatkan persamaan regresi Y = a + bX, perlu dihitung a dan b dengan metode kuadrat kekeliruan terkecil (least square error methods) [12].

=∑ .∑ −∑ .∑_{.∑ − ∑} = .∑ .−∑ .∑

.∑ − ∑ ... (2.36)

Proses analisis statistik meliputi indeks determinasi dan pengujian regresi:

a. Indeks Determinasi (R2₎

Dalam analisis regresi, koefisien korelasi yang dihitung tidak untuk diartikan sebagai ukuran keeratan hubungan variabel bebas (X) dan variabel tidak bebas (Y), sebab dalam analisis regresi asumsi normal bivariat tidak terpenuhi. Untuk itu, dalam analisis regresi agar koefisien korelasi yang diperoleh dapat diartikan maka dihitung

indeks determinasinya, yaitu hasil kuadrat dari koefisien korelasi:

R

2_xy



(

r

_xy

)

2

b. Pengujian Hipotesis Koefisien Regresi Linear Sederhana

Selanjutnya dilakukan pengujian hipotesis secara statistis terhadap koefisien regresi yang diperoleh tersebut. Ada dua jenis pengujian yaitu uji t dan uji F.

Uji t digunakan untuk menguji koefisien regesi secara individual atau untuk menguji ada tidaknya pengaruh variabel bebas (X) terhadap variabel tidak bebas (Y). Uji F digunakan untuk menguji koefisien regresi secara simultan serentak atau untuk menguji keberartian model regresi yang digunakan [13].

H1: ρXY≠ 0 (Terdapat hubungan antara X dan Y)

Statistik uji: = √ − √ −

Kriteria uji: Tolak H0 jika thit≥ ttab atau thit≤ ttab atau terima H0 jika ttab< thit