Group knowledge is not always distributed (neither is it
q
always implicit)
1 *
Wiebe van der Hoek , Bernd van Linder , John-Jules Meyer
Utrecht University, Department of Computer Science, P.O. Box 80.089, 3508 TB Utrecht, The Netherlands
Abstract
In this paper we study the notion of group knowledge in a modal epistemic context. Starting with the standard definition of this kind of knowledge on Kripke models, we show that this definition gives rise to some quite counter-intuitive behaviour. Firstly, using a strong notion of derivability, we show that group knowledge in a state can always, but trivially, be derived from each of the agents’ individual knowledge. In that sense, group knowledge is not really implicit, but rather explicit knowledge of the group. Thus, a weaker notion of derivability seems to be more adequate. However, adopting this more ‘local view’, we argue that group knowledge need not be
distributed over (the members of) the group: we give an example in which (the traditional concept
of) group knowledge is stronger than what can be derived from the individual agents’ knowledge. We then propose two additional properties on Kripke models: we show that together they are sufficient to guarantee ‘distributivity’, while, when leaving one out, one may construct models that do not fulfil this principle. 1999 Elsevier Science B.V. All rights reserved.
Keywords: Group knowledge; Kripke models
1. Introduction
In the field of AI and computer science, the modal system S5 is a well-accepted and by now familiar logic to model the logic of knowledge (cf. Halpern and Moses, 1985; Meyer and van der Hoek, 1995b). Since the discovery of S5’s suitability for epistemic logic, many extensions and adaptations of this logic have been proposed. In this paper we look into one of these extensions, namely a system for knowledge of m agents
*Corresponding author. Tel.:131-30-2531454; fax:131-30-2513791. E-mail address: [email protected] (W. van der Hoek)
q
This is an improved and extended version of van der Hoek et al. (1995). 1
Currently at ABN-AMRO Bank, Amsterdam.
containing a modality for‘group knowledge’. Intuitively, this ‘group knowledge’ (let us write G for it) is not the knowledge of each of the agents in the group, but the knowledge that would result if the agents could somehow ‘combine’ their knowledge. The intuition behind this notion is best illustrated by an example. Let the formula w denote the proposition that P±NP. Assume that three computer scientists are working
on a proof of this proposition. Suppose thatw follows from three lemmas:c1,c2andc3. Assume that scientist 1 has provedc1and therefore knowsc1. Analogously, for agents 2 and 3 regarding c2 and c 53 (c1∧c2)→w, respectively. If these computer scientists would be able to contact each other at a conference, thereby combining their knowledge, they would be able to conclude w. This example also illustrates the relevance of
communication with respect to this kind of group knowledge: the scientists should
somehow transfer their knowledge through communication in order to make the underlying implicit knowledge explicit.
In this paper, we try to make the underlying notions that together constitute G explicit: What does it mean for a group of, say, m agents to combine their knowledge? We start by giving and explaining a clear semantical definition of group knowledge, as given by Halpern and Moses (1985). In order to make some of our points, we distinguish between a global and a local notion of (deductive and semantic) conse-quence. Then we argue that the defined notion of group knowledge may show some counter-intuitive behaviour. For instance, we show in Section 3 that, at the global level, group knowledge does not add deductive power to the system: group knowledge is not always a true refinement of individual knowledge. Then, in Section 4, we try to formalize what it means to combine the knowledge of the members of a group. We give one principle (called the principle of distributivity: it says that G that is derived from a set of premises can always be derived from a conjunction of m formulae, each known by one of the agents) that is trivially fulfilled in our setup. We also study a special case of this principle (called the principle of full communication), and show that this property is not fulfilled when using standard definitions in standard Kripke models. In Section 5 we impose two additional properties on Kripke models: we show that they are sufficient to guarantee full communication; they are also necessary in the sense that one can construct models that do not obey one of the additional properties and that at the same time do not verify the principle under consideration. In Section 6 we round off. Proofs of theorems are provided in Appendix A.
2. Knowledge and group knowledge
G-knowledge may be seen as the G-knowledge being obtained if the agents were fully able to communicate with each other. Actually, instead of being able to communicate with each
other, one may also adopt the idea that the G-knowledge is just the knowledge of one
distinct agent, to whom all the agents communicate their knowledge [this agent was called the ‘wise man’ by Halpern and Moses (1985); a system to model such communication was proposed by van Linder et al. (1994)]. We will refer to this reading of G (i.e., in a ‘send and receiving context’) as ‘a receiving agent’s knowledge’. We start by defining the language that we use.
Definition 2.1. Let P be a non-empty set of propositional variables, and m[N be given. The language + is the smallest superset of P such that:
ifw,c[+ then¬w,(w∧c),Kw,Gw[+ (i#m).
i
The familiar connectives ∨, →,↔ are introduced by definitional abbreviation in the
def def
usual way;¡5p∨ ¬p for some p[P and '5¬¡.
The intended meaning of Kiw is ‘agent i knows w’ and Gw means ‘w is group knowledge of the m agents.’ We assume the following ‘standard’ [the system below was originally introduced by Halpern and Moses (1985)] inference system S5 (G) for them
multi-agent S5 logic extended with the operator G.
Definition 2.2. The logic S5 (G) has the following axioms:m
A1 any axiomatization for propositional logic
A2 (Kiw∧K (iw→c))→Kic
A3 Kiw→w
A4 Kiw→K Ki iw
A5 ¬Kiw→Ki¬Kiw
A6 Kiw→Gw
A7 (Gw∧G(w→c))→Gc
A8 Gw→w
A9 Gw→GGw
A10 ¬Gw→G¬Gw
On top of that, we have the following derivation rules:
R1 £w,£w→c⇒£c
R2 £w⇒£Kw, for all i#m.
i
the group is also known to the receiving agent. Note how the axiom A6 and the rule R2 also induce the principle of necessitation on the operator G. The other axioms express that the receiver has the same reasoning and introspection properties as the other agents of the group. In the group knowledge reading, A6 declares what the members of the group are; the other axioms enforce this group knowledge to obey the same properties that are ascribed to the individual agents.
The derivability relation£ , or£for short, is defined in the usual way. That is, a
S5 (G )m
formulaw is said to be provable, denoted£w, ifw is an instance of one of the axioms or if w follows from provable formulae by one of the inference rules R1 and R2.
To relate this notion of group knowledge to the motivating example of Section 1, in which the group is able to derive a conclusion w from the lemmasc1,c2 andc3, each known by one of the agents, let us consider the following derivation rule which is to be understood to hold for allw,ci, i#m:
R3£(c ∧? ? ?∧c )→w⇒£(K c ∧? ? ?∧K c )→Gw.
1 m 1 1 m m
Theorem 2.3. Let the logic S5 (G)[R3 /A6] be as S5 (G), with axiom A6 replaced bym m
the rule R3. Then, the two systems are equally strong: for all w,
S5 (G)£w⇔S5 (G)[R3 /A6]£w.
m m
From the proof of this theorem, as given by Meyer and van der Hoek (1995b) (p. 263), one can even derive that this equivalence is obtained for any multi-modal logic that is normal with respect to G, i.e. for any logic X containing the axioms A7 and the rules R1 and R29:£w⇒£Gw we have an equivalence between X1A6 and X1R3.
We now define two variants of provability from premises: one in which necessitation on premises is allowed and one in which it is not.
Definition 2.4. Let c be some formula, and let F be a set of formulae. Using the relation£of provability within the system S5 (G) we define the following two relations
m
From a modal logic point of view, one establishes:
2 1
In other words, the deduction theorem holds for£ , not for£ . Note that the relation
1 2 1
£ is more liberal than £ in the sense that £ allows for necessitation on premises,
2 1
where£ only applies necessitation to S5 (G)-theorems. Our definition of£ deviates
m
from standard terminology of premises: in classical logic, the formulas w1, . . . ,wn are called premises in a derivation of c if (w1∧ . . .∧wn)→c is derivable. Thus, premises
1
in our sense in the context of £ play the role of logical axioms [cf. Kaneko and Nagashima (1997), where a related discussion on ‘logical’ versus ‘nonlogical axioms’ leads to a number of (in-)definability results in epistemic logic]. Also, one can prove the following connection between the two notions of derivability from premises.
*
Theorem 2.5. Let hK , . . . ,K1 mj be the set of sequences of epistemic operators. Then
2 1
*
hXwuX[hK , . . . ,K1 mj ,w[Fj£ c⇔F£ c.
From Meyer and van der Hoek (1995a) (Lemma A1), for the one agent case without group knowledge (i.e., S5 ), one even obtains1
2 1
hKwuw[Fj£ c⇔F£ c.
2
From an epistemic point of view, when using£ , we have to view a set of premisesF as a set of additional given (i.e., true) formulae [non-logical axioms, in the terminology
1
of Kaneko and Nagashima (1997)], whereas in the case of £ , F is a set of known formulae (‘logical axioms’). For instance, when describing a game and the knowledge that is involved (see also Bacharach et al., 1997), it would be convenient to express the
1
mutual knowledge of the players as premises under the £ notion of derivability.
Definition 2.6. A Kripke model } is a tuple }5kS,p,R , . . . ,R l where
1 m
1. S is a non-empty set of states,
2. p: S3P→h0,1j is a valuation to propositional variables per state,
3. for all 1#i#m, R 7S3S is an (accessibility) relation. For any s[S and i#m,
i
with R (s) we mean ht[SuR stj.
i i
We refer to the class of Kripke models as_ or, when m is understood, as_. The class
m
of Kripke models in which the accessibility relations R are equivalence relations, isi
denoted by 65 (or by 65).
m
Definition 2.7. The binary relation*between a formulaw and a pair},s consisting of a model } and a state s in } is inductively defined by:
defined by: },s*F⇔},s*w for all w[F. In this paper, a model } is always an 65-model.
The intuition behind the truth definition of G is as follows: if t is a world which is not an epistemic alternative for agent i, then, if the agents would be able to communicate, all the agents would eliminate the state t. This is justified by the idea that the actual, or real state, is always an epistemic alternative for each agent (in65-models, R is reflexive; or,
i
speaking in terms of the corresponding axiom, knowledge is veridical ). Using the wise-man metaphor: this man does not consider any state which has already been abandoned by one of the agents.
A formulaw is defined to be valid in a model}iff},s*w for all s[S; w is valid with respect to 65 iff }*w for all }[65. The formula w is satisfiable in } iff },s*w for some s[S; w is satisfiable with respect to 65 iff it is satisfiable in some }[65. A set of formulae F is valid with respect to 65 iff each formula w[F is valid with respect to65. For a class of models#we define two relations between a set
1 2
of formulae and a formula: F* w iff ;}[#(}*F⇒}*w) and F* w iff
# #
;}[#;s(},s*F⇒},s*w). If the class symbol # is left out, we always mean 65 .
m
Theorem 2.8. (Soundness and Completeness.) Letwbe some formula, and letFbe a set of formulae. The following soundness and completeness results hold.
1. £w ⇔*w,
2 2
2. F£ w ⇔F* w,
1 1
3. F£ w ⇔F* w.
3. Group knowledge is not always implicit
Within the system S5 (G), all agents are considered ‘equal’: if we make no additionalm
assumptions, they all know the same.
Lemma 3.1. For all i, j#m, we have: £Kiw ⇔ £Kjw.
Remark 3.2. One should be sensitive for the comment that Lemma 3.1 is a meta
statement about the system S5 (G), and as such it should be distinguished from them
claim that one should be able to claim within the system S5 (G) that all agents know them
same: i.e., we do not have (nor wish to have) that£Kiw↔Kjw, if i±j. Considering £w
as ‘w is derivable from an empty set of premises’ (cf. our remarks following Definition 2.4), Lemma 3.1 expresses ‘ When no contingent fact is known beforehand, all agents
know the same’. In fact, one easily can prove that ‘ When no contingent facts are given,
Interestingly, we are able to prove a property like that in Lemma 3.1 even when the G operator is involved.
Theorem 3.3. Let X and Y range over hK ,K , . . . ,K ,G1 2 m j. Then: £Xw ⇔£Yw.
Theorem 3.3 has, for both the reading as group knowledge as well as that of a receiving agent for G, some remarkable consequences. It implies that the knowledge in the group is nothing else than the knowledge of any particular agent. We can also phrase this in terms of implicit knowledge. First, let us agree upon what it means to say that group knowledge is implicit:
a
Definition 3.4. Given a notion of derivability £ (where we will typically take
a
a[h1,2j), we say that group knowledge is strongly implicit (under£ ) if there is a
a a
formula w for which we have£ Gw, but for all i#m Z Kiw. It is said to be weakly
a a a
implicit under£ if there is a set of premisesF for whichF£ Gw, butFZ Kiw, for all
i#m.
Thus, Theorem 3.3 tells us that, using£of S5 (G), group knowledge is not strongly
m
implicit! Although counter-intuitive at first, Theorem 3.3 also invites one to reconsider 1
the meaning of£w as opposed to a statementF£ w. When interpreting the case where F 55as ‘initially’ or, more loosely, ‘nothing has happened yet’ (in particular, when no communication of contingent facts has yet taken place), it is perhaps not too strange that all agents know the same and thus that all group knowledge is explicitly present in the knowledge of all agents.
With regard to derivability from premises, we have to distinguish the two kinds of derivation introduced in Definition 2.4.
Lemma 3.5. Let w be a formula,F a set of formulae and i some agent.
1 1
• F£ Gw⇔F£ Kiw,
2 2
• F£ Kiw⇒F£ Gw,
2 2
• F£ Gw£F£ Kiw.
4. Group knowledge is not always distributed
In the previous section we established that group knowledge is in some cases not implicit, but explicit. In particular, for provability per se and for derivation from premises with necessitation on premises, group knowledge is rather uninteresting. The only case where group knowledge could be an interesting notion on its own is that of derivability from premises without necessitation on premises. For this case, we want to formalize the notion of distributed knowledge. Although intuitively clear, a formaliza-tion of distributed knowledge brings a number of hidden parameters to the surface. Informally, we say that the notion of group knowledge is distributed if the group knowledge (apprehended as a set of formulae) equals the set of formulae that can be derived from the union of the knowledge of the agents that together constitute the group.
The following quote is taken from a recent dissertation (Borghuis, 1994):
Implicit knowledge is of interest in connection with information dialogues: if we
think of the dialogue participants as agents with information states represented by epistemic formulae, then implicit knowledge precisely defines the propositions the
participants could conclude to during an information dialogue . . .
Borghuis (1994) means with ‘implicit knowledge’ what we call ‘group knowledge’. We will see in this section that using standard epistemic logic one cannot guarantee that group knowledge is precisely that what can be concluded during an information dialogue.
To do so, we will first formalize the notion of distributivity using the notions of derivability used so far.
4.1. A deductive approach
To formalise what we mean with distributed group knowledge, let us have a second look at derivation rule R3 first. It says that, if w follows from the conjunction of w1, . . . ,wm, then, if we also have K1w1∧? ? ?∧Kmwm, we are allowed to conclude thatw is known by the group, i.e. then also Gw. Now, we are inclined to call group knowledge
distributed if the converse also holds, that is, if everything that is known by the group
does indeed follow from the knowledge of the group’s individuals. Let us, for convenience, say that group knowledge is perfect (over the individuals) if both directions hold. What we now have to do is be precise about the phrase ‘follows from’ and about the role that can be played by premises here. Let us summarize our first approximation to the crucial notions in a semi-formal definition:
Definition 4.1 (first approximation).
1. We say that G represents complete group knowledge if we have that for everyw and w1, . . . ,wm such that (K1w∧? ? ?∧Kmwm) can be derived, and also the implication (w1∧? ? ?∧wm)→w, then we also have that Gw can be derived.
Gw is derivable we can findw1, . . . ,wm such that: (1) together they implyw and (2) the conjunction (K1w∧? ? ?∧Kmw) is derivable.
3. If both items above hold we call the group knowledge represented by G perfect group
knowledge.
Observation 4.2. In S5 (G), using£, G-knowledge is both complete group knowledge
m
and distributed.
The proof of Observation 4.2 shows that it holds for a trivial reason. For distributivity, if £Gw, by Theorem 3.3, we also have£K w, . . . ,£K w, and then distributivity follows
So, to obtain distributivity in a non-trivial way, we should allow for premises. However, we know from the previous section that we then have at least two notions of derivability to consider. Unfortunately, as the following observation summarizes, even when allowing premises, we trivially obtain distributivity.
1 Observation 4.3. If the notion of derivability used in Definition 4.1 is to be F£ c or
2
F£ c, we again obtain distributivity of G-knowledge in a trivial way.
Let us try to understand the source of Observation 4.3. For both w5 1,2, if
w w w
From the two Observations 4.2 and 4.3 above, we conclude that, in order to have an interesting notion of distributed group knowledge, we have to allow for a subtle use of premises and of notions of derivability. Let us therefore introduce the following notation. Let k[h0,1j be a characteristic function in the sense that, for every set F, k ? F 55ifk 50, andFelse. Now, we want to distinguish three types of derivability: one to obtain the (K1w1∧? ? ?∧Kmwm) formulas (the ‘knowledge conclusions’), one to obtain (w1∧? ? ?∧wm)→w (the ‘logical conclusions’) and one to obtain formulas of type Gw (the ‘group knowledge conclusions’). For each type of derivability, we may
1 2
choose to allow for premises or not, and we also choose between £ and£ .
Definition 4.1. Let k,k,k [h0,1j and let K, L and G be variables over h1,2j. For
k l g
each tuple L 5kkk,K,kl,L,kg,Gl we now define the following notions: we say that L-derivable group knowledge is complete if, for all sets of premises F and every formula w:
G K L
k ? F£ Gw⇐'w, . . . ,w : [k ? F£ (K w ∧? ? ?∧K w )&k ? F£ (w ∧? ? ?
g 1 m k 1 1 m m l 1
we say thatL-derivable group knowledge is distributed, if for every set of premisesF, and every w:
G K L
k ? F£ Gw⇒'w, . . . ,w : [k ? F£ (K w ∧? ? ?∧K w )&k ? F£ (w ∧? ? ?
g 1 m k 1 1 m m l 1
∧wm)→w]. (2)
If both (1) and (2) hold for a tuple Land everyF andw, we say that the knowledge represented by G is perfect with respect to L.
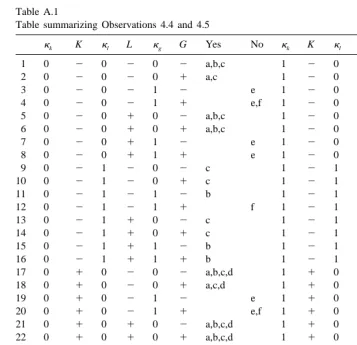
Thus, we have specialized our first attempt to define perfect group knowledge, in notions depending on the choices inL. There are, in principle, 64 such notions, but the following observations give a systematic account of them: the reader may also consult the summarising Table A.1 in Appendix A.
Observation 4.4. For 49 possibilities for L 5kkk,K,kl,L,kg,Glone can show that group knowledge is indeed distributed—but the proofs show that this is only established in a ‘trivial’ manner.
In the observation above, ‘trivial’ refers to the fact distributivity is proven in a way similar to that in Observations 4.2 and 4.3 – for an exhaustive proof, the reader is referred to Appendix A. Those cases are summarized in Table A.1, with an a, b, c or d in the ‘yes’ column.
Observation 4.5. For the 13 of the remaining 15 possibilities for L 5kkk,K,kl,L,kg,Gl one can show that group knowledge is not distributed; they are summarized in Table A.1 with the items e, f and g in the ‘no’ column.
The remaining interesting cases are L 5k1,2,0,L,k1,1l which we take as a starting point for the next section. Note that, in fact, this is only one case, since if k 5l 0, the choice of L5 2,1 is arbitrary. Also note that, apart from the technical results of the observations above, this remaining L seems to make sense: we do not distinguish betweenkkandkg(51), we take premises seriously but we only consider the case where
K5G5 2, so that group knowledge can be called implicit, according to Section 3. Then, according to Observation 4.3 the only sensible choice forklis 0. Let us formulate the notion of distributivity for the remaining L’s:
2 2
F£ Gw⇒'w1, . . . ,wm:F£ (K1w1∧? ? ?∧Kmwm)&£(w1∧? ? ?∧wm)→w. (3)
Thus, the conclusionwshould be an S5 (G)-consequence of the lemma’sm w1, . . . ,wm, for
4.2. A semantic approach
If we try to reformulate (3) semantically, we obtain
If Gwis true in every situation that verifiesF, then there should bew1, . . . ,wm such that (w1∧? ? ?∧wm)→w is valid and (K1w1∧? ? ?∧Kmwm) is true in every situation
verifyingF.
However, we think that the order of quantification in the phrase above deserves some 2
more attention. Consider F 5hK p1 ∨K p2 j. Indeed, we have F* Gp, but does p
follow from formulasw ,w such that (K w ∧K w ) is true in every situation},s forF?
1 2 1 1 2 2
No, obviously not (see Observation 4.6 below or its proof in Appendix A); this is too strong a requirement: instead of finding suchw andw such that every situation},s for
1 2
F satisfies (K1w1∧K2w2), however we are able to find such formula for every situation that verifiesF, since such a situation },s either satisfies K p or K p, so that we can
1 2
take (w ,w ) to be either ( p,¡) or (¡, p). 1 2
2
Observation 4.6. Although we have hK p1 ∨K p2 j£ Gp, there exist no w1,w2 with 2
£(w1∧w2)→p and hK p1 ∨K p2 j£ (K1w1∧K2w2).
Corollary 4.7. Group knowledge is not distributed in the sense of (3).
So, according to the latter Corollary, also the remaining choices forLdo not yield a notion of distributed knowledge. Let us thus push our argument about the order of quantification one step further, by introducing a principle of ‘full communication’:
We say that group knowledge satisfies the principle of full communication if in every situation in which Gw is true one can findw1, . . . ,wm such that (K1w1∧? ? ?∧
Kmwm) also holds in that situation, and, moreover, (w1∧? ? ?∧wm)→w is a valid implication.
Phrased negatively, group knowledge does not satisfy the principle of full communica-tion if there is a situacommunica-tion in which the group knows something, i.e. Gw, wherew does not follow from the knowledge of the individual group members. We will now show that in the logic S5 (G), group knowledge does not satisfy the principle of full communica-m
tion, either.
First, note that the semantic counterpart of full communication reads as follows:
;},s,w 'w, . . .w : [},s*Gw⇒ },s*(K w ∧? ? ?∧K w )& (w ∧? ? ?∧
1 m 1 1 m m 1
2
wm)* w]. (4)
Definition 4.8. Let} be a Kripke model with state s, and i#m. The knowledge set of i in},s is defined by: K(i,},s)5hwu},s*Kwj.
i
2
},s*Gw⇒<K(i,},s)* w. (5)
i
Property (5) expresses that G-knowledge can only be true at some world s if it is derivable from the set that results when putting all the knowledge of all the agents in s together.
For multi-agent architectures in which agents have the possibility to communicate (like, for instance, van Linder et al., 1994) principle (5) is rather relevant. This so-called
principle of full communication captures the intuition of fact discovery (cf. Halpern and
Moses, 1990) through communication. The principle of full communication formalizes the intuitive idea that it is possible for one agent to become a wise man by communicating with other agents: these other agents may pass on formulae from their knowledge that the receiving agent combines to end up with the knowledge that previously was implicit. As such, the principle of full communication seems highly desirable a property for group knowledge. It is questionable whether group knowledge is of any use if it cannot somehow be upgraded to explicit knowledge by a suitable combination of the agents’ individual knowledge sets, probably brought together through communication. Coming back to the example of the three computer scientists and the question whether P±NP, if there is no way for them to combine their knowledge such
that the proof results, it is not clear whether this statement should be said to be distributed over the group at all.
Unfortunately, in the context of S5 (G), the principle of full communication does notm
hold. The following counterexample describes a situation in which group knowledge cannot be upgraded to explicit knowledge (thereby answering a question raised by van Linder et al., 1994).
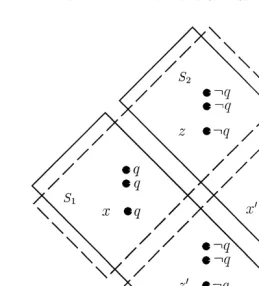
Counterexample 4.9. Let the set P of propositional variables contain the atom q. Consider a Kripke model } such that
• S5hx,x9,z,z9j,
• p( q,x)5p( q,x9)51, p( q,z)5p( q,z9)50 and for all p[P, p( p,x)5p( p,x9) and p( p,z)5p( p,z9) (the precise value, 0 or 1, of p does not matter),
• R is given by the solid lines in Fig. 1, and R is given by the dashed ones (reflexive1 2 arrows are omitted).
Observation 4.10. It holds that (see Appendix A for a justification):
• K(1,},x)5K(2,},x),
• },x*Gq,
• q[⁄ K(1,},x)<K(2,},x)5K(1,},x).
From this last observation it follows that the principle of full communication does not hold in this model: although the formula q is group knowledge, it is not possible to derive this formula from the combined knowledge of the agents 1 and 2. Thus it is not possible for one of these agents to become a wise man through receiving knowledge from the other agent. In terms of Borghuis: the model of Counterexample 4.9 shows that one can have group knowledge of an atomic fact q, although this group knowledge will never be derived during a dialogue between the agents that are involved. The ‘reason’ for this in our example is that the agents have no means in their language to distinguish between x and x9, or between z and z9. In Section 5 we will see that such a negative result can already be obtained in a model in which there are no such ‘copies of the same world’ (see also Fig. 3).
Corollary 4.11. In S5 (G), group knowledge does not satisfy the principle of fullm
communication.
5. Models in which group knowledge is distributed
In this section we will characterize a class of Kripke models, in which G-knowledge
is always distributed, in the sense that they satisfy the principle of full communication.
To be more precise, the models that we come up with will satisfy
2
},s*Gw⇔<K(i,},s)* w. (6)
i
Note that the principle (6) indeed is that of (5), combined with the validity of axiom A6.
Definition 5.1. A Kripke model }5kS,p,R , . . . ,R l is called finite if S is finite;
1 m
moreover, it is called a distinguishing model if for all s,t[S with s±t, there is aws1,t2 such that },s*ws1,t2 and},t±u ws1,t2.
The nice feature of finite distinguishing models is that sets of states can be named:
Lemma 5.2. Let }5kS, . . .l be a finite distinguishing model. Then:
;X,S'a [+;x[S (},x*a ⇔x[X ).
X X
For a given set X, we call aX the characteristic formula for X.
Lemma 5.3. Let}5kS,p,R , . . . ,R lbe a given finite distinguishing model, with s[S.
If one tries to link up the two lemmas above with the principle of full communication, one may take the following point of view. First of all, note that, given a state s, all agents at least share one epistemic alternative, which is s itself. Now, consider the set of epistemic alternatives for agent i in s, R (s). Relative to agent j we can partition R (s)i i
into two subsets: a set Yj7R (s) of worlds that are considered as epistemic alternativesi
for agent j, and a set Xj5R (s)\Y of worlds that are possible alternatives for i, but noti j
for j. Let aXj and aYj be the characteristic formulas for X and Y , respectively. Then,j j
agent i knows that the real world must be in either one of X and Y , i.e. agent i knowsj j
that ¬aXj→aYj, and agent j knows¬aXj. Thus, agent j may inform agent i so to speak which of i’s alternatives can be given up. Now, if all the agents h would communicate this information X to agent i, then finally agent i would end up with those epistemich
alternatives that are considered possible by all of the agents. This argument is made more precise in the (proof of) the following theorem.
Theorem 5.4. Let } be a finite distinguishing model. Then, in }, G-knowledge is
distributed, in the sense that it satisfies (6).
We finally observe that the two properties of Definition 5.1 are in some sense also necessary for distributivity. Let us say that in} group knowledge satisfies the principle of full communication if, for all states s and formulaew, Eq. (6) is satisfied. Then, we know already from Fig. 1 and Observation 4.10 that there is a finite65 model in which
2
this principle of full communication is not valid. One might wonder if there is a distinguishing model that falsifies the same principle (this model should then, by virtue of Theorem 5.4, be infinite). It is tempting to apply the following reasoning to the model } of Fig. 1.
consistent set, and hence, a member of the canonical model } . Also, one has
c c c c
} ,G*(K a↔K a), for all a, } ,G*¬K q and also } ,G*Gq. Thus, } ,G
1 2 1
c
model. This model} moreover is infinite, and distinguishing, by definition (its set of
states is the set of all maximal consistent sets).
c
However, we have to mention here that} is in general not a model of the kind as defined in Definition 2.6; the true definition of },s*Gw is ;t(s,t)[R ⇒},t*w,
G
where R can only be guaranteed to be some subset of R > ? ? ?>R . For more on
G 1 m
this, the reader is referred to van der Hoek and Meyer (1992). But still, we claim the existence of an65 model1 that is distinguishing, in which G-knowledge is defined as
2
in our Definition 2.7, and in which the principle of full communication does not hold. This model1 is provided in Definition A.4 in Appendix A. Let us conclude this section by summarizing the discussion of the last paragraphs:
Observation 5.5.
• There is a finite, not distinguishing model, in which group knowledge does not fulfil the principle of full communication.
• There is a distinguishing model, not finite, in which group knowledge does not fulfil the principle of full communication.
6. Conclusion
We have given formal definitions of what it means for group knowledge to be implicit or to be distributed relative to a group. Basically, group knowledge is implicit, if there is some formula known by the group, but not by any of its members. Here, one has to be precise about the role to be played by premises, and about the notion of derivability that is used to conclude that something is known. It appears that, under the standard notion of derivability in S5 (G), and when no premises are allowed, group knowledge is notm
implicit. The same holds if one allows for applications of the Necessitation rule to premises. Thus, the only case in which group knowledge may be implicit in a group is the case in which premises describe a situation rather than the knowledge present beforehand.
Next, we studied whether group knowledge is always distributed. We made the notion of distributivity precise by saying that a formula is distributed (given some set of premises) if it can somehow, using some notion of derivability and some related set of premises, be derived from the union of the agents’ knowledge. We argued that there was one way of choosing the parameters such that distributivity is not trivialised or directly absent. We gave a semantic account of a variant of distributivity (called the principle of full communication): we then were able to show that this principle was still not guaranteed, in general. Then, we gave two properties of Kripke models that guarantee that group knowledge does allow full communication; we also showed that both properties are, in some sense, needed: giving up one of the properties enables one to falsify the principle mentioned.
properties. For instance, it is also well known that the canonical models for a logic like S5 (G) only have the property that the accessibility relation for G, say R , is a subset ofm G
R > ? ? ?>R , and cannot be guaranteed to be equal to this intersection. In other
1 m
words, this equality is not modally definable, although one can find a complete axiomatization for those models that satisfy it. For more on this, the reader is referred to van der Hoek and Meyer (1992). In that paper, the authors also show that definability of
R > ? ? ?>R 5R is achieved when using graded modal logic. But in this logic, the
1 m G
assumption of distinguishability of a model seems to be unnatural; graded modal logic is typically designed to be able to reason about numbers (and hence copies) of worlds.
Also, in van der Hoek and Meyer (1997) the same authors demonstrate that proving an epistemic logic involving both group knowledge and common knowledge complete with respect to S5 (G)-like models can be quite complicated. Again, distinguishabilitym
of the models has to be given up. To be more precise, given a state },s for c, the technique of filtration in modal semantics often yields a finite distinguishing model}9 with state s9, such that}9,s9still verifiesc, which might suggest af first sight that finite distinguishing models are always obtained. It is not guaranteed, however, that this model } is in the appropriate class, i.e. if } is an 65 (G)-model, }9 need not be.
m
Finally, in a recent manuscript (Lomuscio and Ryan, 1997) a rather surprising property of group knowledge was mentioned in the context of so-called Interpreted
Systems, systems that are widely accepted as a general semantics for distributed systems
(this is also a major approach in Fagin et al., 1995). In such a system, one obtains
Gw↔w, for allw. Since such a system is by definition distinguishing (the states usually differ already on the objective level), in the finite versions the principle of full communication would be automatically obtained, but, at the same time, it might be a too strong, and perhaps optimistic principle: all facts about the world would be eventually obtained by the agents, would they be able to fully communicate.
Acknowledgements
This work was partially supported by ESPRIT WG No. 23531 (FIREworks) and the Human Capital and Mobility network EXPRESS. The contents of this paper evolved by fruitful discussions with and comments from several people, and can thus be conceived as a good example of a body of distributed knowledge, obtained by repeated and fruitful communication. More particularly, Mark Ryan and Elias Thijsse gave useful comments on previous versions of this paper. Frank de Boer gave helpful suggestions to simplify the presentation of the model of Fig. 3. We also thank the participants of LOFT2 (the Second Conference on Logic and the Foundations of the Theory of Games and Decisions) for the inspiring discussion on this paper. Finally, the comments of two anonymous referees of Mathematical Social Sciences helped to further improve our presentation.
Appendix A. Proofs
der Hoek (1995a), where a similar property is proven for an ‘S5 -like’ logic. Let us1
Proof. The ‘⇐’ direction follows immediately from an application of R1 to Kic and axiom A3. The ‘⇒’ direction is proven by induction on the length l(p) of a shortest
2 shortest proof. The same holds for the casec being an S5 (G)-axiom.m
2.2.Suppose c 5Kb with £b. By necessitation, we then also have £Kb and we
j i
2 prove Kc 5K Kb by applying A4 and R1, yielding £Kc and thus WF£ Kc.
i i i i i
2.3.The only other possibility is thatckis obtained by an application of modus ponens tocjandcj→ck11, j#k. Using the induction hypothesis on the proofs forcjand
of the Necessitation rule in a proofp to non-S5 (G)-theorems. We prove, for all n andm
all c:
1 1 1 2
IfF£ chas a proofp with`(p )5n, then WF£ c. (A.2)
1 1
1 2 2 wj[F, by the three steps Kiwj,Kiwj→wj,wj to obtain a proof k(p ) for WF£ w.
1 2
(Note that the resulting proofk(p ) indeed only uses premises from WF.)
1 1 2
• Suppose that (A.2) holds for all p with `(p )#k, and we have a F£ c with a
1 1 1
proof p with `(p )5k11, say p 5kc1. . .cr, cr11, . . .ck11 (5c)l, where cr11 is obtained fromch(h#r) as a result of the last Necessitation step to previous
1 1
• This is a standard result in modal logic; see, for instance, Hughes and Cresswell (1984) or Fagin et al. (1995) and Meyer and van der Hoek (1995b) for this specific multi-agent epistemic logic S5 (G). This property is also referred to as ‘weakm
soundness and completeness’.
• This is the standard notion of adding premises in modal logic. Proofs of this ‘strong soundness and completeness’ result can again be found in Hughes and Cresswell (1984) or Fagin et al. (1995) and Meyer and van der Hoek (1995b).
• For the ⇒-direction, one only has to check that applying Necessitation to premises 1
inF is* -valid. The argument for⇐runs as follows. Suppose that we haveFand
1 2
w for whichFZ w. By Theorem 2.5, we then have WFZ w, where W is defined as in the proof for Theorem 2.5 above. Thus, we find some Kripke model } and world s for which},s*WF and},s±u w. Using a standard argument in modal logic (see, for instance, Theorem 2.12 of Meyer and van der Hoek (1995a)), one may assume that the model } is generated from s: for all w[S there is a path
→
Table A.1
Proof of Observation 4.4. We claim that the following tuplesL 5kkk,K,kl,L,kg,Glmake the notion of group knowledge distributed – but in a trivial way.
(a) Tuples of typek0,K,0,L,0,Gl, i.e. no premises allowed. This was already observed in Observation 4.2, and the argument is given also in Section 4.1.
G
K. Note how this item generalizes (the proof of) Observation 4.3.
(c) TuplesLfor whichk 5g 0 (note how this item generalizes item (a)). Under thisL, suppose that£Gw. Then, by Theorem 3.3, we have£(K1w1∧? ? ?∧Kmwm) and hence
K L
item, we have judged half of all the possibilities to obtain distributed group knowledge as trivial.
G
(d) Here, K5 1 and k 5 kg k. The crucial observation now is that if k ? Fg £ Gw,
K L
thenk ? Fk £ Kiw. Obviously, we also have k ?l £ (w∧? ? ?∧w)→w.
Proof of Observation 4.5. The following tuplesL 5kkk,K,kl,L,kg,Glmake the notion of group knowledge to be not distributed.
(e)k 5 k 5k l 0, k 5g 1. Let F 5hGpj, where p is an atom. Suppose that we would have w1, . . . ,wm for which £(K1w1∧? ? ?∧Kmwm) and £(w1∧? ? ?∧wm)→p. Then
(using A3 and R1) we would also have £p, which we do not.
(f) k 5g 1, G5 1 and, as a first subcase, suppose k 5k 0 and L5 2. Let F 5 1
hp,Gp→qj. We haveF£ Gq. Suppose for this subcase that there arew1, . . .wmwith
K 2
£ (K1w1∧? ? ?∧Kmwm) and hp,Gp→qj£ (w1∧? ? ?∧wm)→q. Then we would
2 2
have hp,Gp→qj£ q. But the fact that hp,Gp→qj±u q is easily verified, and then 2
Theorem 2.8 yields hp,Gp→qj£ q.
(g) As a second subcase to the previous item, suppose, on top ofk 5g 1, G5 1, that k 5k 1, K5 2 and that either k 5l 0 or L5 2. As in the previous item, we then
K
have that if there would bew1, . . .wm for whichhp,Gp→qj£ (K1w1∧? ? ?∧Kmwm),
K 2
andk ?hp,Gp→qj£ (w ∧? ? ?∧w )→q, then we would also havehp,Gp→qj£ q,
l 1 m
which we do not, as argued above.
(h) The remaining tuples areL 5kkk,K,kl,L,kg,Gl5k1,2,0,L,1,2l, with L5 2 2 ,1. That they do not guarantee distributivity of group knowledge follows from Observation 4.6.
Proof of Observation 4.6. In Observation 4.6 we claimed the following: Although we 2
have hK p1 ∨K p2 j£ Gp, there exist no w1,w2 with £(w1∧w2)→p and hK p1 ∨ 2
K p2 j£ (K1w1∧K2w2). Consider the model of Fig. 2 (reflexive arrows are omitted; R is1 denoted with the solid line, R with a dashed one). Suppose that there would be formulas2 w and w of the type described above. Since we both have },s*K p∨K p and
1 2 1 2
},t*K p∨K p, we have},s*(K w ∧K w) and },t*(K w ∧K w ). Thus, we have
1 2 1 1 2 2 1 1 2 2
},u*w1∧w2. However, this is not compatible with£(w1∧w2)→p, thus suchw1andw2
Proof of Observation 4.10. Observation 4.10 claimed about 1 that:
1. K(1,},x)5K(2,},x), 2. },x*Gq,
3. q[⁄ K(1,},x)<K(2,},x)5K(1,},x).
Proof. We first state and prove the following lemma.
Lemma A.2. For all u[hx,zj, and allw: },u*w⇔},u9*w.
Proof of Lemma A.2. Using induction on w. For atoms in P this follows by the definition of the valuation p. The proof for the connectives ∧, ∨ and ¬ is straightforward. So let us assume the statement has been proven for formula c and consider w 5K c. If },x*K c, we have that },u*c for u5x,z. The induction
2 2
hypothesis then yields that},u9*c for u5x,z, and thus},x9*K c. Similar arguments 2
hold for the other direction, as well as for the world z in the model, and also for w 5K c,Gc. End of Proof of Lemma A.2. j
1
Now, the first item of Observation 4.10 is proven as follows. Suppose that c[
K(2,},x), that is, },x*K c. Thus, by definition of K , we have },u*c for u5x,z.
2 2
Then, by the previous lemma, we also have that z9 verifiesc. But then, obviously, we have },x*K c. To see the second item, observe that (x,v)[R >R ⇔v5x. And,
2
but not by agent i. If the agents were able to communicate, agent i could tell agent 1 that each x[X is not a good epistemic alternative, so that the agent 1 can eliminate all
i
worlds x that appear in some set X , thus ending up in exactly those alternatives ini
R (s)> ? ? ?>R (s). Formally, we put Lemma 5.3 to work. Note that R (s)7(X <? ? i.e. t[X , which contradicts the definition of X ). Thus,
i i
• The proof of this claim is provided by the model of Fig. 1.
• This follows from Theorem A.5, presented below.
Before formally introducing our next Kripke model, we need some preliminary notions and notation.
Definition A.3. We now assume that the set of atomic propositions P consists of an atom q together with infinitely atoms p (ii $1). In the following, we will use infinite
binary sequences for the representation of worlds in our model. Here, a binary sequence
is either an infinite sequence s5ks ,s , . . .1 2 l, or a finite sequence s5ks ,s , . . . ,s1 2 nlwith each s [h0,1j. In the finite case, we say that the length l(s) of s is n. Let us denote the
i
set of all the infinite sequences by IBS, and the finite sequences by FBS. It is convenient to define, for a finite sequence u5ku , . . . ,u l and an arbitrary binary sequence v the
Another way of defining u would be as the solution of the equivalence u 5u;u .
v v v
Thus, k0,1,1l 5k0,1,1,0,1,1,0,1,1, . . .l, k1l 5k1,1,1, . . .l and k0l 5k0,0,0, . . .l. We call a sequence t a suffix of a given sequence u iff for some finite sequencev we have
u5v;t (v may be the empty sequencee). Finally, the equivalence relation ; on IBS s
Fig. 3. An infinite distinguishing model for two agents.
We have chosen the worlds x, z, x9and z9as named members of the sets S , S , S and1 2 3
S , respectively. We can choose for these worlds the representatives of the equivalence4 v class that defines the S that contains that world: then, for instance, we get xi 5k1l ,
v
x9 5k0,0,1l , and so on. Then, we putp(u)( q)51 iff u[S1<S , and3 p(u)( p )i 51 iff
ui51. Thus, for instance, in each state u from S , q is true, and, although some of the1
p’s may be false in such a world in S , there is some index k [N, for which all p ’s are
1 u i
v
true, if i$k , since uu ; ks1l . The relations R and R are indicated by the straight and1 2 dotted lines, respectively, and formally defined as follows. R is the equivalence relation1 with the two equivalence classes S <S and S <S , whereas the equivalences classes
1 4 2 3
of R are S <S and S <S .
2 1 2 3 4
Note that the model 1 is a distinguishing infinite model. The relation between the model 1 just defined and the model } of Fig. 1 is already partly suggested by the names of the distinguished worlds. For instance, in both cases, x and x9 are worlds in which q is false, and which are both R and R related to a world of z-type, but not1 2
R >R -related. However, in1, it is not the case that x and x9verify the same formulas,
1 2
which is imposed by the mere fact that 1 is distinguishing (in this case, note that 1,x*p whereas1,x9*¬p ). However, we will be able to prove that, although x and
x9are not equal, the cluster S is ‘similar’ to S , whereas S is in the same sense related1 3 2
The proof of Theorem A.5 proceeds by combining a number of lemmas. First we need an additional definition.
Definition A.6. Let n[N, n$1. The language+ consists of the formulas of which the
n
only propositional atoms are q, p , . . . , p . Also, two sequences u,v[IBS are
n-1 n
equivalent, written u; v if for all i#n, u 5v.
n i i
Now we can state the lemma that guarantees that the clusters S1 and S3 behave similarly (as do S and S ).2 4
Lemma A.7. Let n$1 be given. Then, for every world in S there is an n-equivalent1
world in S , and vice versa3 . The same relation holds between S and S . Put more2 4
Proof. Note that a cluster S contains all sequences with a common suffix. So, as ani
v since by assumption1,x9*F(x), we must have x9; x. A similar argument proves ‘⇐’
n
falsified by x as well as by x9) or it is some p with ii #n and, since x;nx9these two worlds also agree on p . The proof for conjunctions and negations is straightforward, soi
let us now assume that w 5K c, for some c[+ with 1,x*K c. To reach a
1 n 1
contradiction, assume that 1,x9*¬K c. It means that there is some z[S with
1 2
• This is proven by the model of Fig. 1 and Observation 4.10.
• This follows from the model of Fig. 3 and Theorem A.5.
References
Bacharach, M.O.L., Gerard-Varet, L.A., Mongin, P., Shin, H.S. (Eds.), 1997. Epistemic Logic and the Theory of Games and Decisions, Kluwer, Dordrecht.
Borghuis, T., 1994. On the interpretation of modalities in typedl-calculus. PhD thesis, Technical University Eindhoven.
Fagin, R., Halpern, J.Y., Moses, Y., Vardi, M.Y., 1995. Reasoning About Knowlege, MIT Press, Cambridge, MA.
Halpern, J.Y., Moses, Y., 1985. A guide to the modal logics of knowledge and belief. In: Proceedings of IJCAI-85, Los Angeles, CA, pp. 480–490.
Halpern, J.Y., Moses, Y.O., 1990. Knowledge and common knowledge in a distributed environment. J. ACM 37 (3), 549–587.
Halpern, J.Y., Moses, Y., 1992. A guide to the completeness and complexity for modal logics of knowledge and belief. Artificial Intelligence 54, 319–379.
Hughes, G.E., Cresswell, M.J., 1984. A Companion to Modal Logic, Methuen, London.
Kaneko, M., Nagashima, T., 1997. Axiomatic indefinability of common knowledge in finitary logic. In: Bacharach, M.O.L., Gerard-Varet, L.A., Mongin, P., Shin, H.S. (Eds.), Epistemic Logic and the Theory of Games and Decisions, Kluwer, Dordrecht, pp. 69–93.
Levesque, H., 1984. A logic of implicit and explicit belief. In: Proceedings of the National Conference on Artificial Intelligence, pp. 198–202.
Lomuscio, A., Ryan, M., 1997. A note on the relation between interpreted systems and Kripke models. Unpublished manuscript.
Meyer, J.-J., van der Hoek, W., 1995b. Epistemic Logic for AI and Computer Science, No. 41 in Cambridge Tracks in Theoretical Computer Science, Cambridge University Press.
Van der Hoek, W., Meyer, J.-J., 1992. Making some issues of implicit knowledge explicit. Int. J. Found. Comput. Sci. 3 (2), 193–224.
Van der Hoek, W., Meyer, J.-J., 1997. A complete epistemic logic for multiple agents – combining distributed and common knowledge. In: Bacharach, M.O.L., Gerard-Varet, L.A., Mongin, P., Shin, H.S. (Eds.), Epistemic Logic and the Theory of Games and Decisions, Kluwer, Dordrecht, pp. 65–68.
1995. Group knowledge isn’t always distributed. In: Van der Hoek, W., van Linder, B., Meyer, J.-J.Ch. (Eds.), Proceedings of the Bi-annual Israelian Symposium on the Foundation of AI ’95, pp. 191–200.