PENDEKATAN GENERALIZED ADDITIVE MIXED MODELS DALAM PENDUGAAN PARAMETER PADA SMALL AREA ESTIMATION

PENDEKATAN GENERALIZED ADDITIVE MIXED MODELS

DALAM PENDUGAAN PARAMETER PADA SMALL AREA ESTIMATION

1

_{Anang Kurnia dan}

2

_{Khairil A. Notodiputro}

1,2

_{Departemen Statistika, Institut Pertanian Bogor, Jl. Meranti Wing 22 Level 4}

Kampus IPB Darmaga, Bogor – Indonesia 16680

E-mail :

1

_{anangk@ipb.ac.id}

_,

2

_{khairiln@bima.ipb.ac.id}

Diterima 15 Oktober 2007, disetujui untuk diterbitkan 22 Januari 2008

ABSTRACT

Small Area Estimation (SAE) is a statistical technique to estimate parameters of sub-population containing small size of samples with adequate precision. This technique is very important to be developed due to the increasing needs of statistic for small domains, such as districts or villages. Some SAE techniques have been developed in Canada, USA, and UE based on real data. We adapted this technique to produce small area statistic in Indonesia based on national data collected by the Statistics Indonesia (Badan Pusat Statistik). We found that the linear model applied to auxiliary data produced estimates with low precision. In this paper we propose a class of generalized additive mixed model to improve the model of auxiliary data in small area estimation.

Keywords: small area estimation, generalized additive mixed models

1. PENDAHULUAN

Berbagai metode pendugaan area kecil (small area

estimation) telah dikembangkan khususnya menyangkut

metode yang berbasis model (model-based area

estimation). Perhatian yang besar ini terjadi seiring

dengan meningkatnya kebutuhan pemerintah dan para pengguna statistik (termasuk dunia bisnis) terhadap informasi yang lebih rinci, cepat, dan handal, tidak saja untuk lingkup nasional tetapi pada lingkup yang lebih kecil seperti provinsi, kabupaten, bahkan kecamatan atau desa/kelurahan. Bagi kita di Indonesia pentingnya statistik area kecil semakin dirasakan seiring dengan era otonomi daerah dimana sistem ketatanegaraan

bergeser dari sistem sentralisasi ke sistem

desentralisasi. Pada sistem desentralisasi pemerintah daerah memiliki kewenangan yang lebih besar untuk mengatur dirinya sendiri. Kebutuhan statistik pada level kabupaten, dengan demikian, menjadi keniscayaan sebagai dasar bagi pemerintah daerah untuk menyusun sistem perencanaan, pemantauan dan penilaian pembangunan daerah atau kebijakan penting lainnya. Pendugaan area kecil merupakan konsep terpenting dalam pendugaan parameter secara tidak langsung di suatu area yang relatif kecil dalam percontohan survei (survey sampling). Dalam makalah ini area yang dimaksud mungkin saja direpresentasikan oleh objek survei yang jumlahnya sangat kecil sehingga analisis yang didasarkan hanya pada objek-objek tersebut menjadi sangat tidak dapat diandalkan sehingga pendugaan langsung (direct estimation) pada sub-populasi tidak memiliki presisi yang memadai karena

kecilnya jumlah contoh yang digunakan untuk memperoleh dugaan tersebut.

Alternatif metode lain adalah dengan cara

menghubungkan area tersebut dengan area lain melalui model yang tepat. Dengan demikian dugaan tersebut merupakan dugaan tidak langsung (indirect estimation), dalam arti bahwa dugaan tersebut mencakup data dari

domain yang lain. Chand dan Alexander1)

menyebutkan bahwa prosedur pendugaan area kecil pada dasarnya memanfaatkan kekuatan area sekitarnya (neighbouring areas) dan sumber data diluar area yang statistiknya ingin diperoleh. Metode ini memiliki sejarah yang panjang tetapi baru mendapat perhatian dalam beberapa dekade terakhir untuk digunakan sebagai pendekatan pada pendugaan parameter area kecil. Lebih lanjut pengembangan yang sudah dilakukan

dapat dilihat pada Rao2) _.

Dalam makalah ini kita akan mendiskusikan pendugaan area kecil berdasarkan metode tidak langsung atau berdasarkan pada model. Salah satu permasalahan yang ditemukan di dalam penggunaan prosedur ini adalah ketepatan yang rendah jika model linier digunakan untuk menyusun model. Penulis, dalam makalah ini, mengusulkan untuk menggunakan pendekatan generalized additive mixed model (GAMM) untuk meningkatkan akurasi pemodelan yang dilakukan. Pada bagian akhir dari makalah ini juga disajikan kasus pendugaan area kecil dengan menggunakan data pengangguran dari Susenas 2005 dan Podes 2005 pada Kota Bogor - Jawa Barat.

1.1. Pendekatan GAMM dalam Pendugaan Area Kecil

Rao2) _{menyajikan secara intensif ulasan berbagai teknik}

dalam small area estimation yang sering digunakan oleh

peneliti maupun pemakai statistika, termasuk

didalamnya teknik atau pendekatan synthetic,

composite estimator, empirical best unbiased linear predictors, empirical Bayes and hierarchical Bayes.

Seluruh metode-metode tersebut menggunakan

pendekatan parametrik. Dalam bab ini, penulis mendeskripsikan suatu pendekatan nonparametrik,

generalized additive mixed model (GAMM). Pendekatan

GAMM memiliki keuntungan yang lebih dibandingkan dengan pendekatan parametrik khususnya dalam memodelkan pola hubungan peubah respon dengan peubah penjelas (auxiliary variable). Kelebihan tersebut yang selanjutkan digunakan penulis untuk pemodelan yang dilakukan dalam pendugaan area kecil.

Dengan berlandasakan pada model Fay-Herriot pada basic area level model.

yi = xi’β + υi + ei , i = 1, 2, ..., k

dengan β adalah koefisien regresi, υi adalah pengaruh

acak area, dan ei adalah sampling error. Dalam model

ini juga diasumsikan bahwa ei ~ (0, Di), υi ~ (0, A) dan

keduanya bersifat saling bebas dengan Di biasanya

diasumsikan diketahui. Lebih lengkap pembahasan ini

bisa dilihat pada Rao2) _.

Kita asumsikan bahwa yi dan xi memiliki suatu pola

hubungan yang dapat didekati oleh suatu fungsi pemulus m(.). Untuk X sebagai peubah penjelas, maka yi = m(xi) + υi + ei , i = 1, 2, ..., k

dengan υi|X ~ (0, υ(xi)), ei ~ (0, Di), serta ei dengan υi

saling bebas. Fungsi nilai tengah area kecil dapat dituliskan sebagai berikut:

θi(xi) = m(xi) + υi

yang merupakan kombinasi linear dari nilai tengah m(xi)

dan pengaruh acak υi. Kita dapat menggunakan suatu

teknik pendugaan untuk mendapatkan fungsi pemulus seperti menggunakan fungsi pemulus linear meliputi pemulus spline, regresi spline, dan local polynomial regression. Lebih jelas pembahasan secara teknis metode-metode tersebut dapat dilihat pada Hastie dan Tibshirani3) _.

Jika digunakan fungsi pemulus kernel untuk menduga

m(xi), penduga terbaik (best predictor) bagi nilai tengah

area kecil θi dapat dituliskan sebagai berikut

E(θi|yi) = γi yi + (1 - γi) h

mˆ (xi)

dimana γi = υ(xi) / (υ(xi) + Di). Pendekatan pendugaan

MSE bagi penduga parameter tersebut dapat dilakukan dengan mengadopsi pendekatan yang diberikan Prasad

dan Rao4) _{dengan mensubstitusi xi’}β _{dalam model}

linear campuran dengan mˆ _h(xi), sehingga diperoleh

formulasi sebagai berikut :

mse(θˆi) = 2 i u 2 i u D D + ˆ ˆ σ σ +

₍

1-ˆγ

₎

2mse m

(

ˆ _h

_{( )}

x_i

)

+

(

)

-3

( )

2 2 2 i u i u 2D ˆσ + D mse σˆ

2. METODE PENELITIAN

2.1. Model Dasar Pendugaan Area Kecil

Suatu penduga parameter ϒi dari suatu sub-populasi Wi

secara langsung dapat diperoleh berdasarkan anggota contoh pada sub-populasi tersebut (direct/design-based

estimator). Metode pendugaan tersebut menimbulkan

dua permasalahan penting. Pertama, penduga tersebut merupakan penduga tak bias tetapi memiliki ragam yang

besar karena diperoleh dari ukuran contoh yang kecil5) _.

Kedua, apabila pada suatu sub-populasi Wi tidak

terwakili didalam survey, maka tidak memungkinkan dilakukan pendekatan/pendugaan secara langsung.

Fay dan Herriot6) _{secara umum menggunakan model}

linear campuran (linear mixed model) dengan pengaruh acak yang hanya mengandung intersep, dengan kata lain model hanya meliputi pengaruh acak area, untuk menduga rata-rata pendapatan sub-populasi (<1000) dengan menggunakan data sensus 1970 di Amerika Serikat.

Model Fay-Herriot tersebut merupakan model dasar

bagi pengembangan pemodelan area kecil yaitu yi = θi

+ ei ; θi = xi’β + υi, dimana ei dan υi saling bebas

dengan E(ei) = E(υi) = 0 serta Var(ei) = Di dan Var(υi) =

A untuk i = 1, 2, 3, ..., k. Russo7) _{menjabarkan lebih}

lanjut model area kecil dengan memperjelas pengaruh acak sub-populasi di dalam model sebagai berikut : 1. xi = (xi1, xi2, ..., xip) adalah vektor data penyerta

(auxiliary variable)

2. θi = xi’β + ziυi untuk i = 1, 2, ..., k : merupakan

parameter yang menjadi perhatian dan

diasumsikan memiliki hubungan dengan data

penyerta pada (1) sedang υi pengaruh acak

dengan nilai tengah nol dan ragam A.

3. θˆi= θi + ei : penduga langsung untuk sub-populasi

ke-i dengan sampling error

4. θˆ_i= xi’β + ziυi + ei untuk i = 1, 2, ..., k : model

tersebut terdiri dari pengaruh acak dan pengaruh tetap sehingga merupakan bentuk model linear campuran dengan struktur peragam yang diagonal. Model regresi merupakan upaya untuk membentuk model umum dan memanfatkan kekuatan dan keakuratan pendugaan pada level populasi, sedangkan deviasi sub-populasi untuk menangkap kekhasan yang terjadi pada setiap sub-populasi dan bersifat acak. Dengan demikian jika hanya memanfaatkan informasi

umum maka θi = xi’β, dan jika pengaruh umum dan

statistika model pada point (4) diatas melibatkan pengaruh acak akibat desain sampling

(designed-induced, ei) dan pengaruh acak pemodelan

sub-populasi (model-based, υi) serta model tersebut

merupakan bentuk khusus dari model linear terampat (generaizedl linear mixed model).

Ada dua jenis model dasar pada pendugaan area kecil yang dikembangkan dan dapat dipelajari melalui beberapa literatur. Jenis pertama disebut basic area

level model. Jenis ini didasarkan pada ketersediaan

data penyerta yang hanya ada untuk level area tertentu,

katakan xi = (x1i, x2i, …, xpi)’ yang akan digunakan untuk

membangun model θi = xi’β + υi dengan υi ~ N(0, A).

Suatu model yang menggabungkan model berdasarkan

penarikan contoh yang bersesuaian θˆi= θi + ei dimana

i θ

ˆ _{adalah penduga langsung bagi θi dan ei|θi ~ N(0, Di)}

serta Di yang diketahui dengan model θi = xi’β + υi

untuk menghasilkan model gabungan θˆ_i = xi’β + υi + ei

yang tidak lain adalah suatu bentuk khusus dari model linear campuran. Namum demikian, basic area level

model memiliki dua keterbatasan8) _{, yaitu:}

(i) asumsi diketahuinya sampling error σ2ei yang

sangat membatasi, dan

(ii) asumsi E(ei|θi) = 0 mungkin tidak dapat dipenuhi

jika ukuran contoh yang bersesuaian ni kecil dan θi

merupakan fungsi nonlinear.

Jenis kedua disebut basic unit level model, dimana data-data penyerta yang tersedia bersesuaian secara individu dengan data respon, katakan xij = (x1ij, x2ij, …,

xpij)’ sehingga bisa dibangun model regresi tersarang yij

= xij’β + υi + ei dengan υi ~ N(0, A) dan eij ~ N(0, Di).

Lebih lanjut pada makalah ini difokuskan terhadap inferensi pada model basic area level. Ada tiga metode yang biasa digunakan pada pendugaan area kecil yang berbasis model, yaitu EBLUP (Empirical Best Linear

Unbiased Predictor), EB (Empirical Bayes) dan HB

(Hierarchical Bayes). Pendugaan titik pada EBLUP tidak membutuhkan asumsi sebaran, tetapi kenormalan dari pengaruh acak biasa diasumsikan untuk menduga MSE (Mean Squared Error) dari pendugaan. Pendugaan dengan metode EBLUP dan EB bersifat identik berdasarkan kenormalan dan demikian halnya dengan pendugaan dengan HB, hanya saja pengukuran

keragaman dari penduganya dapat berbeda8) _.

2.2. Metode Empirical Best Linear Unbiased Predictor (EBLUP)

Best Linear Unbiased Predictor (BLUP) awalnya

dikembangkan dengan mengasumsikan bahwa

komponen keragaman telah diketahui. Dalam

prakteknya, komponen keragaman sangat sulit untuk diketahui. Untuk itu diperlukan pendugaan terhadap

komponen keragaman ini melalui data contoh. Metode

Empirical Best Linear Unbiased Predictor (EBLUP)

menggantikan komponen keragaman yang tidak

diketahui ini dengan menduganya terlebih dahulu9) _.

Henderson10) _{memperlihatkan bahwa menggantikan}

komponen keragaman di dalam BLUP dengan penduganya dapat menimbulkan bias. Tetapi Kackar

dan Harville11) _{memperlihatkan bahwa 2 pendekatan}

(pertama, menduga komponen keragaman kemudian menggunakannya untuk menduga dan memprediksi parameter-parameter tetap dan komponen-komponen acak) dapat menghasilkan penduga yang tidak berbias9)_.

Fay dan Herriot6) _{mengembangkan model}

i i i

i

x

v

e

y

=

'

β

+

+

sebagai dasar dalam

pengembangan pendugaan area kecil. Selanjutnya

diasumsikan bahwa β dan A tidak diketahui, tetapi D _i

(i = 1, 2, ...., k) diketahui. Penduga terbaik (best

prediction) bagi

θ

_i =x_i'

β

+v_i jika β dan A diketahui adalah

)

,

|

(

ˆ

ˆ

i i i BP i

θ

y

β

D

θ

=

=

x

_i'

β

+

(

1

−

B

_i

)(

y

_i

−

x

_i'

β

)

dengan Bi = Di / (A + Di) untuk i = 1, 2, ..., k sedangkan

MSE(θˆ_iBP) = Var(θi|yi, β, A) = (1 – Bi) Di = g1i(A).

Dalam prakteknya, baik β maupun A biasanya tidak diketahui sehingga untuk kasus A diketahui, β dapat diduga dengan metode kemungkinan maksimum atau

metode momen β* =βˆ A_i( )=(X`V-1<sub>X)</sub>-1 <sub>X`V</sub>-1_{Y dengan V}

= Diag(A + D1, A+ D2, ..., A + Dk). Kemudian dengan

mensubtitusi β dengan β* pada θˆ_iBP, maka diperoleh

)

|

(

ˆ

ˆ

_y

_A

i i BLUP i

θ

θ

=

*

(

1

)(

*)

' '

_β

_β

i i i i

B

y

x

x

+

−

−

=

Menurut Ghosh dan Rao12) _MSE( BLUP

i

θˆ _{) = g1i(A) +}

g2i(A), dengan g2i(A) = (D1)2/(A + Di) [Xi`(X`V-1X)-1Xi].

Jika terlebih dahulu A diduga oleh Aˆ baik

menggunakan metode ML, REML ataupun momen

sehingga dengan mensubtitusi β oleh βˆ dan A oleh Aˆ

terhadap penduga BLUP (θˆiBLUP), maka akan

diperoleh suatu penduga baru

)

ˆ

|

(

ˆ

ˆ

_y

_A

i i EBLUP i

θ

θ

=

ˆ

(

1

ˆ

)(

ˆ

)

' '

_β

_β

i i i i

B

y

x

x

+

−

−

=

Jika didefinisikan MSE dari θˆiEBLUP adalah

MSE( EBLUP i θˆ ) = E( EBLUP i θˆ - θi)2

= Var( EBLUP i θˆ )+(Bias EBLUP i θˆ )2

persamaan tersebut dapat diuraikan menjadi MSE( EBLUP i θˆ ) = MSE( BLUP i θˆ ) + E( EBLUP i θˆ -BLUP i θˆ )2 = H1i(A) + H2i(A) dengan H1i(A) = MSE( BLUP i θˆ ) = g1i(A) + g2i(A) H2i(A) = E( EBLUP i θˆ -BLUP i θˆ )2

Prasad dan Rao4) _{menggunakan ekspansi deret Taylor}

untuk menduga MSE(

EBLUP i θˆ ) dan diperoleh MSE(θˆi_{)PR = g1i( A}ˆ_{) + g2i( A}ˆ_{) + 2g3i( A}ˆ_{) dengan} g3i( Aˆ) =

∑

= + + m j i i i _{A D} D A m D 1 2 2 2 ) ˆ ( ) ˆ ( 2 .

2.3. Metode Empirical Bayes (EB)

Pada metode empirical Bayes, sebaran posterior untuk parameter yang diamati dari data dinotasikan

(

θ |y,β,A

)

f _{i i} adalah hal pertama yang ingin

didapatkan, dengan asumsi parameter model β dan A diketahui. Parameter model diduga oleh sebaran

marginal dari data (yi), dan kesimpulan yang diperoleh

didasarkan pada dugaan sebaran posterior dari θi,

(

θ |y,βˆ,Aˆ

)

f _{i i} .

Model Fay - Herriot untuk model basic area level adalah sebagai berikut : i i T i i

x

β

v

e

y

=

+

+

dengan i

v ~N(0, A)

_{dan i}

e ~N(0, D )

_i , ei dan υi

saling bebas. A dan β diasumsikan tidak diketahui,

tetapi Di (i = 1, 2,…, k) diketahui. Best Predictor (BP)

dari

θ = x 'β + v

_{i i i} jika A dan β diketahui,

berdasarkan penduga composite pada model Fay-Herriot, yaitu : BP i

θ

ˆ

₌ i 1i i 2i

w Y + (1- w )Y

ˆ

ˆ

= xiT β + wi ( yi - xi’β) = xiT β + (1 – Bi)( yi - xi’β) dengan Bi = Di / (A + Di) untuk i = 1, 2,…, k.

Misal

ˆ

θ

_iB merupakan penduga Bayes untuk θi dengan

mengikuti model Bayes : yi |θi ~ N(θi, Di)

θi ~ N(xi’β, A) adalah sebaran prior untuk θi, i = 1, 2, …,

k.

Model Bayes dijelaskan oleh:

(

)

      − − = 2 2 1 exp 2 1 ) | ( _{i i} i i i i y D D y f θ π θ dan

(

)

      − − = 2 2 1 exp 2 1 ) ( θ β π θ π T i i i x A A dan

(

)

(

)

      − −         − − =

∏

= 2 1 2 2 1 exp 2 1 2 1 exp 2 1 ) , | , ( β θ π θ π β θ T i i k i i i i i x A A y D D A y f untuk y = (y1, y2, …, yk)’, θ = (θ1, θ2, …, θk)’. Dengan

penurunan aljabar, kita peroleh bahwa :

(

θ

_i

|

y

_i

,

β,

A

)

~N                 +         + + −1 i i i A 1 D 1 , D A Ay D_ixT_i β ~N

(

)

_       + − + + i i T i i i T i D A AD , β x y D A A β x

Berdasarkan sebaran tersebut dan dengan pendekatan

the squared error loss (pendugaan Bayes menggunakan

konsep nilai harapan), didapatkan bahwa

B i

θˆ

= E

(

θ

_i

|

y

_i

,

β,

A

)

= xi’β + (1 – Bi)( yi - xi’β)

Jika β dan A diduga, maka penduga tersebut menjadi penduga empirical Bayes (EB), yaitu

EB i

θˆ

= E

(

θ

_i

|

y

_i

,

βˆ

,

A

ˆ

)

=

x

βˆ

(

1

)

(

y

i

x

iT

βˆ

)

T i

+

−

B

i

−

dimana , MSE(

θˆ

iEB ) =Var

(

θ

i

|

y

i

,

βˆ

,

A

ˆ

)

= (1 – Bi)Di Penduga

θˆ

BPi dan EB i

θˆ

identik untuk kasus normal.

Jika A diketahui, β dapat diduga dengan menggunakan metode maximum likelihood

log L(β, V)=-½log |V| - ½(Y -Xβ)T _V-1_{(Y -Xβ) dengan}

V = Diag(A + D1, A + D2, …, A + Dk). Turunan dari log

L(β, V) terhadap β adalah dβ d log L(β, V) = XT _V-1 _{(Y -Xβ)} = XT _V-1_{Y –(X}T _V-1_{X)β (=0)} ↔ (XT _V-1_{X)β = X}T _V-1_Y ↔ β = (XT _V-1_X)-1 _XT _V-1_Y

Dalam praktiknya, baik β maupun A biasanya tidak diketahui. A bisa diduga dengan menggunakan

maximum likelihood (ML), restricted/residual maximum likelihood (REML), atau metode momen. Pendugaan A

menggunakan REML konsisten meskipun terdapat

pelanggaran asumsi kenormalan13) _{. Karena β maupun}

A diduga, maka akan ada keragaman pada pendugaan yang diperoleh, sehingga MSE yang didapatkan juga akan meningkat. Untuk mengetahui seberapa besar

peningkatan MSE akibat adanya pendugaan pada β dan

A dapat dihitung menggunakan metode bootstrap14)

maupun metode Jackknife15)_{. Lebih lanjut, perbandingan}

berbagai teknik pendugaan MSE dibahas dalam Rao16) _.

2.4. Generalized Additive (Mixed) Model

Analisis regresi merupakan suatu teknik statistik yang paling luas pemakaiannya. Teknik ini memiliki sifat pendugaan yang sangat baik (powerful tool) jika asumsi-asumsi yang melandasinya terpenuhi, termasuk didalamnya adalah hubungan antara peubah respon dengan peubah penjelas dapat digambarkan dengan suatu fungsi tertentu yang terdefinisi seperti pola garis lurus, berbentuk polinomial, atau berpola eksponensial. Didalam banyak aplikasi, bagaimanapun, untuk memperoleh fungsi-fungsi tersebut secara tepat sangat sulit bahkan banyak gejala menunjukkan bahwa data-data yang diperoleh tidak menunjukkan suatu pola hubungan yang mudah untuk digambarkan.

Untuk mengatasi kesulitan-kesulitan di atas, Stone17)

mengajukan penggunaan model aditif. Model ini menduga pendekatan secara aditif dari fungsi regresi multivariate. Keuntungan penggunaan pendekatan ini paling tidak ada dua hal. Pertama, karena setiap suku aditif diduga secara individu menggunakan pemulus univariate, maka tidak terjadi masalah “curse of

dimensionality”. Yang kedua, pendugaan setiap suku

secara individual dapat menjelaskan bagaimana perubahan variabel respon terhadap perubahan variabel penjelas.

Untuk memperluas penggunaan model aditif dalam

berbagai keluarga sebaran, Hastie dan Tibshirani3)

mengusulkan model aditif terampat (generalized additive

model, GAM). Model ini menghubungkan nilai harapan

peubah respon dengan prediktor aditif melalui fungsi hubung yang tak linear. Model ini memungkinkan sebaran dari peubah respon berasal dari keluarga sebaran eksponensial. Banyak model statistik yang termasuk dalam kelas ini, antara lain model aditif untuk data Gaussian, model logistik non-parametrik untuk data biner, dan model log-linear non-parametrik untuk data Poisson.

Misalkan Y adalah peubah acak respon dan X1, X2, ... ,

Xp adalah gugus peubah penjelas. Prosedur regresi

dapat menduga nilai harapan (expected value) dari Y untuk nili X1, X2, ... , Xp yang telah diketahui. Model regresi linear standar mengasumsikan bentuk linear dari nilai harapan bersyarat sebagai berikut

E(Y|X1…Xp) = β0 + β1 X1 + … + βp Xp

Dengan data contoh, penduga bagi β0, β1, …, βp

umumnya diperoleh dengan menggunakan metode kuadrat terkecil (least squares method).

Model aditif men-general-kan model linear dengan memodelkan nilai harapan bersyarat sebagai

E(Y|X1…Xp) = β0 + s1(X1) + … + sp(Xp)

dengan si(X), i = 1,2, ... , p adalah fungsi pemulusan.

Dipahami bahwa model linear dan aditif tradisional dapat digunakan pada sebagian besar analisis data statistik, namun ada beberapa kasus dimana model-model tersebut tidak sesuai untuk digunakan, misalnya sebaran normal tidak cukup baik untuk memodelkan peubah diskret seperti data pencacahan atau respon yang memiliki batas, seperti proporsi. GAM mengatasi kesulitan tersebut, dengan memperluas penggunaannya ke sebaran lain selain normal. Dengan demikian, GAM bisa diaplikasikan untuk masalah analisis data yang lebih luas.

Sejalan dengan perkembangan teknologi komputasi,

Generalized Additive Mixed Models (GAMM) juga

berkembang untuk melengkapi teknik-teknik pemodelan khususnya model aditif dengan menyertakan pengaruh acak ke dalam model. Hal ini merupakan perluasan secara aditif dari bentuk Generalized Linear Mixed

Models (GLMM) berdasarkan konsep yang

dikembangkan oleh Hastie dan Tibshirani3) _.

3. HASIL DAN PEMBAHASAN

Kajian empirik menggunakan dua gugus data. Data pertama menggunakan data bangkitan yang terdiri dari

32 area kecil dengan υi dan ei masing-masing

dibangkitkan dari sebaran normal dengan rataan 0 dan ragam 1. Peubah yang menjadi perhatian Y,

didefinisikan sebagai fungsi dari X2 _{dan X dimana X}

adalah peubah penyerta. Pendekatan GAMM menunjukkan pendugaan yang lebih baik dibandingkan dengan teknik EBLUP. Nilai mean absolute relative

estimation (MARE) dari pendekatan GAMM adalah

0.0193 sedangkan pendekatan EBLUP adalah 0.0212. Lebih lanjut, nilai relative root mean square error (RRMSE) dari pendekatan GAMM adalah 0.0289 sedangkan pendekatan EBLUP adalah 0.0327

Gugus data kedua, digunakan data yang dikumpulkan oleh BPS khususnya data PODES 2005 sebagai sumber peubah penyerta dan data SUSENAS 2005 sebagai data survey, khususnya untuk Kota Bogor. Peubah yang menjadi perhatian adalah tingkat

pengangguran yang direpresentasikan dengan

persentase tenaga kerja yang tidak sedang bekerja atau tidak memiliki pekerjaan tetap untuk setiap kelurahan di Kota Bogor. Persentasi banyaknya penduduk laki-laki (X2), persentasi rumah tidak permanen (X5), persentasi surat miskin yang dikeluarkan kelurahan (X7), dan persentasi keluarga pra sejahtera dan sejahtera 1 (X8) digunakan sebagai peubah penyerta dalam kajian ini.

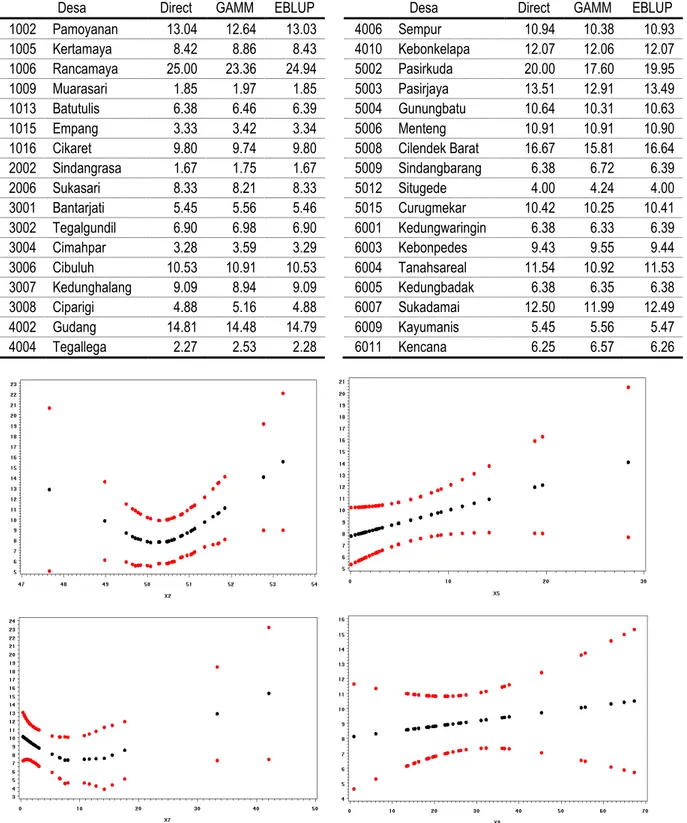
Table 1. Pendugaan Tingkat Pengangguran di Kota Bogor

Desa Direct GAMM EBLUP Desa Direct GAMM EBLUP

1002 Pamoyanan 13.04 12.64 13.03 4006 Sempur 10.94 10.38 10.93 1005 Kertamaya 8.42 8.86 8.43 4010 Kebonkelapa 12.07 12.06 12.07 1006 Rancamaya 25.00 23.36 24.94 5002 Pasirkuda 20.00 17.60 19.95 1009 Muarasari 1.85 1.97 1.85 5003 Pasirjaya 13.51 12.91 13.49 1013 Batutulis 6.38 6.46 6.39 5004 Gunungbatu 10.64 10.31 10.63 1015 Empang 3.33 3.42 3.34 5006 Menteng 10.91 10.91 10.90

1016 Cikaret 9.80 9.74 9.80 5008 Cilendek Barat 16.67 15.81 16.64

2002 Sindangrasa 1.67 1.75 1.67 5009 Sindangbarang 6.38 6.72 6.39 2006 Sukasari 8.33 8.21 8.33 5012 Situgede 4.00 4.24 4.00 3001 Bantarjati 5.45 5.56 5.46 5015 Curugmekar 10.42 10.25 10.41 3002 Tegalgundil 6.90 6.98 6.90 6001 Kedungwaringin 6.38 6.33 6.39 3004 Cimahpar 3.28 3.59 3.29 6003 Kebonpedes 9.43 9.55 9.44 3006 Cibuluh 10.53 10.91 10.53 6004 Tanahsareal 11.54 10.92 11.53 3007 Kedunghalang 9.09 8.94 9.09 6005 Kedungbadak 6.38 6.35 6.38 3008 Ciparigi 4.88 5.16 4.88 6007 Sukadamai 12.50 11.99 12.49 4002 Gudang 14.81 14.48 14.79 6009 Kayumanis 5.45 5.56 5.47 4004 Tegallega 2.27 2.53 2.28 6011 Kencana 6.25 6.57 6.26

Gambar 1. Scater plot peubah penyerta

Tabel 1 menyajikan hasil pendugaan untuk setiap metode yang digunakan pada gugus data kedua. Nilai RRMSE untuk pendugaan langsung (direct estimator), pendekatan GAMM dan EBLUP masing-masing adalah 0.0361, 0.0326 and 0.0335. Seluruh metode pendugaan mengarah ke hasil yang diperoleh oleh teknik pendugaan langsung. Kemungkinan faktor yang

menyebabkan hal tersebut yang utama adalah pengaruh dari kondisi dimana keragaman antar area kecil yang diamati jauh lebih besar dibandingkan dengan keragaman akibat sampling error di dalam setiap area kecil. Walapun demikian, pendekatan GAMM mampu untuk mereduksi pengaruh peubah penyerta yang tidak memiliki pola hubungan linear.

Gambar 1 menyajikan scater plot dari peubah penyerta, dan peubah X2 serta X7 jelas tidak memiliki hubungan yang linear. Kedua peubah tersebut dengan menggunakan pendekatan GAMM diaproksimasi sesuai dengan gambaran yang disajikan pada Gambar 1 tersebut.

4. KESIMPULAN

Berdasarkan kajian yang dilakukan, mampu ditunjukkan

keunggulan generalized additive mixed model

dibandingkan dengan generalized linear mixed model di dalam pendekatan EBLUP, setidaknya dapat ditemukan dalam dua aspek. Pertama, generalized additive mixed

model bersifat bebas dari asumsi kelinearan hubungan

diantara peubah penyerta dan peubah respon sehingga mampu untuk mereduksi masalah jika terjadi ketidaktepatan (misspecification) pemodelan didalam EBLUP. Aspek yang kedua, dengan kemampuannya untuk mengelaborasi pengaruh nonlinear dalam model,

generalized additive mixed model mampu untuk

meng-cover pola-pola yang tersembunyi dari peubah penyerta dan pada akhirnya akan meningkatkan akurasi dari pendugaan yang dilakukan.

UCAPAN TERIMA KASIH

Penelitian ini merupakan bagian dari penelitian Hibah Pasca yang dibiayai oleh Direktorat Jenderal Pendidikan Tinggi Departemen Pendidikan Nasional dengan judul Hibah Pengembangan Pendugaan Area Kecil dan Penerapannya pada Data BPS. Oleh karenanya terima kasih kami ucapkan kepada pihak Dikti dan LPPM-IPB.

DAFTAR PUSTAKA

1. Chand, N. and Alexander, C.H. 1995. Using

Administrative Records for Small Area Estimation in the American Community Survey. US Bureau of

the census.

2. Rao, J.N.K. 2003. Small Area Estimation, New York : John Wiley and Sons.

3. Hastie, T. and Tibshirani, R. 1990. Generalized

Additive Models. London: Chapman and Hall.

4. Prasad, N.G.N. and Rao, J.N.K. 1990. The Estimation of Mean Squared Errors of Small Area Estimators. Journal of American Statistical

Association 85 :163-171.

5. Ramsini, B., Suciu, G., Woodard, S.H., Elliott, M., dan Doss, H. 2001. Uninsured Estimates by County: A Review of Options and Issues.

<www.odh.ohio.gov/Data/OFHSurv/ ofhsrfq7.pdf>, [25 Mei 2005]

6. Fay, R.E. and Herriot, R.A. 1979. Estimates of income for small places: an application of James-Stein procedures to Census data. Journal of the

American Statistical Association, . 74 : 269-277

7. Russo, C., M. Sabbatini dan R. Salvatore. 2005. General linear models in small area estimation : an assessment in agricultural surveys. Paper

presented in The Mexsai

Conference.<www.siap.sagarpa.gob.mx/mexsai/tra

bajos/t44.pdf [29 April 2005]

8. Rao, J.N.K. 1999. Some Recent Advances in Model-Based Small Area Estimation. Survey

Methodology 25 (2) : 175-186.

9. Saei, A. and Chambers, R. 2003. Small area estimation: A Review of Methods Based on the Application of Mixed Models. S3RI Methodology

Working Paper M03/16.

10. Henderson, C.R. 1975. Best linear unbiased estimation and prediction under selection model.

Biometrics 31 : 423-447.

11. Kackar, R.N. and Harville, D.A. 1981. Unbiased of two-stage estimation and prediction procedure for mixed linear models. Communications in Statistics

– Theory and Methods A 10 : 1249-1261.

12. Ghosh, M. and Rao, J.N.K. 1994. Small area estimation : An appraisal”. Statistical Science 9(1) : 55-93.

13. Jiang, J. 1996. REML estimation: Asymptotic behavior and related topics. Annals of Statistics 24 : 255-286.

14. Butar, F.B. and Lahiri, P. 2003. On Measure of Uncertainty of Empirical Bayes Small Area Estimator. Journal of Statistical Planning and

Inference 112 : 63-76.

15. Jiang, J., Lahiri, P. and Wan, S.M. 2002. A Unified Jackknife Theory for Empirical Best Prediction with M-Estimation. Annals of Statistics 30 : 1782-1810. 16. Rao, J.N.K. 2005. Inferential Issues In Small Area

Estimation: Some New Developments. Statistics In

Transition 7 (3) : 513—526.

17. Stone, C.J. 1985. Additive Regression and Other Nonparametric Models. Annals of Statistics 13 : 689–705.