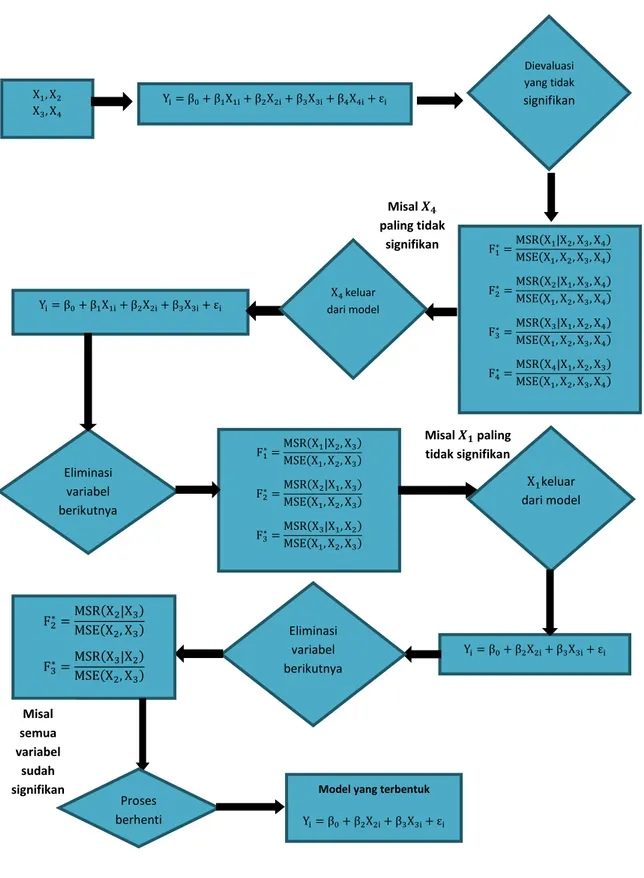
Metode-Metode Pemilihan Persamaan Terbaik Regresi Berganda
Disusun oleh :
Kelompok 3
1.
Arif Anjang Laksono (14611071)2.
Indang Sartika (14611080)3.
Rosi Desmitasari (14611087)4.
Muhammad AtmaYadin (14611088)5.
Aprilinda Puspa dewi Atmaja (14611095)JURUSAN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA
1
Muhammad Atma Yadin rosidesmitasari567@gmail.com
ABSTRAK
Salah satu langkah dalam regresi berganda setelah menentukan pola hubungan antara variabel independen (Y) dengan variabel dependen (X) adalah penentuan persamaan terbaik dari model yang telah dimiliki. Dalam menentukan persamaan yang terbaik terdapat beberapa metode yang dapat membantu untuk mendapatkan persamaan tersebut. Beberapa metode tersebut, yakni metode seleksi maju, metode
penyisihan, metode bertahap, metode semua kombinasi yang mungkin, metode R2
maksimum, dan metode PRESS.
Tujuan dari penulisan ini adalah untuk mengetahui persamaan terbaik regresi dengan menggunakan metode seleksi maju, metode penyisihan, metode bertahap yang menyangkut dengan studi kasus untuk faktor-faktor yang mempengaruhi panjang bayi dengan faktor-faktor yang mempengaruhi adalah usia, panjang waktu lahir, berat badan waktu lahir, dan ukuran dada waktu lahir.
Hasil pembahasan menunjukkan bahwa pada metode seleksi maju dan bertahap, panjang bayi hanya dipengaruhi oleh faktor usia dan berat badan waktu lahir dengan
persamaan regresi nya adalah Ŷ = 20,108+ 0,414X1+ 2,205X3 sedangkan pada metode
penyisihan, panjang bayi hanya dipengaruhi oleh faktor panjang waktu lahir dan berat
badan waktu lahir dengan persamaan regresi nya adalah Ŷ= 2,183+ 0,958X2 + 3,325X3
Kata Kunci: Metode Seleksi Maju, Metode Penyisihan, Metode Bertahap I. PENDAHULUAN
1.1 Latar Belakang
Permasalahan yang sering didapatkan dalam regresi berganda adalah salah dalam menenetukan persamaan terbaik untuk mengestimasi model yang telah dimiliki. Untuk mendapatkan persamaan terbaik yang diinginkan terdapat dua pertimbangan dalam pembentukan model, diantaranya: Agar persamaan regresi bermanfaat untuk tujuan prediksi, seringkali diinginkan persamaan yang memuat sebanyak-banyaknya variabel X (prediktor) yang mempengaruhi variabel Y (respon). Karena pertimbangan biaya untuk mendapatkan informasi, maka digunakan sesedikit mungkin variabel X (prediktor) yang mempengaruhi variabel Y (respon). Untuk itu dibutuhkan metode agar dapat mengakomodasikan dua kepentingan di atas yang digunakan untuk pemilihan
persamaan regresi terbaik. Metode pemilihan persamaan dalam regresi dilakukan dengan teknik pemilihan variabel (variable selection), dimana teknik pemilihan variabel adalah suatu teknik pemilihan subset dari sekelompok variabel independen yang dapat menjelaskan atau memprediksi nilai variabel dependen secara baik, sehingga kontribusi dari variabel independen yang tidak terpilih dapat diabaikan atau mungkin dianggap sebagai kesalahan murni (pure error).
Secara umum, teknik pemilihan variabel terbagi atas metode seleksi variabel satu per satu (Seleksi Maju, Penyisihan, Bertahap), metode semua kombinasi yang mungkin (All possible regression), metode R2 maksimum, dan metode PRESS. Metode seleksi variabel dilakukan dengan cara memasukkan atau mengeliminasi variabel independen satu per satu pada setiap tahapannya. Oleh karena itu, metode ini dapat digunakan untuk jumlah variabel independen yang banyak.
1.2 Rumusan Masalah
Berdasarkan pada latar belakang yang telah dipaparkan oleh penulis, maka terdapat beberapa rumusaan masalah yang dapat disusun, yaitu:
1. Apa yang dimaksud dengan metode seleksi maju, penyisihan, bertahap, semua kombinasi yang mungkin. R2 maksimum?
2. Bagaimana langkah-langkah yang dilakukan dalam penggunaan setiap metode untuk mendapatkan persamaan regresi terbaik?.
3. Apa persamaan yang terbentuk dari studi kasus pada tabel 3.1 yang diselesaikan dengan menggunakan metode seleksi maju, penyisihan, dan bertahap?.
4. Apakah persamaan terbaik yang didaptkan dari metode seleksi maju, metode penyisihan, dan metode mengandung peubah bebas yang sama dalam persamaannya?.
1.3 Tujuan Penulisan
Adapun tujuan penulis dalam penulisan makalah ini adalah:
1. Mengetahui pengertian dari metode seleksi maju, penyisihan, bertahap, semua kombinasi yang mungkin. R2 maksimum.
2. Mengetahui Langkah-langkah yang dilakukan dalam penggunaan setiap metode untuk mendapatkan persamaan regresi terbaik.
3. Mengetahui persamaan terbaik yang terbentuk berdasarkan studi kasus pada tabel 3.1 dengan menggunakan metode seleksi maju, penyisihan, dan bertahap
4. Mengetahui ada atau tidaknya perbedaan persamaan regresi yang didapatkan dari metode seleksi maju, penyisihan, dan bertahap.
II. LANDASAN TEORI 2.1 Koefisien Determinasi
Koefisien determinasi adalah salah satu nilai statistik yang dapat digunakan untuk mengetahui apakah ada hubungan pengaruh antara dua variabel. Nilai koefisien determinasi menunjukkan persentase variasi nilai variabel dependen yang dapat dijelaskan oleh persamaan regresi yang dihasilkan. Koefisien determinasi yang dinyatakan dengan R2 untuk pengujian regresi linier berganda yang mencakup lebih dari dua variabel adalah untuk mengetahui proporsi keragaman total dalam variabel tak bebas (Y) yang dapat dijelaskan atau diterangkan oleh variabel-variabel bebas (X) yang ada dalam model persamaan regresi linier berganda secara bersama-sama. Maka R2 akan ditetukan dengan rumus, yaitu:
𝑅2 = 𝐽𝐾𝑅 𝐽𝐾𝑇 dengan :
𝐽𝐾𝑅 = ( 𝑦̂ − 𝑦)𝑖 2 𝐽𝐾𝑇 = (𝑦𝑖− 𝑦)2
Harga R2 yang diperoleh sesuai dengan variansi yang dijelaskan masing-masing variabel yang tinggal dalam regresi. Hal ini mengakibatkan variasi yang dijelaskan penduga yang disebabkan oleh variabel yang berpengaruh saja (bersifat nyata).
2.2 Uji serempak (uji F)
Sugiyanto (1995:77) menjelaskan bahwa uji serempak dilakukan untuk mengetahui apakah variabel bebas berpengaruh secara bersama-sama terhadap variabel tak bebas. Sebelum pengujian hipotesis maka akan dicari perumusan F hitung terlebih dahulu
𝐹 =𝐽𝐾𝑅/(𝑝 − 1) 𝐽𝐾𝑆/(𝑛 − 𝑝) =
𝑅𝐾𝑅 𝑅𝐾𝑆
dengan:
RKR : Rataan Kuadrat Regresi RKS : Rataan Kuadrat Sisa
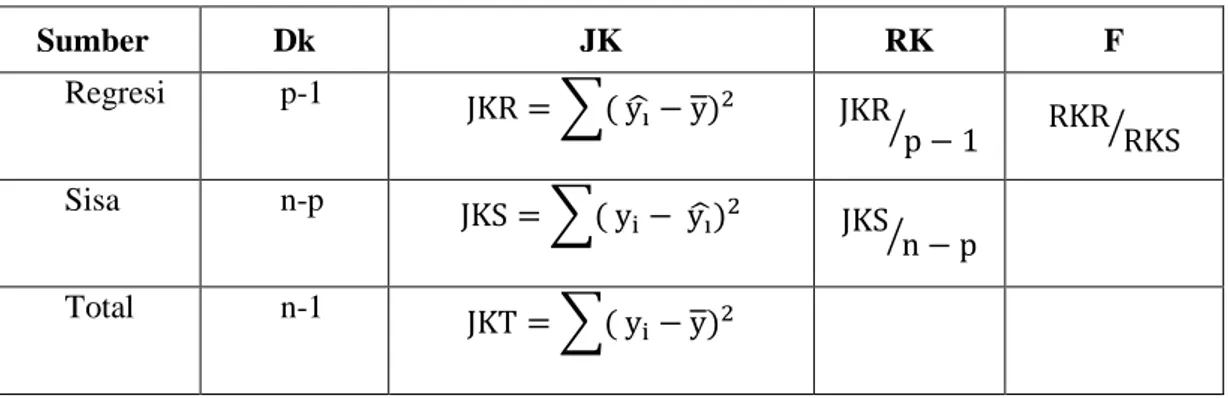
Tabel 2.1 Tabel anova
Sumber Dk JK RK F Regresi p-1 JKR = ∑( y i ̂ − y)2 JKR p − 1 ⁄ RKR⁄RKS Sisa n-p JKS = ∑( y i− ŷ )i 2 JKS n − p ⁄ Total n-1 JKT = ∑( y i− y)2
Pengujian hipotesis yang digunakan adalah sebagai berikut: I. Hipotesis
H0: b1,b2 ,...,bk = 0 (berarti variabel bebas secara bersama-sama tidak mempunyai
pengaruh yang signifikan terhadap variabel tak bebas).
H1 : bj ≠ 0 untuk suatu j = 1,2,..., k (berarti variabel bebas secara bersama-sama
mempunyai pengaruh yang signifikan terhadap variabel tak bebas).
II. Tingkat signifikansi : 𝛼% III. Statistik uji : Fhitung=
𝑅𝐾𝑅 𝑅𝐾𝑆
IV. Daerah kritis : H0 di tolak jika Fhitung>Ftabel(a; p-1,n - p)
V. Kesimpulan : Jika H0 ditolak berarti variabel bebas secara bersama sama
mempunyai pengaruh yang signifikan terhadap variabel tak bebas. 2.2.1 Uji F Parsial untuk Sebuah Parameter
Hipotesis: 𝐻0: 𝛽𝑘 = 0
𝐻1: 𝛽𝑘 ≠ 0
Statistik uji yang umum digunakan adalah statistik t yang berbentuk (Kutner at all, 2004).
𝑡 = 𝑏𝑘 𝑠(𝑏𝑘)
Dimana, s(bk) adalah taksiran standar deviasi dari parameter βk . Kriteria hipotesisnya adalah terima H0 jika thitung ≤ ttabel (1 −
α
2, n − p) sebaliknya
tolak H0 jika thitung> ttabel (1 − α
2, n − p), dimana ttabel (1 − α
2, n − p), merupakan
persentil distribusi t yang sering disebut ttabel. Alternatif untuk statistik uji dalam kasus ini adalah penggunaan Jumlah Kuadrat Ekstra dengan statistik uji.
𝐹 =(𝐽𝐾𝑅 𝑋𝐾|𝑋1, … , 𝑋𝐾−1, 𝑋𝐾+1, … , 𝑋𝑃−1) 1 ÷ (𝐽𝐾𝐸 𝑋1, … , 𝑋𝑃−1) 𝑛 − 𝑝 =(𝑅𝐾𝑅 𝑋𝐾|𝑋1, … , 𝑋𝐾−1, 𝑋𝐾+1, … , 𝑋𝑃−1) 𝑅𝐾𝐸 Kriteria keputusan untuk error 𝛼 :
Terima H0, jika Fhitung ≤ Ftabel (1 − 𝛼; 1; n – p).
Tolak H0 , jika Fhitung>Ftabel (1 − 𝛼; 1; n – p).
Dua statistik uji dari sub bab 2.2.1 adalah ekivalen, kesamaan ini diberikan oleh: 𝐹 = ( 𝑏𝑘
𝑠(𝑏𝑘))
2
= (𝑡)2 2.2.2 Uji F Parsial untuk Beberapa Parameter
Hipotesis
𝐻0: 𝛽𝑞 = 𝛽𝑞+1 = ⋯ = 𝛽𝑝−1 = 0
𝐻1: 𝑝𝑎𝑙𝑖𝑛𝑔𝑠𝑒𝑑𝑖𝑘𝑖𝑡 𝑠𝑒𝑏𝑢𝑎ℎ 𝛽𝑘 ≠ 0, 𝑘 = 𝑞, ⋯ , 𝑝 – 1
Uji statistiknya (statistik 𝐹) menggunakan Jumlah Kuadrat Ekstra (Kutner at all, 2004). 𝐹 =𝐽𝐾𝑅 (𝑋𝑞 , … , 𝑋𝑝−1, |𝑋1, 𝑋2, … , 𝑋𝑝−1) 𝑝 − 𝑞 ÷ 𝐽𝐾𝐸 (𝑋1, … , 𝑋𝑝−1) 𝑛 − 𝑝 =𝑅𝐾𝑅 (𝑋𝑞 , … , 𝑋𝑝−1| 𝑋1, 𝑋2, … , 𝑋𝑃−1) 𝑅𝐾𝐸 Kriteria keputusan untuk error 𝛼 :
Terima H0, jika Fhitung≤ Ftabel (1 − 𝛼; p − q; n – p).
Tolak H0, jika Fhitung>Ftabel(1 − 𝛼; p − q; n – p).
Statistik uji pada sub bab 2.2.2 dapat dilakukan dengan statistik uji alternatif menggunakan koefisien determinasi sebagai berikut:
𝐹 =𝑅(𝑌 | 1,…,𝑝 − 1) 2 − 𝑅 (𝑌 |1,…,𝑞 − 1)2 𝑝 − 𝑞 ÷ 1 − 𝑅(𝑌 | 1,…,𝑝 − 1)2 𝑛 − 𝑞
Dimana R2(Y | 1,…,p − 1) merupakan koefisien determinasi ketika Y diregresikan terhadap semua peubah bebas X dan R(Y |1,…,q − 1)2 merupakan koefisien determinasi ketika Y diregresikan hanya pada sebagian peubah X1, X2, ⋯ , X𝑞−1 (Kutner at all,
2004).
2.3 Koefisien Korelasi
Analisis korelasi adalah studi yang membahas derajat hubungan antara variabel-variabel. Ukuran yang dipakai untuk mengetahui derajat hubungan, terutama data kuantitatif dinamakan koefisien korelasi. Besarnya hubungan antara variabel yang satu dengan variabel yag lain dinyatakan dengan koefisien korelasi yang disimbolkan dengan “r” yang besarnya adalah akar koefisien determinasi. Atau secara matematis dapat ditulis sebagai berikut:
𝑟 = √𝑅2
Koefisien korelasi (r) dapat digunakan untuk:
1. Mengetahui keeratan hubungan (korelasi linier) antara dua variabel.
2. Mengetahui arah hubungan antara dua variabel.
Untuk mengetahui keeratan hubungan antara dua variabel dengan menggunakan koefisien korelasi adalah dengan menggunakan nilai absolut dari koefisien tersebut. Besarnya koefisien korelasi (r) antara dua variabel adalah nol sampai dengan 1. Apabila dua buah variabel mempunyai nilai r = 0, berarti antara dua variabel tersebut tidak ada hubungan. Sedangkan apabila dua buah variabel mempunyai r = ±1, maka dua buah variabel tersebut mempunyai hubungan yang sempurna.
Semakin tinggi nilai koefisien korelasi antara dua buah variabel (semakin mendekati 1), maka tingkat keeratan hubungan antara dua variabel tersebut semakin tinggi. Dan sebaliknya semakin rendah koefisien korelasi antara dua buah variabel (semakin mendekati 0), maka tingkat keeratan hubungan antara dua variabel tersebut semakin lemah.
2.3.1 Koefisien Korelasi Parsial
Koefisien korelasi parsial dimaksudkan untuk menengukur keeratan dua peubah dengan menganggap peubah lainnya adalah tetap atau dikontrol (Pahira,2003). Misalkan terdapat tiga peubah X,Y,Z, maka koefisien parsial antara X dan Y bila Z dikontrol (dipertahankan konstan) didefinisikan sebagai seberikut:
𝑅𝑥𝑦,𝑧
𝑅𝑥𝑦− 𝑅𝑥𝑧 𝑅𝑦𝑧 √1 − 𝑅𝑥𝑧2 √1 − 𝑅
𝑦𝑧2
2.4 Memilih Persamaan Regresi
Apa yang sebenarnya disebut model regresi “terbaik” bergantung sebahagian pada tujuan yang diinginkan dalam membuat model (Tiro, 2002). Kata yang “terbaik” belum tentu tunggal dan masing-masing mempunyai keunggulan dan kelemahan. Kesederhanaan dan keefektifan model merupakan pertimbangan yang akan selalu diperhatikan dalam pemilihan model. Makin besar makin besar pula 𝑣𝑎𝑟(𝑦 ). Ini berarti bahwa bila kemampuan dua atau lebih model sama atau hampir sama dalam menggambarkan persoalan yang hendak dibahas maka akan cenderung dipilih yang paling sedikit mengandung peubah bebas di dalamnya atau paling sederhana (Sembiring, 1995).
2.4.1 Metode Seleksi Maju (Forward)
Secara esensial, metode ini bekerja dengan cara memasukkan peubah bebas satu demi satu menurut urutan besar pengaruhnya terhadap model, kemudian menguji signifikansi parameter regresi dan proses berhenti bila semua peubah bebas yang memenuhi syarat telah masuk ke dalam model yang dibangun (Sembiring, 1995).
Perhatikan bahwa apakah pengaruh (korelasi) positif atau negatif tidak dipersoalkan karena yang diperhatikan hanyalah eratnya hubungan antara suatu peubah bebas dengan 𝑌. Salah satu keuntungannya ialah dapat melihat proses pembentukan model itu tahap demi tahap dimulai dari yang pertama sekali (Sembiring, 1995).
2.4.2 Metode Penyisihan (Eliminasi Mundur)
Variabel peubah bebas (independent) yang pertama kali masuk ke dalam model adalah variabel yang mempunyai korelasi tertinggi dan signifikan dengan variabel
variabel dependent adalah tertinggi kedua dan masih signifikan, dilakukan terus menerus samapi tidak ada lagi variabel independenyang signfikan.
2.4.3 Metode Bertahap (Stepwise)
Metode Bertahap gabungan antara metode seleksi maju dan metode penyisihan, variabel yang pertama kali masuk adalah variabel yang korelasinya tertinggi dan signifikan dengan variabel dependent, variabel yang masuk kedua adalah variabel yang korelasi parsialnya tertinggi dan masih signifikan, setelah variabel tertentu masuk ke dalam model maka variabel lain yang ada di dalam model dievaluasi, jika ada variabel yang tidak signifikan maka variabel tersebut dikeluarkan.
2.4.4 Metode Semua Kombinasi yang Mungkin
Metode ini mengharuskan memeriksa semua kombinasi peubah yang dapat dibuat. Bila ada k peubah bebas (independent) yang tersedia maka kemudian memeriksa persamaan yang terbentuk sebanyak 2k. Kelebihan menggunakan metode ini adalah memungkinkan untuk melihat semua kombinasi. Kelemahannya terletak pada banyaknya pekerjaan yang harus di hadapi. (Sembiring,1995). Dalam metode semua kombinasi yang mungkin untuk menilai suatu kebaikan model maka yang digunakan sebagai patokan adalah:
- 𝑅2 yang disesuaikan, dilambangkan 𝑅2
- 𝑅𝑆2, rataan kuadrat sisa
- Cp Mallows
2.4.4.1 𝐑𝟐- disesuaikan ( 𝑹𝟐)
Salah satu kelemahan 𝑅2 ialah bahwa besarnya dipengaruhi oleh banyaknya peubah bebas dalam model, membesar bersama p, sehingga sulit menyatakan 𝑅2 yang optimum. Suatu cara untuk mengatasi kelemahan tersebut adalah dengan menggunakan apa yang disebut R2- disesuaikan, dengan lamban 𝑅2.
𝑅2 = 𝐽𝐾𝑅 𝐽𝐾𝑇 = 𝐽𝐾𝑅 𝐽𝐾𝑅 + 𝐽𝐾𝑆 = 𝐽𝐾𝑅/𝐽𝐾𝑆 1 + 𝐽𝐾𝑅/𝐽𝐾𝑆 Sedangkan, F =JKR/p−1
𝑅2 = (𝑝 − 1)𝐹/(𝑛 − 𝑝) 1 + (𝑝 − 1)𝐹/(𝑛 − 𝑝) 𝑅2 = 𝐹 𝐹 + (𝑛 − 𝑝)/(𝑝 − 1) kemudian, didapatkan: 𝑅2 = 1 −𝐽𝐾𝑆 𝐽𝐾𝑇 𝑅2 = 1 −𝐽𝐾𝑆/(𝑛 − 𝑝) 𝐽𝐾𝑇/(𝑛 − 1) 𝑅2 = 1 −(𝑛 − 1) (𝑛 − 𝑝) (1 − 𝑅2 )
Nilai koefisien determinasi adjusted (𝑅2)mengukur kontribusi variabel penjelas terhadap variabel respon setelah menghilangkan pengaruh penambahan variabel. Dengan metode ini kita mencari peningkatan 𝑅2 yang cukup besar dan mengabaikan peningkatan 𝑅2 yang tidak begitu besar.
2.4.4.2 Rataan Kuadarat Sisa ( 𝐬𝟐)
Salah satu patokan yang baik digunakan dalam menilai kecocokan suatu model dengan data ialah kuadrat sisa 𝑠2, semakin kecil maka semakin baik. Rataan kuadrat sisa memperhitungkan banyaknya parameter dalam model melalui pembagian dengan derajat kebebasannya (dk). Rataan kuadrat sisa mengkin membesar bila penurunan dalan JKS akibat pemasukan suatu peubah tambahan ke dalam model tidak dapat mengimbangi penurunan dalam derajat kebebasannya.
𝑠2 = 𝐽𝐾𝑆 𝑛 − 𝑝
Nilai rataan kuadrat sisa ( 𝑠2) akan menurun seiring dengan peningkatan jumlah variabel penjelas. Dengan metode ini kita mencari penurunan 𝑠2 yang cukup besar dan mengabaikan penurunan 𝑠2 yang tidak begitu besar. Jadi, menurut patokan ini, berhenti jika 𝑠2 sudah mencapai minimum, model sudah jenuh.
2.4.4.3 Statistik 𝑪𝒑 Mallows
Cp Mallows didasarkan pada total squared error dari n observasi yang
komponen bias dan komponen random error. Dalam ilmu statistik, kriteria Cp Mallows
sering digunakan untuk membantu dalam pemilihan model regresi berganda yang potensial. Statistik Cp didefinisikan sebagai sebuah criteria untuk menaksir ketepatan
ketika model-model dengan jumlah parameter yang dibandingkan. Nilainya diberikan dengan:
𝐶𝑝 =𝐽𝐾𝑆𝑝
𝑠2 − 𝑛 + 2𝑝
Dimana JKSp merupakan residual sum of square suntuk model dengan p-1
variabel. Dalam menggunakan Cp Mallows, dicoba untuk mencari subset model dengan
p independent variable yang menunjukkan nilai Cp yang terkecil dan nilai Cp yang dekat
dengan p. Alasannya adalah karena kumpulan variabel penjelas dengan nilai Cp yang
kecil memiliki total mean squared error yang kecil, dan ketika nilainya juga dekat dengan p maka bias dari model regresi juga kecil.
2.5 Uji Asumsi Klasik
Uji asumsi klasik adalah persyaratan statistik yang harus dipenuhi pada analisis regresi linear berganda yang berbasis ordinary least square (OLS). Jadi analisis regresi yang tidak berdasarkan OLS tidak memerlukan persyaratan asumsi klasik, misalnya regresi logistik atau regresi ordinal. Demikian juga tidak semua uji asumsi klasik harus dilakukan pada analisis regresi linear, misalnya uji multikolinearitas tidak dilakukan pada analisis regresi linear sederhana dan uji autokorelasi tidak perlu diterapkan pada data cross sectional. Uji asumsi klasik juga tidak perlu dilakukan untuk analisis regresi linear yang bertujuan untuk menghitung nilai pada variabel tertentu.
Uji asumsi klasik yang sering digunakan yaitu uji multikolinearitas, uji heteroskedastisitas, uji normalitas, uji autokorelasi. Tidak ada ketentuan yang pasti tentang urutan uji mana dulu yang harus dipenuhi. Analisis dapat dilakukan tergantung pada data yang ada. Sebagai contoh, dilakukan analisis terhadap semua uji asumsi klasik, lalu dilihat mana yang tidak memenuhi persyaratan. Kemudian dilakukan perbaikan pada uji tersebut, dan setelah memenuhi persyaratan, dilakukan pengujian pada uji yang lain.
2.5.1 Uji Normalitas Residual
Uji normalitas adalah untuk melihat apakah nilai residual terdistribusi normal atau tidak. Model regresi yang baik adalah memiliki nilai residual yang terdistribusi normal. Jadi uji normalitas bukan dilakukan pada masing-masing variabel tetapi pada nilai residualnya. Sering terjadi kesalahan yang jamak yaitu bahwa uji normalitas dilakukan pada masing-masing variabel. Hal ini tidak dilarang tetapi model regresi memerlukan normalitas pada nilai residualnya bukan pada masing-masing variabel penelitian.
Uji normalitas dapat dilakukan dengan uji histogram, uji normal P Plot, uji Chi
Square, Skewness dan Kurtosis atau uji Kolmogorov Smirnov. Tidak ada metode yang
paling baik atau paling tepat. Tipsnya adalah bahwa pengujian dengan metode grafik sering menimbulkan perbedaan persepsi di antara beberapa pengamat, sehingga penggunaan uji normalitas dengan uji statistik bebas dari keragu-raguan, meskipun tidak ada jaminan bahwa pengujian dengan uji statistik lebih baik dari pada pengujian dengan metode grafik.
Jika residual tidak normal tetapi dekat dengan nilai kritis (misalnya signifikansi Kolmogorov Smirnov sebesar 0,049) maka dapat dicoba dengan metode lain yang mungkin memberikan justifikasi normal. Tetapi jika jauh dari nilai normal, maka dapat dilakukan beberapa langkah yaitu: melakukan transformasi data, melakukan
trimming data outliers atau menambah data observasi. Transformasi dapat dilakukan ke
dalam bentuk logaritma natural, akar kuadrat, inverse, atau bentuk yang lain tergantung dari bentuk kurva normalnya, apakah condong ke kiri, ke kanan, mengumpul di tengah atau menyebar ke samping kanan dan kiri.
2.5.2 Uji Multikolinearitas
Uji multikolinearitas adalah untuk melihat ada atau tidak korelasi yang tinggi antara variabel-variabel bebas dalam suatu model regresi linear berganda. Jika ada korelasi yang tinggi di antara variabel-variabel bebasnya, maka hubungan antara variabel bebas terhadap variabel terikatnya menjadi terganggu.
Alat statistik yang sering dipergunakan untuk menguji gangguan multikolinearitas adalah dengan variance inflation factor (VIF), korelasi pearson antara variabel-variabel bebas, atau dengan melihat eigenvalues dan condition index (CI).
Beberapa alternatif cara untuk mengatasi masalah multikolinearitas adalah sebagai berikut:
1. Mengganti atau mengeluarkan variabel yang mempunyai korelasi yang tinggi. 2. Menambah jumlah observasi.
3. Mentransformasikan data ke dalam bentuk lain, misalnya logaritma natural, akar kuadrat atau bentuk first difference delta.
2.5.3 Uji Heteroskedastisitas
Uji heteroskedastisitas adalah untuk melihat apakah terdapat ketidaksamaan varians dari residual satu ke pengamatan ke pengamatan yang lain. Model regresi yang memenuhi persyaratan adalah di mana terdapat kesamaan varians dari residual satu pengamatan ke pengamatan yang lain tetapi atau disebut homoskedastisitas.
Deteksi heteroskedastisitas dapat dilakukan dengan metode scatter plot dengan memplotkan nilai ZPRED (nilai prediksi) dengan SRESID (nilai residualnya). Model yang baik didapatkan jika tidak terdapat pola tertentu pada grafik, seperti mengumpul di tengah, menyempit kemudian melebar atau sebaliknya melebar kemudian menyempit. Uji statistik yang dapat digunakan adalah uji Glejser, uji Park atau uji White.
Beberapa alternatif solusi jika model menyalahi asumsi heteroskedastisitas adalah dengan mentransformasikan ke dalam bentuk logaritma, yang hanya dapat dilakukan jika semua data bernilai positif. Atau dapat juga dilakukan dengan membagi semua variabel dengan variabel yang mengalami gangguan heteroskedastisitas.
2.5.4 Uji Autokorelasi
Uji autokorelasi adalah untuk melihat apakah terjadi korelasi antara suatu periode t dengan periode sebelumnya (t -1). Secara sederhana adalah bahwa analisis regresi adalah untuk melihat pengaruh antara variabel bebas terhadap variabel terikat, jadi tidak boleh ada korelasi antara observasi dengan data observasi sebelumnya.
Beberapa uji statistik yang sering dipergunakan adalah uji Durbin-Watson, uji dengan Run Test dan jika data observasi di atas 100 data sebaiknya menggunakan uji
Lagrange Multiplier. Beberapa cara untuk menanggulangi masalah autokorelasi adalah
dengan mentransformasikan data atau bisa juga dengan mengubah model regresi ke dalam bentuk persamaan beda umum (generalized difference equation). Selain itu juga
dapat dilakukan dengan memasukkan variabel lag dari variabel terikatnya menjadi salah satu variabel bebas, sehingga data observasi menjadi berkurang 1.
III. METODE PENELITIAN
Metode yang digunakan dalam penulisan makalah ini adalah studi literatur yaitu dengan mengambil, mengulas, atau membandingkan isi dari penulisan buku, jurnal maupun tulisan yang berkaitan dengan pembahasan pada penulisan makalah ini, dan kasus yang dibahas yaitu tentang pemilihan persamaan terbaik dalan analisis regresi bergandadi bantu dengan software SPSS. Adapun studi kasus yang diambil dalam penulisan makalah ini bersumber dari buku dengan studi kasus nya adalah:
3.1. Studi Kasus
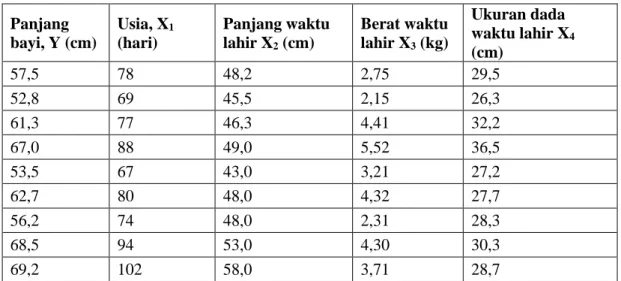
Pada penulisan makalah ini, studi kasus yang diambil oleh penulis adalah data pengukuran 9 bayi. Tujuan percobaan ialah untuk menemukan taksiran persamaan yang cukup baik yang mengaitkan panjang bayi dengan semua atau sebagian peubah bebas. Data pengukuran disajikan dalam tabel 3.1.
Tabel 3.1 Data pengukuran bayi (Walpole & Myers, 1995)
Panjang bayi, Y (cm) Usia, X1 (hari) Panjang waktu lahir X2 (cm) Berat waktu lahir X3 (kg) Ukuran dada waktu lahir X4 (cm) 57,5 78 48,2 2,75 29,5 52,8 69 45,5 2,15 26,3 61,3 77 46,3 4,41 32,2 67,0 88 49,0 5,52 36,5 53,5 67 43,0 3,21 27,2 62,7 80 48,0 4,32 27,7 56,2 74 48,0 2,31 28,3 68,5 94 53,0 4,30 30,3 69,2 102 58,0 3,71 28,7 IV. PEMBAHASAN
Data yang telah disajikan dalam studi kasus dalam tabel 3.1 akan diselesaikan dengan menggunakan tiga metode, yakni metode seleksi maju, metode penyisihan, dan metode bertahap. Adapun tahapan-tahapan dalam analisis regresi sebelum mengestimasi sebuah model regresi dengan menggunakan tiga metode tersebut, yakni:
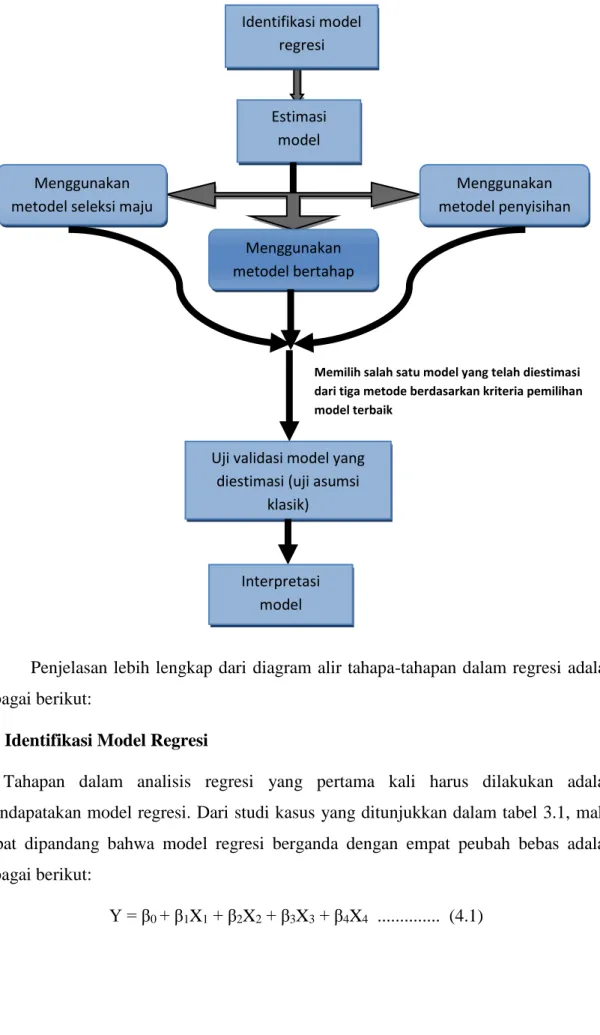
Diagram 4.1 Flowchart tahapan regresi
Penjelasan lebih lengkap dari diagram alir tahapa-tahapan dalam regresi adalah sebagai berikut:
4.1 Identifikasi Model Regresi
Tahapan dalam analisis regresi yang pertama kali harus dilakukan adalah mendapatakan model regresi. Dari studi kasus yang ditunjukkan dalam tabel 3.1, maka dapat dipandang bahwa model regresi berganda dengan empat peubah bebas adalah sebagai berikut: Y = β0+ β1X1 + β2X2 + β3X3 + β4X4 ... (4.1) Identifikasi model regresi Estimasi model Menggunakan
metodel seleksi maju
Menggunakan metodel penyisihan Menggunakan
metodel bertahap
Memilih salah satu model yang telah diestimasi dari tiga metode berdasarkan kriteria pemilihan model terbaik
Uji validasi model yang diestimasi (uji asumsi
klasik)
Interpretasi model
Model regresi berganda pada persamaan 4.1 digunakan dengan memandang bahwa data pada tabel 3.1 memiliki pola hubungan yang linear antara variabel independen dan dependen. Sehingga, estimasi dari model regresi tersebut adalah sebagai berikut:
ŷ = a + b1x1 + b2x2 + b3x3 + b4x4 ... (4.2)
Dari persamaan 4.2, maka dapat dilakukan estimasi koefisien regresi untuk mengestimasi parameter yang terdapat dalam model regresi. Estimasi koefisien regresi berdasarkan pada tabel 3.1 dilakukan dengan tiga metode untuk mendapatkan persamaan terbaik, yakni metode seleksi maju, penyisihan mundur, dan bertahap.
4.2 Estimasi Model Terbaik ( Pemilihan Persamaan Terbaik) 4.2.1 Pemilihan Persamaan Terbaik dengan Metode Seleksi Maju
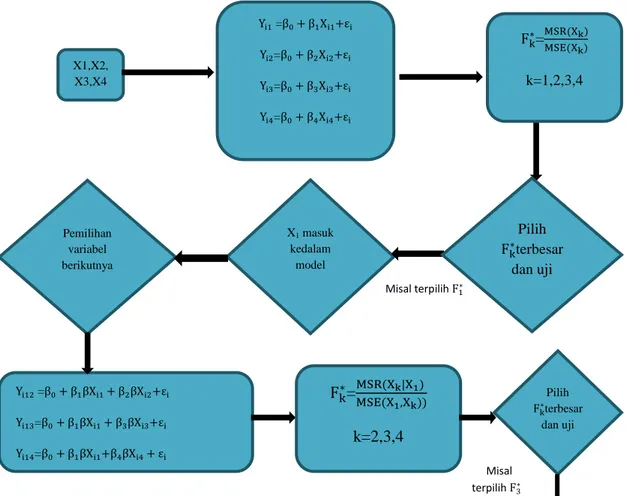
Ilustrasi penggunaan metode seleksi maju adalah sebagai berikut: Diagram 4.2 Flowchart metode seleksi maju
X1,X2, X3,X4 Yi1 =β0+ β1Xi1+εi Yi2=β0+ β2Xi2+εi Yi3=β0+ β3Xi3+εi Yi4=β0+ β4Xi4+εi Pemilihan variabel berikutnya X1 masuk kedalam model Yi12 =β0+ β1βXi1+ β2βXi2+εi Yi13=β0+ β1βXi1+ β3βXi3+εi Yi14=β0+ β1βXi1+β4βXi4+ εi Fk∗=MSR(Xk|X1) MSE(X1,Xk)) k=2,3,4 Misal terpilih F1∗ Pilih Fk∗terbesar dan uji Misal terpilih F3∗ Pilih Fk∗terbesar dan uji Fk∗= MSR(Xk) MSE(Xk) k=1,2,3,4
Penjelasan lebih lengkap dari ilustrasi diagram alir dengan menggunakan metode seleksi maju adalah sebagai berikut:
1. Langkah pertama dilakukan dengan membuat matriks korelasi dari semua variabel yang dimiliki. X3 signifikan ketika X1 sudah ada didalam model X3 masuk ke dalam model Pemilihan variabel berikutnya Yi132=β0+ β1βXi1+ β3βXi3+ β2βXi2+εi Yi134=β0+ β1βXi1+β3βXi3+ β4βXi4+ εi Fk∗= MSR(Xk|X1,X3) MSE(X1,X3,Xk)) k=2,4 Pilih Fk∗terbesar dan uji X2 tidak signifikan Misal terpilih F2∗ X2 tidak masuk ke dalam model Pengujian variabel terakhir(X4) F4∗= MSR(X4|X1,X3) MSE(X1,X3,X4)) Proses berhenti
Model yang terbentuk
Yi=β0+ β1βXi1+ β3βXi3+εi X4 tidak signifikan X4 tidak masuk ke dalam model
Tabel 4.1 Matriks korelasi data tabel 3.1 X1 X2 X3 X4 Y X1 1,000 X2 0,952 1,000 X3 0,534 0,263 1,000 X4 0,390 0,155 0,784 1,000 Y 0,947 0,819 0,761 0,560 1,000
Berdasarkan pada tabel 4.1 terlihat bahwa X1 memberi korelasi terbesar dengan Y,
sehingga X 1 masuk pertama sekali ke dalam model.
2. Setelah matriks korelasi telah dibuat dan salah satu variabel peubah bebas dipilih (X1), maka selanjutnya yang adalah mencari nilai koefisen determinasi, pembuatan
tabel anova, dan pembuatan taksiran persamaan sementara untuk variabel X1 yang
telah masuk terlebih dahulu.
Gambar 4.1 Nilai koefisien determinasi, tabel anova, tabel koefisen regresi X1
Berdasarkan pada gambar 4.1 dapat dilihat bahwa nilai koefisen determinasi (R2) sebesar 0,897 atau 89,7%. Arti dari nilai koefisien determinasi sebesar 89,7% adalah keragaman y yang mampu dijelaskan oleh variabel X1 adalah sebesar 89,7% dan 10,3%
koefisien determinasi adalah keragaman panjang bayi yang mampu dijelaskan oleh usia adalah sebesar 89,7% dan 10,3% lainnya dijelaskan oleh faktor lain di luar model.
Dari gambar 4.1 dapat disusun uji hipotesis untuk X1 yang masuk pertama kali
pada persamaan. 1. Hipotesis
H0 : β1= 0 (variabel bebas X1 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β1 ≠ 0 (variabel bebas X1 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika sig. < tingkat signifikansi atau Fhit > Ftabel.
4. Statistik Uji
Sig.= 0,000 atau Fhit = 𝐾𝑇𝑅 𝐾𝑇𝐺
5. Keputusan
H0 ditolak, karena sig= 0,000 < tingkat signifikansi = 0,05 atau Fhit = 60,950 > Ftabel (1,7,0.05) = 5,59
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.1, dapat dilihat bahwa sig. lebih kecil dari tingkat signifikansi, yaitu 0,000 < 0,05 atau atau Fhit = 60,950 > Ftabel = 5,59 maka
dapat dikatakan bahwa H0 ditolak, artinya bahwa β1 memiliki nilai tidak sama dengan
nol dan dapat dikatakan bahwa usia berpengaruh secara signifikan terhadap panjang bayi.
Berdasarkan pada uji hipotesis nilai β1 tidak sama dengan nol yang artinya
variabel X1 berpengaruh secara signifikan dengan variabel Y, maka dapat diperoleh
taksiran persamaan untuk X1 sebagai variabel peubah bebas yang masuk pertama kali
3. Langkah berikutnya adalah pemeriksaan kuadrat korelasi parsial dengan variabel kontrol nya adalah X1 (r2yxj,x1 untuk j = 2, 3, dan 4).
Tabel 4.2 Kuadrat korelasi parsial dengan X2, X3, dan X4
Xj r2
yxj.x1 Fmasuk
X2 0,720801 15,529 X3 0,885481 46,473 X4 0,417316 4,301
Dari tabel 4.2 terlihat bahwa calon peubah bebas berikutnya yang masuk ialah X3.
Hal ini dikarenakan kuadrat korelasi parsial Y dengan X3 dikontrol terhadap X1 yang
lebih besar diantara peubah bebas lainnya sesuai pada tabel 4.2. Oleh karena itu, dilakukan perhitungan koefisen regresi untuk X1 dan X3 beserta statistik yang
diperlukan.
Tabel 4.3 Koefisien regresi X1 dan X3
Peubah bebas Koefisien regresi Galat
baku F (1,6) Kuadrat korelasi parsial X1 4,136 0,297 208,243 0,972196 X3 0,203 0,029 46,473 0,885481 Tetapan 201,085
Gambar 4.3 Tabel koefisien
Tambahan R2 akibat pemasukan X3 adalah 89,7% - 98,8% = 9,1%, suatu
penambahan yang tidak kecil, artinya bahwa ketika terjadi pemasukkan variabel X3
maka keragaman Y yang mampu dijelaskan oleh model adalah semakin besar, hanya berkisar 1,2% yang dijelaskan oleh faktor lain di luar model. Begitupun s2 bertambah
kecil dari 4,728 menjadi 0,631. Untuk melihat apakah seluruh koefisien regresi signifikan atau berarti ketika terjadi pemasukkan variabel X3, maka perlu dilakukan uji
hipotesis secara keseluruhan (overall). 1. Uji Overall (X1 dan X3)
1. Hipotesis
H0 : β1 = β3= 0 (variabel bebas secara bersama-sama tidak mempunyai pengaruh yang
signifikan terhadap variabel tak bebas)
H1 : Minimal salah satu βi≠ 0, i =1,3 (minimal terdapat salah satu variabel bebas tidak
mempunyai pengaruh yang signifikan terhadap variabel tak bebas)
2. Tingkat Signifikansi α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika sig. < tingkat signifikansi atau Fhit > Ftabel(2,6,0.05).
4. Statistik Uji
Sig.= 0,000 atau Fhit = 𝐾𝑇𝑅 𝐾𝑇𝐺
5. Keputusan
H0 ditolak, karena sig= 0,000 < tingkat signifikansi = 0,05 atau Fhit = 251,650 > Ftabel
= 5,14 6. Kesimpulan
Berdasarkan hasil output pada gambar 4.2, dapat dilihat bahwa sig. lebih kecil dari tingkat signifikansi, yaitu 0,000 < 0,05 atau atau Fhit = 251,650 > Ftabel = 5,14 maka
dapat dikatakan bahwa H0 ditolak, artinya bahwa minimal salah satu dari β1 dan β3
ataupun kedua nya yang memiliki nilai tidak sama dengan nol. Oleh karena itu, perlu dilakukan uji parsial untuk memeriksa apakah koefisien regresi berarti atau tidak. 2. Uji Parsial (X3)
1. Hipotesis
H0 : β3= 0 (variabel bebas X3 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β3 ≠ 0 (variabel bebas X3 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 ditolaj jika Fmasuk (X3)> Ftabel.
4. Statistik Uji Fmasuk (X3) = 𝐽𝐾𝑅 (𝑋3|𝑋1) 1 ∶ 𝐽𝐾𝑆 (𝑋3,𝑋1) 𝑛−𝑝 5. Keputusan
H0 ditolak, karena Fmasuk (X3) = 46,473 > Ftabel(1,6,0.05)= 5,99
6. Kesimpulan
Berdasarkan hasil output pada tabel 4.3, dapat dilihat bahwa Fmasuk (X3) = 46,473 >
Ftabel = 5,99 maka dapat dikatakan bahwa H0 ditolak, artinya bahwa β3 memiliki nilai
4. Langkah selanjutnya kembali lagi seperti pada langkah ketiga, yaitu pemeriksaan kuadrat korelasi parsial dengan variabel kontrol nya adalah X1 dan X3 (r2yxj,x1x3 untuk
j = 2 dan 4).
Tabel 4.4 Kuadrat korelasi parsial dengan X2 dan X4
Xj r2
yxj.x1x3 Fmasuk
X2 0,20974 1,328
X4 0,04884 0,257
Dari tabel 4.4 dapat dilihat bahwa nilai kuadrat korelasi parsial dari X2 lebih besar
dibandinkan dengan X4, namun nilai kuadrat korelasi parsial untuk X2 masih tergolong
rendah. oleh karena itu perlu dilakukan uji hipotesis untuk melihat apakah nilai X2 dan
X4 memenuhi syarat untuk masuk pada persamaan regresi.
3. Uji Parsial (X2)
1. Hipotesis
H0 : β2= 0 (variabel bebas X2 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β2 ≠ 0 (variabel bebas X2 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 jika Fmasuk (X2)> Ftabel.
4. Statistik Uji Fmasuk (X2) = 𝐽𝐾𝑅 (𝑋2|𝑋1𝑥3) 1 ∶ 𝐽𝐾𝑆 (𝑋2,𝑋1,𝑋3) 𝑛−𝑝 5. Keputusan
H0 diterima, karena Fmasuk (X2) = 1,328 < Ftabel(1,5,0.05) = 6,61
6. Kesimpulan
Berdasarkan hasil output pada tabel 4.4, dapat dilihat bahwa Fmasuk (X2) = 1,328 <
Ftabel = 6,61 maka dapat dikatakan bahwa H0 diterima, artinya bahwa β2 memiliki
berarti. Oleh karena itu, X2 tidak memenuhi syarat untuk masuk dalam taksiran
persamaan regresi. 4. Uji Parsial (X4)
1. Hipotesis
H0 : β4= 0 (variabel bebas X4 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β4 ≠ 0 (variabel bebas X4 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 jika Fmasuk (X4)> Ftabel.
4. Statistik Uji Fmasuk (X4) = 𝐽𝐾𝑅 (𝑋4|𝑋1𝑥3) 1 ∶ 𝐽𝐾𝑆 (𝑋4,𝑋1,𝑋3) 𝑛−𝑝 5. Keputusan
H0 diterima, karena Fmasuk (X4) = 0,257< Ftabel(1,5,0.05) = 6,61
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.4, dapat dilihat bahwa Fmasuk (X4) = 0,257 <
Ftabel = 6,61 maka dapat dikatakan bahwa H0 diterima, artinya bahwa β4 memiliki
nilai sama dengan nol atau dapat dikatakan β4 adalah koefisien regresi yang tidak
berarti. Oleh karena itu, X4 tidak memenuhi syarat untuk masuk dalam taksiran
persamaan regresi.
Berdasarkan pada uji hipotesis untuk X2 dan X4 dapat dikatakan bahwa kedua
variabel peubah bebas tersebut tidak memenuhi syarat untuk masuk dalam taksiran persamaan regresi. Oleh karena itu, taksiran persamaan regresi yang diperoleh dari metode seleksi maju ini adalah Ŷ = 20,108 + 0,414x1 + 2,205x3.
3.1.2. Pemilihan Persamaan Terbaik dengan Metode Penyisihan Ilustrasi penggunaan metode penyisihan adalah sebagai berikut:
Diagram 4.2 Flowchart metode penyisihan
X1, X2 X3, X4 Misal 𝑿𝟒 paling tidak signifikan Eliminasi variabel berikutnya Yi= β0+ β1X1i+ β2X2i+ β3X3i+ εi F1∗= MSR(X1|X2, X3) MSE(X1, X2, X3) F2∗= MSR(X2|X1, X3) MSE(X1, X2, X3) F3∗= MSR(X3|X1, X2) MSE(X1, X2, X3) Yi= β0+ β1X1i+ β2X2i+ β3X3i+ β4X4i+ εi F1∗= MSR(X1|X2, X3, X4) MSE(X1, X2, X3, X4) F2∗= MSR(X2|X1, X3, X4) MSE(X1, X2, X3, X4) F3∗= MSR(X3|X1, X2, X4) MSE(X1, X2, X3, X4) F4∗= MSR(X4|X1, X2, X3) MSE(X1, X2, X3, X4) Misal 𝑿𝟏 paling tidak signifikan X4 keluar dari model X1keluar dari model Yi= β0+ β2X2i+ β3X3i+ εi
Model yang terbentuk
Yi= β0+ β2X2i+ β3X3i+ εi Eliminasi variabel berikutnya F2∗= MSR(X2|X3) MSE(X2, X3) F3∗= MSR(X3|X2) MSE(X2, X3) Misal semua variabel sudah signifikan Proses berhenti Dievaluasi yang tidak signifikan
Penjelasan lebih lengkap dari ilustrasi diagram alir dengan menggunakan metode penyisihan adalah sebagai berikut:
1. Langkah pertama yang dilakukan adalah semua peubah bebas (X1, X2, X3, X4)
dimasukkan ke dalam model. Uji seluruh koefisien regresi dengan uji overall. Bila hipotesis tidak ditolak, berarti semua peubah bebas tidak berpengaruh terhadap respons, maka pekerjaan selesai. Misalkan hipotesis ditolak, seperti pada seleksi maju, disini juga digunakan uji-F, hanya saja namanya sekarang disebut Fkeluar.
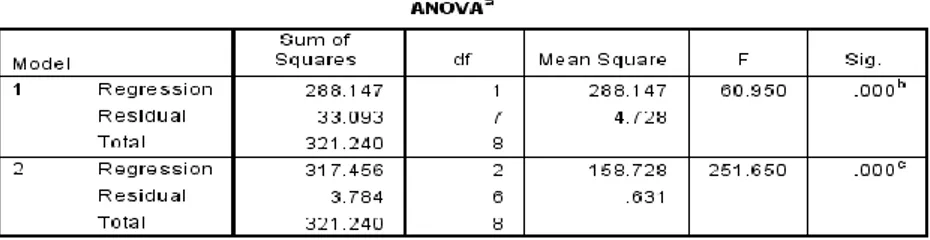
Gambar 4.4 Tabel anova 1. Uji Overall
1. Hipotesis
H0 : β1 = β2 = β3= β4 = 0 (variabel bebas secara bersama-sama tidak mempunyai
pengaruh yang signifikan terhadap variabel tak bebas) H1 : Minimal salah satu βi≠ 0, i =1, 2, 3, 4 (minimal salah satu variabel bebas
mempunyai pengaruh yang signifikan terhadap variabel tak bebas)
2. Tingkat Signifikansi α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika Fhit > Ftabel.
4. Statistik Uji Fhit =
𝐾𝑇𝑅 𝐾𝑇𝐺
5. Keputusan
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.4, dapat dilihat bahwa Fhit = 107,323 >
Ftabel = 6,39 maka dapat dikatakan bahwa H0 ditolak, artinya bahwa terdapat minimal
satu dari βi≠ 0, i =1, 2, 3, 4 ataupun keempatnya nya yang memiliki nilai tidak sama
dengan nol. Oleh karena itu, perlu dilakukan uji parsial untuk memeriksa secara satu per satu koefisien regresi tersebut berarti atau tidak.
2. Langkah selanjutnya yang dilakukan setelah hipotesis nol ditolak adalah pandang tiap peubah bebas seolah-olah sebagai yang paling akhir masuk ke dalam model, ambil yang paling kecil pengaruhnya (kuadrat korelasi parsial paling kecil). Setelah itu lakukan uji parsial dari tiap peubah bebas yang mempunyai pengaruh paling kecil. Jika hipotesis nol ditolak, maka pekerjaan selesai, semua peubah bebas berada dalam model. Bila hipotesis nol diterima maka keluarkan peubah bebas tersebut.
Tabel 4.5 Kuadrat korelasi parsial dengan X1
Xj r2
yxj.x2x3x4 Fkeluar
X1 0,021 0,086
Tabel 4.6 Kuadrat korelasi parsial dengan X2
Xj r2
yxj.x1x3x4 Fkeluar
X2 0,1764 0,854
Tabel 4.7 Kuadrat korelasi parsial dengan X3
Xj r2
yxj.x1x2x4 Fkeluar
X3 0,679 8,432
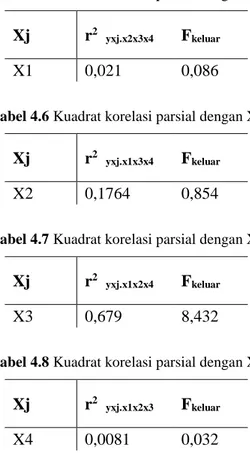
Tabel 4.8 Kuadrat korelasi parsial dengan X4
Xj r2
yxj.x1x2x3 Fkeluar
X4 0,0081 0,032
Berdasarkan pada tabel 4.5 sampai 4.8 dapat dilihat bahwa variabel X4 yang
yang lainnya. Oleh karena itu, perlu dilakukan uji hipotesis, untuk melihat apakah variabel bebas tersebut berarti atau tidak.
2. Uji Parsial (X4)
1. Hipotesis
H0 : β4= 0 (variabel bebas X4 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β4 ≠ 0 (variabel bebas X4 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika Fkeluar (X4)> Ftabel.
4. Statistik Uji Fkeluar (X4) = 𝐽𝐾𝑅 (𝑋4|𝑋1𝑥2𝑥3) 1 ∶ 𝐽𝐾𝑆 (𝑋4,𝑋1,𝑥2,𝑋3) 𝑛−𝑝 5. Keputusan
H0 diterima, karena Fkeluar (X4) = 0,032 < Ftabel(1,4,0.05) = 7,71
6. Kesimpulan
Berdasarkan hasil output pada tabel 4.8, dapat dilihat bahwa Fkeluar (X4) = 0,032 <
Ftabel = 7,71 maka dapat dikatakan bahwa H0 diterima, artinya bahwa β4 memiliki
nilai sama dengan nol atau dapat dikatakan β4 adalah koefisien regresi yang tidak
berarti. Oleh karena itu, X4 tidak memenuhi syarat untuk masuk dalam taksiran
persamaan regresi.
3. Langkah selanjutnya ketika X4 tidak memenuhi syarat untuk masuk dalam taksiran
persamaan regresi, maka terjadi pengulangan lagi seperti pada proses langkah keduaa Pandang lagi dari setiap peubah yang tinggal seolah-olah yang terakhir masuk ke dalam model. Ambil lagi yang terkecil pengaruhnya, uji seperti sediakala. Jika berarti, selesai pekerjaan, dan bila tidak berarti keluarkan peubah tersebut.
Tabel 4.9 Kuadrat korelasi parsial dengan X1
Xj r2
yxj.x2x3 Fkeluar
X1 0,015 0,077
Tabel 4.10 Kuadrat korelasi parsial dengan X2
Xj r2
yxj.x1x3 Fkeluar
X2 0,209 1,328
Tabel 4.11 Kuadrat korelasi parsial dengan X3
Xj r2
yxj.x1x2 Fkeluar
X3 0,676 10,424
Berdasarkan pada tabel 4.9 sampai 4.11 dapat dilihat bahwa variabel X1 yang
memiliki nilai kuadrat korelasi yang paling kecil diantara kuadrat korelasi peubah bebas yang lainnya.
3. Uji Parsial (X1)
1. Hipotesis
H0 : β1= 0 (variabel bebas X1 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β1 ≠ 0 (variabel bebas X1 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika Fkeluar (X1)> Ftabel.
4. Statistik Uji Fkeluar (X1) = 𝐽𝐾𝑅 (𝑋1|𝑥2𝑥3) 1 ∶ 𝐽𝐾𝑆 (𝑋1,𝑥2,𝑋3) 𝑛−𝑝 5. Keputusan
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.9, dapat dilihat bahwa Fkeluar (X1) = 0,077 <
Ftabel = 7,05 maka dapat dikatakan bahwa H0 diterima, artinya bahwa β1 memiliki
nilai sama dengan nol atau dapat dikatakan β1 adalah koefisien regresi yang tidak
berarti. Oleh karena itu, X1 tidak memenuhi syarat untuk masuk dalam taksiran
persamaan regresi.
4. Langkah selanjutnya adalah pengulangan lagi seperti pada proses ketiga dan kedua. Pengulangan ini terjadi karena X1 tidak memenuhi syarat untuk masuk dalam
taksiran persamaan regresi.
Tabel 4.12 Kuadrat korelasi parsial dengan X2
Xj r2
yxj.x3 Fkeluar
X2 0,978 261,061
Tabel 4.13 Kuadrat korelasi parsial dengan X3
Xj r2
yxj.x2 Fkeluar
X3 0,972 203,366
Berdasarkan pada tabel 3.13 sampai 3.14 dapat dilihat bahwa variabel X3 yang
memiliki nilai kuadrat korelasi yang paling kecil diantara kuadrat korelasi peubah bebas yang lainnya. Oleh karena itu, perlu dilakukan uji hipotesis, untuk melihat apakah variabel bebas tersebut berarti atau tidak.
4. Uji Parsial (X3)
1. Hipotesis
H0 : β3= 0 (variabel bebas X3 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β3 ≠ 0 (variabel bebas X3 mempunyai pengaruh yang signifikan terhadap
variabel tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
4. Statistik Uji Fkeluar (X3) = 𝐽𝐾𝑅 (𝑋3|𝑥2) 1 ∶ 𝐽𝐾𝑆 (𝑥3,𝑋2) 𝑛−𝑝 5. Keputusan
H0 ditolak, karena Fkeluar (X3) = 203,366 > Ftabel(1,6,0.05) = 5,99
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.13, dapat dilihat bahwa Fkeluar (X3) = 203,366
> Ftabel = 5,99 maka dapat dikatakan bahwa H0 ditolak, artinya bahwa β3 memiliki
nilai tidak sama dengan nol atau dapat dikatakan β3 adalah koefisien regresi yang
berarti. Oleh karena itu, X3 danX2 memenuhi syarat untuk masuk dalam taksiran
persamaan regresi.
Berdasarkan pada gambar 4.5 terlihat bahwa nilai koefisien determinasi yang diperoleh adalah sebesar 99,1% artinya bahwa keragaman y yang mampu dijelskan oleh X2 dan X3 adalah 99,1% dan sisa nya sebesar 0,9% dijelaskan oleh faktor lain di luar
model. Dari tabel koefisien pada gambar 4.5 diperoleh taksiran persamaan regresi adalah Ŷ = 2,183 + 0,958x2 + 3,325x3.
4.1.3 Pemilihan Persamaan Terbaik dengan Metode Bertahap Ilustrasi penggunaan metode bertahap adalah sebagai berikut:
Diagram 4.4 Flowchart metode bertahap
X1,X2, X3,X4 Yi1 =β0+ β1Xi1+εi Yi2=β0+ β2Xi2+εi Yi3=β0+ β3Xi3+εi Yi4=β0+ β4Xi4+εi Fk∗= MSR(Xk) MSE(Xk) k=1,2,3,4 Pilih 𝐹𝑘∗terbesar dan uji X1 masuk kedalam model Yi12 =β0+ β1βXi1+ β2βXi2+εi Yi13=β0+ β1βXi1+ β3βXi3+εi Yi14=β0+ β1βXi1+β4βXi4+ εi Fk∗= MSR(Xk|X1) MSE(X1,Xk)) k=2,3,4 Misal terpilih 𝐅𝟏∗ Pilih Fk∗terbesar dan uji X3 signifikan ketika X1 sudah ada didalam model Misal terpilih 𝐅𝟑∗ Fk∗= MSR(X1|X3) MSE(X1,X3) uji
Ketika X3 sudah ada
dalam model, apakah
X1 masih signifikan?
Tolak Ho : X1 masih ada dalam model
Gagal tolak H0 : X1 dikeluarkan
Misal tolak H0
X3 masuk
kedalam model
Penjelasan lebih lengkap dari ilustrasi diagram alir dengan menggunakan metode penyisihan adalah sebagai berikut:
1. Langkah pertama yang dilakukan adalah menggunakan seleksi maju untuk melihat peubah bebas pertama yang masuk pertama kali dalam taksiran persamaan regresi, setelah itu lakukan uji hipotesis untuk memeriksa apakah peubah bebas tersebut berarti atau tidak.
Fk∗= MSR(Xk|X1,X3) MSE(X1,X3,Xk)) k=2,4 Yi132=β0+ β1βXi1+ β3βXi3+β2βXi2+ εi Yi134=β0+ β1βXi1+ β3βXi3+β4βXi4+ εi Pilih Fk∗terbesar dan uji X2tidak signifikan ketika X1 dan X3 sudah
ada dalam model
Misal terpilih 𝐅𝟐∗ F4∗= MSR(X4|X1,X3) MSE(X1,X3,X4) Proses berhenti
Model yang terbentuk
Yi=β0+ β1βXi1+ β3βXi3+εi X4tidak signifikan ketika X1 dan X3 sudah ada dalam model X2tidak masuk kedalam model X4tidak masuk kedalam model Pengujian variabel terakhir X4
Tabel 4.14 Matriks korelasi data tabel 3.1 X1 X2 X3 X4 Y X1 1,000 X2 0,952 1,000 X3 0,534 0,263 1,000 X4 0,390 0,155 0,784 1,000 Y 0,947 0,819 0,761 0,560 1,000
Berdasarkan pada tabel 4.14 terlihat bahwa X1 memberi korelasi terbesar dengan
Y, sehingga X1 masuk pertama sekali ke dalam model.
2. Setelah matriks korelasi telah dibuat dan salah satu variabel peubah bebas dipilih (X1), maka selanjutnya yang adalah mencari nilai koefisen determinasi, pembuatan
tabel anova, dan pembuatan taksiran persamaan sementara untuk variabel X1 yang
telah masuk terlebih dahulu.
Gambar 4.6 Nilai koefisien determinasi, tabel anova, tabel koefisen regresi X1
Berdasarkan pada gambar 4.6 dapat dilihat bahwa nilai koefisen determinasi (R2)
sebesar 0,897 atau 89,7%. Arti dari nilai koefisien determinasi sebesar 89,7% adalah keragaman y yang mampu dijelaskan oleh variabel X1 adalah sebesar 89,7% dan 10,3%
lainnnya dijelaskan oleh faktor lain di luar model. Dengan kata lain, arti dari nilai koefisien determinasi adalah keragaman panjang bayi yang mampu dijelaskan oleh usia adalah sebesar 89,7% dan 10,3% lainnya dijelaskan oleh faktor lain di luar model.
Dari gambar 4.6 dapat disusun uji hipotesis untuk X1 yang masuk pertama kali
padaa persamaan. 1. Hipotesis
H0 : β1= 0 (variabel bebas X1 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β1 ≠ 0 (variabel bebas X1 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika sig. < tingkat signifikansi atau Fhit > Ftabel.
4. Statistik Uji
Sig.= 0,000 atau Fhit = 𝐾𝑇𝑅 𝐾𝑇𝐺
5. Keputusan
H0 ditolak, karena sig= 0,000 < tingkat signifikansi = 0,05 atau Fhit = 60,950 > Ftabel =
5,59
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.6, dapat dilihat bahwa sig. lebih kecil dari tingkat signifikansi, yaitu 0,000 < 0,05 atau atau Fhit = 60,950 > Ftabel = 5,59 maka
dapat dikatakan bahwa H0 ditolak, artinya bahwa β1 memiliki nilai tidak sama dengan
nol dan dapat dikatakan bahwa usia berpengaruh secara signifikan terhadap panjang bayi.
2. Langkah berikutnya adalah pemeriksaan kuadrat korelasi parsial dengan variabel kontrol nya adalah X1 (r2yxj,x1 untuk j = 2, 3, dan 4).
Tabel 4.15 Kuadrat korelasi parsial dengan X2, X3, dan X4 Xj r2 yxj.x1 Fmasuk X2 0,720801 15,529 X3 0,885481 46,473 X4 0,417316 4,301
Dari tabel 4.15 terlihat bahwa calon peubah bebas berikutnya yang masuk ialah X3. Hal ini dikarenakan kuadrat korelasi parsial Y dengan X3 dikontrol terhadap X1
yang lebih besar diantara peubah bebas lainnya sesuai pada tabel 4.15. Oleh karena itu, dilakukan perhitungan koefisen regresi untuk X1 dan X3 beserta statistik yang
diperlukan.
Tabel 4.16 Koefisien regresi X1 dan X3
Peubah bebas Koefisien regresi Galat baku F (1,6) Kuadrat korelasi parsial X1 4,136 0,297 208,243 0,972196 X3 0,203 0,029 46,473 0,885481 Tetapan 201,085
Gambar 4.3 Tabel koefisien
1. Uji Parsial (X3)
1. Hipotesis
H0 : β3= 0 (variabel bebas X3 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β3 ≠ 0 (variabel bebas X3 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika Fmasuk (X3)> Ftabel.
4. Statistik Uji Fmasuk (X3) = 𝐽𝐾𝑅 (𝑋3|𝑋1) 1 ∶ 𝐽𝐾𝑆 (𝑋3,𝑋1) 𝑛−𝑝 5. Keputusan
H0 ditolak, karena Fmasuk (X3) = 46,473 > Ftabel(1,6,0.05) = 5,99
6. Kesimpulan
Berdasarkan hasil output pada gambar 3.3, dapat dilihat bahwa Fmasuk (X3) = 46,473 >
Ftabel = 5,99 maka dapat dikatakan bahwa H0 ditolak, artinya bahwa β3 memiliki nilai
tidak sama dengan nol atau dapat dikatakan β3 adalah koefisien regresi yang berarti.
3. Langkah selanjutnya adalah dengan menggunakan metode penyisihan untuk memeriksa apakah kalau tadinya X3 masuk terlebih dahulu pengaruh X1 masih
dikeluarkan dari model dan bila sebaliknya maka X1 boleh tinggal dalam model
sampai pengujian tahap berikutnya. Dari tabel 3.4 dapat dilihat bahwa kuadrat korelasi parsial antara X1 dengan Y yang dikontrol oleh X3 adalah sebesar
0,885481. Angka tersebut menunjukkan korelasi parsial yang besar antara X1
dengan Y setelah X2 berada dalam persamaan, oleh karena itu perlu dilakukan uji
hipotesis untuk memeriksa apakah peubah bebas X1 masih berarti atau tidak ketika
X2 berada di dalam persamaan.
1. Uji Parsial untuk Memeriksa Keberartian X1
1. Hipotesis
H0 : β1= 0 (variabel bebas X1 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β1 ≠ 0 (variabel bebas X1 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 ditolak jika Fkeluar (X1)> Ftabel.
4. Statistik Uji Fkeluar (X1) = 𝐽𝐾𝑅 (𝑋1|𝑋3) 1 ∶ 𝐽𝐾𝑆 (𝑋1,𝑋3) 𝑛−𝑝 5. Keputusan
H0 ditolak, karena Fkeluar (X1) = 208,243 > Ftabel = 5,99
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.16, dapat dilihat bahwa Fkeluar (X1) = 208,243
> Ftabel = 5,99 maka dapat dikatakan bahwa H0 ditolak, artinya bahwa β1 memiliki
nilai tidak sama dengan nol atau dapat dikatakan β1 adalah koefisien regresi yang
berarti ketika X1 masuk di dalam model.
4. Langkah selanjutnya adalah kembali menggunakan metode seleksi maju untuk memilih calon berikutnya yang akan dimasukkan ke dalam persamaan.
Tabel 4.17 Kuadrat korelasi parsial dengan X2 dan X4
Xj r2
yxj.x1x3 Fmasuk
X2 0,20974 1,328
X4 0,04884 0,257
Dari tabel 4.18 dapat dilihat bahwa nilai kuadrat korelasi parsial dari X2 lebih
besar dibandinkan dengan X4, namun nilai kuadrat korelasi parsial untuk X2 masih
tergolong rendah. oleh karena itu perlu dilakukan uji hipotesis untuk melihat apakah nilai X2 dan X4 memenuhi syarat untuk masuk pada persamaan regresi.
2. Uji Parsial (X2)
1. Hipotesis
H0 : β2= 0 (variabel bebas X2 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β2 ≠ 0 (variabel bebas X2 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 jika Fmasuk (X2)> Ftabel.
4. Statistik Uji Fmasuk (X2) = 𝐽𝐾𝑅 (𝑋2|𝑋1𝑥3) 1 ∶ 𝐽𝐾𝑆 (𝑋2,𝑋1,𝑋3) 𝑛−𝑝 5. Keputusan
H0 diterima, karena Fmasuk (X2) = 1,328 < Ftabel(1,5,0.05) = 6,61
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.17, dapat dilihat bahwa Fmasuk (X2) = 1,328 <
Ftabel = 6,61 maka dapat dikatakan bahwa H0 diterima, artinya bahwa β2 memiliki
nilai sama dengan nol atau dapat dikatakan β2 adalah koefisien regresi yang tidak
berarti. Oleh karena itu, X2 tidak memenuhi syarat untuk masuk dalam taksiran
3. Uji Parsial (X4)
1. Hipotesis
H0 : β4= 0 (variabel bebas X4 tidak mempunyai pengaruh yang signifikan terhadap
variabel tak bebas)
H1 : β4 ≠ 0 (variabel bebas X4 mempunyai pengaruh yang signifikan terhadap variabel
tak bebas) 2. Tingkat Signifikansi
α = 5% (0,05). 3. Daerah kritik
H0 jika Fmasuk (X4)> Ftabel.
4. Statistik Uji Fmasuk (X4) = 𝐽𝐾𝑅 (𝑋4|𝑋1𝑥3) 1 ∶ 𝐽𝐾𝑆 (𝑋4,𝑋1,𝑋3) 𝑛−𝑝 5. Keputusan
H0 diterima, karena Fmasuk (X4) = 0,257< Ftabel(1,5,0.05) = 6,61
6. Kesimpulan
Berdasarkan hasil output pada gambar 3.8, dapat dilihat bahwa Fmasuk (X4) = 0,257 <
Ftabel = 6,61 maka dapat dikatakan bahwa H0 diterima, artinya bahwa β4 memiliki
nilai sama dengan nol atau dapat dikatakan β4 adalah koefisien regresi yang tidak
berarti. Oleh karena itu, X4 tidak memenuhi syarat untuk masuk dalam taksiran
persamaan regresi.
Berdasarkan pada uji hipotesis untuk X2 dan X4 dapat dikatakan bahwa kedua
variabel peubah bebas tersebut tidak memenuhi syarat untuk masuk dalam taksiran persamaan regresi, sehingga tidak perlu dilanjutkan layaknya pada metode penyisihan. Oleh karena itu, taksiran persamaan regresi yang diperoleh berdasarkan pada gambar 4.8 dari metode bertahap ini adalah Ŷ = 20,108 + 0,414X1 + 2,025X3.
4.1.4 Kriteria Pemilihan Model Terbaik
Dari tiga metode yang digunakan, metode seleksi maju dan metode bertahap mendapatkan persamaan regresi yang sama, yakni Ŷ = 20,108 + 0,414X1 + 2,025X3
sedangakan persamaan regresi yang didapatkan dari metode penyisihan, yakni Ŷ= 2,183 + 0,958X2 + 3,325X3. Oleh karena itu, untuk melakukan uji validasi dari salah satu
persamaan diantara dua persamaan tersebut, perlu dilakukan pemilihan persamaan regresi berdasarkan kriteria pemilihan model. Kriteria yang digunakan adalah:
1. 𝑅2 terbesar
2. 𝑀𝑆 𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙 𝑡𝑒𝑟𝑘𝑒𝑐𝑖𝑙 (𝑅𝑆2, 𝑟𝑎𝑡𝑎𝑎𝑛 𝑘𝑢𝑎𝑑𝑟𝑎𝑡 𝑠𝑖𝑠𝑎𝑎𝑛) 3. 𝐶𝑝 ~ 𝑝 (𝐶𝑝 mendekati jumlah parameter) dan terkecil
Tabel 4.18 Kriteria pemilihan model
p Peubah dalam model 𝑹 𝟐 𝑴𝑺𝑬 𝑪 𝒑 3 𝑋1, 𝑋3 0,988 atau 98,8% 0,631 2,1066 3 𝑋2, 𝑋3 0,991 atau 99,1% 0,506 1,097
Berdasarkan dari tabel 4.18 dapat dilihat bahwa persaamaan regresi dengan peubah bebas X2 dan X3 memiliki R2 yang lebih besar dan memiliki MSE yang lebih
kecil dibandingkan dengan peubah bebas X1 dan X3. Sedangkan dari nilai Cp dapat
dilihat dari tabel 4.18 bahwa persamaan regresi dengan peubah bebas X1 dan X3
memiliki nilai Cp yang lebih mendekati ke jumlah parameter (3) dibandingkan dengan
peubah bebas X2 dan X3, namun nilai Cp dari peubah bebas X2 dan X3 lebih kecil
dibandingkan dari peubah bebas X1 dan X3. Sehingga dapat dikatakan bahwa persamaan
regresi dengan peubah bebas X2 dan X3 lebih dipilih untuk dilakukan uji validasi untuk
persamaan regresi.
4.3 Uji Validasi untuk Persamaan Terbaik
Tahapan dalam analisis regresi selanjutnya yang harus dilakukan adalah menguji kevalidan (kebenaran) untuk mengetahui apakah persamaan yang telah didapatkan (dalam pengujian kevalidan ini digunakan persamaan yang didapatkan dari metode bertahap) merupakan taksiran yang tepat untuk menaksir model regresi pada persamaan 4.1 atau tidak. Sebuah model dikatakan baik jika telah memenuhi syarat dalam Best
untuk mengetahui apakah model yang didapatkan tergolong sebagai model yang baik karena menghasilkan estimator linear yang tidak bias.
4.3.1 Uji Asumsi Klasik
Uji asumsi klasik terdiri atas beberapa uji, yakni uji normalitas, multikolinearitas, autokorelasi, dan homoskedastisitas. Taksiran persamaan yang akan dilakukan uji asumsi klasik yaitu Ŷ = 2,183 + 0,958X2 + 3,325X3.
4.3.3.1. Uji Normalitas
Gambar 4.4. Uji kolmogorov-smirnov
Pada gambar 4.4 menunjukkan output dari uji kolmogorov-smirnov pada residual dari data pada tabel 3.1 yang bertujuan untuk melihat apakah residual dari data tersebut menyebar secara normal atau tidak. Adapun langkah-langkah untuk uji normalitas adaalah:
1. Hipotesis
H0 : Residual berasal dari distribusi normal
H1 : Residual tidak berasal dari distribusi normal
2. Tingkat Signifikansi α/2 = 0,025.
3. Daerah kritik
H0 ditolak jika Asymp. Sig. (2-tailed) < tingkat signifikansi.
4. Statistik Uji
Asymp. Sig. (2-tailed) = 0,200
5. Keputusan
H0 diterima, karena Asymp. Sig. (2-tailed) = 0,200 > tingkat signifikansi = 0,05
6. Kesimpulan
Berdasarkan hasil output pada gambar 4.4, dapat dilihat bahwa Asymp. Sig.
(2-tailed) lebih besar dari tingkat signifikansi, yaitu 0,200 > 0,025 maka dapat dikatakan
bahwa H0 gagal ditolak, artinya bahwa residual dari data pada tabel 3.1 normal atau
berasal dari distribusi normal. Hal ini mengindikasikan bahwa asumsi untuk residual menyebar normal atau berasal dari distribusi normal telah terpenuhi.
4.3.3.2. Uji Multikolinearitas
Gambar 4.5. Output untuk uji multikolinearitas
Berdasarkan pada gambar 4.5, uji multikolinearitas dilakukan dengan melihat nilai VIF (Variance Inflation Factor) untuk mengukur seberepa besar ragam dari dugaan koefisen regresi akan meningkat apabila antar peubah penjelas terdapat masalah multikolinearitas. Adapun langkah-langkah uji hipotesis untuk mengetahui ada atau tidaknya korelasi antara peubah penjelas (X2 dengan X3 atau variabel panjang waktu
lahir dengan berat waktu lahir). 1. Hipotesis
H0 : ρ= 0 (Tidak terjadi multikolinearitas)
2. Tingkat Signifikansi α = 5% (0,05). 3. Daerah kritik
H0 diterima jika nilai VIF < 10
4. Statistik Uji
Variabel VIF Tanda
Panjang waktu lahir 1,074 < 10
Berat waktu lahir 1,074 < 10
5. Keputusan
Variabel VIF Tanda Keputusan
Usia 1,074 < 10 Gagal Tolak H0
Berat waktu lahir 1,074 < 10 Gagal Tolak H0
6. Kesimpulan
Berdasarkan pada keputusan yang diambil dalam langkah uji hipotesis untuk uji multikolinearitas menunjukkan bahwa nilai VIF dari variabel panjang waktu lahir dan berat waktu lahir kurang dari 10, maka H0 gagal ditolak yang artinya bahwa
tidak terjadi korelasi antara peubah penjelas atau dapat dikatakan tidak terjadi korelasi antara kedua variabel tersebut. Oleh karena itu, data pada tabel 3.1 terbebas dari persoalan multikolinearitas sehingga asumsi no multikolinearitaas terpenuhi. 4.3.3.3. Uji Heterokedastisitas
Berdasarkan pada gambar 4.6 yang menunjukkan plot penyebabaran data dari tabel 3.1, dapat dilihat bahwa data menyebar dan tidak membentuk pola tertentu, sehingga dapat disimpulkan bahwa terdapat kesamaan variansi dari residual satu pengamatan ke pengamatan yang lain tetap atau disebut homoskedastisitas. Untuk memperkuat argumen yang hanya didasarkan secara visual melalui scatterplot, maka dilanjutkan dengan uji glejser.
1. Uji Glejser
Gambar 3.6. Output untuk uji glejser
Adapun langkah-langkah uji hipotesis untuk uji glejser, yaitu: 1. Hipotesis
H0 : variabel independen tidak signifikan mempengaruhi variabel dependen
H1 : variabel independen signifikan mempengaruhi variabel dependen
2. Tingkat Signifikansi α = 5% (0,05) 3. Daerah kritik
H0 ditolak jika sig. < tingkat signifikansi
4. Statistik Uji
Variabel Sig. Tanda α
Panjang waktu lahir 0,107 > 0,05
Berat waktu lahir 0,657 > 0,05
5. Keputusan
Variabel Sig. Tanda α Keputusan
Panjang waktu lahir 0,107 > 0,05 Gagal Tolak H0
6. Kesimpulan
Berdasarkan pada keputusan dalam langkah-langkah uji hipotesis untuk uji glejser dikatakan bahwa gagal tolak H0, karena nilai sig. dari kedua variabel yaitu variabel
panjang waktu lahir dan berat waktu lahir lebih besar dari nilai α. Hal ini berarti, variabel independen tidak signifikan mempengaruhi variabel dependen atau dapat dikatakan variabel panjang waktu lahir dan berat waktu lahir tidak signifikan mempengaruhi variabel panjang bayi. Oleh karena itu terjadi homoskedastisitas, sehingga asumsi kehomogenan ragam sisaan terpenuhi.
3.2.1. Analisis Uji Autokorelasi
Gambar 4.7. Output untuk uji autokorelasi
Gambar 4.8. Tabel Durbin-Watson
Berdasarkan pada gambar 4.7 dapat dilihat nilai durbin-watson yang diperoleh adalah 1,622 dan nilai durbin-lower (dL) serta durbin-upper (dU) berdasarkan pada gambar 4.8 adalah 0,6291 dan 1,6993. Dari nilai-nilai tersebut dapat disusun uji hipotesis untuk mengetahui sisaan dari pengamatan cenderung untuk berkorelasi dengan sisaan yang berdekatan atau tidak. Adapun langkah-langkah uji hipotesisnya, yaitu: 1. Hipotesis
H0 : Tidak terjadi autokorelasi
2. Tingkat Signifikansi α = 5% (0,05) 3. Daerah kritik Kriteria Keterangan 0 < 𝑑 < 𝑑𝐿 Tolak H0 4 − dL < 𝑑 < 4 Tolak H0
dL < 𝑑 < 𝑑𝑈 Tidak ada keputusan 4 − dU < 𝑑 < 4 − 𝑑𝐿 Tidak ada keputusan
dU < 𝑑 < 4 − 𝑑𝑈 Gagal Tolak H0 4. Keputusan Kriteria Keterangan 0 < 2,066 < 0,6291 Tidak Sesuai 3,3709 < 2,066 < 4 Tidak Sesuai 0,6291 < 2,066 < 1,6993 Tidak Sesuai 2,3007 < 2,066 < 3,3709 Tidak Sesuai 1,6993 < 2,066 < 2,3007 Sesuai (Gagal Tolak H0)
5. Kesimpulan
Berdasarkan pada keputusan dalam langkah-langkah uji hipotesis untuk uji autokorelasi dikatakan sesuai dengan kriteria keempat yang menunjukkan bahwa gagal tolak H0, artinya bahwa data cukup random sehingga tidak terdapat masalah
autokorelasi. Hal ini mengindikasikan bahwa asumsi tidak terjadi autokorelasi telah terpenuhi.
Berdasarkan dari kesimpulan dari semua uji klasik yang telah didapat, dapat diketahui bahwa semua uji yang dipersyaratkan untuk analisis regresi linear berganda telah terpenuhi. Artiya persamaan yang didapatkan dari metode bertahap, yakni Ŷ = 2,183 + 0,958X2 + 3,325X3 telah memenuhi semua asumsi klasik dan dapat dikatakan
bahwa persamaan regresi yang digunakan adalah persamaan yang terbaik karena menghasilkan estimator linear yang tidak bias (Best Linear Unbias Estimator/BLUE). 4.4. Interprestasi Model
Setelah kelayakan model, estimasi model regresi linear berganda dilakukan dan diuji pemenuhan syaratnya (uji asumsi klasik), maka tahap terakhir adalah