METODE BIG M
Sering kita menemukan bahwa fungsi kendala tidak hanya dibentuk oleh pertidaksamaan ≤ tapi juga oleh pertidakasamaan ≥ dan/atau persamaan (=). Fungsi kendala dengan pertidaksamaan ≥ mempunyai surplus variable, tidak ada slack variables. Surplus variable tidak bisa menjadi variabel basis awal. Dengan demikian harus ditambahkan satu variabel baru yang dapat berfungsi sebagai variabel basis awal. Variabel yang dapat berfungsi sebagai variabel basis awal hanya slack variables dan artificial variables (variabel buatan).
1. Jika semua fungsi kendala menggunakan pertidaksamaan ≤ maka variabel basis awal semuanya adalah slack variables. Penyelesaian solusi optimal untuk kasus seperti ini dilakukan dengan cara yang sudah diperkenalkan sebelumnya.
2. Jika fungsi kendala menggunakan pertidaksamaan ≥ dan/atau ≤ maka variabel basis awal adalah slack variables dan/atau variabel buatan. Penyelesaian solusi optimal untuk kasus seperti ini dilakukan dengan memilih antara metode Big M, Dua Fase atau
Dual Simpleks.
3. Jika fungsi kendala ada yang menggunakan persamaan maka variabel buatan akan ditemukan pada variabel basis awal. Penyelesaian solusi optimal untuk kasus seperti ini hanya dapat dilakukan dengan memilih antara metode Big M atau Dua Fase. Kita akan bahas metode Big M dalam sub bab ini. Perbedaan metode Big M dengan primal simpleks biasa (teknik penyelesaian yang sudah dipelajari sebelumnya), terletak pada pembentukan tabel awal. Jika fungsi kendala menggunakan bentuk pertidaksamaan ≥, perubahan dari
bentuk umum ke bentuk baku memerlukan satu variabel surplus. Variabel surplus tidak dapat berfungsi sebagai variabel basis awal, karena koefisiennya bertanda negatif. Sebagai variabel basis pada solusi awal, harus ditambahkan satu variabel buatan. Variabel buatan pada solusi optimal harus bernilai 0, karena variabel ini memang tidak ada.
Teknik yang digunakan untuk memaksa variabel buatan bernilai 0 pada solusi optimal adalah dengan cara berikut:
• Penambahan variabel buatan pada fungsi kendala yang tidak memiliki variabel slack, menuntut penambahan variabel buatan pada fungsi tujuan.
• Jika fungsi tujuan adalah maksimisasi, maka variabel buatan pada fungsi tujuan mempunyai koefisien +M; jika fungsi tujuan adalah minimisasi, maka variabel buatan pada fungsi tujuan mempunyai koefisien -M.
• Karena koefisien variabel basis pada tabel simpleks harus bernilai 0, maka variabel buatan pada fungsi tujuan harus digantikan nilai dari fungsi kendala yang memuat variabel buatan tersebut.
Perhatikan contoh di bawah ini. Bentuk Umum Min. z = 4 x1 + x2 Terhadap: 3x1 + x2 = 3 4x1 + 3x2 ≥ 6 x1 + 2x2 ≤ 4 x1, x2 ≥ 0 Bentuk Baku: Min. z = 4 x1 + x2 Terhadap: 3x1 + x2 = 3 4x1 + 3x2 - s1 = 6
x1 + 2x2 + s2 = 4
x1, x2, s1, s2 ≥ 0
Kendala 1 dan 2 tidak mempunyai slack variables, sehingga tidak ada variabel basis awal. Untuk berfungsi sebagai variabel basis awal, pada kendala 1 dan 2 ditambahkan masing-masing satu variabel buatan (artificial variable). Maka bentuk baku Big M-nya adalah:
Min. z = 4 x1 + x2 + MA1 + MA2
Terhadap: 3x1 + x2 + A1 = 3
4x1 + 3x2 - s1 + A2 = 6
x1 + 2x2 + s2 = 4
x1, x2, s1, s2 ≥ 0
1. Nilai A1 digantikan dari fungsi kendala pertama.
A1 = 3 - 3x1 - x2
MA1 berubah menjadi M(3 - 3x1 - x2) 3M-3Mx1-Mx2
2. Nilai A2 digantikan dari fungsi kendala ketiga.
A2 = 6 - 4x1 - 3x2 + s1
MA2 berubah menjadi M(6 - 4x1 - 3x2 + s1)
6M- 4Mx1 - 3Mx2 + Ms1
3. Fungsi tujuan berubah menjadi
Min z = 4x1 + x2 + 3M-3Mx1-Mx2 +6M-4Mx1-3Mx2+Ms1
= (4 -7M)x1+(1 - 4M)x2 + Ms1 +9M
4. Tabel awal simpleks
VB X1 X2 S1 A1 A2 S2 Solusi
z -4 +7M -1 +4M -M 0 0 0 9M
A1 3 1 0 1 0 0 3
S2 1 2 0 0 0 1 4
5. Perhitungan iterasinya sama dengan simpleks sebelumnya. Iterasi-0 VB X1 X2 S1 A1 A2 S2 Solusi Rasio z -4 +7M -1 +4M -M 0 0 0 9M - A1 3 1 0 1 0 0 3 1 A2 4 3 -1 0 1 0 6 3/2 S2 1 2 0 0 0 1 4 2 Iterasi-1 VB X1 X2 S1 A1 A2 S2 Solusi Rasio z 0 (1 +5M)/3 -M (4-7M)/3 0 0 4+2M - X1 1 1/3 0 1/3 0 0 1 3 A2 0 5/3 -1 -4/3 1 0 2 6/5 S2 0 5/3 0 -1/3 0 1 3 9/5 Iterasi-2 VB X1 X2 S1 A1 A2 S2 Solusi Rasio z 0 0 1/5 8/5 – M -1/5 – M 0 18/5 - X1 1 0 1/5 3/5 -1/5 0 3/5 25/3 X2 0 1 -3/5 -4/5 3/5 0 6/5 - S2 0 0 1 1 -1 1 1 1 Iterasi-3 optimal VB X1 X2 S1 A1 A2 S2 Solusi z 0 0 0 7/5-M -M -1/5 17/5
X1 1 0 0 2/5 0 -1/5 2/5
X2 0 1 0 -1/5 0 3/5 9/5
S1 0 0 1 1 -1 1 1
METODE DUA FASE
Metode dua fase digunakan jika variabel basis awal terdiri dari variabel buatan. Disebut sebagai metode dua fase, karena proses optimasi dilakukan dalam dua tahap. Tahap pertama merupakan proses optimasi variabel buatan, sedangkan proses optimasi variabel keputusan dilakukan pada tahap kedua. Karena variabel buatan sebenarnya tidak ada (hanya ada di atas kertas), maka tahap pertama dilakukan untuk memaksa variabel buatan bernilai 0.
Perhatikan kasus berikut: Tahap 1 Min A = A1 + A2 Terhadap: x1 + x2 + A1 = 90 0.001x1 + 0.002x2 + s1 = 0.9 0.09x1 + 0.6x2 -s2 + A2 = 27 0.02x1 + 0.06x2 + s3 = 4.5 x1, x2, s1, s2, s3 ≥ 0
karena A1 dan A2 berfungsi sebagai variabel basis pada solusi awal, maka
koefisiennya pada fungsi tujuan harus sama dengan 0. untuk mencapai itu, gantikan nilai A1 dari fungsi kendala pertama (kendala yang memuat
A1) dan nilai A2 dari fungsi kendala ketiga (kendala yang memuat A2).
Dari kendala -1 diperoleh :
Dari kendala-3 diperoleh:
A2 = 27 - 0.09x1 - 0.6x2 + s2
Maka fungsi tujuan tahap-1 menjadi:
Min A = (90 - x1 - x2) + (27 - 0.09x1 - 0.6x2 + s2) =117 - 1.09x1 - 1.6x2 + s2 Solusi awal VB X1 X2 S1 S2 S3 A1 A2 NK Rasio A 1.09 1.6 0 -1 0 0 0 117 - A1 1 1 0 0 0 1 0 90 90 S1 0.001 0.002 1 0 0 0 0 0.9 450 A2 0.09 0.6 0 -1 0 0 1 27 45 S3 0.02 0.06 0 0 1 0 0 4.5 75 Iterasi1 VB X1 X2 S1 S2 S3 A1 A2 NK Rasio A 0.85 0 0 -11/3 0 0 -8/3 45 - A1 0.85 0 0 10/6 0 1 -10/6 45 52.94 S1 0.0007 0 1 1/300 0 0 -1/300 0.81 1157.14 X2 0.15 1 0 -10/6 0 0 10/6 45 300 S3 0.011 0 0 0.1 1 0 -0.1 1.8 163.634 Iterasi2 optimal VB X1 X2 S1 S2 S3 A1 A2 NK A 0 0 0 -4.8708 0 -1 -1.4625 0 X1 1 0 0 17/12 0 20/17 -17/12 52.94 S1 0 0 1 0.0023417 0 0.0008 -0.0023 0.772942 X2 0 1 0 -1.7542 0 -3/17 1.7542 37.059 S3 0 0 0 0.09358 1 0.01294 -0.084417 1.21766
Tahap 2
Min z = 2 x1 + 5.5 x2
Terhadap: tabel optimal tahap pertama Dari tabel optimal tahap 1 diperoleh: X1 = 52.94 – 17/12s2
X2 = 37.059 + 1.7542s2
Maka fungsi tujuan adalah:
Min z = 2(52.94 – 17/12s2) + 5.5 (37.059 + 1.7542s2)
= -17/6s2 + 9.6481s2 + 309.7045 = 6.814767s2 + 309.7045
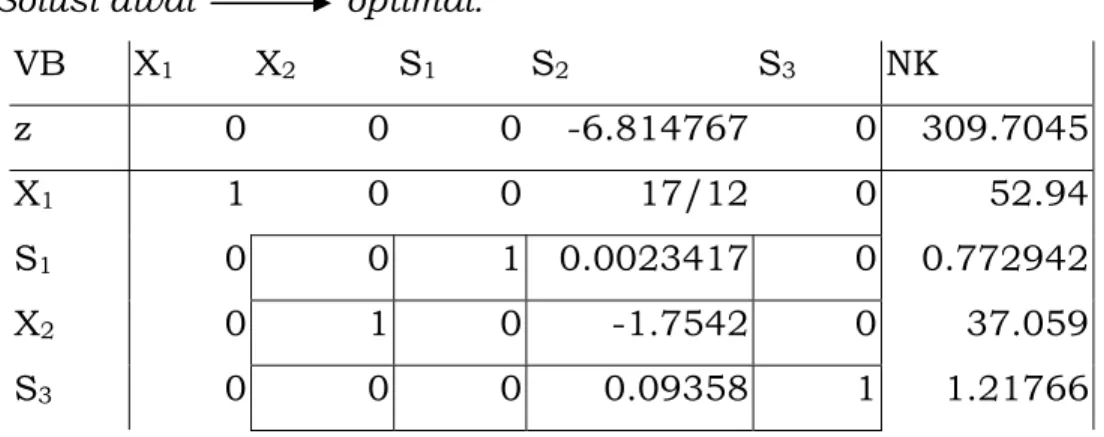
Solusi awal optimal.
VB X1 X2 S1 S2 S3 NK z 0 0 0 -6.814767 0 309.7045 X1 1 0 0 17/12 0 52.94 S1 0 0 1 0.0023417 0 0.772942 X2 0 1 0 -1.7542 0 37.059 S3 0 0 0 0.09358 1 1.21766
Tabel di atas sudah optimal. Solusi optimalnya adalah: X1 = 52.94; x2 = 37.059; dan z = 309.7045
METODE DUAL SIMPLEKS
Metode dual simpleks digunakan jika tabel optimal tidak layak. Jika fungsi kendala ada yang menggunakan pertidaksamaan ≥ dan tidak ada = dalam bentuk umum PL, maka metode dual simpleks dapat digunakan. Kita selesaikan contoh di bawah ini.
Min z = 21x1 + 18x2 + 15x3
Terhadap 90x1 + 20x2 + 40x3 ≥ 200
10x1 + 20x2 + 60x3 ≥ 150
x1, x2, x3 ≥ 0
semua kendala menggunakan pertidaksamaan ≥. Kendala dengan pertidaksamaan ≥ dapat diubah ke pertidaksamaan ≤ dengan mengalikan pertidaksamaan dengan -1. Bentuk umum PL di atas berubah menjadi: Min z = 21x1 + 18x2 + 15x3
Terhadap -90x1 - 20x2 - 40x3 ≤ -200
-30x1 - 80x2 - 60x3 ≤ -180
-10x1 - 20x2 - 60x3 ≤ -150
x1, x2, x3 ≥ 0
Semua fungsi kendala sudah dalam bentuk pertidaksamaan ≤, maka kita kita hanya perlu menambahkan variabel slack untuk mengubah bentuk umum ke bentuk baku/standar. Variabel slack akan berfungsi sebagai variabel basis awal.
Bentuk Baku/standar: Min z = 21x1 + 18x2 + 15x3 + 0s1 + 0s2 + 0s3 Terhadap -90x1 - 20x2 - 40x3 + s1 = -200 -30x1 - 80x2 - 60x3 + s2 = -180 -10x1 - 20x2 - 60x3 + s3 = -150 x1, x2, x3, s1, s2, s3 ≥ 0 VB X1 X2 X3 S1 S2 S3 NK Z -21 -18 -15 0 0 0 0 S1 -90 -20 -40 1 0 0 -200 S2 -30 -80 -60 0 1 0 -180 S3 -10 -20 -60 0 0 1 -150
Tabel di atas optimal tapi tidak layak (ingat, untuk fungsi tujuan minimisasi, tabel sudah optimal jika semua koefisien baris tujuan sudah negatif atau 0). Untuk membuat tabel tersebut layak, kita harus gunakan metode dual simpleks. Langkah-langkah penyelesaian simpleks menggunakan metode dual adalah:
1. Tentukan baris pivot. Baris pivot adalah baris dengan nilai kanan negatif terbesar. Jika negatif terbesar lebih dari satu, pilih salah satu sembarang.
2. Tentukan kolom pivot. Kolom pivot diperoleh dengan terlebih dahulu membagi nilai baris z dengan baris pivot. Dalam hal ini, semua nilai baris pivot dapat menjadi pembagi kecuali nilai 0. Kolom pivot adalah kolom dengan rasio pembagian mutlak terkecil. Jika rasio pembagian mutlak terkecil lebih dari satu, pilih salah satu secara sembarang. 3. Pembentukan tabel berikutnya sama dengan prosedur dalam primal
simpleks.
Gunakan tabel awal simpleks di atas.
¾ Baris pivot adalah baris S1, baris dengan nilai kanan negatif
terbesar. VB X1 X2 X3 S1 S2 S3 NK Z -21 -18 -15 0 0 0 0 S1 -90 -20 -40 1 0 0 -200 S2 -30 -80 -60 0 1 0 -180 S3 -10 -20 -60 0 0 1 -150
¾ Kolom pivot adalah kolom X1
VB X1 X2 X3 S1 S2 S3 NK
Z -21 -18 -15 0 0 0 0
S1 -90 -20 -40 1 0 0 -200
S3 -10 -20 -60 0 0 1 -150 Rasio 21/90 18/20 15/40 0 0 0 - ¾ Iterasi-1: VB X1 X2 X3 S1 S2 S3 NK Z 0 -40/9 -9 -7/30 0 0 140/3 X1 1 2/9 4/9 -1/90 0 0 20/9 S2 0 -220/3 -140/3 -1/3 1 0 -340/3 S3 0 -160/9 -500/9 -1/9 0 1 -1150/9 Rasio - 0.0485 0.19286 0.7 - - ¾ Iterasi-2 VB X1 X2 X3 S1 S2 S3 NK Z 0 0 -611/99 -0.213131 -2/33 0 53.535 X1 0 0 10/33 0.0303 1/330 0 1.8788 X2 0 1 7/11 1/220 -3/220 0 17/11 S3 0 0 -44.2424 -0.0303 -0.02424 1 -100.3030 Rasio - - 0.139498 7.0340 2.500 0 - ¾ Iterasi-3 optimal VB X1 X2 X3 S1 S2 S3 NK Z 0 0 0 -0.208934 -0.0572 -0.13948 67.52628 X1 1 0 0 0.00000014 0.00286 0.006848 1.19173 X2 0 1 0 0.0041127 -0.013986 0.01438 0.102818 X3 0 0 1 0.00068 0.00055 -0.0226 2.267
KASUS KHUSUS DALAM SIMPLEKS
Ada beberapa kasus khusus dalam simpleks. Kadang kala kita akan menemukan bahwa iterasi tidak berhenti, karena syarat optimalitas atau syarat kelayakan tidak pernah dapat dipenuhi. Adakalanya juga
solusi yang dihasilkan antara satu iterasi dengan iterasi berkutnya tidak berbeda. Kasus khusus ini terdiri dari solusi optimal lebih dari satu,
degeneracy, solusi tidak terbatas dan solusi tidak layak. Dua terakhir
dapat terjadi karena kesalahan baik dalam perhitungan iteratif ataupun dalam pembentukan model atau formulasi permasalahan.
Solusi Optimal Lebih dari satu
Ketika fungsi objektif paralel terhadap pembatas yang dipenuhi dalam arti persamaan oleh solusi optimal, fungsi objektif akan mengasumsikan nilai optimal sama pada lebih dari satu titik solusi. Kondisi seperti ini kita kenal dengan solusi optimal lebih dari satu (alternative optima). Perhatikan kasus berikut:
Maks z = 2x1 + 4x2 Terhadap x1 + 2x2 ≤ 5 x1 + x2 ≤ 4 x1, x2 ≥ 0 Tabel awal VB X1 X2 S1 S2 Solusi Rasio Z -2 -4 0 0 0 - S1 1 2 1 0 5 5/2 S2 1 1 0 1 4 2 Iterasi – 1 VB X1 X2 S1 S2 Solusi Rasio Z 0 0 2 0 10 X2 1/2 1 1/2 0 5/2
S2 ½ 0 -1/2 1 3/2
Perhatikan nilai baris z untuk variabel x1 juga menjadi nol saat x2 berubah
menjadi variabel masuk. Jika iterasi tersebut kita lanjutkan dengan memilih x1 sebagai variabel masuk, maka akan didapatkan tabel hasil
iterasi kedua berikut:
Iterasi-2
VB X1 X2 S1 S2 Solusi Rasio
Z 0 0 2 0 10
X2 0 1 1 -1 5/2
X1 1 0 -1 2 3/2
Dalam praktek, pengetahuan akan solusi optimum yang lebih dari satu akan sangat bermanfaat karena manajemen mempunyai kesempatan untuk memilih salah satu sesuai dengan situasi yang mereka miliki tanpa harus merusak nilai tujuan.
Degeneracy
Pada bagian 4.4 di atas, ada kemungkinan saat akan menentukan sel keluar, rasio pembagian terkecil lebih dari satu, dan kita akan memilih salah satu secara sembarang. Jika hal ini terjadi, satu atau lebih variabel akan sama dengan nol (0) pada iterasi selanjutnya. Solusi pada iterasi dimana satu atau lebih variabel mempunyai nilai nol (0) kita sebut sebagai
degeneracy.
Degeneracy terjadi secara praktek karena ada minimum satu fungsi kendala yang redundan. Dalam iterasi, kita dapat mengenalinya dengan cara berikut.
Maks z = 3x1 + 9x2
Terhadap x1 + 4x2 ≤ 8
x1 + 2x2 ≤ 4
x1, x2 ≥ 0
Penyelesaian simpleks kasus di atas adalah:
VB X1 X2 S1 S2 Solusi Rasio
Z -3 -9 0 0 0 -
S1 1 4 1 0 8 2
S2 1 2 0 1 4 2
Kalau anda perhatikan tabel di atas, ada dua kandidat baris pivot, sehingga ada dua kandidat variabel keluar. Kita dapat memilih salah satu. Jika kita pilih baris s1 maka solusi pada iterasi pertama adalah
sebagai berikut:
VB X1 X2 S1 S2 Solusi Rasio
Z -3/4 0 9/4 0 18 -
X2 1/4 1 1/4 0 2 8
S2 1/2 0 1/2 1 0 0
Nilai kanan s2 menjadi 0 dan tabel belum optimum. Variabel x1 menjadi
variabel masuk dan s2 menjadi variabel keluar. Iterasi berikutnya
sebenarnya tidak mengubah solusi optimal, seperti yang ditunjukkan tabel di bawah ini.
Iterasi-2 optimal
VB X1 X2 S1 S2 Solusi
X2 0 1 0 -1/2 2
X1 1 0 1 2 0
Melihat pembatas yang redundan sangat mudah menggunakan solusi grafik. Garis dari fungsi pembatas yang redundan melewati hanya salah satu titik pada daerah penyelesaian yaitu solusi optimal, dan hal ini sebenarnya tidak berarti dalam penentuan solusi optimal. Karena tanpa garis fungsi pembatas itupun, solusi optimal sudah dapat diidentifikasi menggunakan fungsi pembatas yang lain.
Dari sudut pandang teoritis, degeneracy mempunyai implikasi dua. Pertama, berhubungan dengan fenomena pengulangan. Iterasi 1 dan 2 di atas hanya merupakan pengulangan yang memberikan nilai tujuan sama, yaitu 18. Secara umum dapat diterima, pada kasus ini prosedur simpleks akan terus berulang tanpa ada akhir tapi tidak memperbaiki solusi. Kedua, meskipun variabel basis dan non basis berbeda pada setiap iterasi, tetapi nilai semua variabel dalam iterasi adalah sama, yaitu x1 = 0, x2 = 2, s1 = 0, s2 = 0 dan z = 18.
Solusi Tidak Terbatas
Ada kalanya kita menemukan nilai variabel meningkat tak terbatas tanpa melanggar pembatas, artinya ruang solusi tidak terbatas paling tidak untuk satu arah. Sebagai akibatnya, nilai tujuan akan meningkat (untuk kasus maksimisasi) atau menurun (untuk kasus minimisasi) tanpa ada batas. Dalam kasus kita sebut ruang solusi dan nilai tujuan optimum tidak terbatas.
Solusi tidak terbatas hanya mengindikasikan satu hal, yaitu model myang dibangun salah. Mendapatkan keuntungan yang tidak terbatas misalnya tentunya tidak masuk akal. Salah satu yang paling umum yang menyebabkan solusi tidak terbatas adalah tidak memasukan
pembatas yang bukan redundan pada model atau parameter (konstanta) beberapa pembatas tidak dihitung dengan benar. Perhatikan kasus berikut: Maks z = 2x1 + x2 Terhadap x1 - x2 ≤ 10 2x1 ≤ 40 x1, x2 ≥ 0 iterasi-0 VB X1 X2 S1 S2 Solusi Rasio Z -2 -1 0 0 0 S1 1 -1 1 0 10 10 S2 2 0 0 1 40 20 Iterasi-1 VB X1 X2 S1 S2 Solusi Rasio Z 0 -1 0 1 40 S1 0 -1 1 -1/2 -10 X1 1 0 0 ½ 20
Jika iterasi itu diteruskan, tidak akan pernah berhenti. Nilai z akan meningkat terus. Pada tabel awal sebenarnya kita sudah dapat mengidentikasi bahwa nilai tujuan akan meningkat terus tanpa ada batas dengan memperhatikan koefisien pembatas kolom x2 yang bernilai -1 dan
0. Nilai koefisien pembatas ini menunjukkan bahwa x2 dapat dinaikkan
tanpa ada batas, sehingga nilai z juga akan meningkat tanpa ada batas.
Solusi Tidak Layak
Jika pembatas tidak dapat dipenuhi secara bersamaan, maka kita berhadapan dengan solusi tidak layak. Solusi tidak layak tidak akan
pernah terjadi jika semua fungsi kendala menggunakan pertidaksamaan ≤ (asumsikan nilai kanan adalah positif), karena variabel slack selalu memberikan solusi layak. Solusi optimal dapat terjadi jika fungsi pembatas ada yang menggunakan pertidaksamaan ≥, kita menggunakan variabel buatan sebagai variabel basis awal, dimana variabel buatan berdasarkan desainnay tidak memberikan solusi layak bagi model awal. Meskipun dalam prosedur iterasinya kita memaksa variabel buatan bernilai 0 pada solusi optimum, hal ini hanya akan terjadi jika model mempunyai ruang solusi layak. Sering juga terjadi, minimum satu variabel buatan bernilai positif pada solusi optimum. Hal ini mengindikasikan bahwa permasalahan tidak mempunyai solusi layak.
Dari sudut pandang praktikal, solusi tidak layak terjadi karena model tidak diformulasikan dengan benar, dimana beberapa pembatas saling bertentangan. Hal lain yang menyebabkan solusi tidak layak adalah bahwa pembatas tidak dimaksudkan untuk dipenuhi secara bersamaan. Perhatikan kasus berikut:
Maks z = 3x1 + 2x2
Terhadap 2x1 + x2 ≤ 2
3x1 + 4x2 ≥ 12
x1, x2 ≥ 0
Solusi awal dengan metode M besar
VB X1 X2 S1 S2 A1 Solusi Rasio Z -3-3M -2-4M M 0 0 -12M S1 2 1 1 0 0 2 2 A1 3 4 0 -1 1 12 3 Iterasi-1 VB X1 X2 S1 S2 A1 Solusi Rasio Z 1+5M 0 M 2+4M 0 4-4M
X2 2 1 1 0 0 2
A1 -5 0 -1 -4 1 4
Pada iterasi optimal, variabel buatan A1 masih bernilai positif dan