Rancangan Kelompok Tak Lengkap Seimbang (RKTLS) atau Balanced Incompleted Block Design (BIBD)

Rancangan Kelompok Tak Lengkap Seimbang

(RKTLS) atau

Balanced Incompleted Block Design (BIBD)

Pendahuluan

• Rancangan percobaan seperti RBSL, RAKL, dan juga RAL sering mengalami kendala pada perlakuan dengan jumlah yang besar, karena kebutuhan akan banyak satuan percobaan yang menjadi besar.

• Misalkan ketika bekerja menggunakan RAL:

• Misalkan ketika menggunakan RAK:

• Untuk mengatasi masalah yang timbul sehubungan dengan bertambahnya

perlakuan-perlakuan yang dicobakan, maka peneliti cenderung mempergunakan rancangan kelompok tak lengkap.

Rancangan Kelompok Tak Lengkap Seimbang (RKTLS)/

Balanced Incomplete Block Design (BIBD)

• Penggunaan RKTLS sering membantu kesulitan penyediaan satuan-satuan percobaan.

• Apabila dalam rancangan acak kelompok tak lengkap itu terdapat pasangan

perlakuan yang muncul sama banyak dalam percobaan, maka dapat dinyatakan

bahwa proses pemilihan dilakukan secara seimbang, sehingga bentuk percobaan ini menggunakan rancangan kelompok tak lengkap seimbang (RKTLS).

• Dengan demikian apabila semua perlakuan yang akan dicobakan atau

Contoh

• Misal : apabila kita mempunyai 4 perlakuan dan 4 kelompok, maka apabila kita menggunakan RAK harus tersedia satuan percobaan sebanyak 4 x 4 = 16.

Notasi

• Dalam rancangan ini, didefinisikan notasi-notasi:

 _𝑡 = banyaknya perlakuan

 _𝑘 = ukuran kelompok (banyaknya perlakuan dalam setiap kelompok tak lengkap)

 _𝑏 = banyaknya kelompok tak lengkap

 _𝑟𝑖 = banyaknya perulangan untuk setiap perlakuan ke 𝑖 pada seluruh percobaan;

Denah Rancangan

• informasi dari RKTLS:

t: banyak perlakuan yang dicobakan ada 4 (A, B, C, D)

b: banyak kelompok tak lengkap ada 4 (Kelompok 1, 2, 3, 4)

k: ukuran dari kelompok tak lengkap = banyak perlakuan dalam setiap kelompok tak lengkap = 3 (ACD, ABC, BCD, ABD)

Penentuan ulangan pasangan

• Penentuan banyaknya kali setiap pasangan perlakuan muncul dalam rancangan percobaan atau banyaknya kali suatu perlakuan terjadi atau muncul bersama dengan setiap perlakuan yang lain dalam suatu rancangan kelompok tak lengkap sbb:

𝜆 = 𝑟 𝑘 − 1_{𝑡 − 1}

• Apabila dalam RKLTS berlaku 𝑡 = 𝑏, maka rancangan itu disebut bersifat simetrik.

• Perlu diperhatikan bahwa dalam RKTLS:

1. 𝜆 merupakan bilangan bulat.

2. harus berlaku hubungan 𝑡𝑟 = 𝑏𝑘

Pengacakan

• Lakukan pengaturan kelompok dan beri nomor secara acak. Apabila rancangan yang di pilih memiliki ulangan yang terpisah, maka lakukan pengacakan kelompok secara terpisah dan bebas dalam setiap ulangan.

• Lakukan pengacakan perlakuan secara terpisah dan bebas dalam setiap kelompok. Dengan kata lain, lakukan pengacakan posisi dari nomor – nomor perlakuan pada setiap kelompok.

Model linier RKLTS

𝑌_𝑖𝑗 = 𝜇 + 𝜏_𝑖 + 𝛽_𝑗 + 𝑒_𝑖𝑗; 𝑖 = 1, 2, 3, … , 𝑡; 𝑗 = 1, 2, 3, … , 𝑏 Dimana:

Y_ij: nilai pengamatan dari perlakuan ke-i dalam kelompok ke-j.

µ: nilai rata – rata umum

τ_i: pengaruh dari perlakuan ke-i

β_j: pengaruh dari kelompok ke-j

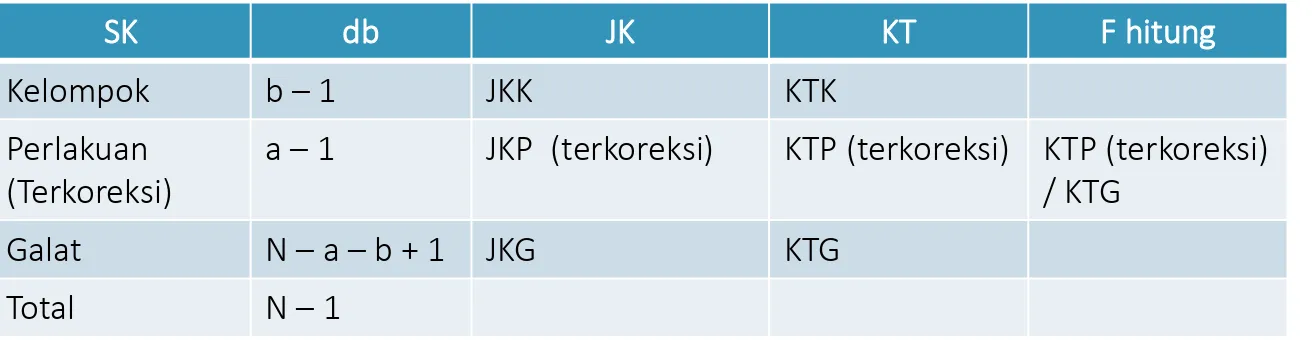
Tabel ANAVA

SK db JK KT F hitung

Kelompok b – 1 JKK KTK

Perlakuan (Terkoreksi)

a – 1 JKP (terkoreksi) KTP (terkoreksi) KTP (terkoreksi) / KTG

Galat N – a – b + 1 JKG KTG

Perhitungan

• JKP (terkoreksi):

𝐽𝐾𝑃 𝑡𝑒𝑟𝑘𝑜𝑟𝑒𝑘𝑠𝑖 = 𝑘 σ𝑖=1𝑡_𝜆𝑡 𝑄𝑖2

• Q_i adalah total terkoreksi untuk perlakuan ke-i, yang di hitung sbb : 𝑄_𝑖 = 𝑦_𝑖∙ − _{𝑘 ෍}1

𝑗=1 𝑏

𝑛_𝑖𝑗𝑦_∙𝑗 ; 𝑖 = 1, 2, 3, … , 𝑡

• n_ij = 1 jika perlakuan i muncul atau terdapat dalam kelompok ke–j

Contoh Penerapan

• Bayangkan bahwa kita akan mencoba 4 macam perlakuan makanan ternak, katakanlah A, B, C, D. oleh karena banyaknya ternak sapi yang tersedia terbatas, yaitu hanya 12 ekor yang terdiri dari 4 kelompok, dimana setiap kelompok terdiri dari 3 ekor sapi, maka kita merencanakan percobaan ini dengan RKTLS (rancangan acak kelompok tak lengkap seimbang).

Contoh data total pertambahan bobot badan ternak sapi :

perlakuan

Kelompok sapi

Total perlakuan

1 2 3 4

A 73 74 - 71 218

B - 75 67 72 214

C 73 75 68 - 216

D 75 - 72 75 222

Total kelompok

Model Linier RAKLTS :

• Dimana :

Y_ij: total pertambahan bobot badan ternak sapi dalam kelompok ke-j yang memperoleh perlakuan ke-i.

µ: rata – rata total pertambahan bobot badan yang sesungguhnya

τ_i: pengaruh perlakuan makanan ke-i terhadap total pertambahan bobot badan sapi

β_j: pengaruh kelompok sapi ke-j terhadap total pertambahan bobot badan

e_ij: pengaruh galat yang muncul dalam kelompok sapi ke-j yang memperoleh perlakuan makanan ke-i.

        



ij i j ij

Penyelesaian

• Hipotesis

 H₀ : 𝜏₁ = 𝜏₂ = ⋯ = 𝜏₄

(tidak ada pengaruh makanan terhadap pertambahan bobot badan ternak sapi)

 H₁ : ∃𝜏_𝑖 ≠ 0

(minimal atau paling sedikit ada satu perlakuan makanan yang pengaruhnya berbeda terhadap pertambahan bobot badan ternak sapi)

t = banyaknya perlakuan makanan = 4 b = banyaknya kelompok tak lengkap = 4

k = ukuran kelompok tak lengkap = banyaknya perlakuan makanan yang terdapat dalam setiap kelompok sapi = 3

r = banyaknya ulangan dari setiap perlakuan makanan = 3 N = banyaknya pengamatan = ar = bk = 4.3 = 12

λ = 2, yang ditentukan berdasarkan formula

Penyelesaian

•

Menentukan Jumlah Kuadrat (JK)

 Faktor Koreksi = FK = (total jenderal)²/banyak pengamatan = (870)²/12 = 63075

 JKT = jumlah kuadrat nilai – nilai pengamatan – FK = (73)²+(74)²+…+(75)² - 63075 = 81

 JKK = (total kelompok)/k – FK = {(221)²+(224)²+(207)²+(218)²}/3 – 63075 = 55

 JKP terkoreksi :

 Dimana Qi adalah total terkoreksi untuk perlakuan ke-i yang dihitung sbb :

• Dapat ditunjukkan bahwa Σ Qi = 0 (nilai σ 𝑄_𝑖 = 0 harus)

• _{𝑄1 = 218 −} 1_{3 1 ∗ 221 + 1 ∗ 224 + 0 ∗ 207 + 1 ∗ 218 = −} 9₃ • _{𝑄2 = 214 −} 1_{3 0 ∗ 221 + 1 ∗ 224 + 1 ∗ 207 + 1 ∗ 218 = −}7₃ • _{𝑄3 = 216 −} 1_{3 1 ∗ 221 + 1 ∗ 224 + 1 ∗ 207 + 0 ∗ 218 = −}4₃ • _{𝑄4 = 222 −} 1_{3 1 ∗ 221 + 0 ∗ 224 + 1 ∗ 207 + 1 ∗ 218 =} 20₃

RKTLS/BIBD R

> hasil = aov(respon~kelompok+perlakuan, data = bobot) # tidak boleh terbalik

> summary(hasil)

Akibat apabila terbalik

> hasil = aov(respon~perlakuan+kelompok, data = bobot) > summary(hasil)

Kelompok terkoreksi

• Apabila diinginkan uji hipotesis untuk kelompok, maka perlu adanya formula untuk kelompok yang terkoreksi.

• Formula untuk JKK (terkoreksi) adalah:

Nilai

𝑄′

_𝑗

BIBD untuk Perlakuan dan Kelompok

Terkoreksi

> hasil1 = aov(respon~perlakuan+kelompok, data = bobot) > drop1(hasil1, test = "F") # kelompok&perlakuan boleh bolak-balik

SV db JK KT F hitung P-value

Kelompok (Terkoreksi)

3 66.083 … 33.889 0.00095

Perlakuan (Terkoreksi)

3 22.75 … 11.667 0.0107

Galat 𝑵 − 𝒕 − 𝒃 + 𝟏

= 𝟏𝟐 − 𝟒 − 𝟒 + 𝟏 = 𝟓

Referensi

• Gaspersz, Vincent, 1991, Teknik Analisis Dalam Penelitian Percobaan, Tarsito, Bandung.