LANDASAN TEORI
2.1 Program Linier
2.1.1 Pengertian Program Linier
Program linear (Linear Programming yang disingkat LP) merupakan salah satu teknik Operasi Riset yang digunakan paling luas dan diketahui dengan baik. LP merupakan metode matematik dalam mengalokasikan sumber daya yang langka untuk mencapai tujuan tunggal seperti memaksimumkan keuntungan atau meminimumkan biaya. LP banyak diterapkan dalam membantu menyelesaikan masalah ekonomi, industri, militer, sosial dan lain-lain. LP berkaitan dengan penjelasan suatu dunia nyata sebagai suatu model matematik yang terdiri atas sebuah fungsi tujuan linear dan sistem kendala linear, (Mulyono, 2004).
Program linear yang diterjemahkan dari Linear Programming (LP) adalah suatu cara untuk menyelesaikan persoalan pengalokasian sumber-sumber yang terbatas diantara aktifitas yang bersaing, dengan cara yang terbaik yang mungkin dilakukan, (Dimyati dan Dimyati, 2004).
Menurut Frederick S. Hiller dan Gerald J. Lieberman, linier programming merupakan suatu model matematis untuk menggambarkan masalah yang dihadapi. Linier berarti bahwa semua fungsi matematis dalam model ini merupakan fungsi-fungsi linier. Pemrograman merupakan sinonim untuk kata perencanaan. Dengan demikian membuat rencana kegiatan-kegiatan untuk memperoleh hasil yang optimal, ialah suatu hasil untuk mencapai tujuan yang ditentukan dengan cara yang paling baik (sesuai dengan model matematis) diantara semua alternatif yang mungkin.
dioptimumkan merupakan suatu penyelesaian atau solusi layak yang mempunyai nilai fungsi tujuan yang dikehendaki. Nilai yang dikehendaki dapat berupa nilai terbesar yaitu fungsi tujuan berupa nilai maksimum sedangkan nilai terkecil yaitu fungsi tujuan berupa nilai minimum.
2.1.2 Model Program Linier
Masalah yang dapat diselesaikan dengan model program linier memiliki ciri-ciri sebagai berikut :
1. Semua variabel penyusunnya bernilai tidak negatif
2. Fungsi obyektif dapat dinyatakan sebagai fungsi linier variabel-variabelnya 3. Kendala dapat dinyatakan sebagai suatu sistem persamaan linier.
Secara matematis, bentuk standard model program linier adalah sebagai berikut: Mencari �= �1,�2,…,� 0 yang memaksimumkan atau meminimumkan
�(�) = �(�1,�2,…,� )
= 1�1+ 2�2+⋯+ �
dengan kendala:
11�1+ 12�2+⋯+ 1 � = 1
21�1+ 22�2+⋯+ 2 � = 2
...
1�1+ 2�2+⋯+ � =
Ciri pertama dipenuhi oleh banyak masalah karena pada umumnya variabel yang digunakan (�1,�2,… ,� ) menyatakan suatu kuantitas (misalnya
jumlah barang, lama waktu, dll) yang hendak dioptimalkan, sedangkan variabel ( 1, 2,… , ) menyatakan biaya. Jelas bahwa nilai-nilai kuantitas tersebut tidak negatif. Akan tetapi bila diinginkan ada variabel yang boleh bernilai negatif, model program linier tetap bisa diselesaikan dengan suatu transformasi.
ditransformasikan ke bentuk linier. Apabila demikian, model program linier dapat digunakan.
2.1.3 Metode Program Linier
Sebenarnya bukan hanya masalah kombinasi produksi saja yang dapat diselesaikan dengan mempergunakan model programasi pangkat satu ini, melainkan segala jenis optimisasi pemanfaatan sumber daya, optimisasi masukan (input) serta optimisasi keluaran (output) dan lain sebagainya.
Metode Program Linier antara lain, yaitu :
a. Metode Grafik untuk pemecahan program linier
Masalah LP dapat diilustrasikan dan dipecahkan dengan grafik jika ia hanya memiliki dua variabel keputusan. Meski masalah-masalah dengan dua variabel keputusan jarang terjadi dalam dunia nyata, penafsiran geometris dari metode grafis ini sangat bermanfaat. Dari sini, kita dapat menarik kesimpulan yang akan menjadi dasar untuk pambentukan metode pemecahan (solusi) yang umum melalui alogaritma simpleks.
b. Metode Simplex
Apabila suatu masalah LP hanya mengandung 2 (dua) kegiatan (atau variabel-variabel keputusan) saja, maka akan dapat diselesaikan dengan metode grafik. Tetapi bila melibatkan lebih dari dua kegiatan maka metode grafik tidak dapat digunakan lagi, sehingga diperlukan metode simplex. Metode simplex merupakan suatu cara yang lazim dipakai untuk menentukan kombinasi optimal dari tiga variabel atau lebih.
c. Metode Transportasi
metode transportasi juga dapat digunakan untuk memecahkan masalah-masalah dunia usaha (bisnis) lainnya, seperti masalah-masalah-masalah-masalah yang meliputi pengiklanan, pembelanjaan modal (capital financing) dari alokasi dana untuk investasi, analisis lokasi, keseimbangan lini perakitan dan perencanaan serta scheduling produksi. Ada beberapa macam metode transportasi, yang semuanya terarah pada penyelesaian optimal dari masalah-masalah transportasi yang terjadi.
d. Metode Penugasan
Seperti masalah transportasi, masalah penugasan (assignment problem) merupakan suatu kasus khusus dari masalah linier programming pada umumnya. Dalam dunia usaha (bisnis) dan industri, manajemen sering menghadapi masalah-masalah yang berhubungan dengan penugasan optimal dari bermacam-macam sumber yang produktif atau personalia yang mempunyai tingkat efisiensi yang beda untuk tugas yang berbeda-beda pula.
Dalam skripsi ini digunakan metode transportasi.
2.2 Kajian Transportasi
2.2.1 Sejarah Permasalahan Transportasi
2.2.2 Persoalan Transportasi
Persoalan transportasi pertama kali diformulasikan sebagai suatu prosedur khusus untuk mendapatkan program biaya minimum dalam mendistribusikan unit yang homogen dari suatu produk atas sejumlah titik penawaran (sumber) ke sejumlah titik permintaan (tujuan). Semua ditempatkan pada sumber dan tujuan yang berbeda secara geografis, (Aminudin, 2008).
Ciri-ciri khusus persoalan transportasi adalah :
1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu.
2. Jumlah barang yang didistribusikan dari setiap sumber dan permintaan oleh setiap tujuan besarnya tertentu.
3. Jumlah barang yang diangkut dari suatu sumber ke suatu tujuan besarnya sesuai dengan permintaan atau kapasitas sumber. Apabila jumlah permintaan tidak sama dengan penawaran maka harus ditambahkan variabel dummy. 4. Biaya pengangkutan komoditas dari suatu sumber ke suatu tujuan besarnya
tertentu.
Data yang dibutuhkan dalam metode transportasi adalah:
1. jumlah persediaan pada setiap daerah sumber dan jumlah permintaan pada setiap daerah tujuan.
2. Biaya transportasi per unit barang dari setiap daerah sumber menuju berbagai daerah tujuan.
Salah satu permasalahan khusus dalam program linier adalah masalah transportasi. Untuk menyelesaikan permasalahan ini digunakan metode transportasi. Dikatakan khusus, karena terletak pada karakteristik utama, yaitu bahwa masalah-masalah tersebut cenderung membutuhkan sejumlah pembatas dan variabel yang sangat banyak sehingga penggunaan komputer dalam menyelesaikan metode simpleksnya akan sangat mahal dibandingkan secara manual, (Fien Zulfikarijah, 2003)
dengan kebutuhannya. Misalnya di suatu tempat asal barang mempunyai jumlah produk yang berlebih sehingga perlu ditransportasikan ke tempat lain yang memerlukannya, (Suyadi Prawirosentono, 2005).
Masalah transportasi merupakan masalah yang sering dihadapi dalam pendistribusian barang. Misalkan ada buah gudang (sumber) yang masing-masing memiliki 1, 2,…, buah barang yang sama. Barang-barang tersebut
hendak di kirim ke buah toko (tujuan) yang masing-masing membutuhkan
1, 2,…, buah barang. Diasumsikan 1+ 2+ …+ = 1+ 2+ …+
. Biasanya karena letak geografis atau jarak yang berbeda, maka biaya pengiriman dari suatu sumber ke tujuan tidaklah sama. Misalkan, adalah
biaya pengiriman dari suatu sumber ke tujuan . Masalahnya adalah bagaimana menentukan pendistribusian barang dari sumber sehingga semua kebutuhan tujuan terpenuhi tetapi dengan biaya yang seminimum mungkin, (Jong Jek Siang, 2014).
2.2.3 Model transportasi
Sebuah model transportasi dari sebuah jaringan dengan m sumber dan n tujuan. Sebuah sumber atau tujuan diwakili dengan sebuah node. Busur yang menghubungkan sebuah sumber dan sebuah tujuan mewakili rute pengiriman barang tersebut. Jumlah penawaran di sumber adalah dan permintaan di tujuan adalah . Biaya unit transportasi antara sumber i dan tujuan j adalah .
Anggaplah � mewakili jumlah barang yang dikirimkan dari sumber ke tujuan
, maka model program linier yang mewakili masalah transprotasi ini secara umum adalah sebagai berikut:
a
−
−
−
b Misalkan ada m buah sumber dan n buah tujuan.
Adapun keterangan pada Gambar 2.1, yaitu:
a. Masing-masing sumber mempunyai kapasitas , = 1,2,3, . . . , .
b. Masing-masing tujuan membutuhkan komoditas sebanyak , = 1,2,3, . . . , .
c. Jumlah satuan (unit) yang dikirimkan dari sumber ke tujuan adalah sebanyak � .
d. Ongkos pengiriman per unit dari sumber ke tujuan adalah . Sumber
= 1
�11
�12
�1
= 2
�21
�22
�2
= 3
� 1
� 2
� −
−
−
tujuan
= 1
= 2
= 3
=
Masalah transportasi pendistribusian berbagai komoditi dari berbagai kelompok pusat penerima yang disebut tujuan sedemikian rupa sehingga meminimalisasi biaya transportasi total. Apabila merupakan biaya distribusi total dan � ( = 1,2,…, ; = 1,2,…, ) adalah jumlah unit yang harus
didistribusikan dari sumber ke tujuan maka dapat diformulasikan sebagai berikut, (Taha Hamdy, 1996):
Fungsi Tunjuan:
� = �
=1 =1
Dengan Kendala: � ; = 1,2,…,
� ; = 1,2,…, � 0 untuk semua i dan j
Kendala yang pertama berarti semua jumlah unit yang di distribusikan tidak boleh melebihi persediaan, sedangkan kendala yang kedua jumlah dari unit yang di distribusikan harus memenuhi permintaan.
2.2.4 Keseimbangan Transportasi
Masalah transportasi dikatakan seimbang (balanced program) apabila jumlah penawaran sama dengan jumlah permintaan. Dapat dituliskan, (Jong Jek Siang, 2014):
=1
=
=1
Fungsi tujuan:
= �
=1 =1
dengan kendala:
� = ; = 1,2,…,
� = ; = 1,2,…, � 0 untuk semua dan Keterangan:
= biaya transportasi per unit barang dari sumber ke tujuan
� = jumlah barang yang didistribusikan dari sumber ke tujuan = jumlah persediaan barang dari sumber
= jumlah permintaan barang oleh tujuan
= banyaknya sumber
= banyaknya tujuan
Kenyataannya, kasus seimbang tidak selalu terjadi. Pada umumnya, masalah yang lebih sering terjadi adalah permasalahan tak seimbang dimana persediaan (supply) lebih besar dari permintaan (demand) atau sebaliknya. Dalam kasus masalah tak seimbang metode solusi transportasi mebutuhkan sedikit modifikasi yaitu dengan menambahkan kolom dummy atau baris dummy untuk menyeimbangkan persediaan dengan permintaan.
Jika permintaan (demand) melebihi persediaan (supply) maka dibuat sumber dummy yang akan memenuhi kekurangan tersebut sebanyak
=1
−
=1
Sebaliknya, jika persediaan (supply) melebihi permintaan (demand) maka dibuat sumber dummy yang akan menyerap kelebihan tersebut sebanyak
=1
−
Biaya transportasi per unit barang dari sumber dummy ke seluruh tujuan adalah nol karena alokasi tersebut tidak mempengaruhi solusi dan pada kenyataanya tidak terjadi pengiriman dari sumber dummy.
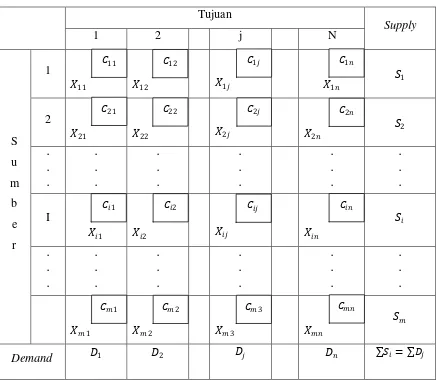
Bentuk umum dari Tabel Transportasi dapat dilihat pada tabel berikut:
Tabel 2.1. Bentuk Umum Tabel Transportasi Tujuan
Model transportasi pada saat dikenali pertama kali, diselesaikan secara manual dengan algoritma yang dikenal sebagai algoritma transportasi.
Langkah – langkah mpengerjaannya adalah sebagai berikut:
1. Mendiagnosis masalah mulai dengan pengenalan sumber, tujuan, parameter dan variabel
2. Seluruh informasi tersebut kemudian dituangkan dalam matriks transportasi Dalam hal ini:
a. Bila kapasitas sumber lebih besar dari permintaan seluruh tujuan maka sebuah kolom dummy perlu ditambahkan untuk menampung kelebihan kapasitas itu.
b. Bila kapasitas seluruh sumber lebih kecil dari sebuah permintaan tujuan maka sebuah baris perlu ditambahkan untuk menyediakan kapasitas semu yang akan memenuhi kelebihan permintaan itu. Jelas sekali bahwa kelebihan permintaan itu tidak bisa dipenuhi.
3. Setelah matriks transportasi terbentuk kemudian dimulai menyusun tabel awal. Metode untuk menyusun tabel awal yaitu:
a. Metode Northwest Corner
Metode Northwest Corner berfungsi untuk menentukan alokasi distribusi awal yang akan membuat seluruh kapasitas sumber teralokasi seluruh tujuan. 4. Setelah didapat penyelesaian awal, maka langkah berikutnya adalah
memeriksa kembali apakah penyelesaian yang didapat sudah optimal atau belum. Tujuan dari evaluasi ini adalah menentukan ada tidaknya pengiriman dari sumber ke tujuan yang lebih baik. Terdapat 2 metode yang dapat digunakan untuk menentukan solusi optimal yaitu:
a. Metode Stepping Stone b. Metode Potensial
2.2.5.1 Algoritma metode Stepping Stone
Langkah-langkah pemecahan masalah menggunakan metode Stepping Stone dengan mengubah alokasi secara trial n eror
Algoritma
1. Mulai
2. Input jumlah p=a dan jumlah g=b 3. i=1 dan j=1
4. Input biaya transportasi 4.1 Selama i<=a maka
-j+1;
4.2 selama j<=b, maka lakukan no 4 4.3 j+1 & i+1
4.4 input = 4.5 j++
4.6 selama j<= b+1, maka lakukan 4.4 4.7 i=1 dan j+1
4.8 Input 4.9 i++
4.10selama i<=a+1, maka lakukan 4.8 5. Alokasi jumlah terbesar dari kiri atas
6. Isi kolom sebelah kanan hingga permintaan terpenuhi
7. Apabila kolom kanan sudah terpenuhi pindahkan kebaris selanjutnya 8. Ulangi langkah 6 dan 7 hingga supplai habis
2.2.5.2Algoritma Metode Potensial
Metode potensial merubah alokasi produksi yang optimal mengguanakan seuatu indeks perbaikan, cara iterasinya sama dengan metode Stepping Stone
Algoritma
1. Mulai
2. Input jumlah p=a danjumlah g=b 3. i=1 dan j=1
4. Input biaya transportasi 4.1 Selama i<=a maka
-j+1;
4.2 selama j<=b, maka lakukan no 4 4.3 j+1 & i+1
4.4 input = 4.5 j++
4.6 selama j<= b+1, maka lakukan 4.4 4.7 i=1 dan j+1
4.8 input 4.9 i++
4.10selama i<=a+1, maka lakukan 4.8 5. Alokasi jumlah terbesar dari kiri atas
6. Isi kolom sebelah kanan hingga permintaan terpenuhi
7. Apabila kolom kanan sudah terpenuhi pindahkan kebaris selanjutnya 8. Ulangi langkah 6 dan 7 hingga supplai habis
9. Biaya transportasi awal = Cij.Xi 10.Tentukan baris dan kolom
11.Hitung indeks perbaikan dan memilih titik tolak perbaikan 12.Selama indeks = negative, makalakukan langkah 9
Ket
= persediaan barang yang diangkut didaerah sumber
= permintaan barang di sejumlah j tujuan.
� = jumlah barang yang diangkut dari sumber ke tujuan
= besarnya biaya transportasi untuk satu unit barang dari sumber ke tujuan
2.2.6 Penyelesaian Feseable Awal
Penyelesaian feasible awal digunakan untuk menentukan penyelesaian awal dalam masalah transportasi maupun masalah transshipment yang telah ditransformasikan ke masalah transportasi. Ada beberapa metode yang biasa digunakan antara lain metode Northwest Corner, metode Least Cost dan metode Vogel’s Approximation (VAM). Namun dalam tulisan ini penulis menggunakan metode Northwest Corner dalam mencari penyelesaian feasible awal.
Jika tabel transportasi terdiri dari baris dan kolom, maka penyelesaian awal harus memenuhi + −1 buah variabel basis (sel yang terisi). Jika penyelesaian awalnya berisi kurang dari + −1 buah variabel basis maka harus ditambahkan variabel dummy agar proses pengecekan keoptimalan dan iterasi dapat dilakukan.
2.2.6.1Metode Northwest Corner
Metode Northwest Corner disebut metode sudut barat laut merupakan metode dimana untuk mengisi tabel awal transportasi dimulai dari sisi barat laut (kiri atas) dengan kuantitas sebanyak-banyaknya disesuaikan dengan jumlah demand dan supply dari baris dan kolom sampai semua kapasitas terpenuhi.
Mulai dari pojok kiri atas, alokasi sebesar �11 = ( 1, 1). Artinya
bila 1 < 1 maka �11= 1; jika 1> 1 maka �11 = 1, selanjutnya yang
mendapat giliran untuk dialokasikan adalah �12sebesar ( 1– 1, 2); kalau �11 = 1 (atau 1 > 1), maka selanjutnya yang mendapat giliran untuk
Prosedur metode ini adalah sebagai berikut: 1. Membuat tabel transportasi.
2. Dimulai dari sel pada sudut kiri atas yang diisi dengan angka sebanyak-banyaknya yang disesuaikan dengan kapasitas dan permintaan.
3. Lakukan langkah yang sama pada langkah (2) untuk mengisi sel-sel lain yang disesuaikan dengan kapasitas dan permintaan sampai seluruh kapasitas dan permintaan terpenuhi.
2.2.7 Pengujian Optimalitas
Setelah tabel awal transportasi dibuat (dengan sembarang metode), langkah berikutnya adalah menguji apakah tabel tersebut sudah optimal. Hal ini dikarenakan solusi awal belum menjamin biaya transportasi telah optimal, untuk itu diperlukan pengujian lebih lanjut yang dilakukan dengan menggunakan uji optimal. Jika sudah optimal maka proses dihentikan dan tabel awal menjadi tabel optimal. Tujuan dari evaluasi ini adalah menentukan ada tidaknya pengiriman dari sumber ke tujuan yang lebih baik.
Terdapat 2 metode yang dapat digunakan untuk pengujian yaitu metode Stepping Stone dan metode potensial atau metode faktor pengali ( multipier). Suatu pengujian dengan menggunakan Stepping Stone dan metode potensial atau metode faktor pengali ( multipier) dikatakan telah optimal apabila sudah tidak ada lagi penghematan biaya (tanda negatif) pada proses eksekusi menggunakan metode-metode tersebut.
2.2.7.1 Metode Stepping Stone
melalui rute transportasi yang saat ini bukan merupakan rute yang ada dalam solusi. Jumlah rute atau sel yang mendapat alokasi harus sebanyak + −1. Prosedur penyelesaian adalah:
1. Setelah memperoleh tabel penyelesaian feasible awal dengan sembarang metode, selanjutnya periksa apakah variabel basis (sel yang terisi) dari tabel awal sudah memenuhi + −1 buah variabel basis, jika berisi kurang dari + −1 buah variabel basis maka harus ditambahkan variabel dummy agar proses pengujian keoptimalan dan iterasi dapat dilakukan.
2. Kotak yang terisi disebut kotak basis, nilainya diberi tanda kurung buka dan tutup seperti (� ), melambangkan baris dan untuk kolom.
3. Kotak yang tidak terisi disebut kotak bukan basis (non-basis cell).
4. Semua kotak memuat biaya angkut per unit barang sebesar dimana 1 unit
barang diangkut dari sumber ke tujuan .
5. = supply atau persediaan barang di sumber , dan = permintaan barang
dari tujuan dan = � jumlah biaya angkut yang harus dibuat minimal.
6. Agar tabel tidak rumit, nilai yang menunjukkan biaya angkut tidak dicantumkan dalam tabel.
7. Dibuat loop tertutup bagi setiap variabel non-basis di mana loop tersebut berawal dan berakhir pada variabel non-basis, dan setiap titik sudut loop tersebut harus merupakan titik-titik yang ditempati oleh variabel-variabel basis dalam tabel transportasi.
8. Dihitung − = jumlah pada loop dengan koefisien (+) dan (−) secara bergantian.
9. Menentukan variabel yang masuk menjadi basis (entering variable) dengan cara memilih nilai − yang terbesar atau Max − .
10. Menentukan variabel yang keluar dari basis dengan cara:
b. Diadakan pengamatan pada dalam loop yang mempunyai koefisien (−).
c. Variabel � yang keluar basis jika dan hanya jika � minimal dari jalur loop.
11. Menentukan harga variabel basis (yang berada di dalam loop yang baru) di mana nilai untuk variabel yang baru masuk basis diambil dari nilai variabel minimal dalam loop.
12. Untuk variabel-variabel basis yang lain yang juga berada dalam loop yaitu: � baru = � lama –� minimal
� baru = � lama + � minimal
13. Untuk variabel-variabel basis yang lain di luar loop harganya tetap dan hitung kembali nilai − untuk variabel non-basis.
14. Diperoleh tabel optimal jika semua − 0.
15. Jika masih ada nilai − 0 , maka dapat ditentukan kembali entering variable dan leaving (variabel yang masuk dan yang keluar).
2.2.7.2 Metode Potensial
Metode potensial merupakan perkembangan dari metode Stepping Stone, karena penentuan segi empat kosong yang bisa menghemat biaya dilakukan dengan prosedur yang lebih pasti dan tepat serta metode ini dapat mencapai hasil optimal lebih cepat, (Subagyo, et al. 2013).
Metode potensial (metode U-V) melakukan evaluasi dari suatu lokasi transportasi secara matriks. Perbedaan utama dari metode potensial dengan metode Stepping-Stone ialah cara mengevaluasi setiap sel dalam matriks. Dalam Stepping-Stone, lingkaran evaluasi harus dicari untuk semua sel, yaitu sebanyak
− + 1sel, yang tidak terletak dalam basis.
Dalam metode potensial, lingkaran evaluasi hanya dicari untuk sel yang mempunyai harga paling negatif pada matriks evaluasi. Dalam proses mencari harga-harga sel evaluasi matriks, metode potensial terlebih dahulu harus menyusun satu matriks perantara. Matriks asli dari transportasi dinyatakan dengan , matriks antara yang akan dijelaskan dinyatakan dengan ,
sedangkan matriks evaluasi dinyatakan dengan .
Berdasarkan alokasi basis, maka sel dari basis dinyatakan dengan .
Sel-sel ini mempunyai jumlah sebanyak + −1. Selanjutnya dicari harga-harga untuk setiap baris dan harga-harga untuk setiap kolom, dengan perantara
persamaan :
+ =
Telah diketahui bahwa jumlah sel yang mendapat alokasi awal atau jumlah sel yang menjadi basis ialah sebanyak + −1, sehingga dengan demikian terdapat + −1 persamaan. Supaya persamaan ini dapat dipecahkan, sebenarnya diperlukan satu persamaan lagi, dan untuk itu diperoleh dengan memilih salah satu harga dari atau dengan konstanta tertentu (biasanya
dipilih salah satu dari harga berikut = 0 atau = 0 ). Setelah harga-harga
dan diketahui, maka dicari harga-harga sel lain yang tidak menjadi basis, yaitu
dengan menggunakan persamaan + = . Matriks yang diperoleh adalah
matriks perantara yang disimbolkan dengan matriks .
Adapun langkah-langkah dalam metode potensial (U-V) adalah:
1. Menentukan nilai untuk setiap baris dan nilai-nilai untuk setiap kolom
dengan menggunakan hubungan + = untuk semua variabel basis
dan menentukan nilai = 0.
2. Menghitung matriks perubahan biaya untuk setiap variabel non basis
3. Apabila hasil perhitungan terdapat nilai negatif, maka solusi belum
optimal. Selanjutnya dipilih � dengan nilai negatif terbesar sebagai entering variabel.
4. Mengalokasikan sejumlah nilai ke entering � variabel sesuai dengan proses Stepping Stone dan ulangi langkah pertama.
2.2.8 Degenerasi dan Redundansi