Perbandingan metode Monte Carlo standar, anthitetic variate, dan control variate pada penentuan harga opsi barrier - USD Repository

PADA PENENTUAN HARGA OPSI BARRIER

SKRIPSI

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh : DIYAH SAYEKTI NIM : 063114017

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

FOR PRICING BARRIER OPTION PRICE

THESIS

Presented As a Partial Fulfillment of The Requirements to Obtain The Sarjana Sains Degree

In Mathematics

by:

DIYAH SAYEKTI NIM : 063114017

MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

2010

Sampai masa tuamu Aku tetap Dia

dan sampai masa putih rambutmu Aku menggendong kamu. Aku telah melakukannya dan mau menanggung kamu terus;

Aku mau memikul kamu dan menyelamatkan kamu.

Janganlah takut , sebab Aku menyertai engkau, Janganlah bimbang, sebab Aku ini Allahmu; Aku akan meneguhkan, bahkan menolong engkau; Aku akan memgang engkau dengan tangan kanan-Ku

yang membawa kemenangan.

Yesaya 46:4,41:10

Kupersembahkan karyaku ini sepenuhnya kepada:

Bapa, Raja, dan Sahabat sejatiku Tuhan Yesus Kristus yang teramat baik, yang selalu menyertai setiap langkahku serta mencurahkan berkat-NYA yang Agung Mulia di dalam hidupku..

Yang bertanda tangan di bawah ini, saya mahasiswa Uniersitas Sanata Dharma:  Nama      : Diyah Sayekti 

Nomor Mahasiswa  : 063114017 

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Uniersitas Sanata  Dharma karya ilmiah saya yang berjudul: 

 

PERBANDINGAN METODE MONTE CARLO STANDAR, ANTHITETIC VARIATE DAN CONTROL VARIATE 

PADA PENENTUAN HARGA OPSI BARRIER 

Beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan  Uniersitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya  dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikan di Internet atau  media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti  kepada saya selama tetap mencantumkan nama saya sebagai penulis. 

 

Demikian pernyataan ini saya buat dengan sebenarnya.  Dibuat di Yogyakarta. 

Pada tanggal: 3 Maret 2010  Yang menyatakan  

 

(Diyah Sayekti) 

(bukan kewajiban) kepada pembeli atau pemegang kontrak itu untuk membeli (opsi beli) atau menjual (opsi jual) suatu aset dengan harga tertentu dalam jangka waktu tertentu. Jenis opsi bermacam-macam anatara lain, opsi Eropa, opsi Amerika, opsi Barrier, opsi Asia, dll. Dalam Skripsi ini akan dibahas opsi barrier, dimana harga dari opsi tersebut akan dihitung menggunakan tiga metode, antar lain metode Monte Carlo standar, Monte Carlo anthitetic variate, dan Monte Carlo control variate.

Prinsip dari metode Monte Carlo dalam mencari harga opsi barrier adalah penggunaan bilangan random berdistribusi normal (0,1) dan hukum bilangan besar. Sedangkan anthitetic variate dan control varite merupakan teknik reduksi variansi dari metode Monte Carlo. Hasil dari ketiga metode tersebut akan dibandingkan satu sama lain. Kesimpulan yang didapatkan adalah harga opsi yang diperoleh dengan metode Monte Carlo anthitetic variate dan control variate lebih akurat dibandingkan dengan metode Monte Carlo standar.

vii

right, but not the obligation, to buy (call option) or to sell (put option) a particular asset at a specified price during a specified period of time. The option type may vary, such as European option, American option, Barrier option, Lookback option, Asian option, etc. This thesis explores the barrier option whose value will be calculated using three methods; the standar Monte Carlo Method, the anthitetic variate Monte Carlo, and the control variate Monte Carlo.

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus atas berkat dan anugerahnya yang telah diberikan sehingga penulis dapat menyelesaikan skripsi ini.

Dalam penulisan skripsi ini, penulis banyak menemui hambatan dan kesulitan. Namun, berkat bantuan dan dukungan dari banyak pihak, akhirnya skripsi ini dapat terselesaikan. Oleh karena itu, penulis ingin mengucapkan terima kasih kepada :

1. Ibu Ch. Enny Murwaningtyas, S.Si, M.Si., selaku dosen pembimbing skripsi yang selalu sabar dan memberi semangat kepada penulis selama penyusunan skripsi ini. 2. Bapak Yosef Agung Cahyanta, S.T., M.T., selaku Dekan Fakultas Sains dan

Teknologi.

3. Ibu Lusia Krismiyati Budiasih S.Si, M.Si, selaku Ketua Program Studi Matematika yang telah banyak membantu dan memberi saran.

4. Ibu M.V. Any Herawati, S.Si., M.Si., selaku dosen pembimbing akademik yang telah banyak membantu dan memberi saran selama penulis kuliah.

5. Bapak Ir. Ignatius Aris Dwiatmoko, M.Sc., selaku penguji yang telah banyak memberikan masukan kepada penulis.

6. Bapak dan Ibu Dosen Fakultas Sains dan Teknologi yang telah memberikan bekal ilmu yang sangat berguna bagi penulis.

7. Bapak Tukijo dan Ibu Linda yang telah memberikan pelayanan administrasi selama penulis kuliah.

8. Mas Susilo Dwiratno yang telah membantu menyiapkan fasilitas laboratorium Tugas Akhir selama penulis mengerjakan skripsi ini..

ix

telah memberikan dukungan, semangat, doa, dan cinta kasih kepada penulis.

11. I Wayan Darmawan terkasih dan keluarga yang telah memberikan dukungan, semangat, doa, dan cinta kasih kepada penulis.

12. Sahabatku Titik Murwani dan Rochi Ifahyani Siagian yang selalu memberi dukungan dan semangat.

13. Teman-teman seangkatan 2006 : Viktor, Galih, Gigih, Ria, Rosa, Lia, Marcel, Atri, Wene, Egi, dan Meta yang telah memberi keceriaan dalam menjalani perkuliahan. 14. Teman-teman angkatan 2005 yang telah memberi semangat dan masukan selama

penulis menjalani kuliah.

15. Tim doa Oikumene: Priskila, Leo, Radit, Gloria, dan Wili yang telah membantu doa sebelum penulis mengikuti ujian pendadaran.

16. Teman – teman Persekutuan Mahasiswa Kristen Oikumene yang telah memberikan dukungan dan semangat.

17. Tim doa GKI Gejayan dan tim doa Keluarga Allah yang telah memberikan dukungan doa.

Penulis juga tidak lupa mengucapkan terima kasih kepada pihak yang membantu penulis dalam penulisan skripsi ini yang tidak bisa disebutkan satu per satu disini. Tiada yang sempurna, demikian juga skripsi ini. Masukan dan kritikan yang membangun untuk kesempurnaan skripsi ini menjadi kehormatan bagi penulis.

HALAMAN JUDUL……… i

HALAMAN JUDUL (INGGRIS)……… i

HALAMAN PERSETUJUAN PEMBIMBING………... ii

HALAMAN PENGESAHAN……….. iii

HALAMAN KEASLIAN KARYA……….. iv

HALAMAN PERSEMBAHAN………... v

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI……… vi

ABSTRAK………... vii

ABSTRACT……….. viii

KATA PENGANTAR………. ix

DAFTAR ISI………. xi

DAFTAR TABEL………. xvii

DAFTAR GAMBAR……….. ix

BAB I PENDAHULUAN A. Latar Belakang………. 1

B. Perumusan Masalah……….. 3

C. Pembatasan Masalah………... 3

D. Tujuan Penulisan………... 4

E. Metode Penulisan………... 4

BAB II LANDASAN TEORI

A. Variabel Random dan Fungsi Probabilitas……… 6

B. Nilai Harapan……… 11

C. Variansi dan Kovariansi……… 17

D. Fungsi Pembangkit Momen……….. 23

E. Fungsi Gamma……….. 24

F. Distribusi Seragam……… 28

G. Distribusi Normal………. 29

H. Fungsi Variabel Random………. 36

I. Distribusi Lognormal………. 40

J. Teorema Limit Pusat……… 42

K. Hukum Bilangan Besar……….. 44

L. Metode Momen……….. 48

M. Nilai Waktu Uang………. 50

1. Nilai Masa Yang Akan Datang……… 50

2. Nilai sekarang……….. 51

BAB III METODE MONTE CARLO, MODEL HARGA SAHAM, DAN OPSI A. Simulasi………. 52

B. Metode Monte Carlo……….. 59

C. Reduksi Variansi Pada Metode Monte Carlo……… 67

D. Model Harga Saham……….. 80

E. Estimasi Volatilitas Pergerakan Harga Saham……….. 95

F. Opsi……… 96

1. Pengertian Opsi……… 96

2. Transaksi Opsi………. 99

3. Opsi Eropa………... 102

BAB IV PENENTUAN HARGA OPSI BARRIER A. Opsi Barrier………... 105

B. Metode Monte Carlo Pada Penentuan Harga Opsi Barrier………108

1. Penentuan Harga Opsi Barrier Menggunakan Metode Monte Carlo Standar……… 108

2. Penentuan Harga Opsi Barrier Menggunakan Metode Monte Carlo Anthitetic Variate……….. 110

3. Penentuan Harga Opsi Barrier Menggunakan Metode Monte Carlo Control Variate……….113

C. Penentuan Harga Opsi Beli Barrier Up and In………..115

1. Penentuan Harga Opsi Beli Barrier Up and In Menggunakan Formula Black Scholes……… 117 2. Penentuan Harga Opsi Beli Barrier Up and In

Menggunakan Metode Monte Carlo Standar,

Barrier Up and In……….124 D. Penentuan Harga Opsi Beli Barrier Up and Out………... 128

1. Penentuan Harga Opsi Beli Barrier Up and Out

Menggunakan Formula Black Scholes……… 130 2. Penentuan Harga Opsi Beli Barrier Up and Out

Menggunakan Metode Monte Carlo Standar,

Anthitetic Variate dan Control Variate………...131

3. Pengaruh Nilai Barrier dan Volatilitas Pada

Harga Opsi beli Barrier Up and Out………134 E. Penentuan Harga Opsi Beli Barrier Down and In……… 136

1. Penentuan Harga Opsi Beli Barrier Down and In

Menggunakan Formula Black Scholes……… 137 2. Penentuan Harga Opsi Beli Barrier Down and In

Menggunakan Metode Monte Carlo Standar,

Anthitetic Variate dan Control Variate………...138

3. Pengaruh Nilai Barrier dan Volatilitas Pada

Harga Opsi beli Barrier Down and In……….141 F. Penentuan Harga Opsi Beli Barrier Down and Out……….. 143

1. Penentuan Harga Opsi Beli Barrier Down and Out

Menggunakan Formula Black Scholes……… 144

Anthitetic Variate dan Control Variate………...145 3. Pengaruh Nilai Barrier dan Volatilitas Pada

Harga Opsi beli Barrier Down and Out……….. 148 G. Penentuan Harga Opsi Jual Barrier Up and In………..150

1. Penentuan Harga Opsi Jual Barrier Up and In

Menggunakan Formula Black Scholes……… 151 2. Penentuan Harga Opsi Beli Barrier Up and In

Menggunakan Metode Monte Carlo Standar,

Anthitetic Variate dan Control Variate………...152

3. Faktor – Faktor Yang Mempengaruhi Harga Opsi Jual

Barrier Up and In……….154

H. Penentuan Harga Opsi Jual Barrier Up and Out………... 159 1. Penentuan Harga Opsi Jual Barrier Up and Out

Menggunakan Formula Black Scholes……… 160 2. Penentuan Harga Opsi Jual Barrier Up and Out

Menggunakan Metode Monte Carlo Standar,

Anthitetic Variate dan Control Variate………...161

3. Pengaruh Nilai Barrier dan Volatilitas Pada

Harga Opsi Jual Barrier Up and Out………... 163 I. Penentuan Harga Opsi Jual Barrier Down and In……… 165

2. Penentuan Harga Opsi Jual Barrier Down and In

Menggunakan Metode Monte Carlo Standar,

Anthitetic Variate dan Control Variate………...167

3. Pengaruh Nilai Barrier dan Volatilitas Pada Harga Opsi Jual Barrier Down and In……… 169

J. Penentuan Harga Opsi Jual Barrier Down and Out……….. 172

1. Penentuan Harga Opsi Jual Barrier Down and Out Menggunakan Formula Black Scholes……… 173

2. Penentuan Harga Opsi Jual Barrier Down and Out Menggunakan Metode Monte Carlo Standar, Anthitetic Variate dan Control Variate………...174

3. Pengaruh Nilai Barrier dan Volatilitas Pada Harga Opsi beli Barrier Down and Out……….. 176

BAB V PENUTUP A. Kesimpulan………. 169

B. Saran………170

DAFTAR PUSTAKA……… 171

LAMPIRAN………...173

Tabel 2.1……… 8

Tabel 3.1……… 57

Tabel 3.2……… 58

Tabel 3.3……… 77

Tabel 3.4……… 85

Tabel 4.1……… 121

Tabel 4.2……… 121

Tabel 4.3……… 131

Tabel 4.4……… 132

Tabel 4.5……… 139

Tabel 4.6……… 139

Tabel 4.7……… 145

Tabel 4.8……… 146

Tabel 4.9……… 152

Tabel 4.10……… 153

Tabel 4.11……… 162

Tabel 4.12……… 162

Tabel 4.13……… 168

Tabel 4.14……… 168

Tabel 4.15……… 174

Gambar 2.1 ..……….. 30

Gambar 3.1 ..……….. 96

Gambar 3.2 ..……….. 98

Gambar 4.1 ..………..106

Gambar 4.2 ..………..107

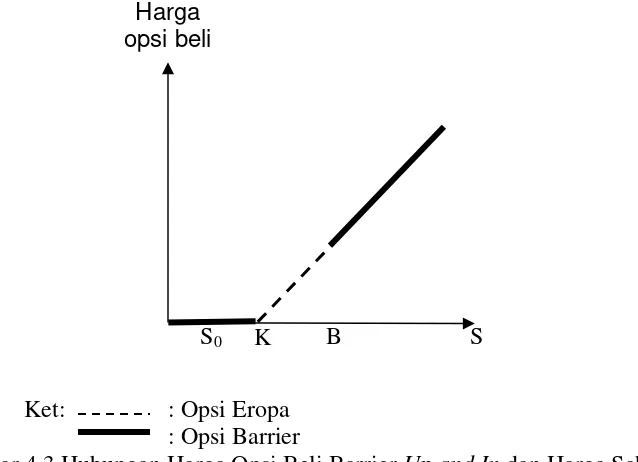
Gambar 4.3 ..………..116

Gambar 4.4 ..………..123

Gambar 4.5 ..………..124

Gambar 4.6 ..………..125

Gambar 4.7 ..………..126

Gambar 4.8 ..………..127

Gambar 4.9 ..………..128

Gambar 4.10 ..………. 129

Gambar 4.11 ..………. 133

Gambar 4.12 ..………. 135

Gambar 4.13 ..………. 136

Gambar 4.14 ..………. 137

Gambar 4.15 ..………. 140

Gambar 4.16 ..………. 142

Gambar 4.17 ..………. 142

Gambar 4.20 ..………. 148 Gambar 4.21 ..………. 149 Gambar 4.22 ..………. 150 Gambar 4.23 ..………. 154 Gambar 4.24 ..………. 155 Gambar 4.25 ..………. 156 Gambar 4.26 ..………. 157 Gambar 4.27..………. 158 Gambar 4.28 ..………. 159 Gambar 4.29 ..………. 160 Gambar 4.30 ..………. 163 Gambar 4.31 ..………. 164 Gambar 4.32 ..………. 165 Gambar 4.33 ..………. 166 Gambar 4.34 ..………. 169 Gambar 4.35 ..………. 170 Gambar 4.36 ..………. 171 Gambar 4.37 ..………. 172 Gambar 4.38 ..………. 175 Gambar 4.39 ..………. 177

A. Latar Belakang

Dunia perdagangan sudah ada sejak zaman purba, sebelum ditemukannya uang bentuk perdagangan pertama kali dilakukan dengan sistem barter (pertukaran langsung). Seiring dengan kemajuan teknologi dan setelah ditemukannya uang, investasi mulai berkembang pesat. Investasi pada hakikatnya merupakan penempatan sejumlah dana pada saat ini dengan harapan untuk memperoleh keuntungan di masa mendatang. Perkembangan dunia investasi tidak saja ditunjukkan oleh semakin meningkatnya jumlah uang yang diinvestasikan ataupun semakin banyaknya jumlah investor yang berinvestasi, tetapi juga ditunjukkan oleh semakin banyaknya alternative-alternatif instrumen investasi yang bisa dijadikan pilihan investor dalam berinvestasi.

opsi yang diperdagangkan tidak terbatas hanya pada opsi saham, tetapi juga opsi indeks saham, opsi kurs valas, opsi komoditas, dan lain-lain.

Opsi yang akan dibahas dalam skripsi ini adalah opsi untuk saham. Oleh karena seiring berjalannya waktu, perjalanan saham cenderung tidak menentu, yakni pergerakan saham yang cenderung liar keatas dan liar kebawah, maka perlu adanya suatu solusi, yaitu dengan memberikan batasan harga tertentu yang nantinya diharapkan dapat meminimalisasi liarnya pergerakan harga saham. Adapun jenis opsi yang dapat memberikan batasan harga tersebut adalah opsi barrier yang berarti opsi penghalang. Opsi barrier merupakan salah satu jenis opsi yang dapat diaktifkan atau dinonaktifkan jika harga pasar saham mencapai suatu level harga tertentu (barrier). Salah satu kelebihan opsi barrier adalah premi opsi barrier lebih murah dibandingkan dengan opsi Eropa.

B. Perumusan Masalah

Pokok – pokok permasalahan yang akan dibahas dalam skripsi ini dirumuskan sebagai berikut:

1. Apa yang dimaksud dengan opsi barrier?

2. Apa yang dimaksud dengan metode Monte Carlo standar, anthitetic variate

dan control variate?

3. Bagaimana cara mencari estimasi harga opsi barrier menggunakan metode Monte Carlo Standar, anthitetic variate dan control variate ?

4. Metode mana yang hasilnya paling mendekati estimasi harga opsi barrier analitik?

C. Pembatasan Masalah

Penulisan ini dibatasi oleh beberapa hal yaitu:

a. Skripsi ini tidak membahas solusi analitis penentuan harga opsi barrier.

b. Deret Taylor – Maclaurin pada pembuktian teorema limit pusat tidak dibahas secara mendalam.

c. Formula Black Scholes untuk opsi Eropa dan opsi barrier tidak dibahas secara mendalam.

d. Teorema 4.3.1 tentang solusi analitis harga opsi barrier diskrit tidak dibuktikan.

D. Tujuan Penulisan

Tujuan yang ingin dicapai dalam penulisan ini adalah menentukan harga opsi barrier dengan metode Monte Carlo standar, Monte Carlo anthitetic variate,

dan Monte Carlo control variate. Kemudian menentukan metode mana yang lebih baik diantara ketiga metode tersebut untuk menentukan estimasi harga opsi barrier.

E. Manfaat Penulisan

Manfaat yang akan diperoleh setelah mempelajari topik ini adalah dapat memahami metode Monte Carlo standar, Monte Carlo anthitetic variate dan

control variate serta penggunaannya dalam pentuan harga opsi barrier.

F. Metode Penulisan

G. Sistematika Penulisan

BAB I: PENDAHULUAN

Dalam bab I dibahas tentang latar belakang, perumusan masalah, pembatasan masalah, tujuan penulisan, metode penulisan, manfaat penulisan, dan sistematika penulisan.

BAB II: LANDASAN TEORI

Dalam bab II akan dibahas tentang variabel random, fungsi probabilitas, nilai harapan, variansi dan kovariansi, fungsi pembangkit momen, distribusi seragam, fungsi gamma, distribusi normal, fungsi variabel random, distribusi lognormal, teorema limit pusat, hukum bilangan besar, metode momen, dan nilai waktu uang.

BAB III: METODE MONTE CARLO, MODEL HARGA SAHAM DAN OPSI

BAB IV: PENENTUAN HARGA OPSI BARRIER

Dalam bab IV akan dibahas opsi barrier dan akan diberikan contoh penentuan harga opsi barrier menggunakan ketiga metode Monte Carlo.

BAB V: PENUTUP

A. Variabel Random dan Fungsi Probabilitas

Gagasan untuk mendefinisikan sebuah fungsi yang dikenal dengan variabel

random timbul karena model-model matematika diekspresikan dalam bentuk

nilai-nilai numeris daripada hasil percobaan asli seperti sisi, warna, atau yang lain.

Definisi 2. 1.1:

Variabel random, misalnya X adalah fungsi yang didefinisikan pada ruang sampel

S, yang memetakan setiap elemen e∈S kebilangan real.

Notasi : X(e)= x,e∈S

R x∈

Untuk lambang variabel random digunakan huruf-huruf kapital X, Y, Z, sedangkan

untuk melambangkan nilai variabel random yang mungkin, digunakan huruf-huruf

kecil yang bersesuaian seperti x, y, z.

Definisi 2.1.2:

Variabel random diskret adalah variabel random yang didefinisikan pada ruang

sampel diskret dan nilainya berhingga atau tak berhingga terbilang. Sedangkan

variabel random kontinu adalah variabel random yang didefinisikan pada ruang

Definisi 2.1.3:

Fungsi f(xi)=P(X =xi),i=1,2,3,K yang menyatakan probabilitas untuk semua

kemungkinan nilai variabel random diskret X disebut fungsi probabilitas.

Fungsi probabilitas tersebut dapat dinyatakan dalam rumus fungsi atau tabel yang memuat pasangan nilai variabel x beserta dengan peluangnya yang disebut dengan distribusi probabilitas.

Contoh 2.1.1:

Sebuah koin dilemparkan sebanyak dua kali dan X adalah variabel random yang menyatakan banyaknya muka yang diperoleh. Variabel random X yang memiliki distribusi probabilitas sebagai berikut:

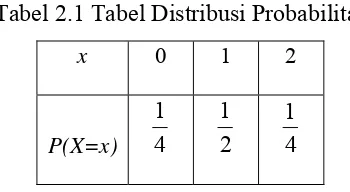
Tabel 2.1 Tabel Distribusi Probabilitas

x 0 1 2

P(X=x) 4 1

2 1

4 1

Definisi 2.1.4

Fungsi f(x) disebut sebagai fungsi probabilitas diskret X bila dan hanya bila memenuhi syarat:

0 ) ( )

(i f x ≥ , untuk ∀x∈N

∑

∀xi i =

x f

ii) ( ) 1

Definisi 2.1.5

Fungsi disebut fungsi densitas bagi variabel random kontinu X bila dan hanya bila memenuhi syarat :

) (x f

(i) f(x)≥0, untuk semua nilai x real.

(ii)

∫

∞

∞ −

=1 ) (x dx f

Definisi 2.1.6

Fungsi distribusi komulatif suatu variabel random diskret X didefinisikan sebagai

∑

∀ = ≤ =

i

x i

x f x

X P x

F( ) ( ) ( ) , untuk ∀x∈N

Fungsi F(x) disebut juga fungsi distribusi.

Definisi 2.1.7

Fungsi distribusi suatu variabel random kontinu X, dengan fungsi densitas f(x) didefinisikan sebagai :

∫

∞ − =

x dt t f x

F( ) ( )

Fungsi densitas f(x) merupakan derivatif dari F(x).

Definisi 2.1.8

Fungsi disebut sebagai fungsi probabilitas gabungan dari variabel random diskret dan bila dan hanya bila memenuhi syarat:

) , (x₁ x₂ f

1

0 ) , ( )

(i f x₁ x₂ ≥ , untuk semua (x₁,x₂)

∑∑

= 1 2 1 ) , ( )

( _{1 2}

x x

x x f ii

(iii)f(x₁,x₂)=P{X₁ = x₁,X₂ = x₂}

Definisi 2.1.9

Fungsi f(x,y) disebut sebagai fungsi densitas gabungan dari variabel random kontinu dan bila dan hanya bila memenuhi syarat:

1 X 2 X 0 ) , ( )

(i f x₁ x₂ ≥ , untuk semua (x₁,x₂)

∫ ∫

∞ ∞ − ∞ ∞ − =1 ) , ( )

(ii f x₁ x₂ dx₁dx₂

(iii) ∈ =

∫∫

A dx dx x x f A X X

p[( ₁, ₂) ] ( ₁, ₂) _{1 2}

untuk setiap daerah A yang diberikan pada bidang xy.

Definisi 2.1.10

Fungsi probabilitas marginal untukX₁ dan X₂ adalah:

∑

= 2 ) , ( )

( _{1 1 2}

1 X X X P X

P dan =

∑

1

) , ( )

( _{2 1 2}

2 X X X P X P

untuk kasus diskrit, dan

∫

∞

∞ −

= _{1 2 2}

1

1(x ) f(x ,x )dx

f dan

∫

∞

∞ −

= _{1 2 1}

2

2(x ) f(x ,x )dx

f

Definisi 2.1.11

Variabel random dan dengan fungsi probabilitas gabungan dikatakan saling bebas jika dan hanya jika

1

X X₂ f(x₁,x₂)

) ( ) ( ) ,

(x₁ x₂ f₁ x₁ f₂ x₂

f =

B. Nilai Harapan

Konsep nilai harapan memegang peranan yang sangat penting dalam

statistika. Nilai harapan dinyatakan dalam definisi berikut,

Definisi 2.2.1:

⎪⎩

⎪

⎨

⎧∑

∫

= ∞

∞ −

n

i

i

ip x p x

x

x f x

xf 1

) ( as probabilit fungsi

dengan diskret

X Jika ), (

) ( densitas fungsi

dengan kontinu

X Jika ), (

=

)

(

X

E

(2.1)

Ditinjau dari segi variabel random yang diskret, maka nilai harapan E(X) merupakan

suatu nilai fungsi linear dari semua unsur didalam domain fungsi dengan peluang

Definisi 2.2.2

Jika X adalah variabel random dan g(X) adalah fungsi dari variabel random X maka,

⎪⎩

⎪

⎨

⎧∑

∫

= ∞ ∞ − n i i

i)p(x ), X p(x)

g(x x f X x f x g 1 as probabilit fungsi dengan diskret Jika ) ( densitas fungsi dengan kontinu Jika ), ( ) ( (2.2) = )] ( [g X E

Teorema 2.2.1

Jika X adalah variabel random dengan fungsi probabilitas f(x), untuk a dan b suatu

konstanta, maka berlaku

a X bE a bX

E( + )= ( )+

Bukti:

Jika X adalah variabel random diskrit maka menurut definisi nilai harapan

∑

= + = + n i i

i a f x

bx a bX E 1 ) ( ) ( ) (

∑

= + = n i i i

if x af x

bx 1 )) ( ) ( (

∑

∑

= = + = n i i n i i

if x af x

bx 1 1 ) ( ) (

∑

∑

= = + = n i i n i i

if x a f x

x b 1 1 ) ( ) ( 1 . ]

[X a

bE +

a X

bE +

= [ ]

Bukti untuk kasus variabel random kontinu dapat dikerjakan secara analog. ■

Teorema 2.2.2

Jika X adalah variabel random dengan fungsi probabilitas f(x), a dan b konstanta, g(X)

dan h(X) fungsi-fungsi variabel random bernilai real, maka

E[ag(x) + bh(x)] = a E[(g(x)] + b E[h(x)]

Bukti :

Jika X adalah variabel random diskrit maka menurut definisi nilai harapan

) ( )] ( ) ( [ )] ( ) ( [ 1 i n i i

i bh x f x

x ag X bh X ag E

∑

= + = +

∑

= + = n i i i i

i f x bh x f x

x ag 1 )] ( ) ( ) ( ) ( [

∑

∑

= = + = n i i i n i i

i f x bh x f x

x ag 1 1 ) ( ) ( ) ( ) (

∑

∑

= = + = n i i i n i i

i f x b h x f x

x g a 1 1 ) ( ) ( ) ( ) ( )] ( [ )] (

[g x bE h x

aE +

=

Nilai harapan sering kali dapat dikatakan sebagai momen ke-k.

Definisi 2.2.3

Momen ke-k dari suatu variabel random X adalah

) (

' k

k = E X

μ

Teorema 2.2.3

Jika terdapat variabel-variabel randomX₁ dan X₂ maka berlaku

] [ ] [ ]

[X₁ X₂ E X₁ E X₂

E + = +

Bukti:

Misalkan dan adalah variabel random diskret dengan fungsi probabilitas

gabungan Dengan menggunakan definisi nilai harapan didapatkan

1 X ( P 2 X ). 2 , 1 X X

∑∑

= = + = + n i n j j i j

i X P X X

X X X E 1 1 2 1 2 1 2

1 ] (( ) ( , ))

[ ) , ( ) , ( 1 1 2 1 2 1 1 2 1 1

∑∑

∑∑

= = = = + = n i n j j i j n i n j j i

iP X X X P X X

X

∑

∑

∑

∑

= = = = + = n i j i n j j n j j i n i

i P X X X P X X

X 1 2 1 1 2 1 2 1 1

1 ( , ) ( , )

Berdasarkan Definisi 2.1.10 maka persamaan diatas menjadi

] [X₁ X₂

E + =

∑

∑

= = + n j j j n i i

iP X X P X

X 1 2 2 1 1

1 ( ) ( )

] [ ]

[X₁ E X₂

E +

=

Teorema 2.2.4

Jika terdapat X₁,X₂,X₃,K,X_n variabel random maka berlaku

] [ ]

[ ] [ ] [ ]

[X₁ X₂ X₃ X_n E X₁ X₂ X₃ X_n

E + + +K+ = + + +K+

Bukti:

Teorema di atas akan dibuktikan menggunakan induksi matematika

1. Rumus benar untuk k = 2, yang ditunjukkan dalam Teorema 2.2.3 .

2. Diasumsikan bahwa rumus benar untuk k <ndimana k > 2.

3. Akan ditunjukkan bahwa rumus benar untuk n=k.

Misalkan Y₁ = X₁+L+X_k−1, Y₂ = X_k sehingga dengan menggunakan Teorema

2.2.3 didapatkan

[

X1 X 1 X

] [

EY1 Y2

]

E +K+ _k− + _k = +

] [ ] [Y₁ EY₂

E +

=

] [ ] [ ]

[ ]

[X₁ X₂ X_{k 1} X_k

E + + + +

= K ₋ ■

Teorema 2.2.5

Apabila X₁ dan X₂ merupakan variabel random yang saling bebas maka

] [ ] [ ] ,

[X₁ X₂ E X₁ E X₂

Bukti:

Misalkan dan adalah variabel random diskret yang saling bebas dengan

fungsi probabilitas gabungan Karena variabel random tersebut saling

bebas maka = , sehingga

1 X P 2 X ). 2 X ). , (X₁ X₂ P

) ( ) ₂

1 P X

,

(X₁ P(X

∑∑

= = = n i n j j i j

iX P X X

X X X E 1 1 2 1 2 1 2

1 ] ( , )

[

∑∑

= = = n i n j j i j

iX P X P X

X 1 1

2 1

2

1 ( ) ( )

∑∑

= = = n i n j j j i

iP X X P X

X 1 1

2 2 1

1 ( ) ( )

)] ( ) ( ) ( )][ (

[ _{21 22 22 2 2}

1

21 1

1 n n

n

i

i

iP X X P X X P X X P X

X + + +

=

∑

= L

∑

∑

= = = n i n j j j i

iP X X P X

X

1 1

2 2 1

1 ( ) ( )

] [ ] [X₁ E X₂ E

=

Bukti untuk kasus variabel random kontinu dapat dikerjakan secara analog. ■

Teorema 2.2.6

Apabila X₁,X₂,X₃,K,X_n merupakan variabel random yang saling bebas maka

] [ ] ][ ][ [ ] , , , ,

[X₁ X₂ X₃ X_n E X₁ X₂ X₃ X_n

Bukti:

Teorema di atas akan dibuktikan menggunakan induksi matematika

1. Rumus benar untuk k =2, yang ditunjukkan dalam Teorema 2.2.5

2. Diasumsikan bahwa rumus benar untuk k <n dimana k > 2.

3. Akan ditunjukkan bahwa rumus benar untuk k =n.

Misalkan Y₁ = X₁KX_n−1 dan Y₂ = X_n sehingga

[

X1 X 1X

]

EY1Y2

E K _{k− k} =

[ ]

.

Karena Y₁ dan Y₂ saling bebas dan dengan menggunakan Teorema 2.2.5 maka

[

X₁ X ₁X

]

E[Y₁]E[Y₂]

E K _{n− n} =

[

X Xn

] [ ]

E Xn

E _{1 −1}

= K

[ ]

X E Xn E

[ ]

Xn

E ₁ [ ₋₁]

= K

Bukti untuk kasus variabel random kontinu dapat dikerjakan secara analog. ■

C. Variansi dan Kovariansi

Pada Bab 2 Bagian B telah dibahas nilai harapan dari variabel random X. Kuantitas

lain yang juga sangat penting dalam probabilitas dan statistik adalah variansi dan

kovariansi. Parameter-parameter tersebut hampir selalu muncul dalam teknik-teknik

analisis statistika elementer maupun lanjut. Variansi dinyatakan dalam definisi

Definisi 2.3.1

Variansi variabel random X adalah :

Var(X) = E[(X-E[X])2]

Teorema 2.3.1

Apabila X merupakan sebuah variabel random maka variansi dari X adalah

2 2

]) [ ( ] [ )

var(X =E X − E X

Bukti:

Berdasarkan Defnisi 2.3.1

] ]) [X 2 E

−

)

var(X =E[(X

] ]) [ ( ] [ 2

[X2 XE X E X 2

E − +

=

] ]) [ [( ]] [ 2 [ ]

[X2 E XE X E E X 2

E − +

=

2 2_{] 2 [ ] [ ] [ ]}

[X E X E X E X

E − +

=

2 2

]) [ ( ]

[X E X

E −

= ■

Teorema 2.3.2

Jika X adalah variabel random dengan fungsi probabilitas f(x), untuk a dan b suatu

konstanta, maka berlaku

Bukti:

Dengan menggunakan Teorema 2.3.1 didapatkan

2 2 ]) [ ( ] ) [( )

var(bX +a =E bX +a − E bX +a

Jika X adalah variabel random diskrit maka menurut definisi nilai harapan

)

var(bX+a = 2

1 2 ) ] [ ( ) ( )

(bx a f x bE X a

n

i

i

i + − +

∑

− ) ] [ 2 ]) [ ( ( ) ( ) 2

( 2 2 2

1 2 2 2 a X abE X E b x f a abx x b n i i i

i + + − + +

=

∑

= ) ] [ 2 ]) [ ( ( )) ( ) ( 2 ) (

( 2 2 2

1 2 2 2 a X abE X E b x f a x f abx x f x b n i i i i i

i + + − + +

=

∑

=

∑

∑

∑

= = = + + = n i i n i i i n i i

i f x abx f x a f x

x b 1 2 1 1 2 2 )) ( ) ( 2 ) ( ) ] [ 2 ]) [ (

(b2 E X 2+ abE X +a2

−

∑

∑

∑

= = = + + = n i i n i i i n i i

i f x ab x f x a f x

x b 1 2 1 1 2 2 )) ( ) ( 2 ) ( ) ] [ 2 ]) [ (

(b2 E X 2+ abE X +a2

− 2 2 2 2 2 2 ] [ 2 ]) [ ( ] [ 2 ]

[X abE X a b E X abE X a

E

b + + − − −

= 2 2 2 2 ]) [ ( ]

[X b E X

E b − = ) ]) [ ( ] [

( 2 2

2 X E X E b − = ) var( 2 X b =

Definisi 2.3.3

Kovariansi antara dua variabel random adalah ukuran sifat asosiasi (hubungan) antara

keduanya. Jika X dan Y merupakan dua variabel random maka kovariansi dari X dan Y

didefinisikan sebagai

Cov(X,Y) = E[(X – E[X])(Y – E[Y])] _(2.3)

Teorema 2.3.3

Jika X dan Y merupakan dua variabel random maka kovariansi dari X dan Y adalah

] [ ] [ ] [ ) ,

cov(X Y =E XY −E X E Y (2.4)

Bukti:

misal : E[X]=μ_X dan E[Y]=μ_Y

Selanjutnya dengan menggunakan Definisi 2.3.2 didapatkan

])] [ ])( [ [( ) ,

cov(X Y = E X −E X Y −EY

)] )(

[(X X Y Y

E −μ −μ

=

] [XY X _Y Y _{X X Y}

E − μ − μ +μ μ

=

] [ ] [ ] [ ]

[XY E X _Y E Y _X E _{X Y}

E − μ − μ + μ μ

=

Y X X

YE X EY

XY

E −μ −μ +μ μ

= [ ] [ ] [ ]

Y X Y X Y X

XY

E −μ μ −μ μ +μ μ = [ ]

Y X

XY

E −μ μ

= [ ]

] [ ] [ ]

[XY E X EY

E −

Dengan melihat Persamaan (2.4) dapat disimpulkan bahwa jika X dan Y saling bebas

maka

0 ) , cov(X Y =

Teorema 2.3.4

Apabila X₁ dan X₂ merupakan variabel random yang saling bebas maka

] var[ ] var[ ]

var[X₁+ X₂ = X₁ + X₂ Bukti:

(

)

[

]

(

)

[

2

]

2 1 2

1 2

1 )

var(X +X =E X +X −E X +X

(

)

[ ] [ ]

(

)

[

2

]

2 1

2

1 X E X E X

X

E + − −

=

[ ]

(

)

(

[ ]

)

(

)

[

2

]

2 2

1

1 E X X E X

X

E − + −

=

[ ]

(

)

(

[ ]

)

(

[ ]

)

(

[ ]

)

[

1 1 2 2

]

2 2 2

2 1

1 E X X E X 2 X E X X E X

X

E − + − + − −

=

[ ]

(

)

[

]

[

(

[ ]

)

2

]

2 2

2 1

1 E X E X E X

X

E − + −

=

[ ]

(

)

(

[ ]

)

[

1 1 2 2

]

2E X −E X X −E X +

( )

1 var

( )

2 2

[

(

1

[ ]

1

)

(

2

[ ]

2

)

]

var X + X + E X −E X X −E X =

( )

var

( )

2cov( , )

var X₁ + X₂ + X₁ X₂ =

Karena X₁ dan X₂ saling bebas maka cov(X₁,X₂)=0 sehingga

( )

var

( )

0

var )

var(X₁ +X₂ = X₁ + X₂ +

=var

( )

X₁ +var

( )

X₂ ■

Teorema 2.3.5

Apabila X₁,X₂,X₃,K,X_nmerupakan variabel random yang saling bebas maka

) var( )

var( ) var( )

var( )

var(X₁ +X₂ +X₃ +K+ X_n = X ₁+ X₂ + X₃ +K+ X_n

Bukti :

Teorema di atas akan dibuktikan menggunakan induksi matematika

1. Persamaan diatas benar untuk k = 2, yang telah ditunjukkan dalam Teorema 2.3.4

2. Diasumsikan bahwa persamaan benar untuk k <n dimana k > 2, selanjutnya

akan ditunjukkan bahwa persamaan benar untuk n = k .

Misalkan Y₁ = X₁+K+X_n−1 dan Y2 = Xn sehingga

) var(

)

var(X₁ +K+X_n−1+ X_n = Y₁ +Y₂ .

Karena Y₁ dan Y₂ saling bebas dan dengan menggunakan Teorema 2.3.3 maka

) var( ) var( )

var(X₁ +K+X_n−1+ X_n = Y₁ + Y₂

) var( )

var(X₁+ +Xn ₁ + Xn

= K ₋

) var( ) var( )

var(X₁ + + X_{n 1} + X_n

= K ₋ ■

Definisi 2.3.4

Korelasi dari dua variabel random X dan Y ditulis ρ(X,Y)dan didefinisikan sebagai

) var( ) var(

) , cov( )

, (

Y X

Y X Y

X =

D. Fungsi Pembangkit Momen

Definisi 2.4.1

Jika X adalah variabel random, maka nilai harapan M_X(t)=E

( )

etX disebut fungsi

pembangkit momen dari X jika nilai harapan tersebut ada untuk semua bilangan real t

dalam interval −h<t<h, untuk h>0.

Teorema 2.4.1

Andaikan adalah variabel random yang saling bebas dengan fungsi

pembangkit momen berturut Bila

maka fungsi pembangkit momen dari U adalah n

X X

X₁, ₂,K,

n X

X₂ +L+

) ( ) (

2

1 t M t

M_{X X} K

). ( , ), ( ), (

2

1 t M t M t

M

n

X X

X K

) (t

n

X X

U = ₁+

) (t

M_U = M

∏

= = n

i X

U t M t

M

i 1

) ( )

(

Bukti:

) ( )

(

2

1 t

M t M

n

X X X

U = + +L+

[

_et(X1 X2 Xn)

]

E + + +

= L

[

_et(X1)_et(X2) _et(Xn)

]

E L

=

karena X_isaling bebas maka

[ ] [ ]

( 1) ( 2)

[ ]

( )

)

( t X t X t Xn

U t Ee Ee Ee

) ( )

( ) (

3 2

1 t M t M t

M_{X X} L _X

=

∏

=

= n

i 1MXi(t) ■

Jika X_i indentik dan independen untuk ∀_i maka

) (t M

i

X =MX(t) sehingga MU(t)=

n X t

M ( )]

[ .

E. Fungsi Gamma

Definisi 2.5.1:

Fungsi Gamma ditulis Γ(k),untuk semua k>0 di definisikan sebagai

(2.6)

∫

∞

− − = Γ

0 1

)

(k tk e tdt

Teorema 2.5.1

Fungsi Gamma memenuhi sifat-sifat:

(i) Γ(k)=(k−1)Γ(k−1) k>1

(ii) Γ(n)=(n−1)! n =1,2,.. (2.7)

Bukti:

(i) Berdasarkan Definisi 2.5.1, didapatkan

∫

∞ − − = Γ 0 1 )

(k tk e tdt

Integral pada (2.8) akan diselesaikan menggunakan integral parsial

dengan memisalkan dan sehingga

dan v . Dengan menggunakan integral parsial tersebut

maka

∫

udv=uv− vdu

2 ) 1 ( − − = k t k du (2.8)

∫

= k−1

t

u dv=e−tdt

t e− − =

∫

∞ − − = Γ 0 1 )

(k tk e tdt

]

( 1) )

( lim

0 2 0

1 −

∫

− −

− ∞ → − + − = a t k a t k

a t e k t e dt

]

∫

− − ∞ → − − ∞ → − + − = a t k a a t k

a t e k t e dt

0 2 0 1 ) 1 ( lim lim + − − = − − ∞

→ ( 0)

lim k 1 a

a a e

∫

− − − a t k dt e t k 0 2 ) 1 ( +

=0 −

∫

− −

a t k dt e t k 0 2 ) 1 ( =( −

∫

− − a t k dt e t k 0 2 ) 1 ) 1 ( ) 1 ( − Γ −

(ii)Pada Sifat (i) telah dibuktikan bahwa Γ(k)=(k−1)Γ(k−1)sehingga secara

rekursif didapatkan

) 1 ( ) 1 ( ) ( = − Γ −

Γ n n n

) 2 ( ) 2 )( 1 ( − − Γ −

= n n n

) 3 ( ) 3 )( 2 )( 1 ( − − − Γ −

= n n n n

M )) 1 ( ( ) 3 )( 2 )( 1 ( − − − − −

= n n n L n n

=(n−1)!

(iii) Dengan menggunakan Definisi 2.5.1, didapatkan

∫

∞ − − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ 0 2 1 2 1 dt e t t

Kemudian dengan memisalkan 2 dan u

t = dt =2udu, maka

∫

∞ − − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ 0 1 2 2 1 2 udu e u u

∫

∞ − = 0 2

2 e u du (2.9)

Misalkan

∫

dan , sedemikian sehingga

∞ − = 0 2 dx e

I x

∫

∞ − = 0 2 dy e I y ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ =

∫

∫

∞ − ∞ − 0 0

2 2 2

dy e dx e

∫∫

∞ ∞ − − = 0 0 2 2 dydx e

e x y

∫∫

∞ ∞ + − = 0 0 ) ( 2 2

dydx

e x y (2.10)

Misalkan x=ρcosϑ dan y=ρcosϑ maka sehingga dengan

mengubah (2.10) ke dalam koordinat polar didapatkan

2 2 2 _{+ =}ρ

y x ϑ ρ ρ π ρ d d e I

∫∫

∞ − = 2 0 0 2 2

∫

∫

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− = − ∞ → 2 0 2 0 ) ( 2 1 lim 2 π ρ _{ρ ϑ} d d e a a

(

)

∫

− − = − ∞ → 2 0 0 2 ( lim 2 1 π ϑ d e e a a

∫

= 2 0 2 1 π ϑ d 2 0 ] [ 2 1 _ϑ π

=

=

⎥⎦ ⎤ ⎢⎣ ⎡ −0

π

2 1

=

I

Karena

∫

∫

∞ ∞

−

− _{= =}

=

0 0 2

1 2 2 π dy e dx e

I x y

maka hasil integral pada (2.9) adalah

∫

∞ − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ 0 2 2 2 1 du e u π 2 1 2 = = π ■

F. Distribusi Seragam

Definisi 2.6.1

Variabel random X dikatakan berdistribusi seragam pada interval (a,b) jika

mempunyai fungsi probabilitas berbentuk

, 1 ) ( a b x f −

= a< x<b

Dengan Nilai harapan

3 )

( 3

) )( (

) ( 3 1

) (

2 2

2 3 3 2

2 b ab a

a b

a b a ab b a b

a b dx a b x X

E

b

a

+ + = −

− + + = − − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

− =

∫

Sehingga dengan menggunakan Teorema 2.3.1 didapatkan variansi distribusi seragam

sebagai berikut,

12 ) ( 4

) ( 3

) (

) var(

2 2

2 2

a b b

a a ab b

X = + + − + = −

G. Distribusi Normal

Distribusi normal sangat penting baik dalam statistika teori maupun terapan.

Distribusi ini pertama kali dipelajari pada abad kedelapan belas, ketika orang

mengamati galat pengukuran berdistribusi simetrik dan berbentuk bel. De Moivre

mengembangkan bentuk matematik distribusi ini pada tahun 1733, sebagai bentuk

limit distribusi binomial. Laplace juga telah mengenal distribusi ini sebelum tahun

1775. Gauss menurunkan persamaan distribusi ini dari suatu studi tentang galat dalam

pengukuran yang berulang-ulang dari kuantitas yang sama, dan mempublikasikannya

pada tahun 1809. Untuk menghormatinya distribusi normal juga dikenal sebagai

distribusi Gauss. Pada abad kedelapan belas dan sembilan belas, berbagai usaha telah

dilakukan untuk membuat distribusi ini sebagai hukum probabilitas yang mendasari

Definisi 2.7.1

Suatu variabel random kontinu X dikatakan berdistribusi normal dengan μ dan

variansi σ2, apabila variabel itu mempunyai fungsi probabilitas yang berbentuk

2

2( )

2 1

2 1 )

( σ μ

π σ

− −

= e x

x

f (2.11)

Dengan

∞ < < ∞

− X ; −∞<μ<∞; σ >0; 14π =3, dan e=2,718

Jika fungsi probabilitas itu digambar, maka diperoleh grafik seperti dalam gambar

dibawah ini dan dinamakan kurva normal.

Gambar 2.1 : kurva normal dengan meanμdan variansi σ2

Berikut ini akan ditinjukkan bahwa distribusi normal memenuhi sifat-sifat fungsi

densitas. Pertama, harus ditunjukkan bahwa μ dan adalah mean dan variansi

dari X.

2

σ

Dengan mensubtitusikan

σ μ − = x

∫

∫

∫

∞ ∞ − ∞ ∞ − ∞ − − ₌ = = 0 2 2 2 2 2 1 2 2 1 ) , ,

(x dx e dz e dz

f

I z z

π π

σ μ

Bila dimisalkan w= z2 2, maka z= 2wdan dz =(w−12 / 2)dw, sehingga

∫

∞ − − = 0 2 1 dw e w I w π

Dengan fungsi gamma didapat

1 ) 2 1 ( 2

1 22

= Γ = =

∫

∞ ∞ − − π π e dz

I z (2.12)

Integran yang diperoleh dengan mensubstitusikan

σ μ − = x

z memegang peranan

yang sangat penting dalam menentukan probabilitas variabel random normal.

Perhitungan menjadi lebih sederhana karena nilai probabilitas telah ditabelkan.

Fungsi densitas hasil transformasi dari X ke Z disebut distribusi normal standar yang

fungsinya, ∞ < < ∞ −

= e− z

z z , 2 1 ) ( 2 2 π φ

kemudian dapat dicari

2 ' 2 2 1 ) ( z e z z − − = π φ ) (z zφ −

= (2.13)

dan ) ( ) ' ( ) ( ) ( ) (

" z z φ' z z φ z

) ( ) ( )

(

" z z2φ z φ z

φ = −

(2.14) )

( ) 1 (z2− φ z

=

Selanjutnya dapat dicari E(Z)dan sebagai berikut, E(Z2)

∫

∞

∞ −

= z z dz Z

E( ) φ( )

dengan menggunakan (2.13) didapatkan

∫

∞

∞ − −

= z dz

Z

E( ) φ'( )

]

∞ ∞ − − = φz

[

(∞)− (−∞)

]

−

= φ φ

=−[0−0]

0

= (2.15)

∫

∞

∞ −

= z z dz

Z

E( 2) 2φ( )

dengan menggunakan (2.14) didapatkan

[

z z

]

dz

∫

∞

∞ −

+ = φ"( ) φ( )

]

z dz

z

∫

∞

∞ − ∞

∞ − + =φ'( ) φ( )

1 1 0 =

+ =

Dengan menggunakan Teorema 2.3.1 maka 2 2 )] ( [ ) ( )

var(Z =E Z − E Z

0 1− =

=0

Sehingga dapat disimpulkan bahwa nilai harapan dan variansi dari variabel random

berdistribusi normal standar adalah 0 dan 1.

Selanjutnya dengan menggunakan Persamaan (2.2) akan dicari nilai harapan

dan variansi dari variabel random X yang berdistribusi normal secara umum.

∫

∞ ∞ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − −

= x x dx

X E 2 2 1 exp 2 1 ) ( σ μ π σ Misal σ μ − = x

z maka x=σz+μdan dx=σdzsehingga diperoleh

∫

∫

∫

∫

∫

∞ ∞ − ∞ ∞ − − − ∞ ∞ − − ∞ ∞ − − ∞ ∞ − − + = + = + = dz e dz e z dz e dz e z dz e z z z z z z 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 ) ( π μ π σ π μ π σ π μ σ ) (X E

Berdasarkan (2.12) telah diketahui bahwa

∫

∞

∞ −

− ₌

dz e z22 2

1

π 1 dan berdasarkan (2.15)

telah diketahui bahwa ( ) 0

2 1 ₂2

= =

∫

∫

∞ ∞ − ∞ ∞ − − dz z z dz e z z φ

π sehingga

1 . 0 . )

(X =σ +μ

μ =

) (X2

E =

∫

∞ ∞ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

− x dx

x 2 2 2 1 exp 2 1 σ μ π σ Misal, σ μ − = x

z maka x=σz+μ dan σdz=dxsehingga diperoleh

dz e z X E z 2 2 1 2 2 2 ) ( ) ( − ∞ ∞ −

∫

+ = π μ σ dz e z

z z2

2 1 2 2 2 2 ) 2 ( − ∞ ∞ −

∫

+ + = π μ μσ σ dz e dz e z dz e

z z2 z2 z2

2 1 2 2 1 2 1 2 2 2 2 2 2 − ∞ ∞ − − ∞ ∞ − − ∞ ∞ −

∫

∫

∫

+ + = π μ π μσ π σ dz e dz e z dz e

z z2 z2 z2

2 1 2 2 1 2 1 2 2 2 1 2 1 2 2 − ∞ ∞ − − ∞ ∞ − − ∞ ∞ −

∫

∫

∫

+ + = π μ π μσ π σ 1 . 0 . 2 2 2 2 1 2 2 2 μ μσ π σ + + = − ∞ ∞ −

∫

dz e z z 2 2 1 2 2 2

2π μ

σ + = ∞ − ∞ −

∫

dz e z z

Berdasarkan (2.16) telah diketahui bahwa ( ) 1

2

1 ₂ 1₂ 2 ₂

= =

∫

∫

∞ ∞ − − ∞ ∞ − dz z z dz e

z z φ

π

sehingga

) (X2

E = σ2 + µ2.

2 2 2 2 2 2 ) ( )] ( [ ) ( σ μ μ σ = − + = −

=E X E X

) var(X

(2.17)

Fungsi pembangkit momen distribusi normal

Dengan menggunakan fungsi probabilitas pada Persamaan (2.11) akan dicari fungsi

pembangkit momen variabel random yang berdistribusi normal. Dengan

menggunakan Definisi 2.4.1

] [ )

( tx

x t E e

M = dx e e x tx 2 2 1 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ∞ ∞ −

∫

= σ μ π σ dx e x tx

∫

∞ ∞ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = π σ σ μ 2 1 2 2 1 dx e x x tx

∫

∞ ∞ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − = π σ σ μ μ 2 1 2 2 ₂ 2 1 dx e x x tx

∫

∞ ∞ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − = π σ σ μ μ σ 2 1 2 2 2 2 2 2 dx e x t x

∫

∞ ∞ − + + − − = 2 2 2 2 2 ) ) ( 2 ( 2

1 σ_σ μ μ

dx e e t t t x

∫

∞ ∞ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − = 2 2 ) ( 2

1 2 2 22

2

1 σ σ μ

μ σ π σ dx e e t x t t

∫

∞ ∞ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − + = 2 2 2 2 2 1 2 2 1 σ μ σ σ μ π σ 2 2 2_t t e σ μ+ =

Jadi FPM dari distribusi normal adalah 2 2 2_t t e σ μ+

H. Fungsi Variabel Random

Salah satu tujuan dari statistika adalah membuat kesimpulan tentang populasi

berdasarkan informasi yang terdapat dalam sampel dan menentukan ukuran yang

sesuai untuk menarik kesimpulan. Topik fungsi variabel random sangat erat kaitannya

dengan tujuan tersebut. Hal ini disebabkan karena statistik yang dipakai untuk

menduga dan mengambil kesimpulan tentang parameter merupakan fungsi dari n

buah pengamatan random yang terdapat dalam sampel.

Sebagai gambaran, dalam masalah pendugaan rata-rata populasi, dari sampel

random berukuran n akan didapatkan pengamatan y1, y2, .., yn. Maka akan digunakan

rata-rata sampel n y y n i i

∑

=

sebagai penduga rata-rata populasi μ. Pertanyaan yang dapat diajukan adalah

seberapa baikah y sebagai panduga dariμ. Jawabannya tergantung pada sifat dari

variabel random Y1, Y2, .., Yn.

Kebaikan dari suatu penduga dapat diukur, misalnya dengan kesalahan

pendugaan, yaitu selisih antara penduga dan parameter yang diduga (dalam hal ini y

dan μ). Karena Y1, Y2, .., Ynadalah variabel-variabel random dalam sampel berulang,

maka Y adalah juga variabel random yang merupakan fungsi dari Y1, Y2, .., Yn.

Dengan demikian, tidak dapat ditentukan secara pasti bahwa kesalahan pendugaan

akan kurang dari suatu bilangan tertentu, misalnya B. Akan tetapi, jika dapat

ditentukan distribusi probilitas dari Y, maka distribusi ini dapat dipakai untuk

menentukan probabilitas bahwa kesalahan pengukuran kurang dari atau sama dengan

B.

Untuk menentukan distribusi probabilitas dari fungsi suatu variabel Y1, Y2, ..,

Yn harus ditemukan terlebih dahulu distribusi probabilitas bersama dari

variabel-variabel random tersebut. Secara umum dapat diasumsikan bahwa sampel diperoleh

berdasarkan pengambilan sampel secara random. Hal ini berarti bahwa pengambilan

sampel dari populasi berhingga akan menghasilkan percobaan yang tidak bebas,

tetapi percobaan ini secara esensial menjadi percobaan bebas jika ukuran populasi

relatif besar dibandingkan dengan ukuran sampelnya.

Pada pembahasan selanjutnya akan diasumsikan bahwa populasi berukuran

dengan yang lainnya. Dengan demikian, baik untuk variabel random diskret maupun

kontinu, distribusi probabilitas bersama Y1, Y2, .., Yn yang berasal dari populasi yang

sama adalah

f(y1, y2, .., yn) = p(y1)p(y2)..p(yn)

Selanjutnya pernyataan “Y1, Y2, .., Yn adalah sampel random dari f(y)”

diartikan sebagai “variabel-variabel random Y1, Y2, .., Yn adalah saling bebas dengan

distribusi bersama f(y)”.

Menentukan Distribusi Probabilitas Fungsi Variabel Random

Untuk menentukan distribusi probabilitas suatu fungsi variabel random dapat

ditempuh dengan 3 metode, yaitu metode fungsi distribusi, metode transformasi, dan

metode fungsi pembangkit momen. Dalam skripsi ini akan digunakan metode

transformasi satu-satu untuk menentukan distribusi probabilitas suatu fungsi variabel

random.

Metode Tranformasi satu-satu

Pertama-tama diasumsikan tranformasi variabel-variabel dalam satu dimensi.

Andaikan u(x) adalah fungsi bernilai real dari variabel x. Jika persamaan y = u(x)

mempunyai persamaan tunggal, misalnya x = w(y), maka tranformasi tersebut adalah

Teorema 2.8.1:

Andaikan X adalah variabel random diskret dengan distribusi probabilitas fx(x) dan Y

= u(x) mendefinisikan trnsformasi satu-satu. Dengan kata lain persamaan Y = u(x)

mempunyai penyelesaian tunggal x = w(y). Maka distribusi probabilitas dari Y adalah

fy(y) = fx(w(y)) y∈B = {y|fy(y)>0} (2.19)

Bukti :

fy(y) = P[Y=y] = P[u(X)=y]=P[X=w(y)]=fx(w(y)) ▄

Teorema 2.8.2:

Andaikan X adalah variabel random kontinu dengan fungsi densitas fx(x), dan Y=u(x)

mendefinisikan transformasi satu-satu A = {x| fx(x)>0} ke B = {y| fy(y)>0} dengan

transformasi invers x = w(y). Jika turunan (d/dy)w(y) kontinu dan tak nol pada B,

maka fungsi densitas dari Y adalah

Fy(y) = fx(w(y)) w(y)

dy d

, y∈B (2.20)

Bukti :

Jika y=u(x) adalah fungsi satu-satu, maka ada dua kemungkinan yaitu monoton naik

atau turun.

Pada kasus monoton naik, u(x) ≤y bila dan hanya bila x≤w(y). Sehingga

FY(y) = P[u(X)≤y] = P[X≤w(y)] = Fx(w(y)), akibatnya

fY(y) = ( ( )) ( )

) ( )) (

( w y

dy d y w F y dw

d y

w F dy

d

x

= fx(w(y)) w(y)

dy d

, karena dalam kasus ini (d/dy)w(y)>0

Pada kasus monoton turun, u(x) ≤y bila dan hanya bila w(y) ≤ x. Sehingga

FY(y) = = P[u(X)≤y] = P[X≥w(y)] = 1-Fx(w(y)), dan

fY(y) = ( ( )) w(y)

dy d y w f_x

−

= ( ( )) w(y) dy

d y w

f_x , karena dalam kasus ini (d/dy)w(y)<0 ▄

Turunan dari w(y) disebut sebagai Jacobian dari transformasi dan disimbolkan dengan J = (d/dy)w(y). Dapat dilihat pula bahwa mentransformasi variabel kontinu

ekuivalen dengan mengganti variabel dalam integral, sehingga metode transformasi

disebut juga metode penggantian peubah.

I. Distribusi Lognormal Teorema 2.9.1:

Jika X adalah variabel random yang berdistribusi normal dengan mean µ dan variansi

σ2

, dan jika X = ln y, maka fungsi densitas untuk Y adalah

f(y) =

⎪⎩

⎪

⎨

⎧

− − _>

0 , 2

1

, 0

2 2 / 2 ) (ln

y e

y

selainnya y μ σ

π σ

Bukti :

Fungsi probabilitas dari distribusi normal adalah

f(x) =

2

2( )

2 1

2

1 _σ μ

π σ

− − x

e . ………. **

Dengan menggunakan persamaan (2.16) akan didapatkan fungsi densitas untuk Y.

fx(x) =

2

2( )

2 1

2

1 _σ μ

π σ

− − x e

Jika x = ln Y maka persamaan ** menjadi

fx(ln y) =

2

2(ln )

2 1

2

1 _σ μ

π σ

−

− y

e

X = w(y) = ln y

w’(y) = 1/y

fy(y) = fx(w(y)) w(y)

dy d

fy(y) = fx(ln y)

y 1

=

2

2(ln )

2 1

2

1 _σ μ

π σ

−

− y

e _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛

y 1

f(y) =

2

2(ln )

2 1

2

1 _σ μ

π σ

−

− y

e y

J. Teorema Limit Pusat

Teorema 2.10.1 (Teorema Limit Pusat):

Andaikan adalah variabel-variabel random yang saling bebas dan

identik dengan

n X X

X₁, ₂,L,

μ =

) (X_i

E dan variansinya _{var( )}=σ2 <∞, maka untuk i

X n→∞

n X Z_n

/

σ μ −

= (2.22)

Akan berdistribusi normal standar.

Bukti: