Ruang Vektor. Modul 1 PENDAHULUAN

Ruang Vektor

Dr. Irawati

alam buku materi pokok Aljabar II ini kita secara perlahan-lahan mulai mengubah pendekatan kita dari pendekatan secara komputasi menjadi pendekatan yang lebih umum. Yang dimaksud dengan pendekatan yang lebih umum adalah penyelesaian masalah yang menuntut bukti, yang tentu saja tidak dapat diselesaikan dengan komputasi rutin. Namun, pendekatan komputasi tidak sepenuhnya kita tinggalkan, melainkan kita pakai untuk mengilustrasikan dan menerapkan teori yang kita bahas.

Pembaca diminta untuk mengerjakan semua soal-soal latihan maupun tes formatif (termasuk menuliskannya dengan rinci), untuk dapat mengikuti semua modul secara utuh dan berkesinambungan.

Secara khusus untuk modul (pokok bahasan) Ruang Vektor ini, skalar yang digunakan lebih umum, yakni himpunan yang memiliki struktur yang sama dengan struktur yang dimiliki oleh himpunan bilangan real.

Secara umum setelah mempelajari modul ini, Anda diharapkan

memahami konsep lapangan, ruang Fp, ruang vektor maupun subruang dan dapat memeriksa apakah suatu himpunan vektor-vektor di suatu ruang vektor bersifat bebas linear atau bergantung linear.

Secara lebih rinci, setelah mempelajari modul ini, Anda diharapkan mampu:

1. memahami konsep lapangan dan ruang Fp;

2. menyelidiki apakah suatu vektor merupakan kombinasi linear dari vektor-vektor yang diberikan;

3. menyelidiki apakah suatu himpunan merupakan suatu ruang vektor atas suatu lapangan;

4. menyelidiki apakah suatu subhimpunan dari suatu ruang vektor merupakan subruang;

D

5. menentukan suatu himpunan bersifat bebas linear atau bergantung linear.

Kegiata n Be laj ar 1

Lapangan, Ruang

_F

p

, dan Ruang Vektor

ada mata kuliah Aljabar Linear Elementer kita telah menggunakan himpunan bilangan nyata (real) sebagai skalar. Sebagaimana dinyatakan sebelumnya pada modul ini, skalar yang digunakan lebih umum, yaitu himpunan yang memiliki struktur yang sama dengan struktur yang dimiliki himpunan bilangan real, yang kita katakan lapangan (field) dengan notasi _F.

Mari kita perhatikan mengenai persyaratan atau ketentuan-ketentuan dari suatu lapangan _F yang didefinisikan sebagai berikut.

Definisi 1.1

Suatu lapangan adalah suatu himpunan tak hampa _F dengan dua operasi, yaitu penjumlahan dan perkalian serta terdapat unsur 0 (nol) dan 1 (satu) di _F sehingga dipenuhi:

(i) ∀x y z, , ∈F, berlaku 1. x + y ∈F (sifat tertutup) 2. x + y = y + x (sifat komutatif) 3. (x + y) + z = x + (y + z) (sifat asosiatif) 4. 0 + x = x (unsur nol) (ii) ∀x y z, , ∈F, berlaku 1. xy∈F (sifat tertutup) 2. xy = yx (sifat komutatif) 3. (xy z) = (x yz) (sifat asosiatif) 4. 1 x = x (unsur satu)

(iii) ∀x y z, , ∈_F, ( x y + ) z = xy + xz (Sifat distributif) (iv) ∀ ∈x _F terdapat secara tunggal z∈F sehingga x + z = 0. (z disebut unsur balikan dari x terhadap operasi penjumlahan). (v) ∀ ∈x F, dengan x ≠ 0 terdapat secara tunggal y∈F sehingga

1

xy= (y dikatakan unsur balikan dari x terhadap operasi perkalian).

Dari definisi di atas terlihat bahwa, suatu lapangan adalah suatu himpunan tak hampa yang berkaitan dengan dua operasi dan memenuhi sifat-sifat (i) s/d (v). Sebagai ilustrasi dari Definisi 1.1, perhatikan contoh berikut:

Contoh 1.1

Lapangan yang kita kenal adalah ¡ = {bilangan yang nyata/real}, ¤ = {bilangan rasional}, dan £ = {bilangan kompleks} terhadap dua operasi, yaitu penjumlahan dan perkalian. Tetapi, himpunan bilangan bulat ¢ bukan merupakan lapangan terhadap dua operasi penjumlahan dan perkalian karena terdapat bilangan bulat a≠0 dan a≠1, tetapi tidak terdapat bilangan bulat b sehingga ab=1 [lihat sifat (v)]. _■

Pandang lapangan F seperti ruang Rn, yang kita bahas pada mata kuliah Aljabar Linear Elementer, sekarang kita definisikan ruang Fp

sebagai berikut. p F = 1 1, , p p α α α α       ∈    _{ }      M L F

Definisi di atas menyatakan bahwa ruang Fpadalah suatu himpunan vektor-vektor, dengan komponen sebanyak p buah dan setiap komponennya merupakan unsur dari lapangan _F.

Selanjutnya, dua operasi penjumlahan dan perkalian skalar juga kita definisikan seperti di ¡ n, sebagai berikut.

1. Operasi Penjumlahan (+) + :Fp×Fp→Fp 1 1 1 1 , p p p p α β α β α β α β      ₊        _{   } _{ } _{   } _{ + }         M M a M

2. Operasi Perkalian Skalar

( )

o :F×Fp→Fp o 1 1 1 , p p p α α αα α α α α αα                 =  _{ }  _{   }                 M a o M M

Dengan menggunakan dua operasi di atas, kita simak suatu definisi tentang konsep kombinasi linear dari vektor-vektor di _Fp.

Definisi 1.2

Misalkan v₁,L , v_n adalah vektor-vektor di _Fp dan α₁,L , α_n adalah skalar-skalar di _F. Vektor di _Fp yang berbentuk

1 1 n n

w=αv +L +α v dikatakan kombinasi linear dari v₁,L ,v_n.

Selanjutnya, himpunan semua kombinasi linear dari v₁,L ,v_n dikatakan span dari v₁,L , v_n dan ditulis

{

1, , n

}

{

1 1 n n 1, , n

}

span v L v = αv +L +α v α L α ∈F

Ilustrasi untuk konsep kombinasi linear dan span yang didefinisikan di atas, akan diperlihatkan pada contoh di bawah ini.

Contoh 1.2

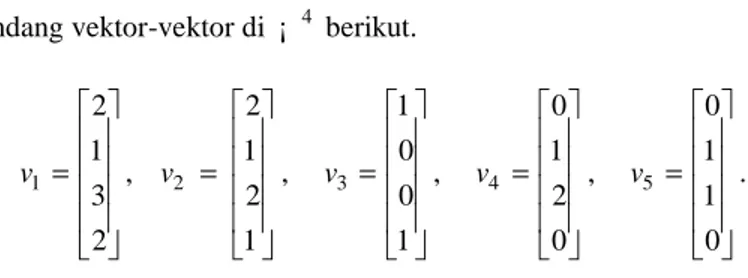
Pandang vektor-vektor di ¡ 4 berikut.

1 2 1 3 2 v       =_{ }     , ₂ 2 1 2 1 v       = _{ }     , ₃ 1 0 0 1 v       = _{ }     , ₄ 0 1 2 0 v       =_{ }     , ₅ 0 1 1 0 v       =_{ }     .

Karena v₁=2v₃+2v₄−v₅ (α₁= 2, α₂=2 dan α₃= −1) maka vl merupakan kombinasi linear dari v3, v4 dan v5.

Jadi, v₁∈span v v v { ,_{3 4}, ₅}, tetapiv₂∉span v v v{ ,_{3 4}, ₅}, karena Sistem Persamaan Linear (SPL) berikut:

2 1 2 2 1 α β γ β γ α =   + =   + =   ₌ 

tidak memiliki solusi, dengan kata lain v tak dapat ditulis sebagai ₂ kombinasi linear dari v v₃, ₄dan .v ₅

_■

Pandang himpunan Fp, yang telah dibahas di atas, beserta operasi penjumlahan dan perkalian skalar. Maka, dapat ditunjukkan bahwa:

(i) ∀u v w, , ∈Fp berlaku sifat-sifat berikut:

1. u+ ∈v Fp (sifat tertutup) 2. u + v = v + u (sifat komutatif) 3. ( u + ) v + w = u + ( v + )w (sifat asosiatif) 4. 0 0 0 0 p u u     ∃ =_{ }∈ ∋ + =     r r M F (vektor nol)

5. ∃ − ∈u Fp ∋ u+ − =( u) 0r (−u vektor balikan dari u) (ii) ∀u v, ∈Fp dan α β, ∈F berlaku

1. α ∈u Fp

2. 1 . v = v

3. α (u + v) = αu + αv 4. (α +β)v = αv + βv 5. (αβ)v = α (βv)

Berikut ini akan kita definisikan pengertian ruang vektor atas lapangan

F secara umum.

Definisi 1.3

Suatu ruang vektor V atas lapangan _F adalah himpunan tak hampa V, yang memuat vektor 0r dan dilengkapi dengan operasi penjumlahan dan perkalian skalar sehingga dipenuhi:

(i) ∀u v w, , ,∈V, berlaku 1. ( ) 2. ( ) 3. ( ) ( ) ( ) 4. 0 ( ) 5. ( ) 0 ( ) u v V sifat tertutup u v v u sifat komutatif u v w u v w sifat asosiatif u u vektor nol

u V u u u vektor balikan dari u

 _{+ ∈}  + = +   + + = + +   + =   _{∃ − ∈ ∋ + − = −}  r r

(ii) u v, ,∈V dan α β, ∈_F berlaku

1. 2. 1 . 3. ( ) ( ) 4. ( ) ( ) 5. ( ) ( ) u V v v u v u v sifat distributif v v v sifat distributif v v α α α α α β α β αβ α β ∈   ₌  + = +   _{+ = +}  = 

Untuk selanjutnya yang dimaksud dengan ruang vektor adalah ruang vektor atas lapangan _F. Dengan lapangan _Fadalah ¡ atau £ , kecuali dengan keterangan yang lebih spesifik.

Setelah kita paham dengan apa yang dimaksud dengan ruang vektor, mari kita lihat salah satu sifat yang berlaku di ruang vektor pada teorema berikut.

Teorema 1.1

Misalkan V suatu ruang vektor. Maka untuk 0, − ∈1 F berlaku: (i) 0v=0,r ∀ ∈v V

Bukti:

Misalkan v∈Vsebarang, maka

(i) 0v=(0+0)v=0v+0v (sifat distributif) 0v + (− (0v)) = (0v + 0v) + (− (0v))

0 =0v+

(

0v+ −

(

(0 )v

)

)

r

(vektor balikan dari 0v) 0r =0v+0r 0r =0v (vektor nol) (ii) 0r =0v=

(

1+ −( 1)

)

v=1.v+ −( 1)v 0r = + −v ( 1)v − + = − + + −v 0r v v ( 1)v − = − +v ( v v)+ −( 1)v − = + −v 0r ( 1)v − = −v ( 1)v _■

Sekarang timbul pertanyaan, apakah subhimpunan dari suatu ruang vektor juga merupakan ruang vektor? Untuk itu, mari kita simak definisi di bawah ini.

Definisi 1.4

Pandang subhimpunan tak hampa U dari suatu ruang vektor V. Kita katakan U sebagai subruang dari V, jika U juga merupakan ruang vektor dengan operasi yang sama seperti operasi di V.

Sekarang akan kita lihat suatu lemma yang lebih operasional untuk menyelidiki apakah suatu subhimpunan tak hampa dari suatu ruang vektor merupakan subruang dari ruang vektor tersebut.

Lemma 1.1

Suatu subhimpunan tak hampa U dari suatu ruang vektor V merupakan suatu subruang, jika dan hanya jika,

(i) jika , 1 2 maka 1 2

(ii) jika dan , maka .

u u U u u U

u U u U

α α

∈ + ∈

Bukti:

Misalkan V suatu ruang vektor dan U adalah subruang dari V maka U juga merupakan ruang vektor (berdasarkan Definisi 1.4), sehingga (i) dan (ii) jelas dipenuhi.

Sebaliknya, misalnya (i) dan (ii) dipenuhi untuk U ⊆ V. Karena U tak hampa maka terdapat u∈U. Dari Teorema 1.1 maka 0u= ∈0r U (karena V suatu ruang vektor). Sifat-sifat ruang vektor dan sifat-sifat yang lain jelas dipenuhi.

Jadi, U merupakan subruang dari ruang vektor V. _■

Untuk pemahaman lebih lanjut tentang konsep ruang dan subruang vektor maupun konsep-konsep yang berhubungan dengan ruang dan subruang vektor ini, baik kita perhatikan beberapa ilustrasi pada Contoh 1.3 di bawah ini.

Contoh 1.3

(1) Misalkan A suatu matriks, dengan unsur pada lapangan _F, berukuran m × n. Pandang ruang baris A yaitu span{ , r_l ⋯, }r_m , dengan merupakan

l, , m

r ⋯ r baris matriks A.

Maka span { ,r_l ⋯, }r_m merupakan subruang dari Fn. Ruang kolom A

yaitu Span { ,k₁⋯,k_n}, dengan k1,⋯,kn merupakan kolom-kolom

matriks A, merupakan subruang dari Fm. _■

(2) Pandang himpunan P yang diekspresikan sebagai

1 0 1 1 n n n n x x x α α α − α − + +L + +

dengan α α_{0 1},L ,α ∈_{n F} dan n bilangan bulat positif.

Operasi penjumlahan dan perkalian skalar didefinisikan sebagai berikut:

(α₀+α₁x+L +α_n−1xn−1+α_nxn)+(β₀+β₁x+L + β_s−1xs−1+ β_sxs) 0 0 0 ( ) n s m i i i i i i i i i i x x x α β α β = = = =

∑

+

∑

=

∑

+ , dengan m = maks (n,s)

1 0 1 1 ( x n xn nxn) α α α α − α − + +L + + 0 0 . n n i i i i i i x x α α αα = = =

∑

=

∑

Maka, dengan operasi seperti di atas, P merupakan ruang vektor dan disebut ruang suku banyak berderajat hingga.

(3) Pandang Mm×n (F) = himpunan semua matriks berukuran m × n dengan

unsur di F. Dengan operasi penjumlahan dan perkalian skalar biasa, Mm× n (F) merupakan suatu ruang vektor.

Misalkan K={ A∈M_{m n×} ( ) _F At = −A }⊂M_{m n×} ( )._F

Akan kita selidiki apakah K merupakan subruang dari Mm× n (F). Jelas,

K≠ ∅, karena matriks O berukuran m×n merupakan unsur K. Misalkan , A B∈K dan α∈F. Berarti At =A dan Bt = −B.

( ) ( ) ( ) ( ) ( ) ( ). t t t t t A B A B A B A B A B A A A A α α α α + = + = − + − = − + = − + = = − = − Berarti A+ ∈B K dan αA∈K.

Jadi, K merupakan subruang dari Mm× n (F).

(4) Misalkan L={A M∈ _{2 2×} ( )_F A−1ada}⊂M_{2 2×} ( )._F Pandang 1 0 1ada, berarti 0 1 A=   A− A∈L   1 1 0 ada, berarti 0 1 B= _− _ B− B∈L −   Tetapi 0 0 0 0 A+ B =_ _

  tak memiliki invers, berarti A+ ∉B L. Jadi, L bukan merupakan subruang dari M_{2 2×} ( )_F .

(5) Pandang V =

{

f :R→R f pemetaan

}

Didefinisikan operasi penjumlahan dan perkalian skalar sebagai berikut: Misalkan f dan gdiV;α∈¡ maka

1) (f+g) ( )x =f x( )+g x( ), ∀ ∈x _R 2) (αf) ( )x =α

(

f x( ) ,

)

∀ ∈x ¡ Pandang dengan: : 0, O O V x x →  ∈  ∀ ∈  a R R R

Misalkan f∈V sebarang maka

(

O+f

)

( )x =O x( )+ f x( )= +0 f x( )= f x( ), ∀ ∈x ¡ Jadi, kita mempunyai O+ =f f, ∀ ∈f V .

Pandang − ∈f V dengan:

(

)

: ( ) , f x f x x − →   − ∀ ∈  a R R R Maka

(

f + −( f) ( )

)

x = f x( ) (+ −f)( )x

(

)

( ) ( ( ) 0 ( ), f x f x O x x = + − = = ∀ ∈R Jadi, f + −( f)=O.

Maka V dengan operasi penjumlahan dan perkalian skalar di atas

merupakan suatu ruang vektor atas ¡ . _■

(6) Misalkan V suatu ruang vektor atas _F. Misalkan pula v v₁, ₂,L ,vn vektor-vektor di V.

Maka, span { ,v v_{1 2},L ,vn} akan membentuk subruang dari V.

(

)

1 1 1 dan n n i i i i i i n i i i i x v y v x y v α β α β = = =  = =     + = +  

∑

∑

∑

demikian sehingga,

{

1, 2, , n

}

x+ ∈y span v v L v ...……….. (1.1) Kemudian, misalkan α∈F, maka

1 . n i i i x v α αα = =

∑

Jadi,

{

1, 2, , n

}

x span v v v α ∈ L ………...….. (1.2)

∴ Dari (1.1) dan ((1.2) maka span v v

{

₁, ₂,L ,vn

}

merupakan subruang

dari V. _■

Setelah membaca materi subpokok bahasan di atas, cobalah kerjakan latihan berikut agar pemahaman Anda lebih mantap.

1) Tentukan subhimpunan dari ¡ n yang merupakan subruang a)

{

( ,r₁L ,r_n) r₁+2r₂+3r₃+L +nr_n=0

}

b)

{

( ,r₁L ,rn) r₁2+r₂2+L + =rn2 1

}

Jelaskan jawaban Anda.

2) Tentukan subhimpunan dari ruang fungsi kontinu dari R ke R yang merupakan subruang

a)

{

f:R→R f kontinu f x, ( )= −f (−x) , ∀ ∈x R

}

b)

{

f:R→R f kontinu f solusi dari PD y", + =y' 2y

}

L A T I H A N

Untuk memperdalam pemahaman Anda mengenai materi di atas, kerjakanlah latihan berikut!

3) Misalkan V suatu ruang vektor. Diketahui w v, ₁,L ,vn di V dan w merupakan kombinasi linear dari v₁,L ,vn. Tunjukkan

{

, ,1 , n

}

span w v L v = span v

{

₁,L ,vn

}

4) Misalkan V suatu ruang vektor. Misalkan pula K dan L subruang dari V sehingga dipenuhi V = K + L. Tunjukkan K ∩ L = {0}, jika dan hanya jika penulisan setiap vektor di V sebagai hasil tambah dari vektor-vektor di K dan L adalah tunggal.

K+ = +L {k l k K l L∈ , ∈ }

Agar latihan Anda terarah dengan baik dan dapat memperkirakan hasil latihan Anda, bacalah rambu-rambu jawaban Latihan.

Petunjuk Jawaban Latihan

1) a) Tulis S =

{

( ,r₁ L ,r_n)∈_Rn r₁+2r₂+L +nr_n=0

}

i) jelas S ⊂ n

¡

ii) (0,L , 0)∈S . Jadi S≠ ∅.

iii) Misalkan ( ,r₁L ,r_n)∈S, berarti r₁+2r₂+L +nr_n=0 dan ( ,s₁ L ,s_n)∈S berarti: 1 2 1 1 2 2 1 2 1 2 2 0 ( ) 2( ) ( ) ( 2 ) ( 2 ) 0 0 0 n n n n n s s ns r s r s n r s r r nr s s ns + + + = + + + + + + = + + + + + + + = + = L L L L Jadi, ( ,r₁L ,rn) ( ,+ s₁L ,sn)=(r₁+ s₁,L ,rn+sn)∈S.

iv) Misalkan ( ,r₁L ,rn)∈S berarti r1+2r2+L +nrn =0 dan . α∈R 1 2 2 n (1 22 n) .0 0. r r n r r r nr α + α +L + α =α + +L + =α = Jadi α( ,r₁L ,rn)=(αr₁,L ,αrn)∈S

b) Tulis K =

{

( ,r₁L , )rn ∈Rn r₁2+L +rn2=1

}

Pandang (1, 0,L , 0)∈¡ n dan 1 + 0 +2 2 L + 0 = 12 . Jadi, (1,0, L ,0) ∈K

Pandang pula (0,1, 0,L , 0)∈_Rn dan 0 + 1 + 0 +2 2 2 L + 0 = 12 . Jadi, (0,1,0, L ,0)∈K, (1,0,L ,0) + (0,1,0,L ,0) = (1,1,0,L ,0). Tetapi, 1 + 1 + 02 2 2+L + 02 ≠ 1 sehingga

(1,0, L ,0) + (0,1,0, L ,0) ∉K Jadi, K bukan subruang dari ¡ n.

2) a) Tulis K =

{

( :f R→R f kontinu, f x( )= − f(− ∀ ∈x) x R

}

i) Pandang f x( ) 0,= ∀ ∈x ¡._ Jelas f kontinu di ¡ . Maka − − = − =f ( x) 0 0.

Jadi, f x( )= − f(− ∀ ∈x), x ¡ . Berarti f ∈K.

K

∴ ≠ ∅

ii) Misalkan f ∈K, berarti f kontinu di ¡ dan

( ) ( ) , .

f x = − −f x ∀ ∈x _R ,

g∈K berarti g kontinu di ¡ dan g x( )= − −g( x) , ∀ ∈x _R. Misalkan pula α∈_R. ( )( ) ( ) ( ) ( )

[

( )

]

( )( ), dan kontinu . f g x f x g x f x g x f g x x f g di + = + = − − + − − = − + − ∀ ∈¡ + ¡ _ Jadi, f+ ∈g K ( )( ) ( ( )) ( ( )) ( ( )) dan kontinu . f x f x f x f x f di R α α α α α = = − − = − − Jadi, α ∈f K.

∴ subruang dari ruang fungsi kontinu dari ke .K R R

b) Tulis K=

{

f : R→R f kontinu, f solusi PD y" + y'=2 y

}

i) Pandang

: dengan ( ) 0, . Jelas kontinu di .

f R→R f x = ∀ ∈x R f R

0.

solusi PD 2 . . . f y" y' y f L L ∴ + = ∴ ∈ ∴ ≠∅

ii) Misalkan f ∈L, berarti f kontinu di _R dan f"+ =f' 2 .f Misalkan pula g∈L, berarti g kontinu di _R dan

2 . g"+ =g' g Misalkan α∈_R. (f +g ") +(f +g ') = f"+g"+ + =f' g' 2f +2g=2(f +g). f +g kontinu di R. . f g L ∴ + ∈ (αf ") +(αf ') =αf"+αf' =α(f"+ f')=α(2 )f =2αf. . f L L α

∴ ∈ ∴ subruang dari fungsi kontinu dari ¡ ke¡ ._ 3) Misalkan x∈span w v

{

, , ,₁ v₂ L ,vn

}

maka x=αw+α1 1v + +L αn nv

untuk suatu α α α, ₁, ₂,L , α ∈n R. Tetapi, w kombinasi linear dari

1 , 2, , n. v v L v

Berarti w =βv₁+β_{2 2}v + +L β_{n n}v untuk suatu β β₁, ₂,L ,β ∈n R.

Jadi, x=α β( _{1 1}v + +L βn nv )+α_{1 1}v + +L αn nv =(αβ α₁+ ₁)v₁+ +L (αβ αn+ n) .vn 1 1 1 { , , } { , , , } { , , }. n n n x span v v span w v v span v v ∴ ∈ ∴ ⊆ L L L

Misalkan y∈span v{ ,₁L ,v_n}. Berarti y = γ_{1 1}v + +L γ_{n n}v untuk suatu

1, , n . γ L γ ∈_R y=γ_{1 1}v + +... γ_{n n}v =γ_{1 1}v + +... γ_{n n}v +0 .w 1 1 1 { , ,..., }. { ,..., } { , ,..., }. n n n y span w v v span v v Span w v v ∴ ∈ ∴ ⊆ 1 1 { ,..., _n} { , ,..., _n}. span v v span w v v ∴ =

4) (⇒) Misalkan x∈V sebarang dengan x = k₁ + l₁ = k₂ + l₂ untuk k₁, k₂∈K dan l l₁, ₂∈L. Maka k₁− = −k₂ l₂ .l₁

Tulis y= − = −k₁ k₂ l₂ .l₁ Karena K dan L subruang, maka k₁− ∈k₂ K dan l₂− ∈l₁ L.

∴ ∈ ∩y K L. Tetapi K∩ =L {0}.

∴ = − = −y k₁ k₂ l₂ l₁ =0. Jadi, k₁=k₂ dan l₁=l₂.

Jadi, penulisan setiap vektor x di V sebagai hasil tambah dari vektor-vektor di K dan L adalah tunggal.

(⇐) Misalkan x∈ ∩K Lsebarang. Berarti x∈K dan x∈L. x∈K, maka x= x + 0 dengan x∈K dan 0∈L.

,

x∈L maka x= + 0 x dengan 0∈K dan x∈L.

Tetapi penulisan x∈V sebagai hasil tambah dari vektor-vektor di K dan adalah tunggal. Jadi, x = 0.

K L {0}.

∴ ∩ =

Pada bagian ini Anda telah mempelajari struktur himpunan yang merupakan dasar dari mata kuliah ini. Ruang vektor disebut juga sebagai struktur ruang linear, karena pada ruang tersebut kita mengerjakan operasi tambah.

Objek atau elemen dari ruang vektor tersebut secara umum tidak harus berbentuk vektor, seperti yang kita kenal. Seperti terlihat pada subpokok bahasan ini, elemen dari ruang vektor dapat berupa matriks, fungsi dan lain sebagainya.

1) Apakah

(

)

1 3 2 0 0 a H b ax bx c dx c       =_{ }∈ + + =  _{ }     

∫

R merupakan ruang vektor?

(Jelaskan jawaban Anda)

R A N G K U M A N

T E S F O R M A T I F 1

2) Tentukan subhimpunan dari Fn di bawah ini yang merupakan subruang dari Fn: (Jelaskan jawab Anda!)

a) 3 0 u v u v w w       ∈ + + = _{ }  _{ }      F b) 3 1 u v u v w w       ∈ + + = _{ }  _{ }      F c) u 2 u v 0 v      ∈ =        F  d) u 2 u2 v2 0 v      ∈ + =        R  e) u 2 u2 v2 0 v      ∈ + =        £ 

3) Mana yang merupakan subruang dari ruang vektor _{Mn n× ( ) F} berikut, (Jelaskan jawab Anda!).

a) Subhimpunan dari _{Mn n× ( ) F} yang memiliki rang 1 (satu). b) Subhimpunan yang memiliki rang 0 (nol).

c) Matriks-matriks yang merupakan solusi dari persamaan

2

.

n M +M = I

d) Matriks-matriks M yang memenuhi t _. M−M =O

4) Misalkan V suatu ruang vektor. Misalkan pula a∈Vdan α∈F. Tunjukkan bahwa:

a) (−α)( )a = −(αa)

b) α(− = −a) (αa)

c) (−α)(− =a) αa

Petunjuk: Sebelum Anda mengerjakan soal 4 di atas, terlebih dahulu tunjukkan sifat berikut:

5) Misalkan V suatu ruang vektor. Misalkan pula K dan L masing-masing subruang dari V.

a) Selidiki apakah K∩L membentuk subruang dari V. b) Selidiki pula apakah K∪L membentuk subruang dari V. c) Jika K+ =L

{

k l k+ ∈K l, ∈K

}

selidiki apakah K+L

merupakan subruang dari V. Jelaskan jawab Anda. (Jika "ya" tunjukkan dan jika "bukan" berikan contoh).

6) Misalkan U U dan W masing-masing subruang dari suatu ruang ₁, ₂ vektor V.

a) Buktikan (U₁∩W)+ (U₂∩W)⊆(U₁+U₂)∩W.

b) Buat suatu contoh di F2 yang menunjukkan bahwa kesamaan pada (a) tidak berlaku.

Cocokkanlah jawaban Anda dengan Kunci Jawaban Tes Formatif 1 yang terdapat di bagian akhir modul ini. Hitunglah jawaban yang benar. Kemudian, gunakan rumus berikut untuk mengetahui tingkat penguasaan Anda terhadap materi Kegiatan Belajar 1.

Arti tingkat penguasaan: 90 - 100% = baik sekali 80 - 89% = baik 70 - 79% = cukup < 70% = kurang

Apabila mencapai tingkat penguasaan 80% atau lebih, Anda dapat meneruskan dengan Kegiatan Belajar 2. Bagus! Jika masih di bawah 80%, Anda harus mengulangi materi Kegiatan Belajar 1, terutama bagian yang belum dikuasai.

Tingkat penguasaan = Jumlah Jawaban yang Benar 100%

Kegiata n Be laj ar 2

Bebas Linear

ari kita pandang subruang-subruang dari ¡ 2 berikut:

{

1 _, 1 _, 2 _, 1

}

1 1 6 5 K =span  _{ }  _− _ _− _   _{ }         ,

{

1 _, 2

}

_dan

{

1 _, 1

}

3 6 3 3 K '=span _− _ _₋ _ K "=span _{ }   _− _         .

Maka, dapat ditunjukkan K =K′′ , tetapi K≠K′.

Mengapa terjadi demikian? Mengapa subruang yang dibangun oleh 4 (empat) vektor, sama dengan subruang yang dibangun oleh 2 (dua) vektor?

Untuk masalah di atas kita katakan K dibangun oleh

1 1 2 1 , , dan 1 1 6 5   −                  ₋           

Pertanyaan-pertanyaan di atas akan dijawab dalam subpokok bahasan ini. Kunci jawaban ada pada konsep bebas linear.

Definisi 1.5

Misalkan V suatu ruang vektor. Himpunan vektor-vektor v v₁, ₂,L ,v_n di V dikatakan bebas linear di V, jika kombinasi linear

1 1v n nv 0

α +L +α = hanya dipenuhi oleh α₁ =α₂=L =αn =0.

Jika

{

v v₁, ₂,L ,vn

}

tidak bebas linear, kita katakan bergantung linear. Berikut ini mari kita perhatikan suatu sifat yang cukup menarik dari himpunan vektor-vektor bergantung linear dan bebas linear di V yang diberikan oleh Lemma 1.2 dan Lemma 1.3 di bawah ini.

Lemma 1.2.

Misalkan V suatu ruang vektor. Misalkan pula

{

v v₁, ₂,...,vn

}

bergantung linear di V. Maka, terdapat j dengan 1≤ ≤j n sehingga vj

merupakan kombinasi linear dari v v1, 2,L ,vj−1,vj+1,L ,vn.

Bukti:

1, 2, , n

v v L v bergantung linear. Berarti terdapat α ≠_j 0; 1≤ ≤j n sehingga

1 1v + 2v2+⋯+ jvj+⋯+ n nv =0 α α α α 1 1 1 1 1 1 jvj v j−vj− j+vj+ n nv ⇔ α = −α −⋯−α −α −⋯−α 1 1 1 1 1 1 j j n j j j n j j j j v v − v + v v − + ⇔ = −α α −⋯−α α −α α −⋯−α α 1 1 1 1 1 1 j j j j j n n v β v β ₋ v ₋ β ₊ v₊ β v ⇔ = +L + + + +L dengan i i j = −α

β _α dan i≠ j atau dengan penulisan lain, yaitu 1 . n j i i i i j v β v = ≠ =

∑

_■ Lemma 1.3

Misalkan V = span

{

w w₁, ₂,⋯,w_n

}

suatu ruang vektor. Misalkan pula

{

v v1, 2,⋯,vr

}

bebas linear di V. Maka r ≤ n.

Bukti:

Akan kita buktikan dengan menggunakan kontradiksi.

Andaikan r > n. Misalkan v_i =α_i1w₁+α_i2w₂+⋯+α_inw_n, ∀ =i 1,⋯, .r Pandang kombinasi linear β_{1 1}v +L +β_rv_r=0, maka

1=⋯= r =0

Selanjutnya

(

)

(

)

1 11w1 12w2 1nwn r r1w1 r2w2 rnwn 0 β α +α +L +α +L +β α +α + L +α = atau

(

α β α β11 1+ 21 2+ L +α βr1 r

)

w1+ L +

(

α β α β1n 1+ 2n 2+ L +α βrn r

)

wn =0 atau 11 1 21 2 1 12 1 22 2 2 1 1 2 2 0 0 0 r r r r n n rn r α β α β α β α β α β α β α β α β α β + + + =   + + + =     _{+ + + =}  L L M L

Tetapi SPL homogen di atas terdiri dari n persamaan dan r variabel, dengan r > n. Maka, SPL di atas memiliki solusi tak hingga banyak (lihat BMP Aljabar Linear Elementer). Hal ini bertentangan karena { ,v_1⋯, }v_r bebas

linear. Jadi, haruslah r≤n. _■

Untuk pemahaman lebih baik tentang konsep bebas dan bergantung linear dari himpunan vektor-vektor di suatu ruang vektor, perhatikan contoh-contoh berikut ini.

Contoh 1.4

(1) Pandang ruang fungsi V=

{

f:R→R f pemetaan

}

.

Misalkan f x( ) 1,= g x( )=ex danh x( )=e2x adalah fungsi-fungsi di V. Akan ditunjukkan bahwa

{

f g h, ,

}

bebas linear di V.

Untuk menunjukkan kebebaslinearan

{

f g h, ,

}

, pandang kombinasi linear:

αf +βg+γh=O

Jadi,

(αf+βg+γh x) ( )=αf x( )+βg x( )+γh x( )

Selanjutnya, untuk x = 0, x = 1 dan x = 2, kita peroleh SPL berikut: 2 2 4 0 0 0 e e e e α β γ α β γ α β γ + + =   + + =   + + = 

Dapat ditunjukkan bahwa solusi SPL di atas adalah α β γ= = =0.

Jadi

{

f g h, ,

}

bebas linear. _■

(2) Pandang ruang fungsi seperti pada Contoh 1.4 nomor (1) di atas. Misalkan

2 2

1( ) cos , 2( ) sin dan ( ) cos 2 .3

f x = x f x = x f x = x

Kita ketahui bahwa: cos 2x=cos2x−sin2x (ini berarti cos 2x

merupakan kombinasi linear dari cos2x dan sin2x), maka berdasarkan Tes Formatif 2 nomor 2 (kebalikan Lemma 1.2) kita peroleh {f₁,f₂,f₃}

bergantung linear. ■

Setelah membaca materi subpokok bahasan di atas, cobalah kerjakan latihan berikut agar pemahaman Anda lebih mantap.

1) Diketahui V suatu ruang vektor atas lapangan _F. Tunjukkan kebalikan Lemma 1.2 senantiasa berlaku.

2) Diketahui V suatu ruang vektor atas lapangan _F. Diketahui pula

{

1, 2, , n

}

X= x x L x bebas linear di V. Selidiki apakah

{

x x₁, ₂,L ,xn

}

bebas linear di V. Jelaskan jawaban Anda!

L A T I H A N

Untuk memperdalam pemahaman Anda mengenai materi di atas, kerjakanlah latihan berikut!

3) Diketahui seperti soal nomor 2. Misalkan pula y∈V. Selidiki apakah

{

x x1, 2,L ,xn,y

}

bebas linear di V. Jelaskan jawaban Anda.

4) Diketahui V suatu ruang vektor atas lapangan _F. Diketahui pula

{

1, 2, , m

}

Y = y y L y membangun V. Selidiki apakah

{

y₂,y₃,L ,ym

}

membangun V. Jelaskan jawaban Anda.

5) Diketahui seperti soal nomor 4. Misalkan pula z∈V . Selidiki apakah

{

y y1, 2,L ,ym,z

}

membangun V. Jelaskan jawaban Anda.

Petunjuk Jawaban Latihan

1) _{1 1 1 1 1 1} 1 0 n j i i j j j j j n n i i j v αv αv α ₋v₋ v α ₊v ₊ α v = ≠ =

∑

⇔ +L + − + + +L = ⇔α_{1 1}v +L +α_j−1v_j−1+ −( 1)v_j+α_j+1v_j+1+ +L α_{n n}v =0

Jadi terdapat α_j = − ≠1 0 di _Fsehingga

1 0. n i i i v α = =

∑

Jadi,

{

v₁,⋯, v_j−1, , v_j v_j+1,⋯, v_n

}

bergantung linear. 2) Pandang kombinasi linear

2 2x n nx 0 α + +L α = ……… (1.3) Maka, 2 2 1 2 2 0=α x +⋯+α_nx_n=0x +α x +⋯+α_nx_n. ………… (1.4) Tetapi, { , x₁ L ,x_n } bebas linear di V. Maka kombinasi linear (1.4) hanya dapat dipenuhi oleh α₂ =⋯= α_n =0. Jadi kombinasi linear (1.3) hanya dipenuhi oleh α₂ =L = α_n =0. Jadi, {x₂,L , } x_n bebas linear di V.

3) Kasus 1.

Jika y ∈span x{ ,₁L ,x_n}, maka y=α_{1 1}x + +L α_{n n}x untuk α_l,_⋯,α_n di F. Menurut soal nomor 1 di atas, maka { ,x_{1 ⋯},x y_n, } bergantung linear.

Kasus 2.

Jika y∉span x{ ,₁⋯,x_n}, andaikan { ,x1 ⋯,x yn, } bergantung linear.

Maka terdapat β₁, ⋯ , β_i−1,β_i+1,⋯,β γ_n, di ,R sehingga

1 . n i j j j j i x β x γ y = ≠

=

∑

+ Jelas γ ≠ 0, karena jika = 0, γ maka

1 n i j j j j i x β x = ≠

=

∑

dan ini berarti { ,x_{1 ⋯}, }x_n bergantung linear. Hal ini bertentangan dengan { ,x_1⋯, }x_n bebas linear.

0. γ ∴ ≠ Jadi, 1 1 1 . n i j j j j i y γ− x γ− β x = ≠ = −

∑

Ini berarti, y∈span x{ ,₁ ⋯,x_n}. Hal ini bertentangan dengan

1

{ , , _n}.

y∉span x ⋯ x Jadi haruslah { ,x1 ⋯,x yn, } bebas linear.

4) Kasus 1.

1 { 2, , n}.

y ∉span y ⋯ y Maka y1∈V tidak dapat ditulis sebagai

kombinasi linear dari {y₂,⋯,y_n}. Jadi {y2,⋯,yn} tidak membangun

V. Kasus 2.

1 { 2, , n},

y ∈span y ⋯ y maka terdapat β2,⋯,βndiF sehingga

1 2 2 n n.

y =β y +⋯+β y Sekarang misalkan x∈V sebarang,

1

{ ,y _⋯, }y_n membangun V berarti terdapat α₁,_⋯, α_n di_F sehingga

1 1 n n x= α y +⋯+α y 1( 2y2 nyn) 2y2 nyn = α β +⋯+β +α +⋯+α 1 2 2 2 1 ( )y ( _{n n})y_n. = α β +α +⋯+ α β +α

Jadi setiap vektor di V dapat ditulis sebagai kombinasi linear dari

2

{y ,⋯, }.y_n Jadi {y2,⋯, }yn membangun V.

5) Misalkan x V∈ sebarang dan { ,y_{1 ⋯},y_m} membangun V. Berarti terdapat α₁,⋯ ,α_m diF sehingga

1 1 m m 1 1 m m 0 ; .

Jadi setiap vektor di V dapat ditulis sebagai kombinasi linear dari

1, , m, .

y _⋯ y z Jadi { ,y_{1 ⋯},y_m, } z membangun V.

Pada bagian ini Anda telah mempelajari sifat bebas linear dan bergantung linear dari kumpulan vektor. Pada kumpulan vektor yang bebas linear, tidak akan berubah sifatnya walaupun anggota dari vektor tersebut dikalikan dengan skalar tidak nol.

1) Misalkan V suatu ruang vektor atas lapangan _F. Misalkan pula {u, v, w} bebas linier di V. Tunjukkan {u v v w u w+ , + , + }bebas linier di V dan

span {u, v, w} = span {u v v w u w+ , + , + }.

2) Misalkan V suatu ruang vektor atas lapangan _F. Misalkan pula

1 2 { ,v v ,L ,v_n}vektor-vektor di V. Jika ₁ 1 1 j j j i v α v = ≠ =

∑

Tunjukkan bahwa { ,v v_{1 2},L ,v_n} bergantung linear.

3) Misalkan V suatu ruang vektor atas lapangan _F. Misalkan pula

1

{ ,v L ,v_n} bebas linier di V dan v∉span v v{ ,_{1 2},L ,v_n}. Tunjukkan bahwa

{

v₁+ v v, ₂+v,L ,vn+v

}

bebas linier.

4) Misalkan V = span { ,v v_{1 2},L ,vn}dan w w1, 2,L ,wn∈V dengan m > n. Tunjukkan

{

w w₁, ₂,L ,wm

}

bergantung linier.

5) Misalkan

{

v v₁, ₂,L ,vn

}

bebas linier di . n

R Misalkan pula A suatu matriks berukuran n × n dan A memiliki invers.

Tunjukkan

{

Av₁, Av₂,L , Avn

}

bebas linear. R A N G K U M A N

T E S F O R M A T I F 2

Cocokkanlah jawaban Anda dengan Kunci Jawaban Tes Formatif 2 yang terdapat di bagian akhir modul ini. Hitunglah jawaban yang benar. Kemudian, gunakan rumus berikut untuk mengetahui tingkat penguasaan Anda terhadap materi Kegiatan Belajar 2.

Arti tingkat penguasaan: 90 - 100% = baik sekali 80 - 89% = baik 70 - 79% = cukup < 70% = kurang

Apabila mencapai tingkat penguasaan 80% atau lebih, Anda dapat meneruskan dengan modul selanjutnya. Bagus! Jika masih di bawah 80%, Anda harus mengulangi materi Kegiatan Belajar 2, terutama bagian yang belum dikuasai.

Tingkat penguasaan = Jumlah Jawaban yang Benar 100%

Kunci Jawaban Tes Formatif

Tes Formatif 1

1) Karena H subhimpunan tak hampa dari ¡ 3, maka untuk menyelidiki apakah H ruang vektor, cukup diselidiki apakah H Subruang dari

3

¡ dengan menggunakan Lemma 1.1. 2) a) subruang. b) bukan subruang. c) bukan subruang. d) bukan subruang. e) bukan subruang. 3) a) bukan subruang. b) subruang. c) bukan subruang. d) bukan subruang.

4) Pertama-tama akan ditunjukkan bahwa pada lapangan _F berlaku 0.α=0 , ∀ ∈α F 0.α= +(0 0)α=0α+0.α (0. ) 0. (0. ) 0. 0. 0 0 0. 0 0. α α α α α α α − + = − + + = + =

Berikutnya akan ditunjukkan bahwa pada lapangan F berlaku

( 1) , ( 1) ( 1) 1. ( 1 1) 0 0 α α α α α α α α α − = − ∀ ∈ − + = − + = − + = = F ( 1)α α ∴ − = − a) (− +α α) .a= − +( α α)a 0. 0 ( 1) ( ) a a αa = = ∴ − = −

b) α(− +a) α a=α(− +a a) . 0 0 ( a) ( a) α α α = = ∴ − = − − c) ( ) ( ) ( ) ( ) ( ) ( ) 0 0 ( ) ( ) a a a a a α α α α α α − − + − = − − + = − = ∴ − − = − 5) a) ya. b) tidak selalu. c) ya. 6) a) Ambil x∈

(

U₁I W

) (

+ U₂I W

)

.

Misalkan x= +y z dengan y∈U₁I W dan z∈U₂I W . Karena y∈U₁ dan z∈U₂, maka x= + ∈y z U₁+U₂. Karena y∈W dan z∈W , maka x= + ∈y z W . Jadi

x

=

y

+

z

∈

(

U

1

+

U

2

)

Ι

W

.

b) Silakan dicoba sebagai latihan.

Tes Formatif 2

1) a) Pandang kombinasi linear

(

u v

) (

v w

) (

u w

)

0

α + +β + +γ + =

(

α γ

) (

u α β

) (

v β γ

)

w 0

∴ + + + + + =

Karena

{

u v w bebas linear, maka , ,

}

0 α γ α β β γ+ = + = + = 0. α β γ ∴ = = =

.

b) Misalkan x∈span u v w

{

, ,

}

. Jadi x=αu+βv+γw =α′

(

u+ +v

)

β′

(

v+w

)

+γ′

(

u+w

)

=

(

α γ′+ ′

) (

u+ α β′+ ′

) (

v+ β γ′+ ′

)

w

Karena

{

u v w bebas linear, maka , ,

}

2)

{

v₁,L ,vn

}

⊂V . 1 n i j j j j i v α v = ≠ =

∑

1 0 n j j i j j i v v α = ≠ ∴

∑

− = 1 0

∴ ∃− ≠ sedemikian hingga kombinasi linear di atas sama dengan nol.

{

v1, ,vn

}

∴ L bergantung linear.

3) Pandang kombinasi linear

(

)

(

)

(

)

1 v1 v 2 v2 v n vn v 0. α + +α + + +L α + =

(

)

1 1v n nv 1 2 n v 0. α α α α α ∴ + +L + + + +L = Jika α₁+ +L α_n ≠0, maka

(

) (

1

)

1 2 n 1 1v n nv v α α+ + +L α − −α − −L α =

{

1, , n

}

. v span v v ∴ ∈ L .

Hal ini bertentangan dengan v∉span v

{

₁,L ,vn

}

.

1 2 n 0 α α α ∴ + + +L = 1 1v n nv 0 α α ∴ + +L =

Karena

{

v₁,L ,vn

}

bebas linear, maka

0

2 1

=

α

=

=

α

=

α

Λ

n

{

v

+

v

v

_n

+

v

}

∴

₁

,

Λ

,

bebas linear. 4) Misalkan 1 n i ij j j w α v = =

∑

, i=1,L ,m Pandang kombinasi linear

1 0 m i i i w β = =

∑

(

)

(

)

1 11 1v 1n nv m m1 1v mn nv 0 β α + +L α + +L β α + +L α =

(

β α1 11+β α2 21+ +L β αm m1

)

v1+ +L

(

β α1 1n+ +L β αm mn

)

vn =0

Jika

{

v₁,L ,vn

}

bebas linear, maka 1 11 m m1 0 β α + +L β α =

Μ

1 1n m mn 0 β α + +L β α = .

m anu dan n persamaan, dengan m>n.

SPL homogen memiliki tak hingga banyak jawab.

{

w1, ,wm

}

∴ L bergantung linear.

Jika

{

v₁,L ,v_n

}

bergantung linear maka dapat direduksi menjadi subhimpunan yang bebas linear. Proses selanjutnya sama dengan di atas.

5) Pandang kombinasi linear

1Av1 nAvn 0

α + +L α =

(

1 1 n n

)

0

A αv + +L α v = Karena A−1 ada, maka

1 1v 2 2v n nv 0

α +α + +L α =

Karena

{

v₁,L ,v_n

}

bebas linear, maka α α₁= ₂=L =α_n =0

{

Av1, ,Avn

}

Daftar Pustaka

Bill Jacob. (1990). Linear Algebra. W.H. Freeman and Company.

Leon, SJ, (1990). Linear Algebra with Application. MacMilan Publishing Company.

Strang, G. (1988). Linear Algebra and Its Application. 3rd edition Academic Press.

Curtin, CW. (1984). Linear Algebra An Introduction Approach. Undergraduate Text in Mathematics Springer verlag.