Bab 3
SISTEM HUKUM KEKEKALAN
LINEAR
3.1
Sistem Linear Hiperbolik
Sistem linear dalam pengertian Tugas Akhir ini adalah suatu sistem hukum kekekalan dengan bentuk umum,
∂tu+ d X α=1 Aα(t)∂xαu= 0 (3.1.1) u(x,0) =u0(x) dimanau:Rd×R→Rm dan Aα ∈
Rm×m adalah matriks fungsi t. Dimensi spasial
sistem linear ini adalah d, sedangkan m adalah dimensi sistem. Sebagai contoh adalah sistem linear dimensi 2 dengan dimensi spasial 2, dengan koefisien konstan berikut ut+ 1 0 0 −1 ux+ 0 1 1 0 uy = 0
Lebih lanjut sistem linear dengan koefisien konstan
∂tu+
X
1≤i≤d
Aα∂xαu= 0 (3.1.2)
disebut hiperbolik jika terdapat C sehingga supξ ∈ R k exp(−iA(ξ))k≤ C dimana
A(ξ) = Pd
α=1ξαAα, lihat Serre[7]. Misalnya sistem berikut
ut+ 1 0 0 2 ux = 0
Sistem di atas adalah hiperbolik. Hal ini dapat ditunjukkan dari perhitungan di bawah ini. Misalkan kita pilihC = 3.
kexp(−iA(ξ))k= exp −iξ 1 0 0 2 = P∞ n=0(−i) n ξn n! 0 0 P∞n=0(−i)n2nξn n! = exp(−iξ) 0 0 exp(−i2ξ) = 2 ≤C,
untuk setiap ξ ∈R. Lebih umum lagi, dengan cara serupa kita dapat menyatakan bahwa sistem yang diagonal bersifat hiperbolik. Suatu sistem disebut hiperbolik kuat jika nilai-nilai eigennya berbeda[4]. Alternatif lain untuk melihat kehiperbo-likan sistem linear adalah melalui dua lemma berikut, lihat [7].
Lemma 3.1. Jika sistem (3.1.1) hiperbolik maka matriks A(ξ) dapat didiagonalkan dengan nilai eigen real untuk semua ξ ∈Rd.
Lemma 3.2.Jika matriksA(ξ)dapat didiagonalkan (misalA(ξ) = P(ξ)D(ξ)P(ξ)−1) dengan nilai eigen real dan pemetaan ξ 7→K(ξ) =kP(ξ)k · kP(ξ)−1k terbatas pada
Rd, maka sistem (3.1.1) hiperbolik.
Dengan asumsi Aα dan Aβ komutatif, suatu sistem u
t+Aαux+Aβuy = 0 akan hiperbolik jika dan hanya jika untuk setiap sistem satu dimensi ut +Aαux = 0 dan ut+Aβux = 0 hiperbolik. Pernyataan ini dapat ditunjukkan sebagai berikut. Pertama, akan ditunjukkan jika sistem satu dimensiut+Aαux= 0 hiperbolik maka
sistem ut+Aαux +Aβuy = 0 juga hiperbolik. Dari asumsi kehiperbolikan pilih C1 >0 dan C2 >0 sehingga ∞ X n=0 ξn 1Anα n! ≤C1 dan ∞ X n=0 ξn 2Anβ n! ≤C2
Untuk sistem ut+Aαux+Aβuy = 0, diperoleh
A(ξ) = ξ1Aα+ξ2Aβ (3.1.3)
, dimana ξ= (ξ1, ξ2), maka
kexp(−iA(ξ))k=kexp(−i(ξ1Aα+ξ2Aβ))k
=kexp(−i(ξ1Aα)·(−iξ2Aβ))k (karena Aα, Aβ komutatif)
≤ ∞ X n=0 ξn 1Anα n! · ∞ X n=0 ξn 2Anβ n! ≤C1·C2
Jadi sistem ut+Aαux+Aβuy = 0 hiperbolik.
Kedua, akan ditunjukkan jika sistem ut+Aαux +Aβuy = 0 hiperbolik maka ut+
Aαu
x = 0 dan ut+Aβuy = 0 hiperbolik. Karena sistem ut+Aαux +Aβuy = 0 hiperbolik, maka terdapat C sehingga supξ∈Rkexp(−iA(ξ))k≤C.
Dengan notasi (3.1.3) sebelumnya
kexp(−i(ξ1Aα))k= ∞ X n=0 (Aα)nξn 1 n! ≤ ∞ X n=0 (ξ1Aα)n+ (ξ2Aβ)n n! ≤C
Jadi, ut+Aαux = 0 hiperbolik. Dengan cara serupa dapat ditunjukkan pula bahwa sistem ut+Aβux = 0 hiperbolik.
3.2
Solusi Sistem Linear Hiperbolik
Suatu sistem linear hiperbolik dengan A =
a11 a12 a21 a22 matriks konstan di R2×2
dapat dituliskan sebagai
u1 u2 t +A u1 u2 x = 0 (3.2.1)
Persamaan di atas dapat diuraikan menjadi dua persamaan yaitu
(u1)t+a11(u1)x+a12(u2)x= 0 (3.2.2)
(u2)t+a21(u1)x+a22(u2)x= 0 (3.2.3)
Misalkan A dapat didiagonalkan, maka A dapat didekomposisi menjadi
R−1A= ΛR−1
dimana Λ =diag[λ1, λ2, ..., λm] adalah matriks diagonal dengan entri nilai eigenA dan R = [r1|r2|...|rm] adalah matriks dari vektor eigen yang berkaitan dengan nilai eigen A. Perhatikan pula bahwa
AR=RΛ
A[r1|...|rm] = [r1|...|rm]Λ
sehingga Arp = λprp, p = 1,2, ..., m(notasi ini akan digunakan pada pembahasan selanjutnya). Untuk mencari solusi dari sistem linear hiperbolik digunakanvariabel karakteristik, yaitu
v =R−1u.
Pertama tulis sistem sebagai
ut+Aux= 0
Kalikan persamaan diatas denganR−1, diperoleh
Substitusikan R−1A= ΛR−1 sehingga
R−1ut+ ΛR−1ux= 0
KarenaR−1 konstan, diperoleh
vt+ Λvx= 0 v1 v2 t + λ1 0 0 λ2 v1 v2 x = 0 sehingga dapat ditulis sebagai
(vp)t+λp(vp)x = 0 p= 1,2
dimana masing-masing persamaan diatas adalah persamaan transport dengan solusi
vp(x, t) =vp(x−λpt,0)
Dengan demikian diperoleh solusi
u(x, t) = Rv(x, t) = [r1|...|rm]v(x, t) = m X p=1 vp(x, t)rp
Dengan demikian (3.2.1) memiliki solusi jika A dapat didiagonalkan. Sebagai ilus-trasi sistem di atas, tinjau persamaan gelombang orde dua :
utt−c2uxx = 0 (3.2.4)
denganc >0 dan syarat awal
u(x,0) =u0(x)
ut(x,0) =u1(x)
Persamaan di atas dapat ditulis sebagai suatu sistem kekekalan skalar orde satu, dengan pemisalan v =ux dan w=ut, diperoleh
dan dari (3.2.4) diperoleh
wt=c2vx (3.2.6)
Persamaan (3.2.5) dan (3.2.6) dapat ditulis sebagai suatu sistem
v w t = w c2v x (3.2.7) v w t + 0 −1 −c2 0 v w x = 0 (3.2.8)
Perhatikan bahwa sistem di atas adalah suatu sistem linear dengan
A= 0 −1 −c2 0
dan syarat awalw(x,0) =u1(x) danv(x,0) =u00(x). MatriksAdapat didiagonalkan dengan nilai eigen λ=±c. Oleh karena itu (3.2.8) adalah sistem linear hiperbolik. MatriksA didekomposisi menjadi A=RΛR−1 dimana
Λ = c 0 0 −c R= 1 1 −c c R−1 = 1 2c c −1 c 1
Untuk mencari solusinya, digunakan variabel karakteristik z
z =R−1 v w = 1 2v− 1 2cw 1 2v+ 1 2cw
Berdasar solusi umum sistem linear hiperbolik, maka pada sistem ini solusinya dapat ditulis sebagai v w =z1(x−ct,0) 1 −c +z2(x+ct,0) 1 c (3.2.9)
atau dapat diuraikan menjadi v(x, t) = 1 2[u 0 0(x−ct) +u 0 0(x+ct)] + 1 2c[u1(x+ct)−u1(x−ct)] (3.2.10) dan w(x, t) = c 2[u 0 0(x+ct)−u 0 0(x−ct)] + 1 2[u1(x+ct) +u1(x−ct)] (3.2.11) Dengan mengetahui solusi untuk v dan w, maka solusi persamaan gelombang dapat dicari dari v = ux atau w = ut. Solusi yang diperoleh ekuivalen dengan solusi d’Alembert dari persamaan gelombang [9], yaitu
u(x, t) = 1 2[u0(x−ct) +u0(x+ct)] + 1 2c Z x+ct x−ct u1(s)ds
Hal ini dapat ditunjukkan dengan menurunkan solusi d’Alembert terhadap x.
v(x, t) = ∂ ∂x( 1 2[u0(x−ct) +u0(x+ct)] + 1 2c Z x+ct x−ct u1(s)ds) = 1 2[u 0 0(x−ct) +u 0 0(x+ct)] + 1 2c[u1(x+ct)−u1(x−ct)]
3.3
Masalah Riemann
Seperti halnya pada bab sebelumnya, masalah Riemann adalah masalah persamaan diferensial dengan syarat awalnya tak kontinu. Sebagai contoh adalah masalah Rie-mann berikut ut+Aux= 0 (3.3.1) u(x,0) = ul,jika x≤0 ur,jika x >0
Penyelesaian masalah Riemann di atas sama halnya pada solusi umum sistem linear hiperbolik, dimana solusinya akan berbentuk u(x, t) =Pm
p=1vp(x−λpt)rp, dimana
tak kontinu, maka akan demikian pula halnya dengan variabel karakteristiknya. Misalkan vp(x,0) = αp,jika x <0 βp,jika x >0 (3.3.2)
Dengan pemisalan di atas diperoleh dua persamaan, yaitu
ul =Rα= m X p=1 αprp (3.3.3) ur =Rβ = m X p=1 βprp (3.3.4)
Solusi untukv(x, t) adalah
v(x, t) =v(x−λpt,0) = αp,jika x−λpt <0 βp,jika x−λpt >0 (3.3.5)
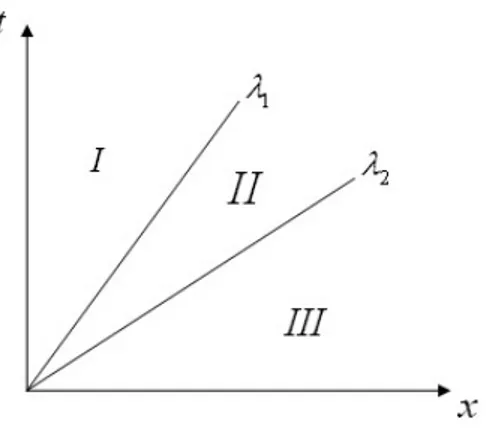
Kita ilustrasikan masalah Riemann pada m = 2. Misalkan λ1 < λ2, maka solusi (3.3.1) adalah u(x, t) = β1r1+β2r2,jika (x, t)∈I β1r1+α2r2,jika (x, t)∈II α1r1+α2r2,jika (x, t)∈III (3.3.6)
dengan daerahI, II, dan III pada gambar (3.1). Secara umum solusi dari (3.3.1) dapat dituliskan sebagai
u(x, t) = P X p=1 βprp+ m X p=P+1 αprp (3.3.7)
Gambar 3.1: Domain pada persamaan (3.2.6)
Untuk mempermudah pemahaman, perhatikan contoh berikut
ut+ 4 0 1 −2 1 0 −2 0 1 ux = 0 (3.3.8)
dengan syarat awal
u(x,0) = 0 1 2 1 2 ,jika x <0 1 2 1 2 0 ,jika x >0
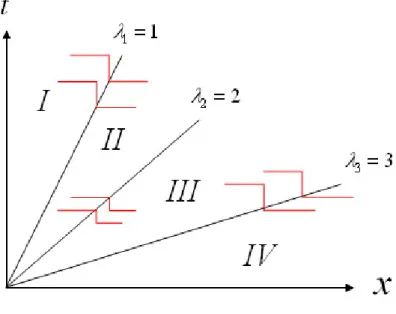
Dengan langkah-langkah seperti yang telah dijelaskan sebelumnya, masalah di atas memiliki solusi u(x, t) = (0,12,12)T, (x, t) di I (0,1,12)T, (x, t) di II (12,0,−1 2) T, (x, t) di III (0,12,0)T, (x, t) di IV = M X p=1 βprp+ 3 X p=M+1 αprp untuk(x−λt)>0 (3.3.9)
dengan daerah I,II,III, dan IV seperti pada gambar (3.2). Nilaiαp,βp dihitung seperti pada bagian (3.3) dan hasilnya adalah α1 = 0, α2 = 12, α3 = −12, β1 = 12,
β2 = 0, dan β3 = 0. Vektor rp adalah vektor karakteristik dari matriks A.
Gambar 3.2: Ilustrasi perambatan diskontinuitas pada sistem linear hiperbolik
3.4
Solusi Lemah dan Kondisi Rankine Hugoniot
Dari bagian (3.3), kita melihat bahwa masalah Riemann dalam sistem linear hiper-bolik dapat memiliki solusi yang memuat diskontinuitas, karenanya diperlukan kon-sep solusi lemah untuk sistem linear. Misalkanuadalah solusi sistem linear (3.1.1), maka u dikatakan solusi lemah jika
hu, ∂tϕ+AT∂xϕi+
Z
R+
u0(x)ϕ(x,0)dx= 0 (3.4.1)
untuk setiap fungsi uji ϕ ∈ C1
0(R×[0,∞),Rm) dan ϕ ≡ 0 di batas dan di luar domain. Dalam notasi ini
hu, ∂tϕ+AT∂xϕi=
Z Z
u·(∂tϕ+AT∂xϕ)dxdt (3.4.2)
yang mengalami diskontinuitas. Pada masalah Riemann (3.3.8) misalnya, solusi dari masalah ini mengalami tiga diskontinuitas dalam tiga arah pula. Perhatikan solusi masalah Riemann (3.3.1). Setiap daerah yang dibatasi oleh x = λpt terjadi perubahan solusi dari αp keβp. Misalkan dari daerah III ke daerah II, solusi hanya mengalami perubahan dari α1 ke β1. Hal ini menunjukkan bahwa ketakkontinuan terjadi pada setiap x=λpt.
Kondisi Rankine Hugoniot pada persamaan skalar menunjukkan besarnya kecepatan perambatan diskontinuitas. Hal serupa pun terjadi pada sistem linear hiperbolik. Diskontinuitas pada solusi sistemut+f(u)x = 0 pun dapat dihitung melalui kondisi Rankine Hugoniot. Perhatikan kondisi Rankine Hugoniot pada persamaan skalar berikut
dxs
dt =
[f(u)]
[u] (3.4.3)
dengan [u] =ur−uldan [f(u)] =f(ur)−f(ul). Karena [u] dan [f(u)] adalah vektor maka persamaan ini tidak berlaku pada sistem. Namun, dari persamaan (3.3.3) dan (3.3.4) kita peroleh [u] =ur−ul =βprp−αprp = (βp−αp)rp (3.4.4) dan [f(u)] =A[u] =A(βp−αp)rp = (βp−αp)Arp = (βp−αp)λprp =λp(βp−αp)rp =λp[u] (3.4.5)
Dengan demikianλp menyatakan kecepatan perambatan diskontinuitas dalam arah