MATERI PERKULIAHAN
MATEMATIKA DISKRET
(Lingkungan Internal MI – UNIKOM)
UNIVERSITAS KOMPUTER INDONESIA
JURUSAN MANAJEMEN INFORMATIKA
DISAJIKAN PADA SEMESTER V
Rencana Perkuliahan
Minggu Materi Tugas
1 03 09 Kosong (PMB, Wisudda) - 2 08 09 Silabi 3 15 09 Himpunan Tugas 4
22 09 Prinsip Inklusi & Eksklusi Tugas
5
13 10 Preposisi Tugas
6
20 10 Induksi Matematika Tugas
7
27 10 Kombinatorial Tugas
8 UTS 9
19 11 Fungsi & Relasi 10
26 11 Sifat Relasi Biner Tugas
11 3 12 Pengantar Graf 12 10 12 Graf 13 17 12 Lintasan Tugas 14
24 12 Mencari Jarak Terpendek
Implementasi Algoritma Floyd dan Djikstra 15
31 12 Kuis
Ketentuan Perkuliahan :
1. Mengikuti edaran Ketua Jurusan MI
2. Tidak ada susulan untuk nilai tugas atau yang lainnya, selain UTS dan UAS.
Ketentuan Penilaian :
UTS : 35 %
UAS : 35 %
Tugas Individu : 30 %
Daftar Pustaka :
1. Liu, C. L, 1995, Dasar-Dasar Matematika Diskret, Gramedia, Jakarta 2. Munir, Rinaldi, 2003, Matematika Diskret, Informatika, Bandung
PREPOSISI
Ilmu logika berkaitan dengan kalimat-kalimat berupa argumen dan hubungan yang ada di antara kalimat tersebut. Ilmu Logika lebih mengarah pada bentuk kalimat (sintaks
)
daripada arti kalimat (semantiks).Preposisi atau kalimat deklaratif adalah kalimat yang mempunyai nilai benar atau salah, tetapi bukan keduanya
Contoh : 2 + 3 = 5
OPERATOR PREPOSISI
Satu atau lebih preposisi dapat dikombinasikan untuk menghasilkan preposisi baru. Preposisi yang diperoleh dari kombinasi tersebut dinamakan preposisi majemuk. Preposisi yang hanya terdiri dari 1 operator dikatakan preposisi atomic. Operator preposisi terdiri dari :
Negasi (Ingkaran) : ~
Konjungsi (Dan) : Λ
Disjungsi (Atau) : V
Implikasi (Jika.. Maka..) : Æ Bi-Implikasi (..Jika hanya jika..) : ↔
Untuk menghindari konotasi berbeda dari preposisi majemuk, maka ditentukan table kebenaran dari preposisi tersebut. Suatu table kebenaran akan memuat 2n kombinasi preposisi. Tabel Kebenaran p q ~ p p Λ q p V q p Æ q p ↔ q B B S S B B B B S S S B S S S B B S B B S S S B B S B B
Soal :
1. Buatlah table kebenaran dari pernyataan berikut : a) ~ (~ p V~ q) b) ~ (~p ↔ q) c) (p Æ q) Λ ~ (p V q) d) p Æ( q Λ ~ p) V q) e) (p Æ q) Λ (~ p V q) f) (~p Λ (~ q Λ r)) V (q Λ r) V (p Λ r) g) (p Λ q) V (~ q Λ r)
2. Tentukan nilai kebenaran dari pernyataan berikut : (nilai p dan q = True, r dan s = False) a) p V ( q Λ r) b) ( p Λ q Λ r) V ~ ((p V q) Λ (r V s) c) (~(p Λ q) V ~ r ) V (((~p Λ q) V ~ r) Λ s) d) ~(p V q) Λ ~(s V r) e) ((~p V q) Λ ~r) Æ (r Λ ~s) EKUIVALENSI
Dua preposisi majemuk disebut ekuivalen secara logika jika keduanya mempunyai tabel kebenaran yang sama. (notasi : ⇔)
Tautologi Æ kalimat yang selalu benar Kontradiksi Æ kalimat yang selalu salah
Kontingensi Ækalimat yang dapat bernilai benar dan salah
Soal :
1. Dengan menggunakan tabel kebenaran periksalah ekuivalensi dari preposisi berikut : a) p Λ q ⇔ ~p V ~q
b) (q V r) ⇔ (p Λ q) V (p Λ r)
c) p V (q V r) ⇔ (p V q) V r
d) (p Λ q) Æ (p V q) ⇔ ~(p Λ q) V (p V q)
e) ~(p Æ q) Æ p ⇔ p
2. Buktikan bahwa pernyataan berikut adalah tautology dengan menggunakan tabel
HUKUM PREPOSISI 1. Hukum Identitas
p V S ⇔ p p Λ B ⇔ p
2. Hukum Dominasi / Null
p Λ S ⇔ S p V B ⇔ B 3. Hukum Negasi p V ~p ⇔ B p Λ ~p ⇔ S 4. Hukum Idempotent p V p ⇔ p p Λ p ⇔ p 5. Hukum Involusi ~(~p) ⇔ p 6. Hukum Absorpsi p V (p Λ q) ⇔ p p Λ (p V q) ⇔ p 7. Hukum Komutatif p V q ⇔ q V p p Λ q ⇔ q Λ p 8. Hukum Asosiatif p V (q V r) ⇔ (p V q) V r p Λ (q Λ r) ⇔ (p Λ q) Λ r 9. Hukum Distributif p V (q Λ r) ⇔ (p V q) Λ (p V r) p Λ (q V r) ⇔ (p Λ q) V(p Λ r) 10.Hukum De Morgan ~(p Λ q) ⇔ ~p V ~q ~(p V q) ⇔ ~p Λ ~q
Varians Preposisi
Variasi preposisi terdapat 3 bentuk, yaitu : konvers, invers dan kontraposisi. Variasi preposisi merupakan variasi dari bentuk : p Æ q
Konvers : q Æ p Invers : ~p Æ ~q Kontraposisi : ~q Æ ~p p q ~ p ~ q p Æ q q Æ p ~p Æ ~q ~q Æ ~p B B S S B B B B B S S B S B B S S B B S B S S B S S B B B B B B Contoh : p : A merupakan bujursangkar
q : A merupakan empat persegi panjang
p Æ q : Jika A merupakan bujursangkar maka A merupakan empat persegi panjang
q Æ p : Jika A merupakan empat persegi panjang maka A merupakan bukan bujursangkar
~p Æ ~q : Jika A merupakan bujursangkar maka A merupakan bukan empat persegi panjang
~q Æ ~p : Jika A merupakan bukan empat persegi panjang maka A merupakan bukan bujursangkar
Soal Misalkan :
p : David sedang berada di taman q : David ada di dalam rumah r : David sedang mengerjakan PR s : David sedang mendengarkan radio
1. Nyatakan kalimat berikut dalam bentuk preposisi :
a) Jika David ada di dalam rumah dan tidak mengerjakan PR, ia pasti mendengarkan radio
b) Jika David tidak ada di dalam rumah, maka ia sedang mengerjakan PR di taman c) Jika David tidak ada di dalam rumah, maka ia pasti tidak sedang mendengarkan
radio, tetapi sedang berada di taman.
2. Nyatakan preposisi berikut dalam bentuk kalimat : a) (p Æ ~r) V (q Æ s)
b) (p Λ r ) Æ ~q
HIMPUNAN
Himpunan didefinisikan sebagai kumpulan objek-objek yang berbeda. Objek yang terdapat dalam himpunan disebut elemen atau anggota himpunan.
Penulisan anggota himpunan dapat dilakukan dengan :
a) Menuliskan semua anggota himpunan di dalam kurung kurawal Contoh: A = {1, 2, 3, 5, 7}
B = {a, i, u, e, o}
b) Menuliskan notasi pembentuk himpunan yang mencakup karakteristik himpunan. Contoh : A = {x | x semua bilangan prima bernilai kurang dari 10}
B = { x | x merupakan huruf vokal} Diargram Venn
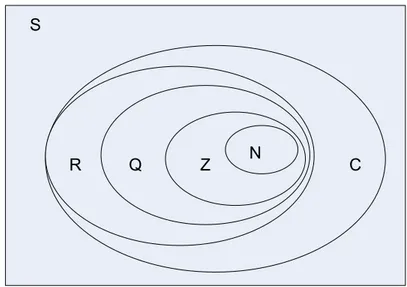
Diagram Venn adalah grafis yang menyatakan keadaan himpunan. Diperkenalkan oleh John Venn.
S
Z N Q
R N C
N : himpunan bilangan asli Z : himpunan bilangan bulat Q : himpunan bilangan rasional R : himpunan bilangan real C : himpunan bilangan kompleks S : himpunan semesta
MACAM HIMPUNAN
1. Himpunan Kosong : { } atau ∅
Himpunan Kosong merupakan himpunan yang tidak memiliki satupun anggota (null set) 2. Himpunan Bagian : ⊆
Himpunan Bagian merupakan himpunan yang anggotanya merupakan anggota dari himpunan yang lain.
Teorema :
a) Suatu himpunan memiliki satu himpunan bagian yang merupakan himpunan itu
sendiri
b) Himpunan kosong merupakan himpunan bagian dari semua himpunan c) Berlaku sifat transitif
3. Himpunan Sama : =
Himpunan (yang) sama merupakan himpunan yang memiliki jumlah anggota dan jenis anggota yang tepat sama, walau tidak berurutan.
A = B ↔ A ⊆ B dan B ⊆ A
4. Himpunan Kuasa : ℘
Himpunan Kuasa merupakan himpunan yang anggotanya merupakan semua himpunan bagian dari himpunan tersebut, termasuk himpunan kosong dan himpunan itu sendiri. Jumlah banyaknya anggota himpunan kuasa = 2n .
Jumlah dan banyaknya suatu elemen dinyatakan dalam kardinalitas (| |)
5. Himpunan Semesta : S atau U(nion)
Himpunan semesta adalah himpunan semua objek yang dibicarakan. Soal
1. Diketahui A suatu himpunan, dengan anggota semua bilangan prima antara 4 hingga 15. Sebutkan ℘ (A).
OPERASI HIMPUNAN
Operasi Himpunan Penyelesaian Visualisasi
Irisan A ∩ B = {x | x∈A dan x∈B}
Gabungan A U B = {x | x∈A atau x∈B}
Komplemen Ac = {x | x∈ S, x∉ A}
Selisih (Difference A - B = {x |x∈A atau x∉B}
Beda Setangkup (Symmetric Difference) A ⊕ B = {x | x∈(AUB), x∉ (A∩B)} S A B S A B A S S S A B A B
Soal
Diketahui : S = {x | semua bilangan antara 1 s/d 21}
A= {x | semua bilangan prima lebih kecil dari 20} B = {x | semua bilangan ganjil antara 6 s/d 17} C = {2, 4, 7, 9, 13, 15} D = {1, 9, 12, 14, 16, 18} 1. A ∪ Bc∩ D = 2. (B ⊕ C) c – A = 3. D ⊕ A – (B ∩ A) = 4. C – (A – B) c = 5. C c⊕ B ∪ A c = HUKUM HIMPUNAN 1. Hukum Identitas A ∪∅ = A A ∩ S = A
2. Hukum Dominasi / Null
A ∩∅ = ∅ A ∪ S = S 3. Hukum Komplemen A ∪ ~A = S A ∩ ~A = ∅ 4. Hukum Idempotent A ∪ A = A A ∩ A = A 5. Hukum Involusi ~(~A) = A 6. Hukum Absorpsi A ∪ (A ∩ B) = A A ∩ (A ∪ B) = A 7. Hukum Komutatif A ∪ B = B ∪ A A ∩ B = B ∩ A
8. Hukum Asosiatif A ∪ (B ∪ C) = (A ∪ B) ∪ C A ∩ (B ∩ C) = (A ∩ B) ∩ C 9. Hukum Distributif A ∪ (B ∩ C) ⇔ (A ∪ B) ∩ (A ∪ C) A ∩ (B ∪ C) ⇔ (A ∩ B) ∪ (A ∩ C) 10.Hukum De Morgan ~(A ∩ B) ⇔ ~A ∪ ~B ~(A ∪ B) ⇔ ~A ∩ ~B
PRINSIP INKLUSI & EKSLUSI
Jika terdapat dua atau lebih himpunan yang akan digabungkan, maka harus diperhatikan apakah himpunan tersebut saling beririsan atau tidak, jika beririsan maka gabungan himpunan tersebut harus dikurangi dengan irisannya.
a) Jika Saling Lepas n(A∪ B) = |A| + |B|
n(A∪ B∪ C) = |A| + |B| + |C|
b) Jika saling Beririsan
n(A∪ B) = |A| + |B| - |A∩ B|
n(A∪ B∪ C) = |A| + |B| + |C| - |A∩ B| - |A∩ C| - |B∩ C| + |A∩ B∩ C|
Bentuk Umum :
|A1∪ A2∪.. ∪ An| = Σ | Ai| - Σ |Ai ∩ Aj| + (-1)n-1 |A1 ∩ A2 ∩.. ∩ An| i 1≤ I≤ j≤ n
Contoh :
1. Pada suatu pertemuan, yang dihadiri 30 wanita, 17 orang keturunan Jawa, 16 orang keturunan Sunda dan 5 orang bukan keturunan Jawa maupun sunda. Berapa banyak yang merupakan keturuan Jawa dan Sunda.
Misal : A = himpunan wanita keturunan Jawa
n(A) = 17, n(B) = 16, n(A∪ B)c = 5 n(A∪ B) = n(S) - n(A∪ B)c n(A∪ B) = |A| + |B| - |A∩ B| (30 – 5) = 17 + 16 - x 25 = 33 – x x = 33 – 25 x = 8
2. Banyaknya bilangan antara 1 s/d 300 yang tidak habis dibagi oleh 2, 3, 5 Misal : A = himpunan bilangan yang habis dibagi 2
B = himpunan bilangan yang habis dibagi 3 C = himpunan bilangan yang habis dibagi 5
n(A) = 300/2 = 150, n(A∩ B) = 300/(2 . 3) = 50 n(B) = 300/3 = 100, n(A∩ C) = 300/(2 . 5) = 30 n(C) = 300/5 = 60 n(B∩ C) = 300/(3 . 5) = 20 n(A∩ B∩C )= 300/(2 . 3 . 5) = 10
Bilangan yang tidak habis dibagi 2, 3, 5 = = n(S) – n(A∪ B∪ C) = n(S) – (n|A| + n|B| + n|C| - n |A∩ B| - n |A∩ C| - n |B∩ C| +n|A∩ B∩ C|) = 300 – (150 + 100 + 60 – 50 – 30 – 20 + 10) = 300 – 220 = 80 S A 9 8 8 5 B 10 S 80 20 40 40 10 20 A B C 80
3. Terdapat 1232 mahasiswa mengambil kuliah bahasa Inggris, 879 mengambil kuliah bahasa Perancis, dan 114 mengambil kuliah bahasa Jerman. 103 mengambil bahasa Inggris dan Perancis, 23 orang mengambil kuliah Inggris dan Jerman, 14 orang kuliah Perancis dan Jerman. Jika 2092 orang mengambil paling sedikit satu kuliah bahasa saja, berapa banyak mahasiswa yang mengambil ketiga bahasa tersebut, dan gambarkan diagram Venn-nya.
Misal : A = himpunan mahasiswa mengambil kuliah bahasa Inggris B = himpunan mahasiswa mengambil kuliah bahasa Perancis C = himpunan mahasiswa mengambil kuliah bahasa Jerman
n(A) = 1232 n(A∩ B) = 103 n(A∪ B∪ C) = 2092 n(B) = 879 n(A∩ C) = 23 n(C) = 114 n(B∩ C) = 14 n(A∪ B∪ C) = |A| + |B| + |C| - |A∩ B| - |A∩ C| - |B∩ C| + |A∩ B∩ C| 2092 = 1232 + 879 + 114 – 103 – 23 – 14 + x x = 2092 – 2225 + 140 x = 7
Soal
1. Diantara 130 mahasiswa, 60 memakai topi di dalam kelas, 51 memakai syal, dan 30 memakai topi dan syal, Diantara 54 orang yang memakai sweater, 26 memakai topi, 21 memakai syal dan 12 memakai syal dan topi. Berapa mahasiswa yang tidak memakai sweater dan syal, namun memakai topi?, Gambarkan diagram Venn-nya.
7 S 1113 16 96 769 7 84 A B C 90
2. Diantara 100 mahasiswa, 32 mempelajari matematika, 20 mempelajari fisika, 45
mempelajari biologi, 15 mempelajari matematika dan biologi, 7 mempelajari matematika dan fisika, 10 mempelajari fisika dan biolagi, dan 30 tidak mempelajari satu pun diantara ketiga bidang tersebut. Berapa mahasiswa yang mempelajari hanya satu diantara ketiga bidang tersebut ?, Gambarkan diagram Venn-nya.
3. 30 Mobil dirakit disebuah pabrik. Pilihan yang tersedia adalah radio, AC dan Power Window. Diketahui bahwa 15 mobil mempunyai radio, 8 mobil mempunyai AC dan 6 mobil mempunyai power window. Selain itu 3 diantaranya mempunyai ketiga pilihan. Berapa mobil yang tidak memiliki pilihan sama sekali.
KOMBINATORIAL
Ilmu kombinatorik ditujukan untuk mengetahui perkiraan jumlah operasi komputasi untuk mengetahui waktu proses dan besar kapasitas data. Kombinatorial adalah cabang matematika yang mempelajari pengaturan objek-objek.
Kaidah Dasar perhitungan kombinatorial, adalah sebagai berikut : 1. Perhitungan Secara Langsung
a. Kaidah Penjumlahan (m + n)
“Bila percobaan kesatu mempunyai m hasil percobaan yang mungkin terjadi, percobaan kedua mempunyai n hasil percobaan yang mungkin terjadi. Maka bila hanya satu percobaan yang dilakukan akan terdapat m + n kemungkinan hasil percobaan.”
Contoh :
Sekelompok mahasiswa terdiri dari 4 pria dan 3 wanita. Berapa jumlah cara memilih satu orang yang mewakili kelompok tersebut.
Æ 4 + 3 = 7 cara
b. Kaidah Perkalian (m x n)
“Bila percobaan kesatu mempunyai m hasil percobaan yang mungkin terjadi, percobaan kedua mempunyai n hasil percobaan yang mungkin terjadi. Maka bila percobaan kesatu dan kedua akan terdapat m x n kemungkinan hasil percobaan. “
Contoh :
Sekelompok mahasiswa terdiri dari 4 pria dan 3 wanita. Berapa jumlah cara memilih satu wakil pria dan satu wakil wanita.
Æ 4 x 3 = 12 cara
c. Perluasan rumusan (a) dan (b)
“Percobaan untuk nomor (a) dan (b) tidak terbatas hanya dua percobaan, tetapi lebih dari dua percobaan.”
p1 + p2 + p3 + .. + pn
Contoh :
1. Jika ada 10 pertanyaan yang dijawab B/S, berapakah kemungkinan kombinasi jawaban yang dapat dibuat.
Æ B/S terdapat 2 alternatif, n = 10 2 10 = 1024
2. Terdapat 6 buku bahasa Inggris, 3 buku bahasa Perancis dan 10 buku bahasa Indonesia.
a) Berapa jumlah cara memilih 3 buku dengan bahasa berbeda?
Æ 6 x 3 x 10 = 180
b) Berapa jumlah cara memilih 1 buku secara sembarang ?
Æ 6 + 3 + 10 = 18
3. Berapa banyak bilangan ganjil antara 100 dan 1000 a) Jika semua angka tidak berulang.
Æ
5 x 8 x 8 = 320
b) Jika semua angka boleh berulang.
Æ 5 x 9 x 10 = 450 2. Perhitungan dengan rumus
a. Permutasi b. Kombinasi
PERMUTASI
Permutasi adalah penyusunan objek-objek dalam suatu urutan tertentu. Prinsip Dasar Penghitungan Permutasi :
1) Setiap unsure dari n unsure, dapat dipilih sebagai unsure pertama sehingga terdapat n cara untuk memilih unsure pertama
2) Jika unsure pertama itu sudah dipilih, maka setiap dari sisanya, yaitu (n-1) unsure dapat dipilih sebagai unsure kedua, terdapat (n-1) cara untuk memilih unsure kedua
Satuan (1, 3, 5, 7, 9) = 5 puluhan (0. . 9) – 2 = 8 Ratusan (1. . 9) - 1 = 8
3) Untuk memilih unsure ketiga, yaitu (n-2) cara. Dan untuk menempatkan unsure kesatu dan kedua ada : n. (n-1) . (n-2), sehingga didapat :
Pn = P (n,n) = n . (n-1) . (n-2) ... 3 . 2 . 1! = n!
Teknik perhitungan permutasi : 1. Permutasi dari keseluruhan n unsure
“ Jika n bilangan bulat positif, maka hasil perkalian bilangan tersebut dari 1 s/d n disebut n faktorial“
P(n,n) = n!
2. Permutasi dari sebagian objek berbeda, dimana tidak semua objek tersebut digunakan. “Jumlah permutasi dari suatu himpunan yang terdiri dari n objek yang berbeda dan yang diambil sekaligus sebanyak r objek tanpa pengulangan.“
P(n,r) = n ! . (n-r)!
3. Permutasi dengan pengulangan
“Terdapat n pangkat r cara untuk menyusun r objek ke dalam n objek berbeda”.
P(n,r) = nr
KOMBINASI
Kombinasi adalah suatu subset pilihan dari objek-objek tanpa menghiraukan urutan objek yang bersangkutan.
Teknik Penghitungan Kombinasi :
1. Kombinasi dari seluruh objek yang berbeda
“Jumlah kombinasi dari suatu set yang terdiri dari n objek yang berbeda dan diambil sebanyak n objek, maka akan sama dengan 1.”
C(n,r) = 1!
2. Kombinasi dari n objek yang berbeda, dipilih r objek tanpa menghiraukan susunannya, dengan syarat : 0 < r < n
C(n,r) = n ! . r!(n-r)!
3. Kombinasi dengan pengulangan
“Masalah pengambilan r objek dari i benda yang berbeda dengan membolehkan
pengambilan berulang, dapat dipandang sebagai penggunaan r tanda yang sama untuk menandai n benda yang berbeda, dan setiap benda dapa ditandai lebih dari satu kali.
C(n+r-1,r) = (n+r-1) ! r!(n-1)!
Contoh :
1) Sebuah bioskop mempunyai jajaran kursi per baris. Tiap baris terdiri dari 6 kursi. Jika dua orang akan duduk, berapa banyak pengaturan tempat duduk yang mungkin pada satu baris?
Æ P(6,2) = 6! = 6! = 6.5.4.3.2.1! = 6 . 5 = 30 (6-2)! 4! 4 . 3 . 2 . 1!
2) Terdapat perlombaan lari dengan jumlah peserta tujuh orang. Berapa kemungkinan peserta mendapatkan medali. Æ P(7,3) = 7! = 7! = 7. 6.5.4.3.2.1! = 7 . 6 . 5 = 210 (7-3)! 4! 4 . 3 . 2 . 1! 3) P(n,4) = 110. P(n-2,2) , n? Æ n ! = 110 . (n-2)! (n-4)! (n-4)! n.(n-1).(n-2)! = 110 . (n-2)! (n-4)! (n-4)! n(n-1)=110 n2-n-110 = 0 (n-11)(n+10) = 0 n = 11, n = -10 4) P(n,4) = 9 . P(n,3) Æ n ! = 9 . n ! (n-4)! (n-3)! n ! = 9 . n ! . (n-4)! (n-3).(n-4)! n-3 = 9 n = 12
Soal
1) Terdapat koleksi buku : 4 buku basis data, 3 buku matematika, dan 6 buku pemrograman a) Berapa kemungkinan dapat dipilih 2 buku dengan tema berbeda
b) Berapa kemungkinan terambil 3 buku dengan salah satunya adalah buku permrograman
2) Berapa kemungkinan 5 digit angka genap dapat disusun, dengan syarat digit pertama adalah angka ganjil dan tidak terjadi pengulangan.
3) P(n,r) = 336 C(n,r) = 56 , n?, r? 4) P (n,r) = 6720 C(n,r) = 56, n?, r? 5) P(n,r) = 60 C(n,r) =10, n?, r?
6) Diketahui himpunan bilangan {1, 2, 3, 5, 8, 9}. Berapa banyak kemungkinan bilangan terdiri dari 5 digit, dengan ketentuan digit ke-3 selalu ganjil
INDUKSI MATEMATIKA
Serangkaian langkah-langkah perhitungan untuk membuktikan suatu pernyataan matematika benar, dan berlaku untuk semua nilai n. (n adalah bilangan bulat positif)
Langkah Pembuktian terbagi 2, yaitu : 1. Basis Induksi
Untuk pernyataan dengan nilai dasar bernilai benar. P(no) selalu benar
2. Langkah Induksi
Untuk pernyataan semua nilai benar sehingga jika nilai tersebut ditambah satu maka pernyataan tetap benar.
Jika p(k) benar untuk k ≥ no maka p(k+1) selalu benar Contoh :
1. 1 + 2 + .. + n = n ( n+1) , untuk n ≥ 1 2
Maka untuk nilai basis : 1) Nilai Basis
no = 1 Æ 1 = 1. (1+1)
2
1 = 1 . 2 , Terbukti no = 1 bernilai benar 2 2) Langkah induksi n = k Æ 1 + 2 + . . + k = k (k+1) 2 n = k+1 Æ1 + 2 + . . + k + (k+1) = k(k+1) + (k+1) 2 = k(k+1) + 2 . (k+1) 2 2 = (k2 + k) + (2k+2) 2 = k2 + 3k + 2 2 = (k+1) (k+2) 2 Misal : k = 1 Æ (1+1) . (1+2) = 3 2
2. 2 + 4 + 6 + . . + 2n = n(n+1)
Maka untuk nilai basis : 1) Nilai Basis
no = 1 Æ 2 = 1. (1+1)
1 = 1 . 2 , Terbukti no = 1 bernilai benar 2) Langkah induksi n = k Æ 2 + 4 + . . + 2k = k (k+1) n = k+1 Æ2 + 4 + . . + k + 2(k+1) = k(k+1) + 2(k+1) = (k2 + k) + (2k+2) = k2 + 3k + 2 = (k+1) (k+2) Misal : k = 1 Æ (1+1) . (1+2) = 2. 3 = 6 3. 1 + 2 + 22 + .. + 2 n = 2n+1 – 1
Maka untuk nilai basis : 1) Nilai Basis
no = 0 Æ 1 = 20+1 - 1) 1 = 21 - 1
1 = 1, Terbukti no = 0 bernilai benar
2) Langkah induksi n = k Æ 1 + 2 + 22 + .. + 2 k = 2k+1 – 1 n = k+1 Æ1 + 2 + 22 + .. + 2 k + 2k+1= 2k+1 – 1 + 2k+1 = 2 . (2k+1) - 1 = 2 . 2k .. 2 - 1 = 2k+2 - 1 Misal : k = 1 Æ 21+2 – 1 = 23 - 1 = 2. 3 = 8 – 1 = 7
Soal 1. 4 + 8 + 12 + . . + 4 n = 2n(n+1) 2. 1 + 5 + 9 + . . + (4n-3) = n (2n-1) 3. 12 + 32 + 52 + . . + (2n-1)2 = n (2n+1)(2n-1) 3 4. 2 + 5 + 8 + . . + (3n-1) = n(3n+1) 2 5. 5 + 10 + 15 + . . + 5n = 5n(n+1) 2 6. 12 + 22 + 32 + . . + n2 = n(n+1).(2n+1) 2 7. 1.2 + 2.3 + 3.4 + . . + n(n+1) = n(n+1)(n+2) 3 8. 13 + 23 + 33 + . . + n3 = n2 (n+1) 2 4 9. 2 + 22 + 23 + .. + 2 n = 2n+1 – 2 10.1 + 2 + 3 + . . + n < 1/8 (2n+1) 2 11. 1 + 1 + 1 + . . + 1 = n . 1 . 2 2 . 3 3 . 4 n(n+1) n+1 12. 12 + 22 + . . + n2 = n(n+1) 1 . 3 3 . 5 (2n-1)(2n+1) 2(2n+1) 13. 1 + 2 + . . + 1 = n . 1 . 3 3 . 5 (2n-1)(2n+1) 2n+1 14. 1 + 1 + 1 + . . + 1 = n . 1 . 4 4 . 7 7 . 10 (3n-2)(3n+1) 2n+1
FUNGSI
Teorema 1 :
Misal A dan B adalah himpunan suatu fungsi dari A ke B adalah pe
nandaan tepat satu kali dari satu elemen dari himpunan A, ke setiap elemen dari himpunan B.
F(a) = b Jika b unik dan elemen dari B ditandai oleh fungsi f dari elemen a di A
f : A Æ B fungsi dari A ke B.
Teorema 2 :
Jika f adalah fungsi dari A ke B, disebut f memetakan A ke B, maka A adalah domain dari f , dan B adalah kodomain dari f.
Jika f(a) = b maka b adalah image (daerah bayangan) dari a, dan a adalah pre-image (daerah bayangan awal) dari b. Range dari f adalah seluruh images dari A.
Macam Fungsi
Fungsi Visualisai one to one (injective)
onto (surjective)
correspondence one to one (bijective) a b c 1 2 3 4 a b c 1 2 3 4 a b c 1 2 3 4 d e d
Into
Contoh :
Tentukan macam-macam fungsi berikut :
1) A = {1, 2, 3}, B = {u, v, w} dan R = {{1, u}, {2, v}, {3, w}} 2) A = {1, 2, 3, 4}, B = {u, v, w}, dan R = {{1, u}, {2, v}, {3, w}} 3) A = {1, 2, 3}, B = {u, v, w}, dan R = {{1, u}, {1, v}, {2, v}, {3, w}} 4) A= {1, 2, 3}, B = {u, v, w}, dan R = {{1, u}, {2, u}, {3, w}}
Soal
Diketahui : A dan B adalah suatu himpunan, A = {1, 2, 3, 4} dan B = {u, v, w, x} Jika R adalah himpunan pemetaan dari A ke B, maka tentukan macam fungsi berikut :
1) R = {{1, v}, {2, u}, {3, v}, {4, w}} 2) R = {{1, x}, {2, u}, {3, v}, {4, w}} 3) R = {{1, u}, {2, u}, {3, v}, {4, w}} 4) R = {{1, u}, {1, v}, {2, w}, {3, x}, {4, x}} a b c 1 2 3 4
RELASI
Relasi biner R antara A dan B adalah himpunan bagian dari A X B. Notasi : R ⊆ (A X B)
A X B = {(a, b) | a ∈ A dan b ∈ B}
Jika (a,b) ∈ R, maka dituliskan a R b, artinya a dihubungkan dengan b oleh R Jika (a,b) ∈ R, maka dituliskan a R b, artinya a tidak dihubungkan dengan b oleh R.
Representasi Relasi Jenis Visualisasi A = {a, b, c} B = {1, 2, 3, 4} R = {(a,1), (b,2), (b,4), (c,3)} Diagram Panah Tabel Relasi A B a 1 b 2 b 4 c 3 A = {a, b, c, d}
R = {(a,a), (a,d), (b,b), (b,c), (c,a), (c,c), (d,c)} Matriks
mij = 1 jika (ai, bj) ∈ R
mij = 0 jika (ai, bj) ∉ R M =
1 0 0 1 0 1 1 0 1 0 1 0 0 0 1 0 a b c 1 2 3 4
Graf berarah
Relasi yang dapat direpresentasikan dalam graf berarah adalah relasi pada satu himpunan dan bukan dari satu himpunan ke himpunan yang lain.
In-degree dari suatu titik adalah jumlah anak panah yang masuk atau berakhir pada titik itu Out-degree dari suatu titik adalah jumlah anak pannah yang keluar dari titik itu
a b c d
In-degree 2 1 3 1
Out-degree 2 2 2 1
SIFAT RELASI BINER 1. Relasi Refleksif (Reflexif)
Relasi R pada himpunan A disebut reflexif jika (a,a)∈ R untuk setiap a ∈ A.
Irreflexif : Jika terdapat a∈A sedemikian sehingga (a,a) ∉ A
2. Relasi Setangkup (Symmetric)
Relasi R pada himpunan A disebut setangkup jika terdapat (a,b) ∈ R, maka (b,a) ∈R,
untuk semua a,b∈ R.
Not Symmetric : Jika (a,b) ∈ R sedemikian sehingga (b,a) ∉R untuk semua a,b ∈R
3. Relasi Tolak Setangkup (Anti Symmetric)
Relasi R pada himpunan A disebut tolak setangkup jika (a,b) ∈R dan (b,a) ∈R, hanya jika a=b, untuk semua a,b∈ R
A symmetric : Jika a ≠ b untuk (a,b) ∈R sedemikian sehingga (b,a) ∈R
4. Relasi Menghantar (Transitif)
Relasi R pada himpunan A disebut transitif jika (a,b) ∈ R dan (b,c) ∈R maka (a,c) ∈R
untuk semua a,b,c ∈R.
5. Relasi Equivalence
Relasi R pada himpunan A disebut equivalensi, jika mempunyai sifat reflexif, simetrik dan transitif.
d c
b a
6. Relasi Partisi
Relasi partisi adalah cara membagi sesuatu hal menjadi beberapa kelas yang berbeda. Pembagian kelas yang berbeda disebut Partisi.
7. Class Equivalence
Relasi R pada himpunan A adalah relasi equivalensi. Himpunan dari semua elemen yang direlasikan atau berrelasi pada tiap elemen a dari A disebut class equivalensi dari a. Kelas equivalensi dari a yang bersesuaian dengan R dinotasikan [a]/R
Soal
1. Misal : A = {1, 2, 3, 4}
R1 = {(1,1), (1,2), (2,1), (2,2), (2,4), (3,1), (3,4), (4,1), (4,4)} R2 = {(1,1), (1,2), (1,4), (2,1), (2,2), (3, 3), (4,1), (4,3)}
b) Gambarkan relasi R1 dalam bentuk matriks c) R1 x R2 = d) R1 ∩ R2 = e) R1 – R2 = f) R1 c⊕ R2 ∪ R1 c = 2. Misal : A = {1, 2, 3, 4} R1 = {(1,1), (1,2), (2,1), (2,2), (2,4), (3,3), (4,2), (4,4)} R2 = {(1,1), (1,2), (1,4), (2,1), (2,2), (3, 3), (4,1), (4,3)}
Sebutkan sifat relasi biner pada R1 dan R2.
3. Misal : A = {1, 2, 3, 4, 5, 6}
R1 = {(1,1), (1,2), (2,1), (2,2), (3,3), (3,5), (4,4), (5,3), (5,5), (6,6)}
GRAF
Graf G(V,E) didefinisikan sebagai pasangan himpunan (V,E), dengan V adalah
himpunan berhingga dan tidak kosong dari simpul-simpul (verteks atau node). Dan E adalah himpunan berhingga dari busur (vertices atau edge).
Contoh :
V = {v1, v2, v3, v4} E = {e1, e2, e3, e4, e5}
E = {(v1,v2), (v1,v2), (v1,v3), (v2,v3), (v3,v3)}
ISTILAH GRAF
Gelang (loop) yaitu busur yang berawal dan berakhir pada simpul yang sama.
Busur ganda (multiple edge) yaitu suatu busur yang menghubungkan simpul yang sama
Ketetanggaan (adjacent) : dua buah simpul dikatakan bertetangga, jika terdapat busur e dengan ujung awal dan akhir adalah v1 dan v2. ( e=(v1,v2) )
Kehadiran (incident) : suatu busur dikatakan hadir pada suatu simpul, jika busur tersebut menghubungkan simpul tersebut.
Derajat (degree) yaitu banyaknya busur yang ada pada suatu simpul v. ( d(v) )
Simpul terminal adalah simpul yang berderajat 1
Simpul terpencil adalah simpul yang berderajat 0, dan tidak bertetangga dengan simpul lain.
n = |V| = kardinalitas simpul
m = |E| = kardinalitas busur e4 e3 e2 e5 e1 V4 V3 V2 V1
MACAM GRAF
Graf dapat dikelompokkan menjadi beberapa kategori, yaitu : 1. Graf Kosong (Null graph)
Graf kosong adalah graf dengan himpunan busur merupakan himpunan kosong. Contoh :
● ● ● ●
N4
2. Graf Sederhana (simple graph)
Graf sederhana adalah graf yang tidak mempunyai gelang (loop) dan/atau sisi ganda (multiple edge)
Terdapat beberapa macam graf sederhana, yaitu : a) Graf lengkap (complete graph)
Graf lengkap adalah graf dengan setiap pasang simpulnya saling bertetangga, dengan jumlah busur (m) = (n.(n-1))/2.
Contoh :
b) Graf teratur (regular graph)
Graf teratur adalah graf yang semua simpul dalam graf trsebut berderajat sama, dengan jumlah busur (m) = (n.r)/2, dan r adalah nilai derajat simpul.
Contoh : K3
K4
c) Graf Lintasan (paths)
Graf lintasan adalah graf yang bentuknya menyerupai garis lurus, m=n-1. Contoh :
d) Graf lingkaran (Cycles)
Graf lingkaran adalah graf yang bentuknya menyerupai lingkaran, dengan m=n Dinotasikan dengan Cn
Contoh :
e) Graf Roda (Wheels)
Graf Roda adalah graf lingkaran yang setiap simpulnya dihubungkan dengan simpul di tengah lingkaran. Dinotasikan dengan Wn Contoh : W6 K3 K4 K5 P4 C2
3. Graf tidak sederhana (unsimple graph)
Graf tidak sederhana adalah graf yang mempunyai gelang (loop) dan/atau sisi ganda (multiple edge)
1. Graf Ganda (Multigraph) adalah graf yang mempunyai sisi ganda 2. Graf Semu (Pseudograph) adalah graf yang mempunyai gelang / loop
Contoh :
4. Graf dengan kekhususan tertentu 1. Graf Petersen
Graf Petersen adalah graf teratur yang mempunyai derajat simpul 3 pada semua simpulnya.
Contoh :
2. Graf Planar
Graf Planar adalah graf yang dapat digambarkan pada suatu bidang datar dengan busur-busur yang tidak saling memotong.
Contoh :
3. Graf Bipartite
Graf bipartite adalah graf G dengan himpunan simpulnya dapat dibedakan dan dipisahkan menjadi dua himpunan bagian, yaitu V1 dan V2, sedemikian sehingga
K4
K6 K4
setiap busur di G menghubungkan ke satu simpul di V1 ke satu simpul di V2, dengan kata lain setiap pasang simpul di V1 tidak bertetangga, dan setiap pasang simpul di V2 juga tidak bertetangga.
Dinotasikan Sebagai G(V1, V2) ↔ Kn,m
Jika setiap simpul di V1 bertetangga dengan semua simpul di V2, maka disebut graf bipartite lengkap (complete bipartite graph)
Contoh :
4. Graf Berarah (Directed graph)
Graf berarah adalah graf yang semua busurnya mempunyai arah. Contoh :
5. Graf Berbobot (Weighted graph)
Graf berbobot adalah graf yang setiap sisinya diberi sebuah harga (bobot) tertentu. Contoh : 6 7 4 10 4 8 e d b a K2,3 K2,3 c
Graf Tidak Sederhana 1. Graf Ganda (multigraph)
Graf yang mempunyai sisi ganda 2. Graf Semu (pseudograph)
Graf yang mempunyai gelang/loop Representasi Graf dalam bentuk Matriks 1. Matriks Adjacent
Msimpul x simpul
2. Matriks Incident
Isimpul x busur
Isomorfisma
Isomorfik adalah dua buah benda yang sama tetapi secara geometri bersifat berbeda. Dua buah graf G1 dan G2 dikatakan mempunyai isomorfisma (isomorfiks), jika terdapat pemetaan satu-satu antara simpul-simpul di G1 dan simpul-simpul di G2, dan dipenuhinya syarat : (1) jumlah busur masing graf sama, (2) jumlah node masing-masing graf sama, (3) terdapat kesesuaian antara busur-busur di dalam kedua graf tersebut
Contoh : G1 G4 G2 G3 G5 G6
Graf Komplemen
Komplemen graf (Gc) adalah suatu graf sederhana dengan simpul yang sama dengan himpunan simpul graf G, dan memenuhi syarat bahwa dua buah simpul di Gc bertetangga, jika dan hanya jika kedua simpul tidak bertetangga di G, sehingga Gc dan G akan membentuk
graf lengkap Contoh :
LINTASAN
Sederetan busur atau simpul atau busur dan simpul secara berselang seling yang membentuk sambungan yang tidak putus pada graf G.
Macam Lintasan 1. Lintasan Sederhana
Lintasan yang setiap simpul yang dilalui berbeda 2. Lintasan Tertutup
Lintasan yang berawal dan berakhir di simpul yang sama 3. Lintasan Terbuka
Lintasan yang berawal dan berakhir di simpul berbeda
Jalan (walk) adalah sederetan busur-busur yang membentuk sambungan yang tidak putus di G
K2,3 Komplemen K2,3
Lintasan (path) adalah sederetan busur dan simpul berselang-seling dari simpul awal v0 ke simpul akhir vn, sedemikian sehingga e1 = (v0,v1), e2 = (v1,v2), …, en=(vn-1,vn), adalah
busur-busur dalam graf.
Panjang suatu lintasan adalah banyaknya busur-busur pada jalan tersebut.
Penulisan lintasan pada graf sederhana, hanya menuliskan simpul-simpul yang dilalui, sedangkan pada graf dengan sisi ganda, harus menuliskan urutan busur dan simpul secara berselang-seling sesuai dengan jalan yang dilalui.
Lintasan sederhana adalah lintasan yang setiap simpul yang dilalui berbeda (atau setiap busur yang dilalui hanya satu kali).
Lintasan tertutup (closed path) adalah lintasan yang berawal dan berakhir pada simpul yang sama.
Lintasan terbuka (open path) adalah lintasan yang berawal dan berakhir pada simpul yang berbeda.
Contoh :
Jalan antara v1 dan v4 di G1: e3 atau e1-e2-e4-e7 atau e1-e6-e7
Lintasan v1 dan v4 di G1: e3 atau e1-e2-e4-e7 atau e1-e6-e7
Lintasan v1 dan v4 di G2: e3 atau e1-v5-e2-v2-e4-e2-v3-e7 atau e1- v5-e6-v3-e7
Lintasan sederhana : v1- v5-v3-v4
Lintasan tertutup : v1- v5-v2-v3-v4-v1
Lintasan terbuka : v1- v5-v2-v3-v4
Definisi Keterhubungan dalam graf :
Suatu graf G disebut terhubung (connected) apabila setiap pasang simpul sembarang, misal: u dan v, di G mempunyai suatu lintasan dari simpul u menuju simpul v.
Lintasan tertutup adalah lintasan dengan simpul awal dan simpul akhir lintasan sama (u=v). Contoh: e7 e6 e4 e3 e2 e1 V3 V2 V1 V4 V5 e5 G1 e9 e8 e8 V2 e7 e6 e4 e3 e2 e1 V3 V1 V4 V5 e5 G2
Graf G1 adalah graf terhubung, sedangkan G2 merupakan graf tidak terhubung (disconnected graf)
Graf Euler
Lintasan Euler adalah lintasan yang melalui masing-masing busur dalam graf tepat satu kali. Bila lintasan tersebut kembali ke simpul asal, membentuk lintasan tertutup, maka lintasan itu
dinamakan sirkuit Euler.
Graf yang mempunyai sirkuit Euler dinamakan graf Euler, dan graf yang mempunyai lintaan Euler dinamakan graf semi-Euler.
Graf Hamilton
Lintasan Hamilton adalah lintasan yang melalui setiap simpul di dalam graf tepat satu kali. Bila lintasan itu kembali ke simpul awal dan membentuk lintasan tertutup maka disebut
sirkuit Hamilton
Graf yang memiliki sirkuit Hamilton dinamakan graf Hamilton, sedangkan graf yang memiliki lintasan Hamilton disebut graf semi Hamilton.
G1 G2 G3 G1 G2 G3 e7 e6 e4 e3 e2 e1 V3 V2 V1 V4 V5 e5 G1 V2 e6 e4 e2 e1 V3 V1 V4 V5 G2
APLIKASI GRAF
MENCARI JARAK TERPENDEK (SHORTEST PATH)
Banyak permasalahan transportasi dimodelkan sebagai bentuk graf, yaitu graf yang mempunyai berat ( weighted graf). Kota digambarkan sebagai simpul, hubungan antar kota digambarkan sebagai busur, dan jarak antar kota sebagai berat dari gambar.
Algoritma Djikstra
Terdapat beberapa algoritma untuk mencari jalur terpendek, diantaranya adalah yang dikemukakan oleh E. Djikstra pada tahun 1959. Algoritma ini digunakan untuk mencari jalur terpendek yang menghubungkan dua buah simpul dalam suatu graf, sehingga sering disebut single pair’s shortest path. Langkah-langkah yang digunakan sebagai berikut :
a) Iterasi pertama, simpul awal = vi, beri label untuk simpul yang lain, yaitu :
1. Jika simpul vj dengan j∈{ v1, v2, v3, .., vn}terhubung dengan vi oleh suatu busur (vi, vj), maka label untuk vj = d(vj)= panjang busur tersebut
2. Jika vj tidak terhubung dengan vi maka d(vi) = ∞
b) Iterasi kedua, pilih simpul dengan label minimum dari hasil iterasi pertama sebagai simpul awal, label untuk setiap simpul lain ditentukan dengan membandingkan nilai labelnya dengan jumlah nilai label simpul awal ditambahkan dengan panjang busur antara simpul awal dengan simpul tersebut, atau :
d’(vk) = min{d(vk), d(vj)+a(vj, vk)}
dengan vj : simpul awal
vk : simpul yang dicari labelnya d’(vk) : nilai label yang baru
d(vk) : nilai label hasil iterasi sebelumnya d(vj) : nilai label hasil iterasi sebelumnya a(vj,vk) : panjang busur
Contoh :
Penyelesaian : Iterasi 1
Posisi awal di simpul a.
d(a) = 0, d(b) = 4, d(c) = 3, d(d) = 7, d(e) = ∞, d(f) = ∞, Minimum di c, maka jalur yang didapat (a,c)
Iterasi 2
Posisi awal di c
d(b) = min {d(b), d(c)+ a(c, b)} = min {4, 3+∞} = 4 d(d) = min {d(d), d(c)+ a(c, d)} = min {7, 3+∞} = 7 d(e) = min {d(e), d(c)+ a(c, e)} = min {∞, 3+3} = 6 d(f) = min {d(f), d(c)+ a(c, f)} = min {∞, 3+∞} = ∞
Minimum di b, jalur yang didapat (a, b) Iterasi 3
Posisi awal di b
d(d) = min {d(d), d(b)+ a(b, d)} = min {7, 4+4} = 7 d(e) = min {d(e), d(b)+ a(b, e)} = min {6, 4+2} = 6 d(f) = min {d(f), d(b)+ a(b, f)} = min {∞, 4+∞} = ∞
Minimum di e, jalur yang didapat (b, e) atau (c, e) Iterasi 4
Posisi awal di e
d(d) = min {d(d), d(e)+ a(e, d)} = min {7, 6+∞} = 7 d(f) = min {d(f), d(e)+ a(e, f)} = min {∞, 6+5} = 11 Minimum di d, jalur yang didapat (a, d)
d 4 b 4 7 3 c 3 2 e 5 f 2 a
Iterasi 5
Posisi awal di d
d(f) = min {d(f), d(d)+ a(d, f)} = min {11, 7+2} = 9 Minimum di f, Iterasi dihentikan, jalur yang didapat (d, f) Maka jalur terpendek dari a ke f adalah {(a, d), (d, f)} dengan panjang 9. Algoritma Djikstra
Procedure Djikstra (G: berat graf terhubung, dengan semua berat graf positif)
{G mempunyai busur a=v0, v1, ..,vn dan berat w(vi,vj) = ∞, jika (vi,vj) tidak terhubung dengan busur lain} for i:=1 to n
L(vi):= ∞ L(a):=0 S:={}
{simpul telah diinisialisasi sehingga simpul a adalah kosong dan simpul lainnya adalah ∞, dan S adalah himpunan kosong}
while z ∉S begin
u:=a simpul tidak ada dalam S dengan L(u) minimal S :=S ∪{u}
For semua busur v tidak ada dalam S If L(u)+w(u,v) < L(v) then L(v) :=L(u)+w(u,v)
{menambahkan simpul ke S dengan nilai minimal dan mengubah nilai busur yang tidak berada di S}
end. {Lz)=panjang dari jalur terpendek dari a ke z}
Algoritma Floyd
Algoritma yang juga sering digunakan untuk menentukan panjang jalur terpendek untuk setiap pasangan simpul adalah algoritma Floyd, sering disebut dengan all pair’s shortest path algoritma. Langkah-langkah dalam algoritma Floyd :
a) Setiap simpul diberi nomor dari 1, 2, .., n. Susun matriks D0 yang masing-masing elemennya menunjukkan panjang busur terpendek yang menghubungkan simpul tersebut. (elemen i, j menunjukkan panjang busur terpendek yang menghubungkan vi dengan vj). Jika tidak ada busur yang menghubungkan vi dengan vj, maka d0ij = ∞ dan d0
ii = 0
b) Lakukan iterasi sebanyak n kali dimana setiap iterasi disusun matrik Dm(m∈{1,2,..,n}) dari matriks Dm-1 dengan rumus :
c) Catat setiap jalur yang didapat dari setiap iterasi. Akhiri iterasi setelah m=n, sehingga Dn menunjukkan panjang jalur terpendek yang menghubungkan simpul I dengan simpul j. Contoh : Penyelesaian : Iterasi 0 Matriks d0 = 0 4 3 7 ∞ ∞ 4 0 ∞ 4 2 ∞ 3 ∞ 0 ∞ 3 ∞ 7 4 ∞ 0 ∞ 2 ∞ 2 3 ∞ 0 5 ∞ ∞ ∞ 2 5 0 Iterasi 1 Matriks d1 = 0 4 3 7 ∞ ∞ 4 0 7 4 2 ∞ 3 7 0 10 3 ∞ 7 4 10 0 ∞ 2 ∞ 2 3 ∞ 0 5 ∞ ∞ ∞ 2 5 0 Iterasi 2 Matriks d2 = 0 4 3 7 6 ∞ 4 0 7 4 2 ∞ 3 7 0 10 3 ∞ 7 4 10 0 6 2 6 2 3 6 0 5 ∞ ∞ ∞ 2 5 0 d 4 b 4 7 3 c 3 2 e 5 f 2 a
Iterasi 3 Matriks d3 = 0 4 3 7 6 ∞ 4 0 7 4 2 ∞ 3 7 0 10 3 ∞ 7 4 10 0 6 2 6 2 3 6 0 5 ∞ ∞ ∞ 2 5 0 Iterasi 4 Matriks d4 = 0 4 3 7 6 9 4 0 7 4 2 6 3 7 0 10 3 12 7 4 10 0 6 2 6 2 3 6 0 5 9 6 12 2 5 0 Iterasi 5 Matriks d5 = 0 4 3 7 6 9 4 0 7 4 2 6 3 7 0 9 3 8 7 4 9 0 6 2 6 2 3 6 0 5 9 6 8 2 5 0 Iterasi 6 Matriks d6 = 0 4 3 7 6 9 4 0 7 4 2 6 3 7 0 9 3 8 7 4 9 0 6 2 6 2 3 6 0 5 9 6 8 2 5 0 Soal
Carilah jarak terpendek dari a ke z dengan algoritma Floyd dan Djikstra, dan tuliskan jalurnya.
Tugas Matematika Diskret
1. Diketahui sejumlah pernyataan sebagai berikut : p : Isi kuliahnya menarik
q : Soal-soal latihannya menantang r : Kuliahnya menyenangkan
Terjemahkan kalimat majemuk tersebut ke dalam notasi simbolik :
a) jika isi kuliahnya tidak menarik dan soal-soal latihannya tidak menantang, maka kuliahnya tidak enak.
b) Isi kuliahnya menarik jika dan hanya jika soal-soal latihannya menantang dan kuliahnya menyenangkan.
Buatlah kalimat majemuknya berdasarkan notasi simbolik berikut : a) ~p ↔ ~r V ~q
b) ~(p ∧q) V (~q V r)
2. Gambarkan tabel kebenaran dari pernyataan berikut : p ∧ (q V r) ) ⇔ (p ∧ q) V (q ∧ r) 3. Diketahui : S = {x | 0 < x < 15}
A = {x | x < 15, x ∈ bilangan prima} B = { x | x < 15, x ∈ bilangan asli genap} C = { x | 3x – 2 < 30, x ∈ bilangan asli} D = { 1, 4, 7, 10, 12, 13}
Tentukan himpunan berikut : a) Ac ∩ (C – B) =
b) Ac ⊕ ((D ∪ C) – B) =
4. Diantara 50 mahasiswa di dalam kelas, 26 memperoleh nilai A dari ujian pertama dan 21 orang memperoleh nilai A dari ujian kedua. Jika 17 mahasiswa tidak memperoleh nilai A dari ujian pertama maupun ujian kedua, berapa banyak mahasiswa yang memperoleh dua kali nilai A dari ujian kedua itu ?, gambarkan diagram Venn-nya.
5. Diketahui himpunan bilangan 1 antara 1 s.d 100, berapa banyak bilangan yang tidak habis dibagi 2 dan 5. Gambarkan diagram Venn-nya. (Yang dimaksud habis dibagi adalah hasil pembagian merupakan bilangan bulat dan bukan pecahan).
6. P(n,r) = 840
7. Diketahui suatu himpunan A = {0, 1, 2, 4, 5, 6, 7, 9}. Dari himpunan tersebut dapat dibentuk angka yang terdiri dari 5 digit dengan ketentuan merupakan bilangan genap yang berada diantara 30000 s/d 80000.
8. Tentukan rumus untuk menghitung ½ + ¼ + 1/8 + .. + 1/(2n) dengan memeriksa nilai-nilai ekspresi untuk n yang lebih kecil, kemudian induksi matematika untuk membuktikan hal itu.
9. Untuk tiap relasi pada A = {1, 2, 3, 4}, tentukan apakah relasi tersebut reflexif, setangkup, tak setangkup dan menghantar.
a) {(2,2), (2,3), (2,4), (3,2), (3,3), (3,4)} b) {(2,4), (4,2)} c) {(1,1), (2,2), (3,3), (4,4)} d) {(1,3), (1,4), (2,3), (2,4), (3,1), (3,4)} 10.Diketahui A = {1, 2, 3, 4, 5}, R = {(1,1), (1,2), (2,1), (2,2), (3,3), (4,4), (5,5)} Tentukan a/[R].