i
REGRESI PIECEWISE UNTUK MASALAH INTERVENSI
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun oleh :
DIMAS ADI SETIAWAN
NIM : 093114011
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
v
HALAMAN PERSEMBAHAN
Tulisan ini dipersembahkan untuk Orang tua, sahabat, teman, dan orang yang
selalu mendukung dalam proses penulisan.
Teruntuk :
TUHAN YESUS KRISTUS yang selalu ada di saat penulis membutuhkan
pertolongan-Nya.
Ibu Lusia Luveniasmi dan Bapak Ambrosius Sarjono yang telah membesarkan,
mendidik dengan penuh cintak kasih, kesabaran dan doa,…
Cosmas Jerry Anggoro yang telah menemani dalam proses penulisan skripsi ini,
vi
ABSTRAK
Regresi piecewise merupakan pengembangan dari model regresi linier sederhana ke dalam model regresi linier berganda yang menggunakan variabel dummy. Regresi piecewise adalah salah satu model regresi linier berganda yang cocok untuk masalah data pada jangkauan nilai variabel yang berbeda. Pada model regresi piecewise terdapat breakpoint yang digunakan untuk menentukan garis regresi untuk setiap perubahan kemiringan pada fungsi linier. Model regresi piecewise dengan k breakpoint dapat dituliskan sebagai berikut:
𝑌𝑖 = 𝛼1+ 𝛽1𝑋𝑖 + 𝛽2(𝑋𝑖 − 𝑋1∗)𝐷1𝑖+ 𝛽3(𝑋𝑖 − 𝑋2∗)𝐷2𝑖+ ⋯ + 𝛽𝑘(𝑋𝑖 − 𝑋𝑘−1∗ )𝐷𝑘𝑖 + 𝑢𝑖
𝐷1𝑖 = {1, 𝑗𝑖𝑘𝑎 𝑋𝑖 > 𝑋1 ∗ 0, 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
𝐷2𝑖 = {1, 𝑗𝑖𝑘𝑎 𝑋0, 𝑙𝑎𝑖𝑛𝑛𝑦𝑎𝑖 > 𝑋2∗
⋮
𝐷𝑘𝑖 = {1, 𝑗𝑖𝑘𝑎 𝑋0, 𝑙𝑎𝑖𝑛𝑛𝑦𝑎𝑖 > 𝑋𝑘−1∗
vii
ABSTRACT
Piecewise regression is a development of the simple linear regression model to the multiple linear regression model using dummy variables. Piecewise regression is one of multiple linear regression model that appropriate for different range of variable values. In piecewise regression model there are breakpoints that are used to determine the slope of the regression for each change in linear functions. Piecewise regression models contain k breakpoints can be written as follows:
𝑌𝑖 = 𝛼1+ 𝛽1𝑋𝑖 + 𝛽2(𝑋𝑖 − 𝑋1∗)𝐷1𝑖+ 𝛽3(𝑋𝑖 − 𝑋2∗)𝐷2𝑖+ ⋯
+ 𝛽𝑘(𝑋𝑖 − 𝑋𝑘−1∗ )𝐷𝑘𝑖 + 𝑢𝑖
𝐷1𝑖 = {1, 𝑋𝑖 > 𝑋1 ∗
0, 𝑜𝑡ℎ𝑒𝑟𝑠
𝐷2𝑖 = {1, 𝑋𝑖 > 𝑋2 ∗
0, 𝑜𝑡ℎ𝑒𝑟𝑠
⋮
𝐷𝑘𝑖 = {1, 𝑋𝑖 > 𝑋𝑘−1 ∗
0, 𝑜𝑡ℎ𝑒𝑟𝑠
Assumptions in multiple regression can be used to test the piecewise regression model, except no multicollinearity assumption because there is only one independent variable in the model.
viii
KATA PENGANTAR
Segala puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus, Guru Yang Agung atas petunjuk dan pertolongan-Nya sehingga penulis dapat menyelesaikan skripsi ini.
Skripsi ini penulis susun untuk memenuhi salah satu syarat memperoleh gelar Sarjana Program Studi Matematika, Jurusan Matematika, Fakultas Sains dan Teknologi di Universitas Sanata Dharma Yogyakarta.
Dalam proses penyusunan skripsi ini ada banyak kesulitan dan hambatan yang penulis alami. Namun dengan bantuan berbagai pihak semua kesulitan dan hambatan tersebut dapat teratasi dengan baik. Untuk itu, pada kesempatan ini penulis dengan penuh ketulusan ingin mengucapkan terima kasih kepada :
1. Ir. Ig. Aris Dwiatmoko, M.Sc, selaku Dosen pembimbing yang telah membimbing dengan sabar dan memberikan masukan dan koreksi yang sangat bermanfaat selama proses penyusunan skripsi ini.
2. Paulina Heruningsih Prima Rosa, S.Si., M.Sc., selaku Dekan Fakultas Sains dan Teknologi.
ix
4. Y. G. Hartono, S.Si., M.Sc., selaku Dosen penguji yang telah memberikan masukan-masukan dan koreksi.
5. Ch. Enny Murwaningtyas, S.Si., M.Si, selaku Dosen penguji yang telah memberikan masukan-masukan dan koreksi.
6. Bapak dan Ibu Dosen Program Studi Matematika yang telah memberikan ilmu yang berguna kepada penulis.
7. Bapak Zaerilus Tukija, Bapak Ignatius Tri Widaryanta, dan Ibu Erna Linda Santyas Rahayu yang telah memberikan pelaayanan administrasi selama penulis kuliah.
8. Perpustakaan Universitas Sanata Dharma yang memberikan fasilitas dan kemudahan kepada penulis.
9. Ibu Lusia Luveniasmi, Bapak Ambrosius Sarjono yang selalu mendoakan anak-anaknya dimanapun berada dan Cosmas Jerry Anggoro yang selalu menemani saat penulis mengerjakan skripsi ini. Luciana Putri Renliastuti yang selalu memberikan semangat kepada penulis.
10.Teman-teman program matematika angkatan 2009: Sekar, Yohana, Erlika, Ida, Etik, Doweek, Jojo,Ochi dan angkatan 2008: Etus, Moyo, Widi terima kasih atas segala bantuan, dukungan dan kebersamaannya selama ini.
xii
DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN KEASLIAN KARYA ... v
HALAMAN PERSEMBAHAN... vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI ... xii
DAFTAR ISI ... xiii
DAFTAR GAMBAR ... xvii
xiii
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 4
C. Tujuan Penulisan ... 4
D. Batasan Masalah... 4
E. Manfaat Penulisan ... 5
F. Sistematika Penulisan ... 5
BAB II REGRESI BERGANDA ... 7
A. Model Regresi Berganda ... 7
B. Model Linier ... 8
1. Linier dalam variabel ... ... 9
2. Linier dalam parameter ... ... 9
C. Pendugaan Model Regresi ... 10
D. Matriks Variansi-Kovariansi dari 𝛽̂ ... 13
E. Koefisien Determinasi (R2) ... 15
F. Asumsi-asumsi dalam Regresi ... 20
1. Tidak ada heteroskedastisitas ... ... 20
2. Tidak ada otokorelasi ... ... 23
3. Tidak ada multikolinieritas ... ... 26
xiv
G. Regresi dengan Variabel Dummy ... ... 36
H. Masalah Intervensi ... ... 39
BAB III REGRESI PIECEWISE ... .. 42
A. Pengantar ... 42
B. Model Regresi Piecewise ... 45
1. Model regresi piecewise untuk satu breakpoint ... 46
2. Model regresi piecewise untuk dua breakpoint ... 46
3. Model regresi piecewise untuk k breakpoint ... .. 47
C. Asumsi Regresi Piecewise ... 49
1. Kebebasan galat ... 49
2. Kenormalan galat ... 50
3. Galat memiliki variansi homogen ... 51
D. Potensi Pencilan (Outlier) ... 53
E. Pendugaan Model Regresi Piecewise ... 60
F. Pengujian Model Regresi Piecewise ... 67
1. Kebebasan galat (tidak ada otokorelasi) ... 67
2. Kenormalan galat ... 68
3. Galat memiliki variansi homogen ... 69
BAB IV APLIKASI REGRESI PIECEWISE ... 71
xv
B. Contoh 4.1 ... 72
C. Menentukan Titik Patahan (breakpoint) ... 72
D. Menentukan Model Regresi Piecewise ... 74
1. Persamaan garis regresi sebelum titik ke 12 ... 74
2. Persamaan garis regresi antara titik ke 13-64 ... ... 74
3. Persamaan garis regresi antara titik ke 65-87 ... 75
4. Persamaan garis regresi setelah titik ke 87 ... 75
E. Menentukan Model Regresi Piecewise yang Kontinu Pada Breakpoint ... 75
1. Mencari titik 𝑋1∗... 76
a. Menentukan persamaan garis regresi sebelum titik ke 14 .... 76
b. Menentukan persamaan garis regresi antara titik ke 15-64... 77
2. Mencari titik 𝑋2∗... 77
3. Mencari titik 𝑋3∗... 78
a. Menentukan persamaan garis regresi pada titik 65-89... 78
b. Menentukan persamaan garis regresi antara titik 90-108... 79
F. Menentukan Model Regresi Piecewise ... 80
G. Pengujian Model Regresi Piecewise ... . 81
1. Kebebasan galat (tidak ada otokorelasi) ... 82
2. Tidak ada Heteroskedastisitas ... 83
xvi
H. Potensi Outlier ... 87 I. Pengggunaan Model untuk mepredikisi... 88 J. Contoh 4.2 ... 90
BAB V PENUTUP
A. Kesimpulan... 101 B. Saran... 101
DAFTAR PUSTAKA
xvii
DAFTAR GAMBAR
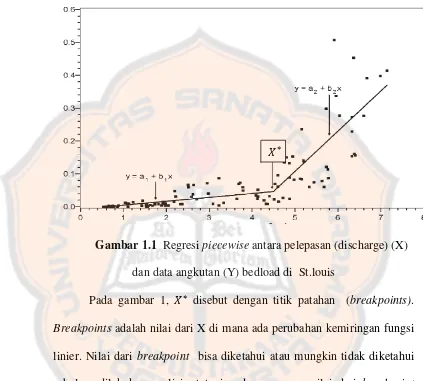
Gambar 1.1 Regresi piecewise antara pelepasan (discharge) (X) dan data angkutan
(Y) bedload di St.louis ... 3
Gambar 2.1 Homoskedastisitas ... 20
Gambar 2.2 Heteroskedastisitas ... 21
Gambar 2.3 Grafik Saham... 40
Gambar 3.1 Hubungan antara penjualan tiket (Y) pada saat hari biasa dengan saat mendekati liburan (X) ... 43
Gambar 3.2 Hubungan kurs rupiah terhadap USD ... 44
Gambar 3.3 Scatterplot galat tidak normal ... 51
Gambar 3.4 Scatterplot galat normal ... 58
Gambar 3.5 Galat bersifat homogen ... 52
Gambar 3.6 Galat tidak bersifat homogen ... 53
Gambar 3.7 Scatterplot data contoh 3.1 ... 57
Gambar 3.8 Scatterplot data simulasi Regresi Piecewise ... 62
Gambar 4.1 Grafik Kurs Rupiah ... 72
Gambar 4.2 Garis hubungan persamaan garis regresi ... 87
xviii
DAFTAR TABEL
Tabel 2.1 Perhitungan statistik uji Kolmogorov-Smirnov ... 31
Tabel 3.1 Data simulasi ... 57
Tabel 3.2 Data simulasi 0-7 ... 61
Tabel 3.3 Data simulasi 8-14 ... 61
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Peramalan erat kaitannya dengan statistika. Terdapat dua jenis model peramalan yang utama, yaitu: model deret berkala (time series) dan model regresi (kausal). Tujuan model peramalan deret berkala adalah menemukan pola dalam deret data, mengekstrapolasikan pola dalam data dan mengekstrapolasikan pola tersebut ke masa depan. Model regresi mengasumsikan bahwa faktor yang diramalkan menunjukkan suatu hubungan sebab-akibat dengan satu atau lebih variabel bebas. Tujuan dari model regresi adalah menemukan bentuk hubungan tersebut dan menggunakannya untuk meramalkan nilai mendatang dari variabel tak bebas. Analisis regresi berfokus pada pembelajaran yang berkaitan dengan satu variabel, variabel tak bebas, satu atau lebih variabel tak bebas, variabel explanatory, dengan maksud untuk menaksir atau meramalkan nilai rata-rata hitung atau nilai rata-rata variabel tak bebas. Analisis regresi juga digunakan untuk menganalisis hubungan antar variabel. Hubungan tersebut dapat ditulis dalam model persamaaan yang menghubungkan variabel tak bebas Y dengan satu atau lebih variabel bebas X.
yang terdapat hubungan variabel tak bebas Y dengan satu varibel bebas X. Model regresi berganda adalah model yang terdapat hubungan antara variabel tak bebas Y dengan lebih dari satu variabel bebas X. Model regresi berganda dapat memuat variabel dummy, yaitu variabel yang bersifat kualitatif. Variabel ini tidak bisa diukur, maka yang dapat dilakukan adalah memberikan nilai yang berfungsi sebagai atribut atau kategori misalnya 0 dan 1.
yang berbeda (Ryan, Sandra E.; Porth, Laurie S. 2007). Pada gambar di bawah ini diberikan contoh penerapan regresi piecewise.
Gambar 1.1 Regresi piecewise antara pelepasan (discharge) (X) dan data angkutan (Y) bedload di St.louis
Pada gambar 1, 𝑋∗ disebut dengan titik patahan (breakpoints). Breakpoints adalah nilai dari X di mana ada perubahan kemiringan fungsi linier. Nilai dari breakpoint bisa diketahui atau mungkin tidak diketahui sebelum dilakukan analisis, tetapi pada umumnya nilai dari breakpoint tidak diketahui dan harus dilakukan estimasi parameter. Fungsi regresi pada breakpoint mungkin tidak kontinu, tetapi model dapat ditulis sedemikian sehingga fungsi itu kontinu pada semua titik termasuk breakpoint.
B. Rumusan Masalah
Berdasarkan uraian di atas, maka permasalahan dalam tugas akhir ini adalah sebagai berikut:
1. Apa yang dimaksud dengan masalah intervensi 2. Apa yang dimaksud dengan regresi piecewise?
3. Bagaimana menerapkan regresi piecewise dalam analisis regresi yang mengandung unsur-unsur intervensi?
C. Tujuan Penulisan
Berdasarkan rumusan masalah di atas, tujuan dari penulisan tugas akhir ini adalah sebagai berikut:
1. Memahami apa yang dimaksud dengan regresi piecewise.
2. Dapat menggunakan regresi piecewise dalam analisis regresi yang mengandung unsur-unsur intervensi.
D. Batasan Masalah
Agar penulisan mencapai tujuan yang dimaksud, maka perlu ada batasan mengenai permasalahan yang diangkat. Adapun batasan masalahnya adalah sebagai berikut:
2. Tidak semua materi prasayarat regresi dibahas secara rinci kecuali untuk beberapa topik yang berhubungan langsung dengan regresi piecewise.
E. Manfaat Penulisan
Adapun manfaat yang diharapkan penulis dalam tugas akhir ini adalah sebagai berikut:
1. Mengetahui bahwa analisis regresi juga dapat dipengaruhi oleh adanya pengaruh dari luar.
2. Dapat memberi masukan kepada para pengambil keputusan terkait dengan masalah adanya pengaruh dari luar dalam analisis regresi.
F. Sistematika Penulisan
BAB I Pendahuluan
A. Latar Belakang Masalah B. Rumusan Masalah C. Tujuan Penulisan D. Pembatasan Masalah E. Manfaat Penulisan F. Sistematika Penulisan
BAB II Analisis Regresi
C. Penduga Model Regresi
D. Matriks Variansi-Kovariansi dari 𝜷̂ E. Koefisien Determinasi (R2)
F. Pengujian Hipotesis
G. Asumsi-asumsi dalam Regresi H. Regresi dengan Variabel Dummy I. Masalah Intervensi
BAB III Regresi Piecewise
A. Pengantar
B. Model Regresi Piecewise
C. Asumsi-asumsi Regresi Piecewise D. Potensi Outlier
E. Pendugaan Model Regresi Piecewise F. Pengujian Hipotesis Regresi Piecewise
BAB IV Aplikasi Regresi Piecewise
A. Data
B. Model Regresi Piecewise C. Analisis Regresi Piecewise
BAB V Penutup
BAB II
ANALISIS REGRESI
Bagian ini hanya membahas regresi berganda beserta penduganya, pendugaan model regresi, matrik variansi-kovariansi, koefisien determinasi, regresi dengan variabel dummy, masalah intervensi, dan asumsi-asumsi dalam model regresi.
A. Model Regresi Berganda
Model regresi berganda merupakan model yang menggambarkan hubungan antara satu variabel tak bebas Y dengan beberapa variabel bebas 𝑋2, … , 𝑋𝑘. Persamaan Fungsi Regresi Populasi (FRP) k-variabel meliputi hubungan antara variabel tak bebas Y dengan k-variabel bebas 𝑋2, … , 𝑋𝑘, dapat ditulis sebagai berikut:
𝑌𝑖 = 𝛽1 + 𝛽2𝑋2𝑖+ 𝛽3𝑋3𝑖+ ⋯ + 𝛽𝑘𝑋𝑘𝑖+ 𝑢𝑖 (2.1)
di mana,
𝑌𝑖 : variabel tak bebas
𝛽1 : konstanta
𝛽𝑗 : koefisien regresi dari variabel bebas ke-j
𝑋𝑗𝑖 : nilai variabel bebas ke-j pada pengamatan ke-i
𝑢𝑖 : galat (error) ke-i
Salah satu cara menduga parameter regresi berganda adalah dengan menggunakan pendekatan matriks. Model pada persamaan (2.1) dapat ditulis dalam bentuk matriks, sebagai berikut:
[
Persamaan (2.2) dapat ditulis dalam notasi matriks sebagai berikut:
𝒚 = 𝑿𝜷 + 𝒖 (2.3)
di mana,
𝒚 : vektor kolom n x 1dari variabel tak bebas 𝑿 : matriks n x k dari variabel bebas dan konstanta
𝜷 : vektor kolom k x1 dari parameter yang tidak diketahui 𝒖 : vektor kolom n x 1 dari galat
B. Model Linier
1. Linier dalam variabel
Penafsiran linieritas ini mengisyaratkan bahwa nilai harapan bersyarat, 𝐸(𝑌|𝑋𝑖) adalah fungsi linier dari variabel bebas, 𝑋𝑖. Contoh model yang bukan linier dalam variabel: 𝐸(𝑌|𝑋𝑖) = 𝛽1+ 𝛽2𝑋𝑖2. Persamaan tersebut bukan merupakan fungsi linier sebab variabel bebas X berpangkat dua. Dengan kata lain, suatu fungsi dikatakan linier dalam variabel, jika 𝑋𝑖 hanya berpangkat satu.
2. Linier dalam parameter
Penafsiran linieritas ini mengisyaratkan bahwa nilai harapan, E(Y|X), adalah fungsi linier dari parameter 𝛽𝑖, jika 𝛽𝑖 nampak hanya dengan pangkat satu dan tidak dikalikan atau dibagi dengan parameter lain. Contoh model yang bukan merupakan fungsi linier dalam parameter: 𝐸(𝑌|𝑋𝑖) = 𝛽1 + 𝛽2𝛽3𝑋𝑖. Persamaan tersebut bukan fungsi linier dalam
parameter karena 𝛽2 berpangkat 𝛽3, tetapi fungsi tersebut linier dalam variabel bebas, 𝑋𝑖.
Istilah regresi linier sederhana ditunjukkan pada penggunaan satu variabel tak bebas sebagai fungsi linier dari satu variabel bebasnya. Secara umum, model regresi disimbolkan sebagai berikut ini:
𝐸(𝑌|𝑋𝑖) = 𝑓(𝑋𝑖) (2.4)
𝑓(𝑋𝑖) = 𝛽1+ 𝛽2𝑋𝑖 (2.5)
Dengan demikian, persamaan FRP dapat ditulis sebagai berikut ini:
𝐸(𝑌|𝑋𝑖) = 𝛽1+ 𝛽2𝑋𝑖 (2.6)
Pengertian dari persamaan (2.6) adalah nilai rata-rata bersyarat Y dengan X tertentu merupakan fungsi linier dari 𝑋𝑖, dan persamaan tersebut adalah Fungsi Regresi Populasi Linier atau FRP Linier. Dalam suatu model regresi akan ditentukan parameter yang tidak diketahui besarnya atau dikenal dengan parameter regresi, yaitu 𝛽1 dan 𝛽2, 𝛽1 adalah intersep dan 𝛽2 adalah koefisien kemiringan.
Persamaan regresi merupakan fungsi linier dalam parameter maupun variabel. Pada skripsi ini hanya dibahas model liner dalam parameter. Dapat dilihat dari persamaan (2.1), bahwa parameter dari persamaan regresi hanya berpangkat satu. Selain linier dalam parameter, persamaan (2.1) juga linier dalam variabel. Dapat dilihat bahwa variabel dalam persamaan regresi (2.1) hanya berpangkat satu.
C. Pendugaan Model Regresi
Persamaaan (2.3) dapat ditulis menjadi: 𝒚 = 𝑿𝜷̂ + 𝒖̂
𝒖̂ = 𝒚 − 𝑿𝜷̂ (2.7)
Dari persamaan (2.7) dapat juga ditulis sebagai barikut:
𝒖̂ = 𝒚 − 𝒚̂ (2.8) Sehingga pendugaan MKT dengan meminimumkan jumlah kuadrat galat dapat ditulis menjadi:
∑ 𝑢̂𝑖2 = (𝒚 − 𝑿𝜷̂)𝟐 (2.9)
Meminimunkan jumlah kuadrat galat ∑ 𝑢̂𝑛𝑖 𝑖2 sama dengan meminimumkan 𝒖̂𝑻𝒖̂ karena
𝜕(𝒖̂𝑻𝒖̂)
𝜕𝜷̂ = 0
𝜕(𝒚𝑻𝒚−𝟐(𝑿𝜷̂)𝑻𝒚+(𝑿𝜷̂)𝑻𝑿𝜷̂)
𝜕𝜷̂ = 0
𝜕𝒚𝑻𝒚
𝜕𝜷̂ −
2𝜕(𝑿𝜷̂)𝑻𝒚
𝜕𝜷̂ +
𝜕(𝑿𝜷̂)𝑻𝑿𝜷̂
𝜕𝜷̂ = 0
0- 𝟐𝑿𝑻𝒚 + 𝟐𝑿𝑻𝑿𝜷̂ = 0
𝟐𝑿𝑻𝑿𝜷̂= 𝟐𝑿𝑻𝒚
𝑿𝑻𝑿𝜷̂= 𝑿𝑻𝒚
𝜷̂= (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒚 (2.11)
D. Matriks Variansi-Kovariansi dari 𝜷̂
Perhitungan nilai variansi-kovariansi dari komponen-komponen vektor 𝜷̂ sangat berguna untuk pengambilan kesimpulan statistis (statistical inference). Definisi matriks variansi-kovariansi dari 𝛽̂ adalah:
Dari persamaan (2.14) 𝜎2 tidak diketahui, sehingga diduga dengan 𝜎̂2. Dalam kasus dua variabel dan tiga variabel penduga untuk 𝜎̂2 adalah
sebagai berikut:
𝜎̂2 = ∑ 𝑢̂𝑖2
𝑛 − 2 dan 𝜎̂2 = ∑ 𝑢̂𝑖2
𝑛 − 3
Pada kasus k-variabel penduga untuk 𝜎̂2 adalah sebagai berikut:
𝜎̂2 = ∑ 𝑢̂𝑖2
𝑛 − 𝑘 (2.15)
Dengan mengingat bahwa ∑ 𝑢̂𝑖2 = 𝒖̂𝑻𝒖̂, dimana 𝑢̂𝑖 = 𝑌𝑖 − 𝑌̂𝑖, maka 𝑌𝑖 = 𝑌̂𝑖 + 𝑢̂𝑖 .
Karena 𝒖̂𝑻𝒖̂ = 𝒚𝑻𝒚 − 𝟐(𝑿𝜷̂)𝑻𝒚 + (𝑿𝜷̂)𝑻𝑿𝜷̂dan (𝑿𝑻𝑿)𝜷̂ = 𝑿𝑻𝒚 maka 𝒖̂𝑻𝒖̂dapat ditulis menjadi:
𝒖̂𝑻𝒖̂ = 𝒚𝑻𝒚 − 𝟐(𝑿𝜷̂)𝑻𝒚 + (𝑿𝜷̂)𝑻𝑿𝜷̂
= 𝒚𝑻𝒚 − 𝟐𝜷̂𝑻𝑿𝑻𝒚 + 𝜷̂𝑻𝑿𝑻𝑿𝜷̂
= 𝒚𝑻𝒚 − 𝟐𝜷̂𝑻𝑿𝑻𝒚 + 𝜷̂𝑻𝑿𝑻𝒚
= 𝒚𝑻𝒚 − 𝜷̂𝑻𝑿𝑻𝒚 (2.16)
Dengan mensubtitusikan persamaan (2.16) ke dalam persamaan (2.15) maka diperoleh:
𝜎̂2 = 𝒚𝑻𝒚 − 𝜷̂𝑻𝑿𝑻𝒚
𝑛 − 𝑘
Jadi diperoleh rumus untuk mencari Var-cov(𝜷̂), yaitu:
Var-cov(𝜷̂) = 𝒚
𝑻𝒚−𝜷̂𝑻𝑿𝑻𝒚
E. Koefisien Determinasi (R2)
Setelah menentukan var-cov dari 𝜷̂, langkah selanjutnya adalah menentukan seberapa besar data dapat dijelaskan dengan model regresi. diberikan diagram Venn untuk memberikan gambaran mengenai konsep koefisien determinasi.
irisan antara variasi Y dan variasi X. Pada gambar diagram Venn menunjukkan bahwa irisan antara varisi Y dan variasi X meningkat, ini berarti meningkat pula proporsi variasi Y yang dapat dijelaskan oleh X. Ketika lingkaran Y dan lingkaran X berhimpit, ini dapat dikatakan bahwa nilai R2 =1, karena 100 persen dari variasi Y dapat dijelaskan oleh X. Sebaliknya, ketika lingkaran Y dan lingkaran X tidak berhimpit dan tidak beririsan, ini dapat dikatakan bahwa nilai R2 =0, artinya variasi Y tidak dapat dijelaskan oleh X.
Koefisien determinasi adalah koefisien yang menjelaskan besarnya persentase variansi Y yang dapat dijelaskan dengan model. Koefisien determinasi dapat digunakan untuk menentukan kebaikan model. Untuk menghitung 𝑅2, diberikan persamaan
𝑦𝑖 = 𝑦̂𝑖 + 𝑢̂𝑖 (2.18)
Dengan mengkuadratkan dan menjumlahkan persamaan (2.18), maka persamaan (2.18) dapat ditulis menjadi:
∑ 𝑦𝑖2 = ∑(𝑦̂𝑖+ 𝑢̂𝑖)2
= 𝛽̂22∑ 𝑥𝑖2+ ∑ 𝑢̂𝑖2, (2.19)
Sebelum membuktikan persamaan (2.19), selebihnya akan dibuktikan dahulu bahwa ∑ 𝑦̂𝑖𝑢̂𝑖 = 0 dan diberikan bahwa 𝑦̂𝑖 = 𝛽̂2𝑥𝑖 dan 𝛽̂2 = ∑ 𝑥𝑖𝑦𝑖⁄∑ 𝑥𝑖2, maka
= 𝛽̂2∑ 𝑥𝑖𝑢̂𝑖
= 𝛽̂2∑ 𝑥𝑖( 𝑦𝑖− 𝑦̂𝑖)
= 𝛽̂2∑ 𝑥𝑖( 𝑦𝑖− 𝛽̂2𝑥𝑖)
= 𝛽̂2∑ 𝑥𝑖𝑦𝑖 − 𝛽̂22∑ 𝑥𝑖2
= 𝛽̂22∑ 𝑥𝑖2− 𝛽̂22∑ 𝑥𝑖2
= 0
Setelah membuktikan ∑ 𝑦̂𝑖𝑢̂𝑖 = 0, selanjutnya akan dibuktikan untuk persamaan (2.19):
∑ 𝑦𝑖2 = ∑(𝑦̂
𝑖+ 𝑢̂𝑖)2
= ∑(𝑦𝑖2+ 2𝑦̂𝑖𝑢̂𝑖 + 𝑢̂𝑖2)
= ∑ 𝑦̂𝑖2+ 2 ∑ 𝑦̂𝑖𝑢̂𝑖 + ∑ 𝑢̂𝑖2 , ∑ 𝑦̂𝑖𝑢̂𝑖 = 0
= ∑ 𝑦̂𝑖2+ ∑ 𝑢̂𝑖2
= 𝛽̂22∑ 𝑥𝑖2+ ∑ 𝑢̂𝑖2 (2.20)
1. 𝛽̂22∑ 𝑥𝑖2 yang disebut sebagai jumlah kuadrat dari regresi atau jumlah kuadrat yang dapat dijelaskan oleh regresi (ESS) dan
2. ∑ 𝑢̂𝑖2 yang disebut sebagai jumlah kuadrat galat (RSS)
Dengan kata lain, komponen jumlah kuadrat total (TSS) dapat diuraikan menjadi ESS dan RSS, yaitu
TSS = ESS + RSS (2.21) Persamaan (2.21) dapat dipakai untuk mendefinisikan konsep koefisien determinasi, yaitu:
𝑅2 = ∑(𝑌̂𝑖 − 𝑌̅𝑖)2
∑(𝑌𝑖 − 𝑌̅𝑖)2,
= 𝐸𝑆𝑆
𝑇𝑆𝑆 (2.22)
Dalam notasi matrik TSS dan ESS dapat ditulis menjadi, TSS= ∑ 𝑦𝑖2 = ∑(𝑌𝑖 − 𝑌̅𝑖)2
∑ 𝑌𝑖2− ∑ 𝑌̅𝑖2
∑ 𝑌𝑖2− 𝑛 𝑌̅2
𝒚𝑻𝒚 − 𝑛𝑌̅2 (2.24)
= 𝛽̂22∑ 𝑥𝑖2
Dalam kasus tiga variabel diberikan 𝑌 = 𝛽1+ 𝛽2𝑋2𝑖+ 𝛽3𝑋3𝑖+ 𝑢𝑖, ESS dapat ditulis menjadi:
ESS = ∑(𝑌𝑖 − 𝑌̅𝑖)2
= 𝛽̂2∑ 𝑦𝑖𝑥2𝑖+ 𝛽̂3∑ 𝑦𝑖𝑥3𝑖
Dalam kasus k-variabel diberikan 𝑌 = 𝛽1+ 𝛽2𝑋2𝑖+ 𝛽3𝑋3𝑖+ ⋯ + 𝛽𝑘𝑋𝑘𝑖+ 𝑢𝑖, ESS dapat ditulis menjadi:
ESS = ∑(𝑌𝑖 − 𝑌̅𝑖)2
= 𝛽̂2∑ 𝑦𝑖𝑥2𝑖+ 𝛽̂3∑ 𝑦𝑖𝑥3𝑖+ ⋯ + 𝛽̂𝑘∑ 𝑦𝑖𝑥𝑘𝑖
= 𝜷̂𝑻𝑿𝑻𝒚 − 𝑛𝑌̅2
Secara umum koefisien determinasi (𝑅2) didefinisikan sebagai berikut: 𝑅2 = 𝐸𝑆𝑆
𝑇𝑆𝑆
= 𝜷̂𝑻𝑿𝑻𝒚 − 𝑛𝑌̅2 𝒚𝑻𝒚 − 𝑛𝑌̅2
Setelah menentukan koefisien determinasi 𝑅2, lanjutkan dengan pengujian hipotesis untuk menguji apakah ada pengaruh X terhadap Y.
Dalam menguji model regresi terdapat asumsi-asumsi berikut ini: 1. Tidak ada Heteroskedastisitas
2. Tidak ada Otokorelasi 3. Tidak ada Multikolinieritas 4. Kenormalan galat
Selanjutnya akan dijelaskan lebih lanjut mengenai asumsi-asumsi dalam regresi.
1. Tidak ada Heteroskedastisitas
Asumsi ini dapat juga disebut dengan asumsi homoskedastisitas. Homoskedastisitas merupakan salah satu asumsi penting dari model regresi linier. Dalam model regresi linier, varian galat harus bersifat homoskedastisitas, artinya variansi dari variabel galat 𝑢𝑖 adalah suatu angka konstan yang sama dengan 𝜎2 ditulis sebagai berikut:
𝐸(𝑢𝑖2) = 𝜎2 𝑖 = 1, 2, … , 𝑛 (2.29)
Diberikan gambar model regresi dua variabel yang menunjukkan homoskedastisitas:
tabungan
Gambar 2.1. Homoskedastistas
Pada gambar di atas menunjukkan hubungan antara variabel respon Y dengan variabel bebas X. Variabel respon Y adalah tabungan, variabel respon X adalah pendapatan. Terlihat bahwa variansi dari 𝑌𝑖 (yang sama dengan variansi 𝑢𝑖) tergantung pada nilai 𝑋𝑖, tetapi variansi tetap sama. Diberikan gambar untuk masalah heteroskedastisitas:
Gambar 2.2. Heteroskedastisitas
Dari gambar di atas menunjukkan bahwa variansi dari 𝑌𝑖 meningkat dengan meningkatnya X. Keadaan ini yang menyebabkan variansi tidak sama, jadi terdapat heteroskedstisitas.
Definisi 2.4:
𝐸(𝑢𝑖2) = 𝜎𝑖2 𝑖 = 1, 2, … 𝑛 (2.30)
Pada umumnya, heteroskedastisitas sering terjadi pada model-model yang menggunakan data cross- sectional dari pada data runtun waktu. Di mana galat yang bersifat heteroskedastisitas berubah seiring perubahan
tabungan
pengamatan ke-i. Konsekuensi dari keberadaan heteroskedastisitas adalah metode MKT akan menghasilkan penduga yang bias untuk nilai variasi galat dan degan demikian untuk variasi koefisien regresi. Akibatnya uji t, uji F dan estimasi nilai variabel dependen menjadi tidak valid.
Cara mendeteksi adanya heteroskedastisitas adalah dengan menggunakan uji Rank Spearman (Gujarati, 406). Langkah pengujiannya sebagai berikut:
1. Dapatkan nilai 𝑢𝑖 dari model regresi
2. Dengan mengabaikan tanda dari ui, yang berarti mendapatkan nilai absolut |ui|, dapatkan nilai korelasi Rank Spearman antara nilai absolut ini dengan setiap variabel independen dalam model dengan rumus:
rs adalah koefisien korelasi Rank Spearman, di selisih ranking, dan n adalah banyaknya data atau pengamatan.
3. Uji Rank Spearman a. Hipotesis
𝐻𝑜 = tidak ada masalah heteroskedastisitas
𝐻1= ada masalah heteroskedastisitas
H0 ditolak bila statistik t < - t(/2, N-2) atau t > t(/2, N-2)
d. Menghitung statistik t (t-hitung) masing-masing nilai korelasi Rank Spearman dengan rumus sbb:
r
Masalah heteroskedastisitas terkait dengan variansi dari galat (error) yang tidak konstan. Metode tranformasi logaritma sering digunakan untuk mengatasi masalah heterskedastisitas.
2. Tidak ada Otokorelasi
Otokorelasi adalah sebuah kasus khusus dari korelasi. Otokorelasi dapat didefinisikan sebagai korelasi antara galat dari pengamatan, baik dalam bentuk observasi deret waktu atau observasi cross-sectional (Gujarati, 442). Untuk mendefinisikan otokorelasi, terlebih dahulu didefinisikan nilai kovarian sebagai berikut:
Definisi 2.2:
Cov(𝑢𝑖, 𝑢𝑗) = 𝐸[𝑢𝑖 − 𝐸(𝑢𝑖)][𝑢𝑗− 𝐸(𝑢𝑗)]
= 𝐸(𝑢𝑖, 𝑢𝑗)
Sementara itu untuk nilai otokorelasi populasi (𝜌)didefinisikan sebagai berikut:
Definisi 2.3:
𝜌 = 𝐶𝑜𝑣(𝑢𝑖, 𝑢𝑗) √𝑣𝑎𝑟(𝑢𝑖)√𝑣𝑎𝑟(𝑢𝑗)
= 𝐸(𝑢𝑖, 𝑢𝑗) 𝑣𝑎𝑟(𝑢𝑖)
dengan 𝑖 ≠ 𝑗.
Bagian penyebut dapat berubah menjadi 𝑣𝑎𝑟(𝑢𝑖) karena berdasarkan asumsi homoskedastisitas, di mana variansi galat diasumsikan konstan. Karena pada model regresi diasumsikan tidak ada otokorelasi, maka diharapkan nilai 𝜌 = 0 atau 𝐸(𝑢var(𝑢𝑖,𝑢𝑗)
𝑖) = 0. Maka dengan kata lain
𝐸(𝑢𝑖, 𝑢𝑗) = 0. Sementara kita tahu bahwa 𝐸(𝑢𝑖, 𝑢𝑗) = Cov(𝑢𝑖, 𝑢𝑗). Jadi
Salah satu cara mendeteksi adanya otokorelasi dapat dilakukan dengan menggunakan uji Durbin-Watson (Gujarati, 467). Diberikan rumus untuk uji Durbin-Watson:
𝑑 =
∑ (𝑢
𝑁𝑡=2∑
𝑡− 𝑢
𝑡−1)
2𝑢
𝑡 𝑁 𝑡=1Dimana,
𝑢𝑡 : nilai galat yang diperoleh dari proses MKT biasa
𝑢𝑡−1 : nilai galat yang mundur sebanyak satu satuan waktu
Setelah mendapatkan nilai 𝑑, langkah selanjutnya adalah membandingkan nilai 𝑑 dengan nilai-nilai kritis dari DL dan DU dari tabel statistik Durbin-Watson. Kriteria pengujiannya adalah sebagai berikut: 1. Jika 𝑑 < 4dL, berarti ada otokorelasi posiitif
2. Jika 𝑑 > 4dL, berarti ada otokorelasi negatif
3. Jika dU < 𝑑 < 4 – dU, berarti tidak ada otokorelasi positif atau negatif 4. Jika dL ≤ 𝑑 ≤ dU atau 4 – dU ≤ 𝑑 ≤ 4 – dL, pengujian tidak
meyakinkan
Masalah otokorelasi dapat di tangani dengan cara melakukan tranformasi pembedaan pertama pada data. Proses pembedaan (diferencing) dapat ditulis sebagai berikut:
𝑌𝑡− 𝑌𝑡−1 = 𝛽2(𝑋𝑡− 𝑋𝑡−1) + (𝑢𝑡− 𝑢𝑡−1)
∆𝑌𝑡 = 𝛽2∆𝑋𝑡+ 𝑣𝑡
3. Tidak ada Multikolinieritas
Istilah multikolinieritas mula-mula ditemukan oleh Ragnar Frisch. Multikolinieritas terjadi jika ada hubungan linier yang sempurna diantara beberapa atau semua variabel-varibel bebas dalam regresi (Gujarati, 342). Untuk regresi dengan k-variabel bebas 𝑋1, 𝑋2, … , 𝑋𝑘 (di mana 𝑋1=1 untuk semua pengamatan yang memungkinkan unsur intersep), suatu hubungan linier dikatakan ada apabila kondisi berikut ini dipenuhi:
𝜆1𝑋1+ 𝜆2𝑋2+ ⋯ + 𝜆𝑘𝑋𝑘 = 0 (2.25)
di mana 𝜆1, 𝜆2, … , 𝜆𝑘 adalah konstanta yang tidak semua bernilai nol. Persamaan (2.25) merupakan persamaan yang mengandung multikolinieritas sempurna. Diberikan persamaan yang mengandung multikolinieritas tetapi tidak sempurna, sebagai berikut:
𝜆1𝑋1+ 𝜆2𝑋2+ ⋯ + 𝜆𝑘𝑋𝑘+ 𝑢𝑖 = 0 (2.26)
di mana 𝑢𝑖 adalah galat stokastik.
𝑋2𝑖 = −𝜆𝜆12𝑋1𝑖−𝜆𝜆32𝑋3𝑖− ⋯ −𝜆𝜆𝑘2𝜆𝑘𝑖 (2.27)
persamaan di atas menunjukan bahwa 𝑋2 berhubungan linier secara pasti dengan variabel lain atau 𝑋2 dapat diperoleh dari kombinasi linier dari variabel X lainnya. Persamaan (2.25) mengandung multikolinieritas yang sempurna. Pada keadaan seperti ini, koefisien dari korelasi antara variabel 𝑋2 dan kombinasi linier di sisi kanan pada persamaan (2.27) sama dengan
satu.
Pada persamaan (2.26), diasumsikan bahwa 𝜆2 ≠ 0. Maka persamaan dapat ditulis menjadi:
𝑋2𝑖 = −𝜆𝜆12𝑋1𝑖−𝜆𝜆32𝑋3𝑖− ⋯ −𝜆𝜆𝑘2𝜆𝑘𝑖+𝜆12𝑢𝑖 (2.28)
Persamaan di atas menunjukkan bahwa 𝑋2 tidak ada kombinasi linier yang pasti dari X lainnya dikarenakan 𝑋2 juga ditentukan oleh galat stokastik 𝑢𝑖.
Diberikan cotoh data yang mengandung multikolinieritas:
𝑋2 𝑋3 𝑋3
∗
10 50 52
15 75 75
18 90 97
30 150 152
jelas bahwa 𝑋3𝑖 = 5𝑋2𝑖. Jadi, ada multikolinieritas sempurna antara 𝑋2 dan 𝑋3 karena koefisien korelasi sama dengan satu. Variabel 𝑋3∗ diperoleh dari 𝑋3 dengan hanya menambahkan bilangan 2, 0, 7, 9, 2. Analisis regresi mengasumsikan tidak adanya multikolinieritas. Jika asumsi tidak dipenuhi maka kita akan mengalami kesulitan saat pendugaan koefisien regresi. Efek dari adanya multikolinieritas adalah standard error dari koefisien regresi tinggi sehingga model buruk bila dipakai untuk memprediksi. Salah satu cara mendeteksi adanya multikolinieritas adalah dengan cara menghitung Variance Inflation Factor (VIF) pada model regresi (Gujarati, 351). Langkah-langkahnya yaitu:
1. Lakukan regresi 𝑋𝑖 dengan X yang lain dan hitunglah koefisien determinasi (𝑅2).
2. Hitung VIF 𝛽̂𝑖 = 1 (1 − 𝑅⁄ 𝑖2) .
3. Bila ada VIF >10, maka ada multikolinieritas.
Salah satu cara untuk menanggulangi adanya multikolinieritas adalah dengan menghilangkan salah satu variabel yang berkorelasi. Jika ada variabel yang VIF>10 maka variabel dapt dihilangkan dari model regresi.
Regresi linier mengasumsikan bahwa galat 𝑢𝑖 mengikuti distribusi normal (Gujarati, 108) dengan
Rata-rata :𝐸(𝑢𝑖) = 0 (2.31)
Variansi : 𝐸(𝑢𝑖) = 𝜎2 (2.32) Cov (𝑢𝑖, 𝑢𝑗): 𝐸(𝑢𝑖, 𝑢𝑗) = 0 𝑖 ≠ 𝑗 (2.33)
Asumsi ini dapat ditulis menjadi:
𝑢𝑖~ 𝑁(0, 𝜎2) (2.34)
Kenormalan galat dapat di dieteksi menggunakan uji Kolmogorov-Smirnov dan melihat pada scatterplot galat. Jika plot galat mengikuti garis lurus kenormalan maka mengindikasikan bahwa data berdistribusi normal. Pengujian yang paling sering digunakan untuk mendeteksi kenormalam galat adalah uji Kolmogorov-Smirnov. Berikut ini merupakan Langkah-langkah pengujian Kolmogorov-Smirnov:
a. Pengujian hipotesis
𝐻0: 𝐹(𝑋) = 𝐹0(𝑋) (data berdistribusi normal)
𝐻1: 𝐹(𝑋) ≠ 𝐹0(𝑋) (data tidak berdistribusi normal)
b. Menentukan tingkat signifikansi 𝛼 c. Menentukan stastistik uji
𝐷ℎ𝑖𝑡𝑢𝑛𝑔 = 𝑚𝑎𝑘𝑠𝑖𝑚𝑢𝑚|𝐹𝑛(𝑋) − 𝐹0(𝑋)|
Dengan,
𝐹0(𝑋) = fungsi distributif kumulatif dibawah 𝐻0 P(Z<Zi)
d. Menentukan kriteria pengujian
𝐻0 ditolak jika 𝐷ℎ𝑖𝑡𝑢𝑛𝑔 > 𝐷(𝛼,𝑛), n= banyaknya pengamatan
e. Menetukan kesimpulan
Contoh 2.1
Diberikan data sebagai berikut:
73.9 74.2 74.6 74.7 75.4 76.0 76.0 76.0 76.5 76.6 76.9 77.3 77.4 77.7
Uji apakah data tersebut berdistribusi normal dengan menggunakan uji Kolmogorov-Smirnov.
Penyelesaian:
a. Pengujian Hipotesis
𝐻0: 𝐹(𝑋) = 𝐹0(𝑋) (data berdistribusi normal)
𝐻1: 𝐹(𝑋) ≠ 𝐹0(𝑋) (data tidak berdistribusi normal)
b. Menentukan tingkat signifikansi 𝛼 c. Menentukan statistik Uji
dimana, 𝑆=1,227. Perhitungan statistik uji Kolmogorov-Smirnov diberikan pada tabel dibawah ini:
Tabel 2.1 Perhitungan statistik uji Kolmogorov-Smirnov
Xi Fkum Fn(x)
f. Menentukan kesimpulan
Karena nilai D= 0.1302 < 0.314, maka 𝐻0 diterima. Dapat dikatakan bahwa data tersebut berdistribusi normal.
Dengan asumsi kenormalan, pendugaan MKT 𝛽̂ akan memiliki sifat ideal sebagai penduga yang baik dan memiliki sifat Best Linier Unbiased Estimator (BLUE). Menurut teorema Gauss-Markov, sifat-sifat BLUE tersebut adalah:
a. Linier (Linierity), artinya bahwa nilai penduga merupakan fungsi linier.
b. Tak bias (unbiasedness), artinya bahwa nilai penduga sesuai dengan nilai parameter.
c. Variansi minimum dari 𝛽̂ artinya bahwa nilai penduga memiliki variansi sampel terkecil dibandingkan penduga-penduga linier tak bias lainya.
Bukti: 1. Linier
Dari persamaan (2.11) kita mempunyai penduga dari 𝛽, sebagai berikut:
𝜷̂ = (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒚
𝜷̂ = 𝑪𝒚 (2.35) Dari persamaan (2.34) dapat ditulis ke dalam bentuk skalar,
𝛽̂𝑗 = 𝑐𝑗1𝑌1+ 𝑐𝑗2𝑌2+ 𝑐𝑗3𝑌3+ ⋯ + 𝑐𝑗𝑛𝑌𝑛 (2.36)
dimana, 𝑌𝑖 adalah contoh pengamatan dan 𝑐𝑗𝑖merupakan konstanta dalam baris j pada matrik C berukuran k x n. Terbukti bahwa nilai dari penduga merupakan fungsi linier.
2. 𝛽̂ penduga tak bias
Diberikan 𝜷̂ = (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒚 dan 𝒚 = 𝑿𝜷 + 𝒖, subtisusikan 𝑦 ke dalam persamaan 𝜷̂.
𝜷̂ = (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒚
= (𝑿𝑻𝑿)−𝟏𝑿𝑻(𝑿𝜷 + 𝒖)
= (𝑿𝑻𝑿)−𝟏𝑿𝑻𝑿𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖, , (𝑿𝑻𝑿)−𝟏𝑿𝑻𝑿 = 𝟏
= 𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖
Dilanjutkan proses berikutnya, yaitu mencari nilai harapan dari 𝛽̂
Terbukti bahwa 𝛽̂ merupakan penduga yang tak bias 3. 𝛽̂ Penduga mempunyai varansi minimum
𝒗𝒂𝒓 − 𝒄𝒐𝒗(𝜷̂) = 𝑬{[𝜷̂ − 𝑬(𝜷̂)][𝜷̂ − 𝑬(𝜷̂)]𝑻
= 𝑬{[𝜷̂ − 𝜷][𝜷̂ − 𝜷]𝑻}
𝑬(𝜷̂) = 𝑬(𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖)
= 𝑬(𝜷) + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝑬(𝒖)
= 𝑬(𝜷) , 𝑬(𝒖) = 𝟎
= 𝑬{[𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 − 𝜷][𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 − 𝜷]𝑻}
= 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖][(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖]𝑻
= 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 𝒖𝑻𝑿 {(𝑿𝑻𝑿)−𝟏]
= (𝑿𝑻𝑿)−𝟏𝑿𝑻 𝑬(𝒖 𝒖𝑻) 𝑿 (𝑿𝑻𝑿)−𝟏
= (𝑿𝑻𝑿)−𝟏𝑿𝑻 𝝈𝟐𝑰 𝑿 (𝑿𝑻𝑿)−𝟏 , 𝑬(𝒖 𝒖𝑻) = 𝝈𝟐𝑰
= 𝝈𝟐 (𝑿𝑻𝑿)−𝟏
Dimisalkan 𝜷̂∗ merupakan penduga tak bias lain dari 𝜷, dapat ditulis menjadi:
𝜷̂∗ = [(𝑿𝑻𝑿)−𝟏𝑿𝑻+ 𝑪]𝒚 (2.37)
dimana, 𝐶 merupakan konstanta. Subtistusikan 𝒚 = 𝑿𝜷 + 𝒖 kedalam persamaan (2.36).
𝜷̂∗ = [(𝑿𝑻𝑿)−𝟏𝑿𝑻+ 𝑪]𝒚
= [(𝑿𝑻𝑿)−𝟏𝑿𝑻+ 𝑪][𝑿𝜷 + 𝒖]
= 𝑪𝑿𝜷 + 𝑪𝒖 + (𝑿𝑻𝑿)−𝟏𝑿𝑻 𝑿𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖
= 𝑪𝑿𝜷 + 𝑪𝒖 + 𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖
= 𝜷 + 𝑪𝑿𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖 (2.38)
Jika 𝜷̂∗ nilai penduga tak bias 𝜷 , maka 𝑪𝑿 = 0. Hal ini dapat dibuktikan dengan langkah sebagai berikut:
𝑬(𝜷̂∗ ) = 𝑬[𝜷 + 𝑪𝑿𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖]
𝜷 = 𝑬(𝜷) + 𝑬(𝑪𝑿𝜷) + 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖] + 𝑬(𝑪𝒖)
𝜷 = 𝜷 + 𝑪𝑿 𝑬(𝜷) + 𝑬(𝒖)(𝑿𝑻𝑿)−𝟏𝑿𝑻+ 𝑪 𝑬(𝒖)
𝜷 = 𝜷 + 𝑪𝑿 𝑬(𝜷) , 𝑬(𝒖) = 𝟎
𝜷 − 𝜷 = 𝑪𝑿 𝑬(𝜷)
0 = 𝑪𝑿 𝜷
𝑪𝑿 = 0
Sehingga persamaan 𝑪𝑿 𝜷 = 𝟎, ini hanya dapat dipenuhi bila CX=0 Dari persamaan (2.37) dapat ditulis menjadi:
𝜷̂∗ = 𝜷 + 𝑪𝑿𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖
𝜷̂∗ − 𝜷 = 𝑪𝑿𝜷 + (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖
𝜷̂∗ − 𝜷 = (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖 , 𝑪𝑿 = 𝟎
Dengan mengikuti definisi, 𝑣𝑎𝑟 − 𝑐𝑜𝑣 (𝜷̂∗) maka:
𝒗𝒂𝒓 − 𝒄𝒐𝒗 (𝜷̂∗)
= 𝑬[(𝜷̂∗ − 𝜷)(𝜷̂∗ − 𝜷)𝑻]
= 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖][(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖]𝑻
= 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 + 𝑪𝒖][𝒖𝑻𝑿 (𝑿𝑻𝑿)−𝟏+ 𝒖𝑻𝑪𝑻] ,(𝑨𝑩)𝑻= 𝑨𝑻𝑩𝑻
= 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 𝒖𝑻𝑿 (𝑿𝑻𝑿)−𝟏+ (𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 𝒖𝑻𝑪𝑻+ 𝑪𝒖𝒖𝑻𝑿 (𝑿𝑻𝑿)−𝟏+
= 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 𝒖𝑻𝑿 (𝑿𝑻𝑿)−𝟏] + 𝑬[(𝑿𝑻𝑿)−𝟏𝑿𝑻𝒖 𝒖𝑻𝑪𝑻]+
𝑬[𝑪𝒖𝒖𝑻𝑿 (𝑿𝑻𝑿)−𝟏] + 𝑬[𝑪𝒖𝒖𝑻𝑪𝑻]
=(𝑿𝑻𝑿)−𝟏𝑿𝑻𝑬(𝒖 𝒖𝑻)𝑿 (𝑿𝑻𝑿)−𝟏+ (𝑿𝑻𝑿)−𝟏𝑿𝑻𝑬(𝒖 𝒖𝑻)𝑪𝑻+
𝑪 𝑬(𝒖𝒖𝑻)𝑿 (𝑿𝑻𝑿)−𝟏+ 𝑪 𝑬(𝒖𝒖𝑻)𝑪𝑻
=(𝑿𝑻𝑿)−𝟏𝑿𝑻𝝈𝟐𝑰 𝑿 (𝑿𝑻𝑿)−𝟏+ (𝑿𝑻𝑿)−𝟏𝑿𝑻𝝈𝟐𝑰 𝑪𝑻+ + 𝑪 𝝈𝟐𝑰𝑿 (𝑿𝑻𝑿)−𝟏+
𝑪𝝈𝟐𝑰 𝑪𝑻 , 𝑬(𝒖 𝒖𝑻) = 𝝈𝟐𝑰
=𝝈𝟐(𝑿𝑻𝑿)−𝟏𝑿𝑻𝑿 (𝑿𝑻𝑿)−𝟏+ 𝝈𝟐(𝑿𝑻𝑿)−𝟏𝑿𝑻𝑪𝑻+ 𝝈𝟐𝑪𝑿 (𝑿𝑻𝑿)−𝟏+ 𝝈𝟐𝑪𝑪𝑻
=𝝈𝟐(𝑿𝑻𝑿)−𝟏+ 𝝈𝟐(𝑿𝑻𝑿)−𝟏𝑿𝑻𝑪𝑻+ 𝝈𝟐𝑪𝑿 (𝑿𝑻𝑿)−𝟏+𝝈𝟐𝑪𝑪𝑻
=𝝈𝟐(𝑿𝑻𝑿)−𝟏+ 𝝈𝟐(𝑿𝑻𝑿)−𝟏(𝑪𝑿)𝑻+ 𝝈𝟐𝑪𝑿 (𝑿𝑻𝑿)−𝟏+ 𝝈𝟐𝑪𝑪𝑻
=𝝈𝟐(𝑿𝑻𝑿)−𝟏+ 𝝈𝟐𝑪𝑪𝑻 , 𝑪𝑿 = 𝟎
=𝒗𝒂𝒓 − 𝒄𝒐𝒗(𝜷̂) + 𝝈𝟐𝑪𝑪𝑻 , 𝝈𝟐𝑪𝑪𝑻 > 0 (2.40) Persamaan (2.38) menunjukkan bahwa matrik variansi-covariansi merupakan penduga linier dari 𝜷̂∗, ini sama untuk matrik variansi-covariansi MKT pada penduga 𝜷̂ ditambah 𝜎2𝐶𝐶𝑇. Dengan membandingkan 𝑣𝑎𝑟 − 𝑐𝑜𝑣(𝜷̂) dengan 𝑣𝑎𝑟 − 𝑐𝑜𝑣 (𝜷̂∗) , 𝜷̂ memiliki var-cov terkecil diantara penduga tak bias yang lain artinya 𝜷̂ memiliki variansi yang minimum.
Dengan melihat asumsi kenormalan, dalam analisis regresi linier pendugaan MKT 𝛽̂𝑖 juga berdisitribusi normal dengan rata-rata 𝛽𝑖 dan variansi 𝜎2. Dengan menggeneralisasikan dalam k-variabel dapat ditunjukkan bahwa
Rata-rata :𝐸(𝛽̂𝑖) = 𝛽𝑖
𝜷̂ ~ 𝑁(𝜷, 𝜎2(𝑿′𝑿)−1)
G. Regresi dengan Variabel Dummy
Variabel dummy juga dikenal dengan nama variabel indikator, variabel kualitatif atau variabel biner. Variabel dummy adalah variabel yang digunakan untuk mengamati ada atau tidak adanya pengaruh dalam variabel bebas. Dalam analisis regresi variabel bebas tidak hanya dipengaruhi oleh variabel kuantitatif (misalnya: pendapatan, harga, dll) tetapi juga dapat dipengaruhi oleh variabel kualitatif ( misalnya: jenis kelamin, agama, dll). Variabel kualitatif tidak dapat diukur, tetapi hanya bisa ditandai sifatnya antara ada dan tidak ada. Contoh faktor-faktor kualitatif, antara lain: ras, warna kulit, perang, dan lain-lain.
Untuk menjelaskan proses analisis regresi dengan variabel-variabel dummy, diberikan contoh kasus model regresi sederhana yang variabel bebasnya diwakili oleh variabel dummy. Andaikan diilakukan penelitian pada penentuan standar gaji seorang karyawan ditentukan berdasarkan pada tingkat pendidikannya. Situasi ini digambarkan melalui model regresi sederhana yang terdiri dari dua variabel, yaitu gaji karyawan sebagai variabel terikat (Y) dan tingkat pendidikan sebagai variabel kualitatif (D).
𝑌𝑖 = 𝛼 + 𝛽𝐷𝑖 + 𝑢𝑖 (2.41)
di mana,
𝑌𝑖 : gaji karyawan ke-i
𝐷𝑖 : variabel dummy
Diberikan nilai 1 jika karyawan telah tamat SLTA atau berpendidikan di atas SLTA, nilai 0 jika karyawan tidak tamat atau berpendidikan di bawah SLTA.
𝐷𝑖 = {1, 𝑡𝑎𝑚𝑎𝑡 𝑆𝐿𝑇𝐴 0, 𝑡𝑖𝑑𝑎𝑘 𝑡𝑎𝑚𝑎𝑡 𝑆𝐿𝑇𝐴
Dengan menggunakan asumsi variabel galat (𝑢𝑖)yang memenuhi asumsi dasar MKT, maka dari pendugaan (2.41) diperoleh:
𝐸(𝑌𝑖|𝐷𝑖 = 0) = 𝛼
𝐸(𝑌𝑖|𝐷𝑖 = 1) = 𝛼 + 𝛽
SLTA dengan rerata gaji karyawan yang tidak tamat SLTA. 𝛼 + 𝛽 mencerminkan rerata gaji karyawan yang sudah tamat SLTA.
Pada contoh di atas hanya memakai satu varaiabel dummy dan tidak ada variabel bebas lainnya dalam persamaan regresi tersebut. Model-model yang hanya mengandung variabel dummy sebagai variabel bebasnya, disebut model analisis variansi (Analysis of Variance Model (ANOVA)). Model-model ANOVA, umumnya dipakai dalam bidang ilmu sosiologi, psikologi pendidikan, dan penelitian dasar. Dalam bidang ekonometri, model regresi biasanya mengandung campuran antara variabel kuantitatif dan variabel kualitatif. Model-model semacam ini disebut dengan model analisis kovarian (Analysis of Covarian Model (ANCOV))
H. Masalah Intervensi
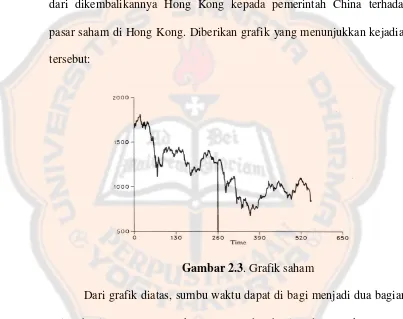
Pengumuman ini yang menyebabkan kekhawatiran penduduk dan investor di Hong Kong. Akibatnya dollar Hong Kong anjlok ke level terendah di pasar valuta asing. Pasar saham juga ikut mengalami penurunan jauh lebih rendah dibandingkan krisis ekonomi global di tahun 1973. Pada situasi seperti ini, analsis intervensi dapat digunakan yaitu untuk menilai dampak dari dikembalikannya Hong Kong kepada pemerintah China terhadap pasar saham di Hong Kong. Diberikan grafik yang menunjukkan kejadian tersebut:
Gambar 2.3. Grafik saham
BAB III
REGRESI PIECEWISE
A. Pengantar
Regresi piecewise dapat digunakan dalam kasus intervensi, tetapi tidak semua kasus intervensi dapat menggunakan regresi piecewise. Sebagaimana telah dibahas di bab II, model ini hanya dapat digunakan dalam kasus intervensi, di mana pengaruh intervensi berdampak langsung, sehingga akan terlihat pengaruh sebelum dan setelah intervensi. Regresi piecewise adalah suatu metode regresi di mana nilai-nilai peubah bebas disekat ke dalam interval dan suatu ruas garis yang cocok diprediksi untuk masing-masing interval.
Model regresi piecewise merupakan pengembangan dari model regresi linier sederhana ke dalam model regresi linier berganda yang menggunakan variabel dummy. Metode ini bekerja secara baik ketika hubungan antara variabel tak bebas dengan variabel intak bebas linier. Ketika menganalisa hubungan antara variabel bebas Y dan variabel tak bebas X, untuk segmen (range) yang berbeda dari X, dapat terjadi hubungan linier yang berbeda.
kemerosotaan, ini dikarenakan adanya krisis moneter dan ekonomi (Eka Nuvitasari, 2007). Pada kasus demikian dapat digunakan regresi piecewise. Terdapat dua bagian, yaitu: bagian pertama sebelum terjadinya krisis moneter dan bagian kedua setelah terjadi krisis moneter dan ekonomi. Ini lah yang dinamakan regresi piecewise.
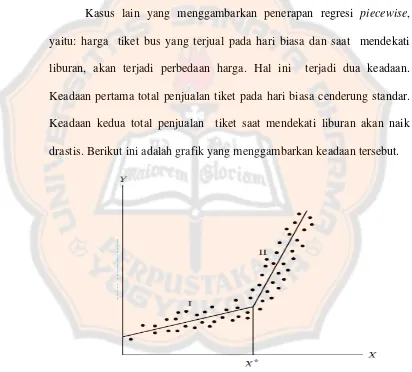
Kasus lain yang menggambarkan penerapan regresi piecewise, yaitu: harga tiket bus yang terjual pada hari biasa dan saat mendekati liburan, akan terjadi perbedaan harga. Hal ini terjadi dua keadaan. Keadaan pertama total penjualan tiket pada hari biasa cenderung standar. Keadaan kedua total penjualan tiket saat mendekati liburan akan naik drastis. Berikut ini adalah grafik yang menggambarkan keadaan tersebut.
Gambar 3.1 Hubungan antara penjualan tiket (Y) pada saat hari biasa dengan saat mendekati liburan (X)
saat hari biasa dengan saat mendekati liburan juga dipengaruhi adanya faktor mudik atau pulang kampung. 𝑋∗ merupakan titik yang menjelaskan keadaan tersebut yaitu intervensi terjadinya mudik. Pada grafik di atas, garis regresi di bagi menjadi dua segmen, yaitu: segmen I dan segmen II. Segmen I merupakan keadaan di mana belum dipengaruhi faktor mudik, sedangkan segmen II merupakan keadaan di mana kemiringan garis meningkat, ini dipengaruhi oleh faktor mudik.
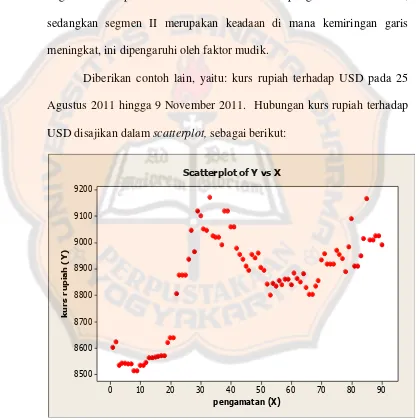
Diberikan contoh lain, yaitu: kurs rupiah terhadap USD pada 25 Agustus 2011 hingga 9 November 2011. Hubungan kurs rupiah terhadap USD disajikan dalam scatterplot, sebagai berikut:
Gambar 3.2 Hubungan kurs rupiah terhadap USD
Dari scatterplot di atas terlihat bahwa setelah pengamatan ke-20 yaitu pada tanggal 13 September 2011 terjadi perubahan kemiringan fungsi linier.
Diperkirakan juga setelah pengamatan ke-35 yaitu pada tanggal 28 September 2011 terjadi perubahan kemiringan fungsi linier. Perubahan kemiringan terjadi dikarenakan pada sekitar tanggal 13 September 2011 terjadi krisis ekonomi di dunia sehingga terjadi penurunan nilai dollar Amerika, kasus tersebut yang menyebabkan nilai kurs rupiah meninggi.
B. Model Regresi Piecewise
1. Model regresi piecewise untuk satu breakpoint
Model regresi piecewise untuk satu breakpoint merupakan model regresi piecewise yang paling sederhana. Model ini hanya menduga dua persamaan untuk dua segmen yang berbeda. Berikut ini, diberikan persamaan regresi untuk satu breakpoint:
𝑌𝑖 = 𝛽01+ 𝛽11𝑋𝑖+ 𝑢𝑖, 𝑘𝑒𝑡𝑖𝑘𝑎 𝑋𝑖 ≤ 𝑋∗
𝑌𝑖 = 𝛽02+ 𝛽12𝑋𝑖+ 𝑢 𝑖 ,𝑘𝑒𝑡𝑖𝑘𝑎 𝑋𝑖 > 𝑋∗
Persamaan di atas dapat ditulis dalam model regresi berganda menjadi:
𝑌𝑖 = 𝛼1+ 𝛽1𝑋𝑖 + 𝛽2(𝑋𝑖 − 𝑋∗)𝐷𝑖 + 𝑢𝑖 (3.1)
di mana,
𝛼1 = 𝛽01
𝛽1 = 𝛽11
𝛽12= 𝛽01+ 𝛽02
𝛽2 = 𝛽01𝑋− 𝛽∗ 02
𝐷𝑖 = {1, 𝑗𝑖𝑘𝑎 𝑋𝑖 > 𝑋 ∗ 0, 𝑗𝑖𝑘𝑎 𝑋𝑖 ≤ 𝑋∗
2. Model regresi piecewise untuk dua breakpoint
Model regresi piecewise untuk dua breakpoint adalah pengembangan dari model regresi piecewise satu breakpoint dengan penambahan satu breakpoint, persamaan regresi, dan parameter. Diberikan persamaan regresi untuk dua breakpoint, yaitu:
𝑌̂𝑖 = 𝛽01+ 𝛽11𝑋𝑖 ; 𝑋𝑖 ≤ 𝑋1∗
𝑌̂𝑖 = 𝛽02+ 𝛽12𝑋𝑖 ; 𝑋1∗ < 𝑋𝑖 ≤ 𝑋2∗
𝑌̂𝑖 = 𝛽03+ 𝛽13𝑋𝑖 ; 𝑋𝑖 > 𝑋2∗
Dari persamaan regresi di atas dapat ditulis dalam model regresi berganda menjadi:
3. Model regresi piecewise untuk k breakpoint
Diberikan persamaan regresi untuk k breakpoint, yaitu:
𝑌̂𝑖 = 𝛽01+ 𝛽11𝑋𝑖; 𝑋𝑖 ≤ 𝑋1∗
𝑌̂𝑖 = 𝛽02+ 𝛽12𝑋𝑖 ; 𝑋1∗ < 𝑋𝑖 ≤ 𝑋2∗
⋮
𝑌̂𝑖 = 𝛽0𝑘+ 𝛽1𝑘𝑋𝑖 ; 𝑋𝑖 > 𝑋𝑘−1∗
Dari persamaan regresi tersebut, dapat ditulis dalam model regresi berganda menjadi:
𝑌𝑖 = 𝛼1+ 𝛽1𝑋𝑖 + 𝛽2(𝑋𝑖 − 𝑋1∗)𝐷1𝑖+ 𝛽3(𝑋𝑖 − 𝑋2∗)𝐷2𝑖+ ⋯
+ 𝛽𝑘(𝑋𝑖 − 𝑋𝑘−1∗ )𝐷𝑘𝑖 + 𝑢𝑖 (3.3)
di mana,
𝛼1 = 𝛽01
𝛽1 = 𝛽11
𝛽1𝑘 = 𝛽01+ 𝛽02+ ⋯ . +𝛽0𝑘
𝛽2 = 𝛽01𝑋− 𝛽02 1∗
𝛽3 = 𝛽02𝑋− 𝛽03 2∗
⋮
𝛽𝑘 =𝛽0𝑘−1𝑋 − 𝛽0𝑘 𝑘−1∗
𝐷1𝑖 = {1, 𝑗𝑖𝑘𝑎 𝑋𝑖 > 𝑋1 ∗
𝐷2𝑖 = {1, 𝑗𝑖𝑘𝑎 𝑋𝑖 > 𝑋2 ∗
0, 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
⋮
𝐷𝑘𝑖 = {1, 𝑗𝑖𝑘𝑎 𝑋𝑖 > 𝑋𝑘−1 ∗
0, 𝑙𝑎𝑖𝑛𝑛𝑦𝑎
Persamaan (3.3) merupakan regresi piecewise untuk k breakpoint.
C. Asumsi-asumsi Regresi Piecewise
Dari bab II telah diberikan asumsi-asumsi model regresi linier yang bersifat umum. Regresi piecewise memiliki asumsi-asumsi klasik yang sebagian merupakan asumsi-asumsi yang ada dalam bab II. Dalam menentukan model regresi piecewise, asumsi-asumsi dalam regresi harus diperhatikan. Menurut Ryan, Sandra E dan Porth, Laurie S (2007) asumsi-asumsi yang ada harus diperhatikan dalam menentukan model regresi piecewise adalah sebagai berikut:
1. Kebebasan galat (tidak ada otokorelasi) 2. Kenormalan galat
3. Galat memiliki variansi homogen (homoskedastisitas)
1. Kebebasan galat
Kebebasan galat ini berarti bahwa nilai dari galat tidak ada hubungan ke nilai selanjutnya. Netter dan lainya (1990) mengatakan bahwa jika data berkorelasi, koefisien regresi masih tak bias tetapi mungkin tidak efisien, dan kesalahan kuadrat rata-rata dan standar deviasi dari parameter mungkin dapat diabaikan. Plot dari galat seharusnya tidak menunjukkan adanya pola. Pengujian ada atau tidaknya kebebasan galat dilakukan pada persamaan garis regresi sebelum breakpoint dan persamaan garis setelah breakpoint. Dikarenakan model regresi piecewise merupakan gabungan dari garis regresi yang sepotong-sepotong jadi untuk lebih singkatnya pengujian kebebasan galat atau tidak adanya otokorelasi dapat dilakukan pada model regresi Piecewise yang diperoleh.
Kebebasan galat juga dapat disebut dengan tidak ada aoutokorelasi. Asumsi ini juga sudah dibahas dalam bab II. Cara mendeteksi adanya galat yang tidak bebas atau adanya otokorelasi dapat menggunakan uji Durbin-Watson yang telah dibahas dalam bab II.
2. Kenormalan Galat
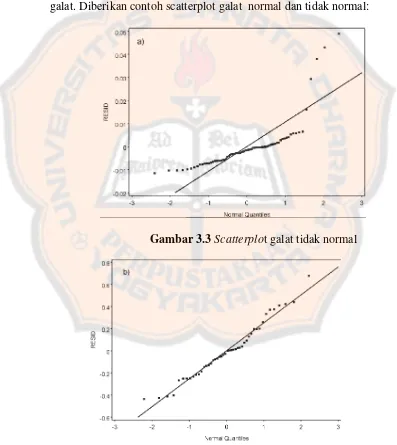
pengujian langsung terhadap model yang diperoleh tanpa melakukan pengujian pada persamaan garis regresi sebelum breakpoint dan setelah breakpoint. Untuk memeriksa normalitas dapat menggunakan uji Kolmogorov-Smirnov. Langkah-langkah pengujian Kolmogorov-Smirnov sudag dijelaskan dalam bab II. Selain itu juga dapat dilihat scatterplot dari galat. Diberikan contoh scatterplot galat normal dan tidak normal:
Gambar 3.3 Scatterplot galat tidak normal
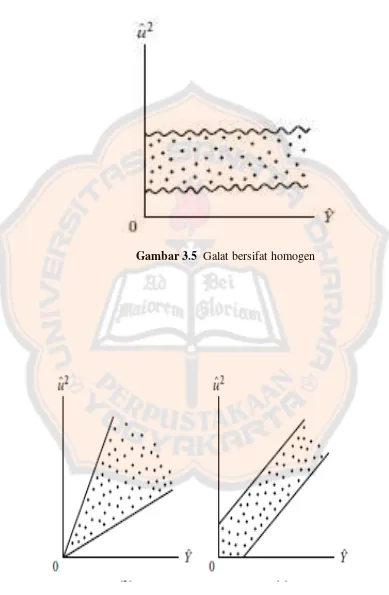
3. Galat memiliki variansi homogen (homoskedastisitas)
Gambar 3.5 Galat bersifat homogen
Galat memiliki sifat homogen ini sama saja dengan tidak adanya heteroskedsatisitas. Cara mendeteksi adanya galat yang tidak bersifat homogen atau adanya heteroskedastisitas dapat menggunakan uji Rank Spearman yang mana pengujian ini sudah dibahas dalam bab II.
D. Potensi Pencilan (Outlier)
Outlier adalah pengamatan yang jauh dari pusat data atau kumpulan data yang mungkin berpengaruh besar terhadap koefisien regresi. Outlier dapat disebut juga dengan pencilan. Pemeriksaan potensi pencilan merupakan hal yang sangat penting dalam analisis apapun. Salah satu analisis yang harus memperhatikan potensi pencilan adalah analisis regresi piecewise. Dalam analisis regresi piecewise pencilan harus diperiksa karena ini mungkin dapat mempengaruhi model dugaan, juga mempengaruhi dalam menentukan lokasi breakpoint. Pencilan dapat dilihat dalam scatterplot data. Jika terdapat data yang terletak jauh dari kumpulan data yang lain, dapat dikatakan bahwa mungkin data tersebut termasuk pencilan. Metode ini juga mempunyai kelemahan, yaitu keputusan bahwa sebuah data merupakan pencilan sangat bergantung pada pendapat seorang peneliti, karena metode ini hanya mengandalkan visualisasi grafis, unutk itu dibutuhkan seseorang yang ahli dan berpengalaman dalam mengiterpretasikan plot tersebut.
menggunakan metode grafis, jika terdapat data yang terletak jauh dari kumpulan data yang lain, mungkin data tersebut merupakan pencilan. Cara mendeteksi apakah data tersebut merupakan pencilan atau tidak dapat menggunakan metode Residual Studentization ( galat yang distudenkan). Untuk mendeteksi pencilan, diperlukan suatu matriks yang dinamakan matriks Hat. Matriks ini dilambangkan dengan H, matriks Hat dapat ditulis dalam bentuk matrik
H = 𝑿 (𝑿𝑻𝑿)−𝟏𝑿𝑻 (3.4)
Dalam menduga model regresi, model penduga Y dapat ditulis sebagai berikut:
𝒀̂ = 𝑿𝜷̂ (3.5) Persamaan (3.5) dapat ditulis menjadi
𝒀̂ = 𝑿𝜷̂
= 𝑿(𝑿𝑻𝑿)−𝟏𝑿𝒚
= H y (3.6) Elemen matriks H dilambangkan dengan ℎ𝑖𝑗, yang merupakan elemen baris ke-i dan elemen baris ke-j pada matriks H. Elemen diagonal matriks H dilambangkan dengan ℎ𝑖𝑖. ℎ𝑖𝑖 juga dapat disingkat menjadi ℎ𝑖.
Langkah-langkah metode Residual Studentization adalah sebagai berikut:
a. Uji hipotesis
𝐻1= pengamatan ke-i merupakan pencilan
b. Tingkat signifikansi 𝛼 c. Statistik uji
𝑡𝑖 = 𝑢𝑖√(𝑛 − 𝑝)𝑀𝑆𝐸(1 − ℎ𝑛 − 𝑝 − 1
𝑖𝑖) − 𝑢𝑖2
dengan,
𝑝= banyaknya variabel bebas
𝑛= banyaknya data d. Kriteria uji
𝐻0 ditolak jika 𝑡𝑖 > 𝑡(𝛼 2;𝑛−𝑝−1)⁄ .
e. kesimpulan
Setelah melakukan pengujian Residual Studenization dan diperoleh data yang termasuk pencilan, dilanjutkan langkah apakah data pencilan tersebut berpengaruh pada model. Salah satu metode yang digunakan untuk mengetahui apakah data yang termasuk pencilan tersebut berpengaruh pada model, yaitu: The Difference In Fit Statistic (DFITS).
The Difference In Fit Statistic (DFITS) ini digunakan untuk mengamati
pengaruh pengamatan ke-i pada nilai penduga 𝑌̂𝑖. Langkah-langkah pengujian DFITS adalah sebagai berikut:
a. Uji hipotesis
𝐻0= pengamatan ke-i tidak berpengaruh 𝐻1= pengamatan ke-i berpengaruh
c. Statistik uji
𝐷𝐹𝐼𝑇𝑆𝑖 = √1 − ℎℎ𝑖𝑖 𝑖𝑖 𝑢𝑖√
𝑛 − 𝑝 − 1
(𝑛 − 𝑝)𝑀𝑆𝐸(1 − ℎ𝑖𝑖) − 𝑢𝑖2
d. Menentukan kriteria pengujian
𝐻0 ditolak jika 𝐷𝐹𝐼𝑇𝑆𝑖 > 2√𝑝 𝑛⁄
e. Menentukan kesimpulan
Setelah melakukan beberapa pengujian di atas, jika terdapat data yang termasuk dalam pencilan dan data tersebut berpengaruh pada model, maka data tersebut harus tidak perlu dihapus. Sebaliknya, jika diperoleh data yang termasuk dalam pencilan tetapi data tersebut tidak berpengaruh terhadap model maka data dihapus.
Contoh 3.1
Diberikan data sebagai berikut:
Tabel 3.1 data simulasi
X 0 1 2 3 4 5 6 7 8 9 10
Penyelesaian:
Terlebih dahulu memplotkan data tersebut, hal ini dilakukan dengan tujuan supaya terlihat apakah ada pencilan atau tidak, diperoleh scatterplot sebagai berikut:
Gambar 3.7 Scatterplot data contoh 3.1
Dari gambar 10, terlihat bahwa pada data ke-5 teletak jauh dari kumpulan data asli, sehingga data ke-5 tersebut mungkin termasuk dalam pencilan. Selanjutnya lakukan pengujian untuk data ke-5, apakah data ke-5 termasuk pencilan dan mempengaruhi model. Pertama dilakukan pengujian dengan menggunakan metode Residual Studentization (galat yang distudenkan). Langkah-langkah pengujian:
10 8
6 4
2 0
25
20
15
10
5
0
X
Y
a. Uji hipotesis
𝐻0= pengamatan ke-i bukan pencilan 𝐻1= pengamatan ke-i merupakan pencilan
b. Menentukan tingkat signifikansi 𝛼 c. Menentukan statistik uji
𝑡5 = 𝑢5√(𝑛 − 𝑝)𝑀𝑆𝐸(1 − ℎ𝑛 − 𝑝 − 1
𝑖𝑖) − 𝑢52
𝑡5 = 14,3155√(11 − 1)25,30(1 − 0,1) − (14,3155)11 − 1 − 1 2
𝑡5 = 8,913
dengan,
𝑝= banyaknya variabel bebas
𝑛= jumlah data
d. Menentukan kriteria uji
𝐻0 ditolak jika 𝑡5 > 𝑡(𝛼 2;𝑛−𝑝−1)⁄ . Dimana 𝑡(0,025 10)⁄ = 2,228
e. Menentukan kesimpulan
Karena nilai 𝑡5=8,913>2,228, maka 𝐻0 ditolak, jadi dapat disimpulkan bahwa pengamtan ke-5 merupakan pencilan.
a. Uji hipotesis
𝐻0= pengamatan ke-i tidak berpengaruh 𝐻1= pengamatan ke-i berpengaruh
b. Menetukan tingkat signifikansi 𝛼
c. Menentukan statistik uji
𝐷𝐹𝐼𝑇𝑆𝑖 = √1 − ℎℎ𝑖𝑖 𝑖𝑖 𝑢𝑖√
𝑛 − 𝑝 − 1
(𝑛 − 𝑝)𝑀𝑆𝐸(1 − ℎ𝑖𝑖) − 𝑢𝑖2
𝐷𝐹𝐼𝑇𝑆5 = √1 − 0,1 0,1 (8,913)
𝐷𝐹𝐼𝑇𝑆5 = 2,97
d. Menentukan kriteria pengujian
𝐻0 ditolak jika 𝐷𝐹𝐼𝑇𝑆𝑖 > 2√𝑝 𝑛⁄ , 2√𝑝 𝑛⁄ = 2√1 11⁄ =0,666
e. Menentukan kesimpulan
Karena nilai 𝐷𝐹𝐼𝑇𝑆5=2,97>0,666, maka 𝐻0 ditolak, jadi dapat disimpulkan bahwa pengamtan ke-5 tidak mempunyai pengaruh terhadap model.