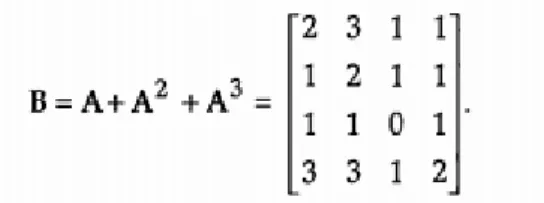5. Representasi Matrix

1

5. Representasi Matrix

Oleh : Ade Nurhopipah

Pokok Bahasan :

1. Matrix Ketetanggaan

2. Walk Pada Graph dan Digraph 3. Matrix Insidensi

Sumber :

Aldous, Joan M. ,Wilson, Robin J. 2004. Graph and Applications. Springer: UK.

Kita telah mempelajari cara merepresentasikan sebuah graph atau digraph sebagai sebuah diagram yang memuat sejumlah vertex dan dihubungkan dengan edge atau arc. Representasi permasalahan dengan diagram ini sangat berguna untuk banyak situasi, terutama jika kita ingin melihat struktur graph atau digraph secara keseluruhan. Namun jika kita memiliki graph atau digraph yang memiliki ukuran besar dan kompleks, kita membutuhkan cara representasi graph atau digraph dalam bentuk lain yang lebih sesuai.

Salah satu cara representasi yang mungkin dilakukan adalah dengan membuat sebuah tabel yang mengindikasikan pasangan vertex yang bertetangga, atau vertex mana yang insiden dengan suatu edge/arc. Pada metode ini kita menyajikan graph atau digraph dengan array segiempat yang disebut matrix. Pada bagian ini, kita akan membahas tentang dua matrix yang dapat merepresentasikan graph atau digraph yaitu matrix ketetanggaan dan matrix insidensi.

Matrix Ketetanggaan (Adjacency Matrices)

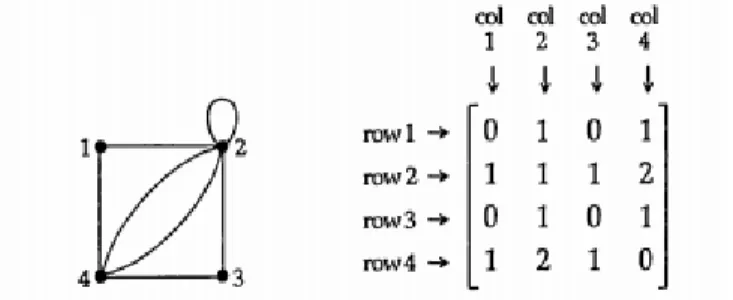
Perhatikan contoh pada Gambar 5.1. Kita memiliki graph dengan empat vertex dan kita akan merepresentasikannya dengan sebuah matrix dengan empat baris dan empat kolom.

Gambar 5.1 Contoh representasi matrix ketetanggan untuk graph

Angka yang muncul dalam matrix pada Gambar 5.1 mengacu pada jumlah edge yang menghubungkan vertex yang berkoresponden dengan graph sebagai berikut.

2 Vertex 1 dan 2 dihubungkan dengan 1 edge, sehingga angka 1 muncul pada baris 1 kolom 2, dan pada baris 2 kolom 1.

Vertex 2 dan 4 dihubungkan dengan 2 edge, sehingga angka 2 muncul pada baris 2 kolom 4, dan pada baris 4 kolom 2.

Vertex 1 dan 3 dihubungkan dengan 0 edge, sehingga angka 0 muncul pada baris 1 kolom 3, dan pada baris 3 kolom 1

Vertex 2 dihubungkan dengan dirinya sendiri dengan 1 edge, sehingga angka 1 muncul pada baris 2 kolom 2.

Definisi 5.1

Misalkan G adalah sebuah graph dengan n vertex yang dilabeli 1,2,3,...,n.

Matix ketetanggaan dari G atau A(G) adalah matrix nxn di mana entri pada baris i kolom j adalah jumlah edge yang menghubungkan vertex i dan vertex j.

Latihan 5.1

1. Tulislah matrix ketetanggaan dari graph berikut.

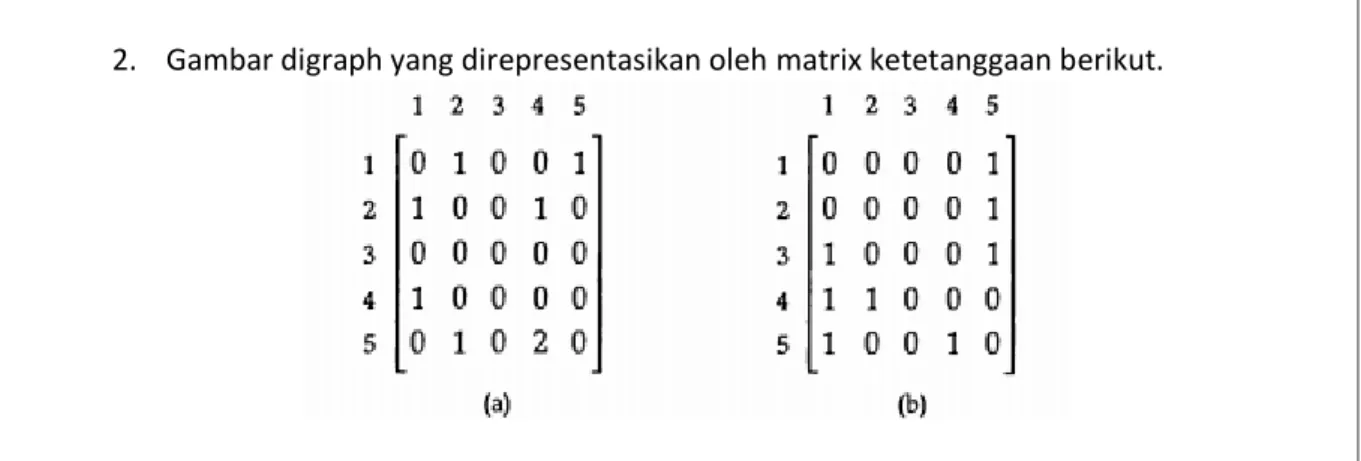
2. Gambar graph yang direpresentasikan oleh matrix ketetanggaan berikut.

Matrix ketetanggaan dari sebuah graph adalah matrix simetris pada diagonal utamanya (kiri atas ke kanan bawah). Untuk graph tanpa loop, diagonal utama matrix semua berisi 0. Jumlah dari semua elemen pada baris atau kolom tertentu pada matrix tersebut menyatakan derajat vertex dari baris dan kolom yang mewakilinya.

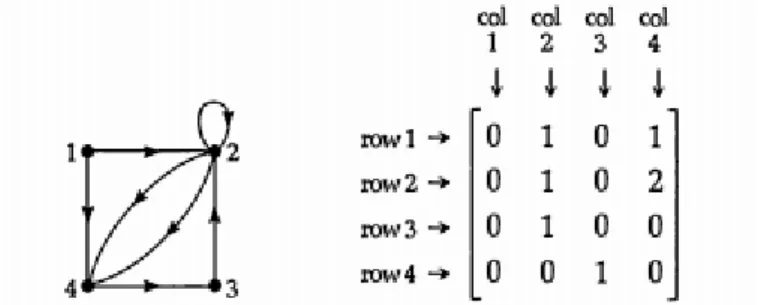
3 Representasi matrix untuk digraph, analog dengan representasi matrix untuk graph. Sebagai contoh perhatikan Gambar 5.2. Kita memiliki digraph dengan empat vertex yang akan direpresentasikan oleh matrix dengan empat baris dan empat kolom.

Gambar 5.2 Contoh representasi matrix ketetanggan untuk digraph

Angka yang muncul dalam matrix mengacu pada jumlah arc yang menghubungkan vertex yang berkoresponden dengan digraph sebagai berikut.

Vertex 1 ke 2 dihubungkan dengan 1 arc, sehingga angka 1 muncul pada baris 1 kolom 2. Vertex 2 ke 4 dihubungkan dengan 2 arc, sehingga angka 2 muncul pada baris 2 kolom 4. Vertex 1 ke 4 dihubungkan dengan 1 arc, sehingga angka 1 muncul pada baris 1 kolom 4. Vertex 4 ke 1 dihubungkan dengan 0 arc, sehingga angka 0 muncul pada baris 4 kolom 1.

Vertex 2 dihubungkan dengan dirinya sendiri dengan 1 arc, sehingga angka 1 muncul pada baris 2 kolom 2.

Definisi 5.2

Misalkan D adalah sebuah digraph dengan n vertex yang dilabeli 1,2,3,...,n.

Matix ketetanggaan dari D atau A(D) adalah matrix nxn di mana entri pada baris i kolom j adalah jumlah arc dari vertex i ke vertex j.

Latihan 5.2

4 2. Gambar digraph yang direpresentasikan oleh matrix ketetanggaan berikut.

Matrix ketetanggaan dari digraph biasanya tidak simetris pada diagonal utamanya. Jumlah entri pada sebuah baris merupakan derajat keluar dari vertex yang mewakilinya, dan jumlah entri pada sebuah kolom menunjukan derajat masuk pada vertex yang mewakilinya.

Walk dalam Graph dan Digraph

Kita dapat membangun walk yang ada dalam graph atau digraph dengan menggunakan matrix ketetanggan. Pada contoh berikut, kita akan fokuskan pembahasan untuk digraph. Cara dan hasil yang sama dapat diturunkan untuk walk dalam graph.

Gambar 5.3 Contoh representasi matrix ketetanggan untuk digraph

Pada Gambar 5.3, ditunjukan tabel yang berisi jumlah walk dengan panjang 1 antara setiap pasangan vertex pada digraph. Perhatikan contoh berikut.

Jumlah walk dari a ke c dengan panjang 1 adalah 0, sehingga angka 0 muncul pada baris 1 kolom 3. Jumlah walk dari b ke a dengan panjang 1 adalah 1, sehingga angka 1 muncul pada baris 2 kolom 1. Jumlah walk dari d ke b dengan panjang 1 adalah 2, sehingga angka 2 muncul pada baris 4 kolom 2. Perhatikan bahwa suatu walk dengan panjang 1 merupakan sebuah arc pada digraph, sehingga tabel tersebut tidak lain sama dengan matrix ketetanggaan dari digraph tersebut.

Selanjutnya, mari kita perhatikan walk dengan panjang 2 dan 3. Sebagai contoh, terdapat dua walk yang berbeda dengan panjang 2 dari a ke b, karena ada sebuah arc dari a ke d dan ada dua buah arc dari d ke b. Begitu juga terdapat dua walk berbeda dengan panjang 3 dari d ke d, karena ada dua arc dari d ke b, dan ada satu walk dengan panjang 2 dari b ke d,

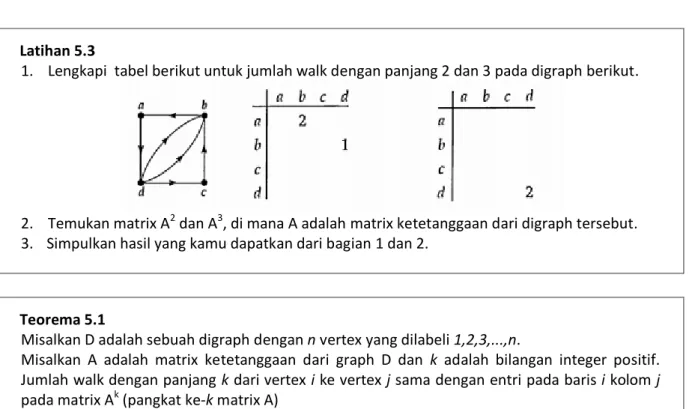
5 Latihan 5.3

1. Lengkapi tabel berikut untuk jumlah walk dengan panjang 2 dan 3 pada digraph berikut.

2. Temukan matrix A2 dan A3, di mana A adalah matrix ketetanggaan dari digraph tersebut. 3. Simpulkan hasil yang kamu dapatkan dari bagian 1 dan 2.

Teorema 5.1

Misalkan D adalah sebuah digraph dengan n vertex yang dilabeli 1,2,3,...,n.

Misalkan A adalah matrix ketetanggaan dari graph D dan k adalah bilangan integer positif. Jumlah walk dengan panjang k dari vertex i ke vertex j sama dengan entri pada baris i kolom j pada matrix Ak (pangkat ke-k matrix A)

Bukti

Bukti teorema 5.1 dilakukan dengan induksi matematika. Langkah 1

Pernyataan untuk k=1 adalah benar, karena jumlah walk dengan panjang 1 dari vertex i ke vertex j adalah jumlah arc dari vertex i ke vertex j , dan ini sama dengan aij yang merupakan entri pada baris i dan kolom j pada matrix ketetanggaan A.

Langkah 2

Kita asumsikan bahwa k>1, dan pernyataan tersebut benar untuk semua bilangan integer yang lebih kecil dari k. Kita ingin membuktikan bahwa pernyataan tersebut juga benar untuk semua bilangan integer k.

Misalkan terdapat sebuah walk dengan panjang k dari vertex i ke vertex j. Walk ini memiliki walk dengan panjang k-1 dari vertex i ke suatu vertex r yang bertetangga dengan vertex j, diikuti dengan suatu walk dengan panjang 1 dari vertex r ke vertex j seperti ditunjukan pada Gambar5.4.

6 Jumlah walk dengan panjang k-1 dari vertex i ke vertex r adalah entri dari baris i kolom r dari matrik Ak-1, (dinotasikan dengan 𝑎𝑖𝑟𝑘−1). Karena jumlah walk dengan panjang 1 dari vertex r ke

vertex j adalah arj, maka, jumlah walk dengan panjang k dari vertex i ke vertex j melalui vertex r

adalah 𝑎𝑖𝑟𝑘−1𝑎𝑟𝑗.

Sekarang, jumlah total walk dengan panjang k dari vertex i ke vertex j sama dengan, jumlah walk melalui vertex 1 + jumlah walk melalui vertex 2 + ….

jumlah walk melalui vertex r + …+ jumlah walk melalui vertex n. atau,

𝑎_𝑖1𝑘−1𝑎1𝑗+ 𝑎𝑖2𝑘−1𝑎2𝑗+ ⋯ + 𝑎𝑖𝑟𝑘−1𝑎𝑟𝑗+ ⋯ + 𝑎𝑖𝑛𝑘−1𝑎𝑛𝑗

Dengan aturan perkalian matrix, kita tahu bahwa rumus ini merupakan entri pada baris i dan kolom j pada matrix Ak-1A = Ak.

Pernyataan ini adalah benar untuk semua bilangan integer positif lebih kecil dari k, maka ia pun benar untuk bilangan integer k.

Dengan prinsip induksi matematika, pernyataan pada teorema 5.1 tersebut adalah benar untuk setiap bilangan integer positif k.

Latihan 5.4

Tuliskan matrix ketetanggaan A untuk digraph berikut, lalu hitunglah A2, A3, A4! Temukan pula jumlah walk dengan panjang 1,2,3 dan 4!

Apakah ada walk dengan panjang 1, 2, 3 atau 4 dari d ke b?

Matrix ketetanggaan dapat pula dipakai sebagai cara untuk menentukan apakah sebuah digraph merupakan digraph yang terhubung kuat atau bukan. Kita mengetahui bahwa suatu digraph terhubung kuat jika ada path dari setiap pasang vertexnya. Sebagai contoh pada digraph sebelumnya kita memperoleh walk dengan panjang 1,2 dan 3. Kita perhatikan bahwa walk (termasuk path) dengan panjang 1, 2 dan 3 di antara dua vertex yang berbeda diberikan oleh entri matrix pada elemen non-diagonalnya.

7 Dengan memperhatikan matrix tersebut, kita mengetahui bahwa setiap pasangan vertex dihubungkan dengan setidaknya sebuah path dengan panjang 1,2, atau 3, sehingga digraph tersebut terhubung kuat. Kita dapat mengecek ini lebih mudah dengan menyajikan sebuah matrix B yang diperoleh dengan cara menjumlahkan tiga matrix tersebut.

Gambar 5.6 Matrix B penjumlahan dari A, A2 dan A3

Misalnya kita menotasikan bij dengan entri untuk baris i kolom j pada matrix B, maka setiap

entri bij adalah jumlah total walk dengan panjang 1, 2 dan 3 dari vertex i ke vertex j. Semua entri

non diagonalnya adalah positif, artinya setiap pasangan vertex yang berbeda dihubungkan dengan path, sehingga digraph tersebut adalah digraph yang terhubung kuat.

Teorema 5.2

Misalkan D adalah digraph dengan n vertex yang dilabeli 1,2,3,.., n, misalkan A adalah matrix ketetanggaan dari matrix D, dan B adalah sebuah matrix yang didefinisikan sebagi berikut.

B= A+A2+A3+...An-1

Maka D terhubung kuat jika dan hanya jika setiap entri non diagonal pada matrix B adalah positif, atau bij >0, untuk i≠j.

Bukti

Ada dua pernyataan yang harus dibuktikan.

a. Jika setiap entri non-diagonal pada B positif, maka D terhubung kuat.

Misalkan D adalah digraph yang memenuhi kondisi tersebut, dan misalkan setiap entri non diagonal di B adalah positif, maka bij >0 untuk i≠j, maka 𝑎𝑖𝑗𝑘 > 0 untuk suatu k≤n-1. Maka ada

suatu walk dengan panjang paling besar n-1 dari vertex i ke vertex j, sehingga digraph D adalah digraph yang terhubung kuat.

b. Jika digraph D terhubung kuat, maka setiap entri non-diagonal pada B adalah positif.

Misalkan D adalah digraph yang terhubung kuat yang memenuhi kondisi tersebut, maka ada sebuah path dari suatu vertex ke vertex lain. Karena D memiliki n vertex, maka sebuah path memiliki panjang paling besar n-1. Oleh karena itu, 𝑎𝑖𝑗𝑘 > 0 untuk setidaknya satu nilai dari

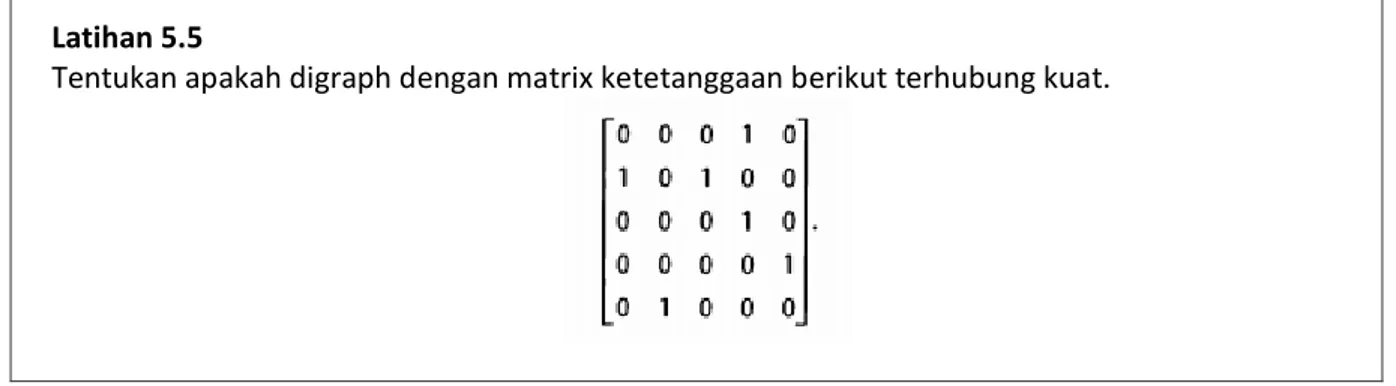
8 Latihan 5.5

Tentukan apakah digraph dengan matrix ketetanggaan berikut terhubung kuat.

Matrix Insidensi

Pada bagian ini kita akan membatasi pembahasan untuk graph dan digraph yang tidak memiliki loop. Jika matrix ketetanggaan pada graph dan digraph melibatkan ketetanggaan antar vertex, maka pada matrix insidensi kita melibatkan insidensi vertex dengan edge atau arc.

Gambar 5.7 Representasi matrix insidensi untuk graph

Perhatikan contoh pada Gambar 5.7. Kita memiliki graph dengan empat buah vertex yang berlabel dan enam edge yang berlabel. Perhatikan matrix insidensi yang terbentuk. Kita memiliki empat buah baris dan enam buah kolom. Setiap angka yang muncul pada matrix tersebut adalah bilangan 0 atau 1, tergantung pada vertex dan edge yang diwakilinya apakah insiden satu sama lain atau tidak. Sebagai contoh,

Vertex (1) insiden dengan edge 4 sehingga angka 1 muncul pada baris ke 1 kolom 4. Vertex (2) tidak insiden dengan edge 4 sehingga angka 0 muncul pada baris ke 2 kolom 4.

Definisi 5.3

Misalkan G adalah graph tanpa loop dengan n vertex yang dilabeli (1), (2), ..., (n) dan m edge yang dilabeli 1,2,3,..,m.

Matrix insidensi dari G atau I(G) adalah matrix berukuran nxm dimana entri pada baris i kolom j adalah sebagai berikut.

9

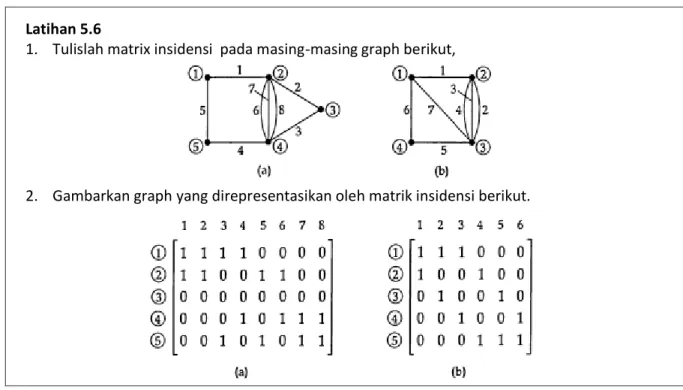
Latihan 5.6

1. Tulislah matrix insidensi pada masing-masing graph berikut,

2. Gambarkan graph yang direpresentasikan oleh matrik insidensi berikut.

Pada matrix insidensi sebuah graph tanpa loop, setiap kolom mengandung tepat dua buah angka 1, yang menggambarkan bahwa suatu edge menghubungkan tepat dua buah vertex. Jumlah bilangan pada sebuah baris sama dengan derajat vertex yang diwakilinya.

Jika dalam matrix ketetanggaan sebuah digraph melibatkan ketetanggaan dua buah vertex, maka dalam matrix insidensi sebuah digraph, kita melibatkan insidensi vertex dengan arc. Pada matrix insidensi digraph kita harus memperhatikan apakah sebuah arc insiden dari, insiden ke atau tidak insiden dengan sebuah vertex.

Gambar 5.8 Representasi matrix insidensi untuk digraph

Perhatikan contoh pada Gambar 5.8. Pada digraph tersebut kita memiliki sebuah digraph dengan empat vertex berlabel dan enam arc berlabel. Pada matrix insidensi yang dihasilkan kita mempunyai sebuah matrix yang memiliki empat baris dan enam kolom.

10 Setiap angka yang muncul pada matrix adalah 1, -1 atau 0 tergantung pada apakah arc yang berkoresponden insiden ke, insiden dari atau tidak insiden dengan vertex tersebut. Perhatikan contoh sebagai berikut.

Arc 4 insiden dari vertex (1), sehingga angka 1 muncul pada baris ke 1 kolom ke 4. Arc 5 insiden ke vertex (4), sehingga angka -1 muncul pada baris ke 4 kolom ke 5. Arc 4 tidak insiden dari vertex (2), sehingga angka 0 muncul pada baris ke 2 kolom ke 4.

Definisi 5.4

Misalkan D adalah digraph tanpa loop dengan n vertex yang dilabeli (1), (2), ..., (n) dan m arc yang dilabeli 1,2,3,..,m.

Matrix insidensi dari D atau I(D) adalah matrix berukuran nxm di mana entri pada baris i kolom j adalah sebagai berikut.

{

1 , jika arc 𝑗 insiden dari vertex 𝑖 −1, jika arc 𝑗 insiden ke vertex 𝑖 0, selainnya

Latihan 5.7

1. Tulislah matrix insidensi pada masing-masing digraph berikut.

2. Gambarkan digraph yang direpresentasikan oleh matrik insidensi berikut.

Dalam matrix insidensi digraph tanpa loop, setiap kolom memiliki tepat sebuah nilai 1 dan sebuah nilai -1, yang menggambarkan bahwa sebuah arc tersebut insiden dari sebuah vertex ke vertex lain. Jumlah angka 1 pada setiap baris menggambarkan derajat keluar dari vertex yang berkoresondensi dan jumlah angka -1 pada setiap baris menggambarkan derajat masuk dari vertex tersebut.

11

Studi Kasus

Interval Graph

Interval graph adalah graph yang menggambarkan situasi yang melibatkan penyusunan suatu data dengan susunan kronologi. Pada graph ini vertex berkoresponden dengan objek yang sedang disusun, dan edge berkoresponden dengan pasangan vertex yang bertumpang tindih dengan cara tertentu.

Arkeologi

Pada akhir abad ke-19, para arkeolog tertarik terhadap artefak yang ditemukan pada beberapa kuburan di Mesir. Untuk menentukan usia artefak tersebut, mereka berasumsi bahwa jika dua artefak berbeda ditemukan bersama-sama dalam satu kuburan, maka periode waktu keduanya pasti bertumpang tindih.

Suatu pendekatan yang menjanjikan untuk masalah ini adalah dengan merepresentasikan data ini dalam graph, di mana vertex mewakili artefak dan edge mewakili pasangan artefak yang muncul bersama-sama dalam satu kuburan. Misalkan kita memiliki enam buah artefak, dan kondisi apakah kedua artefak tersebut muncul dalam satu kuburan disajikan dalam Gambar 5.9. Pada Gambar tersebut ditunjukan bahwa kita dapat membuat matrix ketetanggaan dari situasi yang diberikan. Jika dua buah artefak muncul dalam kuburan yang sama maka kita beri nilai 1 jika tidak kita beri nilai 0. Dengan matrix ketetanggaan tersebut kita dapat membuat graphnya.

Gambar 5.9 Contoh representasi matrix ketetanggaan dalam arkeologi

Untuk merepresentasikan graph tersebut ke dalam bentuk kronologis, kita membangun suatu himpunan interval dengan sebuah garis yang berkoresponden dengan periode waktu munculnya artefak tersebut. Artefak diwakili dengan suatu interval dan dan pasangan artefak yang muncul bersama dalam sebuah kuburan diwakili dengan interval yang overlapping (saling bertumpang tindih) seperti ditunjukan pada Gambar 5.10.

12 Pada Gambar 5.10 ditunjukan bahwa vertex yang mewakili artefak a dan b bertetangga, sehingga interval keduanya bertumpang tindih. Vertex yang mewakili artefak a dan f tidak bertetangga, sehingga intervalnya tidak tumpeng tindih. Graph yang memberikan suatu gambaran interval seperti ini disebut graph interval.

Latihan 5.8

Gambarlah suatu graph dan interval graph yang muncul dengan himpunan interval berikut. (1,2), (3,4), (5,6), (7,8), (1,6), (2,7), (3,8).

Genetika

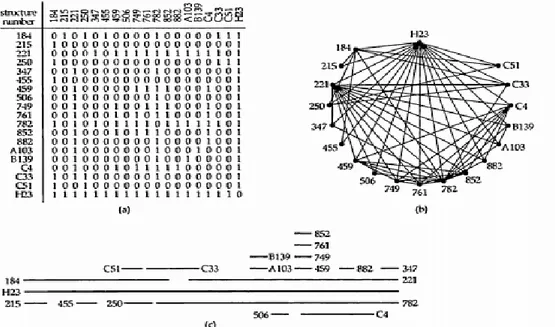
Untuk beberapa waktu, genetika menganggap kromosom sebagai sebuah susunan linier dari suatu gen. Suatu pertanyaan muncul dalam bidang genetika yaitu apakah struktur yang benar dalam gen disusun dalam sebuah susunan yang linier. Masalah ini disebut sebagai Benzer’s problem. Sayangnya struktur ini terlalu detail untuk diteliti secara langsung. Oleh karena itu untuk mengetahuinya, dipelajari perubahan pada struktur gen secara keseluruhan yang dikenal sebagai mutasi.

Dalam menganalisa struktur genetik suatu bakteri yang disebut phage T4, Seymour Benzer memperlihatkan suatu mutasi yang dihasilkan saat suatu bagian dari sebuah gen hilang. Dia mempelajari mutasi di mana segmen yang hilang bertumpang tindih, dan menyajikan hasilnya dalam bentuk matrix overlap yang ditunjukan oleh Gambar 5.11. Matrix berukuran 19x19 pada Gambar 5.11 adalah matrix ketetanggaan, di mana vertex mewakili mutasi dan edge mewakili pasangan mutasi dengan segmen hilang yang bertumpang tindih. Pada Gambar tersebut juga ditunjukan graph interval yang muncul dari matrix ketetangaan tersebut.

13 Rantai Markov

Rantai Markov telah dipakai dalam berbagai bidang misalnya dalam genetika, statistika, ilmu komputer dan sosiologi. Berikut diberikan contoh penggunaan rantai Markov dengan masalah seorang pemabuk yang berada di antara dua pub. Setiap menit dia memiliki satu dari tiga perilaku berikut.

1. Dia bergeser 10 meter ke pub pertama dengan peluang 1₂. 2. Dia bergeser 10 meter ke pub kedua dengan peluang 1₃. 3. Dia diam dimana dia berada dengan peluang 1₆.

Prosedur seperti ini disebut sebagai suatu walk acak satu dimensi. Kita mengasumsikan bahwa dua pub tersebut dalam kondisi melenakan (menyerap), dalam arti jika sang pemabuk sampai di sana, maka dia akan tetap disana. Permasalahan tersebut ditunjukan pada Gambar 5.12.

Gambar 5.12 Contoh masalah rantai Markov

Misalkan jarak antara dua pub adalah lima puluh meter, kita menotasikan E1, E2 ,..,E6 sebagai

posisi di mana sang pemabuk dapat berhenti.

Posisi pertama E4 dapat dijelaskan dengan vektor x = [0,0,0,1,0,0].

Peluang posisi pemabuk setelah satu menit diberikan oleh vektor [0,0,1₂, 1₆, 1₃] Peluang posisi pemabuk setelah dua menit diberikan oleh vektor [0, 1₄, 1₆, 13₃₆, 1₉, 1₉].

Sebagai contoh peluang sang pemabuk berada di posisi E4 setelah dua menit dapat dihitung sebagai

berikut (1₂×1₃) + (1₆×₆1) + (1₃×1₂) = 13₃₆.

Untuk menyajikan masalah posisi setelah k menit, kita dapat menyajikannya dengan sebuah matrix transisi. Missal pij adalah peluang bahwa dia bergerak dari Ei ke Ej dalam satu menit. Peluang pij disebut peluang transisi, dan matrix P berukuran yang 6x6 dimana entri pada baris i kolom j

adalah pij dikenal sebagai matrix transisi. Secara umum, sebuah matrix transisi adalah matrix

segiempat yang setiap barisnya memuat bilangan tidak negatif yang disebut probabilitas transisi dengan jumlah 1.

Peluang posisi setelah satu menit pada permasalahan di atas ditunjukan pada gambar 5.13. Setelah k menit peluang tersebut ditunjukan oleh vector xPk. Bentuk ini adalah sebuah rantai Markov yang memuat matrix transisi P berukuran nxn, dan vektor barix x berukuran 1xn. Komponen ke-i dari xPk merepresentasikan peluang bahwa sang pemabuk diposisi Ei setelah k menit.

14 Gambar 5.11 Contoh sebuah rantai Markov

Pada masalah ini, jita berkonsentrasi bagaimana kita bisa beralih dari suatu status ke status lain, dan berapa lama waktu untuk mencapainya. Sebagai contoh, pada permasalah di atas, sang pemabuk dapat bergerak dari E4 ke E1 dalam tiga menit dan dari E4 ke E6 dalam dua menit. Namun

sang pemabuk tidak akan bisa bergerak dari posisi E1 ke E4 karena asumsi kita bahwa kedua pub

bersifat menyerap.

Pada masalah ini, perhatian utama kita adalah pada probabilitas pij, saat ia tidak bernilai 0.

Kita dapat merepresentasikan situasi ini ke dalam digraph, di mana vertex mewakili status dan arc menunjukan ke mana kita dapat bergerak dari satu status ke status yang lain dalam satu menit. Matrix ketetanggaan dari masalah rantai Markov diperoleh dengan mengganti semua nilai tidak nol dari entri dalam matrix transisi P dengan angka 1. Jika setiap status Ei direpresentasikan oleh vertex vi, maka kita mendapat digraph yang berasosiasi dengan matrix transisinya. Matrix ketetanggaan dan

digraph yang diperoleh untuk masalah tersebut ditunjukan pada Gambar 5.12.

Gambar 5.12 Contoh representasi digraph untuk rantai Markov

Pada masalah ini, kita dapat bergerak dari status Ei ke ststus Ej dalam sebuah rantai Markov

jika dan hanya jika terdapat sebuah path dari vi ke vj dalam digraph yang berasosiasi dengannya.

Waktu minimal yang dibutuhkan untuk melakukannya adalah panjang path terpendek yang ada. Sebuah rantai Markov di mana kita dapat bergerak dari satu status ke status lainnya disebut rantai Markov irreducible (tidak tereduksi). Rantai Markov irreducible jika hanya jika digraph yang berasosiasi dengannya terhubung kuat. Rantai Markov yang dicontohkan di atas tidak irreducible. Sebagai contoh, tidak ada path dari v1 ke vertex lainnya.

Latihan 5.9

1. Misalkan dalam masalah pemabuk di atas, pub 1 menolaknya, segera setelah ia sampai kesana. Tulislah matrix transisi yang dihasilkan dan digraph yang berasosiasi dengannya. Tentukan apakah rantai Markov yang dihasilkan irreducible.