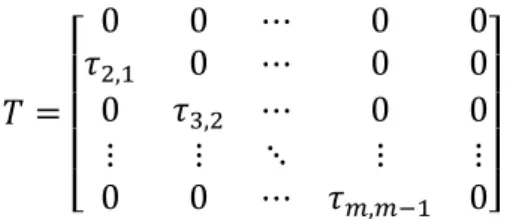TUGAS ANALISIS MATRIKS
APLIKASI TEOREMA PERRON FROBENIUS PADA MODEL MATRIKS
POPULASI LESLIE
Fani Puspitasari 201 16019
Program Studi Magister Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Teknologi Bandung 2016
1. PENDAHULUAN
Teori matriks dan Aljabar Linear memiliki beberapa peranan penting dalam aplikasi masalah real, salah satu contohnya adalah dalam bidang matematika biologi, yaitu dinamika populasi. Populasi dapat didefinisikan sebagai kumpulan tanaman, binatang, atau organisme lainnya (satu spesies) yang tinggal bersama dan bereproduksi. Dinamika populasi adalah suatu keilmuan yang mempelajari bagaimana suatu populasi berubah seiring waktu dan bagaimana mereka berinteraksi dengan faktor biotik dan faktor abiotik di lingkungannya. Faktor- faktor lingkungan tersebut mempengaruhi laju kelahiran, laju kematian dan bahkan fekunditas dari populasi, hal inilah yang menjadi pertanyaan bagi peneliti dalam mempelajari dinamika populasi.
Besarnya perubahan jumlah populasi dalam kurun waktu tertentu akan dapat ditentukan jika dari hasil pengamatan selama kurun waktu tertentu tersebut laju pertumbuhan populasinya diketahui. Dalam hal ini diasumsikan bahwa laju pertumbuhan populasi hanya disebabkan oleh adanya proses kelahiran dan kematian, dan dianggap tidak ada proses migrasi (populasi tertutup).
Secara matematis, laju pertumbuhan populasi yang dikelompokkan berdasarkan distribusi umur dan dalam kurun waktu yang sama, dapat dibawa ke dalam bentuk matriks persegi. Matriks tersebut disebut Matriks Leslie. Model Matriks Leslie merupakan suatu model matematika yang dapat digunakan untuk menentukan pertumbuhan populasi serta distribusi umur populasi dari waktu ke waktu. Model Leslie ini memperhitungkan perbedaan tingkat fertilitas dan kebertahanan hidup populasi di tiap kelompok umur. Jika distribusi populasi mula-mula diketahui, dan laju pertumbuhan populasinya telah diperoleh, maka akan dapat ditentukan distribusi umur populasi pada sebarang waktu ke depan menggunakan matriks Leslie
Teori matriks yang dipakai dari mata kuliah Analisis Matriks dalam memodelkan matriks Leslie adalah Teorema Perron Frobenius dan Matriks Tak Negatif. Dengan teorema Perron Frobenius, diberikan bukti sederhana dari teorema dasar demografi pada bab pembahasan.
2. PEMBAHASAN
Model Leslie dengan struktur umur adalah model dari pembagian kelas-kelas individu
berdasarkan kronologis umur. Model ini mengklasifikasikan individu ke dalam kelas umur dengan panjang partisi sama besar, asumsikan . Perhatikan ilustrasi berikut
dengan kelas umur dan interval umur sebagai berikut
Misalkan ( ) menyatakan jumlah individu pada kelas umur ke- pada waktu
Model matriks Leslie diberikan oleh
( ) ( )
disebut Matriks Leslie (Matriks Proyeksi) berukuran dengan entri-entri tak negatif. Matriks Leslie diberikan oleh
Dengan [ ]
adalah Matriks Fertilitas dimana menyatakan jumlah individu yang baru lahir, sehingga
matriks memuat fertilitas per kapita dari setiap kelas umur di baris pertama. dan
Kelas-Umur (
)
Umur
Tabel 1: pembagian kelas umur dan interval umur dalam populasi
(1)
[
]
adalah Matriks Transisi dimana adalah peluang individu dengan umur yang
bertahan selama satu satuan waktu (dan pindah dari kelas ke kelas ) dan diasumsikan bahwa tidak ada individu yang hidup lebih dari satuan waktu.
Sehingga persamaan matriks model Leslie di atas menjadi
[ ( ) ( ) ( ) ] [ ] [ ( ) ( ) ( ) ]
Secara umum, persamaan matriks dalam bentuk rekursif diberikan oleh ( ) ( ) ( )
Dengan
∑
Pertidaksamaan terakhir menyatakan bahwa penjumlahan entri-entri setiap kolom dari tidak lebih besar dari satu, artinya jumlah individu dari kelas yang didistribusikan ke setiap kelas (termasuk sendiri) pada waktu , tidak akan melebihi jumlah individu yang ada di kelas pada waktu .
Model Leslie dapat diilustrasikan oleh siklus hidup (berikut, dengan adalah individu yang lahir, dan Tj adalah peluang individu yang bertahan dari kelas umur ke kelas umur .
Misalkan terdapat 4 kelas umur,
1
T
12
T
23
T
34
F
2F
3F
1F
4Gambar 1: Siklus hidup dengan 4 kelas umur
(3)
Matriks Leslie sebagai Matriks Tak Negatif
Suatu matriks dikatakan tak negatif jika setiap entrinya tak negatif. Notasikan sebagai himpunan yang beranggotakan vektor . Karena elemen dari maktriks Leslie tak negatif, maka matriks Leslie merupakan matriks tak negatif, artinya solusi ( ) pada persamaan (3) dengan nilai awal ( ) akan tetap tak negatif untuk setiap Definisi 2.1
Matriks persegi dikatakan tak tereduksi jika terdapat matriks permutasi yang memenuhi ( ) untuk suatu ( ) ( ) ( ), .
Matriks Leslie sebagai matriks tak negatif dikatakan tak tereduksi jika dan hanya jika setiap kelas umur dapat dilewati oleh setiap kelas umur lainnya, artinya terdapat path yang menghubungkan satu node ke node lainnya pada siklus hidup model Leslie (lihat gambar 1) Definisi 2.2
Matriks tak tereduksi dikatakan primitif jika terdapat k 0 sehingga k
A positif
Matriks Leslie sebagai matriks tak tereduksi dikatakan primitif jika faktor persekutuan terbesarnya bernilai 1 untuk setiap loop pada grafik siklus hidup model Leslie. Loop adalah
path yang memiliki titik awal dan titik akhir yang sama dan melewati setiap node paling
banyak satu kali.
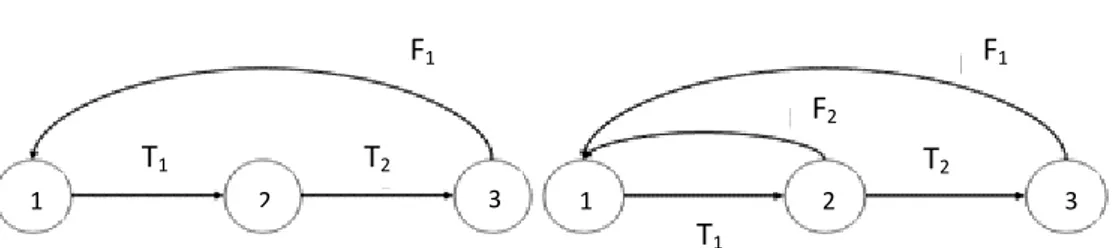
Perhatikan gambar berikut
Gambar 2: Siklus hidup pada gambar kiri tidak primitif karena hanya terdapat satu loop (sehingga tereduksi) dan memiliki panjang 3. Siklus hidup pada gambar kanan primitif karena memiliki 2 loop dengan panjangnya masing-masing 2 dan 3, sehingga fpb nya adalah 1.
Teorema Perron Frobenius dan Teorema Dasar Demografi Populasi
Nilai eigen dari matriks Leslie dengan nilai modulus terbesar disebut nilai eigen dominan. Nilai modulus dari nilai eigen dominan ini disebut radius spektral dari , dinotasikan dengan ( ).
Teorema Perron Frobenius mengimplikasikan bahwa jika matriks Leslie adalah matriks tak negatif dan tak tereduksi, maka Radius spektral ( ) dari adalah nilai eigen dengan
T1 T2 T2
T1
F1 F1
F2
vektor eigen tak negatif terkait. Sedangkan matriks tak tereduksi dikatakan primitif jika ( ) strictly dominant.
Asumsikan nilai-nilai eigen dari matriks Leslie bernilai real dan berbeda satu sama lain, dan misal ( ) . Pada model ini, radius spektral ( ) disebut laju pertumbuhan. Karena berdasar asumsi bahwa nilai eigen berbeda, maka vektor eigen terkait juga berbeda, tulis vektor populasi awal ( ) sebagai kombinasi linear dari vektor-vektor eigen matriks Leslie
k i i iw c x 1 ) 0 (Dimana koefisien ci ditentukan dari vektor awal ( ) dan adalah vektor eigen terkait.
Terapkan matriks Leslie pada persamaan di atas, dan lakukan iterasi sebagai berikut
k i i i i k i i i k i i iw cPw c w c P Px x 1 1 1 ) 0 ( ) 1 (
k i i i i k i i i i k i i i i w c Pw c w c P Px x 1 2 1 1 ) 1 ( ) 2 ( : :
k i i t i i k i i t i i k i i t i i w c Lw c w c P t Px t x 1 1 1 1 1 ) 1 ( ) ( Sehingga vektor populasi pada saat adalah penjumlahan berbobot dari t i
. Teorema 2.1
Misal adalah matriks Leslie dengan model ( ) (persamaan 1). Misalkan matriks tak negatif tak tereduksi dan primitif dengan radius spektral ( ) , maka
( )
Dimana adalah vektor eigen terkait dengan nilai eigen terbesar Teorema ini disebut Teorema Dasar Demografi Populasi
Bukti:
Karena setiap nilai eigen dari matriks Leslie berbeda, misal ( ) r12 3 .
sehingga untuk , nilai eigen terbesar akan mendominasi persamaan berikut (5)
t t k k t t k i i t i i t w r c w r c w c r w r c r t x saat 0 2 2 2 2 1 1 1 ) ( atau dapat ditulis
1 1 ) ( lim cw r t x t t Teorema 2.2
Misal persamaan matriks dipenuhi oleh persamaan (3) dan berdasarkan asumsi (4). Jika ( ) maka seluruh solusi memenuhi ( )
Teorema 2.3
Misal persamaan matriks dipenuhi oleh persamaan (3) dan berdasarkan asumsi (4). Asumsikan primitif. Jika ( ) 1 maka seluruh solusi dengan nilai awal ( ) ( ) memenuhi | ( )|
Dari teorema 2.1 dan teorema 2.3 , dapat dilihat bahwa berapapun nilai awal ( ) populasi akan tumbuh secara eksponensial tanpa batas jika ( ) dan pertumbuhan populasi akan menurun dengan cepat jika ( )
Laju Reproduksi Rasio ( )
Radius spektral ( ) dari matriks transisi adalah nilai modulus terbesar nilai eigen . Karena dalam populasi tak ada peluang individu dapat hidup selamanya, maka asumsikan ( ) untuk setiap nilai awal ( ), asumsi ini ekivalen dengan
( ) Berdasar asumsi (7) , diperoleh
( )
Misal ( ) , maka
( ) ( ) ( ) ( )
Persamaan (9) memiliki interpretasi biologi, yakni jika peluang individu bertahan selama waktu adalah , maka ekspektasi jumlah keturunan yang dihasilkan individu baru pada waktu ke- adalah , dengan adalah jumlah keturunan yang baru lahir. Radius spektral (7)
(8)
dari ( ( ) ( ( ) )) disebut laju reproduksi rasio atau lebih sering dikenal
dengan notasi .
3. REFERENSI
[1] Leslie, P.H.: On the uses of matrices in certain population mathematics, Biometrika 35, 213-212 (1945)
[2] Cushing, J.M.: Matrix Models and population dynamics, 5-12
[3] Li, Chi-Kwong dan Schneider, H.: Application of Perron –Frobenius theory to population dynamics