ANALISIS MODEL MATRIKS LESLIE DAN PENERAPANNYA DALAM MEMPREDIKSI JUMLAH DAN LAJU PERTUMBUHAN POPULASI PEREMPUAN SKRIPSI HAFIZA BALQIS

(1)

ANALISIS MODEL MATRIKS LESLIE DAN PENERAPANNYA DALAM MEMPREDIKSI JUMLAH DAN LAJU PERTUMBUHAN

POPULASI PEREMPUAN

SKRIPSI

HAFIZA BALQIS 160803055

PROGRAM STUDI S1 MATEMATIKA DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2021

Universitas Sumatera Utara

(2)

SKRIPSI

DIAJUKAN UNTUK MELENGKAPI TUGAS AKHIR DAN MEMENUHI SYARAT MENCAPAI GELAR SARJANA SAINS

HAFIZA BALQIS 160803055

PROGRAM STUDI S1 MATEMATIKA DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2021

(3)

PERNYATAAN ORISINALITAS

SKRIPSI

Saya menyatakan bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Januari 2021

Hafiza Balqis 160803055

(4)

(5)

ii

ABSTRAK

Matriks Leslie merupakan suatu model yang digunakan untuk memprediksi laju pertumbuhan populasi perempuan. Matriks Leslie diperkenalkan oleh P.H Leslie pada tahun 1945. Terdapat tiga komponen penting dalam matriks Leslie yaitu jumlah penduduk perempuan, tingkat kesuburan dan tingkat ketahanan hidup.

Menentukan laju pertumbuhan populasi dicari nilai eigen positif . Tiga kasus yang berkaitan dengan nilai eigen positif , yaitu populasi cenderung meningkat jika , populasi cenderung menurun jika dan populasi akan stabil jika . Tulisan ini memprediksi jumlah dan laju pertumbuhan populasi perempuan di Kelurahan Sukaramai I. Dari penelitian yang dilakukan, diperoleh nilai eigen sebesar 0,7217. Oleh karena itu jumlah populasi perempuan cenderung mengalami penurunan pada tahun berikutnya.

Kata kunci: Model matriks Leslie, Pertumbuhan populasi, Nilai eigen

(6)

ANALYSIS OF THE LESLIE MATRIX MODEL AND APPLICATION IN PREDICTING GROWTH AMOUNT AND RANGE

FEMALE POPULATION

ABSTRACT

Leslie Matrix is a model used to predict the growth rate of the female population.

Leslie matrix is introduced by P.H Leslie in 1945. There are three significant components in Leslie matrix which are the number of female population, the fertility rates,and the survival rates. determine the population growth rate searching for positive eigenvalue. There are three cases are related to positve eigen values of , which tends to increase if , the population tends to decrese if and the population will be stable if . This study, predicts population size and growth rate in Sukaramai I sub-district. in this study, the eigenvalue was 0,7212. therefore, the number of female population tends to decline in the following years.

Keyword : Leslie Matrix Model, Population Growth, Eigenvalue

(7)

iv

PENGHARGAAN

Puji dan syukur penulis ucapkan kehadirat Allah SWT yang telah memberikan rahmat serta karunia-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul “Analisis Model Matriks Leslie dan Penerapannya dalam Memprediksi Jumlah dan Laju Pertumbuhan Populasi Perempuan”. Tujuan penulisan skripsi ini adalah sebagai salah satu syarat untuk memperoleh gelar Sarjana Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

Pada kesempatan ini penulis ingin mengucapkan terima kasih kepada pihak yang telah membantu keberhasilan penyusunan skripsi ini baik secara langsung maupun tidak langsung. Penulis mengucapkan terima kasih sebesar-besarnya kepada:

1. Bapak Prof. Dr. Runtung, S.H., M.Hum selaku Rektor universitas Sumatera Utara.

2. Bapak Prof. Dr. Kerista Sebayang, M.S selaku Dekan FMIPA serta seluruh Staf pegawai di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

3. Bapak Dr. Suyanto, M.Kom dan Bapak Drs. Rosman Siregar, M.Si selaku Ketua dan Sekretaris jurusan matematika serta seluruh Bapak dan Ibu dosen yang telah mendidik penulis selama menjalani pendidikan di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

4. Ibu Dr. Mardiningsih, M.Si selaku dosen pembimbing yang senantiasa membantu, membimbing dan mengarahkan penulis dalam menyelesaikan skripsi ini.

5. Bapak Dr. Sawaluddin, M.IT dan Bapak Drs. Ujian Sinulingga, M.Si selaku dosen pembanding yang memberikan kritik dan saran yang membangun dalam menyelesaikan skripsi penulis.

6. Seluruh dosen dan pegawai Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

(8)

7. Teristimewa kepada kedua orang tua tercinta Ayahanda Ir. Ahyar, Ibunda Fitri, Abangda Muhammad Buchari, S.T yang telah memberikan kasih sayang yang tiada akhir, motivasi serta dukungan do’a.

8. Seluruh rekan-rekan mahasiswa angkatan 2016 Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, terkhusus kepada Dinna Khairunisyah Nasution, Dea Kusuma Umaeni Sulfa, Fini Ardiani Br. Damanik, Firza Yunara, Khairunnisa Rangkuti, Muthia Rachma Afifah, Sintya Surya Ningsih dan Maharani Beruh.

Terim kasih penulis ucapkan kepada seluruh pihak yang telah membantu dalam proses pembuatan skripsi.

Medan, Januari 2021

Hafiza Balqis

(9)

vi

DAFTAR ISI

Halaman

PENGESAHAN SKRIPSI I

ABSTRAK Ii

ABSTRACT Iii

PENGHARGAAN Iv

DAFTAR ISI Vi

DAFTAR TABEL Viii

DAFTAR GAMBAR Ix

DAFTAR LAMPIRAN X

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Rumusan Masalah 2

1.3 Batasan Masalah 3

1.4 Tujuan Penelitian 3

1.5 Manfaat Penelitian 3

BAB 2 TINJAUAN PUSTAKA 4

2.1 Matriks 4

2.1.1 Definisi Matriks 4

2.1.2 Jenis-jenis Matriks 4

2.1.3 Nilai Eigen dan Vektor Eigen 6

2.1.4 Diagonalisasi 7

2.2 Bilangan Kompleks 8

2.2.1 Definisi Bilangan Kompleks 8

2.2.2 Bentuk Polar dan Eksponen dari Bilangan Kompleks 8

2.2.3 Pangkat dari Bilangan Kompleks 9

2.3 Model Matriks Leslie 10

2.4 Karakteristik Model Matriks Leslie 14

BAB 3 METODE PENELITIAN 15

3.1 Metodologi Penelitian 15

3.2 Kerangka Penelitian 16

BAB 4 HASIL DAN PEMBAHASAN 17

4.1 Analisa Model 17

4.2 Model Matriks Leslie dalam Memprediksi Jumlah Populasi 18 4.3 Penerapan Model Matriks Leslie Pada Pertumbuhan Populasi 29

4.3.1 Data Penduduk Perempuan 30

4.3.2 Model Matriks Leslie 31

4.3.3 Proyeksi Jumlah Populasi 35

4.3.4 Nilai Eigen dan Vektor Eigen 40

BAB 5 KESIMPULAN DAN SARAN 43

5.1 Kesimpulan 43

(10)

5.2 Saran 43

DAFTAR PUSTAKA 44

(11)

viii

DAFTAR TABEL No

Tabel Judul Halaman

2.1 Penentuan Kelas Umur 10

2.2 Parameter dalam Model Matriks Leslie 11

4.1 Data Penduduk Perempuan di Kelurahan Sukaramai I

tahun 2014-2016 30

4.2 Tingkat Kesuburan dan Tingkat Ketahanan Hidup

Perempuan di Kelurahan Sukaramai I Tahun 2014-2016 34

4.3 Nilai Eigen Matriks Leslie L 40

(12)

DAFTAR GAMBAR No

Gambar Judul Halaman

2.1 Bidang Kompleks 8

3.1 Diagram Kerangka Penelitian 16

4.1 Grafik Fungsi ( ) 20

(13)

x

DAFTAR LAMPIRAN No

Lampiran Judul Halaman

1 Data Kelahiran Anak Berdasarkan Umur Ibu Saat

Melahirkan di Kelurahan Sukaramai I Tahun 2014-2016 45 2 Data Kematian Perempuan di Kelurahan Sukaramai I

tahun 2014-2016 46

3 Mencari Nilai Eigen Menggunakan Software MATLAB 49 4 Surat Izin Penelitian dari Kelurahan Sukaramai I 50

(14)

1.1 Latar Belakang

Matriks Leslie adalah salah satu model pertumbuhan populasi yang paling umum digunakan oleh para ahli demografi. Model ini menjelaskan pertumbuhan jenis kelamin perempuan pada populasi manusia atau hewan dalam model ini perempuan (manusia) atau betina (hewan) dibagi menjadi kelas-kelas umur dalam durasi waktu yang sama. Dalam model matriks Leslie proses kelahiran dan kematian tergantung oleh umur dan menjadi bagian yang penting dalam pertumbuhan populasi.

Proyeksi penduduk bukan merupakan ramalan jumlah penduduk tetapi suatu perhitungan ilmiah yang didasarkan pada asumsi dari komponen-komponen laju pertumbuhan penduduk, yaitu kelahiran, kematian dan ketahanan hidup. Ketiga komponen inilah yang menentukan besarnya jumlah penduduk dan struktur umur penduduk pada masa yang akan datang. Untuk menentukan masing-masing asumsi data yang menggambarkan tren pada masa lampau hingga saat ini, faktor–

faktor yang mempengaruhi komponen-komponen itu, dan hubungan antara satu komponen dengan yang lain serta target yang diharapkan tercapai pada masa yang akan datang.

Nilai eigen dan vektor eigen berperan penting untuk menentukan dinamika populasi jangka panjang serta untuk menentukan apakah populasi meningkat, menurun atau konstan. nilai eigen digunakan untuk mendefinisikan angka pertumbuhan populasi, atau memberikan informasi yang berharga tentang keadaan populasi sedangkan vektor eigen menunjukkan kestabilan distribusi umur.

Brittney et.al (2013) meneliti tentang Leslie Matrices and Women Population in the United States of America yaitu proyeksi selama tahun 2010 yang di peroleh menggunakan model matriks Leslie yang dibangun dari tingkat kesuburan dan

(15)

2

kelangsungan hidup dibandingkan dengan data yang disediakan untuk populasi perempuan, pada masing-masing data memiliki nilai eigen yang lebih besar sehingga memenuhi kesimpulan teorema Perron-Frobenius (yang mengklaim bahwa setiap masing-masing data yang berbentuk matriks dengan entri real non- negatif memiliki nilai eigen real terbesar yang tunggal). Terdapat penelitian tentang model matriks Leslie yaitu penelitian Dewi dan Ratri (2017) menggunakan matriks Leslie untuk memprediksi jumlah dan laju pertumbuhan penduduk di Jawa Timur pada tahun 2021, sehingga diperoleh hasil jumlah dan laju pertumbuhan perempuan cenderung mengalami peningkatan atau dapat dikatakan laju pertumbuhan populasi cenderung bernilai positif.

Kelurahan Sukaramai I merupakan salah satu kelurahan di kota Medan yang berada di Kecamatan Medan Area. Dengan mengetahui proyeksi jumlah dan laju pertumbuhan penduduk apakah pertumbuhan penduduk meningkat, menurun atau tetap stabil tahun kedepannya. Sehingga akan berpengaruh terhadap pembangunan yang dilaksanakan yang berutujuan untuk menyediakan kebutuhan sandang dan pangan sebagai kebutuhan dasar, berbagai fasilitas pendidikan, kesehatan dan berbagai sarana sosial lainnya yang cukup dan merata dalam rangka peningkatan kesejahteraan. Berdasarkan uraian tersebut, penulis memberi tulisan ini dengan judul “Analisis Model Matriks Leslie dan Penerapannya dalam Memprediksi Jumlah dan Laju Pertumbuhan Populasi Perempuan”.

1.2 Rumusan Masalah

Jumlah penduduk pada suatu wilayah cenderung terus meningkat. Pesatnya pertambahan penduduk memicu berbagai masalah sehingga akan memicu angka pengangguran yang tinggi dan menimbulkan kemiskinan. Dengan adanya proyeksi penduduk pemerintah dapat mempertimbangkan kebijakan yang akan diambil untuk masa depan.

Perubahan jumlah pada suatu populasi dipengaruhi oleh kelahiran, kematian, ketahanan hidup dan kesuburan, dengan adanya proses tersebut dapat menentukan pertumbuhan populasi akan meningkat, menurun atau cenderung stabil pada tahun

(16)

berikutnya. Sehingga pada penelitian ini penulis akan menggunakan model matriks Leslie untuk memprediksi jumlah dan laju pertumbuhan populasi perempuan di Kelurahan Sukaramai I.

1.3 Batasan Masalah

Berdasarkan rumusan masalah di atas maka penulisan penelitian ini dibatasi oleh:

1. Data matriks Leslie yang tersedia dalam tugas akhir hanya untuk memprediksi jumlah dan laju pertumbuhan populasi perempuan di Kelurahan Sukaramai I Kecamatan Medan Area Kota Medan Provinsi Sumatera Utara dengan menggunakan data jumlah penduduk perempuan berdasarkan kelompok umur, jumlah kelahiran anak berdasarkan umur ibu saat melahirkan dan jumlah kematian perempuan berdasarkan umur pada tahun 2014-2016.

2. Penelitian ini difokuskan dalam analisis dan penerapan matriks Leslie pada pertumbuhan populasi perempuan.

1.4 Tujuan Penelitian

Tujuan penelitian ini adalah menganalisis dan menerapkan model matriks Leslie dalam memprediksi jumlah dan laju pertumbuhan populasi perempuan di kelurahan Sukaramai I.

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah:

1. Dapat memberikan sumbangan pemikiran berupa informasi apakah perubahan jumlah penduduk pada tahun berikutnya selalu meningkat, menurun atau tetap sehingga pemerintah memperoleh gambaran jumlah penduduk serta dapat menjalankan program-program yang ada.

2. Bagi penulis penelitian ini merupakan penerapan teori-teori yang telah diperoleh dibangku kuliah sehingga diharapkan dapat memberikan pengalaman dan menambah pengetahuan.

(17)

BAB 2

TINJAUAN PUSTAKA 2.1 Matriks

2.1.1 Definisi Matriks

Matriks adalah susunan segiempat dari skalar-skalar yang biasanya dinyatakan dalam bentuk sebagai berikut:

[

] (2.1)

Baris – baris dari matriks A semacam ini adalah m deretan horizontal yang terdiri dari skalar-skalar:

( ) ( ) ( ) Dan kolom – kolom dari adalah deretan vertikal yang terdiri dari skalar- skalar:

[

] [

]

Elemen , yang disebut entri atau elemen , muncul pada baris dan kolom . Seringkali menuliskan matriks tersebut hanya sebagai [ ]. Suatu matriks dengan baris dan kolom disebut sebagai matriks .

2.1.2 Jenis – jenis Matriks

Berikut adalah beberapa jenis matriks:

1. Matriks Bujur Sangkar

Matriks bujur sangkar yaitu suatu matriks yang banyak barisnya sama dengan banyak kolomnya. Barisan elemen disebut diagonal utama dari matriks bujur sangkar A tersebut

(18)

Contoh:

[

]

Matriks A merupakan matriks bujur sangkar berukuran 3.

2. Matriks Diagonal

Matriks diagonal yaitu matriks bujur sangkar yang semua entri di luar diagonal utama bernilai nol.

Contoh:

[

]

3. Matriks Satuan (Matriks Identitas)

Matriks satuan yaitu matriks diagonal yang yang entri-entri pada diagonal utamanya adalah bilangan satu dan entri-entri lainnya adalah bilangan nol.

Matriks satuan dilambangkan dengan , dimana adalah ordo dari matriks tersebut.

Contoh:

[ ]

4. Matriks Skalar

Matriks skalar yaitu matriks diagonal yang semu entri pada diagonal utamanya bernilai sama tetapi tidak nol.

Contoh:

[ ]

5. Matriks Nol

Matriks nol yaitu matriks yang semua entrinya bernilai nol.

(19)

6

Contoh:

[ ] 6. Matriks Invers

Jika dan matriks-matriks bujur sangkar berordo dan berlaku , maka invers dari ditulis dan sebaliknya adalah invers dari , ditulis .

Contoh:

Buktikan bahwa invers dari matriks * + adalah * + Bukti:

* + * + *

+ * +

7. Matriks Simetris

Matriks bujursangkar disebut matriks simetris jika elemen untuk semua i dan j, sehingga apabila di transpose akan menghasilkan matriks semula yaitu .

Contoh:

[

] dan [

], karena maka adalah simetris.

2.1.3 Nilai Eigen dan Vektor Eigen

Misalkan A adalah suatu matriks , maka sebuah vektor taknol pada disebut vektor eigen (eigen vector)dari jika adalah sebuah kelipatan skalar dari ;

Jelasnya,

(2.2)

(20)

Untuk skalar sebarang . Skalar disebut nilai eigen (eigen value) dari , dan disebut sebagai vektor eigen dari yang terkait dengan .

Untuk memperoleh nilai eigen dari sebuah matriks , , ditulis kembali sebagai

(2.3)

Atau secara ekuivalen

( ) (2.4) agar dapat menjadi nilai eigen, harus terdapat satu solusi taknol dari persamaan ini. Akan tetapi persamaan (2.4) memilki solusi taknol jika dan hanya jika

( ) (2.5) Persamaan ini disebut persamaan karakteristik matriks ; skalar-skalar yang memenuhi persamaan ini adalah nilai-nilai eigen . Apabila diperluas lagi, determinan ( ) adalah sebuah polinomial dalam variabel yang disebut sebagai polinomial karakteristik matriks .

Beberapa kasus dapat terjadi pada sebuah populasi yang terkait dengan nilai eigen positif dari matriks Leslie, yaitu popluasi akan bertambah jika nilai eigen positif lebih besar dari satu, populasi akan berkurang jika nilai eigen positif kurang dari satu dan populasi stabil jika nilai eigen positif sama dengan satu. Jadi, nilai eigen sangat penting untuk mendefinisikan angka pertumbuhan populasi, atau memberikan informasi yang berharga tentang keadaan populasi sedangkan vektor eigen menunjukkan kestabilan distribusi umur.

2.1.4 Diagonalisasi

Suatu matriks berorde , disebut dapat didiagonalisasi jika terdapat matriks singular dan suatu matriks diagonal sedemikian sehingga

(2.6) Dikatakan bahwa mendiagonalisasi .

Terdapat beragam permasalahan didalam ilmu matematika terapan yang membutuhkan perhitungan pangkat tinggi dari sebuah matriks bujursangkar. Jika adalah sebuah matriks Leslie dan adalah sebuah matriks yang dapat dibalik maka

( )

(21)

8

Untuk bilangan bulat positif sebarang

( ) (2.7)

Dari persamaan (2.7), jika dapat didiagonalisasikan, dan adalah sebuah matriks diagonal, maka

( ) (2.8) Dengan menyelesaikan persamaan (2.8) untuk memperoleh akan menghasilkan

(2.9)

2.2 Bilangan Kompleks

2.2.1 Definisi Bilangan Kompleks

Bilangan kompleks adalah bilangan kompleks yang berbentuk:

atau , dan bilangan real dan

Bilangan kompleks dinyatakan dengan huruf , sedangkan dan menyatakan bilangan real. Jika menyatakan sembarang bilangan kompleks, maka dinamakan bagian real dan bagian imajiner dari . Bagian real dan bagian imajiner dari bilangan kompleks dinyatakan dengan Re( ) dan Im( ).

2.2.2 Bentuk Polar dan Eksponen dari Bilangan Kompleks

Selain dinyatakan dalam bentuk ( ), bilangan kompleks dapat dinyatakan sebagai koordinat kutub, yaitu ( ).

Gambar 2.1 Bidang Kompleks Adapun hubungan antara keduanya, ( ) dan ( ) yaitu:

(22)

( )

adalah sudut antara sumbu- positif dengan . Sehingga √ | | Diperoleh bentuk polar bilangan yaitu:

( ) ( ) cis

Dua bilangan kompleks ( ) dan ( ) dikatakan sama jika dan . Selain penulisan bilangan kompleks ( ) ( ) cis , dapat dituliskan dalam rumus Euler (eksponen), yaitu .

2.2.3 Pangkat dari Bilangan Kompleks

Diketahui bahwa bilangan kompleks dalam bentuk polar adalah ( ).

Jika ( ) dan ( ) , maka diperoleh hasil perkalian sebagai berikut:

[ ( )][ ( )]

[( ) ( )]

[ ( ) ( )]

Sehingga,

( ) Jika diketahui:

( ) ( )

( ) untuk asli

Maka, secara induksi matematika, diperoleh perkalian

[ ( ) ( )]

Akibatnya jika ( ) maka

( ) (2.10) Khusus untuk , disebut Dalil De-Moivre

( ) , dengan asli.

(23)

10

2.3 Model Matriks Leslie

Matriks Leslie ditemukan oleh seorang pakar Ekologi bernama P.H Leslie pada tahun 1945. Pada matriks Leslie, untuk mengetahui model pertumbuhan suatu populasi ada beberapa asumsi harus terpenuhi yaitu:

1. Dibutuhkan jumlah populasi perempuan

2. Usia maksimum yang dapat dicapai suatu populasi 3. Kelompok usia dari populasi

4. Daya tahan hidup (survival rate) tiap kelompok usia menuju tahap usia selanjutnya diketahui

5. Angka kelahiran (age birth) untuk tiap kelompok usia diketahui 6. Distribusi umur awal (Initial Age Distribution) diketahui.

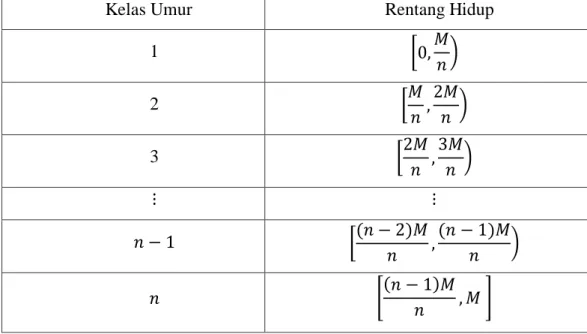
Pada model penelitian ini penduduk dibagi menjadi kelas-kelas umur dalam durasi waktu yang sama. Dengan umur maksimum yang dicapai oleh sebarang perempuan pada suatu populasi adalah tahun dan membagi populasi tersebut menjadi kelas umur, sehingga tiap kelas mempunyai durasi tahun. Sebagai contoh dapat dilihat pada tabel 2.1.

Tabel 2.1 Penentuan kelas umur

Kelas Umur Rentang Hidup

1 [ )

2 [

)

3 [

)

[( ) ( )

)

*( )

+

Andaikan diketahui jumlah perempuan dalam masing – masing dari kelas tersebut dalam waktu . Secara khusus, misalkan terdapat ^{( )} perempuan

(24)

di dalam kelas pertama, ^{( )} perempuan di dalam kelas kedua, dan seterusnya.

Dengan bilangan-bilangan ini, membentuk sebuah vektor kolom:

^{( )} [ ^{( )}

( ) ( )]

(2.11)

Vektor kolom ini disebut sebagai vektor distribusi umur awal (initial age distribution vector). Dengan berjalannya waktu, jumlah perempuan pada tiap kelas berubah karena tiga proses biologis, yaitu lahir, mati dan penuaan. Cara untuk mempelajari proses pertambahan umur adalah dengan mengobservasi populasi dalam waktu diskrit, misalnya, . Model Leslie mempersyaratkan bahwa durasi antara dua waktu observasi yang berurutan sama dengan durasi interval umur, yaitu:

(2.12)

Dengan asumsi ini seluruh perempuan pada kelas ke-( ) pada waktu sebelumnya berada dalam kelas kepada waktu .

Proses kelahiran dan proses kematian diantara dua waktu pengamatan yang berturutan dapat dijelaskan dengan menggunakan parameter demografis seperti pada Tabel 2.2

Tabel 2.2 Parameter dalam Model Matriks Leslie

Parameter Model Keterangan

Jumlah rata – rata dari anak perempuan yang dilahirkan oleh seseorang wanita selama dia berada dalam kelompok umur ke-i

Banyaknya perempuan dalam kelompok umur ke-i yang dapat diharapkan masih hidup dan

(25)

12

sampai ke kelompok umur ke-i

Berdasarkan definisinya, maka akan diperoleh bahwa untuk dan untuk . Dapat dilihat bahwa, tidak boleh adanya

yang sama dengan nol, karena jika hal ini terjadi maka tidak akan ada wanita yang masih hidup sesudah kelompok umur ke-i. Dianggap bahwa sedikitnya ada satu yang positif sehingga akan terjadi kelahiran. Setiap kelompok umur dimana nilai yang bersangkutan adalah positif dinamakan kelompok umur subur (fertile age class). Didefinisikan vektor distribusi umur ^{( )} pada waktu dengan

( )

[ ^{( )}

( ) ( )]

(2.13)

Dimana ^{( )} adalah banyaknya wanita dalam kelompok umur ke-i pada waktu . Pada waktu , perempuan dalam kelompok umur pertama adalah anak perempuan yang lahir diantara waktu dan waktu . Sehingga, dapat dituliskan

{

}

{

} {

}

{

}

(26)

Secara sistematis dapat dituliskan dalam persamaan berikut:

( ) ^{( )} ^{( )} ^{( )} (2.14) Perempuan - perempuan pada kelas umur ke-( ) pada waktu adalah wanita dalam kelompok kepada waktu yang masih hidup pada waktu . Sehingga,

{

} {

}

{

}

Secara sistematis,

( ) ^{( )} (2.15) Dengan menggunakan notasi matriks, persamaan (2.14) dan (2.15) dapat dituliskan dalam bentuk

[ ^{( )}

( ) ( ) ( )] [

][

^{( )}

( ) ( ) ( )]

(2.16)

Atau secara lebih ringkas

( ) ^{( )} dengan (2.17) Dimana adalah matriks Leslie

[

]

(2.18)

Dari persamaan (2.18) akan dihasilkan

(27)

14

( ) ^{( )}

( ) ^{( )} ^{( )}

(2.19)

Jika diketahui distribusi umur awal ^{( )} dan matriks Leslie , maka dapat ditentukan distribusi umur perempuan pada sebarang waktu pada masa mendatang.

2.4 Karakteristik Model Matriks Leslie

Walaupun persamaan (2.19) memberikan distribusi umur dari populasi pada sebarang waktu, namun persamaan itu tidak segera memberikan suatu gambaran umum mengenai dinamika dari proses pertumbuhan tersebut. Untuk itu perlu diselidiki nilai – nilai eigen dan vektor – vektor eigen dari matriks Leslie tersebut.

Nilai – nilai eigen dari adalah akar – akar dari polinomial karakteristiknya.

Polinomial karakteristik dari matriks Leslie adalah

( ) (2.20) Untuk menentukan akar-akar dari polinomial ini, dapat digunakan fungsi sebagai berikut:

( ) (2.21)

(28)

3.1 Metodologi Penelitian

Penelitian ini dilakukan dengan langkah–langkah sebagai berikut:

1. Mengkaji model matriks Leslie

Adapun yang dikaji mengenai model matriks Leslie yaitu, langkah-langkah penentuan model matriks Leslie, parameter dalam model matriks Leslie dan nilai eigen dan vektor eigen pada model matriks Leslie.

2. Pengumpulan data

Mengumpulkan data mengenai jumlah penduduk perempuan berdasarkan kelompok umur, jumlah kelahiran anak berdasarkan umur ibu saat melahirkan, dan jumlah kematian perempuan di Kelurahan Sukaramai I 3. Mencari nilai tingkat kesuburan dan ketahanan hidup

Mencari nilai tingkat kesuburan ( ) yaitu rata-rata jumlah anak perempuan yang lahir dari tiap wanita ketika si ibu berada dalam kelas umur ke-i dan Mencari nilai tingkat ketahanan hidup ( ) yaitu perbandingan wanita pada kelas umur ke-i yang diharapkan dapat bertahan dan mencapai kelas umur ke-(i+1).

4. Menentukan model matriks Leslie menggunakan persamaan (2.18).

5. Menentukan nilai eigen dari matriks Leslie untuk memproyeksi laju pertumbuhan populasi. Dari nilai–nilai eigen dicari nilai eigen positif. Tiga kasus yang muncul berkaitan dengan nilai dari nilai eigen positif :

a. Suatu populasi akhirnya meningkat jika b. Suatu populasi akhirnya berkurang jika c. Suatu populasi cenderung stabil jika 6. Membuat kesimpulan dan saran.

(29)

16

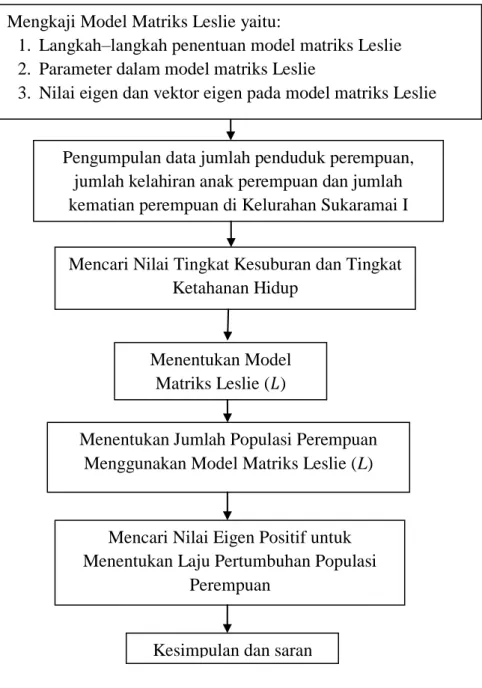
3.2 Kerangka Penelitian

Penelitian ini disusun secara sistematis pada Gambar 3.1 berikut:

Gambar 3.1 Diagram Kerangka Penelitian Pengumpulan data jumlah penduduk perempuan,

jumlah kelahiran anak perempuan dan jumlah kematian perempuan di Kelurahan Sukaramai I

Mencari Nilai Tingkat Kesuburan dan Tingkat Ketahanan Hidup

Menentukan Model Matriks Leslie ( )

Menentukan Jumlah Populasi Perempuan Menggunakan Model Matriks Leslie (L)

Mencari Nilai Eigen Positif untuk Menentukan Laju Pertumbuhan Populasi

Perempuan

Kesimpulan dan saran Mengkaji Model Matriks Leslie yaitu:

1. Langkah–langkah penentuan model matriks Leslie 2. Parameter dalam model matriks Leslie

3. Nilai eigen dan vektor eigen pada model matriks Leslie

(30)

4.1 Analisa Model

Matriks Leslie adalah salah satu model yang menjelaskan pertumbuhan perempuan pada suatu populasi, dimana perempuan pada populasi tersebut dibagi kedalam kelompok umur yang kurun waktunya sama. Populasi diwakilkan oleh vektor dengan elemen untuk setiap kelas umur dimana setiap elemen menunjukkan jumlah individu di kelas tersebut. Dalam model matriks Leslie diasumsikan bahwa laju pertumbuhan populasi hanya disebabkan oleh proses kelahiran dan kematian perempuan dan dianggap tidak ada migrasi masuk atau keluar pada populasi yang diteliti.

Bentuk analisis yang digunakan dalam penulisan skripsi ini adalah menganalisis apakah sudah terpenuhi syarat-syarat pada model matriks Leslie sehingga dapat menggunakan model matriks Leslie untuk permasalahan populasi penduduk perempuan. Kemudian mencari nilai tingkat kesuburan ( ) yaitu rata- rata jumlah anak perempuan yang lahir dari tiap perempuan ketika ibu berada dalam kelas umur ke- dan mencari tingkat ketahanan hidup ( ) yaitu perbandingan perempuan pada kelas umur ke- yang diharapkan dapat bertahan dan mencapai kelas umur ke-( ). Setelah nilai tingkat kesuburan ( ) dan nilai tingkat ketahanan hidup ( ) telah didapat, selanjutnya memprediksi jumlah populasi perempuan dengan menggunakan populasi awal perempuan. Kemudian untuk mengetahui laju pertumbuhan populasi perempuan dicari nilai eigen positif dari model matriks Leslie menggunakan MATLAB sehingga dapat juga diketahui vektor yang berkaitan dengan nilai eigen positif.

Adapun ciri-ciri dari model matriks Leslie yaitu:

1. Matriks Leslie merupakan matriks bujursangkar dengan jumlah baris dan kolom yang sama dengan vektor populasi yang memiliki elemen

2. Sebuah matriks Leslie mempunyai sebuah nilai eigen positif tunggal . Nilai eigen ini mempunyai multiplisitas 1 dan sebuah vektor eigen yang seluruh entri-entrinya adalah positif

(31)

18

3. Jika adalah suatu nilai eigen positif yang tunggal dari sebuah matriks Leslie L dan adalah sebarang nilai eigen bilangan real atau bilangan kompleks dari L maka | |

4. Jika dua entri yang berurutan dan dalam baris pertama dari sebuah matriks Leslie L tidak sama dengan nol maka nilai eigen positif dari L adalah dominan.

4.2 Model Matriks Leslie dalam Memprediksi Jumlah Populasi

Model matriks Leslie merupakan model pertumbuhan populasi yang digunakan para ahli demografi dikembangkan pada tahun 1945 oleh P.H Leslie.

Adapun bentuk umum dari model matriks Leslie yaitu:

[

]

(4.1)

Dimana:

: Jumlah rata – rata dari anak perempuan yang dilahirkan oleh seseorang perempuan selama dia berada dalam kelompok umur ke- .

: Banyaknya perempuan dalam kelompok umur ke- yang dapat diharapkan masih hidup dan sampai ke kelompok umur ke- .

Mengetahui suatu gambaran umum tentang dinamika proses pertumbuhan yang terjadi perlu adanya penyelidikan nilai eigen dan vektor-vektor eigen dari matriks Leslie. Persamaan karakteristik matriks Leslie adalah

( ) | |

|| [

] [

]

||

(32)

|| [

] [

]

||

|| [

]

||

= (4.2) Untuk menganalisis akar-akar dari persamaan polinomial ini, digunakan fungsi sebagai berikut:

( ) (4.3)

Dengan menggunakan fungsi ini, persamaan karakteristik ( ) , sehingga ( )

(

)

( ) ( )

Maka didapatkan hasil

( ) untuk (4.4)

(33)

20

Karena semua elemen dan bernilai positif, jika nilai-nilai eigen dari matriks Leslie L disubstitusikan ke persamaan matriks pertumbuhan populasi, dimisalkan bernilai positif dari sampai , maka nilai dari ( ) akan menuju monoton turun seperti gambar

Gambar 4.1 Grafik Fungsi ( )

Terdapat suatu yang tunggal yaitu sehingga ( ) . Matriks Leslie L memiliki sebuah nilai eigen positif yang mempunyai multiplisitas 1 yang artinya tidak ada nilai eigen dengan yang bernliai sama dengan atau dapat dikatakan bahwa bukanlah akar yang diulang untuk persamaan karakteristik tersebut. Sehingga berikut teorema yang berkaitan dengan vektor eigen yang bersesuaian dengan .

Teorema 4.2.1

Sebuah matriks Leslie L mempunyai sebuah nilai eigen positif tunggal . Nilai eigen ini mempunyai multiplisitas 1 dan sebuah vektor eigen yang seluruh entri-entrinya adalah positif.

Bukti:

Misalkan merupakan sebuah vektor eigen dari matriks Leslie L yang mempunyai nilai eigen positif tunggal , sehingga memenuhi persamaan ( )

Misalkan

(34)

[ ] Sehingga,

( [

] [

])

([

] [

])[ ] [ ]

[

][ ] [ ]

[

( )

] [ ]

( ) (4.5) → (4.6)

→ (4.7)

→

(4.8) →

(4.9)

(35)

22

Substitusikan persamaan (4.6), persamaan (4.7), persamaan (4.8), dan persamaan (4.9) ke persamaan (4.5).

( )

(

)

( )

Diketahui bahwa merupakan suatu vektor eigen yang bersesuaian dengan . Dari persamaan (4.10) jika , maka vektor eigen yang bersesuaian dengan merupakan vektor nol, sehingga diperoleh

[

]

( )

Karena memiliki multiplisitas 1, maka vektor eigen yang berhubungan dengan merupakan multiplisitas .

Akan diperlihatkan bahwa perilaku jangka panjang dari distribusi umur populasi ditentukan oleh nilai eigen positif .

(36)

Teorema 4.2.2

Jika adalah suatu nilai eigen positif yang tunggal dari sebuah matriks Leslie L dan adalah sebarang nilai eigen bilangan real atau bilangan kompleks dari L maka | | .

Bukti:

Diketahui bahwa adalah nilai eigen positif yang tunggal, sehingga adalah nilai eigen yang bisa berupa bilangan real atau bilangan kompleks. Misalkan terbukti bahwa | | . Kemudian diambil sebarang dengan √ , untuk membuktikan | | sama dengan memperlihatkan | | . Syarat perlu agar adalah sebuah nilai eigen, harus merupakan solusi dari sistem persamaan

( )

( ) untuk

( )

( ) ( )

( )

( ) ( )

( )

( ( ) ( )) ( ( ) ( ))

( ( ) ( ))

( ) ( ) ( )

Sehingga

( ) ( )

( )

(37)

24

( ) ( )

( )

Diambil bagian yang real, maka

( ) ( )

( )

Karena adalah nilai eigen sehingga memenuhi persamaan ( ) yaitu,

( )

Sehingga,

( ) ( ) ( )

(

) ( ) ( ) ( ) Persamaan (4.12) berlaku jika , diperoleh karena sehingga | | yang berarti | | .

Contoh 4.2.3 (matriks Leslie tanpa nilai eigen dominan) Misalkan

[

]

Maka persamaan polinomial karakteristik dari L adalah ( ) | |

(38)

| [

] [

]|

|[

] [

]|

Nilai eigen dari L kemudian menjadi solusi dari yaitu:

, ^√ ^√

Ketiga nilai eigen di atas memiliki nilai absolut 1, sehingga nilai eigen positif tunggal tidak dominan

Untuk menjadikan nilai eigen dominan, diperlukan yang memenuhi

| | . Oleh karena itu syarat dari teorema 4.2.2 tidak cukup kuat untuk membuktikan bahwa nilai eigen dari matriks Leslie adalah dominan.

Teorema 4.2.4

Jika dua entri yang berurutan dan dalam baris pertama dari sebuah matriks Leslie L tidak sama dengan nol maka nilai eigen positif dari L adalah dominan.

Bukti:

Dikatakan nilai eigen dominan jika | | tidak boleh | | atau| | . Menurut definisi dan dengan , misalkan jadi dan sehingga akan ditunjukkan | | dengan dimana positif. Untuk membuktikannya dilakukan secara kontradiksi yaitu diasumsikan .

→

Sehingga, ( )

(39)

26

Diperoleh dan

Jika persamaan dikalikan dengan , maka berarti atau . Berdasarkan persamaan (4.12) yaitu

( ) ( ) ( )

Diperoleh nilai dan . Pernyataan tersebut bertentangan dengan asumsi yang menyatakan dan . Berarti pengandaian salah sehingga

| | .

Jika suatu populasi perempuan memiliki dua kelas usia subur yang berurutan, maka matriks Leslie L memiliki sebuah nilai eigen yang dominan.

Kasus tersebut merupakan suatu kasus populasi yang realistik, jika durasi dari kelas-kelas umur relatif kecil. Diasumsikan bahwa L dapat didiagonalisasi. Dalam kasus ini L memiliki nilai eigen yaitu , yang tidak harus berbeda dan vektor-vektor eigen independen yang linear yaitu . Dibentuk sebuah matriks dimana kolom-kolomnya adalah vektor-vektor eigen dari L.

[ | | | | ] ( ) Diagonalisasi L seperti pada persamaan (2.9) dinyatakan dengan persamaan

[

]

Untuk dengan sehingga persamaan menjadi

[

]

Untuk vektor distribusi umur awal ^{( )}, diperoleh

(40)

( ) [

]

( )

Diketahui bahwa ^{( )} ^{( )}, sehingga

^{( )} [

]

( ) ( )

Misalkan

^{( )}

[ ]

( )

Substitusikan persamaan (4.13) dan (4.15) ke persamaan (4.14)

( ) [ | | | | ] [

][ ]

( ) [ | | | | ] [

] Kedua ruas dikalikan dengan sehingga

(41)

28

( ) [ | | | | ] [

]

( )

[

( )

]

( )

[

( )

( ) ]

[ ]

( )

[

( )

( ) ]

( )

Karena adalah nilai eigen dominan, sehingga | | untuk . Diperoleh

(| |) → ketika → untuk .

Oleh karena itu

(42)

→

( ) [

]

( ) ( )

Entri dari vektor kolom ^{( )} adalah suatu konstanta , dimana merupakan sebuah konstanta positif yang hanya bergantung pada vektor distribusi umur awal

( ). Substitusikan persamaan (4.13) dan persamaan (4.15) ke persamaan (4.16), diperoleh

→

( ) [ | | | | ] [

][ ]

→

( ) [ | | | | ] [ ]

→

( ) ( )

Dari persamaan (4.17) diperoleh suatu pendekatan

( ) ( ) Untuk nilai yang besar, dari persamaan (4.18) diperoleh

( ) ( ) Dengan membandingkan persamaan (4.18) dan persamaan (4.19) diperoleh

( ) ^{( )} ( ) Untuk nilai-nilai waktu yang besar, tiap vektor distribusi umur merupakan kelipatan skalar dari vektor distribusi umur sebelumnya, besaran skalar tersebut

(43)

30

merupakan nilai eigen positif dari matriks Leslie. Akibatnya, proporsi dari perempuan tiap kelas umur menjadi konstan.

4.3 Penerapan Model Matriks Leslie Pada Laju Pertumbuhan Populasi Pada penelitian ini akan menentukan proyeksi laju pertumbuhan suatu populasi penduduk perempuan disuatu daerah. Adapun laju pertumbuhan populasi penduduk perempuan yang digunakan sebagai berikut:

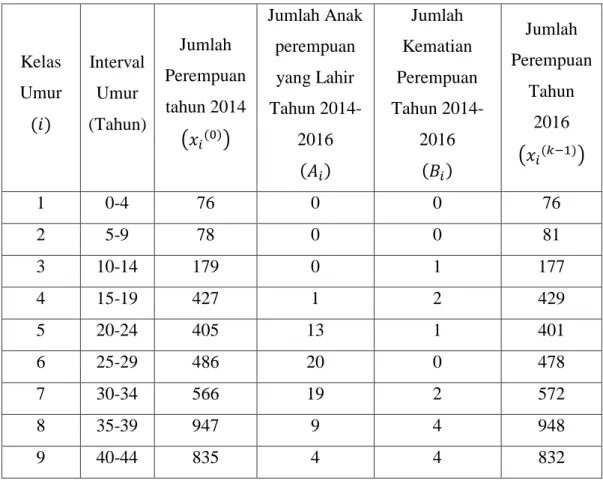
4.3.1 Data Penduduk Perempuan

Data yang digunakan penulis pada penelitian ini merupakan data penduduk perempuan di Kelurahan Sukaramai I Kecamatan Medan Area Kota Medan Provinsi Sumatera Utara pada tahun 2014-2016. Adapun data yang diperoleh yaitu jumlah penduduk perempuan pada tahun 2014 dan 2016 berdasarkan kelompok umur, kelahiran anak berdasarkan umur ibu saat melahirkan dan data kematian populasi perempuan.

Tabel 4.1 Data Penduduk Perempuan di Kelurahan Sukaramai I Tahun 2014-2016

Kelas Umur

( )

Interval Umur (Tahun)

Jumlah Perempuan tahun 2014

( ^{( )})

Jumlah Anak perempuan yang Lahir Tahun 2014-

2016 ( )

Jumlah Kematian Perempuan Tahun 2014-

2016 ( )

Jumlah Perempuan

Tahun 2016 ( ^{( )})

1 0-4 76 0 0 76

2 5-9 78 0 0 81

3 10-14 179 0 1 177

4 15-19 427 1 2 429

5 20-24 405 13 1 401

6 25-29 486 20 0 478

7 30-34 566 19 2 572

8 35-39 947 9 4 948

9 40-44 835 4 4 832

(44)

10 45-49 776 0 7 820

11 50-54 534 0 3 542

12 55-59 90 0 17 93

13 60-64 71 0 14 76

14 65+ 83 0 57 89

Jumlah 5.595 66 112 5614

4.3.2 Model Matriks Leslie

Model matriks Leslie dibentuk berdasarkan tingkat kesuburan ( ) dan ketahanan hidup ( ). Dimana merupakan rata-rata jumlah anak perempuan yang lahir dari tiap perempuan ketika si ibu berada dalam kelas umur ke- dimana untuk , sehingga

( ) ( ) ( ) Dari data penduduk perempuan pada Tabel 4.1 diperoleh tingkat kesuburan ( ) menggunakan persamaan (4.21) sebagai berikut:

( ) ( )

( )

(45)

32

( )

merupakan perbandingan perempuan pada kelas umur ke- yang diharapkan dapat bertahan dan mencapai kelas umur ke-( ) dimana untuk ( ). adalah rata-rata jumlah kematian dari tiap kelompok umur, sehingga

_{( )} ( ) ( )

dan

( ) ( ) ( ) Dari data penduduk perempuan pada Tabel 4.1 diperoleh tingkat ketahanan hidup ( ) menggunakan persamaan (4.22) dan (4.23) sebagai berikut:

(46)

( )

Oleh karena itu,

(47)

34

( ) ( ) ( )

( )

( ) ( ) ( ) ( )

( ) ( ) ( )

( )

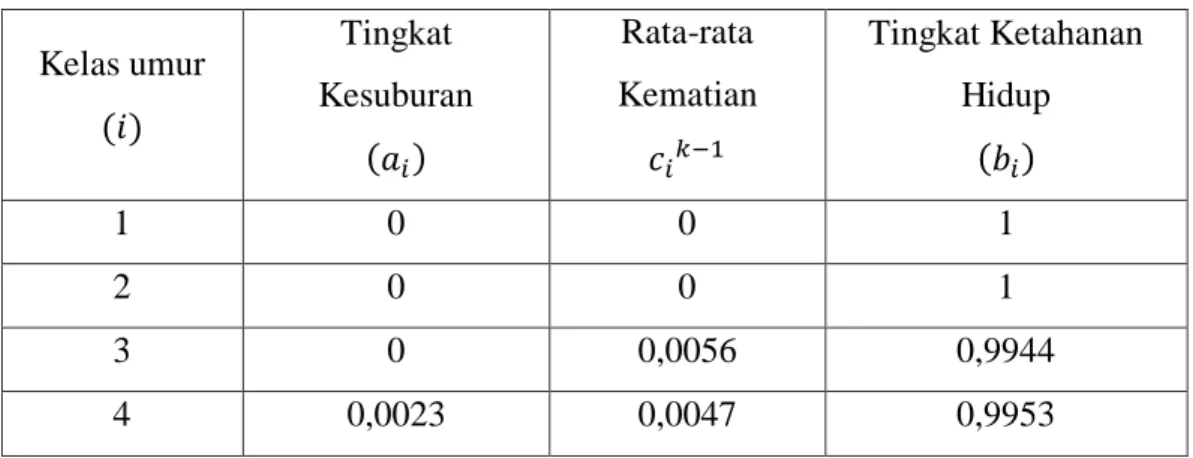
Tabel 4.2 Tingkat Kesuburan dan Tingkat Ketahanan Hidup Perempuan di Kelurahan Sukaramai I Tahun 2014-2016

Kelas umur ( )

Tingkat Kesuburan

( )

Rata-rata Kematian

Tingkat Ketahanan Hidup

( )

1 0 0 1

2 0 0 1

3 0 0,0056 0,9944

4 0,0023 0,0047 0,9953

(48)

5 0,0324 0,0025 0,9975

6 0,0411 0 1

7 0,0336 0,0035 0,9965

8 0,0095 0,0042 0,9958

9 0,0048 0,0048 0,9952

10 0 0,0090 0,9910

11 0 0,0056 0,9944

12 0 0,1889 0,8111

13 0 0,1972 0,8028

14 0 0,6285 0,3313

Dari Tabel 4.2 diperoleh model matriks Leslie yang berukuran yang elemen-elemennya terdiri dari tingkat kesuburan ( ) dan tingkat ketahanan hidup ( ).

[

]

4.3.3 Proyeksi Jumlah Populasi

Dengan menggunakan persamaan (2.19), yaitu:

( ) ^{( )}

( ) ^{( )} ^{( )}

(49)

36

Dari persamaan diatas diperoleh model pertumbuhan populasi perempuan di Kelurahan Sukaramai I pada tahun berikutnya, dimana ^{( )} adalah jumlah perempuan pada tahun 2016 sebagai jumlah populasi awal.

( ) ^{( )}

[

]

[ ] [

]

( )

( ) ^{( )}

(50)

[

]

[ ] [

]

( )

( ) ^{( )}

[

]

(51)

38

[ ] [

]

( )

( ) ^{( )}

[

]

(52)

[ ] [

]

^{( )}

( )

( ) ^{( )}

[

]

(53)

40

[ ] [

]

( )

Berdasarkan perhitungan di atas proyeksi jumlah populasi perempuan diperoleh

( ) ^{( )} ^{( )} ^{( )} ^{( )} . Oleh karena itu dapat diketahui bahwa jumlah populasi berkurang yaitu pada tahun 2017, 2018, 2019, 2020, dan 2021.

4.3.4 Nilai Eigen dan Vektor Eigen

Untuk mengetahui laju pertumbuhan populasi perempuan di Kelurahan Sukaramai I, diperlukan perhitungan dari matriks Leslie L. Dengan menggunakan program Matlab diperoleh nilai eigen untuk matriks Leslie L seperti tabel 4.3 berikut:

Tabel 4.3 Nilai Eigen Matriks Leslie L Nilai Eigen

0 0 0 0 0

(54)

0,7217

Berdasarkan Tabel 4.3 diketahui 14 nilai eigen yang terdiri dari 5 nilai eigen bernilai nol, 8 nilai eigen bernilai kompleks dan 1 nilai eigen bernilai real.

Diperoleh satu-satunya nilai eigen real yang positif yaitu . Oleh karena itu diperoleh vekto eigen yang bersesuaian dengan nilai eigen tersebut.

[

] [

]

Dengan menggunakan persamaan (4.20), diperoleh persamaan pendekatan untuk distribusi umur pembatas:

( ) ^{( )}

Sehingga,

(55)

42

( ) ^{( )} Untuk nilai yang besar.

Oleh karena itu jika para perempuan di Kelurahan Sukaramai I tetap melahirkan dan meninggal seperti tahun 2014-2016, maka setiap lima tahun jumlah perempuan akan menurun sebesar .

(56)

BAB 5 PENUTUP 5.1 Kesimpulan

Dari hasil pembahasan dalam skripsi ini dapat diambil kesimpulan sebagai berikut:

1. Dari hasil penelitian, diperoleh nilai tingkat kesuburan ( ) dan tingkat ketahanan hidup ( ) sehingga dapat diprediksi jumlah populasi perempuan menggunakan model matriks Leslie.

2. Didapati prediksi populasi perempuan di Kelurahan Sukaramai I menggunakan model matrik Leslie, yaitu ^{( )} ^{( )}

( ) ^{( )} ^{( )} dapat dilihat bahwa tiap tahunnya jumlah populasi perempuan berkurang yaitu pada tahun 2017, 2018, 2019, 2020, dan 2021. Nilai eigen dari matriks Leslie yang terbentuk dari data tersebut bernilai 0,7217. Hal ini berarti bahwa jumlah populasi cenderung mengalami penurunan pada tahap selanjutnya atau dengan kata lain laju pertumbuhan populasi perempuan di Kelurahan Sukaramai I cenderung negatif. Serta diperoleh pendekatan untuk distribusi umur pembatas:

( ) ^{( )} Untuk nilai yang besar.

5.2 Saran

Pada tugas akhir ini hanya terdapat tiga faktor yang digunakan untuk perhitungan matriks Leslie yaitu jumlah populasi perempuan, tingkat ketahanan hidup dan tingkat kesuburan. Padahal perpindahan penduduk juga dapat mempengaruhi populasi perempuan. Sehingga untuk penelitian selanjutnya, sebaiknya peneliti dapat memodifikasi model matriks Leslie dengan mengikut sertakan perpindahan penduduk.

(57)

DAFTAR PUSTAKA

Anggreini, D., dan Hastari, R.C. 2017. Penerapan Matriks Leslie pada Angka Kelahiran dan Harapan Hidup Wanita di Propinsi Jawa Timur.

Phytagoras: Jurnal Pendidikan Matematika vol 7 No.2: 109 – 122

Anton, H., dan Rorres, A. 2014. Aljabar Linear Elementer Edisi kedelapan..

Jakarta: Erlangga

Anton, H., dan Rorres, A. 2014. Aljabar Linear Elementer Versi Aplikasi Edisi kedelapan. Jakarta: Erlangga

Leon, Steven J, 1998. Aljabar Linear dan Aplikasinya, Edisi Kelima. Jakarta:

Erlangga

Lipschutz, Seymour dan Marc Lipson. 2004. Teori dan Soal Aljabar Linier, Edisi Ketiga. Jakarta: Erlangga

Nelson, Denise and Antonija. 2013. Leslie Matrices and Women Population in the United States of America Georgia Journal of Sience Vol 71 No.2: 158 – 166

Sanusi, W., Sukarna dan Nur R. 2018. Matriks Leslie dan Aplikasinya dalam Memprediksi Jumlah dan Laju Pertumbuhan Penduduk di Kota Makassar.

Journal of Mathematics, Computations and Statistics Vol 1 No.2: 142 – 154 Sumarti, N., Mharta A. Wardana dan Nuning N. Population Growth Models of

Forest Trees for Conservation Management: Case of Teak (Tectona Grandis) Forest in Begal, East Java, Indonesia. Hayati Journal of Biosciences Vol 25 No.4: 169 - 177

Sutojo, T dkk. 2010. Teori dan Aplikasi Aljabar Linier dan Matriks. Yogyakarta:

Andi Offset.

Yuliani, S., Rahayu B.V dan Mashuri. 2012. Penerapan Diagonalisasi Matriks dan Matriks Leslie dalam Memproyeksikan Jumlah Populasi Perempuan.

UNNES Journal of Mathemtics Vol 1 No. 1