ANALISIS IMPLEMENTASI MATRIKS LESLIE PADA MODEL PEMANENAN POPULASI HEWAN
SKRIPSI
ADE IRMAYANTI 160803054
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2020
ANALISIS IMPLEMENTASI MATRIKS LESLIE PADA MODEL PEMANENAN POPULASI HEWAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat memperoleh gelar Sarjana Sains
ADE IRMAYANTI 160803054
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2020
i
ii ANALISIS IMPLEMENTASI MATRIKS LESLIE PADA MODEL
PEMANENAN POPULASI HEWAN
ABSTRAK
Matriks Leslie merupakan suatu matriks guna memprediksi jumlah dan laju pertumbuhan populasi tertentu. Faktor-faktor yang mempengaruhi pertumbuhan populasi adalah tingkat kesuburan, tingkat ketahanan hidup, dan batas maksimal umur populasi. Penelitian model pemanenan ini bertujuan untuk mengetahui kebijakan pemanenan dari masing-masing kelas umur suatu populasi saat pemanenan tiap tahun. Metode penelitian diawali dengan mengkaji dan menganalisis matriks Leslie dan karakteristiknya, lalu matriks tersebut diterapkan pada model pemanenan sehingga dapat diaplikasikan ke salah satu contoh populasi hewan tertentu. Model pemanenan ini hanya dapat memperhitungkan populasi hewan betina karena sifatnya yang dapat berkembangbiak. Model ini memiliki nilai-nilai yang dapat menghasilkan panen berkesinambungan, nilai eigen dominan dan vektor eigen akan memberikan keterangan mengenai vektor distribusi umur dari populasi setelah waktu panen. Pemanenan seragam dapat dilakukan apabila peluang pemanenan dari tiap kelas umur dalam suatu populasi adalah sama. Kebijakan pemanenan seragam yang berkesinambungan adalah ⁄ . Sedangkan pemanenan kelas umur termuda dilakukan dengan memanen populasi yang berada pada kelas umur termuda yaitu terletak pada kelas pertama. Kebijakan pemanenan kelas umur termuda yang berkesinambungan adalah ⁄ .
Kata kunci: matriks Leslie, model pemanenan, nilai eigen, vektor eigen
iii ANALYSIS OF IMPLEMENTATION OF THE LESLIE MATRIX IN ANIMAL
POPULATION HARVESTING MODEL
ABSTRACT
Leslie matrix is a matrix use to predict number and rate of population growth. The factors which influence the population growth are fertility rate, the survival rate, and maximum age of the population. This study is about harvesting model aims to know the harvesting policy of each age class of population at harvest each year. The research method will started by examine and analyze Leslie matrix and its characteristics, then the matrix applied to harvesting model so that it can be applied to one example of animal population. This harvesting model can only take into account of female animal population cause its reproductive. This model has
values that can produce sustainable harvests, eigen value and eigen vector will providing information about the age distribution vector of population after harvest time. Uniform harvesting can be done if fraction of harvesting for each class in the population are the same. The policy of harvesting uniform which sustainable is ⁄ . Meanwhile, harvesting the youngest age class can be done with harvest the population where in the youngest age class is located in the first class. The policy of harvesting the youngest age class which sustainable is ⁄ .
Keywords : Leslie matrix, harvesting model, eigen value, eigen vector
iv
v Ade Irmayanti
DAFTAR ISI
Halaman
PENGESAHAN SKRIPSI i
ABSTRAK ii
ABSTRACT iii
PENGHARGAAN iv
DAFTAR ISI v
DAFTAR TABEL vii
DAFTAR GAMBAR viii
DAFTAR LAMPIRAN ix
BAB 1 PENDAHULUAN
1.1 Latar belakang 1
1.2 Perumusan Masalah 3
1.3 Batasan Masalah 3
1.4 Tujuan Penelitian 3
1.5 Manfaat Penelitian 3
BAB 2 TINJAUAN PUSTAKA
2.1 Matriks 4
2.1.1 Jenis-jenis Matriks 4
2.1.2 Perkalian Matriks 6
2.1.3 Diagonalisasi Matriks 6
2.2 Nilai Eigen dan Vektor Eigen 6
2.3 Matriks Leslie 9
2.4 Karakteristik Matriks Leslie 12
2.5 Model Pemanenan 17
BAB 3 METODOLOGI PENELITIAN
3.1 Jenis Penelitian 21
3.2 Metodologi Penelitian 21
BAB 4 PEMBAHASAN
4.1 Nilai Eigen Matriks Leslie 23
4.2 Karakteristik Model Pemanenan 26
4.3 Pemanenan Seragam 28
4.4 Pemanenan Kelas Umur Termuda 29
4.5 Aplikasi Model Pemanenan pada Populasi Kambing 30 4.5.1 Pemanenan Seragam pada Populasi Kambing 33 4.5.2 Pemanenan Kelas Umur Termuda pada Populasi
Kambing
34
vi BAB 5 KESIMPULAN DAN SARAN
5.1 Kesimpulan 36
5.2 Saran 36
DAFTAR PUSTAKA 37
LAMPIRAN 39
vii DAFTAR TABEL
Nomor
Tabel Judul Halaman
2.1 Penentuan kelas umur 7
4.1 Tingkat kelahiran dan tingkat ketahanan hidup populasi kambing
30
4.2 Nilai eigen matriks Leslie 32
viii DAFTAR GAMBAR
Nomor
Gambar Judul Halaman
2.1 Grafik fungsi 13
2.2 Ilustrasi gagasan mendasar model pemanenan 18
ix DAFTAR LAMPIRAN
Nomor
Lampiran Judul Halaman
1 Mencari nilai eigen dengan aplikasi MATLAB 39
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Model matematika dapat didefinisikan sebagai suatu konstruksi matematis yang didesain guna mempelajari fenomena tertentu dalam dunia nyata. Matematika sebagai bahasa simbol yang universal, sangat erat hubungannya dengan kehidupan nyata. Kenyataan membuktikan bahwa untuk menyelesaikan masalah-masalah dalam kehidupan sehari-hari, matematika mempunyai peranan yang sangat penting. Di dalam dunia nyata terkadang terdapat masalah-masalah yang sulit untuk diselesaikan dalam sistemnya. Metode-metode matematika diperlukan untuk mempermudah penyelesaian masalah tersebut.
Konsep-konsep dalam aljabar linier bersifat abstrak sehingga tidak jelas manfaatnya. Aplikasi aljabar linier banyak digunakan untuk memecahkan persoalan dibidang matematika maupun diluar bidang matematika. Sebagai contoh penggunaan matriks memudahkan dalam membuat analisis masalah-masalah ekonomi (model ekonomi liontif), fisika (keseimbangan benda getar), biologi (genetika terapan), demografi (penggunaan matriks Leslie untuk memproyeksikan jumlah populasi), peternakan (pemanenan populasi hewan).
Matriks Leslie merupakan suatu matriks yang memiliki bentuk unik, yaitu berbentuk matriks persegi yang entri-entrinya telah ditentukan. Entri dari baris pertama terdiri dari tingkat kesuburan populasi, sub-diagonalnya berisi tingkat ketahanan hidup populasi dan entri yang lain bernilai nol. Matriks Leslie ditemukan oleh seorang pakar Ekologi bernama Leslie pada tahun 1945. Adanya perubahan jumlah dari suatu populasi disebut pertumbuhan populasi. Model matriks Leslie merupakan salah satu dari antara model-model yang paling umum mengenai pertumbuhan populasi oleh para ahli demografi. Model ini mengasumsikan bahwa ukuran populasi untuk setiap tahap hanya tergantung kepada populasi perempuan (manusia) atau betina (hewan) dan tergantung kepada fraksi tingkat kesuburan dan ketahanan hidup satu populasi tersebut dari satu tahun ke tahun berikutnya.
Penggunaan model matriks Leslie dengan karakteristiknya telah mampu memberikan solusi pemecahan masalah dalam penelitian untuk memprediksi jumlah
2
dan laju pertumbuhan populasi dalam perhitungan skala tahunan akan cenderung meningkat, menurun atau tetap. Faktor-faktor yang digunakan pada perhitungan matriks Leslie adalah tingkat kesuburan, harapan hidup dan batas hidup populasi betina.
Dalam penelitian ini matriks Leslie diaplikasikan dalam bidang peternakan yaitu untuk menghitung pemanenan populasi hewan. Istilah memanen (harvesting) berarti menghilangkan atau pengambilan sekelompok hewan dari populasinya untuk tujuan lain. Pemanenan populasi hewan ini mengacu dengan yang disebut sebagai kebijakan pemanenan berkesinambungan. Sehingga populasi hewan tidak berkurang dengan adanya kebijakan tersebut, hanya kelebihan pertumbuhannya saja yang dihilangkan.
Sebagai contoh, seorang peternak memiliki populasi ayam. Anggap jangka setahun populasi ayam telah memiliki pertumbuhan yang sudah diperhitungkan dengan model Leslie. Dengan adanya pertumbuhan ini, diambil sekelompok ayam dari populasinya untuk dipanen menurut kebijakan pemanenan yang baik. Panen yang dimaksud dalam penelitian adalah hewan-hewan yang dikeluarkan oleh peternak dari populasi asalnya.
Anggraini (2018) meneliti tentang strategi pemanenan pada kelompok umur termuda pada angka kesuburan dan harapan hidup populasi hewan yaitu populasi domba betina dengan menggunakan matriks Leslie menyimpulkan kebijaksanaan pemanenan dari kelompok umur yang termuda (0-1 tahun) pada populasi domba betina adalah sebesar 17,9% atau 179 ekor setiap tahun dari populasi tersebut.
Pada umumnya pertumbuhan suatu makhluk hidup merupakan proses yang berlangsung kontinu atau sinambung. Namun demikian, kajian populasi perlu juga didekati dari tinjauan waktu diskrit. Penggunaan pola diskrit didasarkan pula atas pengamatan populasi yang pada umumnya dilakukan selang-selang periode tertentu seperti sehari, seminggu, dan sekian satuan waktu menurut rancangan peneliti yang bersangkutan. Berdasarkan pertimbangan tersebut, penyusunan model-model pertumbuhan selain didasarkan atas solusi-solusi secara kontinu perlu dievaluasi lebih mendalam dengan pemecahan secara diskrit.
Berdasarkan uraian tersebut, penelitian ini diberi judul “Analisis Implementasi Matriks Leslie pada Model Pemanenan Populasi Hewan”.
3
1.2 Perumusan Masalah
Matriks Leslie diimplementasikan dalam hal pertumbuhan populasi. Pemanenan pada populasi hewan dapat terjadi jika adanya pertumbuhan pada populasi tersebut.
Pemanenan sebaiknya mengacu pada kebijakan pemanenan yang sangat penting dalam bidang peternakan. Hal ini dikarenakan dapat memberikan keuntungan maksimal dan berkelanjutan serta tidak terjadi kepunahan dari populasi hewan yang dipanen. Oleh karena itu, permasalahan yang akan dibahas adalah mengimplementasikan matriks Leslie dalam hal pemanenan populasi hewan untuk mengetahui kebijakan pemanenan.
1.3 Batasan Masalah
Penelitian ini difokuskan dalam analisis penerapan matriks Leslie pada model pemanenan populasi hewan dalam bidang peternakan. Pemanenan mengacu pada kebijakan pemanenan berkesinambungan.
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah mengkaji dan menganalisis model pemanenan populasi hewan yang tumbuh menurut model matriks Leslie serta mengetahui kebijakan pemanenan pada kelompok umur tertentu dalam setiap masa panen.
1.5 Manfaat Penelitian
Bermanfaat dalam menambah informasi, wawasan dan pengetahuan yang secara khusus berkaitan dengan masalah pemanenan pada populasi hewan sehingga dapat memantapkan pemahaman materi dan menjadi referensi yang berhubungan dengan masalah didalamnya. Selain itu, peternak juga dapat melihat bagaimana mengetahui laju pertumbuhan ternakannya dan mengetahui strategi pemanenan yang tepat.
BAB 2
TINJAUAN PUSTAKA
2.1 Matriks
Suatu matriks adalah jajaran empat persegi panjang dari bilangan-bilangan yang disebut dengan entri dari matriks berdasarkan baris dan kolom serta diletakkan dalam dua tanda kurung siku. Bila adalah matriks yang mempunyai baris dan kolom (bertipe ), maka dapat ditulis sebagai
[
] (2.1)
2.1.1 Jenis-Jenis Matriks
Ada beberapa jenis matriks yang perlu diketahui, yaitu : a. Matriks Baris
Matriks baris adalah matriks yang hanya terdiri dari satu baris saja.
Contoh: [ ] b. Matriks Kolom
Matriks kolom adalah matriks yang hanya terdiri dari satu kolom saja.
Contoh: [ ] c. Matriks Bujur Sangkar
Matriks bujur sangkar adalah matriks yang jumlah barisnya sama dengan jumlah kolomnya. Karena sifatnya yang demikian ini, dalam matriks bujur sangkar dikenal dengan istilah elemen diagonal yang berjumlah dengan matriks berukuran , yaitu
Contoh: [
], dengan elemen diagonal d. Matriks Diagonal
Matriks diagonal adalah matriks bujur sangkar yang semua elemen diluar diagonal utamanya adalah nol. Dalam hal ini tidak disyaratkan bahwa elemen diagonal tak harus nol.
5
Contoh: [ ] e. Matriks Segitiga
Matriks segitiga adalah matriks bujur sangkar yang elemen-elemen dibawah atau diatas elemen diagonal bernilai nol. Jika yang bernilai nol adalah elemen-elemen dibawah elemen diagonal maka disebut matriks segitiga atas dan sebaliknya, jika yang bernilai nol adalah elemen-elemen diatas elemen diagonal disebut matriks segitiga bawah.
Contoh: [
], merupakan matriks segitiga atas
[
], merupakan matriks segitiga bawah f. Matriks Identitas
Matriks identitas adalah mariks yang semua elemen diagonalnya bernilai satu.
Contoh: [ ] g. Matriks Nol
Matriks nol adalah matriks yang semua entrinya bernilai nol.
Contoh: * + h. Matriks Transpose
Jika adalah matriks , maka transpose dari dinyatakan dengan yang didefinisikan sebagai matriks yang didapatkan dengan mempertukarkan baris-baris dan kolom-kolom dari .
Contoh: [
] [ ] i. Kelipatan Skalar
Jika adalah matriks sebarang dan adalah skalar sebarang, maka hasilkali adalah matriks yang diperoleh dari perkalian setiap entri pada matriks dengan bilangan .
Contoh: [
] [
] [
]
6
2.1.2 Perkalian Matriks
Jika adalah matriks dan adalah matriks , maka hasilkali adalah matriks yang entri-entrinya ditentukan dengan mencari entri pada baris dan kolom dari yang kemudian akan dikalikan entri-entri yang bersesuaian dari baris dan kolom tersebut dan kemudian dijumlahkan hasilnya.
(2.2)
2.1.3 Diagonalisasi Matriks
Sebuah matriks bujur sangkar dikatakan dapat didiagonalisasi jika terdapat sebuah matriks yang dapat dibalik sedemikan sehingga adalah sebuah matriks diagonal, maka dikatakan dapat mendiagonalisasi matriks .
(2.3)
adalah matriks diagonal yang memiliki nilai-nilai eigen dari matriks sebagai entri-entri diagonal utamanya.
Untuk menghitung pangkat sebuah matriks yang dapat didiagonalisasi, sebarang bilangan bulat positif, maka Persamaan (2.3) menjadi
dengan hukum asosiatif dan , adalah matriks identitas, diperoleh
(2.4)
sedemikian sehingga
(2.5)
2.2 Nilai Eigen dan Vektor Eigen
Jika adalah matriks bujur sangkar , maka sebuah vektor taknol pada disebut vektor eigen dari apabila adalah sebuah kelipatan skalar dari , yaitu
(2.6)
Skalar dinamakan nilai eigen dari dan disebut sebagai vektor eigen dari yang bersesuaian dengan . Untuk mencapai nilai eigen dari matriks yang berukuran , dapat dituliskan kembali Persamaan (2.6) sebagai
7
atau secara ekuivalen
(2.7)
Agar sistem tersebut memiliki solusi tak nol, maka syarat yang harus dipenuhi adalah
| | (2.8)
Persamaan (2.8) disebut persamaan karakteristik matriks . Skalar-skalar yang memenuhi persamaan ini merupakan nilai-nilai eigen dar matriks . Apabila diperluas, determinan adalah sebuah polinomial dalam variabel yang disebut sebagai polinomial karakteristik matriks . Jika adalah nilai eigen dari suatu matriks , maka multiplisitas aljabar adalah banyaknya sebagai akar dari persamaan polinomial karakteristik matriks . Sedangkan multiplisitas geometri adalah dimensi ruang eigen yang bersesuaian dengan .
Contoh:
[
]
Untuk mencari nilai eigen dari matriks digunakan Persamaan (2.8)
| |
|[
] [
]|
|[
]|
Diperoleh dan , artinya multiplisitas aljabar dari matriks adalah 3.
Selanjutnya untuk mencari vektor eigen dari matriks yang bersesuaian dengan yaitu dengan menggunakan Persamaan (2.7)
8
[
] [ ] [ ] Untuk , persamaan diatas menjadi
[
] [ ] [ ] Oleh karena itu, sistem ini memperoleh hasil
Berdasarkan nilai , dan , vektor eigen yang terkait dengan adalah vektor tak nol yang berbentuk
* + [ ]
sehingga [ ] adalah basis untuk ruang eigen yang bersesuaian dengan Untuk , persamaan diatas menjadi
[
] [ ] [ ] Oleh karena itu, sistem ini memperoleh hasil
Berdasarkan nilai , dan , vektor eigen yang terkait dengan adalah vektor-vektor tak nol yang berbentuk
* + [ ] [ ]
sehingga [ ] dan [ ] adalah basis untuk ruang eigen yang bersesuaian dengan
Jadi vektor-vektor eigen dari matriks adalah [ ] [ ] dan [ ] , yang artinya matriks memiliki multiplisitas geometri sebanyak 3.
9
2.3 Matriks Leslie
Model matriks Leslie merupakan salah satu model yang digunakan oleh para ahli demografi, yang ditemukan oleh seorang pakar Ekologi bernama P.H Leslie pada tahun 1940-an. Model ini menjelaskan pertumbuhan populasi perempuan. Dalam model ini perempuan (manusia) atau betina (hewan) dibagi kelas-kelas umur dalam durasi waktu yang sama. Untuk mengetahui pertumbuhan populasi dengan matriks Leslie dipengaruhi oleh tingkat kesuburan dan tingkat ketahanan hidup betina dari suatu populasi, proses ini dapat menentukan pertumbuhan populasi yang terjadi, apakah populasi akan meningkat, menurun, atau cenderung stabil.
Apabila terdapat batasan dari umur hidup hewan betina pada populasi tertentu adalah tahun dan populasi dibagi menjadi kelas umur, maka tiap-tiap kelas umur memiliki rentang umur tahun. Sebagai contoh dapat dilihat pada Tabel 2.1
Tabel 2.1 Penentuan kelas umur Kelas umur Rentang umur
[ )
[
)
[
)
[ )
*
+
Misalnya diketahui jumlah betina pada tiap kelas dari ke- kelas tersebut pada waktu . Secara khusus, misalkan, ( pada awal tahun) betina dalam kelas pertama, ( pada awal tahun) betina di dalam kelas kedua, ( pada awal tahun) betina di dalam kelas ketiga, dan seterusnya. Dengan bilangan ke- ini akan dibentuk suatu vektor kolom
10
[
]
(2.9)
Vektor Persamaan (2.9) dinamakan vektor distribusi umur mula-mula (initial age distribution vector). Dengan berjalannya waktu, banyaknya betina di dalam setiap kelompok dari ke- kelompok tersebut akan berubah karena tiga proses biologis, yakni: kelahiran, kematian dan pertambahan usia. Dengan perhitungan ketiga proses ini secara kuantitatif, dapat dilihat bagaimana memproyeksikan vektor distribusi umur mula-mula tersebut ke masa mendatang.
Cara yang paling mudah mempelajari proses penuaan adalah dengan mengamati populasi pada waktu-waktu diskrit, misalnya Model matriks Leslie memberikan syarat bahwa kurun waktu diantara dua waktu pengamatan yang berurutan adalah sama seperti kurun waktu dari selang (interval) umur. Dengan demikian ditetapkan
⁄ ⁄
⁄
Dengan ketetapan ini, maka semua betina dalam kelas ke- pada waktu
telah berada dalam kelompok ke- pada waktu .
Didefinisikan sebagai tingkat kesuburan betina yaitu rata-rata jumlah anak betina yang lahir dari kelompok umur saat waktu ke . Didefinisikan sebagai tingkat ketahanan hidup betina yaitu peluang betina yang dapat bertahan hidup dari kelas umur sampai saat waktu ke .
Dalam penelitian diasumsikan bahwa paling sedikit terdapat satu kelas umur dari tingkat kesuburan yang bernilai positif, dan tingkat ketahanan hidup tidak boleh sama dengan nol, serta diasumsikan tidak adanya migrasi pada populasi tersebut.
11
Berdasarkan batasan di atas, diketahui bahwa paling sedikit satu kelas umur dari , karena jika , untuk setiap pada kelas tersebut tidak ada kelahiran terjadi. Kelas umur yang punya nilai disebut kelas umur kesuburan. Diketahui , karena jika , maka tidak ada betina yang bisa bertahan hidup ke kelas berikutnya. Selanjutnya didefinisikan vektor distribusi umur pada waktu
[
]
(2.10)
Didefinisikan ( pada tahun ke- ) adalah jumlah betina dalam kelas umur ke- pada waktu . Pada waktu , betina-betina dalam kelas umur pertama adalah anak dari betina-betina yang lahir diantara waktu dan waktu . Sehingga dapat dibentuk menjadi
{
}
{
} {
}
{
} atau secara matematis
(2.11)
Betina-betina pada kelas umur ke- dengan pada waktu adalah betina pada kelas ke- pada waktu yang masih hidup pada waktu . Sehingga ditetapkan
{
}
{
}
{
}
atau secara matematis
(2.12)
12
Dengan menggunakan notasi matriks, Persamaan (2.11) dan (2.12) dapat dituliskan kembali menjadi
[
] [
][
] atau singkatnya
(2.13)
adalah matriks Leslie.
[
] Dari Persamaan (2.13) akan dihasilkan
(2.14)
Berdasarkan Persamaan (2.14), jika diketahui distribusi umur awal dan matriks Leslie , maka dapat ditentukan distribusi umur betina dalam populasi tertentu pada sebarang waktu di masa mendatang.
2.4 Karakteristik Matriks Leslie
(Montshiwa, 2007) Nilai eigen dan vektor eigen berperan penting untuk menentukan dinamika populasi jangka panjang serta dapat menentukan apakah populasi meningkat, menurun atau konstan. Beberapa kasus dapat terjadi pada sebuah populasi yang terkait dengan nilai eigen positif dari matriks Leslie, yaitu populasi akan bertambah jika nilai eigen positif lebih besar dari satu, populasi akan berkurang jika nilai eigen positif kurang dari satu dan populasi stabil jika nilai eigen positif sama dengan satu. Sehingga, nilai eigen sangat penting untuk mendefinisikan angka pertumbuhan populasi atau memberikan informasi tentang keadaan populasi sedangkan vektor eigen menunjukkan kestabilan distribusi umur.
13
Meskipun Persamaan (2.14) menunjukkan distribusi umur dari suatu populasi pada setiap waktu, namun tidak serta-merta memberikan gambaran umum mengenai dinamika proses pertumbuhan yang terjadi. Sehingga, harus ditentukan nilai eigen dan vektor eigen dari matriks Leslie. Nilai eigen dari adalah akar-akar dari polinomial karakteristiknya.
| |
||
[
] [
]
||
||
[
] [
]
||
|| [
]
||
(2.15) Dimisalkan persamaan polinomial berikut untuk memudahkan menganalisis akar- akarnya
(2.16) Persamaan karakteristik dapat ditulis untuk
Gambar 2.1 Grafik fungsi
Oleh karena semua dan adalah tak negatif, dapat dilihat bahwa berkurang secara monoton untuk . Akibatnya, mendekati nol ketika
14
. Sehingga, seperti yang terlihat pada Gambar 2.1, terdapat sebuah yang tunggal, misalnya , sedemikian rupa sehingga . Dalam hal ini, matriks memiliki sebuah nilai eigen positif yang unik. Dilihat bahwa memiliki multiplisitas satu yaitu bukan merupakan akar berulang dari persamaan karakteristik.
[
⁄
⁄
⁄
⁄ ]
(2.17)
Oleh karena mempunyai multiplisitas satu, maka ruang eigen yang bersesuaian mempunyai dimensi satu, demikian pula vektor eigen yang brsesuaian merupakan multiplisitas . Beberapa teorema yang berkaitan mengenai nilai eigen, yaitu
Teorema 1: Sebuah matriks Leslie mempunyai sebuah nilai eigen positif unik . Nilai eigen ini mempunyai multiplisitas satu dan sebuah vektor eigen yang seluruh entri-entrinya adalah positif.
Teorema 2: Jika adalah suatu nilai eigen positif yang unik dari sebuah matriks Leslie dan adalah sebarang nilai eigen bilangan real atau bilangan kompleks dari , maka | | .
Dalam kasus ini, akan disebut dengan nilai eigen dominan. Namun, akan dinyatakan suatu syarat yang mendukung yaitu apabila terdapat dua entri yang berurutan dan pada baris pertama sebuah matriks Leslie adalah tidak nol.
Sehingga, jika suatu populasi mempunyai dua kelas umur subur yang berurutan, maka matriks Leslie-nya memiliki nilai eigen yang dominan.
Definisi: Diberikan sebagai nilai eigen dari matriks Leslie , disebut sebagai nilai eigen dominan dari jika
| | | |
Diasumsikan dapat didiagonalisasi. Matriks Leslie memiliki nilai eigen dan vektor eigen yang bersesuaian. Dibentuk sebuah matriks yang setiap kolomnya adalah vektor-vektor eigen dari .
[ | | | | ]
15
Terdapat adalah invers matriks dari . Diagonalisasi matriks Leslie berbentuk
[
]
(2.18)
Dari Persamaan (2.18), dapat dihasilkan
[
]
(2.19)
Misal terdapat vektor distribusi awal dari populasi tertentu, sehingga diperoleh
[
]
(2.20)
Berdasarkan Persamaan (2.14), Persamaan (2.20) menjadi
[
]
(2.21)
Kedua ruas pada Persamaan (2.21) dibagi dengan , diperoleh
[
( )
( ) ( )
]
(2.22)
Diketahui adalah nilai eigen dominan dari matriks Leslie, sehingga ( ) untuk
Sedemikian sehingga
( ) saat Dengan ini, akan dibentuk sebuah limit yaitu
16
( ) [
]
(2.23)
Dimisalkan hasil perkalian
[ ] Persamaan (2.23) akan menjadi
( ) [
][ ]
( ) [ | | | | ] [
][ ]
( ) [ | | | | ] [ ]
( ) ( )
Dari limit diatas diperoleh suatu hampiran
(2.24)
Sedemikian sehingga
(2.25)
untuk nilai-nilai yang cukup besar. Hal ini menunjukkan bahwa untuk nilai waktu yang besar, tiap vektor distribusi umur adalah kelipatan skalar dari vektor distribusi
17
umur sebelumnya, nilai skalar tersebut merupakan nilai eigen positif yang dominan dari matriks Leslie.
Tiga kasus yang muncul berkaitan dengan nilai eigen positif :
i. Jika diketahui , maka populasi pada semua kelas umur cenderung menurun
ii. Jika diketahui , maka populasi pada semua kelas umur cenderung tetap iii. Jika diketahui , maka populasi pada semua kelas umur cenderung
meningkat
Kasus dari matriks Leslie secara khusus merupakan kasus yang menarik karena menunjukkan suatu populasi yang memiliki pertumbuhan populasi nol (zero population growth). Untuk distribusi umur awal manapun, populasi ini mendekati sebuah limit distribusi umur yang merupakan kelipatan dari vektor eigen . Berdasarkan Persamaan (2.16), merupakan sebuah nilai eigen jika dan hanya jika
(2.26)
Persamaan berbentuk
(2.27)
disebut laju reproduksi bersih (net reproduction rate) dari suatu populasi. Dengan demikian, sebuah populasi memiliki pertumbuhan populasi nol jika dan hanya jika laju reproduksi bersihnya bernilai satu.
2.5 Model Pemanenan
Memanen berarti menghilangkan sekelompok hewan dari populasinya. Kata
“memanen” yaitu hewan-hewan yang dihilangkan dari populasinya untuk tujuan yang lain. Menurut definisi, suatu kebijakan pemanenan dimana sebuah populasi hewan dipanen secara periodik dikatakan berkesinambungan jika hasil dari tiap panen selalu sama dan distribusi umur dari populasi yang tersisa setelah setiap panen tetap sama.
Sebagaimana dijelaskan sebelumnya, penelitian ini hanya akan membahas populasi perempuan atau populasi betina. Jika jumlah hewan jantan dalam tiap kelas umur sama dengan jumlah hewan betina, suatu asumsi yang wajar untuk kebanyakan populasi, maka kebijakan tersebut juga berlaku bagi populasi jantan.
18
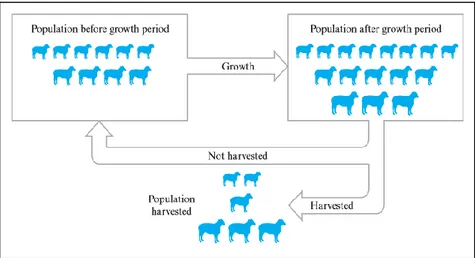
Gambar 2.2 Ilustrasi gagasan mendasar model pemanenan
Populasi tersebut mengalami suatu periode pertumbuhan yang akan dijelaskan dengan matriks Leslie. Pada akhir dari periode pertumbuhan, fraksi tertentu dari tiap kelas umur dipanen sedemikian rupa sehingga populasi yang tidak dipanen mempunyai distribusi umur yang sama dengan populasi semula. Siklus ini diulang setelah tiap panen sehingga hasilnya berkesinambungan. Durasi dari suatu panen diasumsikan relatif pendek dibandingkan dengan periode pertumbuhannya, sehingga pertumbuhan atau perubahan apapun yang terjadi pada populasi selama periode panen dapat diabaikan. Pada beberapa populasi, hanya hewan-hewan betina termuda yang mempunyai nilai ekonomis, sehingga peternak cenderung hanya memanen hewan-hewan betina dari kelas umur termuda.
Untuk menjelaskan model pemanenan secara matematis, dimisalkan
[ ]
(2.28)
sebagai vektor distribusi umur dari populasi awal periode pertumbuhan. Dengan demikian, adalah jumlah populasi betina di dalam kelas ke- yang tidak dipanen.
Sebagaimana model Leslie sudah mempersyaratkan bahwa durasi tiap kelas umur harus identik dengan durasi periode pertumbuhan.
Sebagai contoh, jika suatu populasi dipanen satu kali dalam setahun, maka populasi tersebut dibagi menjadi kelas-kelas umur satu tahun. Jika adalah suatu matriks Leslie yang menggambarkan pertumbuhan populasi tertentu, maka vektor adalah vektor distribusi umur dari populasi pada akhir periode pertumbuhan, tepat
19
sebelum periode panen. Jika , untuk , adalah fraksi dari populasi betina dari kelas ke- yang telah dipanen, maka untuk membentuk sebuah matriks diagonal digunakan bilangan sehingga diperoleh
[
]
yang disebut matriks pemanenan (harvesting matrix). Dalam hal ini, memanen bisa saja dengan tanpa hasil ( ), seluruhnya ( ), atau suatu fraksi ( ) dari masing-masing dari kelas. Oleh karena jumlah hewan pada kelas ke- sesaat sebelum tiap panen adalah entri ke- dari vektor , dapat dibentuk bahwa entri ke- dari vektor kolom
[
]
(2.29)
adalah jumlah hewan betina yang dipanen dari kelas ke- .
Dari definisi kebijakan pemanenan berkesinambungan, diketahui
[
] [ ] [
]
atau secara matematis
(2.30)
Didefinisikan harus merupakan sebuah vektor eigen dari matriks yang bersesuaian dengan nilai eigen satu. Hal ini dapat memberikan batasan-batasan tertentu pada nilai-nilai dan . Misalkan matriks Leslie dari suatu populasi adalah
[
] Sehingga matriks berbentuk
20
([
] [
])[
]
([
][
])
[
]
(2.31)
Dapat dilihat bahwa matriks merupakan matriks dengan bentuk matematis yang sama dengan matriks Leslie.
BAB 3
METODOLOGI PENELITIAN
3.1 Jenis Penelitian
Jenis penelitian yang digunakan adalah kajian pustaka yaitu salah satu jenis penelitian yang memanfaatkan sumber kepustakaan untuk memperoleh informasi.
Metodologi penelitian dilakukan dengan mengumpulkan dan mempelajari beberapa literatur berupa buku-buku serta jurnal-jurnal yang berkaitan dengan penelitian guna menyelesaikan permasalahan yang akan diselidiki.
3.2 Metodologi Penelitian
Adapun beberapa langkah yang dilakukan dalam penelitian ini adalah 1. Studi Pustaka
Mengumpulkan serta mempelajari berbagai sumber informasi berupa buku-buku ataupun jurnal-jurnal yang isinya terkait dengan model matriks Leslie serta penerapannya dalam model pemanenan populasi hewan.
2. Mengkaji model matriks Leslie dan karakteristiknya
Beberapa yang harus dikaji dalam model ini yaitu pengertian dan langkah-langkah untuk membentuk matriks Leslie, parameter-parameter yang mendasari bentuk matriks Leslie, dan nilai eigen untuk mengetahui laju pertumbuhan populasi serta vektor eigen untuk mengetahui kestabilan distribusi umur. Adapun teorema- teorema yang berkaitan dengan nilai eigen akan dibuktikan secara berurutan.
3. Mengkaji dan menganalisis model pemanenan
Menerapkan model matriks Leslie pada pemanenan populasi hewan dan karakteristiknya, serta mengkaji strategi pemanenan khusus yaitu pemanenan seragam berdasarkan Persamaan (2.30) dan pemanenan kelas umur termuda berkaitan dengan laju reproduksi bersih pada Persamaan (2.27)
4. Mengaplikasikan model pemanenan
Model pemanenan akan diaplikasikan dengan salah satu contoh populasi hewan.
a. Diberikan data berupa tingkat kelahiran dan tingkat ketahanan hidup suatu populasi yaitu populasi kambing berdasarkan kelas umur yang dibuat secara random menggunakan Microsoft Excel.
22
b. Membuat matriks Leslie dari data yang telah ada dan menentukan vektor distribusi umur awal berdasarkan subbab (2.3) untuk mengetahui distribusi umur populasi pada sebarang waktu di masa depan.
c. Menentukan nilai eigen dari matriks Leslie menggunakan Persamaan (2.15) untuk memprediksi laju pertumbuhan populasinya. Jika polinomial karakteristik dengan pangkat tinggi serta sukar dalam perhitungannya, akan lebih mudah mencari nilai eigen nya menggunakan aplikasi MATLAB.
d. Menentukan kebijakan pemanenan yang berkesinambungan, baik pemanenan seragam maupun pemanenan kelas umur termuda.
5. Kesimpulan
Membuat kesimpulan berdasarkan kajian pembahasan yaitu mengenai kebijakan pemanenan yang berkesinambungan pada model pemanenan.
BAB 4 PEMBAHASAN
4.1 Nilai Eigen Matriks Leslie
Matriks Leslie dengan karakteristiknya telah mampu memberikan solusi pemecahan masalah tertentu. Parameter yang digunakan pada perhitungan matriks Leslie adalah batas maksimal umur suatu populasi, angka kesuburan, dan peluang ketahanan hidup dari populasi betina. Jika dimisalkan adalah nilai eigen positif yang dominan dari matriks Leslie, maka nilai digunakan untuk memprediksi laju pertumbuhan populasi tertentu, apakah akan cenderung menurun, meningkat atau stabil.
Sebelum mengkaji karakteristik model pemanenan, akan dibuktikan teorema- teorema mengenai nilai eigen dalam karakteristik matriks Leslie. Dengan dibuktikannya teorema-teorema tersebut akan memudahkan pencarian vektor eigen , artinya ditribusi kestabilan umur populasi akan diperoleh. Seperti yang sudah disebutkan pada bab sebelumnya, terdapat 2 teorema diantaranya
Teorema 1: Sebuah matriks Leslie mempunyai sebuah nilai eigen positif unik . Nilai eigen ini mempunyai multiplisitas satu dan sebuah vektor eigen yang seluruh entri-entrinya adalah positif.
Bukti:
Dimisalkan
[ ]
(4.1)
Diberikan sebagai suatu vektor eigen dari yang bersesuaian dengan yang memenuhi
([
] [
])
24
[
][ ] [ ]
[
] [ ]
Diperoleh
(4.2)
(4.3)
(4.4)
(4.5)
Substitusi Persamaan (4.3), (4.4), dan (4.5) ke Persamaan (4.2)
( ) Dengan demikian
(4.6)
Diketahui merupakan vektor tak nol yang bersesuaian dengan . Dari Persamaan (4.6), jika , maka vektor eigen yang berhubungan dengan adalah vektor nol. Sedemikan sehingga dimisalkan , diperoleh
Sehingga diperoleh vektor eigen berbentuk
25
[
]
(4.7)
Diperoleh bahwa ruang eigen dari mempunyai dimensi satu, sehingga terbukti bahwa multiplisitasnya sama dengan satu serta diperoleh elemen-elemen dari vektor eigen merupakan bilangan positif. Dengan adanya teorema ini akan memberikan informasi mengenai keberadaan nilai eigen positif. Dapat dilihat bahwa perilaku jangka panjang dan distribusi umur populasi ditentukan oleh nilai eigen dan vektor eigen -nya.
Teorema 2: Jika adalah suatu nilai eigen positif yang unik dari sebuah matriks Leslie dan adalah sebarang nilai eigen bilangan real atau bilangan kompleks dari , maka | | .
Bukti:
Diambil sebarang
Akan dibuktikan bahwa .
Dari Persamaan (2.16), diketahui , sehingga diperoleh
Dengan diambilnya bagian real dari kedua persamaan diperoleh
26
Sedemikian sehingga
Dengan inilah diambil kesimpulan bahwa
dan | |
Diketahui bahwa , sehingga terbukti bahwa untuk sebarang yang merupakan bilangan real ataupun kompleks berlaku | | .
4.2 Karakteristik Model Pemanenan
Berdasarkan penjelasan yang ada bahwa terdapat sebuah syarat penting dan cukup dalam matriks Leslie supaya memiliki nilai eigen bernilai satu yaitu laju reproduksi bersihnya bernilai satu (Persamaan 2.26).
Dimisalkan dan matriks berbentuk seperti Persamaan (2.31) | |
[
] n
Dengan menghitung laju reproduksi bersih dari dan ditetapkan sama dengan satu, dihasilkan
[
] (4.8) Persamaan (4.8) memberikan batasan seberapa besar fraksi pemanenan yang diperkenankan. Hanya yang memenuhi Persamaan (4.8) dan terletak di dalam interval [ ] sehingga bisa menghasilkan panen yang berkesinambungan.
Apabila terpenuhi pada Persamaan (4.8) maka matriks mempunyai nilai eigen (yang diinginkan). Pembahasan lebih lanjut, nilai eigen ini memiliki kelipatan satu, sebagaimana nilai eigen positif dari matriks Leslie
27
selalu memiliki kelipatan satu (Teorema 1). Hal ini menunjukkan bahwa hanya terdapat satu vektor eigen independen linear yang memenuhi Persamaan (2.30).
Dimisalkan
[ ]
Diberikan merupakan suatu vektor eigen dari yang memenuhi
[
( )
] [ ]
Diperoleh
( )
(4.9)
(4.10)
(4.11)
(4.12) Substitusi Persamaan (4.10), (4.11), dan (4.12) ke Persamaan (4.9)
( )
Dengan demikian
(4.13)
Menurut Persamaan (4.13), jika , maka vektor eigen merupakan vektor nol.
Sedemikan hingga dimisalkan , diperoleh
28
Sehingga diperoleh vektor eigen berbentuk
[
]
(4.14)
Ditinjau dari keseluruhan, terdapat sebuah ambiguitas atau keraguan dalam banyaknya hewan betina di dalam populasi setelah tiap panen. Hal ini dapat ditentukan dengan sebuah syarat tambahan, seperti batasan ekologi atau ekonomi.
Sebagai contoh, untuk populasi tertentu yang secara ekonomis didukung oleh si pemanen, populasi terbesar yang dicapai oleh pemanen diantara dua waktu panen akan menentukan konstanta tertentu yang dikalikan dengan untuk menghasilkan vektor yang berhubungan dengan Persamaan (2.30). Untuk populasi hewan liar, habitat alamiah dari populasi akan menentukan seberapa besar jumlah populasi yang dapat terjadi di antara dua waktu panen.
4.3 Pemanenan Seragam
Dengan banyaknya populasi, akan sukar untuk membedakan hewan-hewan dengan umur yang spesifik. Apabila hewan-hewan diambil secara acak, maka dapat diasumsikan bahwa fraksi yang sama dari tiap kelas umur telah dipanen. Oleh karena itu, ditetapkan
Persamaan (2.30) akan direduksi menjadi
(
) (4.15)
Jadi, ( ) harus merupakan nilai eigen positif unik dari matriks pertumbuhan Leslie .
(
)
Untuk memperoleh fraksi pemanenan , secara ekuivalen menjadi
⁄ (4.16)
29
Vektor pada hal ini adalah sama dengan vektor eigen dari matriks Leslie yang bersesuaian dengan nilai eigen , yaitu
[
⁄
⁄
⁄
⁄ ]
(4.17)
Dari Persamaan (4.17), diketahui bahwa semakin besar , semakin besar pula peluang dari hewan-hewan yang dapat dipanen tanpa menurunkan jumlah populasi. Sehingga diperlukan agar fraksi pemanenan terletak di dalam interval [ ]. Hal inilah yang diinginkan, sebagaimana merupakan syarat agar populasi dari tiap kelas akan meningkat.
4.4 Pemanenan Kelas Umur Termuda
Dalam beberapa populasi, hanya populasi hewan betina termuda yang mempunyai nilai ekonomis, sehingga peternak cenderung ingin memanen hewan-hewan betina pada kelas umur termuda. Berdasarkan hal tersebut, ditetapkan
Persamaan (4.8) direduksi menjadi
adalah laju reproduksi bersih dari populasi, secara ekuivalen
⁄ (4.18)
Dari Persamaan (4.18) diketahui kebijakan pemanenan berkesinambungan hanya mungkin jika . Hal ini diterima karena hanya jika maka populasi akan bertambah. Dari Persamaan (4.14), vektor distribusi umur setelah tiap panen adalah
[ ]
(4.19)
30
4.5 Aplikasi Model Pemanenan pada Populasi Kambing
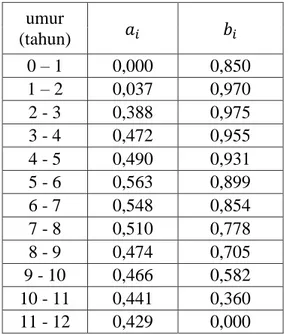
Berikut ini merupakan contoh pertumbuhan populasi kambing. Diketahui umur maksimal kambing adalah 12 tahun dan jumlah awal kambing adalah 100 ekor untuk setiap kelas umur. Diketahui parameter-parameter yang tersedia dalam Tabel 4.1 adalah tingkat kesuburan dan tingkat ketahanan hidup dari suatu populasi. Pada contoh ini, data pada tabel tersebut dibuat dengan Microsoft Excel yang nilai-nilainya telah ditentukan menggunakan nilai random agar mempermudah hasil perhitungan.
Tabel 4.1 Tingkat kelahiran dan tingkat ketahanan hidup populasi kambing umur
(tahun)
0 – 1 0,000 0,850 1 – 2 0,037 0,970 2 - 3 0,388 0,975 3 - 4 0,472 0,955 4 - 5 0,490 0,931 5 - 6 0,563 0,899 6 - 7 0,548 0,854 7 - 8 0,510 0,778 8 - 9 0,474 0,705 9 - 10 0,466 0,582 10 - 11 0,441 0,360 11 - 12 0,429 0,000 tingkat kesuburan (birth rate)
tingkat ketahanan hidup (survival rate)
Bentuk matriks Leslie dari data pada Tabel 4.1 adalah
[
] Bentuk vektor distribusi umur awal adalah
31
[
] [ ]
Jumlah populasi awal dari kambing adalah 1200 ekor. Untuk mengetahui jumlah kambing betina pada tahun pertama, kedua dan seterusnya dapat dihitung dengan menggunakan Persamaan (2.14). Jumlah kambing betina pada tahun pertama yaitu
[
]
Diperoleh prediksi jumlah populasi kambing pada tahun petama adalah sebesar 1368 ekor. Hal ini berarti pertumbuhan populasi diprediksikan meningkat sebesar 168 ekor pada tahun pertama.
[ ]
Diperoleh prediksi jumlah populasi kambing pada tahun kedua adalah sebesar 1502 ekor. Hal ini berarti pertumbuhan populasi diprediksikan meningkat sebesar 134 ekor pada tahun kedua dari tahun pertama atau sebesar 302 ekor dari awal tahun.
32
Dilakukan cara yang sama untuk perhitungan pertumbuhan populasi tahun-tahun berikutnya.
Untuk memprediksi laju pertumbuhan dari populasi kambing digunakan nilai eigen dari matriks Leslie, yaitu
| |
|
|
|
|
|
|
|
|
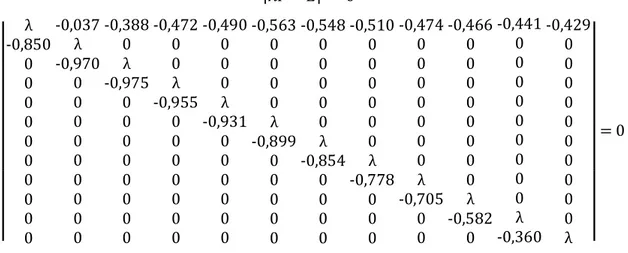
Perhitungan dilakukan menggunakan Persamaan (2.15), diperoleh [
]
Dari persamaan karakteristik diatas diselesaikan dengan menggunakan aplikasi MATLAB yang algoritmanya telah dilampirkan pada Lampiran 1 guna memperoleh nilai-nilai eigen yang terangkum dalam Tabel 4.2
Tabel 4.2 Nilai eigen matriks Leslie Nilai Eigen
1.180027596483179e+000
5.628234231383071e-001 + 5.514423691506808e-001i 5.628234231383071e-001 - 5.514423691506808e-001i
33
2.453901731077905e-001 + 7.031572841003201e-001i 2.453901731077905e-001 - 7.031572841003201e-001i -1.331128808544938e-001 + 7.259427053077278e-001i
-1.331128808544938e-001 - 7.259427053077278e-001i -3.737767187662345e-001 + 5.605423506131189e-001i -3.737767187662345e-001 - 5.605423506131189e-001i
-6.631651748299201e-001
-5.597552074519956e-001 + 3.044629819665216e-001i
-5.597552074519956e-001 - 3.044629819665216e-001i
Dari semua nilai eigen yang dihasilkan, nilai eigen yang dominan adalah , sedemikian sehingga nilai eigen ini menunjukkan pertumbuhan populasi kambing akan cenderung meningkat.
4.4.1 Pemanenan Seragam pada Populasi Kambing
Dari Persamaan (4.16) dan nilai eigen dominan sebesar 1,180, fraksi pemanenan adalah
⁄
Kebijakan pemanenan seragam dengan artinya sebanyak itulah kambing akan dipanen untuk tiap kelasnya. Dari Persamaan (4.17), vektor distribusi umur dari kambing tersebut adalah
[ ]
[ ]
[ ]
Dari dapat dipastikan bahwa untuk 100 kambing dalam setiap kelas umur, pada kelas umur 0-1 tahun sebanyak 17,7 atau 18 ekor kambing yang akan dipanen. Pada kelas umur 1-2 tahun sebanyak 12,8 atau 13 ekor kambing akan
34
dipanen. Pada kelas umur 2-3 tahun sebanyak 10,5 atau 11 ekor kambing akan dipanen dan seterusnya. Banyaknya kambing yang akan dipanen untuk semua kelas umur secara keseluruhan berjumlah 73 ekor dari 1200 ekor kambing dalam satu tahun. Jadi, kebijakan pemanenan berkesinambungan seragam pada populasi kambing sebesar 6,08% dari seluruh populasi untuk tiap tahunnya.
4.4.2 Pemanenan Kelas Umur Termuda pada Populasi Kambing
Untuk mengetahui kebijakan pemanenan berkesinambungan pada pemanenan ini, akan dicari nilai yaitu laju reproduksi bersih dari populasi kambing tersebut (Persamaan (2.27)), diperoleh
Dicari fraksi pemanenan dari Persamaan (4.18), diperoleh ⁄
Vektor distribusi umur dari kambing tersebut setelah tiap panen menurut Persamaan (4.19) adalah
35
[ ]
[ ]
Vektor yaitu vektor distribusi umur pada saat tepat sebelum panen.
Jumlah keseluruhan entri dalam vektor sebesar 8,707, sehingga pada entri pertama yaitu 2,588 adalah 29,7% dari jumlah populasi. Hal ini berarti tepat sebelum tiap panen, 29,7% dari populasi kambing berada pada kelas umur termuda. Sehingga keseluruhan populasi kambing yang dipanen tiap tahun sebesar 61,4% dari 29,7%
yaitu 18,2%. Jadi, kebijakan pemanenan berkesinambungan populasi kambing pada kelas umur termuda adalah sebesar 18,2% dari seluruh populasi. Jika untuk 1200 ekor kambing maka kambing yang akan dipanen sebanyak 218 ekor setiap tahunnya.
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Dalam model pemanenan, terdapat banyak pilihan untuk nilai-nilai yang akan menghasilkan panen berkesinambungan. Tetapi saat nilai tersebut terpilih, maka distribusi umur dari populasi setelah tiap panen secara unik ditentukan oleh vektor eigen . Pada pemanenan seragam, nilai-nilai adalah sama yaitu , artinya fraksi dari populasi betina yang dipanen untuk setiap kelas umur adalah sama. Sehingga kebijakan pemanenan seragam yang berkesinambungan adalah ⁄ . Hasil penelitian dalam kasus ini, sehingga diperoleh sebesar atau . Pada pemanenan kelas umur termuda, nilai-nilai adalah 0 dan adalah , artinya populasi hewan pada kelas pertama atau termudalah yang akan dipanen karena dinilai memiliki nilai ekonomis yang tinggi pada beberapa populasi. Sehingga kebijakan pemanenan kelas umur termuda yang berkesinambungan adalah ⁄ , R merupakan laju reproduksi bersih dari populasi hewan betina tertentu. Dalam pengaplikasian pada kasus ini diperoleh serta sebesar .
5.2 Saran
Penelitian selanjutnya diharapkan meneliti model pemanenan lebih lanjut agar hasil maksimal dalam memprediksi pemanenan karena model ini berasumsi bahwa terdapat dukungan ekonomis pada populasi tertentu oleh pemanen. Sehingga, pemanenan akan optimal sesuai dengan kebijakan yang berkesinambungan.
37
DAFTAR PUSTAKA
Anggreini, D., Hastari, R.C. 2017. Penerapan Matriks Leslie pada Angka Kelahiran dan Harapan Hidup Wanita di Provinsi Jawa Timur. PHYTAGORAS (Jurnal Pendidikan Matematika). 12(2) : 109-122.
Anton, H., dan Rorres, A. 2014. Aljabar Linier Elementer Edisi Kedelapan. Jakarta:
Erlangga.
Anton, H., dan Rorres, A. 2014. Aljabar Linier Elementer Versi Aplikasi Edisi Kedelapan. Jakarta: Erlangga.
Corazon, C., M., Muda, Y., Hasanah, Nurul. 2016. Aplikasi Matriks Leslie untuk Memprediksi Jumlah dan Laju Pertumbuhan Perempuan di Provinsi Riau pada Tahun 2017. Jurnal Sains Matematikan dan Statistika. 1(2). UIN Suska Riau.
Leon, J. Steven. 2001. Aljabar Linier dan Aplikasinya Edisi Kelima. Jakarta:
Erlangga.
Nelson, B., Reid, D.T., Tangar, A. 2013. Leslie Matrices and Women Population in the United States of Americ. Georgia Journal of Scienc. 71(2) : Article 6.
Pratama, Y., Pribahandono, B., dan Kusumastuti, N. 2013. Aplikasi Matriks Leslie untuk Memprediksi Jumlah dan Laju Pertumbuhan Suatu Populasi. Buletin Ilmiah Math. Stat. Dan Terapannya. 2(3) : 163-172.
Sampurna, B., Santosa, Y., Rahmat, U.M. 2014. Pendugaan Parameter Demografi dan Model Pertumbuhan Monyet Ekor Panjang (Macaca fascicularis) di Pulau Peucang, Taman Nasional Ujung Kulon. Media Konservasi. 19(2) : 95-104.
Santosa R. Gunawan. 2008. Aljabar Linier Dasar. Yogyakarta: Penerbit Andi.
Sanusi, W., Sukarna, Ridiawati, N., 2018. Matriks Leslie dan Aplikasinya dalam Memprediksi Jumlah dan Laju pertumbuhan Penduduk di Kota Makassar.
Journal of Computations and Statistics. 1(2) : 142-154.
Sumarti, N., Wardana, M.A., Nurani, N. 2018. Population Grwoth Models of Forest Trees for Conservation Management: Case of Teak (Tectona Grandis) Forest in Begal, East Java, Indonesia. HAYATI Journal of Biosciences.
25(4): 169-177.
38
Yuliana, S., Rahayu, Mashuri. 2012. Penerapan Diagonalisasi Matriks dan Matriks Leslie dalam Memproyeksikan Jumlah Populasi Perempuan. UNNES Journal of Mathematics. 1(1). Universitas Negeri Malang.
39
LAMPIRAN
Lampiran 1. Mencari nilai eigen pada aplikasi MATLAB
Perintah yang diketik beserta hasil yang diperoleh pada command window di aplikasi MATLAB untuk mencari nilai eigen matriks Leslie. Dimulai dengan membuat matriks Leslie pada Microsoft Excel seperti
Kemudian data matriks Leslie diatas disimpan dalam file csv program Microsoft Excel. Misal data disimpan dengan nama file Leslie. Perintah yang diketik pada aplikasi MATLAB adalah
>> A=xlsread('Leslie.csv');
format long e
>> eigenA=eig(A) eigenA =
1.180027596483179e+000
5.628234231383071e-001 +5.514423691506808e-001i 5.628234231383071e-001 -5.514423691506808e-001i 2.453901731077905e-001 +7.031572841003201e-001i 2.453901731077905e-001 -7.031572841003201e-001i -1.331128808544938e-001 +7.259427053077278e-001i -1.331128808544938e-001 -7.259427053077278e-001i -3.737767187662345e-001 +5.605423506131189e-001i -3.737767187662345e-001 -5.605423506131189e-001i -6.631651748299201e-001
-5.597552074519956e-001 +3.044629819665216e-001i -5.597552074519956e-001 -3.044629819665216e-001i