PSALM: Program Simulasi untuk Sistem Linier
Hany FerdinandoJurusan Teknik Elektro, Fakultas Teknologi Industri, Universitas Kristen Petra [email protected]
Abstrak
Dalam mempelajari Sistem Linier, mahasiswa banyak menemui kesulitan untuk membayangkan beberapa konsep, seperti manipulasi sinyal, konvolusi, deret Fourier, dll. John Hopkin University (JHU) telah menyediakan sebuah web yang dapat dipakai untuk mempelajari hal-hal tersebut. Solusi ini mensyaratkan penggunaan internet karena semuanya berbasis web dan menggunakan java script. Solusi web JHU ini menginspirasi lahirnya PSALM (Petra Software for Linear System). PSALM memuat beberapa modul seperti manipulasi sinyal, demo konvolusi diskrit dan kontinyu, dekomposisi sinyal untuk deret Fourier, konsep phasor, kestabilan pada bidang Z dan kestabilan pada bidang s. PSALM terbukti telah membantu mahasiswa untuk mempelajari sistem linier dengan baik.
Kata kunci : PSALM, sistem linier, simulasi
1. Pendahuluan [Times New Roman 10, bold] Dalam kuliah Sistem Linier, ada banyak kesalahan umum yang dilakukan mahasiswa karena tidak mengetahui konsep dengan benar. Beberapa mahasiswa mengatakan bahwa kuliah ini sulit dibayangkan. Beberapa yang lain mengatakan bahwa mereka memerlukan bimbingan yang intensif sedangkan sebagian besar memilih belajar malam hari.
PSALM didanai oleh Program Hibah Kompetisi A2 Jurusan Teknik Elektro Universitas Kristen Petra. Tujuan utama pembuatan PSALM adalah memfasilitasi mahasiswa untuk belajar sistem linier secara mandiri. Tidak semua hal mampu diakomodasi oleh PSALM, sehingga untuk mempelajari Sistem Linier dengan baik masih memerlukan dukungan program lain seperti MATLAB atau Maple.
Secara umum Sistem Linier terdiri dari 4 bagian besar, yaitu dasar sinyal dan sistem, analisis Fourier, transformasi Z dan transformasi Laplace. Oleh karena dasar sinyal dan sistem harus dipahami dengan baik, maka PSALM terfokus pada bagian ini. 2. Pengenalan PSALM
PSALM singkatan dari Petra Software for Linear System, yang terdiri dari 7 modul: manipulasi sinyal, dekomposisi sinyal, konvolusi diskrit dan kontinyu, phasor, kestabilan pada bidang Z dan s.
PSALM dirancang untuk dipergunakan tanpa instalasi dan dibagikan secara bebas kepada siapa pun. Dengan demikian, PSALM ini dapat dikembangkan untuk dijadikan modul praktikum kuliah Sistem Linier.
Bagian berikut akan menjelaskan modul-modul yang terdapat dalam PSALM. Setiap bagian akan dilengkapi dengan contoh penggunaan. Gambar 1 menunjukkan layar pembukaan PSALM dengan
default bahasa Indonesia. Pengguna bisa menggantinya menjadi bahasa Inggris.
Gambar 1. Tampilan awal PSALM 3. Manipulasi Sinyal
Modul ini membantu mahasiswa untuk mempelajari prinsip dasar manipulasi sinyal seperti pencerminan, pergeseran, penguatan dan pelemahan. Selain itu, pengguna juga bisa menggabungkan semuanya itu dalam satu persoalan untuk ditemukan hasil manipulasinya.
Manipulasi sinyal yang dilakukan dalam Matlab mengharuskan pengguna menuliskan fungsi matematika dari sinyal yang akan dimanipulasi, Karmen, et a;l (2007). Hal yang sama juga dilakukan untuk Maple. Bagi pengguna yang mengalami kesulitan dalam menemukan sinyal, hal ini tentu saja
merepotkan. Hal ini diatasi dalam PSALM dengan menggambar sinyal tersebut pada bidang yang tersedia.
Apabila sinyal telah digambar, maka klik pada “process” akan membuat PSALM menampilkan hasil manipulasinya. Hasil ini sesuai dengan isi parameter A, a, b dan c yang dimasukkan pengguna.
Parameter A dan c dipergunakan untuk manipulasi amplitudo dan offset pada sinyal. Parameter b dan c dipergunakan untuk manipulasi pada sumbu waktu, misalnya pergeseran.
Sebagai contoh dipergunakan sinyal pada gambar 2. Dengan manipulasi x(-t+3). Dalam hal ini, A=1, a=-1, b=3 dan c=0. Hasil manipulasi ini ditunjukkan pada gambar 3a.
Gambar 2. Contoh sinyal yang dimanipulasi
Gambar 3a. PSALM untuk manipulasi x(-t+3)
Gambar 3b. PSALM untuk manipulasi -3x(2t-5)+1
Gabungan antara manipulasi amplitude dan sumbu waktu juga dapat dilakukan dalam modul ini . Misalnya, manipulasi -3x(2t-5)+1, maka parameter yang dimasukkan adalah A=-3, a=2, b=-5 dan c=1. Hasil manipulasi ditampilkan pada gambar 3b.
Modul ini dilengkapi dengan “clear all” dan “clear result”. Tombol pertama membersihkan layar untuk bentuk sinyal yang baru sedangkan tombol kedua dipergunakan untuk membersihkan hasilnya saja dengan tetap mempertahankan sinyal yang dimanipulasi.
4. Konvolusi Diskrit dan Kontinyu
Permasalahan yang timbul dalam konvolusi adalah kesulitan untuk membayangkan proses yang terjadi. Dalam konvolusi, salah satu sinyal harus dimanipulasi terlebih dahulu, Ferdinando (2010) Modul ini memberikan visualisasi proses tersebut untuk pasangan sinyal yang dapat dipilih.
Mula-mula pengguna diminta untuk memilih pasangan sinyal yang akan dipergunakan. Setelah dipilih, kedua sinyal siap divisualisasikan dengan cara menggerakkan mouse ke kiri dan ke kanan. Lihat Gambar 4.
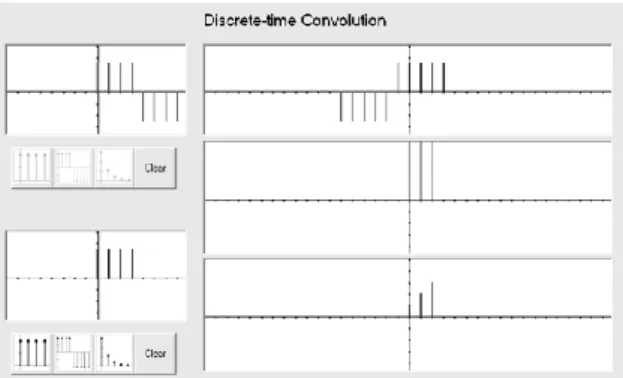
Gambar 4. Modul konvolusi diskrit dalam PSALM Bagian teratas menunjukkan bahwa ada sinyal yang tetap dan ada sinyal yang bergerak. Hal ini menegaskan kembali bahwa hanya satu sinyal yang dimanipulasi.
Bagian tengah menunjukkan perkalian antar komponen yang bersesuaian. Apabila semua hasil perkalian ini dijumlahkan, maka hasil tunggal akan diletakkan pada posisi waktu yang sesuai dengan posisi pointer mouse.
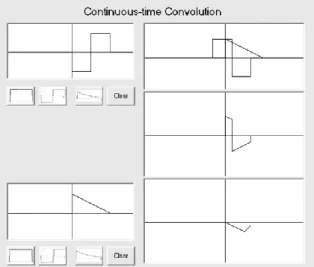
Hal yang sama juga berlaku pada konvolusi kontinyu sebagaimana ditampilkan pada gambar 5.
Bagian tengah menunjukkan hasil perkalian antara kedua sinyal setelah salah satu mengalami pergeseran. Jika luasan daerah tersebut dihitung, maka akan diperoleh nilai tunggal yang diletakkan pada posisi waktu yang sama dengan posisi pointer mouse (seperti konvolusi diskrit).
-1 1
Gambar 5. Modul konvolusi kontinyu dalam PSALM
5. Dekomposisi Sinyal
Dalam analisis Fourier, konsep utama yang diberikan adalah melakukan dekomposisi sinyal. Sinyal yang ada dipecah-pecah menjadi sinyal sinusoidal yang apabila dijumlahkan akan menghasilkan sinyal yang semula, Ferdinando (2010). Dengan kata lain, seseorang bisa membuat sebuah sinyal dengan menjumlahkan sinyal pembentuknya.
Gambar 6a. Penjumlah 3 sinyal sinusoidal untuk menghasilkan sinyal gigi gergaji.
Gambar 6b. Penjumlah 10 sinyal sinusoidal untuk menghasilkan sinyal gigi gergaji.
Melalui modul ini, mahasiswa belajar bahwa jumlah sinyal yang digabungkan menentukan kualitas sinyal yang dihasilkan. Semakin banyak sinyal yang dijumlahkan, maka semakin mendekati sinyal yang diinginkan. Hal ini ditunjukkan oleh gambar 6a dan 6b.
Pengguna dapat mengubah jumlah sinyal yang digunakan untuk melihat pengaruhnya terhadap kualitas sinyal yang dihasilkan. Selain itu, pengguna dapat memilih dua jenis sinyal yang lain, yaitu sinyal kotak dan segitiga.
Melalui modul ini, pengguna juga dapat mengamati bahwa dalam beberapa kasus, penjumlahkan ini hanya menggunakan sinyal dengan bilangan harmonic ganjil atau genap. Hal ini dapat diperlihatkan pada saat menambah satu sinyal yang dipergunakan tetapi tidak terjadi perubahan bentuk sinyal penjumlahannya.
6. Phasor
Aplikasi analisis Fourier pada rangkaian menggunakan bantuan phasor dalam perhitungan. Permasalahannya adalah mahasiswa belum dapat membayangkan seperti apa phasor itu, terutama bagi mereka yang baru pertama kali belajar tentang sinyal dalam domain frekuensi.
Phasor dinyatakan dalam bentuk magnitude dan sudut fasa. Oleh karena itu, sebuah phasor hanya mewakili sinyal sinusoidal dengan satu frekuensi.
Gambar 7a. Visualisasi Phasor dengan fasa positif Magnitude phasor dalam gambar 7 adalah jari-jari lingkaran bagian sebelah kiri. Jari-jari-jari ini menentukan besarnya amplitude sinyal sinusoidal yang dihasilkan pada bagian sebelah kanan. Perhatikan gambar 7b.
Gambar 7b. Visualisasi Phasor dengan fasa positif dan magnitude yang lebih kecil.
Sudut fasa adalah sudut yang terbentuk antara jari-jari dengan sumbu x positif. Bagian ini merupakan penunjuk dimulainya sinyal sinusoidal tersebut.
Tombol „+‟ dan „-„ memberi kesempatan pengguna untuk belajar bahwa ada relasi antara putaran phasor dengan frekuensi sinyal yang diwakilinya. Semakin tinggi frekuensi sinyalnya, semakin cepat putaran phasor tersebut. Gambar 7c menunjukkan perubahan frekuensi yang terjadi saat tombol tersebut ditekan.
Gambar 7c. Visualisasi Phasor dengan fasa positif dan frekuensi yang lebih besr.
7. Eksplorasi Bidang Z
Bidang Z memiliki cirri khas pada unit circle atau sebuah lingkaran berpusat di titik asal dengan jari-jari satu satuan. Analisis kestabilan pada bidang Z sangat dipengaruhi oleh unit circle dan daerah konvergensi atau RoC (Region of Convergence), Gabel (1987).
Melalui modul ini, pengguna bisa melihat hubungan antara unit circle dengan RoC. Oleh karena RoC dipengaruhi oleh posisi pole, maka dalam modul ini pengguna dapat menggeser posisi pole untuk melihat kestabilan pada bidang Z.
Gambar 8a menunjukkan sistem kausal dengan n>=0. Bagian sebelah kiri terlihat bahwa RoC ini memuat unit circle sehingga sinyal di sebelah kanan menjadi semakin kecil saat waktu bertambah besar.
Gambar 8a. Posisi pole dan RoC yang membuat sistem menjadi stabil untuk n>=0
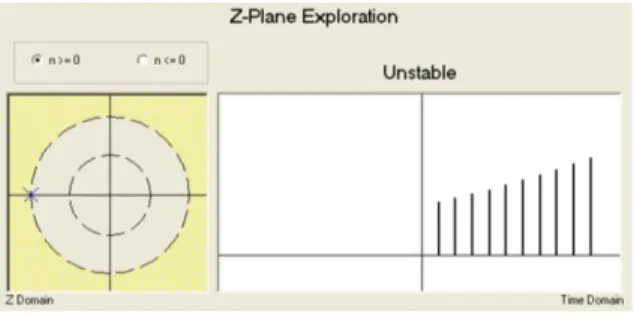
Kondisi yang tidak stabil ditunjukkan pada gambar 8b. Saat RoC tidak lagi memuat unit circle, maka amplitudo sinyal menjadi semakin besar saat waktu bertambah besar juga.
Gambar 8b. Posisi pole dan RoC yang membuat sistem menjadi tidak stabil untuk n>=0 Modul ini juga menyediakan eksplorasi bidang Z untuk n<0. Pengguna bisa melihat hubungan antara RoC dan unit circle pada kondisi ini, lihat gambar 8c dan 8d.
Gambar 8c. Posisi pole dan RoC yang membuat sistem menjadi stabil untuk n<0
Gambar 8d. Posisi pole dan RoC yang membuat sistem menjadi tidak stabil untuk n<0 Gambar 8c memperlihatkan situasi untuk sistem yang stabil karena RoC memuat unit circle. Hal ini konsisten dengan untuk n>=0. Kondisi RoC yang tidak memuat unit circle pada n<0 juga menunjukkan gejala yang sama dengan kondisi n>=0.
8. Eksplorasi Bidang s
Bidang s dipergunakan dalam transformasi Laplace. Modul ini dibuat dengan tujuan agar pengguna bisa melihat pengaruh posisi pole terhadap kestabilan sistem. Aturan umum menyatakan bahwa sistem dikatakan stabil apabila pole terletak di sebelah kiri bidang s, Gabel (1987).
PSALM menggunakan sistem orde 2 untuk menjelaskan hal ini. Kedua pole yang saling
conjugate diletakkan pada bidang s. Posisi pole pasti
simetris terhadap sumbu horizontal.
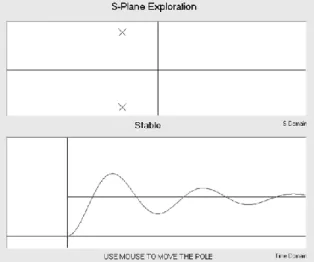
Pengguna dapat menggeser posisi salah satu pole (karena pole yang lain akan mengikuti) untuk melihat pengaruhnya terhadap kestabilan sistem. Kestabilan sistem ditunjukkan pada bagian bawah modul ini. Gambar 9a menunjukkan posisi pole yang membuat sistem menjadi stabil. Gambar 9b menunjukkan posisi pole yang lain, tetapi tetap membuat sistem menjadi stabil. Pengguna bisa memperhatikan bahwa posisi pole sangat berpengaruh terhadap kestabilan sistem.
Gambar 9a. Posisi pole yang membuat sistem menjadi stabil
Gambar 9b. Posisi pole yang membuat sistem menjadi stabil
Apabila diperhatikan lebih seksama, walaupun kedua sistem pada gambar 9a dan 9b stabil, terlihat bahwa keduanya tetap berbeda. Salah satu yang dapat diamati adalah perbedaan rise time dan
maximum overshoot pada kedua gambar tersebut.
Jadi, modul ini juga dapat membantu pengajaran
pada sistem pengendalian yang juga memerlukan analisa kestabilan.
9. Diskusi
PSALM dirancang sebagai bentuk visualisasi pembelajaran Sistem Linier. Hal ini perlu dilakukan karena banyak konsep dasar Sistem Linier sulit dibayangkan.
Semua modul dalam PSALM dirancang agar dapat memberikan penjelasan secara interaktif. Dengan demikian, pengguna dapat belajar secara mandiri konsep dasar dalam Sistem Linier.
Oleh karena itu, keberadaan PSALM tidak bisa berdiri sendiri. Instruktur harus menyediakan semacam penuntun seperti buku praktikum yang dapat dibuat sendiri. Hal ini diketahui pada awal implementasi penggunaan PSALM dalam pengajaran.
Proses belajar konsep dasar dalam Sistem Linier akan lebih cepat pada saat handout tersebut disediakan. Perbedaan antara implementasi tanpa dan dengan handout telah dilakukan selama 4 semester. Berdasarkan pengamatan itu, handout yang dibuat terbukti membantu proses pembelajaran. Pada modul manipulasi sinyal, pengguna bisa menggunakannya untuk belajar secara mandiri. Soal dapat dirancang sendiri, lalu dikerjakan. Hasilnya dicocokkan dengan perhitungan PSALM.
Salah satu kelemahan modul ini terletak pada gaya belajar pengguna. Seharusnya, pengguna mencoba terlebih dahulu dengan menghitung sendiri, baru melihat hasilk perhitungan PSALM. Gaya belajar yang biasanya dilakukan adalah langsung melihat hasil perhitungan PSALM tanpa melakukan perhitungan secara mandiri.
Modul konvolusi baik kontinyu maupun diskrit masih harus dikembangkan lagi. Implementasi yang sudah dilakukan masih sebatas memberikan informasi prinsip dan cara konvolusi. Pengguna masih belum dapat menggunakan sinyal yang dirancang sendiri.
Secara umum, respon mahasiswa yang pernah menggunakan PSALM sangat positif. Oleh karena itu, PSALM dibagikan secara gratis untuk dapat lebih banyak membantu proses pembelajaran Sistem Linier.
10. Kesimpulan
PSALM adalah sebuah program visualisasi yang terinspirasi web-based simulation yang dibuat oleh John Hopkins University. Program yang
portable ini sangat mudah digunakan dan tidak
memerlukan sambungan internet.
Instruktur yang menggunakan PSALM perlu melengkapinya dengan sebuah handout yang dirancang sesuai dengan kebutuhan penggunanya. Keberadaan handout ini sangat membantu, bahkan dapat mempercepat proses belajar.
Modul manipulasi sinyal merupakan salah satu modul yang menarik karena pengguna bisa melakukan berbagai macam percobaan dengan sinyal yang digambar sendiri. Hal ini membuka peluang bagi pengguna untuk belajar secara mandiri. Satu hal yang perlu diwaspadai dalam hal ini adalah gaya belajar yang salah. Pengguna harus melakukan perhitungan secara mandiri baru melihat hasil perhitungan PSALM secara visual. Apabila hal ini tidak dilakukan, maka PSALM menjadi tidak bermanfaat.
Modul konvolusi memerlukan pengembangan lebih lanjut sehingga pengguna bisa melakukan percobaan seperti halnya pada modul manipulasi sinyal.
Dalam implementasi di kelas, PSALM telah mendapat respon yang positif. Hal ini membuka peluang yang lebih besar untuk mengembangkan
PSALM menjadi salah satu alat bantu belajar untuk Sistem Linier.
Daftar Pustaka:
Ferdinando, Hany. (2010): Dasar-dasar Sinyal dan
Sistem. Penerbit Andi, Jogjakarta.
Gabel, Robert A., Richard A Roberts. (1987):
Signals and Linear Systems, 3rd ed. New York.
Karmen, Edward R., Bonnie S. Heck. (2007):
Fundamental of Signals and Systems Using the Web and MATLAB, 3rd ed. Upper Saddle River,
NJ.
Ucapan Terima kasih
Proyek PSALM didanai oleh Program Hibah Kompetisi A2 Jurusan Teknik Elektro, Universitas Kristen Petra melalui skema Hibah Pengajaran.