BAB 3 ENTROPI DARI BEBERAPA DISTRIBUSI

(1)

ENTROPI DARI BEBERAPA DISTRIBUSI

Untuk lebih memahami mengenai entropi, pada bab ini akan diberikan perhitungan entropi untuk beberapa distribusi diskrit dan kontinu.

3.1 Distribusi Diskrit

Pada sub bab ini dibahas rataan, variansi dan entropi dari beberapa distribusi baik diskrit maupun kontinu.

a. Geometri (p)

Misalkan X menyatakan peubah acak yang berdistribusi Geometri dengan parameter (p) dan fungsi densitas peluang

( ) (

¹

)

¹^, ^{1, 2,...}

0 , lainnya

p p k k

P X k

k

⎧ − − =

= = ⎨⎪

⎪⎩

Rataan : µ =

( )

¹

0

1 ^k

k

kp p

∞ −

=

∑

− ⁼¹_p

Variansi : σ² = ²

( )

¹

0

1 1 ^k

k

k p p

p

∞ −

=

⎛ − ⎞ −

⎜ ⎟

⎝ ⎠

∑

⁼

⁽

^{1- p}_p²

⁾

Entropi: H(X=x)

( ( )

¹

) ⁽ ⁾

¹

0

log 1 1

n k k

k

p p ⁻ p p ⁻

=

∑

− − ⁼⁻^log^p⁻¹⁻_p^p^{log 1}

⁽

⁻^p

⁾

23

(2)

BAB III ENTROPI DARI BEBERAPA DISTRIBUSI DAN HASIL SIMULASI 24

Pada distribusi geometri ini, entropi dapat mudah dihitung seperti halnya menghitung rataan dan variansinya dengan entropi ini berlaku untuk p∈ (0,1).

Tabel perhitungan entropi untuk distribusi geometri dengan beberapa nilai p, (dengan basis dua) ditampilkan di bawah ini.

p H

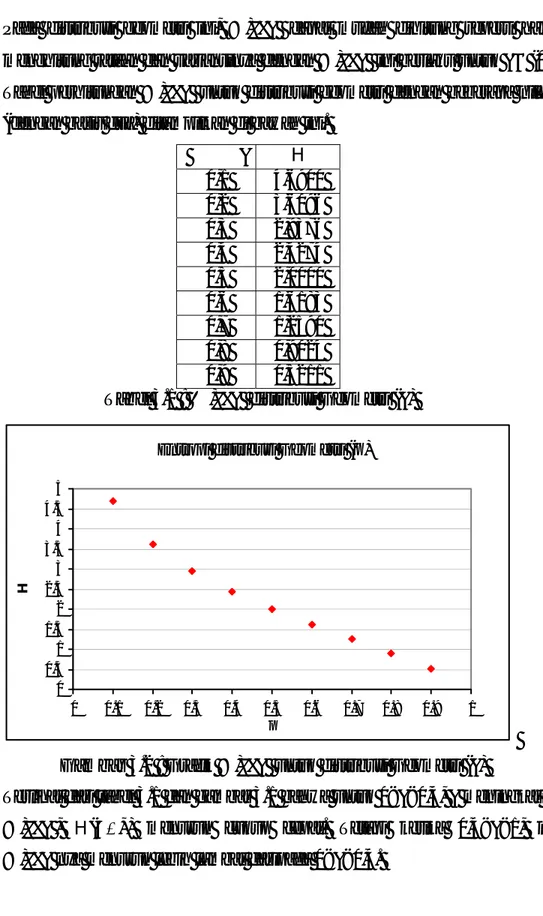
0,1 4,6900 0,2 3,6096 0,3 2,9376 0,4 2,4274 0,5 2,0000 0,6 1,6183 0,7 1,2590 0,8 0,9024 0,9 0,5211 Tabel 3.1 : Entropi distribusi Geometri (p)

Entropi distribusi Geometri (p )

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

p

H

Gambar 3.2 : Grafik entropi untuk distribusi Geometri (p)

Terlihat dari tabel 3.1 dan gambar 3.1 bahwa untuk 0<p<0,4, p meningkat dan entropi, H(X=x) menurun cukup cepat. Tetapi ketika 0,4<p<1, nilai entropinya menurun lebih lambat daripada 0<p<0,4.

(3)

a. Binomial (n, p)

Misalkan X menyatakan peubah acak yang berdistribusi Binomial dengan parameter (n,p) dan fungsi padat peluang

( ) (

¹

)

, 0,1, 2,...,

0 , lainnya

k n k

n p p k

P X k k

k

⎧⎛ ⎞ − − =

= = ⎨⎝ ⎠⎪⎜ ⎟

⎪⎩

n

Rataan :

( ) ( )

( )

( ) ( ) ( )

0

1

! 1

! !

1 ! 1

1 ! !

n k n k

k

n k n k

k

k n p p

k n k

np n p p np

k n k

µ ⁻

=

− −

=

= −

−

= − −

− −

∑

⁼

Variansi : ²

( ) ( ) ( )

²

(

0

! 1 1

! !

n k n k

k

k np n p p np p

k n k

σ ⁻

=

= − − = −

∑

−

⁾

Entropi: H(X=x) n k 0

log (1 ) (1 )

n k n k k

k

n n

p p p p

k k

− −

=

⎛⎛ ⎞ ⎞⎛ ⎞

= ⎜⎜ ⎟ − ⎟⎜ ⎟

⎝ ⎠ ⎝ ⎠

⎝ ⎠

∑

⁻

0

(1 ) log log( ) (1 ) log(1 )

n k n k

k

n n

p p np p n p

k k

−

=

⎛ ⎞ ⎛ ⎞

= ⎜ ⎟ − ⎜ ⎟− − −

⎝ ⎠ ⎝ ⎠

∑

⁻^p

Entropi dari distribusi binomial ini mempunyai bentuk yang cukup rumit karena dibutuhkan perhitungan logaritma dari kombinasi (n,k) berbeda dengan mean dan variansinya. Oleh karena itu, penggunaan software seperti Maple akan lebih memudahkan mencari entropinya. Di gambar berikut ditampilkan

entropi untuk beberapa p dengan n sebesar 50 kali.

(4)

Entropi Distribusi Binomial (n,p )

0 20 40 60 80 100 120

0 10 20 30 40 50 60

n

H

p=0,03 p=0,25 p=0,5 p=0,6 p=0,99

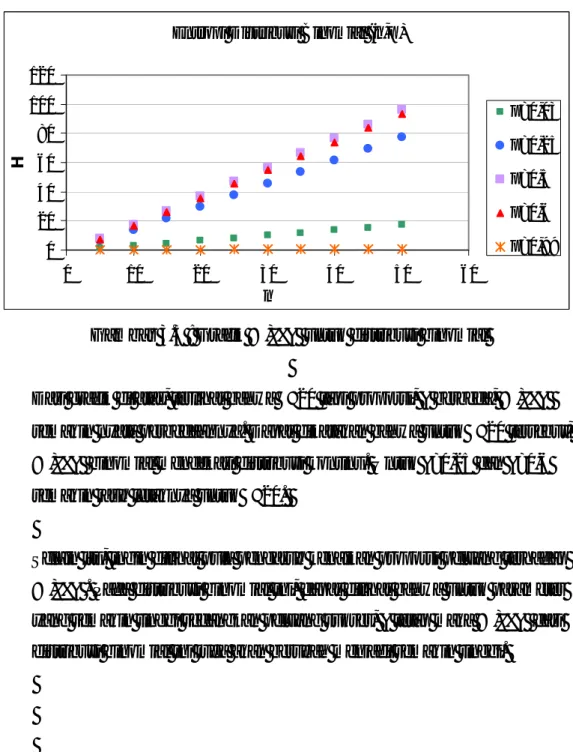
Gambar 3.3 : Grafik entropi untuk distribusi binomial

Dari grafik di atas, terlihat bahwa n≥20 tapi proporsi, p berbeda, entropi semakin nyata perbedaannya. Dapat dikatakan bahwa untuk n≥20 tersebut, entropi binomial mendekati distribusi kontinu. Untuk p=0,25 dan p=0,6 semakin jauh letaknya untuk n≥20.

Selain itu, ingin dilihat pula pengaruh kenaikan proporsi peluang terhadap entropi. Pada distribusi binomial ini, dapat dilihat bahwa untuk parameter n yang semakin tinggi sedangkan peluang sukses, p tetap maka entropi dari distribusi binomial ini juga akan berubah menjadi semakin tinggi.

(5)

Sebagai perbandingan, parameter n ditetapkan sebesar 20 sedangkan proporsi peluangnya meningkat maka hasil perhitungan dapat dilihat pada tabel di

bawah ini.

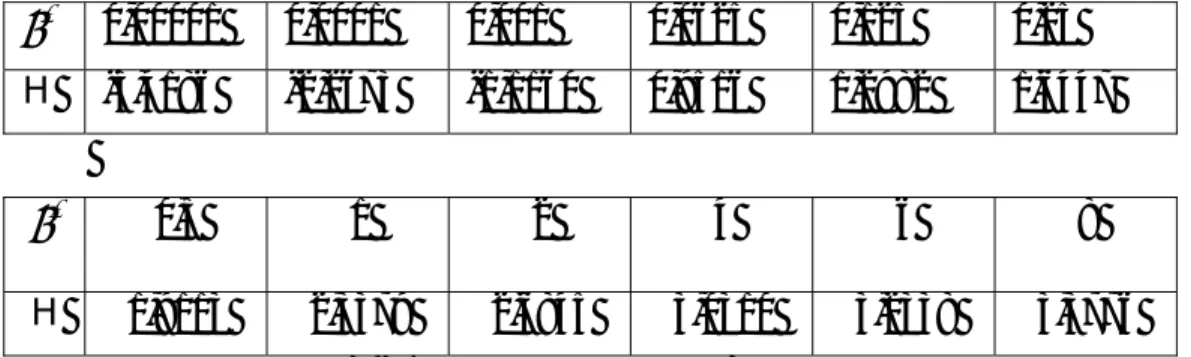
p 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5

H 16,3547 21,7038 26,0086 29,4606 32,1750 34,2258 35,6608 36,5108 36,7923

p 0,55 0,6 0,65 0,7 0,75 0,8 0,85 0,9

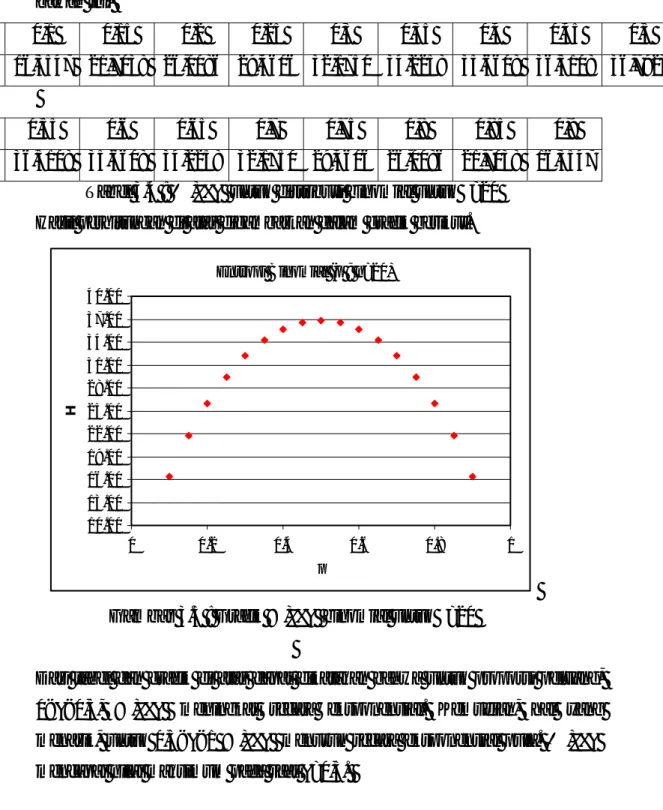
H 36,5108 35,6608 34,2258 32,1750 29,4606 26,0086 21,7038 16,3547 Tabel 3.4 : Entropi untuk distribusi binomial untuk n=20

Hasil perhitungan di atas digambarkan dalam grafik berikut.

Entropi Binomial (p ; n=20)

10.00 13.00 16.00 19.00 22.00 25.00 28.00 31.00 34.00 37.00 40.00

0 0.2 0.4 0.6 0.8 1

p

H

Gambar 3.5 : Grafik entropi binomial untuk n=20

Dari tabel dan grafik di atas dapat dikatakan bahwa untuk proporsi peluang, 0<p<0,5, entropi meningkat secara eksponensial. Kemudian, hal yang

menarik, untuk 0,5<p<1 entropi menurun secara eksponensial pula. Entropi mencapai nilai maksimum pada saat p=0,5.

(6)

BAB 3 ENTROPI DARI BEBERAPA DISTRIBUSI 27

n

1 2 3 4 5 6 7 8 9 10

0,1 0,4689 1,1179 1,8349 2,592 3,3768 4,1822 5,0036 5,8379 6,6827 7,5363 0,2 0,7219 1,7639 2,9266 4,1552 5,4259 6,7262 8,048 9,3863 10,7373 12,0986 0,3 0,8813 2,1826 3,6424 5,1835 6,7735 8,3956 10,0403 11,7016 13,3754 15,0592 0,4 0,9709 2,4219 4,0542 5,7756 7,5484 9,3536 11,1811 13,0245 14,88 16,7449 p

0,5 1 2,5 4,1887 5,9694 7,8018 9,6666 11,5534 13,4558 15,3701 17,2936

n

11 12 13 14 15 16 17 18 19 20

0,1 8,3973 9,2647 10,1376 11,0152 11,8971 12,7827 13,6716 14,5634 15,4578 16,3547 0,2 13,4683 14,8448 16,2271 17,6143 19,0056 20,4006 21,7987 23,1997 24,603 26,0086 0,3 16,7508 18,4489 20,1524 21,8604 23,5724 25,2877 27,0059 28,7267 30,4498 32,175 0,4 18,6173 20,4959 22,3797 24,2678 26,1597 28,0548 29,9528 31,8533 33,7561 35,6609 p

0,5 19,2245 21,1615 23,1036 25,0499 27,0001 28,9535 30,9096 32,8684 34,8293 36,7923 Tabel 3.6 : Entropi untuk distribusi Binomial (n,p) dengan 2 sebagai basis logaritma

(7)

b. Poisson (λ)

Misalkan X menyatakan peubah acak yang berdistribusi Poisson dengan parameter (λ) dan fungsi padat peluang,

( )

, 0,1, 2,...

!

0 , lainnya e k

P X k k k

k

λλ

⎧ −

⎪ =

= = ⎨

⎪⎩

Rataan : µ =

( )

1

0 ! 1 1

k k

ke e

k k

λλ λλ λ

− −

∞ ∞

−

= =

= − !

∑ ∑

⁼^λ

Variansi : σ²=

( )

²

0 !

k

k e

k

λλ λ ⁻

∞

=

∑

− ⁼^λ

Entropi : H(X=x) =

0

log ! !

k k

k

e e

k k

λλ λλ

− −

∞

=

⎛ ⎞

⎜ ⎟

⎝ ⎠

∑

⁼

⁽ ⁾ ^{( )}

0

log ! 1 log

!

k

e k

k

λ λ

λ λ ⁻ ^∞

=

− +

∑

Entropi untuk distribusi Poisson mempusnyai kerumitan dalam perhitungan yang tidak sederhana dan memerlukan analisis yang lebih kuat.

3.1 Distribusi Kontinu a. Uniform (a,b)

Misalkan X menyatakan peubah acak yang berdistribusi uniform dengan fungsi distribusi,

1 , ( )

0, lainnya a x b

f x b a

x

⎧ < <

=⎪⎨ −

⎪⎩

Rataan : µ = 1

2

b

a

x dx a b b a

= +

∫

−

Variansi : σ²= ² ¹ ² ¹

( )

²

2 12

b

a

x dx a b b a

b a

⎛ ⎞−⎛ + ⎞ = −

⎜ − ⎟ ⎜⎝ ⎟⎠

⎝

∫

⎠

(8)

Entropi: H(X=x) 1 1 ln

b

a

b a b a dx

⎛ ⎞

= −

∫

− ⎜⎝ − ⎟⎠

^ln ¹ ^{ln b a}

( )

b a

⎛ ⎞

= − ⎜⎝ − ⎟⎠= −

Dari perhitungan tersebut, entropi untuk distribusi uniform hanya ditentukan oleh lebar intervalnya.

b. Normal N(α,β²)

Misalkan X menyatakan peubah acak yang berdistribusi normal dengan parameter (α,β²) dan fungsi padat peluang,

( ) ( )

²

2

1 exp 2 2

f x x α

β π β

⎛ − ⎞

= ⎜−

⎜ ⎟

⎝ ⎠

⎟ , -∞ < x < ∞

Rataan : µ =

( )

²

2

1 exp 2 2

x x α dx

β π β

∞

−∞

⎛ − ⎞

⎜− ⎟

⎜ ⎟

⎝ ⎠

∫

^{= α}

Variansi : σ²=

( )

²

( )

²

2

1 exp 2 2

x x α dx

α β π β

∞

−∞

⎛ − ⎞

⎜ ⎟

− ⎜− ⎟

⎝ ⎠

∫

⁼^β²

Untuk menghitung entropi dari distribusi-distribusi kontinu, digunakan basis logaritmanya adalah e sehingga

Entropi : H(X=x)

2 2

1 1

2 2

1 1

2 log 2

x x

e e

α α

β β

β π β π

⎛ − ⎞ ⎛ − ⎞

∞ − ⎜ ⎟ − ⎜ ⎟

⎝ ⎠ ⎝ ⎠

−∞

⎛ ⎞

⎜ ⎟

= − ⎜ ⎟

⎝ ⎠

∫

^dx

( )

(

²

) ⁽ ⁾

1 1

1 ln 2 ln 2

2 πβ 2 π

= + = + β

Entropi dari distribusi normal tidak bergantung pada nilai mean melainkan pada standar deviasi. Apabila digambarkan dalam kurva maka entropi untuk distribusi normal meningkat untuk standar deviasi yang meningkat, dengan mean yang sama.

(9)

Gambar 3.7 : Grafik entropi distribusi Normal

Untuk lebih memperjelas, diambil contoh kasus distribusi Normal dengan mean tetap yaitu 7, tetapi variansi meningkat. Hasilnya ditabelkan seperti di bawah ini.

β² 0,00001 0,0001 0,001 0,0625 0,125 0,25 H -3,4186 -2,2673 -1,1160 0,9516 1,2982 1,6447

β² 0,5 1 2 4 6 8

H 1,9113 2,3379 2,6845 3,0310 3,2338 3,3776

Tabel 3.8 : Hasil perhitungan entropi distribusi normal

Dari tabel di atas dapat dilihat bahwa untuk variansi yang meningkat maka nilai entropi juga meningkat. Entropi distribusi normal akan bernilai negatif untuk variansi yang cukup kecil. Grafik yang didapat juga tampak seperti pada Gambar 3.5.

(10)

c. Gamma (θ,α)

Fungsi padat peluang dari distribusi Gamma adalah

( ) ( )

1

, 0 0 , lainnya

x

x e x

f x

x

θ α

θ αθ

− −

⎧⎪⎪ >

= ⎨Γ⎪

⎪⎩

(3.1)

Rataan :

( ) ( ) ( )

( )

1

1 1

1

x x

x x e dx xx e dx

θ α

θ θ

µ α θ θα

θ α θ α θ

∞ − − ∞ − −

−∞ −∞

Γ +

= = =

Γ Γ Γ

∫ ∫

⁼ ^(3.2)

Variansi : ²

( ) ( )

² ¹

x

x x e d

θ α

θ

x 2

σ αθ θα

θ α

∞ − −

−∞

= − =

∫

Γ (3.3)

Entropi : H(X=x)

( ) ( )

1 1

0

ln

x x

x e x e

dx

θ α θ α

θ θ

θ α θ α

− −

∞ ⎛ − ⎞ −

⎜ ⎟

= − ⎜⎜Γ ⎟⎟Γ

⎝ ⎠

∫

(3.4)

^{= +}^θ ^ln

(

^{α θ}^Γ

( ) )

^{+ −}

(

¹ ^{θ ψ θ}

) ( )

(3.5) dengan ^ψ

( )

^k adalah fungsi digamma,

( ) ( )

( )

' θ

ψ θ θ

=Γ

Γ .

Pada distribusi Gamma, rataan dan variansi dapat dihitung dengan mudah, sedangkan pada entropinya muncul fungsi digamma. Hal ini menjadi lebih sulit karena diperlukan turunan dari fungsi gamma, terlebih untuk α bukan bilangan bulat.

Kasus khusus dari distribusi Gamma adalah distrbusi eksponensial. Untuk mendapatkan distribusi eksponensial, ditetapkan θ =1 pada persamaan (3.6),

sehingga fungsi padat peluangnya menjadi

( )

^, ⁰

0 , lainnya

x

e x

f x

x

α

⎧ −

⎪ >

= ⎨⎪

⎩

(11)

Rataan : µ =

x

xe ^αdx α

∞ −

−∞

∫

⁼_α¹ ^∞ ^{xe dx}⁻^α^x

−∞

∫

⁼^α

Variansi : σ²=

( )

²

x

x α e ^αdx α

∞ −

−∞

∫

− ⁼_α¹ ^∞

⁽

^x ^α

⁾

²^{e dx}⁻^α^x

−∞

∫

− ^{= α}²

Entropi : H(X=x)

0

ln

x x

e e

α α dx

α α

− −

∞ ⎛ ⎞

⎜ ⎟

= −

∫

⎜⎜⎝ ⎟⎟⎠

( )

0

1 ln ln

x x

e α eα α ⎞dx λ

∞ − ⎛ ⎛⎜ ⎜ − ⎞⎟− ⎟

⎝ ⎠

⎝ ⎠ ^{1 ln}

( )

= −

∫

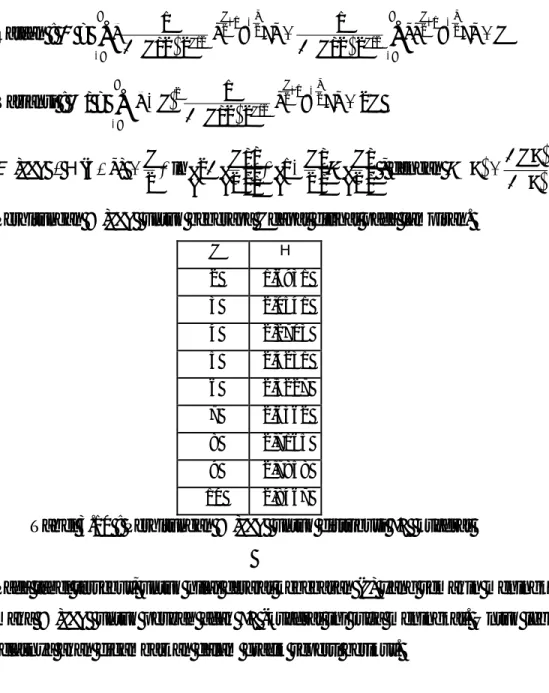
^{= +} ^α

Entropi untuk distribusi eksponensial ini akan menjadi negatif untuk α yang kecil, seperti dapat terlihat pada grafik.

Gambar 3.9 : Grafik entropi distribusi eksponensial

Kasus lain dari distribusi Gamma yaitu distribusi chi kuadrat yang diperoleh dengan

2

θ = r dan α= sehingga persamaan (3.6) menjadi 2

( ) ( )

2 1 2 / 2

1 , 0

/ 2 2

0 , lainnya

r x

r x e x

r f x

x

− −

⎧ < < ∞

= ⎨⎪Γ

⎪⎩

(12)

Rataan : µ =

( ) ( )

1 1

2 2 2 2

/ 2 / 2

1 1

/ 2 2 / 2 2

r x r x

r r

x x e dx xx e dx r

r r

∞ − − ∞ − −

−∞ −∞

= =

Γ Γ

∫ ∫

Variansi : σ ² = _−∞^∞

∫ (

^{x r}⁻

) ( )

² ^Γ ^r^{/ 2 2}¹ ^r^{/ 2} ^{x e d}²^r⁻¹ ⁻²^x ^x⁼²^r

Entropi : H(X=x) ln 2 1

2 2 2

r ^⎛ ^{⎛ ⎞}r ^⎞ ^⎛ r^{⎞ ⎛ ⎞}ψ

= + ⎜⎝ Γ⎜ ⎟⎝ ⎠⎟⎠+ −⎜⎝ ⎟ ⎜ ⎟⎠ ⎝ ⎠2

r , dengan

( ) ( ) ( )

a ' a ψ =^Γ a

Γ . Perhitungan entropi untuk beberapa r dapat dilihat pada lampiran.

r H

2 1,6931 3 2,0541 4 2,2703 5 2,4231 6 2,5227 7 2,6362 8 2,7165 9 2,7858 10 2,8467

Tabel 3.10 : Perhitungan entropi untuk distribusi chi kuadrat

Pada tabel tersebut, untuk nilai derajat kebebasan (r) yang semakin meningkat maka entropi untuk peubah acak chi-kuadrat ini juga meningkat. Untuk lebih

jelasnya akan digambarkan dalam grafik seperti berikut.

(13)

Entropi khi kuadrat

1.0 1.5 2.0 2.5 3.0

0 2 4 6 8 10 1

r

H

2

Gambar 3.11 : Grafik entropi untuk distribusi chi kuadrat (r)

Dari grafik, entropi pada distribusi chi kuadrat akan meningkat dengan derajat kebebasan yang meningkat pula. Hal ini dapat dilihat karena informasi yang terkandung juga semakin banyak.

c. Pareto (α,θ)

Distribusi Pareto sering digunakan untuk bidang-bidang yang berhubungan dengan sosial, asuransi, geofisika dan sains. Salah satu contohnya adalah frekuensi kata-kata untuk teks yang panjang, di mana kata-kata pendek sering digunakan dan kata yang panjang jarang digunakan. Fungsi padat peluang dari distribusi Pareto dituliskan

( ) ( )

¹^{, 0}

0 , lainnya f x x x

x

α α

αθ θ ⁺

⎧ >

=⎪⎨ +

⎪⎩ Rataan : µ =

( )

¹ ¹

x dx

x

α α

αθ θ

θ α

∞

+

−∞

= −

∫

+

(14)

Variansi : σ ² =

( )

2

1 1

x dx

x

α α

θ αθ

α θ

∞

+

−∞

⎛ − ⎞ =

⎜ − ⎟

⎝ ⎠ +

∫ ₍

_α ₋₁^{θ α}

_{) (}

²² _α ₋₂

₎

Entropi : H(X=x)

( )

¹

( )

¹

0

ln dx

x x

α α

αθ αθ

θ θ

∞

+ +

⎛ ⎞

⎜ ⎟

= −

∫

⎜⎝ + ⎟⎠ +

ln α ¹ 1

θ α

= ⎛ ⎞⎜ ⎟+

⎝ ⎠ +

Untuk distribusi Pareto, bentuk entropi lebih sederhana dan dapat dengan mudah dihitung seperti halnya mean dan variansi.

d. Lognormal (α,β )

Contoh penggunaan distribusi lognormal yaitu pada long-term return rate pada investasi barang. Fungsi padat peluang dari distribusi lognormal adalah

( ) ( )

²

2

ln( ) 1 exp

2 2 f x x

x

α β π β

⎛ − ⎞

⎜ ⎟

= ⎜− ⎟

⎝ ⎠

, −∞ < < ∞x

Rataan : µ =

( )

² ₂

2

ln( )

1 1

exp exp

2 2

2

x x dx

x

α α β

β π β

∞

−∞

⎛ − ⎞ ⎛ ⎞

⎜− ⎟ = ⎜ ⎟

⎜ ⎟ ⎝ ⎠

⎝ ⎠

∫

⁺

Variansi : 2 2 ²

( )

²

2

ln( )

1 1

exp exp

2 2 2

x x dx

x

σ α β α

β π β

∞

−∞

⎛ − ⎞

⎛ ⎛ ⎞⎞ ⎜ ⎟

=

∫

⎜⎝ − ⎜⎝ + ⎟⎠⎟⎠ ⎜⎝− ⎟⎠

⁼

(

^exp

( )

^β² ⁻^{1 exp 2}

) ⁽

^{α β}⁺ ²

⁾

Entropi :

H(X=x)=

( )

²

( )

²

2 2

0

ln( ) ln( )

1 1

ln exp exp

2 2

x x

x x dx

α α

β β

β π β π

∞ ⎛⎜ ⎛⎜ − ⎞⎟⎞⎟ ⎛⎜ − ⎞⎟

− − −

⎜ ⎟ ⎜ ⎟

⎜ ⎝ ⎠⎟ ⎝ ⎠

⎝ ⎠

∫

(

²

) (

²

)

1 1 1

ln 2 ln 2

2 2 πβ α 2 π βe

= + + = +α

Entropi untuk distribusi lognormal bergantung pada parameter α dan β.

(15)

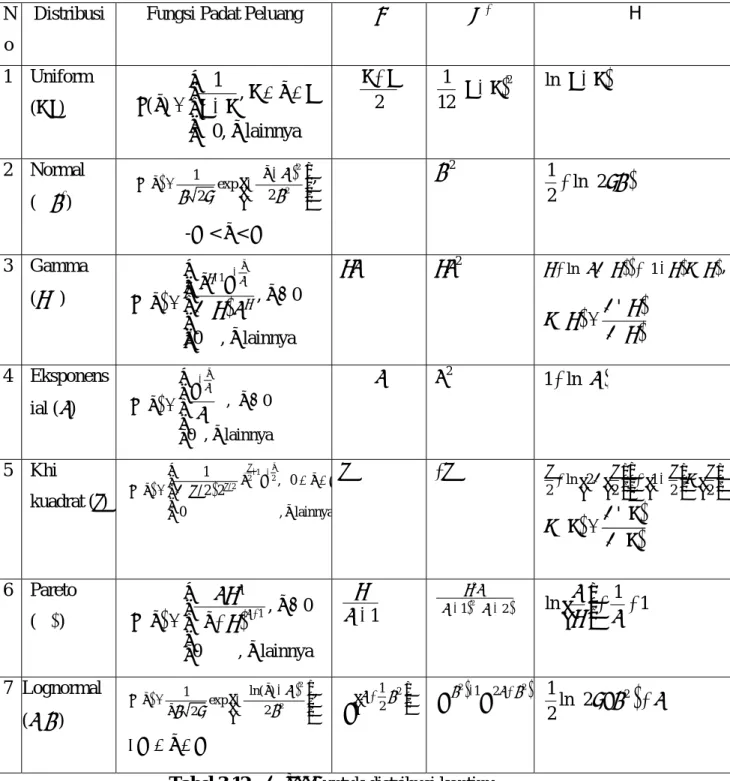
Entropi dari beberapa distribusi kontinu pada Bab 3 ditampilkan pada tabel berikut.

N o

Distribusi Fungsi Padat Peluang µ σ² ^H

1 Uniform (a,b)

1 , ( )

0, lainnya a x b

f x b a

x

⎧ < <

=⎪⎨ −

⎪⎩

2

a b+ ¹

( )

²

12 b a− ^{ln b a}

(

⁻

)

2 Normal (α,β²)

( ) ( )²

2

1 exp 2 2

f x x α

β π β

⎛ − ⎞

⎜ ⎟

= ⎜⎝− ⎟⎠

, -∞ < x < ∞

α β² ¹ ^{ln 2}

( )

2+ πβ

3 Gamma

(θ,α)

( ) ( )

1

, 0 0 , lainnya

x

x e x

f x

x

θ α

θ αθ

− −

⎧⎪⎪ >

= ⎨Γ⎪

⎪⎩

θα θα² ^θ⁺^ln

(

^{α θ}^Γ( )

)

^{+ −}(¹ ^{θ ψ θ}) ( )^,

( ) ( ) ( )

' θ

ψ θ θ

=Γ Γ 4 Eksponens

ial (α)

( )

^, ⁰

0 , lainnya

x

e x

f x

x

α

⎧ −

⎪ >

= ⎨⎪

⎩

α α² ^{1 ln}⁺

( )

^α

5 Khi

kuadrat (r) ^{( )} ⁽ ⁾

21 2 / 2

1 , 0

/ 2 2

0 , lainnya

r x

r x e x

r f x

x

− −

⎧ < < ∞

= ⎨⎪Γ

⎪⎩

r 2r _{ln 2} ₁

2 2 2

r r r

⎛ ⎛ ⎞⎞ ⎛ ⎞ ⎛ ⎞ψ + ⎜⎝ Γ⎜ ⎟⎝ ⎠⎟⎠+ −⎜⎝ ⎟ ⎜ ⎟⎠ ⎝ ⎠

( )

2 r

( ) ( )

a ' a ψ =^Γ a

Γ 6 Pareto

(α,θ)

( ) ( )

¹^{, 0}

0 , lainnya f x x x

x

α α

αθ θ ⁺

⎧ >

=⎪⎨ +

⎪⎩

1 θ

α − ⁽ ^{) (} ⁾

2

12 2

θ α

α− α− 1

ln α 1

θ α

⎛ ⎞ + +

⎜ ⎟⎝ ⎠

7 Lognormal (α,β )

( ) ( )²

2

ln( ) 1 exp

2 2 f x x

x

α β π β

⎛ − ⎞

⎜ ⎟

= ⎜⎝− ⎟⎠

,

−∞ < < ∞ x

1 2

e

^α 2^β

⎛ + ⎞

⎜ ⎟

⎝ ⎠ _e

( ) (

^β² ⁻¹_e²^{α β}⁺ ²

)

¹^{ln 2}

(

²

)

2 π βe +α

Tabel 3.12 : Entropi untuk distribusi kontinu

(16)

3.2 Entropi dari Bivariat normal

Untuk kasus bivariat, diambil contoh distribusi bivariat normal dengan fungsi padat peluang untuk mean, µX dan µY serta variansi σX dan σY dituliskan

( )

2 2

1 1

, exp 2

2 1 2 1

y y

x x

x x y y

x y

y y

x x

f x y µ ρ µ µ µ

σ σ σ σ

πσ σ ρ ρ

⎛ − ⎡⎛ − ⎞ ⎛ − ⎞⎛ − ⎞ ⎛ − ⎞ ⎤⎞

⎜ ⎢ ⎥⎟

= ⎜ ⎜ ⎟ − ⎜ ⎟⎜⎜ ⎟ ⎜⎟ ⎜+ ⎟⎟ ⎟

⎢ ⎥

− ⎝ − ⎣⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎝ ⎠ ⎦⎠

−∞ < < ∞ , x −∞ < < ∞y (3.11) Entropi untuk peubah acak yang berdistribusi bivariate normal adalah

H(x,y)

( )

2 2

1 1

exp 2

2 1 2 1

y y

x x

x x y y

x y

y y

x x

µ µ dxdy

µ ρ µ

σ σ σ σ

πσ σ ρ ρ

∞ ∞

−∞ −∞

⎛ − ⎡⎛ − ⎞ ⎛ − ⎞⎛ − ⎞ ⎛ − ⎞ ⎤⎞

⎜ ⎢ ⎥⎟

=

∫ ∫

− ⎜⎝ − ⎢⎣⎜⎝ ⎟⎠ − ⎜⎝ ⎟⎜⎠⎝⎜ ⎟ ⎜⎟ ⎜⎠ ⎝⁺ ⎟⎟⎠ ⎥⎦⎟⎠

Terlihat bahwa entropi untuk kasus bivariat kontinu semakin sulit untuk dihitung secara manual. Hal ini terpengaruh juga oleh bentuk fungsi padat peluang dari distribusi bivariat normal.