Teknik Pengambilan Sampel Dan Ukuran Sampel

(1)

Teknik Pengambilan Sampel

Dr. Zaenal Fanani, SE.,MSA., Ak

Email:

[email protected] S

HP Simpati: 08125296854

1

(2)

Sampel ?

p

sesuatu hal

yang dijadikan

_Populasi

adalah

sebagian

dari

yang dijadikan

sebagai unit

analisis

Populasi bisa berupa

Sampel n

Populasi bisa berupa

kumpulan manusia

atau benda

2

(3)

Alasan Pengambilan Sampel

g

p

1. Keterbatasan waktu, biaya, tenaga

,

y ,

g

yang dimiliki peneliti.

2. Penelitiannya bersifat penjajagan.

3. Setiap unsur dalam populasi dianggap

memiliki karakter yang sama (homogen).

(4)

B k

Syarat sampel yang baik

Banyak

Jumlah

Sampel

Karak-teristik

teristik

sampel

Sedikit

Tingkat kesalahan

Banyak

(5)

Ukuran Sampel

p

1. Biaya, waktu, tenaga yang tersedia

2. Derajat keseragamanan (homogenitas)

3. Rancangan analisis – deskriptif,

korelasi komparasi

korelasi, komparasi.

4. Banyaknya unsur dalam populasi

(6)

Pedoman Menentukan Jumlah

1. Rumus Slovin

• n =

Besar

sampel

Kita akan meneliti pengaruh upah terhadap semangat kerja pada karyawan PT. Cucak Rowo. Di dalam PT tersebut terdapat 130 orang karyawan. Dengan tingkat kesalahan pengambilan sampel sebesar 5%, berapa jumlah sampel minimal yang harus diambil ?

(7)

2. Interval Penaksiran

• Untuk menaksir parameter rata-rata

µ

(Untuk Populasi yang tidak diketahui)

2

Seorang mahasiswa akan menguji suatu hipotesis yang menyatakan bahwa Indek Prestasi Mahasiswa Jurusan S1 Keperawatan adalah 2,7. dari 30 sampel percobaan dapat diperoleh informasi bahwa standar

dari 30 sampel percobaan dapat diperoleh informasi bahwa standar deviasi indek Prestasi mahasiswa adalah 0,25 Untuk menguji hipotesisi ini berapa jumlah sampel yang diperlukan jika kita menginginkan tingkat keyakinan sebesar 95% dan error estimasi µ kurang dari 0,05,?

(8)

• Untuk menaksir parameter proporsi P

Kita akan meperkirakan proporsi mahasiswa yang

menggunakan angkutan kota waktu pergi kuliah.

Berapa sampel yang diperlukan jika dengan tingkat

kepercayaan 95% dan kesalahan yang mungkin

terjadi 0,10 ?

(9)

3. Pendekatan Isac Michel

a. Untuk menentukan sampel untuk menaksir

2 parameter rata-rata µ

Seorang mahasiswa akan menguji suatu hipotesis yang menyatakan bahwa Indek Prestasi Mahasiswa Jurusan S1 Keperawatan yang berjumlah 175 mahasiswa adalah 2,7. Dari 30 sampel percobaan dapat diperoleh informasi bahwa standar deviasi Indek Prestasi mahasiswa diperoleh informasi bahwa standar deviasi Indek Prestasi mahasiswa adalah 0,25 Untuk menguji hipotesisi ini berapa jumlah sampel yang diperlukan jika kita menginginkan tingkat keyakinan sebesar 95% dan error estimasi µ kurang dari 5 persen ?

(10)

B. Untuk menentukan sampel untuk menaksir

p

parameter proporsi P

Z

Kita akan meperkirakan proporsi mahasiswa jurusan manajemen

unsoed yang berjumlah 175 orang. Brdasarkan penelitian pendahuluan diperolh data proporsi mahasiswa manajemen unsoed menggunakan diperolh data proporsi mahasiswa manajemen unsoed menggunakan angkutan kota waktu pergi kuliah adalah 40%. Berapa sampel yang diperlukan jika dengan tingkat kepercayaan 95% dan derajat

penyimpangan sebesar 0,10.?

(11)

Sampel Ideal (Gay, 1984)

p

(

y,

)

Ukuran minimal sampel yang dapat diterima:

p

y

g

p

1. Penelitian deskriptif:sampel minimal 10%

populasi, namun untuk populasi yang

sangat kecil diperlukan minimal 20%

2. Penelitian korelasi: minimal 30 subjek.

3 Penelitian ex post fakto atau penelitian

3. Penelitian ex post fakto atau penelitian

kausal komparatif:minimal 15 subjek per

kelompok.

(12)

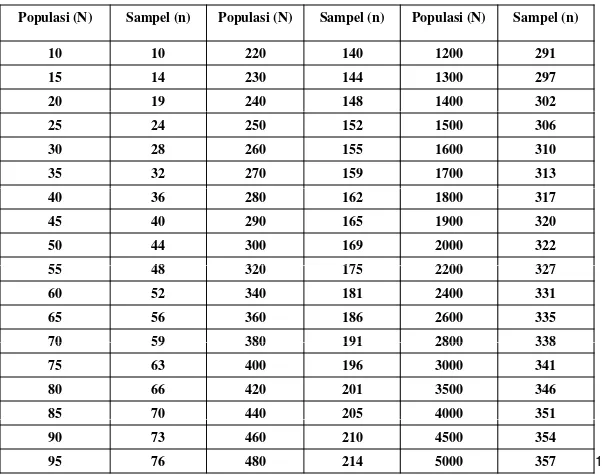
Tabel jumlah sampel berdasarkan jumlah populasi

Populasi (N) Sampel (n) Populasi (N) Sampel (n) Populasi (N) Sampel (n)

10 10 220 140 1200 291

15 14 230 144 1300 297

20 19 240 148 1400 302

25 24 250 152 1500 306

30 28 260 155 1600 310

35 32 270 159 1700 313

40 36 280 162 1800 317

45 40 290 165 1900 320

50 44 300 169 2000 322

55 48 320 175 2200 327

60 52 340 181 2400 331

65 56 360 186 2600 335

70 59 380 191 2800 338

75 63 400 196 3000 341

80 66 420 201 3500 346

85 70 440 205 4000 351

12

90 73 460 210 4500 354

(13)

Populasi (N) Sampel (n) Populasi (N) Sampel (n) Populasi (N) Sampel (n)

100 80 500 217 6000 361

110 86 550 226 7000 364

120 92 600 234 8000 367

130 97 650 242 9000 368

140 103 700 248 10000 370

150 108 750 254 15000 375

160 113 800 260 20000 377

170 118 850 265 30000 379

180 123 900 269 40000 380

190 127 950 274 50000 381

200 132 1000 278 75000 382

210 136 1100 285 1000000 384

13

(14)

Bentuk pengambilan sampel

Sampel Sampel

Acak

Tidak Acak

Setiap unsur

yang ada dalam

Setiap unsur

yang ada dalam

populasi diberi

kesempatan

t

l

yang ada dalam

populasi tidak

diberi

kesempatan

t

l

atau peluang

yang sama untuk

bisa diambil

atau peluang

yang sama untuk

bisa diambil

14

(15)

Kapan peneliti sebaiknya mengambil sampel

secara acak dan tidak acak?

Ketika peneliti

bermaksud untuk

menggeneralisasikan

gg

_{Ketika peneliti}

hasil penelitiannya

maka ambilah sampel

Ketika peneliti

tidak bermaksud untuk

menggeneralisasikan

secara acak dan

representatif

gg

hasil penelitiannya

atau ketika jumlah

populasi tidak

di-ketahui secara pasti

maka ambilah sampel

15

(16)

Teknik pengambilan sampel

e

pe ga b a sa pe

Sampel Acak :

Sampel Tidak Acak :

Sampel Acak Sederhana

Sampel Acak Distratakan

Sampel “kemudahan”

Sampel “pertimbangan”

p

Sampel Klaster

p

g

Sampel Bola Salju

Sampel Sistematis

(17)

Kerangka Sampling

Daftar yang berisikan informasi dari setiap

unsur dalam populasi

Misalnya : Populasi adalah mahasiswa STIE Indonesia.

Di dalam kerangka sampling harus ada daftar dari

S l

h

i

STIE I d

i

l

k

l i d i

Seluruh mahasiswa STIE Indonesia, lengkap mulai dari nama,

Alamat, nomor pokok, fakultas, jurusan, dlsb.

Misaln a Pop lasi adalah ib r mah tangga di Kecamatan

Misalnya : Populasi adalah ibu rumah tangga di Kecamatan

Gubeng. Di dalam kerangka sampling harus ada daftar dari

Seluruh nama ibu rumah tangga penduduk kecamatan

Gubeng dan alamatnya

(18)

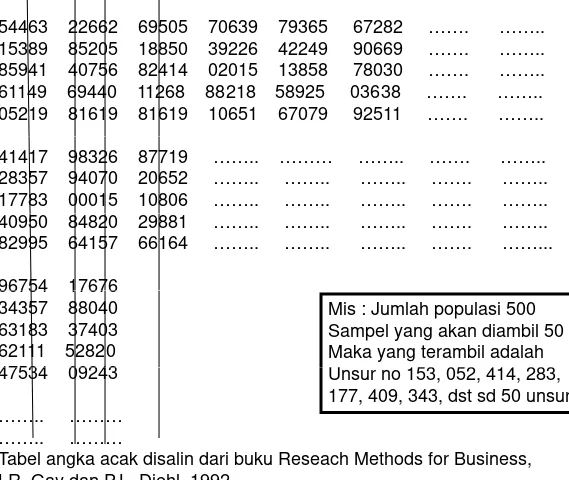
Alat pengambilan sampel

secara acak

• Daftar angka acak (random)

• Undian

• Kalkulator / komputer

(19)

54463 22662 69505 70639 79365 67282 ……. ……..

Mis : Jumlah populasi 500 Sampel yang akan diambil 50 Maka yang terambil adalah U 153 052 414 283 47534 09243

…….. ……… …….. ………

Unsur no 153, 052, 414, 283, 177, 409, 343, dst sd 50 unsur

19

(20)

Sampel Acak Sederhana

Jika setiap unsur dalam populasi dianggap sama (homogen)

oleh peneliti. Atau perbedaan-perbedaan yang ada dalam setiap

unsur populasi tidak dianggap penting oleh peneliti, dan jumlah

unsur dalam populasi tidak begitu banyak.

Langkah-langkah :

1. Susun kerangka sampling

2 Tetapkan jumlah sampel

2. Tetapkan jumlah sampel

3. Tentukan alat pengambilan sampel

4. Pilih sampel sampai dengan jumlah sampel terpenuhi

(21)

Sampel Acak Distratakan

(Proposional dan Tidak Proposional)

(

p

)

Jika unsur populasi heterogen Mis. heterogen dalam jenis kelamin,

pendidikan, pendapatan, status pekerjaan, dlsb; dan keanekaragaman

t

b t b

k

b

i

li i

liti

k

tid k

tersebut bermakna bagi analisis penelitiannya maka agar tidak

terambil hanya dari kelompok/strata tertentu saja, gunakan cara ini.

Langkah-langkah :

1. Susun kerangka sampling.

2 Bagi kerangka sampling ke dalam strata yang

2. Bagi kerangka sampling ke dalam strata yang

dikehendaki.

3. Tentukan jumlah sampel secara keseluruhan.

4 T

t k

j

l h

l d l

ti

t t

4. Tentukan jumlah sampel dalam setiap stratum.

5. Pilih sampel dari setiap stratum secara acak.

21

(22)

Sampel Sistematis

Jika jumlah unsur dalam populasi sedemikian besar dan dianggap

homogen, dan ketika peneliti tidak mempunyai alat pengambilan

sampel secara acak yang baik, pakailah cara ini. Peneliti menentukan

unsur dalam populasi yang “keberapa” yang akan diambil

unsur dalam populasi yang keberapa yang akan diambil

sebagai sampel

Langkah-langkah :

1 S

k

li

1. Susun kerangka sampling

2. Tetapkan jumlah sampel yang akan diambil.

3. Tentukan kelas interval (k) dengan cara membagi jumlah

unsur dalam populasi dengan jumlah sampel yang

dikehendaki. Mis : N = 50000 orang, n = 500 orang maka

k = 10.

4 Pilih sampel ke satu dengan cara acak – mengundi unsur

4. Pilih sampel ke satu dengan cara acak mengundi unsur

populasi yang kesatu s/d kesepuluh. Kalau sampel kesatu

jatuh ke unsur populasi ketiga, maka sampel kedua adalah

unsur populasi yang ke 13

22

p p

y

g

(23)

Sampel Klaster

Ukuran populasinya tidak terbatas (tidak diketahui dengan pasti).

Tidak tersedia kerangka sampling atau tidak memungkinkan untuk

dibuat kerangka samplingnya. Unsur-unsur populasi tersebar, baik

fi

il

h d i i t tif

secara geografis maupun secara wilayah administratif

Langkah-langkah :

1 Susun kerangka sampling

1. Susun kerangka sampling

2. Tetapkan jumlah sampel yang akan diambil.

3. Bagi kerangka sampling ke dalam strata yang

dikehendaki, biasanya lebih dari satu strata

4. Tentukan jumlah sampel dalam setiap stratum.

5. Pilih sampel dari setiap stratum secara acak

(24)

Sampel Wilayah

Ketika peneliti dihadapkan pada situasi di mana unsur populasi

tersebar di berbagai wilayah yang relatif saling berjauhan, maka

cara pengambilan sampel wilayah dapat diterapkan. Misalkan,

peneliti ingin mengetahui pandangan masyarakat Jawa Barat

terhadap program keluarga berencana.

Langkah-langkah :

1. Susun kerangka sampel yang menggambarkan

wilayah-wilayah. Mis. Propinsi Jawa Barat yang

l

k

d

K b

t

K

t

d

D

lengkap dengan Kabupaten, Kecamatan, dan Desa.

2. Tentukan wilayah yang akan dijadikan sampel – Kabupaten?,

Kecamatan?, Desa?

3 Tentukan berapa wilayah yang akan dijadikan sampel

3. Tentukan berapa wilayah yang akan dijadikan sampel

4. Pilih wilayah yang akan dijadikan sampel dengan cara acak

5. Telitilah semua unsur sampel yang ada dalam

wilayah sampel penelitian.

24

wilayah sampel penelitian.

(25)

Sampel Tidak Acak

Sampel yang mudah dilakukan

Pengambilan sampel dengan cara ini cukup

g

p

g

p

Memadai untuk penelitian yang sifatnya

penjajagan

Langkah-langkah :

1. Tetapkan secara khusus populasi penelitian

2 Tetapkan jumlah sampel yang akan diambil

2. Tetapkan jumlah sampel yang akan diambil

3. Pergilah ke tempat yang banyak terdapat unsur populasi

4. Bagikanlah kuesioner kepada setiap unsur populasi

yang dijumpai

(26)

Sampel berdasarkan

ti b

t t

t

pertimbangan tertentu

Peneliti menentukan suatu unsur dalam populasi

dijadikan sampel, berdasarkan pertimbangan tertentu,

yaitu karena “kaya akan

informasi”

“Seorang kepala sekolah dijadikan sampel penelitian

Seorang kepala sekolah dijadikan sampel penelitian

ketika peneliti yakin bahwa informasi atau data

yang ingin diperolehya akan banyak di miliki

oleh kepala sekolah tadi”

(27)