BAB 1 PENDAHULUAN
1.1 LATAR BELAKANG
Graf merupakan salah satu cabang ilmu matematika yang dapat digunakan
dalam membantu persoalan diberbagai bidang seperti masalah komunikasi,
transportasi, distribusi, aliran air, aliran listrik dan lain sebagainya. Salah satu
kegunaan graf yang cukup penting adalah dalam hal pemilihan path terpendek dimana
untuk mencari path terpendek dari simpul t (simpul awal) ke simpul s (simpul tujuan)
adalah mencari jalur yang berbeda dari simpul t ke s dengan bobot yang seminimal
mungkin. Bobot dalam graf adalah nilai yang diberikan pada setiap jalurnya. Bobot
tersebut dapat menyatakan diameter, panjang, jarak antar tempat, waktu pengiriman,
ongkos pengiriman dan lain sebagainya.
Persoalan Travelling Salesman Problem (TSP) termasuk persoalan yang sangat
terkenal di dalam teori graf. Persoalan ini diilhami oleh masalah seorang pedagang
yang berkeliling mengunjungi sejumlah kota. Persoalan ini menentukan sirkuit
terpendek yang harus dilalui oleh seorang pedagang bila pedagang itu berangkat dari
sebuah kota asal dan menyinggahi setiap kota tepat satu kali dan kembali ke kota asal
keberangkatan (Rinaldi Munir, 2003: 355).
Dalam Travelling Salesman Problem terdapat beberapa algoritma diantaranya
adalah algoritma Branch and Bound, algoritma Nearest Neighbor dan algoritma
Cutting Plane. Algoritma Branch and Bound adalah sebuah teknik penyelesaian
langkah-langkah untuk semua kemungkinan solusi tanpa mempertimbangkannya satu
demi satu. Algoritma Nearest Neighbor adalah algoritma heuristic yang mudah untuk
diimplementasikan dan biasanya menghasilkan hasil yang bermutu. (William J. Cook,
masalah program integer linier yang berawal optimal. (Ir. Tjutju Dimyati.
1987:178). Berikut adalah sedikit gambaran tentang kelebihan dan kekurangan
beberapa algoritma yang digunakan untuk menyelesaikan permasalahan Travelling
Salesman problem.
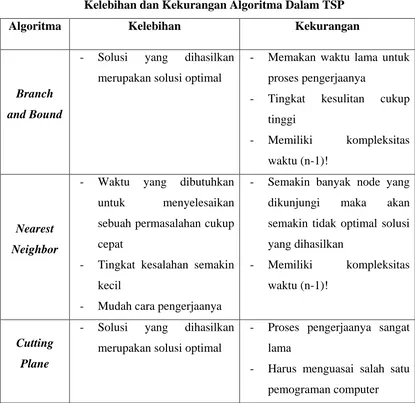
Tabel 1.1
Kelebihan dan Kekurangan Algoritma Dalam TSP
Algoritma Kelebihan Kekurangan
Branch
and Bound
- Solusi yang dihasilkan
merupakan solusi optimal
- Memakan waktu lama untuk
proses pengerjaanya
- Tingkat kesulitan cukup
tinggi
- Memiliki kompleksitas
waktu (n-1)!
Nearest
Neighbor
- Waktu yang dibutuhkan
untuk menyelesaikan
sebuah permasalahan cukup
cepat
- Tingkat kesalahan semakin
kecil
- Mudah cara pengerjaanya
- Semakin banyak node yang
dikunjungi maka akan
semakin tidak optimal solusi
yang dihasilkan
- Memiliki kompleksitas
waktu (n-1)!
Cutting
Plane
- Solusi yang dihasilkan
merupakan solusi optimal
- Proses pengerjaanya sangat
lama
- Harus menguasai salah satu
pemograman computer
PT. Coca Cola Bottling Indonesia yang beralamat di Jalan KL.Yos Sudarso
Km.14 Simpang Martubung Medan adalah perusahaan yang bergerak di bidang
industri pembuatan minuman ringan. Barang produksinya meliputi Coca Cola, Sprite,
Barat, Medan Utara dan Medan Selatan. Kantor penjualan Medan memiliki
outlet-outlet yang penjualannya langsung pada konsumen.
Sistem pendistribusian pada PT. Coca Cola Bottling Indonesia Medan diawali
dengan pendataan pemesanan yang dilakukan oleh seorang sales sehingga pada proses
pendistribusian, setiap truk sudah diisi barang produksi dengan maksimal.
Pendistribusian dilakukan dengan cara memenuhi permintaan pada setiap lokasi outlet
tanpa mempertimbangkan jarak tempuh sehingga waktu distribusi menjadi lama dan
pengiriman produk menjadi terlambat. PT. Coca Cola Bottling Indonesia Medan
belum memiliki penyusunan rute sehingga dapat berubah sewaktu-waktu yang
berdampak pada ketidaktepatan waktu dalam pendistribusian. Oleh karena itu perlu
dilakukan penyusunan rute yang dapat mempersingkat jarak tempuh dan akhirnya
berdampak pada penghematan biaya distribusi bagi perusahaan.
Untuk penyelesaian persoalan diatas digunakan dua algoritma yang
dibandingkan yaitu algoritma Branch and Bound dan algoritma Nearest Neighbor
dimana indikator pembandingnya adalah kompleksitas waktu dan jarak terpendek
yang dihasilkan sehingga algoritma yang memiliki waktu eksekusi minimum dan
menghasilkan jarak terpendek yang menjadi algoritma terbaik.
Berdasarkan kondisi-kondisi di atas maka penulis memilih judul Tugas Akhir ini
sebagai: “Menentukan Rute Optimal Pendistribusian Produk Minuman pada PT.
Coca Cola Bottling Indonesia Medan dengan Menggunakan Algoritma Branch
and Bound dengan Algoritma Nearest Neighbor.’’
1.2 PERUMUSAN MASALAH
Permasalahan yang dirumuskan dalam penelitian ini adalah bagaimana menentukan
rute optimal pendistribusian produk minuman pada PT. Coca Cola Bottling Indonesia
Medan dengan menggunakan Algoritma Branch and Bound dengan Algoritma Nearest
1.3 BATASAN MASALAH
Agar permasalahan tidak menyimpang dari pokok permasalahan maka perlu dibuat
pembatasan masalah yaitu:
1. Pekerjaan yang dianalisa adalah pendistribusian produk minuman di dalam wilayah
Binjai.
2. Perhitungan dilakukan untuk menentukan rute dengan jarak tempuh yang tersingkat
dari rute yang telah ada.
3. Rute yang dianalisa adalah rute yang biasanya dilalui oleh pegawai pada waktu
yang sama untuk wilayah Binjai.
4. Objek Penelitian hanya pada rute satu salesman yang terdiri dari grosir, kantin
lembaga, institusi dan rumah makan.
5. Kondisi jalan dan kepadatan lalu-lintas setiap harinya adalah normal.
6. Hanya meneliti 1 Truk, salesman juga berpengalaman dan memahami tugasnya
dalam mendistribusikan produk ke outlet-outlet.
7. Satu liter bahan bakar untuk alat angkut dapat menempuh jarak rata-rata 9 km.
1.4 TINJAUAN PUSTAKA
Aulia Rahma (2006) dalam jurnalnya menuliskan Travelling Salesman Problem
sebagai salah satu permasalahan optimasi yang bersifat klasik dan Non-Deterministic
Polynomial-time Complete (NPC), di mana tidak ada penyelesaian yang paling
optimal selain mencoba seluruh kemungkinan penyelesaian yang ada. Permasalahan
ini melibatkan seorang travelling salesman yang harus melakukan kunjungan sekali
pada semua kota dalam sebuah lintasan sebelum dia kembali ke titik awal, sehingga
perjalanannya dikatakan sempurna.
Hamdy A. Taha (2007) menjelaskan Travelling Salesman Problem
berhubungan dengan pencarian rute terpendek atau rute terdekat pada n-kota dan dij
yang merupakan jarak antara kota i ke kota j, di mana setiap kota hanya dikunjungi
sekali. Beberapa metode yang digunakan dalam menyelesaikan masalah Travelling
Secara khusus penyelesaian permasalahan Travelling Salesman Problem dapat
dimodelkan / didefinisikan sebagai berikut :
Minimumkan :
∑
dengan kendala :
∑
1.
X
ij semua bilangan cacah, maka problema disebutproblema program bilangan cacah murni.
2.
X
ijsebagian bilangan cacah dan yang lainnya bolehtidak, maka disebut problema bilangan cacah campuran.
3.
X
ijsalah satu nol atau satu, problema disebut problemaprogram bilangan cacah nol-satu (Siagian, 1987).
n
= jumlah kota / lokasi / pelanggan yang akandikunjungi (n tidak termasuk tempat asal, yang
c
ij= biaya / jarak travelling dari kota i ke kota jTinjauan Singkat Mengenai Branch and Bound dengan Nearest Neighbor
Pada dasarnya pendekatan Branch and Bound terdiri dari dua prosedur utama yaitu
branching dan bounding. Branching adalah proses mempartisi masalah yang besar
menjadi dua atau lebih masalah kecil (subproblem), sedangkan Bounding adalah
proses menghitung batas bawah pada solusi optimal dari subproblem yang
bersangkutan. Pemrosesan Bounding function yang digunakan hanya dilakukan pada
branch yang baik dan branch yang buruk tidak akan diproses dengan harapan branch
yang baik akan memberikan hasil yang optimal diproses selanjutnya.
Metode Branch and Bound (cabang dan batas) adalah salah satu metode untuk
menghasilkan penyelesaian optimal pemrograman liniear yang menghasilkan
variabel-variabel keputusan bilangan bulat. Sesuai dengan namanya, metode ini membatasi
penyelesaian optimum yang akan menghasilkan bilangan pecahan dengan cara
membuat cabang atas dan bawah bagi masing-masing variabel keputusan yang
bernilai pecahan agar bernilai bulat sehingga setiap pembatasan akan menghasilkan
cabang baru.
Algoritma Branch and Bound diusulkan pertama kali oleh A.H.Land dan
A.G.Doig pada tahun 1960. Sebenarnya algoritma ini dibuat untuk pemrograman
linier (liniear programing). Branch and Bound merupakan metode yang membagi
permasalahan menjadi subregion yang mengarah ke solusi (branching) dengan
membentuk sebuah struktur pohon pencarian (search tree) dan melakukan pembatasan
semua cabang tree yang menuju solusi, sedangkan proses bound merupakan
menghitung node dengan memperhatikan batas constraint.
Prosedur di dalam branch and bound dilakukan secara berulang secara rekursif
hingga membentuk sebuah pohon pencarian (search tree) dan melakukan proses
bounding dengan menentukan batas atas (upper bound) dan batas bawah (lower
bound).
Ketika tangkai pohon (node) dicabangkan, satu atau lebih node ditambahkan
ke job yang ada di depannya. Pemilihan node untuk cabang yang memiliki jumlah job
paling besar. Sebuah lower bound untuk makespan dihitung berdasarkan
masing-massing node yang dihasilkan.
Konsep utama yang mendasari metode ini adalah dengan membagi dan
menyelesaikan (divide and coquer). Pembagian (pencabangan) dilakukan dengan
membagi gugus dari keseluruhan penyelesaian layak menjadi anak gugus yang lebih
kecil dan kemudian menjadi anak gugus yang lebih kecil lagi (Frederick.S.Hilier dan
Gerald.J.Lieberman, 1994).
Langkah-langkah penyelesaian dengan metode Branch and Bound, yaitu:
1. Gambarkan problem dengan diagraph G = (V,E).
2. Cij
di mana C
= nilai (cost) pada edge (i,j)
ij
3. Dengan definisi nilai (cost) di atas, bangun Cost Matrix dari TSP.
= ∞, jika tidak ada edge antara i dan j.
4. Lakukan reduksi terhadap Cost Matrix , di dapat Reduced Cost Matrix.
5. Gunakan fungsi pembatas (bound) untuk membangun Search Tree dari Reduced
Cost Matrix.
6. Dan seterusnya hingga didapat solusi yang diinginkan.
Pada metode Nearest Neighbor pemilihan lintasan akan dimulai pada lintasan
yang memiliki nilai jarak paling minimum setiap melalui kota, kemudian akan
memilih kota selanjutnya yang belum dikunjungi dan memiliki jarak yang paling
minimum.
1. Buat peta aliran yang menggambarkan letak-letak outlet penjualan beserta jarak
antar oulet.
2. Proses pengerjaan dengan melihat outlet dengan jarak terpendek. Setiap mencapai
satu outlet, algoritma ini akan memilih outlet selanjutnya yang belum dikunjungi
dan memiliki jarak yang paling minimum.
3. Perhitungan nilai optimal dengan menjumlah jarak dari awal sampai akhir
perjalanan.
1.5 TUJUAN PENELITIAN
Tujuan penelitian ini adalah untuk menentukan rute optimal pendistribusian produk
minuman pada PT. Coca Cola Bottling Indonesia Medan dengan menggunakan
Algoritma Branch and Bound dengan Algoritma nearest Neighbor.
1.6 MANFAAT PENELITIAN
1. Untuk menambah pengetahuan peneliti dan juga menambah wawasan pembaca
mengenai penggunaan Algoritma Branch and Bound dengan Algoritma Nearest
Neighbor pada Travelling Salesman Problem.
2. Sebagai bahan masukan pada PT. Coca Cola Bottling Indonesia Medan dalam
menentukan rute optimal pendistribusian produk sehingga dapat menimalkan biaya
pengeluaran.
1.7 METODOLOGI PENELITIAN
Metode penelitian yang digunakan dalam penelitian ini adalah metode survey dengan
langkah-langkah sebagai berikut:
1. Melakukan studi jurnal, buku, dan artikel di internet yang berubungan dengan
Algoritma Branch and Bound dan Algoritma Nearest Neighbor pada Travelling
Salesman Problem (TSP).
2. Mengumpulkan data program pendistribusian barang yang bersumber dari PT.
3. Mengolah data dengan menggunakan algoritma Branch and Bound dengan
algoritma Nearest Neighbor dan membandingkan hasil dari kedua algoritma
tersebut.
4. Penarikan kesimpulan, yakni konsep pendistribusian mana yang terbaik untuk