Penerapan Jaringan Saraf Tiruan Untuk Memprediksi Pergerakan Harga Minyak Mentah Dunia Menggunakan Metode Backpropagation

BAB 2

TINJAUAN PUSTAKA

2.1 Jaringan Saraf Tiruan

Jaringan saraf tiruan (JST) pertama kali diperkenankan oleh

informasi yang memiliki karakteristik-karakteristik menyerupai jaringan saraf biologi

[2].

Dengan meniru sistem jaringan biologis maka sistem jaringan saraf tiruan

memiliki 3 karakteristik utama, yaitu [1]:

1. Arsitektur jaringan

Merupakan pola keterhubungan antara neuron. Keterhubungan neuron

-neuron inilah yang membentuk suatu jaringan.

2. Algoritma Pembelajaran

Merupakan metode untuk menentukan nilai bobot hubungan. Ada dua jenis

metode utama, yaitu metode pelatihan atau pembelajaran (memorisasi) dan

metode pengenalan atau aplikasi.

3. Fungsi Aktivasi

Merupakan fungsi untuk menentukan nilai keluaran (output) berdasarkan

nilai total masukan (input) pada neuron. Fungsi aktivasi suatu algoritma

jaringan dapat berbeda dengan fungsi aktivasi algoritma jaringan lain.

2.1.1 Arsitektur jaringan saraf tiruan

Satu sel saraf dapat dimodelkan secara matematis seperti diilustrasikan oleh Gambar

Synaptic weights

fungsi aktivasi (activation function) dan keluaran (output). Secara matematis, dapat

digambarkan sebuah neuron dengan menuliskan pasangan persamaan sebagai berikut:

Gambar 2.1. Model Neuron[1]

f(.) = fungsi aktivasi atau elemen pemroses

y = sinyal keluaran.

Beberapa konsep yang berhubungan dengan pemrosesan informasi tersebut

seperti yang disebutkan di atas, yaitu:

1. Input

Nilai numerik atau representasi suatu atribut merupakan input dari

jaringan. Beberapa tipe data seperti teks, gambar dan suara dapat juga

digunakan sebagai input.

2. Output

Output jaringan berisi solusi untuk permasalahan.

3. Bobot (weights)

Unsur kunci Jaringan saraf tiruan adalah bobot. Bobot menunjukkan suatu

banyaknya koneksi yang memindahkan data dari satu lapisan ke lapisan

yang lainnya. Bobot sangat penting karena menyimpan pola pembelajaran

dari informasi.

4. Fungsi Penjumlahan

Fungsi penjumlahan merupakan perkalian setiap nilai input dengan

bobotnya.

5. Fungsi Aktivasi

Fungsi aktivasi merupakan hubungan antara tingkat aktivasi internal dan

output yang bisa berupa linier atau non-linier

Arsitektur pada jaringan saraf tiruan menggambarkan jumlah neuron dan

hubungan bobot yang dipakai dan fungsi aktivasi. Secara umum arsitektur jaringan

saraf dapat dibedakan menjadi tiga kelas yang berbeda, yaitu jaringan umpan-maju

lapisan tunggal (single layer feedforward network atau perceptron), jaringan

umpan-maju lapisan jamak (multilayer perceptron) dan jaringan dengan lapisan kompetitif

[6].

2.1.2 Jaringan saraf tiruan backpropagation

Terdapat banyak ide dan definisi yang berhubungan dengan “belajar”. Taksonomi

proses belajar dalam jaringan saraf tiruan dibagi secara umum menjadi dua bagian [5]:

1. Supervised learning

Supervised learning adalah proses belajar yang membutuhkan guru. Yang

dimaksud guru disini adalah sesuatu yang memiliki pengetahuan tentang

lingkungan. Guru bisa direpresentasikan sebagai sekumpulan sampel

input-ouput.

2. Unsupervised learning

Sesuai dengan namanya, unsupervised atau self-organized learning tidak

membutuhkan guru untuk memantau proses belajar. Dengan kata lain,

tidak ada sekumpulan input-output atau fungsi tertentu untuk dipelajari

Jaringan saraf tiruan backpropagation dikategotikan sebagai supervised

learning yang melakukan pembelajaran sehinggamemberikan output yang masuk akal

jika diberi masukan serupa (tidak harus sama) dengan pola yang dipakai dalam

pelatihan. Sifat generalisasi ini membuat pelatihan lebih efisien karena tidak perlu

dilakukan pada semua data [9].

Backpropagation dibentuk dengan membuat generalisasi aturan pelatihan

dalam model widrow-hoff dengan cara menambahkan layer tersembunyi. Kata

backpropagation merujuk pada cara bagaimana gradien perubahan bobot dihitung.

Suatu jaringan saraf tiruan backpropagation memproses informasi masukan

pada setiap neuron. Pada gambar 2. ditunjukkan arsitektur JST backpropagation

dengan tiga layer dimana unit masukan X, unit hidden layer Z, dan unit keluaran Y.

Sedangkan v0j adalah nilai bias untuk hidden layer Z dan wok adalah nilai bias untuk

keluaran Y.

Y₁ Y_k Y_m

w₀₁ w₁₁ w_j1 w_p1 w_0k w_1k w_jk w_pk w_0m w_1m w_jm w_pm

Z₁ Z_j Z_p

X₁ X_i X_n

v₀₁ v₁₁ v_i1 v_n1 v_0j v_1j v_ij v_nj v_0p v_1p v_ip v_np

1

1

Gambar 2.2. Arsitektur Jaringan Saraf Tiruan dengan Backpropagation[7] Keterangan:

X = Masukan (input)

V = Bobot lapisan tersembunyi

n = Jumlah unit pengolah lapisan tersembunyi

Z = Lapisan tersembunyi (hidden layer)

Y = Keluaran (output)

2.1.3 Fungsi Aktivasi

Sebuah sinyal aktivasi diperlukan oleh suatu neuron untuk menyalakan atau

memadamkan penjalaran sinyal dari neuron tersebut. Sinyal aktivasi dalam jaringan

saraf tiruan ditentukan oleh suatu fungsi aktivasi.

Fungsi aktivasi merupakan fungsi pengolah jumlahan data masukan menjadi

data keluaran. Karakteristik pada fungsi aktivasi dari backpropagation adalah

continue, dapat diturunkan, dan tidak menurun secara monoton. Fungsi aktivasi untuk

algoritma backpropagation adalah sebagai berikut [6]:

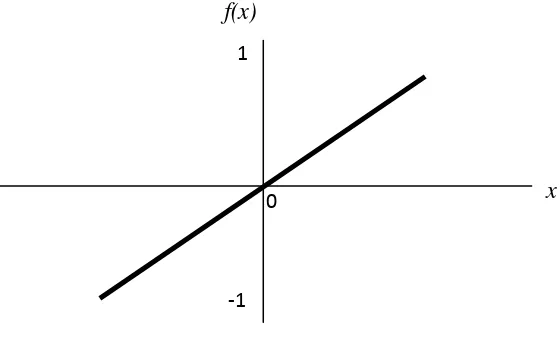
1. Linier atau Purelin

Fungsi linier akan membawa masukkan ke keluaran yang sebanding. Fungsi ini

didefinisikan:

Ilustrasi fungsi liner digambarkan pada gambar 2.3 berikut ini:

Gambar 2.3. Fungsi Aktivasi Linier -1

1

0 x

f(x) x

2. Sigmoid Biner atau Logsig

Fungsi ini memiliki sifat nonlinier sehingga sangat baik diterapkan dalam

penyelesaian masalah yang kompleks. Keluaran dari fungsi sigmoid biner berupa

bilangan biner (0 atau 1) atau nilai yang berada di antara 0 sampai 1. Sigmoid biner

memiliki range dari [0,1] dan didefinisikan :

)

dan fungsi turunannya adalah :

f'(x)= f₁(x)[1− f₁(x)]

Ilustrasi fungsi sigmoid biner digambarkan pada gambar 2.4 berikut ini:

Gambar 2.4. SigmoidBiner[11]

3. Sigmoid Bipolar atau Tansig

Sigmoid Bipolar memiliki range dari (-1,1) dan didefinisikan :

1

dan turunan fungsi adalah :

Ilustrasi fungsi sigmoid bipolar digambarkan pada gambar 2.5 berikut ini:

Gambar 2.5. Sigmoid Bipolar[12]

2.1.4 Algoritma pembelajaran metode backpropagation

Proses pelatihan backpropagation meliputi tiga tahap, yaitu tahap umpan maju

(feedforward), tahap umpan mundur, dan tahap update bobot dan bias[7]. Algoritma

backpropagation diuraikan sebagai berikut:

Fase I: Propagasi Maju

Selama propagasi maju, sinyal masukan (= xi ) dipropagasikan ke layer tersembunyi

menggunakan fungsi aktivasi yang ditentukan. Keluaran dari setiap unit layer

tersembunyi (= zj ) tersebut selanjutnya dipropagasikan maju lagi ke layer

tersembunyi di atasnya menggunakan fungsi aktivasi yang ditentukan. Demikian

seterusnya hingga menghasilkan keluaran jaringan (=yk ). Berikutnya, keluaran

jaringan (= yk ) dibandingkan dengan target yang harus dicapai (= tk ). Selisih dari tk

terhadap yk yaitu ( tk – yk ) adalah kesalahan yang terjadi. Jika kesalahan ini lebih

kecil dari batas toleransi yang ditentukan, maka iterasi dihentikan. Akan tetapi apabila

kesalahan masih lebih besar dari batas toleransinya, maka bobot setiap garis dalam

jaringan akan dimodifikasi untuk mengurangi kesalahan yang terjadi. -1

x f(x)

Fase II: Propagasi Mundur

Berdasarkan kesalahan tk – yk , dihitung faktor δk (k = 1,2,..., m ) yang dipakai untuk mendistribusikan kesalahan di unit yk ke semua unit tersembunyi yang terhubung

langsung dengan yk . δk juga dipakai untuk mengubah bobot garis yang berhubungan langsung dengan unit keluaran.

Dengan cara yang sama, dihitung faktor δj ( j = 1,2,…, p ) di setiap unit di layer

tersembunyi sebagai dasar perubahan bobot semua garis yang berasal dari unit

tersembunyi di layerdi bawahnya. Demikian seterusnya hingga semua faktor δ di unit

tersembunyi yang berhubungan langsung dengan unit masukan dihitung.

Fase III: Perubahan Bobot

Setelah semua faktor δ dihitung, bobot semua garis dimodifikasi bersamaan.

Perubahan bobot suatu garis didasarkan atas faktor δ neuron di layer atasnya. Sebagai contoh, perubahan bobot garis yang menuju ke layer keluaran didasarkan atas δk yang ada di unit keluaran. Ketiga fase terebut diulang-ulang terus hingga kondisi

penghentian dipenuhi. Umumnya kondisi penghentian yang sering dipakai adalah

jumlah iterasi atau kesalahan. Iterasi akan dihentikan jika jumlah iterasi yang

dilakukan sudah melebihi jumlah maksimum iterasi yang ditetapkan, atau jika

kesalahan yang terjadi sudah lebih kecil dari batas toleransi yang diijinkan. Algoritma

pelatihan untuk jaringan dengan satu layer tersembunyi (dengan fungsi aktivasi

sigmoid biner) adalah sebagai berikut [4]:

Langkah 0 : Inisialisasi semua bobot dengan bilangan acak kecil.

Langkah 1 : Jika kondisi penghentian belum terpenuhi, lakukan langkah 2 – 9.

Langkah 2 : Untuk setiap pasang data pelatihan, lakukan langkah 3 – 8.

Fase I : Propagasi maju

Langkah 3 : Tiap unit masukan menerima sinyal dan meneruskannya ke unit

tersembunyi di atasnya.

Langkah 4 : Hitung semua keluaran di unit tersembunyi j

Langkah 5 : Hitung semua keluaran jaringan di unit k

Fase II : Propagasi mundur

Langkah 6 : Hitung faktor δ unit keluaran berdasarkan kesalahan di setiap unit keluaran yk ( k = 1,2,…,m ). δk merupakan unit kesalahan yang akan dipakai dalam perubahan bobot layer dibawahnya (langkah 7). Hitung suku perubahan bobot wkj

(yang akan dipakai nanti untuk merubah bobot wkj) dengan laju perceptron α

Δwkj=αδk zj ; k = 1,2,…,m ; j = 0,1,…, p

Langkah 7 : Hitung faktor δ unit tersembunyi berdasarkan kesalahan di setiap unit

tersembunyi zj ( j = 1,2,…, p ).

Faktor δ unit tersembunyi :

δj= δ_netj f ’(z_netj) = δ_netj zj ( 1– zj )

Hitung suku perubahan bobot Vji (yang akan dipakai nanti untuk merubah bobot Vji).

Δvji= α δj xi ; j = 1,2,…,p ; I = 0,1,…,n

Fase III : Perubahan bobot

Langkah 8 : Hitung semua perubahan bobot.

Perubahan bobot garis yang menuju ke unit keluaran :

Wkj (baru) = Wkj (lama) + ΔWkj ( k = 1,2,…,m ; j = 0,1,…,p )

Vji (baru) = Vji (lama) + Δvji ( j = 1,2…,p ; I = 0,1,…,n )

Setelah selesai dilakukan, jaringan dapat dipakai untuk pengenalan pola. Dalam hal

ini, hanya propagasi maju (langkah 4 dan 5) saja yang dipakai untuk menentukan

keluaran jaringan. Apabila fungsi aktivasi yang dipakai bukan sigmoid biner, maka

langkah 4 dan 5 harus disesuaikan. Demikian juga turunannya pada langkah 6 dan 7.

2.1.5 Preprocessing dan postprocessing

1. Min dan Max

Sebelum dilakukan pelatihan, seringkali dilakukan penskalaan pada input dan target

sedemikian hingga data input dan target tersebut masuk dalam satu range tertentu[5].

Fungsi premnmx digunakan untuk menskala input dan output sedemikian hingga

data-datanya akan terletak pada range [1,1].

Systax:

[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t), atau

[pn,minp,maxp] = premnmx(p), atau

[tn,mint,maxt] = premnmx(t)

Dengan p adalah hasil input, dan t adalah matriks output. Fungsi ini akan

menghasilkan:

pn : matriks input yang ternormalisasi (terletak pada range [-1,1])

tn : matriks target yang ternormalisasi (terletak pada range [-1,1])

minp : nilai minimum pada matriks input asli(p).

maxp : nilai maksimum pada matriks input asli(p).

mint : nilai minimum pada matriks target asli(p).

maxt : nilai maksimum pada matriks target asli(p).

Apabila matriks yang sudah ternormalisasi ini ingin dikembalikan kebentuk aslinya,

maka dapat digunakan fungsi postmnmx.

Systax:

[p] = postmnmx (pn,minp,maxp), atau

[t] = postmnmx (tn,mint,maxt)

Dengan p dan t adalah matriks yang telah didenormalisasi.

Apabila pada jaringan saraf tiruan yang telah dilatih menggunakan premnmx untuk

preprocessing, maka apabila ada data input baru yang akan disimulasikan, data baru

tersebut juga harus disesuaikan dengan nilai minimum dan maksimum dari jaringan.

Untuk keperluan ini, dapat digunakan fungsi tramnmx.

2. Mean dan standar deviasi

Selain dengan meletakkan data input dan target pada range tertentu, proses

normalisasi juga dapat dilakukan dengan bantuan mean dan standar deviasi[5]. Fungsi

prestd akan membawa data ke bentuk normal dengan mean=0 dan deviasi standar=1.

Syntax:

[pn,meanp,stdp,tn,meant,stdt] = prestd(p,t), atau

[pn,meanp,stdp] = prestd(p), atau

[tn,meant,stdt] = prestd(t)

Dengan p adalah hasil input, dan t adalah matriks output. Fungsi ini akan

menghasilkan:

pn : matriks input yang ternormalisasi (terletak pada range [-1,1])

tn : matriks target yang ternormalisasi (terletak pada range [-1,1])

meanp : mean pada matriks input asli(p).

stdp : standar deviasi pada matriks input asli(p)

meant : mean pada matriks input target(t).

stdt : standar deviasi pada matriks target asli(p)

Apabila matriks yang sudah ternormalisasi ini ingin dikembalikan kebentuk aslinya,

maka dapat digunakan fungsi poststd.

Systax:

[p,t] = poststd(pn,meanp,stdp,tn,meant,stdt), atau

[t] = poststd (tn,meant,stdt)

Dengan p dan t adalah matriks yang telah didenormalisasi.

Apabila pada jaringan saraf tiruan yang telah dilatih menggunakan trastd untuk

preprocessing, maka apabila ada data input baru yang akan disimulasikan, data baru

tersebut juga harus disesuaikan dengan nilai mean dan standar deviasi dari jaringan.

Untuk keperluan ini, dapat digunakan fungsi trastd.

2.2 Aplikasi Backpropagation Dalam Prediksi

Prediksi adalah perkiraan tentang sesuatu yang akan terjadi pada waktu yang akan

datang yang didasarkan pada data waktu sekarang dan waktu lampau (historical

data)[4].

Prediksi merupakan suatu proses untuk memperkirakan kejadian ataupun

perubahan di masa yang akan datang[11]. Dalam suatu proses kegiatan, proses

prediksi ini merupakan awal dari rangkaian kegiatan, dan sebagai titik tolak kegiatan

berikutnya. Permodelan time series sering sekali dikaitkan dengan proses prediksi

(forecasting) suatu nilai karakteristik tertentu pada periode kedepan, melakukan

pengendalian suatu proses ataupun untuk mengenali pola perilaku sistem[15].

Dengan mendeteksi pola dan kecendrungan data time series, kemudian

memformulasikannya dalam suatu model, maka dapat digunakan untuk memprediksi

data yang akan datang. Model dengan akurasi yang tinggi akan menyebabkan nilai

prediksi cukup valid untuk digunakan sebagai pendukung dalam proses pengambilan

keputusan.

Salah satu metode prediksi yang berkembang saat ini adalah menggunakan

jaringan saraf tiruan (artificial neural network), dimana jaringan saraf tiruan telah

menjadi penelitian yang menarik dan banyak digunakan untuk menyelesaikan masalah

pada beberapa bidang kehidupan. Salah satu diantaranya adalah untuk analisis data

Salah satu jaringan pada JST yang dapat diaplikasikan dengan baik dalam

bidang prediksi (forecasting) adalah backpropagation. Prediksi yang sering kita dengar adalah prediksi jumlah penjualan, nilai tukar, valuta asing, prediksi besarnya

aliran air sungai, dll[4].

Secara umum, masalah prediksi dapat dinyatakan sebagai berikut: Diketahui

sejumlah data runtun waktu (time series) x1, x2, …, xn. Masalahnya adalah

memperkirakan berapa harga xn+1 berdasarkan x1, x2, …, xn.

Dengan backpropagation, record data dipakai sebagai data pelatihan untuk

mencari bobot yang optimal. Untuk itu kita perlu menetapkan besarnya periode

dimana data berfluktuasi secara teratur. Besarnya periode ini kita tentukan secara

intuitif. Misalnya: perminggu, perbulan, perempat bulan atau pertahun.

Bagian tersulit dari memprediksi sesuatu menggunakan jaringan saraf tiruan

backpopagation adalah menentukan jumlah layer (dan unitnya). Tidak ada teori yang

dengan pasti yang dapat dipakai. Tapi secara praktis dicoba jaringan yang kecil

terlebih dahulu (misalnya terdiri dari satu layer tersembunyi dengan beberapa unit

saja). Jika gagal (kesalahan tidak turun dalam epoch yang besar), maka jaringan

diperbesar dengan menambahkan unit tersembunyi atau bahkan menambah layer

tersembunyi.

2.3 Prediksi Harga Minyak Mentah Dunia

Energi adalah mesin pertumbuhan ekonomi yang utama dan minyak bumi adalah

primadonanya karena kemudahan dan fleksibilitas penggunaannya paling tinggi

dibandingkan energi lainnya. Minyak bumi telah berperan besar dalam memajukan

negara-negara industri yang mengkonsumsinya dalam jumlah besar dan harga murah

sedangkan dewasa ini negara-negara ekonomi baru yang sedang tumbuh juga sangat

memerlukan namun pada situasi pasokan yang sudah sedikit dan pada harga yang jauh

Kecukupan pasokan dan harga minyak yang stabil sangat diperlukan dalam

mendorong pertumbuhan ekonomi maupun kegiatan usaha. Karena itu harga yang

dapat diprediksi dengan baik akan sangat bermanfaat bagi banyak pihak, baik

pemerintah, badan usaha maupun investor agar semua kegiatan dapat direalisasikan

sesuai rencana[14].

Sebaliknya, harga minyak yang naik-turun saat ini, sering membuat cemas

para pelaku ekonomi bahkan dapat mengancam stabilitas pertumbuhan perekonomian

jika tidak di-manage dengan baik. Pada kenyataannya pergerakan harga minyak dalam

runut waktu tertentu dapat digolongkan data time series yang umumnya dapat

dipahami dengan melihat pola kejadian di masa lalu dan saat ini.

Pada pengamatan data time series harga minyak, terdapat beberapa reverensi

yang dapat diambil, yaitu harga dari pasar minyak mentah dunia. Dari beberapa pasar

minyak mentah yang terbesar antara lain: WTI (West Texas Intermediate), NYMEX

(New York Mercantile Exchange), Brent North Sea, Tapis, Minas[10].

2.4 Tinjauan Penelitian yang Relevan

Berikut ini penelitian tentang jaringan saraf tiruan backpropagation, khususnya

penggunaan dalam hal prediksi:

1. Penelitian oleh Dini Otaviani ini membahas tentang penggunaan jaringan saraf

tiruan backpropagation untuk memprediksi kurs mata valuta asing. Hasil dari

penelitian ini, jaringan saraf tiruan backpropagation dapat memprediksi nilai

kurs valuta asing dengan faktor penentu keberhasilan pelatihan antara lain:

jumlah layer, jumlah neuron dan parameter pelatihan. Pelatihan perbulan

menghasilkan pencapaian yang baik, namun pada pelatihan periode lain seperti

harian atau mingguan kurang baik karena data pelatihan yang kurang banyak

2. Penelitian oleh Edy Suprianto ini mengimplementasikan algoritma

Backpropagation untuk memprediksi harga saham. Dalam penelitian ini

dilakukan beberapa prediksi dalam bentuk harian, dengan empat variabel input

yaitu nilai tertinggi, terendah, penutupan dan volume. Dari hasil penelitian

algoritma backpropagation bisa digunakan karena sifatnya yang adaptif karena

jaringan berusaha mencapai kestabilan kembali untuk mencapai output yang