BAB 1
PENDAHULUAN
1.1 Latar Belakang
Keamanan dan kerahasiaan saat mengirimkan data penting sangat dibutuhkan, baik
untuk kepentingan perusahaan, kelompok maupun individu. Berbagai algoritma
kriptografi dikembangkan untuk memenuhi permintaan tersebut. Salah Satunya ialah
Rivest Shamir Adleman (RSA) yang memanfaatkan kunci publik dan kunci privat.
Rivest Shamir Adleman (RSA) adalah salah satu teknik kriptografi modern
yang ditemukan pada tahun 1978 oleh Ron Rivest, Adi Shamir dan Leonard Adleman.
RSA merupakan algoritma kriptografi yang asimetris dimana RSA menggunakan
sepasang kunci, yaitu kunci publik biasanya disebut “e” dan “n” dan kunci privat
biasanya disebut “d”. Kunci publik dibentuk dengan mengalikan 2 buah bilangan
prima yang disebut “p” dan “q”. Algoritma ini dikategorikan sebagai algoritma
kriptografi yang aman, karena memiliki bit kunci yang panjang. Semakin panjang bit
kunci maka semakin sulit pula untuk dipecahkan.
Namun masalah timbul ketika kunci privat tersebut hilang. Penerima pesan
tidak bisa mendekripsi pesan yang diterima. Oleh sebab itu perlu dilakukan hacking
pada data tersebut. Hacking ialah proses menganalisa suatu sistem untuk mengetehui
cara kerja serta kelemahan pada sistem tersebut tetapi tidak memanfaatkan kelemahan
tersebut untuk hal kejahatan. Selanjutnya diperlukan metode untuk memfaktorkan
kunci publik menjadi kunci privat agar data penting tersebut dapat didekripsi untuk
kepentingan proses hacking.
Dalam hal ini, metode yang digunakan untuk memfaktorkan kunci publik
adalah metode Pollard ρ (baca: rho). Metode ini dipilih untuk menemukan faktor
prima dari bilangan bulat yang besar dengan hanya menggunakan jumlah lokasi
memori yang konstan (Sutomo, 2005). Metode Pollard ρ mengintegrasikan sebuah
fungsi polynomial di dalam modulo N (bilangan yang akan difaktorkan) dan sebuah
seed (bilangan pembangkit). Umumnya fungsi yang digunakan ialah f(x) = x2+1
dalam metode ini, sehingga membuka peluang untuk penelitian. Dengan metode ini,
akan ditemukan faktor prima “n” yaitu “p” dan “q”, sehingga perhitungan lebih lanjut
untuk mendapatkan kunci private “d” dapat dilakukan.
Penelitian sebelumnya dari Prasasti Imani yang berjudul Analisis Keamanan
Kriptosistem Kunci Publik RSA (Imani, 2002) menunjukkan bahwa kunci publik RSA
dapat difaktorisasi. Selain itu penelitian oleh B.R. Ambedkar dan S.S. Bedi dengan
judul A New Factorization Method to Factorize RSA Public Key Encryption
(Ambedkar & Bedi 2011) menunjukkan bahwa metode faktorisasi baru yang
didasarkan pada metode Pollard ρ dapat dikembangkan untuk mempercepat proses
faktorisasi kunci publik RSA.
Berdasarkan latar belakang di atas, maka penulis akan mencoba melakukan
penelitian dengan judul “Simulasi Pencarian Kunci Private dengan Metode
Modifikasi Pollard Rho pada Algoritma Kriptografi RSA” yang berfokus pada
algoritma kriptografi RSA kunci tunggal (unmodified) tanpa adanya modifikasi
apapun, sehingga dengan faktorisasi n dapat dihasilkan p dan q.
1.2 Perumusan Masalah
Berdasarkan latar belakang di atas, maka rumusan masalah pada penelitian ini adalah:
1. Bagaimana merancang sebuah program yang dapat menemukan kunci privat (d)
untuk keperluan dekripsi data dengan bermodalkan kunci publik (e, n) yang telah
di-publish oleh sistem kriptografi RSA biasa (unmodified) menggunakan metode
Pollard ρ.
2. Bagaimana efektifitas dan efisiensi metode Pollard ρ dalam memfaktorkan n
untuk mendapatkan p dan q ditinjau dari segi waktu dan panjang kunci.
1.3 Batasan Masalah
Batasan masalah dalam pengerjaan skripsi ini adalah sebagai berikut:
1. Pengujian bilangan prima menggunakan algoritma Miller-Rabin.
2. Perhitungan Greatest Common Divisor (GCD) menggunakan algoritma Euclid.
3. Sistem memfaktorkan kunci n menjadi p dan q dengan menggunakan metode
Pollard ρ. Kemudian kunci private dapat ditemukan menggunakan algoritma RSA
4. Ukuran maksimal kunci publik ialah 32 digit dimana pengujian dilakukan pada n
dimulai dari 4 digit sampai 32 digit dengan increment 4.
5. Modifikasi Pollard ρ dilakukan pada penentuan fungsi polynomial dengan seed
bernilai 2. Fungsi polynomial yang digunakan yaitu:
4.1. x2 + 1 (Fungsi standard Pollard ρ)
4.2. x2 + 12x + 11
4.3. x2 + 2x + 23
4.4. 3x2 + 4x + 1
4.5. x2 – x + 1
6. Dekripsi hanya dapat dilakukan pada data teks yang dienkripsi menggunakan
sistem kriptografi RSA biasa (unmodified) dengan format *txt, *doc, *docx dan
*rtf.
7. Bahasa pemrograman yang digunakan adalah C#.
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah sebagai berikut:
1. Membuat aplikasi untuk menemukan kunci privat dengan bermodalkan kunci
publik yang menerapkan metode Pollard ρ serta dekriptor data berupa teks,
dimana data tersebut dienkripsi menggunakan sistem kriptografi RSA biasa
(unmodified).
2. Mengetahui tingkat keamanan algoritma RSA ditinjau dari segi panjang kunci dan
waktu untuk memfaktorkan kunci publik menggunakan metode Pollard ρ.
3. Mengetahui peran fungsi polynomial pada metode Pollard ρ.
4. Mengetahui kelebihan dan kekurangan dari metode Pollard ρ.
1.5 Manfaat Penelitian
Manfaat dari penelitian ini yaitu:
1. Mempercepat proses faktorisasi metode Pollard ρ ditinjau dari segi waktu dan
tahap yang dibutuhkan dalam faktorisasi kunci publik RSA.
2. Mengetahui tingkat keamanan RSA ditinjau dari segi panjang kunci dalam
3. Penelitian ini diharapkan dapat bermanfaat bagi pengguna sistem kriptografi RSA
dalam menemukan kunci privat yang hilang dengan bermodalkan kunci publik
agar proses dekripsi dapat dilakukan.
1.6 Metode Penelitian
Tahapan yang dilakukan dalam penelitian ini adalah:
1. Studi Literatur
Penulisan tugas akhir ini diawali dengan terlebih dahulu melakukan pembelajaran
literatur pada sejumlah buku, artikel, paper, jurnal, makalah maupun situs internet
mengenai RSA dan metode Pollard ρ.
2. Analisa Data
Pada tahap ini akan dilaksanakan penganalisaan data yang diperlukan dalam
pembuatan tugas akhir ini.
3. Perancangan Sistem
Pada tahap ini akan dilaksanakan perancangan flowchart, antar muka dan
perancangan sistem dengan menggunakan metode Pollard ρ pada RSA.
4. Implementasi Sistem
Pada tahap ini akan dilaksanakan pengkodean (coding).
5. Pengujian Sistem
Dalam tahap ini dilakukan pengujian terhadap sistem berdasarkan hasil analisis
data dan perancangan sistem.
6. Dokumentasi
Dalam tahap ini dilakukan penyusunan laporan dari hasil analisis dan perancangan
1.7 Diagram Alir Sistem
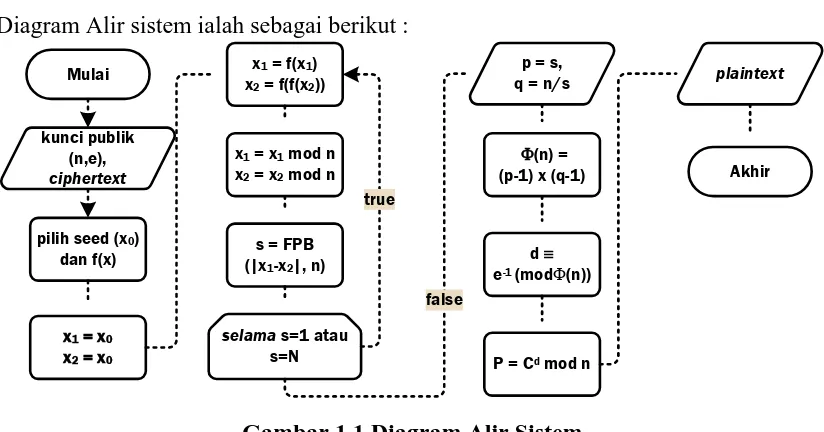
Diagram Alir sistem ialah sebagai berikut :
Mulai
Gambar 1.1 Diagram Alir Sistem
Dari Gambar 1.1 dapat dilihat proses dari pemecahan kunci menggunakan metode
Pollard ρ pada sistem yang akan dibangun. Input kunci publik (n,e) dan ciphertext.
Pilih seed (x0) dan fungsi polinomial. Jika s = 1 atau s = N, maka hitung x1 = f(x1) dan
x2 = f(f(x2)). Lalu hitung x1 = x1 mod N dan x2 = x2 mod N. Lalu kemudian lakukan
perhitungan FPB untuk mencari faktor yaitu s = (|x1- x2|, n). Jika s ≠ 1 dan s ≠ N,
maka kedua faktor N ialah p = s dan q = N/s. Hitung Φ (n) = (p - 1) · (q - 1). Lakukan
perhitungan kunci privat dengan rumus d ≡ e -1 (mod Φ (n)). Kemudian dekripsi
ciphertext yang telah diinput dengan rumus P = C d mod n. Maka akan didapat nilai
plaintext dari ciphertext yang telah di-input.
1.8 Sistematika Penulisan
Sistematika penulisan dari skripsi ini terdiri dari beberapa bagian utama
sebagai berikut:
BAB 1: PENDAHULUAN
Bab ini akan menjelaskan mengenai latar belakang pemilihan judul skripsi
“Simulasi Pencarian Kunci Private dengan Metode Modifikasi Pollard Rho
pada Algoritma Kriptografi RSA”, rumusan masalah, batasan masalah, tujuan
penelitian, manfaat penelitian, metode penelitian, flowchart penelitian dan
sistematika penulisan.
BAB 2: TINJAUAN PUSTAKA
Bab ini berisi dasar teori-teori yang digunakan dalam analisis, perancangan
dan implementasi skripsi.
BAB 3: ANALISIS DAN PERANCANGAN SISTEM
Bab ini berisi analisis terhadap fokus permasalahan penelitian dan
perancangan terhadap pencarian kunci private pada algoritma kriptografi RSA
dengan menggunakan metode modifikasi Pollard ρ.
BAB 4: IMPLEMENTASI DAN PENGUJIAN SISTEM
Bab ini berisi teknik implementasi dari perancangan yang telah dibuat dan
pengujian terhadap implementasi. Pengujian dilakukan untuk membuktikan
perangkan lunak dapat berjalan sesuai dengan spesifikasi yang telah ditentukan
di tahapan analisis.
BAB 5: KESIMPULAN DAN SARAN
Bab ini akan memuat kesimpulan isi dari keseluruhan uraian bab-bab
sebelumnya dan saran-saran dari hasil yang diperoleh yang diharapkan dapat