Pemodelan masalah ekologi dengan persamaan Lotka-Volterra termodifikasi dan penyelesaian numerisnya menggunakan metode Beda Hingga Eksak

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PEMODELAN MASALAH EKOLOGI DENGAN PERSAMAAN LOTKAVOLTERRA TERMODIFIKASI DAN PENYELESAIAN NUMERISNYA MENGGUNAKAN METODE BEDA HINGGA EKSAK Skripsi. Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika. Oleh: Especially Angelina Kono NIM: 153114027. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA YOGYAKARTA 2019 i.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. MODELING OF ECOLOGY PROBLEMS WITH MODIFIED LOTKAVOLTERRA EQUATIONS AND THEIR NUMERICAL SOLUTIONS USING EXACT FINITE DIFFERENCE METHODS. Thesis. Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains in Mathematics. By: Especially Angelina Kono NIM: 153114027. MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY SANATA DHARMA UNIVERSITY YOGYAKARTA 2019 ii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. HALAMAN PERSEMBAHAN. “You can’t go back and change the beginning, but you can start where you are and change the ending”. -C. S. Lewis“Nothing is permanent so you should love what you got”. -Thiru Kumar-. Skripsi ini saya persembahkan untuk Tuhan Yang Maha Esa yang selalu memberkati saya, kedua orang tua tercinta dan kakak saya terkasih, dan juga untuk semua orang yang selalu mendoakan saya.. vii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRAK. Skripsi ini membahas tentang penyelesaian suatu masalah ekologi khususnya masalah kompetisi antara dua populasi yang dimodelkan secara matematis ke dalam bentuk persamaan diferensial yaitu, persamaan diferensial Lotka-Volterra termodifikasi. Persamaan diferensial Lotka-Volterra termodifikasi merupakan suatu sistem persamaan diferensial biasa nonlinear orde satu. Metode numerik yang digunakan dalam skripsi ini adalah metode beda hingga eksak yang merupakan salah satu metode beda hingga tak standar. Penyelesaian yang dihasilkan oleh metode beda hingga eksak ini akan disimulasikan dan dibandingkan dengan dua metode lain, yaitu metode Euler dan metode Heun. Setelah dilakukan simulasi diperoleh bahwa metode beda hingga eksak memiliki hasil yang lebih akurat dan yang paling mendekati penyelesaian eksaknya. Hasil simulasi tersebut menunjukkan bahwa seiring dengan membesarnya waktu (t) laju pertumbuhan dari kedua populasi semakin menurun.. Kata Kunci: Persamaan diferensial, persamaan diferensial Lotka-Volterra termodifikasi, metode beda hingga eksak, metode beda hingga nonstandar.. viii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRACT. This thesis discusses the solution of an ecological problem especially the problem of competition between two populations which are mathematically modeled into the form of differential equations, namely, modified Lotka-Volterra differential equations. The modified Lotka-Volterra differential equations are a system of first-order nonlinear ordinary differential equations. The numerical method used in this paper is the exact finite difference method which is one of nonstandard finite difference methods. The solutions produced by this exact finite difference method will be simulated and compared with two other methods, namely, the Euler’s method and the Heun’s method. After the simulation is obtained, the exact finite difference method has more accurate results and the closest to the exact solution. The results of this simulation show that as time (t) increases the growth rate of the two populations decreases.. Keywords: Differential equations, modified Lotka-Volterra differential equations, exact finite difference methods, nonstandard finite difference methods.. ix.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. KATA PENGANTAR Puji dan Syukur saya ucapkan kepada Tuhan Yesus karena dengan kuasa dan rahmat-Nyalah saya dapat menyelesaikan skripsi ini dengan tepat waktu. Skripsi ini dibuat dengan tujuan memenuhi syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma. Penulis menyadari bahwa penulis melibatkan banyak pihak yang bersedia membantu dalam menghadapi berbagai macam kesulitan, tantangan dan hambatan. Oleh karena itu pada kesempatan ini penulis mengucapkan terima kasih kepada: 1.. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku Dekan Fakultas Sains dan Teknologi dan selaku Dosen Pembimbing Akademik dan juga dosen pembimbing skripsi.. 2.. Bapak Hartono, S.Si., M.Sc., Ph.D., selaku Kaprodi Matematika.. 3.. Romo Prof. Dr. Frans Susilo, SJ., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc, Bapak Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si. dan Ibu M. V. Any Herawati, S.Si., M.Si., selaku dosen-dosen Prodi Matematika yang telah membimbing dan memberikan banyak pengetahuan kepada penulis selama proses perkuliahan.. 4.. Bapak/Ibu dosen/karyawan Fakultas Sains dan Teknologi yang telah berdinamika bersama selama penulis berkuliah.. 5.. Kedua orang tua tercinta, Bapak Alex dan Mama Erna dan juga Kakak Dodi yang selalu memberi semangat dan dukungan kepada penulis selama proses perkuliahan dan pengerjaan skripsi.. 6.. Teman-teman Prodi Matematika Angkatan 2015: Rani, Fithri, Edhi, Rio, Yion, Yofi, Ayu, Sasmi, Laura, Florens, Devi, Lya, Sapi, Ana dan Priska. Khususnya Putri, Brigit, Vania dan Arel yang selalu membantu, memberi masukan dan memberi semangat kepada penulis dalam proses pengerjaan skripsi dan berjuang bersama selama kuliah empat tahun. Terima kasih telah membagikan begitu banyak ilmu dan cerita yang kalian miliki. x.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR ISI HALAMAN JUDUL .................................................................................................... i HALAMAN PERSETUJUAN DOSEN PEMBIMBING ........................................ iii HALAMAN PENGESAHAN ....................................................................................iv PERNYATAAN KEASLIAN KARYA ..................................................................... v PERNYATAAN PERSETUJUAN ............................................................................vi HALAMAN PERSEMBAHAN ................................................................................vii ABSTRAK ................................................................................................................ viii ABSTRACT ................................................................................................................ix KATA PENGANTAR .................................................................................................x DAFTAR ISI ..............................................................................................................xii DAFTAR GAMBAR ................................................................................................. xv DAFTAR TABEL ....................................................................................................xvii BAB I PENDAHULUAN ........................................................................................... 1 A. Latar belakang ..................................................................................... 1 B. Rumusan Masalah ................................................................................ 3 C. Batasan Masalah .................................................................................. 3 D. Tujuan Penulisan ................................................................................. 3 E. Manfaat Penulisan................................................................................ 3 F. Metode Penulisan................................................................................. 3 G. Sistematika Penulisan .......................................................................... 3 BAB II PERSAMAAN DIFERENSIAL DAN TURUNAN NUMERIK ............... 5 A. Turunan ............................................................................................... 5 B. Persamaan Diferensial .......................................................................... 7 1.. Definisi Persamaan Diferensial ....................................................... 7. 2.. Klasifikasi Persamaan Diferensial ................................................... 7. C. Fungsi Bebas Linear dan Bergantung Linear ...................................... 10 xii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. E. Determinan Matriks ........................................................................... 12 1.. Determinan Matriks 2 × 2 ............................................................ 12. 2.. Determinan Matriks n × n ............................................................ 13. F. Nilai Eigen ......................................................................................... 14 G. Turunan Numerik ............................................................................... 15 1.. Pendekatan Turunan Orde Satu Menggunakan Beda Maju ............ 16. 2.. Pendekatan Turunan Orde Satu Menggunakan Beda Mundur ........ 17. 3.. Pendekatan Turunan Orde Satu Menggunakan Beda Tengah......... 18. H. Metode Euler ..................................................................................... 19 I.. Metode Heun ..................................................................................... 20. J.. Metode Biseksi .................................................................................. 22. BAB III SISTEM PERSAMAAN DIFERENSIAL LOTKA-VOLTERRA TERMODIFIKASI DAN METODE BEDA HINGGA EKSAK ............................ 24 A. Sistem Persamaan Lotka-Volterra Termodifikasi ............................... 24 1.. Persamaan Diferensial Lotka-Volterra .......................................... 24. 2.. Persamaan Diferensial Lotka-Volterra Termodifikasi.................... 26. B. Metode Beda Hingga Eksak ............................................................... 27 1.. Skema Beda Hingga Eksak ........................................................... 28. 2.. Contoh Skema Beda Hingga Eksak ............................................... 30. 3.. Aturan Pemodelan Beda Hingga Nonstandar................................. 39. 4.. Perbandingan Penyelesaian ........................................................... 40. BAB IV PENYELESAIAN NUMERIS SISTEM PERSAMAAN DIFERENSIAL LOTKA-VOLTERRA TERMODIFKASI ............................................................... 50 A. Penyelesaian Numeris Sistem Persamaan Diferensial Lotka-Volterra Termodifikasi dengan Metode Beda Hingga Eksak ............................ 50 B. Simulasi Numeris ............................................................................... 58 C. Pembahasan Hasil Simulasi................................................................ 68 BAB V PENUTUP .................................................................................................... 69 A. Kesimpulan ........................................................................................ 69 B. Saran.................................................................................................. 70 xiii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR PUSTAKA ................................................................................................ 71 LAMPIRAN PROGRAM .......................................................................................... 73 1.. Program Bab III ................................................................................. 73. 2.. Program Bab IV ................................................................................. 76. xiv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR GAMBAR. Gambar 2.1.1 Grafik ilustrasi pendekatan turunan orde satu dengan beda maju. .................................................................... 17 Gambar 2.1.2 Grafik ilustrasi pendekatan turunan orde satu dengan beda mundur. ................................................................................... 18 Gambar 2.1.3 Grafik ilustrasi pendekatan turunan orde satu dengan beda tengah. .................................................................. 19 Gambar 3.4.1 Grafik simulasi numeris persamaan (3.56) dengan menggunakan metode Euler, metode Heun dan metode beda hingga eksak dengan 𝑦(0) = 1 dan 𝛥𝑡 = 0.1. ................................................ 40 Gambar 3.4.2 Grafik simulasi numeris persamaan (3.56) dengan batas minimum dan maksimum sumbu-y dan sumbu-x adalah 0.585, 0.615 dan 0.468, 0.502. ............................................................................ 41 Gambar 3.4.3 Grafik simulasi numeris persamaan (3.57) dengan menggunakan metode beda hingga standar dan metode beda hingga eksak dengan 𝑦(0) = 1, 𝑦 ′ (0) = 1, dan 𝛥𝑡 = 0.1. ............................. 43 Gambar 3.4.4 Grafik simulasi numeris persamaan (3.57) dengan batas minimum dan maksimum sumbu-y dan sumbu-x adalah 1.39, 1.415 dan 0.59, 0.95.................................................................................. 44 Gambar 3.4.5 Grafik simulasi numeris persamaan (3.58) dengan menggunakan metode Euler, metode Heun dan metode beda hingga eksak dengan 𝑦(0) = 1, 𝛥𝑡 = 0.1 dan 𝜆1 = 1 dan 𝜆2 = 2. ................. 47 Gambar 3.4.6 Grafik simulasi numeris persamaan (3.58) dengan batas minimum dan maksimum sumbu-y dan sumbu-x adalah 0.68, 0.76 dan 0.35, 0.65.................................................................................. 48 Gambar 4.1.1 Grafik penyelesaian metode beda hingga eksak untuk persamaan (4.1) dengan 𝛥𝑡 = 0.1. .............................................................. 60 Gambar 4.1.2 Grafik penyelesaian metode beda hingga eksak untuk persamaan (4.1) dengan 𝛥𝑡 = 0.01. ............................................................ 61 Gambar 4.1.3 Grafik penyelesaian metode beda hingga eksak untuk persamaan (4.1) dengan 𝑡 = 0 sampai 𝑡 = 10, dan 𝛥𝑡 = 0.01. .................. 62 Gambar 4.1.4 Grafik penyelesaian persamaan (4.1) dengan menggunakan metode Euler dengan 𝛥𝑡 = 0.1. ............................................................. 63 xv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. Gambar 4.1.5 Grafik penyelesaian metode Euler untuk persamaan (4.1) dengan 𝑡 = 0 sampai 𝑡 = 10 dan 𝛥𝑡 = 0.01. ....................................... 64 Gambar 4.1.6 Grafik penyelesaian persamaan (4.1) dengan menggunakan metode Heun dengan 𝛥𝑡 = 0.1 .............................................................. 66 Gambar 4.1.7 Grafik penyelesaian metode Heun untuk persamaan (4.1) dengan 𝑡 = 0 sampai 𝑡 = 10 dan 𝛥𝑡 = 0.01. ....................................... 67. xvi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR TABEL. Tabel 3.4.1 Error hasil perhitungan dari persamaan (3.56) ................................. 43 Tabel 3.4.2 Error hasil perhitungan dari persamaan (3.57) ................................. 46 Tabel 3.4.3 Error hasil perhitungan dari persamaan (3.58) ................................. 49 Tabel 4.1.1 Hasil perhitungan dari persamaan (4.48) dengan ∆𝑡 = 0.1 .............. 60 Tabel 4.1.2 Hasil perhitungan dari persamaan (4.53) dengan ∆𝑡 = 0.1 .............. 64 Tabel 4.1.3. Hasil perhitungan dari persamaan (4.54) dengan ∆𝑡 = 0.1 ............. 67. xvii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB I PENDAHULUAN Pada bab ini akan dibahas latar belakang, rumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan juga sistematika penulisan. A. Latar belakang Matematika merupakan salah satu ilmu pengetahuan yang banyak diterapkan dalam kehidupan sehari-hari dan juga diterapkan dalam berbagai bidang ilmu pengetahuan, salah satunya adalah dalam bidang biologi. Contoh penerapan matematika dalam bidang biologi adalah pada masalah ekologi. Ekologi merupakan cabang ilmu biologi yang mempelajari tentang populasi dan komunitas yang terdiri atas manusia, hewan, dan tumbuhan serta interaksinya satu sama lain dan juga interaksinya dengan lingkungan sekitar. Masalah ekologi sudah dimodelkan ke dalam bentuk matematis, contohnya adalah model mangsa-pemangsa dan model Lotka-Volterra. Kedua model ini sering digunakan untuk menyelesaikan masalah-masalah nyata seperti hubungan dinamis antara zebra dan kelinci, kompetisi di pasar, total permintaan produk di pasar (Gorvett, 2014), dan masalah-masalah nyata lainnya. Model mangsa-pemangsa dan model Lotka-Volterra ini berupa persamaan diferensial. Persamaan diferensial adalah persamaan yang menyatakan hubungan antara suatu fungsi dengan turunan-turunannya. Persamaan diferensial ini dapat dibedakan menjadi dua berdasarkan banyak variabel bebasnya, yaitu persamaan diferensial biasa, dan persamaan diferensial parsial. Dalam skripsi ini akan dibahas persamaan diferensial biasa yang merupakan model dari masalah kompetisi. Persamaan diferensial biasa adalah persamaan diferensial yang hanya memuat satu variabel bebas. Salah satu persamaan diferensial yang menyatakan model mangsa-pemangsa, kompetisi, dan mutualisme adalah persamaan diferensial LotkaVolterra (Mickens, 2018). Skripsi ini akan membahas persamaan diferensial LotkaVolterra yang termodifikasi dan penyelesaian numerisnya.. 1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 2. Persamaan diferensial Lotka-Volterra terdiri atas sepasang persamaan diferensial nonlinear orde satu, yang sering digunakan untuk menggambarkan dua populasi yang berinteraksi. Persamaan diferensial Lotka-Volterra termodifikasi juga terdiri atas sepasang persamaan diferensial nonlinear orde satu. Bentuk dari persamaan diferensial Lotka-Volterra adalah 𝑑𝑥 = 𝑟1 𝑥 − 𝑎11 𝑥 2 − 𝑎12 𝑥𝑦, 𝑑𝑡 𝑑𝑦 = 𝑟2 𝑦 − 𝑎21 𝑥𝑦 − 𝑎22 𝑦 2 , 𝑑𝑡 dan bentuk dari persamaan diferensial Lotka-Volterra termodifikasi yang akan dibahas dalam skripsi ini adalah 𝑑𝑥 = 𝑟1 √𝑥 − 𝑎11 𝑥 − 𝑎12 √𝑥 √𝑦 , 𝑑𝑡 𝑑𝑦 = 𝑟2 √𝑦 − 𝑎21 √𝑥 √𝑦 − 𝑎22 𝑦, 𝑑𝑡 dimana 𝑟1 , 𝑟2 , 𝑎11 , 𝑎22 , 𝑎12 , 𝑎21 adalah parameter konstan, dan x(t) dan y(t) adalah variabel terikat (Mickens, 2018). Tidak semua persamaan diferensial mudah diselesaikan secara analitis. Banyak persamaan diferensial yang sulit untuk diselesaikan secara analitis, salah satu contohnya adalah model dari persamaan diferensial Lotka-Volterra termodifikasi yang merupakan persamaan diferensial nonlinear. Meskipun demikian, persamaan diferensial Lotka-Volterra termodifikasi dapat diselesaikan dengan metode numeris. Ada beberapa metode numeris yang dapat digunakan. untuk. menyelesaiakan. persamaan. diferensial. Lotka-Volterra. termodifikasi misalnya metode Euler, Heun, beda hingga, beda hingga eksak, dan metode-metode lainnya. Skripsi ini akan menggunakan metode beda hingga eksak untuk menyelesaikan persamaan diferensial Lotka-Volterra termodifikasi. Metode beda hingga eksak ini akan menghasilkan suatu skema numerik dengan menggunakan beda hingga maju..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 3. B. Rumusan Masalah Rumusan masalah dalam skripsi adalah: 1. Bagaimana mengkonstruksi metode beda hingga eksak untuk suatu persamaan diferensial? 2. Bagaimana menyelesaikan sistem persamaan diferensial Lotka-Volterra termodifikasi secara numeris menggunakan metode beda hingga eksak? C. Batasan Masalah Dalam skripsi ini akan dibahas mengenai bagaimana mengkonstruksi model diskret menggunakan metode beda hingga eksak dari suatu masalah ekologi, yaitu interaksi yang terjadi antara rusa dan zebra yang dimodelkan secara matematis ke dalam bentuk persamaan diferensial Lotka-Volterra termodifikasi. D. Tujuan Penulisan Tujuan penulisan skripsi adalah: 1. Memaparkan model diskret yang dikonstruksi menggunakan metode beda hingga eksak. 2. Mencari penyelesaian numeris persamaan diferensial Lotka-Voltera termodifikasi dengan metode beda hingga eksak.. E. Manfaat Penulisan Manfaat. yang. diperoleh dari skripsi. ini. adalah. mengetahui cara. mengkonstruksi model diskret dari suatu persamaan diferensial khususnya persamaan diferensial Lotka-Volterra termodifikasi dengan menggunakan metode beda hingga eksak.. F. Metode Penulisan Skripsi ini ditulis berdasarkan kajian pustaka, seperti jurnal-jurnal matematika dan buku-buku matematika, serta praktik pemrograman MATLAB.. G. Sistematika Penulisan Skripsi ini disusun dengan sistematika sebagai berikut: BAB I PENDAHULUAN.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 4. A.. Latar Belakang. B.. Rumusan Masalah. C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F.. Metode Penelitian. G. Sistematika Penulisan BAB II PERSAMAAN DIFERENSIAL DAN TURUNAN NUMERIK A. Turunan B. Persamaan Diferensial C. Fungsi Bebas Linear dan Bergantung Linear D. Wronskian E. Determinan Matriks F.. Nilai Eigen. G. Turunan Numerik H.. Metode Euler. I.. Metode Heun. J.. Metode Biseksi. BAB III SISTEM PERSAMAAN DIFERENSIAL LOTKA-VOLTERRA TERMODIFIKASI DAN METODE BEDA HINGGA EKSAK A. Sistem Persamaan Lotka-Volterra Termodifikasi B. Metode Beda Hingga Eksak BAB. IV. PENYELESAIAN. NUMERIS. SISTEM. PERSAMAAN. DIFERENSIAL LOTKA-VOLTERRA TERMODIFIKASI A. Penyelesaian Numeris Sistem Persamaan Diferensial Lotka-Volterra Termodifikasi dengan Metode Beda Hingga Eksak B. Pembahasan Hasil Simulasi BAB V PENUTUP A. Kesimpulan B. Saran DAFTAR PUSTAKA.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB II PERSAMAAN DIFERENSIAL DAN TURUNAN NUMERIK. Pada bab ini akan dibahas landasan teori yang digunakan dalam penulisan skripsi ini. Landasan teori tersebut meliputi: turunan, persamaan diferensial, fungsi bebas linear dan bergantung linear, Wronskian, determinan matriks, nilai eigen, turunan numerik, metode Euler dan metode Heun.. A. Turunan Pada subbab ini akan dibahas mengenai definisi turunan dan aturan rantai.. Definisi 2.1.1 Misalkan suatu fungsi 𝑓 terdefinisi pada interval terbuka yang memuat titik 𝑎, maka turunan fungsi 𝑓 di titik 𝑎 yang dinotasikan 𝑓 ′ (𝑎) adalah 𝑓 ′ (𝑎) = lim. 𝑓(𝑎+ℎ)−𝑓(𝑎). (2.1). ℎ. ℎ→0. dengan ketentuan limit tersebut ada.. Contoh 1. Tentukan turunan di titik 𝑥 = 3 dengan fungsi 𝑓(𝑥 ) = 𝑥 + 2. Penyelesaian: 𝑓(3 + ℎ) − 𝑓(𝑎) ℎ→0 ℎ. 𝑓′(3) = lim. = lim. ℎ→0. 1 7 (3 + ℎ + 2) − 3 ℎ. 3 − (3 + ℎ) 3(3 + ℎ) = lim ℎ→0 ℎ −ℎ ℎ→0 3ℎ(3 + ℎ). = lim. 5.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 6. −1 ℎ→0 3(3 + ℎ). = lim. =−. 1 9 1. 1. Jadi, nilai turunan fungsi 𝑓(𝑥) = 𝑥 + 2 di titik 𝑥 = 3 adalah − 9. Aturan Rantai Misalkan 𝑦 = 𝑓(𝑢), 𝑢 = 𝑔(𝑥), dan turunan 𝑓 ′ (𝑢) dan 𝑔′ (𝑥 ) ada, maka fungsi komposisi yang didefinisikan dengan 𝑦 = 𝑓(𝑔(𝑥 )) mempunyai turunan yang diberikan dengan 𝑦 ′ (𝑥 ) = 𝑓 ′ (𝑢)𝑔′ (𝑥 ), atau 𝑑𝑦 𝑑𝑦 𝑑𝑢 = . 𝑑𝑥 𝑑𝑢 𝑑𝑥 Pembuktian aturan rantai dapat dibaca pada (Swokowski, 1980:115).. Contoh Jika 𝑦 = 𝑢2 dan 𝑢 = 𝑥 + 1, maka cari 𝑦 ′ (𝑥). Penyelesaian: Diketahui 𝑦 = 𝑢2 dan 𝑢 = 𝑥 + 1, 𝑦 ′ (𝑢) = 2𝑢, 𝑢′ (𝑥 ) = 1. Sehingga menurut aturan rantai di atas 𝑑𝑦 𝑑𝑦 𝑑𝑢 = 𝑑𝑥 𝑑𝑢 𝑑𝑥 = (2𝑢)( 1) = 2𝑢 = 2(𝑥 + 1) Jadi, 𝑦 ′ (𝑥 ) = 2(𝑥 + 1)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 7. B. Persamaan Diferensial Pada subbab ini akan dibahas definisi dari persamaan diferensial dan klasifikasi persamaan diferensial.. 1. Definisi Persamaan Diferensial Pada bagian ini akan dibahas terlebih dahulu definisi dari persamaan diferensial dan contohnya.. Definisi 2.1.2 Persamaan diferensial adalah persamaan yang menyatakan hubungan antara suatu fungsi dengan turunan-turunannya. Contoh persamaan diferensial 𝑑𝑦 − 18𝑥 = 6 𝑑𝑥. (2.2). 𝑑 3 𝑦 𝑑𝑦 + − 3𝑦 = 0 𝑑𝑡 3 𝑑𝑡. (2.3). 𝜕 2 𝑢 𝜕𝑢 − =0 𝜕𝑥 2 𝜕𝑡. (2.4). 𝜕 2 𝑢 𝜕 2 𝑢 𝜕𝑢 + = 𝜕𝑥 2 𝜕𝑦 2 𝜕𝑡. (2.5). 2. Klasifikasi Persamaan Diferensial Persamaan diferensial dapat diklasifikasikan berdasarkan banyaknya variabel bebas dan orde persamaan diferensial.. Definisi 2.1.3 Persamaan diferensial biasa adalah persamaan diferensial yang memuat turunan biasa dan hanya memuat satu variabel bebas..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 8. Contoh Persamaan (2.2) adalah persamaan diferensial biasa dengan variabel bebasnya adalah 𝑥 dan variabel terikatnya adalah 𝑦. Persamaan (2.3) juga merupakan persamaan diferensial biasa.. Definisi 2.1.4 Persamaan diferensial parsial adalah persamaan diferensial parsial yang memuat turunan parsial dan terdapat lebih dari satu variabel bebas.. Contoh Persamaan (2.4) adalah persamaan diferensial parsial dengan 𝑢 adalah variabel terikat, sedangkan 𝑥 dan 𝑡 adalah variabel bebas. Persamaan (2.5) juga merupakan persamaan diferensial parsial.. Definisi 2.1.5 Klasifikasi persamaan diferensial berdasarkan orde: Orde dari suatu persamaan diferensial adalah orde turunan tertinggi yang terdapat pada persamaan diferensial. Berdasarkan Roger (1982:76) suatu persamaan diferensial orde ke-𝑛 dapat ditulis ke dalam bentuk 𝑑𝑛 𝑦 𝑑𝑦 𝑑 𝑛−1 𝑦 = 𝑓 (𝑥, 𝑦, , … , ). 𝑑𝑥 𝑛 𝑑𝑥 𝑑𝑥 𝑛−1. (2.6). Contoh Persamaan (2.2) adalah persamaan diferensial biasa orde satu karena turunan tertinggi yang terdapat pada persamaan di atas adalah turunan pertama. Persamaan (2.3) adalah persamaan diferensial biasa (PDB) orde tiga, persamaan (2.4) dan (2.5) adalah persamaan diferensial parsial (PDP) orde dua.. Persamaan diferensial biasa juga dapat diklasifikasikan lagi berdasarkan linearitasnya..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 9. Definisi 2.1.6 Persamaan diferensial biasa orde 𝑛, dengan variabel bebas 𝑥 dan variable terikat 𝑦 dikatakan linear jika dapat ditulis ke dalam bentuk 𝑑𝑛 𝑦 𝑑 𝑛−1 𝑦 𝑑𝑦 𝑎0 (𝑥 ) 𝑛 + 𝑎1 (𝑥 ) 𝑛−1 + ⋯ + 𝑎𝑛−1 (𝑥 ) + 𝑎𝑛 (𝑥)𝑦 = 𝑟(𝑥 ), 𝑑𝑥 𝑑𝑥 𝑑𝑥. (2.7). dengan 𝑎0 tidak sama dengan 0.. Contoh Persamaan (2.2) dan (2.3) adalah persamaan diferensial biasa linear. Dapat diamati bahwa pada kedua persamaan tersebut variabel terikat dan turunan-turunannya berpangkat satu, tidak ada perkalian antara variabel terikat dengan turunanturunannya, serta tidak ada bentuk nonlinear dari variable terikat maupun bentuk nonlinear dari turunan-turunannya.. Definisi 2.1.7 Suatu persamaan diferensial biasa dikatakan nonlinear jika persamaan diferensial tersebut tidak linear.. Contoh Berikut ini adalah persamaan diferensial biasa yang nonlinear: 3. 𝑑𝑦 − 18𝑦 2 = 0 𝑑𝑥. (2.8). 𝑑3𝑦 𝑑𝑦 2 + ( ) − 3𝑦 = 0 𝑑𝑡 3 𝑑𝑡. (2.9). 𝑑3𝑦 𝑑 2 𝑦 𝑑𝑦 + ( 2 ) ( ) − 3𝑦 = 0 𝑑𝑡 3 𝑑𝑡 𝑑𝑡. (2.10).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 10. Persamaan (2.8) adalah persamaan nonlinear karena variable terikat 𝑦 yang terdapat dalam persamaan tersebut berpangkat dua dengan bentuk 18𝑦 2. Persamaan (2.9) 𝑑𝑦 2. adalah persamaan nonlinear karena terdapat bentuk ( 𝑑𝑡 ) , yang mana memuat pangkat dua dari turunan pertamanya. Persamaan (2.10) juga nonlinear karena 𝑑2 𝑦. 𝑑𝑦. bentuk ( 𝑑𝑡 2 ) ( 𝑑𝑡 ), yang mana memuat perkalian antara turunan kedua dan turunan pertama.. C. Fungsi Bebas Linear dan Bergantung Linear Pada subbab ini akan dibahas definisi dari fungsi yang bebas linear dan bergantung linear.. Definisi 2.1.8 Fungsi 𝑦1 (𝑡), 𝑦2 (𝑡), … , 𝑦𝑛 (𝑡) dikatakan bergantung linear pada interval I, jika ada konstanta 𝑐1 , 𝑐2 , … , 𝑐𝑛 yang tidak semuanya nol atau dengan kata lain ada 𝑐𝑖 ≠ 0 untuk suatu atau beberapa 𝑖 dengan 𝑖 = 1,2, … , 𝑛, sehingga menyebabkan 𝑐1 𝑦1 (𝑡) + 𝑐2 𝑦2 (𝑡) + ⋯ + 𝑐𝑛 𝑦𝑛 (𝑡) = 0. (2.11). untuk semua t pada interval I.. Definisi 2.1.9 Fungsi 𝑦1 (𝑡), 𝑦2 (𝑡), … , 𝑦𝑛 (𝑡) dikatakan bebas linear pada interval 𝐼, jika 𝑐1 𝑦1 (𝑡) + 𝑐2 𝑦2 (𝑡) + ⋯ + 𝑐𝑛 𝑦𝑛 (𝑡) = 0. (2.12). untuk semua 𝑡 pada interval 𝐼 yang berakibat 𝑐1 = 𝑐2 = ⋯ 𝑐𝑛 = 0. D. Wronskian Pada subbab ini akan dibahas definisi dari Wronskian dan teorema yang berhubungan dengan Wronskian. Definisi 2.1.10 Misalkan 𝑓1 , … , 𝑓𝑛 merupakan fungsi-fungsi yang terdiferensial 𝑛 − 1 kali. Fungsi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 11. 𝑓1 (𝑥) 𝑓 ′ (𝑥) 𝑊 [𝑓1 , … , 𝑓𝑛 ](𝑥) ≔ | 1 ⋮ (𝑛−1) 𝑓1 (𝑥). 𝑓2 (𝑥) 𝑓2′ (𝑥) ⋮ (𝑛−1) 𝑓2 (𝑥). ⋯ ⋯ ⋯ ⋯. 𝑓𝑛 (𝑥) 𝑓𝑛′ (𝑥) | ⋮ (𝑛−1) 𝑓𝑛 (𝑥). (2.13). disebut Wronskian dari 𝑓1 , … , 𝑓𝑛 . Contoh Misalkan diketahui 𝑓1 = sin(𝑥 ) , 𝑓2 = cos(𝑥) dan 𝑓3 = −sin(𝑥) yang terdiferensial dua kali. Tentukan Wronskian dari 𝑓1 , 𝑓2 , 𝑓3 . Penyelesaian: Diketahui 𝑓1 = sin(𝑥 ) , 𝑓2 = cos(𝑥) dan 𝑓3 = −sin(𝑥), sehingga menurut definisi 2.3.5 Wronskian dari 𝑓1 , 𝑓2 , 𝑓3 adalah sin(𝑥) 𝑊 [ 𝑓1 , 𝑓2 , 𝑓3 ] = | cos(𝑥) −sin(𝑥). cos(𝑥) −sin(𝑥) −cos(𝑥). −sin(𝑥) −cos(𝑥)| sin(𝑥). (2.14). Teorema 2.1.11 Misalkan {𝑓1 , … , 𝑓𝑛 } menjadi suatu himpunan fungsi-fungsi yang terdiferensial 𝑛 − 1 kali. Himpunan fungsi-fungsi {𝑓1 , … , 𝑓𝑛 } tersebut adalah bebas linear jika dan hanya jika 𝑊 [𝑓1 , … , 𝑓𝑛 ](𝑥) ≠ 0. Jika himpunan fungsi-fungsi tersebut tidak bebas linear, maka himpunan fungsi-fungsi tersebut dikatakan bergantung linear. Contoh Tentukan apakah kedua himpunan berikut ini bebas linear atau bergantung linear dengan menggunakan Wronskian. a). {𝑒 −𝑡 , 𝑒 −2𝑡 }. b.) {𝑥 + 2, 𝑥 − 3, 𝑥 + 1}. Penyelesaian:. a.) Wronskian adalah sebagai berikut: 𝑊 (𝑡 ). −𝑡. = | 𝑒 −𝑡 −𝑒. 𝑒 −2𝑡 | −2𝑒 −2𝑡.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 12. = 𝑒 −𝑡 (−2𝑒 −2𝑡 ) − 𝑒 −2𝑡 (−𝑒 −𝑡 ) = −2𝑒 −3𝑡 + 𝑒 −3𝑡 = −𝑒 −3𝑡 Hasil dari Wronskiannya adalah −𝑒 −3𝑡 , sehingga menurut Teorema 2.1.11 himpunan fungsi pada nomor a) adalah bebas linear. b.) Wronskiannya adalah sebagai berikut: 𝑊 (𝑡 ). 𝑥+2 =| 2 0. 𝑥−3 −3 0. 𝑥+1 1 | 0. = (𝑥 + 2)(−3)(0) + (𝑥 − 3)(1)(0) + (𝑥 + 1)(2)(0) − (𝑥 − 3)(2)(0) − (𝑥 + 2)(1)(0) − (𝑥 + 1)(−3)(0) =0 Hasil dari Wronskiannya adalah 0, sehingga menurut Teorema 2.1.11 himpunan fungsi pada nomor b adalah bergantung linear.. E. Determinan Matriks Pada subbab ini akan dibahas definisi determinan dan cara mencari determinan 2 × 2 dan 𝑛 × 𝑛. 1. Determinan Matriks 𝟐 × 𝟐 Diketahui matriks berukuran 2 × 2 𝑎 𝐴=[ 𝑐. 𝑏 ], 𝑑. nilai 𝑎𝑑 − 𝑏𝑐 disebut determinan matriks 𝐴 dan ditulis sebagai berikut 𝑎 det(A) = det [ 𝑐 (Budhi, 1995:77).. 𝑏] = 𝑎𝑑 − 𝑏𝑐, 𝑑.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 13. Contoh Diketahui suatu matriks 2 × 2 yaitu 𝐴=[. 2 4 ]. 5 2. Tentukanlah determinan dari matriks 𝐴. Penyelesaian: 2 4 det(A) = det [5 2] = (2 × 2) − (4 × 5) = 4 − 20 = −16. Jadi, determinan dari matriks 𝐴 adalah −16. 2. Determinan Matriks 𝒏 × 𝒏 Pada bagian ini cara mencari atau menghitung determinan matriks 𝑛 × 𝑛 akan menggunakan minor dan kofaktor dengan 𝑛 ≥ 3.. Definisi 2.1.12 Diketahui matriks 𝐴 berukuran 𝑛 × 𝑛. Minor 𝑀𝑖𝑗 adalah determinan dari matriks berukuran (𝑛 − 1) × (𝑛 − 1) yang diperoleh dari matriks 𝐴 dengan menghapus baris ke-𝑖 dan kolom ke-𝑗. Sedangkan kofaktor 𝐴𝑖𝑗 = (−1)𝑖+𝑗 𝑀𝑖𝑗 (Budhi, 1995:89).. Teorema 2.1.13 Diketahui matriks berukuran 𝑛 × 𝑛. Nilai determinan matriks 𝐴 dapat dihitung dengan cara perluasan baris ke-𝑖 det(A) = 𝑎𝑖1 𝐴𝑖1 + 𝑎𝑖2 𝐴𝑖2 + ⋯ + 𝑎𝑖𝑛 𝐴𝑖𝑛 = (−1)𝑖+1 𝑎𝑖1 𝑀𝑖1 + (−1)𝑖+2 𝑎𝑖2 𝑀𝑖2 + ⋯ + (−1)𝑖+𝑛 𝑎𝑖𝑛 𝑀𝑖𝑛 , sedangkan perluasan untuk kolom ke-𝑗 adalah det(A) = 𝑎1𝑗 𝐴1𝑗 + 𝑎2𝑗 𝐴2𝑗 + ⋯ + 𝑎𝑛𝑗 𝐴𝑛𝑗 = (−1)1+𝑗 𝑎1𝑗 𝑀1𝑗 + (−1)2+𝑗 𝑎2𝑗 𝑀2𝑗 + ⋯ + (−1)𝑛+𝑗 𝑎𝑛𝑗 𝑀𝑛𝑗 . Pembuktian pernyataan ini dapat dilihat pada (Budhi, 1995:90)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 14. Contoh Hitunglah nilai determinan dari matriks berikut ini 1 0 0 −1 𝐵=[ 3 4 1 2. 0 −2 0 0 ]. 5 7 4 −1. Penyelesaian: 1 0 det(𝐵) = det [ 3 1. 0 −1 4 2. 0 0 5 4. −2 0 ], 7 −1. perhitungan determinan matriks 𝐵 akan menggunakan perluasan baris ke-2. Sehingga determinan matriks 𝐵 dapat ditulis det(B) = (−1. )2+2. 𝑎22 𝑀22. 1 = (−1)(−1) det [3 1. 0 −2 1 5 7 ] = −det [3 4 −1 1. 0 5 4. −2 7] −1. Selanjutnya akan dihitung determinan matriks 3 × 3 yang dihasilkan di atas dengan menggunakan perluasan baris juga 1 0 −det [3 5 1 4. −2 ( )1+1 1 det [5 7 ] = − ( −1 4 −1. 7 ] ( )1+3 ( ) 3 + −1 −2 det [ −1 1. 5]) 4. = −((−5 − 28) + (−2)(12 − 5)) = 47 Jadi, det(B) = 47.. F. Nilai Eigen Bilangan real 𝜆 merupakan nilai eigen dari matriks 𝐴 jika dan hanya jika 𝜆 memenuhi persamaan karakteristik |𝐴 − 𝜆𝐼 | = 0, Pembuktian pernyataan ini dapat dilihat pada (Budhi, 1995:269).. Contoh Carilah nilai eigen dari matriks.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 15. 3 𝐴=[ 6. 5]. 2. Penyelesaian: Langkah pertama bentuk matriks 3−𝜆 𝐴 − 𝜆𝐼 = [ 6. 7 ], 2−𝜆. sehingga determinan dari matriks 𝐴 − 𝜆𝐼 adalah 0 = 𝐴 − 𝜆𝐼 = (3 − 𝜆)(2 − 𝜆) − (6)(7) = 𝜆2 − 5𝜆 + 6 − 42 = 𝜆2 − 5𝜆 − 36 = (𝜆 + 4)(𝜆 − 9). Jadi, matriks 𝐴 mempunyai dua nilai eigen yaitu 𝜆1 = −4 dan 𝜆2 = 9. G. Turunan Numerik Sebelum membahas turunan numerik akan terlebih dahulu dibahas ekspansi deret Taylor.. Teorema 2.1.14 Misalkan 𝑓 adalah sebuah fungsi yang turunan ke 𝑛 + 1, yaitu 𝑓 (𝑛+1) , ada pada interval [𝑎, 𝑏], dan 𝑥0 𝜖 [𝑎, 𝑏]. Untuk setiap 𝑥 𝜖 [𝑎, 𝑏] ada 𝜉 (𝑥 ) diantara 𝑥0 dan 𝑥 dengan 𝑓(𝑥 ) = 𝑃𝑛 (𝑥 ) + 𝑅𝑛 (𝑥),. (2.15). dimana 𝑃𝑛 (𝑥 ) = 𝑓(𝑥0 ) + 𝑓 ′ (𝑥0 )(𝑥 − 𝑥0 ) +. 𝑓′′ (𝑥0) 2!. (𝑥 − 𝑥 0 )2 + ⋯ +. dan 𝑅𝑛 (𝑥 ) =. 𝑓 (𝑛+1) (𝜉(𝑥)) (𝑥 − 𝑥0 )𝑛+1 . (𝑛 + 1)!. 𝑓(𝑛) (𝑥0 ) 𝑛!. ( 𝑥 − 𝑥 0 )𝑛.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 16. Persamaan (2.15) secara umum dapat ditulis ke dalam bentuk sebagai berikut: 𝑓 (𝑥𝑖+1 ) = 𝑓(𝑥𝑖 ) + 𝑓 ′ (𝑥𝑖 )(𝑥 − 𝑥𝑖 ) + 𝑓(𝑛) (𝑥𝑖 ) 𝑛!. 𝑓′′ (𝑥𝑖 ) 2!. (𝑥 − 𝑥 𝑖 )2 + ⋯ +. (𝑥 − 𝑥𝑖 )𝑛 + 𝑅𝑛 (𝑥),. atau 𝑓 (𝑥𝑖+1 ) = 𝑓(𝑥𝑖 ) + 𝑓 ′ (𝑥𝑖 )Δ𝑥 +. 𝑓′′ (𝑥𝑖 ) 2!. (Δ𝑥)2 + ⋯ +. 𝑓(𝑛) (𝑥𝑖 ) 𝑛!. (Δ𝑥)𝑛 +. (2.16). 𝑅𝑛 (𝑥 ), dimana Δ𝑥 = 𝑥 − 𝑥𝑖 . 1. Pendekatan Turunan Orde Satu Menggunakan Beda Maju Jika kita memotong deret Taylor setelah turunan orde satu pada persamaan (2.16) maka akan diperoleh 𝑓 (𝑥𝑖+1 ) = 𝑓 (𝑥𝑖 ) + 𝑓 ′ (𝑥𝑖 )Δ𝑥 + 𝑅1 ,. (2.17). dimana 𝑓 ′′ (𝜉 ) 2 𝑅1 𝑓 ′′ (𝜉 ) 𝑅1 = Δ𝑥 atau = Δ𝑥. 2! Δ𝑥 2 Jika ruas kiri dan kanan persamaan (2.16) kita bagi dengan Δ𝑥 akan diperoleh 𝑓 (𝑥𝑖+1 ) 𝑓(𝑥𝑖 ) 𝑓 ′ (𝑥𝑖 )(𝑥 − 𝑥𝑖 ) 𝑅1 = + + Δ𝑥 Δ𝑥 Δ𝑥 Δ𝑥 atau 𝑓 ′ (𝑥 𝑖 ) ≈. 𝑓 (𝑥𝑖+1 ) − 𝑓 (𝑥𝑖 ) 𝑅1 − , Δ𝑥 Δ𝑥. atau 𝑓 ′ (𝑥 𝑖 ) ≈. 𝑓 (𝑥𝑖+1 ) − 𝑓(𝑥𝑖 ) + 𝑂(Δ𝑥). Δ𝑥. (2.18). Persamaan (2.18) adalah pendekatan turunan numerik orde satu dengan menggunakan beda maju. Ilustrasi grafis dari pendekatan numerik beda maju ditunjukkan oleh Gambar 2.1.1..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 17. 𝑓(𝑥). Δ𝑥. 𝑥𝑖. 𝑥𝑖−1. 𝑥. 𝑥𝑖+1. Gambar 2.1.7 Grafik ilustrasi pendekatan turunan orde satu dengan beda maju.. 2. Pendekatan Turunan Orde Satu Menggunakan Beda Mundur Deret Taylor dapat diekspansi mundur untuk menghitung nilai sebelumnya berdasarkan nilai sekarang. Jika deret Taylor pada persamaan (2.16) diekspansi mundur maka akan diperoleh: 𝑓 (𝑥𝑖−1 ) = 𝑓(𝑥𝑖 ) − 𝑓 ′ (𝑥𝑖 )Δ𝑥 +. 𝑓′′ (𝑥𝑖 ) 2!. (Δ𝑥 )2 − ⋯ +. 𝑓(𝑛) (𝑥𝑖 ) 𝑛!. (Δ𝑥)𝑛 +. (2.19). 𝑅𝑛 (𝑥 ), Jika kita memotong deret Taylor setelah turunan orde satu pada persamaan (2.20) maka akan diperoleh: 𝑓 (𝑥𝑖−1 ) = 𝑓 (𝑥𝑖 ) − 𝑓 ′ (𝑥𝑖 )Δ𝑥 + 𝑅1 ,. (2.21). dengan melakukan operasi aljabar pada persamaan (2.19) akan peroleh 𝑓 ′ (𝑥 𝑖 ) ≈. 𝑓 (𝑥𝑖 ) − 𝑓 (𝑥𝑖−1 ) 𝑅1 − , Δ𝑥 Δ𝑥. atau 𝑓 ′ (𝑥 𝑖 ) ≈. 𝑓(𝑥𝑖 ) − 𝑓(𝑥𝑖−1 ) + 𝑂(Δ𝑥 ). Δ𝑥. (2.22). Persamaan (2.22) adalah pendekatan turunan numerik orde satu dengan menggunakan beda mundur. Ilustrasi grafis dari pendekatan numerik beda mundur ditunjukkan oleh Gambar 2.1.2..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 18. 𝑓(𝑥). Δ𝑥 𝑥𝑖−1. 𝑥𝑖+1. 𝑥𝑖. 𝑥. Gambar 2.1.8 Grafik ilustrasi pendekatan turunan orde satu dengan beda mundur.. 3. Pendekatan Turunan Orde Satu Menggunakan Beda Tengah Pendekatan turunan numerik yang ketiga ini atau beda tengah diperoleh dengan cara mengurai ekspansi deret Taylor maju dengan ekspansi deret Taylor mundur. Atau dengan kata lain pendekatan beda tengah diperoleh dengan cara pendekatan ratarata beda maju dan beda mundur. Jika persamaan (2.16) dikurang persamaan (2.19) akan diperoleh: 𝑓 ′ (𝑥 𝑖 ) ≈. 𝑓(𝑥𝑖+1 ) − 𝑓(𝑥𝑖−1 ) + 𝑂(Δ𝑥 2 ) 2Δ𝑥. (2.23). Persamaan (2.23) adalah pendekatan turunan numerik orde satu dengan menggunakan beda tengah. Ilustrasi grafis dari pendekatan numerik beda tengah ditunjukkan oleh Gambar 2.1.3. 𝑓(𝑥). 2Δ𝑥 𝑥𝑖−1. 𝑥𝑖. 𝑥𝑖+1. 𝑥. Gambar 2.1.9 Grafik ilustrasi pendekatan turunan orde satu dengan beda tengah..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 19. H. Metode Euler Dipandang suatu persamaan diferensial 𝑦 ′ (𝑡) = 𝑓 (𝑡, 𝑦), 𝑦(𝑡0 ) = 𝑦0. (2.24). dan diasumsikan bahwa penyelesaian dari persamaan (2.24) di atas dapat ditulis dalam bentuk deret Taylor, yaitu 𝑦(𝑡) = 𝑦(𝑡0 ) + 𝑦 ′ (𝑡0 )(𝑡 − 𝑡0 ) +. 𝑦 ′′ (𝑡0 )(𝑡 − 𝑡0 )2 + ⋯. 2. (2.25). Ketika 𝑦 ′ (𝑡0 ) = 𝑓(𝑡0 , 𝑦(𝑡0 )) dan Δ𝑡 = 𝑡1 − 𝑡0 disubstitusikan ke persamaan (2.25) akan menghasilkan bentuk 𝑦(𝑡1 ) sebagai berikut 𝑦(𝑡1 ) = 𝑦(𝑡0 ) + Δ𝑡 𝑓(𝑡0 , 𝑦(𝑡0 )) +. 𝑦 ′′ (𝑡0 )(Δ𝑡)2 + ⋯. 2. (2.26). Jika kita memilih Δ𝑡 yang cukup kecil, maka kita bisa mengabaikan suku yang memuat (Δ𝑡)2 beserta suku-suku yang ordenya lebih tinggi dan akan diperoleh 𝑦(𝑡1 ) = 𝑦(𝑡0 ) + Δ𝑡 𝑓(𝑡0 , 𝑦(𝑡0 )),. (2.27). yang mana merupakan aproksimasi Euler. Sehingga secara umum langkah untuk metode Euler adalah 𝑡𝑘+1 = 𝑡𝑘 + Δ𝑡, 𝑦𝑘+1 = 𝑦𝑘 + Δ𝑡 𝑓(𝑡𝑘 , 𝑦𝑘 ),. (2.28). dengan 𝑘 = 0, 1, … , 𝑛 − 1, untuk mendapatkan 𝑦1 , 𝑦2 , 𝑦3 , … , 𝑦𝑛 .. Contoh Gunakanlah metode Euler untuk menyelesaikan aproksimasi masalah nilai awal dari persamaan 𝑦 ′ = 𝑅𝑦 pada interval [0,1] dengan 𝑦(0) = 𝑦0 dan 𝑅 adalah konstanta. Penyelesaian: Dipilih selisih jaraknya adalah Δ𝑡 dan berdasarkan persamaan (2.28) akan diperoleh persamaan beda untuk masalah nilai awal tersebut adalah 𝑦𝑘+1 = 𝑦𝑘 + Δ𝑡(𝑅𝑦𝑘 ) atau.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 20. 𝑦𝑘+1 = 𝑦𝑘 (1 + Δ𝑡𝑅). Jika kita mengurutkan nilai-nilai dari penyelesain tersebut secara rekursif, akan diperoleh 𝑦1 = 𝑦0 (1 + Δ𝑡𝑅) 𝑦2 = 𝑦1 (1 + Δ𝑡𝑅) = 𝑦0 (1 + Δ𝑡𝑅)2 𝑦3 = 𝑦2 (1 + Δ𝑡𝑅) = 𝑦0 (1 + Δ𝑡𝑅)3 ⋮ 𝑦𝑛 = 𝑦𝑛−1 (1 + Δ𝑡𝑅) = 𝑦0 (1 + Δ𝑡𝑅)𝑛 atau secara umum skema Euler untuk masalah nilai awal tersebut menghasilkan nilai 𝑦𝑘 = 𝑦0 (1 + Δ𝑡𝑅)𝑘 , untuk 𝑘 = 0, 1, … , 𝑛.. I.. Metode Heun. Penyelesaian numerik dari suatu persamaan diferensial dengan masalah nilai awal dapat diselesaikan dengan metode Euler. Selain dengan menggunakan metode Euler dapat juga menggunakan metode Heun yang mana merupakan peningkatan dari metode Euler. Misalnya diketahui 𝑦 ′ (𝑡) = 𝑓 (𝑡, 𝑦), 𝑦(𝑡0 ) = 𝑦0 ,. (2.29). dengan menggunakan metode Heun langkah pertama yang dihitung adalah nilai dari 𝑦̃𝑘+1 dan yang terakhir adalah menghitung pendekatan dari 𝑦𝑘+1 . Secara umum langkah untuk metode Heun adalah 𝑦̃𝑘+1 = 𝑦𝑘 + Δ𝑡 𝑓 (𝑡𝑘 , 𝑦𝑘 ) 𝑦𝑘+1. Δ𝑡 = 𝑦𝑘 + [𝑓 (𝑡𝑘 , 𝑦𝑘 ) + 𝑓(𝑡𝑘+1 , 𝑦̃𝑘+1 )], 2. dimana Δ𝑡 adalah selisih jarak dan 𝑡𝑘+1 = 𝑡𝑘 + Δ𝑡.. (2.30).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 21. Contoh Gunakanlah metode Heun untuk menyelesaikan aproksimasi masalah nilai awal dari persamaan 𝑦 ′ = 𝑅𝑦 pada interval [0,1] dengan 𝑦(0) = 𝑦0 dan 𝑅 adalah konstanta. Penyelesaian: Dipilih selisih jarak Δ𝑡 dan berdasarkan persamaan (2.30) akan diperoleh persamaan beda untuk masalah nilai awal tersebut adalah 𝑦̃𝑘+1 = 𝑦𝑘 + Δ𝑡 𝑅𝑦𝑘 , 𝑦𝑘+1 = 𝑦𝑘 +. Δ𝑡 [𝑅𝑦𝑘 + (𝑦𝑘 + Δ𝑡 𝑅𝑦𝑘 )], 2. atau 𝑦̃𝑘+1 = 𝑦𝑘 (1 + Δ𝑡𝑅), 𝑦𝑘+1 = 𝑦𝑘 (1 +. Δ𝑡 [𝑅 + 1 + Δ𝑡𝑅]). 2. Sehingga persamaan beda untuk persamaan (2.30) bisa ditulis dalam satu bentuk saja, yaitu 𝑦𝑘+1 = 𝑦𝑘 (1 +. Δ𝑡 [𝑅 + 1 + Δ𝑡𝑅]). 2. Jika kita mengurutkan nilai-nilai dari penyelesaian tersebut secara rekursif, akan diperoleh 𝑦1 = 𝑦0 (1 +. Δ𝑡 [𝑅 + 1 + Δ𝑡𝑅]) , 2. 2 Δ𝑡 Δ𝑡 𝑦2 = 𝑦1 (1 + [𝑅 + 1 + Δ𝑡𝑅]) = 𝑦0 (1 + [𝑅 + 1 + Δ𝑡𝑅]) 2 2. ⋮ 𝑦𝑛 = 𝑦𝑛−1 (1 +. 𝑛 Δ𝑡 Δ𝑡 [𝑅 + 1 + Δ𝑡𝑅]) = 𝑦0 (1 + [𝑅 + 1 + Δ𝑡𝑅]) 2 2. atau secara umum skema Heun untuk masalah nilai awal tersebut menghasilkan nilai.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 22. 𝑦𝑘 = 𝑦0 (1 +. 𝑘 Δ𝑡 [𝑅 + 1 + Δ𝑡𝑅]) . 2. untuk 𝑘 = 0, 1, … , 𝑛.. J.. Metode Biseksi Teorema 2.1.15. Jika terdapat fungsi 𝑓 yang kontinu pada interval tertutup [𝑎, 𝑏] dan 𝑓(𝑎). 𝑓(𝑏) < 0, maka ada 𝑐 ∈ (𝑎, 𝑏) sehingga berlaku 𝑓 (𝑐 ) = 0. Bukti: Diketahui bahwa 𝑓 (𝑎). 𝑓(𝑏) < 0 hal ini terjadi ketika 𝑓 (𝑎) < 0 dan 𝑓(𝑏) > 0. Didefinisikan suatu himpunan 𝐸 = {𝑥 ∈ [𝑎, 𝑏] ∶ 𝑓(𝑥 ) < 0}. dan himpunan tersebut tidak kosong karena 𝑎 ∈ 𝐸 dan 𝐸 mempunyai batas atas 𝑏. Misalkan 𝑓(𝑐) ≠ 0 karena 𝑓 kontiniu pada 𝑐 terdapat 𝛿 > 0 sedemikian sehingga |𝑥 − 𝑐 | < 𝛿 dan 𝑥 ∈ [𝑎, 𝑏] sehingga mengakibatkan 1 |𝑓(𝑥) − 𝑓(𝑐)| < |𝑓(𝑐)|. 2 Jika 𝑓(𝑐 ) < 0, maka 𝑐 ≠ 𝑏 dan 1 𝑓 ( 𝑥 ) = 𝑓 (𝑐 ) + 𝑓 (𝑥 ) − 𝑓 (𝑐 ) < 𝑓 (𝑐 ) − 𝑓 (𝑐 ), 2 1. Untuk semua 𝑥 ∈ [𝑎, 𝑏] sehinga |𝑥 − 𝑐 | < 𝛿. Jadi 𝑓(𝑥 ) < 2 𝑓(𝑐 ) < 0. Karena ada 𝑥 ∈ 𝐸 dengan 𝑥 > 𝑐, yang mana kontradiksi dengan fakta bahwa 𝑐 adalah batas atas dari 𝐸. Jika 𝑓(𝑐 ) > 0, maka 𝑐 ≠ 𝑎 dan 1 𝑓 ( 𝑥 ) = 𝑓 (𝑐 ) + 𝑓 (𝑥 ) − 𝑓 (𝑐 ) > 𝑓 (𝑐 ) − 𝑓 (𝑐 ), 2 1. untuk semua 𝑥 ∈ [𝑎, 𝑏], sehingga |𝑥 − 𝑐 | < 𝛿. Jadi, 𝑓(𝑥 ) > 2 𝑓(𝑐 ) > 0. Ada 𝛽 > 0 sehingga 𝑐 − 𝛽 ≥ 𝑎 dan 𝑓 (𝑥 ) > 0 untuk 𝑐 − 𝛽 ≤ 𝑥 ≤ 𝑐..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 23. Pada kasus ini, 𝑐 − 𝛽 < 𝑐 adalah batas atas dari 𝐸. Karena 𝑐 adalah batas atas dan 𝑓 (𝑥 ) > 0 untuk 𝑐 − 𝛽 ≤ 𝑥 ≤ 𝑐, yang mana kontradiksi bahwa 𝑐 merupakan batas paling atas. Karena 𝑐 ≠ 𝑎, 𝑏 maka terbukti bahwa 𝑓(𝑐 ) = 0. Diberikan suatu fungsi 𝑓 yang kontinu pada interval [𝑎, 𝑏] dan 𝑐 ∈ (𝑎, 𝑏) merupakan akar karakteristik dari fungsi 𝑓. Langkah pertama dalam metode biseksi yaitu menentukan nilai tengah, yaitu 𝑐=. 𝑎+𝑏 , 2. selanjutnya menganalisis kemungkinan-kemungkinan yang akan muncul: 1. Jika 𝑓(𝑎). 𝑓(𝑐) < 0, maka akar dari fungsi f terletak diantara 𝑎 dan 𝑐, 2. Jika 𝑓(𝑎). 𝑓(𝑐) > 0, maka akar dari fungsi f terletak diantara 𝑐 dan 𝑏, 3. Jika 𝑓(𝑎). 𝑓(𝑐) = 0, maka 𝑎 atau 𝑐 adalah akar real dari fungsi 𝑓..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB III SISTEM PERSAMAAN DIFERENSIAL LOTKA-VOLTERRA TERMODIFIKASI DAN METODE BEDA HINGGA EKSAK. Pada bab ini akan dibahas sistem persamaan diferensial Lotka-Volterra termodifikasi dan metode beda hingga eksak yang akan digunakan untuk menyelesaikan persamaan diferensial Lotka-Volterra termodifikasi.. A. Sistem Persamaan Lotka-Volterra Termodifikasi Dalam subbab ini akan dibahas model dari persamaan diferensial LotkaVolterra khususnya untuk model kompetisi dan juga akan dipaparkan hasil modifikasi dari persamaan diferensial Lotka-Volterra.. 1.. Persamaan Diferensial Lotka-Volterra. Misalkan 𝑥 menggambarkan jumlah populasi rusa pada waktu 𝑡 dan 𝑦 menggambarkan jumlah populasi zebra pada waktu 𝑡. Rusa merupakan hewan herbivora yang bertahan hidup dengan mengkonsumsi tumbuh-tumbuhan. Kita dapat mengasumsikan laju pertumbuhan rusa per kapita (tanpa adanya zebra) memiliki nilai konstan 𝑟1 , dengan 𝑟1 > 0, tetapi dengan adanya zebra akan mengurangi laju pertumbuhan rusa per kapita. Jika kita mengasumsikan bahwa laju pertumbuhan rusa berkurang sejumlah 𝑎12 𝑦 yang sebanding dengan jumlah zebra, dengan 𝑎12 > 0, maka laju pertumbuhan rusa per kapita yang dihasilkan adalah 𝑟1 − 𝑎12 𝑦. Persamaan pertumbuhan rusa adalah 𝑑𝑥 = (𝑟1 − 𝑎12 𝑦)𝑥. 𝑑𝑡. (3.1). Misalkan zebra bergantung sepenuhnya pada tumbuh-tumbuhan sebagai satusatunya sumber makanan. Tanpa adanya rusa, kita mengasumsikan laju pertumbuhan zebra per kapita memiliki nilai konstan 𝑟2 , dengan 𝑟2 > 0, tetapi adanya rusa akan menurunkan laju pertumbuhan zebra per kapita sejumlah 𝑎21 𝑥 yang sebanding dengan jumlah rusa, dengan 𝑎21 > 0. Laju pertumbuhan zebra per. 24.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 25. kapita yang dihasilkan adalah 𝑟2 − 𝑎21 𝑥, sehingga persamaan pertumbuhan zebra adalah 𝑑𝑦 = (𝑟2 − 𝑎21 𝑥)𝑦. 𝑑𝑡. (3.2). Persamaan (3.1) dan persamaan (3.2) menghasilkan model kompetisi sebagai berikut: 𝑑𝑥 = (𝑟1 − 𝑎12 𝑦)𝑥, { 𝑑𝑡 𝑑𝑦 = (𝑟2 − 𝑎21 𝑥)𝑦. 𝑑𝑡. (3.3). Jika kita mengasumsikan bahwa sumber makanan rusa dan zebra yang awalnya tidak terbatas menjadi terbatas maka laju pertumbuhan per kapita rusa (tanpa adanya zebra dan tanpa adanya kompetisi antar rusa dalam memperoleh makanan) memiliki nilai konstan 𝑟1 , dengan 𝑟1 > 0. Dengan adanya zebra dan kompetisi antar rusa dalam perebutan makanan (tumbuhan) akan mengurangi laju pertumbuhan per kapita rusa. Jika kita mengasumsikan bahwa laju pertumbuhan rusa berkurang sejumlah 𝑎12 𝑦 yang sebanding dengan jumlah zebra, dengan 𝑎12 > 0 dan sejumlah 𝑎11 𝑥 yang sebanding dengan jumlah rusa, dengan 𝑎11 > 0, maka laju pertumbuhan rusa per kapita yang dihasilkan adalah 𝑟1 − 𝑎11 𝑥 − 𝑎12 𝑦. Model pertumbuhan rusa menjadi 𝑑𝑥 = 𝑟1 𝑥 − 𝑎11 𝑥 2 − 𝑎12 𝑥𝑦, 𝑑𝑡. (3.4). Hal yang sama juga terjadi pada zebra. Jika diasumsikan sumber makan menjadi terbatas maka laju pertumbuhan zebra per kapita (tanpa adanya rusa dan kompetisi antara zebra dalam memperoleh makanan) memiliki nilai konstan 𝑟2 , dengan 𝑟2 > 0. Dengan adanya rusa akan menurunkan laju pertumbuhan zebra per kapita sejumlah 𝑎21 𝑥, dengan 𝑎21 > 0 yang sebanding dengan jumlah rusa. Akan tetapi, dengan adanya kompetisi antara zebra dalam memperoleh makanan akan mengakibatkan laju pertumbuhan zebra per kapita menurun sejumah 𝑎22 𝑦, dengan 𝑎22 > 0 yang sebanding dengan jumlah zebra. Laju pertumbuhan zebra per kapita yang dihasilkan adalah 𝑟2 − 𝑎21 𝑥 − 𝑎22 𝑦, sehingga persamaan pertumbuhan zebra adalah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 26. 𝑑𝑦 = 𝑟2 𝑦 − 𝑎21 𝑥𝑦 − 𝑎22 𝑦 2 . 𝑑𝑡. (3.5). Berdasarkan persamaan (3.4) dan persamaan (3.5) diperoleh persamaan diferensial Lotka-Volterra untuk masalah kompetisi yang didefinisikan dengan bentuk 𝑑𝑥 = 𝑟1 𝑥 − 𝑎11 𝑥 2 − 𝑎12 𝑥𝑦, 𝑑𝑡 𝑑𝑦 = 𝑟2 𝑦 − 𝑎21 𝑥𝑦 − 𝑎22 𝑦 2 , 𝑑𝑡. (3.6a) (3.6b). 𝑥(0) = 𝑥0 > 0, 𝑦(0) = 𝑦0 > 0, dimana 𝑟1 , 𝑟2 , 𝑎11 , 𝑎22 , 𝑎12 , 𝑎21 adalah parameter konstan positif untuk kasus dinamika rusa-zebra ini dan 𝑥(𝑡) dan 𝑦(𝑡) adalah variabel terikat. Pada umumnya nilai dari parameter yang diberikan bisa bernilai positif, nol atau negatif bergantung pada kasus yang dihadapi. Kita menganggap 𝑥(𝑡) dan 𝑦(𝑡) menggambarkan besarnya masing-masing populasi.. 2.. Persamaan Diferensial Lotka-Volterra Termodifikasi Kita telah mengetahui bahwa persamaan (3.6) merupakan persamaan. diferensial Lotka-Volterra khususnya untuk masalah kompetisi. Persamaan diferensial Lotka-Volterra tersebut akan dimodifikasi dengan mengganti x dan y masing-masing dengan √𝑥 dan √𝑦, sehingga kita akan memperoleh persamaan diferensial Lotka-Volterra termodifikasi sebagai berikut 𝑑𝑥 = 𝑟1 √𝑥 − 𝑎11 𝑥 − 𝑎12 √𝑥 √𝑦, 𝑑𝑡 𝑑𝑦 = −𝑟2 √𝑦 + 𝑎21 √𝑥 √𝑦 − 𝑎22 𝑦, 𝑑𝑡. (3.7a) (3.7b). bisa dilihat bahwa persamaan (3.6) dan (3.7) memiliki koefisien yang sama yaitu 𝑟1 , 𝑟2 , 𝑎11 , 𝑎12 , 𝑎21 , 𝑎22 . Penggantian 𝑥 menjadi √𝑥 dan 𝑦 dan menjadi √𝑦 diajukan oleh Mickens (2018) untuk dijadikan sebagai model kasus uji keefektifan metode beda hingga eksak..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 27. B. Metode Beda Hingga Eksak Sebelum membahas metode beda hingga eksak, akan dibahas terlebih dahulu model diskret dari persamaan diferensial biasa 𝑑𝑦 = 𝑓(𝑦, 𝜆), 𝑑𝑡. (3.8). dimana 𝜆 adalah suatu parameter. Model beda hingga paling umum untuk persamaan (3.8) merupakan turunan diskret orde pertama yang ditunjukkan dalam bentuk sebagai berikut: 𝑦𝑘+1 − 𝑦𝑘 = 𝐹(𝑦𝑘 , 𝑦𝑘+1 , 𝜆, Δ𝑡), 𝜙(Δ𝑡, 𝜆). (3.9). turunan diskret pada sisi kiri adalah generalisasi dari bentuk 𝑑𝑦 𝑦𝑘+1 − 𝑦𝑘 → . 𝑑𝑡 Δ𝑡. (3.10). Berdasarkan persamaan (3.9), kita peroleh dimana fungsi penyebut 𝜙(Δ𝑡, 𝜆) mempunyai sifat 𝜙(Δ𝑡, 𝜆) = Δ𝑡 + 𝑂(Δ𝑡 2 ),. (3.11). 𝜆 = tetap, Δ𝑡 → 0. Bentuk persamaan (3.9) di atas merupakan turunan diskret yang didasarkan pada definisi turunan (2.1) yang mana dapat digeneralisasi sebagai berikut 𝑑𝑦 𝑦[𝑡 + 𝜓1 (Δ𝑡)] − 𝑦(𝑡) = lim , Δ𝑡→0 𝑑𝑡 𝜓2 (Δ𝑡) dimana 𝜓𝑖 (Δ𝑡) = Δ𝑡 + 𝑂(Δ𝑡 2 ), Δ𝑡 → 0; 𝑖 = 1,2. Contoh dari fungsi 𝜓(Δ𝑡) yang memenuhi kondisi ini adalah. 𝜓(Δ𝑡) =. Δ𝑡, sin(Δ𝑡) , 𝑒 Δ𝑡 − 1, 1 − 𝑒 −Δ𝑡 , 1−𝑒 −𝜆Δ𝑡 𝜆. ,. {dan lainnya.. (3.12).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 28. Perlu diperhatikan dalam pengambilan limit Δ𝑡 → 0 untuk memperoleh turunan, penggunaan salah satu dari 𝜓(Δ𝑡) akan mengarah pada hasil biasa dari suatu turunan pertama 𝑑𝑦 𝑦[𝑡 + 𝜓1 (Δ𝑡)] − 𝑦(𝑡) 𝑦(𝑡 + Δ𝑡) − 𝑦(𝑡) = lim = lim . Δ𝑡→0 Δ𝑡→0 𝑑𝑡 𝜓2 (Δ𝑡) Δ𝑡. 1.. (3.13). Skema Beda Hingga Eksak. Dipandang bentuk umum persamaan diferensial orde satu 𝑑𝑦 = 𝑓(𝑦, 𝑡, 𝜆), 𝑦(𝑡0 ) = 𝑦0 , 𝑑𝑡. (3.14). dimana 𝑓 (𝑦, 𝑡, 𝜆) sedemiakan sehingga persamaan (3.14) memiliki penyelesaian tunggal pada interval, 0 ≤ 𝑡 < 𝑇 dan 𝜆 adalah parameter pada interval 𝜆1 ≤ 𝜆 ≤ 𝜆2 dengan 𝜆1 dan 𝜆2 adalah konstanta. Penyelesaiannya dapat ditulis sebagai berikut: 𝑦(𝑡) = 𝜙(𝜆, 𝑦0 , 𝑡0 , 𝑡). (3.15). dimana 𝜙 (𝜆, 𝑦0 , 𝑡0 , 𝑡0 ) = 𝑦0 . Dipandang model diskret dari persamaan (3.14) 𝑦𝑘+1 = 𝑔(𝜆, Δ𝑡, 𝑦𝑘 , 𝑡𝑘 ),. (3.16). dimana 𝑡𝑘 = 𝑘. Δ𝑡, 𝑦𝑘 ≈ 𝑦(𝑡𝑘 ). Penyelesaian dari persamaan (3.16) dapat ditulis dalam bentuk 𝑦𝑘 = 𝜓(𝜆, Δ𝑡, 𝑦0 , 𝑡0 , 𝑡𝑘 ),. (3.17). dimana 𝜓(𝜆, Δ𝑡, 𝑦0 , 𝑡0 , 𝑡0 ) = 𝑦0 .. Definisi 3.1.1 Persamaan (3.14) dan (3.16) dikatakan memiliki penyelesaian umum yang sama jika dan hanya jika.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 29. 𝑦𝑘 = 𝑦(𝑡𝑘 ), untuk sebarang Δ𝑡 > 0 dan untuk semua 𝑘.. Definisi 3.1.2 Suatu skema beda hingga eksak adalah suatu skema yang menghasilkan penyelesaian beda tertentu yang mana penyelesaian umum dari persamaan beda hingga tersebut sama dengan penyelesaian diferensial terkait.. Teorema 3.1.3 Persamaan diferensial 𝑑𝑦 = 𝑓 (𝑦, 𝑡, 𝜆), 𝑦(𝑡0 ) = 𝑦0 , 𝑑𝑡. (3.18). mempunyai skema beda hingga eksak yang diekspresikan dengan bentuk sebagai berikut 𝑦𝑘+1 = 𝜙(𝜆, 𝑦𝑘 , 𝑡𝑘 , 𝑡𝑘+1 ),. (3.19). dimana fungsi 𝜙 sama dengan fungsi pada persamaan (3.15). Bukti: Diasumsikan penyelesaian umum untuk persamaan (3.18) didefinisikan sebagai berikut 𝑦(𝑡) = 𝜙(𝜆, 𝑦0 , 𝑡0 , 𝑡) dimana 𝑦0 adalah nilai dari 𝑥(𝑡) saat 𝑡 = 𝑡0 . Nemytski and Stepanov (1969) mengatakan 𝑓 (𝑓(𝑥, 𝑡1 ), 𝑡2 ) = 𝑓 (𝑥, 𝑡1 + 𝑡2 ),. (3.20). sehingga berdasarkan persamaan (3.20) di atas dapat kita tulis 𝑓 (𝑓 (𝑦, 𝑡, 𝜆), Δ𝑡, 𝜆) = 𝑓(𝑦, 𝑡 + Δ𝑡, 𝜆),. (3.21). dengan nilai awalnya adalah 𝑦(𝑡) = 𝑦𝑡 . Berdasarkan pembahasan di atas diperoleh penyelesaian untuk persamaan (3.21) adalah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 30. 𝑦(𝑡 + Δ𝑡) = 𝜙(𝜆, 𝑦(𝑡), 𝑡, 𝑡 + Δ𝑡). Jika kita mensubstitusi 𝑡 → 𝑡𝑘 , 𝑦(𝑡) → 𝑦𝑘 , maka penyelesaian untuk persamaan (3.21) akan menjadi (3.22). 𝑦𝑘+1 = 𝜙(𝜆, 𝑦𝑘 , 𝑡𝑘 , 𝑡𝑘+1 ).. Persamaan (3.22) merupakan persamaan beda biasa yang dibutuhkan yang mana persamaan (3.22) memiliki penyelesaian umum yang dengan persamaan (3.18).. 2.. Contoh Skema Beda Hingga Eksak. Diberikan suatu himpunan fungsi-fungsi yang bebas linear {𝑦 (𝑖) (𝑡)} ; 𝑖 = 1, 2, … , 𝑁,. (3.23). dimana fungsi-fungsi tersebut selalu mungkin membangun persamaan beda linear orde 𝑁, yang memiliki fungsi diskret yang sesuai sebagai penyelesaian. Diberikan (𝑖). 𝑦𝑘 ≡ 𝑦 (𝑖) (𝑡𝑘 ),. (3.24). 𝑡𝑘 = (Δ𝑡)𝑘;. sehingga determinan berikut ini memberikan persamaan yang diperlukan 𝑦𝑘 | 𝑦𝑘+1 ⋮ 𝑦𝑘+𝑛. 𝑦𝑘1 1 𝑦𝑘+1 ⋮ 1 𝑦𝑘+𝑛. 2 𝑦𝑘+1 2 𝑦𝑘+1 ⋮ 2 𝑦𝑘+𝑛. ⋯ ⋯ ⋮ ⋯. 𝑦𝑘𝑛 𝑛 𝑦𝑘+1 | = 0. ⋮ 𝑛 𝑦𝑘+𝑛. Bukti dan penjelasan tentang hal tersebut diberikan oleh Mickens (1990).. Contoh 1 Dipandang suatu fungsi 𝑦 (1) (𝑡) = 𝑒 −𝜆𝑡 ,. (3.25). dimana fungsi tersebut merupakan suatu penyelesaian untuk persamaan diferensial orde satu 𝑑𝑦 = −𝜆𝑦. 𝑑𝑡 Persamaan beda yang sesuai adalah. (3.26).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 31. det |. 𝑦𝑘 𝑦𝑘+1. 𝑦 =| 𝑘 | 𝑦𝑘+1 (1). 𝑒 −𝜆Δ𝑡𝑘. (1). 𝑦𝑘. 𝑦𝑘+1. 𝑒. −𝜆Δ𝑡(𝑘+1). 𝑦𝑘 | = 𝑒 −𝜆Δ𝑡𝑘 | 𝑦𝑘+1. 1. 𝑒. −𝜆Δ𝑡 |. = 𝑒 −𝜆Δ𝑡𝑘 [𝑒 −𝜆Δ𝑡 𝑦𝑘 − 𝑦𝑘+1 ] = 0 atau dapat ditulis 𝑦𝑘+1 = 𝑒 −𝜆Δ𝑡 𝑦𝑘 .. (3.27). Persamaan (3.27) di atas adalah persamaan beda hingga eksak atau skema beda hingga eksak yang sesuai untuk persamaan (3.26). Bentuk dari skema eksak di atas dapat ditulis ke dalam bentuk yang lebih konstruktif dengan melakukan operasi aljabar pada persamaan (3.27) sebagai berikut: 𝑦𝑘+1 = 𝑒 −𝜆Δ𝑡 𝑦𝑘 atau 𝑦𝑘+1 − 𝑦𝑘 + 𝑦𝑘 = 𝑒 −𝜆Δ𝑡 𝑦𝑘 atau 𝑦𝑘+1 − 𝑦𝑘 = 𝑒 −𝜆Δ𝑡 𝑦𝑘 − 𝑦𝑘 atau 𝜆. 𝑦𝑘+1 − 𝑦𝑘 = 𝜆 (𝑒 −𝜆Δ𝑡 𝑦𝑘 − 𝑦𝑘 ) atau 𝑦𝑘+1 − 𝑦𝑘 = −𝜆 (. −𝑒 −𝜆Δ𝑡 𝑦𝑘 +𝑦𝑘 𝜆. ). atau 𝑦𝑘+1 − 𝑦𝑘 = −𝜆 (. −𝑒 −𝜆Δ𝑡 +1 𝜆. ) 𝑦𝑘. atau 𝑦𝑘+1 − 𝑦𝑘 = −𝜆 (. 1−𝑒 −𝜆Δ𝑡 𝜆. ) 𝑦𝑘. atau 𝑦𝑘+1 − 𝑦𝑘 = −𝜆𝑦𝑘 . 1 − 𝑒 −𝜆Δ𝑡 ( ) 𝜆. (3.28).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 32. Setelah melakukan operasi aljabar pada persamaan (3.27) diperoleh persamaan (3.28). Sebagai catatan metode Euler standar untuk persamaan (3.26) adalah 𝑦𝑘+1 − 𝑦𝑘 (3.29) = −𝜆𝑦𝑘 . Δ𝑡 Contoh 2 Dipandang persamaan diferensial osilator harmonik 𝑑2𝑦 + 𝑦 = 0. 𝑑𝑡 2. (3.30). Persamaan diferensial di atas memiliki dua penyelesaian yang bebas linear yaitu 𝑦 (1) (𝑡) = cos(𝑡) ,. 𝑦 (2) (𝑡) = sin(𝑡),. atau dalam bentuk kompleks ditulis 𝑦̅ (1) (𝑡) = 𝑒 𝑖𝑡 ,. 𝑦̅ (2) (𝑡) = 𝑒 −𝑖𝑡 .. Untuk memperoleh persamaan beda yang sesuai kita terapkan cara yang sama seperti pada contoh 1 𝑦𝑘 det [𝑦𝑘+1 𝑦𝑘+2. 𝑒 𝑖Δ𝑡𝑘 𝑒 𝑖Δ𝑡(𝑘+1) 𝑒 𝑖Δ𝑡(𝑘+2). 𝑒 −𝑖Δ𝑡𝑘 𝑒 −𝑖Δ𝑡(𝑘+1) ] = 0 𝑒 −𝑖Δ𝑡(𝑘+2). Menggunakan aturan minor dan kofaktor diperoleh 𝑦𝑘 (𝑒 𝑖Δ𝑡(𝑘+1) 𝑒 −𝑖Δ𝑡(𝑘+2) − 𝑒 −𝑖Δ𝑡(𝑘+1) 𝑒 𝑖Δ𝑡(𝑘+2) ) − 𝑒 𝑖Δ𝑡𝑘 (𝑦𝑘+1 𝑒 −𝑖Δ𝑡(𝑘+2) − 𝑒 −𝑖Δ𝑡(𝑘+1) 𝑦𝑘+2 ) + 𝑒 −𝑖Δ𝑡𝑘 (𝑦𝑘+1 𝑒 𝑖Δ𝑡(𝑘+2) − 𝑒 𝑖Δ𝑡(𝑘+2) 𝑦𝑘+2 ) = 0 atau 𝑦𝑘 (𝑒 −𝑖Δ𝑡 − 𝑒 𝑖Δ𝑡 ) − 𝑦𝑘+1 (𝑒 −2𝑖Δ𝑡 − 𝑒 2𝑖Δ𝑡 ) + 𝑦𝑘+2 (𝑒 −𝑖Δ𝑡 − 𝑒 𝑖Δ𝑡 ) = 0 atau 𝑦𝑘 ((cos(Δ𝑡) − 𝑖 sin(Δ𝑡)) − (𝑐𝑜𝑠(Δ𝑡) + 𝑖 sin(Δ𝑡))) − 𝑦𝑘+1 ((cos(2Δ𝑡) − 𝑖 𝑠𝑖𝑛(2Δ𝑡)) − ((cos(2Δ𝑡) + 𝑖 𝑠𝑖𝑛(2Δ𝑡))) + 𝑦𝑘+2 ((cos(Δ𝑡) − 𝑖 sin(Δ𝑡)) − ((cos(Δ𝑡) + 𝑖 sin(Δ𝑡))) = 0 atau.

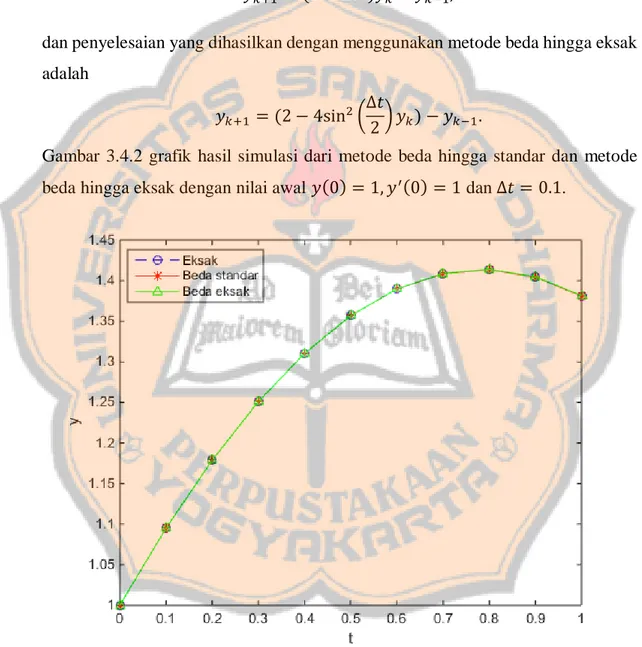
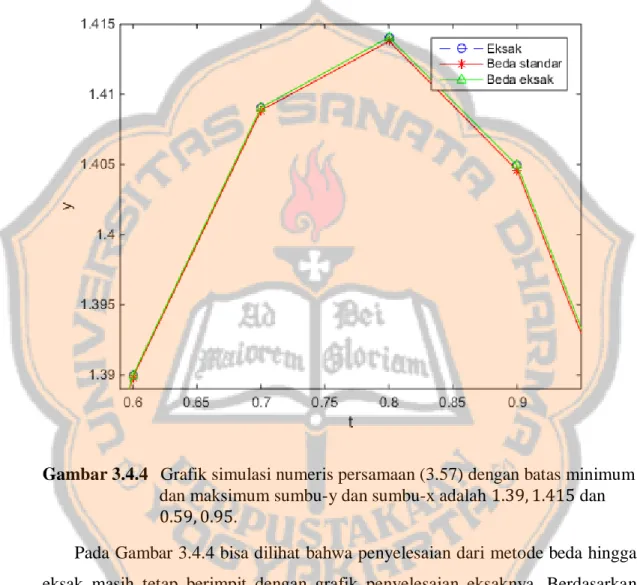
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 33. 𝑦𝑘 (−2𝑖 sin(Δ𝑡)) − 𝑦𝑘+1 (−2𝑖 sin(2Δ𝑡)) + 𝑦𝑘+2 (−2𝑖 sin(Δ𝑡)) = 0 atau sin(Δ𝑡)𝑦𝑘 − sin(2Δ𝑡) 𝑦𝑘+1 + sin(Δ𝑡) 𝑦𝑘+2 = 0 atau sin(Δ𝑡)𝑦𝑘 − 2sin(Δ𝑡) cos(Δ𝑡) 𝑦𝑘+1 + sin(Δ𝑡) 𝑦𝑘+2 = 0 atau 𝑦𝑘 − 2 cos(Δ𝑡) 𝑦𝑘+1 + 𝑦𝑘+2 = 0.. (3.31) Δ𝑡. Persamaan cos(2Δ𝑡) = 1 − 2sin2 Δ𝑡 yang mengakibatkan cos Δ𝑡 = 1 − 2sin2 ( 2 ) sehingga diperoleh 𝑦𝑘 − 2(1 − 2sin2 (. Δ𝑡 ))𝑦𝑘+1 + 𝑦𝑘+2 = 0. 2. (3.32). Pada persamaan (3.32) kita menggeser indeks k satu satuan ke bawah dan akan kita peroleh 𝑦𝑘−1 − 2(1 − 2sin2 (. Δ𝑡 ))𝑦𝑘 + 𝑦𝑘+1 = 0, 2. (3.33). Δ𝑡 )) 𝑦𝑘 −𝑦𝑘−1 . 2. (3.34). atau dapat ditulis 𝑦𝑘+1 = 2 (1 − 2sin2 (. Persamaan (3.34) di atas adalah persamaan beda hingga eksak atau skema beda hingga eksak yang sesuai untuk persamaan (3.30). Persamaan (3.34) juga dapat ditulis ke dalam bentuk yang lebih konstruktif. Jadi, dengan cara yang sama pada contoh 1 akan diperoleh persamaan sebagai berikut: 𝑦𝑘−1 − 𝑦𝑘+1 − 2𝑦𝑘 = −𝑦𝑘 Δ𝑡 2 4sin ( 2 ). (3.35). Setelah melakukan operasi aljabar pada persamaan (3.34) diperoleh persamaan (3.35). Sebagai catatan bahwa metode beda hingga standar untuk persamaan (3.30) adalah 𝑦𝑘−1 − 𝑦𝑘+1 − 2𝑦𝑘 = −𝑦𝑘 , Δ𝑡 2. (3.35a).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 34. Persamaan (3.35a) akan menjadi pembanding metode beda hingga eksak untuk menyelesaikan persamaan (3.30).. Cara yang digunakan untuk meperoleh atau mengkonstruksi skema beda eksak pada contoh 1 dan contoh 2 tidak dapat digunakan untuk mengkonstruksi skema beda eksak untuk persamaan diferensial yang nonlinear. Berikut ini adalah langkah-langkah yang akan diterapkan untuk mengkonstruksi skema beda eksak untuk persamaan diferensial nonlinear: 1.. Dipandang suatu sistem dari 𝑁 pasang persamaan diferensial biasa orde satu 𝑑𝑌 = 𝐹 (𝑌, 𝑡, 𝜆), 𝑌(𝑡0 ) = 𝑌0 , 𝑑𝑡. (3.36). dimana 𝑌, 𝐹 adalah vektor kolom berdimensi 𝑁 yang komponen ke-𝑖 adalah (𝑌)𝑖 = 𝑦 (𝑖) (𝑡), (𝐹)𝑖 = 𝑓 (𝑖) [𝑦 (1) , 𝑦 (2) , … , 𝑦 (𝑁) ; 𝑡, 𝜆]. 2.. Penyelesaian umum untuk persamaan (3.36) dinyatakan dengan 𝑌(𝑡) = Φ(λ, 𝑌0 , 𝑡0 , 𝑡) dimana (1). (2). (𝑁). 𝑦 (𝑖) (𝑡) = 𝜙 (𝑖) [λ, 𝑦0 , 𝑦0 , … , 𝑦0 , 𝑡0 , 𝑡]. 3.. Persamaan beda eksak yang sesuai dengan persamaan diferensial diperoleh dengan membuat substitusi berikut 𝑌 (𝑡) → 𝑌𝑘+1 , 𝑌 = 𝑌(𝑡0 ) → 𝑌𝑘 , { 0 𝑡0 → 𝑡𝑘 , 𝑡 → 𝑡𝑘+1 .. Contoh 3 Dipandang persamaan diferensial logistik umum dengan suatu nilai awal 𝑑𝑦 = 𝜆1 𝑦 − 𝜆2 𝑦 2 , 𝑑𝑡 dimana 𝜆1 dan 𝜆2 adalah konstanta.. 𝑦(𝑡0 ) = 𝑦0. (3.37).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 35. Penyelesaian untuk masalah nilai awal dari persamaan (3.37) di atas adalah 𝑦 (𝑡 ) =. 𝜆1 𝑦0 . (𝜆1 − 𝑦0 𝜆2 )𝑒 −𝜆1 (𝑡−𝑡0 ) + 𝜆2 𝑦0. (3.38). Berdasarkan langkah nomor 3 di atas kita akan mensubstitusikan 𝑡0 → 𝑡𝑘 ,. 𝑡 → 𝑡𝑘+1 ,. 𝑦0 → 𝑦𝑘 ,. 𝑦(𝑡) → 𝑦𝑘+1 ,. ke persamaan (3.38) sehingga diperoleh 𝑦𝑘+1 =. 𝜆1 𝑦𝑘 , (𝜆1 − 𝑦𝑘 𝜆2 )𝑒 −𝜆1 Δ𝑡 + 𝜆2 𝑦𝑘. (3.39). Persamaan (3.39) di atas adalah persamaan beda hingga eksak atau skema beda hingga eksak yang sesuai untuk persamaan (3.37). Persamaan (3.39) dapat ditulis ke dalam bentuk yang lebih konstruktif. Dengan melakukan operasi aljabar pada persamaan (3.39) akan diperoleh persamaan sebagai berikut: 𝑦𝑘+1 − 𝑦𝑘 = 𝜆1 𝑦𝑘 − 𝜆2 𝑦𝑘+1 𝑦𝑘 . 𝑒 𝜆1 Δ𝑡 − 1 ( ) 𝜆1. (3.40). Sebagai catatan bahwa metode Euler maju untuk persamaan (3.37) adalah 𝑦𝑘+1 − 𝑦𝑘 (3.40a) = 𝜆1 𝑦𝑘 − 𝜆2 𝑦𝑘 𝑦𝑘 . Δ𝑡 Persamaan (3.40a) akan menjadi pembanding metode beda hingga eksak untuk menyelesaikan persamaan (3.37). Selanjutnya akan dibahas skema beda hingga eksak untuk sistem dari dua pasang persamaan diferensial biasa linear. Dipandang sistem persamaan diferensial 𝑑𝑢 = 𝛼𝑢 + 𝛽𝑤, 𝑑𝑡 𝑑𝑤 = 𝛾𝑢 + 𝛿𝑤, 𝑑𝑡 dengan kondisi nilai awal 𝑢0 = 𝑢(𝑡0 ), dan syarat. 𝑤0 = 𝑤(𝑡0 ),. (3.41a) (3.41b).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 36. 𝛼𝛿 − 𝛽𝛾 ≠ 0. Sebelum membahas skema beda eksak dari persamaan (3.41) di atas akan terlebih dahulu dibahas penyelesaian umum dari persamaan (3.41) yang diperoleh secara analitik. Misalkan: 𝑢 = 𝐴𝑒 𝜆𝑡 ,. 𝑣 = 𝐵𝑒 𝜆𝑡 ,. 𝑑𝑢 = 𝐴𝜆𝑒 𝜆𝑡 , 𝑑𝑡. 𝑑𝑣 = 𝐵𝜆𝑒 𝜆𝑡 . 𝑑𝑡. (3.42). Jika persamaan (3.42) disubstitusikan ke persamaan (3.41) maka persamaan (3.41) akan menjadi 𝐴𝜆𝑒 𝜆𝑡 = 𝛼𝐴𝑒 𝜆𝑡 + 𝛽𝐵𝑒 𝜆𝑡 , 𝐵𝜆𝑒. 𝜆𝑡. = 𝛾𝐴𝑒. 𝜆𝑡. (3.43). 𝜆𝑡. + 𝛿𝐵𝑒 ,. atau 𝐴𝜆 = 𝛼𝐴 + 𝛽𝐵,. (3.44). 𝐵𝜆 = 𝛾𝐴 + 𝛿𝐵, atau (𝜆 − 𝛼 )𝐴 + 𝛽𝐵 = 0,. (3.45). 𝛾𝐴 + (𝜆 − 𝛿 )𝐵 = 0. Selanjutnya akan dicari nilai eigen dari persamaan (3.45) diatas sehingga berdasarkan persamaan (3.45) dapat membentuk matriks yang determinannya sama dengan 0 yaitu det [. 𝜆−𝛼 𝛾. 𝛽 ] = 0. 𝜆−𝛿. (3.46). Persamaan (3.46) dapat diperluas menjadi suatu persamaan kuadrat, yaitu 𝜆2 − (𝛼 + 𝛿 )𝜆 + (𝛼𝛿 − 𝛽𝛾) = 0, dengan menggunakan rumus kuadratik dapat diperoleh nilai akar-akar dari persamaan (3.47) 𝜆1,2 = atau. (𝛼 + 𝛿 ) ± √(𝛼 + 𝛿 )2 − 4(𝛼𝛿 − 𝛽𝛾) , 2.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 37. (3.47). 2𝜆1,2 = (𝛼 + 𝛿 ) ± √(𝛼 + 𝛿 )2 − 4(𝛼𝛿 − 𝛽𝛾).. Apabila nilai dari 𝜆1 dan 𝜆2 disubstitusi ke persamaan (3.45) maka akan di peroleh 𝛽 , 𝜆1 − 𝜆2. 𝐴1 =. 𝐵1 =. 𝛽 𝐴2 = , 𝜆1 − 𝜆2. 𝜆1 − 𝛼 , 𝜆1 − 𝜆2. (3.48). 𝜆2 − 𝛼 𝐵2 = . 𝜆1 − 𝜆2. Menurut Ross (1984:303) penyelesaian umum dari persamaan (3.41) dapat ditulis ke dalam bentuk 𝑢(𝑡) = 𝑐1 𝐴1 𝑒 𝜆1 𝑡 + 𝑐2 𝐴2 𝑒 𝜆2 𝑡 , 𝑤 (𝑡) = 𝑐1 𝐵1 𝑒. 𝜆1 𝑡. + 𝑐2 𝐵2 𝑒. 𝜆2 𝑡. (3.49). .. Apabila persamaan (3.48) disubstitusi ke persamaan (3.49) maka akan diperoleh 𝑢(𝑡) = 𝑐1 (. 𝛽 𝛽 ) 𝑒 𝜆1 𝑡 + 𝑐2 ( ) 𝑒 𝜆2 𝑡 , 𝜆1 − 𝜆2 𝜆1 − 𝜆2. (3.50). 𝜆1 − 𝛼 𝜆 𝑡 𝜆2 − 𝛼 𝜆 𝑡 𝑤 (𝑡) = 𝑐1 ( ) 𝑒 1 + 𝑐2 ( )𝑒 2 . 𝜆1 − 𝜆2 𝜆1 − 𝜆2 Diketahui bahwa kondisi nilai awal dari persamaan (3.41) adalah 𝑢0 = 𝑢(𝑡0 ),. 𝑤0 = 𝑤(𝑡0 ),. dengan menggunakan kondisi nilai awal tersebut dapat dicari nilai dari 𝑐1 dan 𝑐2 , sehingga dengan melakukan operasi aljabar akan diperoleh masing-masing 𝑢0 𝑒 −𝜆1 𝑡0 (𝜆2 − 𝛼 ) 𝑐1 = − + 𝑤0 𝛽. dan. 𝑐2 = (. 𝑢0 (𝜆1 − 𝛼) − 𝑤0 ) 𝑒 −𝜆2 𝑡0 . 𝛽. Hasil dari substitusi nilai 𝑐1 dan 𝑐2 yang telah diperoleh ke persamaan (3.50) adalah sebagai berikut: 𝑢 (𝑡 ) = − (. 𝛽 𝜆1 −𝜆2. ) [(. 𝜆2 −𝛼 𝛽. ) 𝑢0 − 𝑤0 ] 𝑒 𝜆1 (𝑡−𝑡0 ) + (. 𝛽 𝜆1 −𝜆2. ) [(. 𝜆2 −𝛼 𝛽. ) 𝑢0 −. (3.51a). 𝑤0 ] 𝑒 𝜆2 (𝑡−𝑡𝑜 ) , 𝑤(𝑡) = − ( 𝜆1 −𝛼 ) [(𝜆2 −𝛼 ) 𝑢0 − 𝑤0 ] 𝑒 𝜆1 (𝑡−𝑡0 ) + ( 𝜆2 −𝛼 ) [(𝜆1 −𝛼 ) 𝑢0 − 𝜆 −𝜆 𝛽 𝜆 −𝜆 𝛽 1. 2. 𝑤0 ] 𝑒 𝜆2 (𝑡−𝑡0 ) , dimana. 1. 2. (3.51b).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 38. 2𝜆1,2 = (𝛼 + 𝛿 ) ± √(𝛼 + 𝛿 )2 − 4(𝛼𝛿 − 𝛽𝛾) . Persamaan (3.51) di atas merupakan penyelesaian umum dari persamaan (3.41).. Skema beda eksak untuk persamaan (3.41) diperoleh dengan membuat substitusi berikut pada persamaan (3.51a) dan persamaan (3.51b): 𝑡0 → 𝑡𝑘 = Δ𝑡(𝑘), 𝑡 → 𝑡𝑘+1 = Δ𝑡(𝑘 + 1), 𝑢0 → 𝑢𝑘 , 𝑢(𝑡) → 𝑢𝑘+1 , 𝑤0 → 𝑤𝑘 , { 𝑤(𝑡) → 𝑤𝑘+1 .. (3.52). Hasil dari substitusi di atas adalah sebagai berikut: 𝑢𝑘+1 = − ( 𝜆. 𝛽. 1 −𝜆2. ) [(. 𝜆2 −𝛼 𝛽. ) 𝑢𝑘 − 𝑤𝑘 ] 𝑒 𝜆1 Δ𝑡 + (𝜆. 𝛽. 1 −𝜆2. ) [(. 𝜆2 −𝛼 𝛽. ) 𝑢𝑘 −. (3.53a). 𝑤𝑘 ] 𝑒 𝜆2 Δ𝑡 , 𝑤𝑘+1 = − ( 𝜆1 −𝛼 ) [(𝜆2 −𝛼 ) 𝑢𝑘 − 𝑤𝑘 ] 𝑒 𝜆1 Δ𝑡 + ( 𝜆2 −𝛼 ) [(𝜆1 −𝛼 ) 𝑢𝑘 − 𝜆 −𝜆 𝛽 𝜆 −𝜆 𝛽 1. 2. 1. 2. (3.53b). 𝑤𝑘 ] 𝑒 𝜆2 Δ𝑡 . Dengan melakukan operasi aljabar pada persamaan (3.53a) dan persamaan (3.53b) akan diperoleh persamaan sebagai berikut: 𝑢𝑘+1 − 𝜓𝑢𝑘 = 𝛼𝑢𝑘 + 𝛽𝑤𝑘 , 𝜙. (3.54). 𝑤𝑘+1 − 𝜓𝑤𝑘 = 𝛾𝑢𝑘 + 𝛿𝑤𝑘 , 𝜙. (3.55). dimana 𝜓 ≡ 𝜓(𝜆1 , 𝜆2 , Δ𝑡) =. 𝜆1 𝑒 𝜆2 Δ𝑡 − 𝜆2 𝑒 𝜆1 Δ𝑡 , 𝜆1 − 𝜆2. 𝜙 ≡ 𝜙(𝜆1 , 𝜆2 , Δ𝑡) =. 𝑒 𝜆1 Δ𝑡 − 𝑒 𝜆2 Δ𝑡 . 𝜆1 − 𝜆2. Ruas kiri dari persamaan (3.54) dan persamaan (3.55) merupakan turunan diskret laju satu untuk persamaan (3.41a) dan persamaan (3.41b), yaitu 𝑑𝑢 𝑢𝑘+1 − 𝜓𝑢𝑘 → , 𝑑𝑡 𝜙.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 39. 𝑑𝑤 𝑤𝑘+1 − 𝜓𝑤𝑘 → . 𝑑𝑡 𝜙. 3.. Aturan Pemodelan Beda Hingga Nonstandar. Berdasarkan subbab sebelumnya yang membahas skema beda hingga eksak untuk suatu persamaan diferensial khususnya persamaan diferensial biasa, diberikan aturan atau syarat untuk mengkonstruksi model-model diskret yang berlaku untuk persamaan diferensial biasa dan persamaan diferensial parsial, sebagai berikut: 1.. Orde dari turunan diskret harus persis sama dengan orde dari turunan persamaan diferensial terkait.. 2.. Fungsi penyebut untuk turunan diskret harus secara umum dinyatakan dalam bentuk fungsi yang lebih rumit dari selisih jarak atau Δ𝑡 yang biasa digunakan. Misalkan pada contoh 1, 2 dan 3 fungsi penyebut untuk turunan diskretnya adalah (. 3.. 1−𝑒 −𝜆Δ𝑡 𝜆. Δ𝑡. ) , 4sin2 ( 2 ),. 𝑒 𝜆1 Δ𝑡 −1 𝜆1. .. Bentuk nonlinear harus secara umum dimodelkan secara nonlokal pada komputasi grid atau kisi. Misalnya pada persamaan (3.2.5) pada contoh 3 bentuk 𝑦 2 diaproksimasi pada dua titik yang berbeda 𝑦 2 → 𝑦𝑘+1 𝑦𝑘 , dengan indeks 𝑘 bersesuaian dengan langkah variabel bebasnya. Hal ini juga berlaku untuk persamaan diferensial parsial nonlinear misalnya bentuk 𝑢2 diaproksimasi pada dua titik yang berbeda yaitu 𝑘 𝑘+1 𝑢2 → 𝑢𝑚−1 𝑢𝑚 ,. dengan indeks 𝑘 dan 𝑚 bersesuaian dengan langkah dari dua variabel bebas yang berbeda. 4.. Penyelesaian khusus dari persamaan diferensial juga harus menjadi penyelesaian diskret dari model-model beda hingga.. 5.. Persamaan beda hingga seharusnya tidak memiliki penyelesaian yang tidak sesuai dengan penyelesaian dari persamaan diferensial..

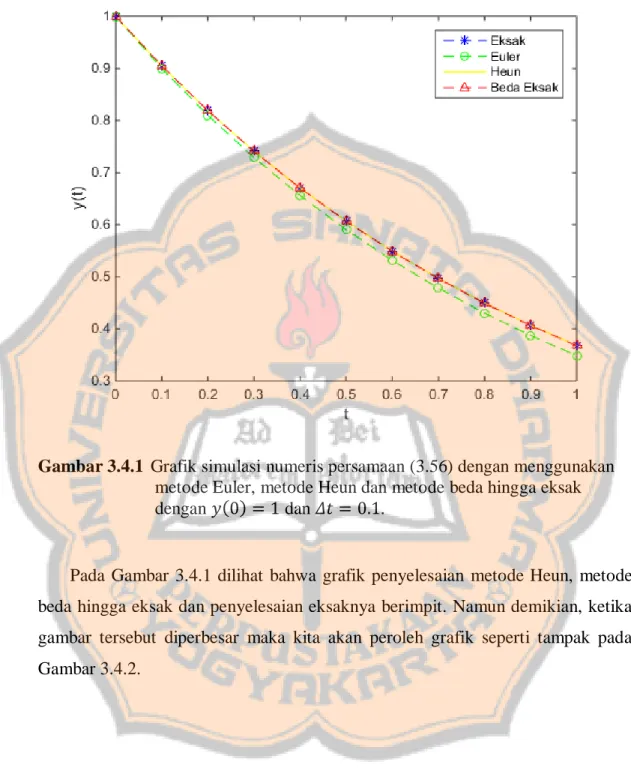
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 40. 4.. Perbandingan Penyelesaian. Pada bagian ini akan dibandingkan penyelesaian metode Euler, metode Heun, beda hingga standar dan penyelesaian dari metode beda hingga eksak dengan menggunakan program MATLAB. Akan dilihat dari ketiga penyelesaian tersebut yang mendekati penyelesaian eksaknya atau penyelesaian yang diperoleh secara analitik. Untuk membandingkan penyelesaian ini akan digunakan contoh 1 yaitu persamaan (3.26), contoh 2 persamaan (3.30) dan contoh 3 yaitu persamaan (3.37).. Contoh 1 Diketahui persamaan diferensial dengan suatu nilai awal 𝑑𝑦 = −𝑦, 𝑑𝑡. 𝑦(0) = 1.. (3.56). Akan dicari nilai 𝑦1 , 𝑦2 , 𝑦3 , … , 𝑦10 dari penyelesaian analitik dan penyelesaian dari metode Euler, metode Heun, dan metode beda hingga eksak. Penyelesaian eksak dari persamaan diferensial di atas adalah 𝑦 = 𝑒 −𝑡 , penyelesaian yang dihasilkan dengan menggunakan metode Euler untuk persamaan di atas adalah 𝑦𝑘+1 = −Δ𝑡𝑦𝑘 + 𝑦𝑘 . Penyelesaian yang dihasilkan dengan menggunakan metode Heun untuk persamaan di atas adalah 𝑦̃𝑘+1 = 𝑦𝑘 + Δ𝑡 𝑓(𝑡𝑘 , 𝑦𝑘 ), 𝑦𝑘+1 = 𝑦𝑘 +. Δ𝑡 (𝑓(𝑡𝑘 , 𝑦𝑘 + 𝑓 (𝑡𝑘+1 , 𝑦̃𝑘+1 ), 2. dengan 𝑓 (𝑡, 𝑦) = −𝑦. Sedangkan penyelesaian yang dihasilkan dengan menggunakan metode beda hingga eksak adalah 𝑦𝑘+1 = 𝑒 −Δ𝑡 𝑦𝑘 . Gambar 3.4.1 menunjukkan grafik hasil simulasi dari metode Euler, metode Heun, dan metode beda hingga eksak dengan nilai awal 𝑦(0) = 1 dan Δ𝑡 = 0.1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 41. Gambar 3.4.1 Grafik simulasi numeris persamaan (3.56) dengan menggunakan metode Euler, metode Heun dan metode beda hingga eksak dengan 𝑦(0) = 1 dan 𝛥𝑡 = 0.1.. Pada Gambar 3.4.1 dilihat bahwa grafik penyelesaian metode Heun, metode beda hingga eksak dan penyelesaian eksaknya berimpit. Namun demikian, ketika gambar tersebut diperbesar maka kita akan peroleh grafik seperti tampak pada Gambar 3.4.2..

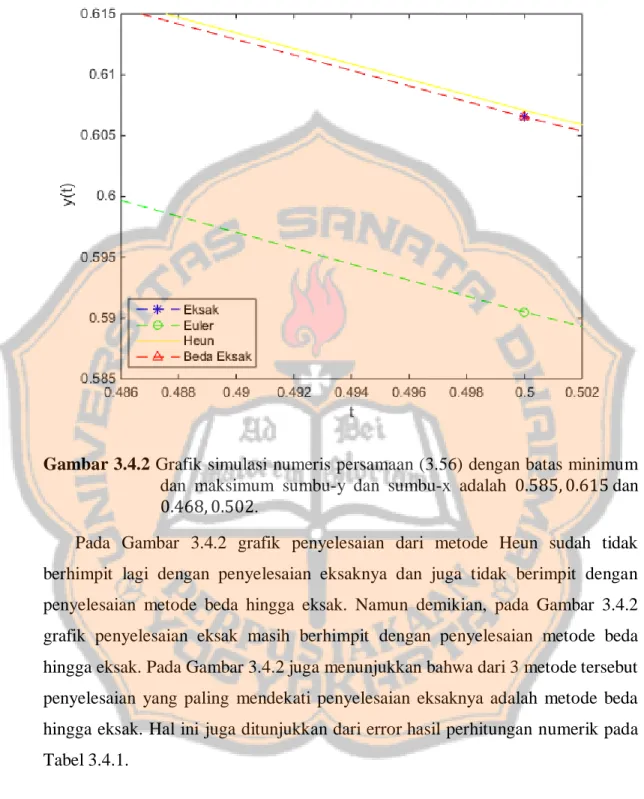
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 42. Gambar 3.4.2 Grafik simulasi numeris persamaan (3.56) dengan batas minimum dan maksimum sumbu-y dan sumbu-x adalah 0.585, 0.615 dan 0.468, 0.502. Pada Gambar 3.4.2 grafik penyelesaian dari metode Heun sudah tidak berhimpit lagi dengan penyelesaian eksaknya dan juga tidak berimpit dengan penyelesaian metode beda hingga eksak. Namun demikian, pada Gambar 3.4.2 grafik penyelesaian eksak masih berhimpit dengan penyelesaian metode beda hingga eksak. Pada Gambar 3.4.2 juga menunjukkan bahwa dari 3 metode tersebut penyelesaian yang paling mendekati penyelesaian eksaknya adalah metode beda hingga eksak. Hal ini juga ditunjukkan dari error hasil perhitungan numerik pada Tabel 3.4.1..