PEMODELAN MATEMATIKA PENGARUH IMUNOTERAPI TERHADAP PENYAKIT TUMOR

(1)

PEMODELAN MATEMATIKA PENGARUH IMUNOTERAPI

TERHADAP PENYAKIT TUMOR

SKRIPSI

Untuk Memenuhi Sebagai Syarat Guna Memperoleh Derajat Sarjana S – 1

Program Studi Matematika

Disusun oleh:

MOHAMMAD ARIF MAULIDA 10610022

PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI SUNAN KALI JAGA YOGYAKARTA

(2)

(3)

(4)

(5)

v

HALAMAN MOTTO

”Barang siapa keluar untuk mencari ilmu maka dia berada di jalan Allah”

(6)

vi

HALAMAN PERSEMBAHAN

Kupersembahkan karya sederhana ini kepada

Keponakanku tersayang

Ahmad Hably Hudaya

Dan

(7)

vii

KATA PENGANTAR

Puji syukur penulis panjatkan kehadirat Allah SWT, yang telah melimpahkan rahmat dan hidayah-Nya, sehingga skripsi yang berjudul “Pemodelan Matematika Pengaruh Imunoterapi terhadap Penyakit Tumor” dapat terselesaikan guna memenuhi syarat untuk memperoleh gelar Sarjana Matematika di Program Studi Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Sunan Kalijaga Yogyakarta. Sholawat serta salam senantiasa tercurah kepada Nabi Muhammad SAW sebagai cahaya bagi seluruh alam.

Penulis menyadari skripsi ini tidak akan selesai tanpa dukungan, bantuan, bimbingan dan arahan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terimakasih kepada:

1. Bapak Prof. Drs. Yudian Wahyudi, M.A.,Ph.D., selaku Rektor Universitas Islam Negeri Sunan Kalijaga Yogyakarta.

2. Bapak Dr. Murtono M.Si., selaku Dekan Fakultas Sains dan Teknologi Univeristas Islam Negeri Sunan Kalijaga Yogyakarta.

3. Bapak Dr. M Wakhid Musthofa M.Sc., selaku ketua Prodi Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Yogyakarta.

4. Bapak Noor Saif Muhammad Mussafi, M.Sc selaku Dosen Penasehat Akademik Program Studi Matematika Universitas Islam Negeri Sunan Kalijaga Yogyakarta.

(8)

viii

5. Bapak Sugiyanto, M.Si selaku Dosen Pembimbing Skripsi, atas bimbingan dan arahannya, yang memberikan semangat serta berkenan meluangkan waktunya sehingga skripsi ini dapat terselesaikan.

6. Bapak/Ibu Dosen dan Staf Fakultas Sains dan Teknologi Universitas Islam Negeri Sunan Kalijaga Yogyakarta, atas ilmu, bimbingan dan pelayanan yang diberikan selama perkuliahan hingga skripsi ini terselesaikan.

7. Ibunda ku tercinta, Ibu Sunarti yang senantiasa memberikan doa, semangat serta dukungan materiilnya.

8. Kakak-kakakku yang selalu memberikan dukungan baik spiritual maupun material.

9. Teman-temanku Keluarga Kudus Yogyakarta yang telah banyak menyumbangkan pikiran dan waktunya.

10. Teman seperjuangan Matematika 2010 Cahyo, Alfi, Hasan, Ikhsan, Azzun dan lainnya yang tidak dapat saya sebutkan satu per satu.

11. Semua pihak yang tidak dapat penulis sebutkan semua, yang telah membantu dalam penyusunan skripsi ini.

Penulis menyadari bahwa penyusunan skripsi ini masih banyak kekurangan dan kesalahan. Namun penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak.

Yogyakarta, 23 Mei 2017 Penulis,

Mohammad Arif Maulida 10610022

(9)

ix DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PENGESAHAN ... ii

HALAMAN PERSETUJUAN ... iii

SURAT PERNYATAAN KEASLIAN SKRIPSI ... iv

HALAMAN MOTTO ... v

HALAMAN PERSEMBAHAN ... vi

KATA PENGANTAR ... vii

DAFTAR ISI ... ix

DAFTAR GAMBAR ... xii

DAFTAR TABEL ... xiii

ABSTRACT ... xv INTISARI ... xvi BAB I PENDAHULUAN ... 1 1.1. Latar Belakang ... 1 1.2. Rumusan Masalah ... 3 1.3. Batasan Masalah ... 4 1.4. Tujuan Penelitian ... 4 1.5. Manfaat Penelitian ... 4 1.6. Tinjauan Pustaka ... 5

(10)

x

1.7. Sistematika Penelitian ... 8

BAB II LANDASAN TEORI ... 9

2.1. Tinjauan Medis ... 9

2.1.1. Tumor ... 9

2.1.2. Imunoterapi ... 11

2.2. Tinjauan Matematis ... 12

2.2.1. Operasi Matriks ... 12

2.2.2. Nilai Eigen dan Vektor Eigen ... 14

2.2.3. Persamaan Diferensial ... 16

2.2.4. Sistem persamaan diferensial ... 18

2.2.5. Solusi Sistem Persamaan Diferensial ... 20

2.2.6. Titik Ekuilibrium ... 21

2.2.7. Kestabilan Titik Ekuilibrium ... 23

2.2.8. Potret Fase Sistem Linear ... 27

2.2.9. Kriteria Routh-Hurwitz ... 32

2.2.10. Pemodelan Matematika ... 34

2.2.11. Mekanisme Mechaelis Menten ... 36

BAB III METODOLOGI PENELITIAN ... 40

BAB IV PEMBAHASAN ... 43

4.1. Pembentukan Model ... 43

4.2. Titik Ekuilibrium ... 48

4.2.1. Titik Ekuilibrium Bebas Tumor ... 52

4.2.2. Titik Ekuilibrium Endemi ... 54

4.3. Analisis Kestabilan Titik Ekuilibrium ... 63

(11)

xi

3.2.2 Kestabilan Titik Ekuilibrium Terinfeksi Tumor ... 68

4.4. Simulasi Model ... 82

4.4.1 Simulasi Tumor dengan Imunoterapi ... 83

4.4.2 Simulasi Tumor tanpa Imunoterapi ... 87

4.5. Interpretasi Solusi ... 91 BAB V PENUTUP ... 92 5.1 Kesimpulan... 92 5.2 Saran ... 93 DAFTAR PUSTAKA ... 94 LAMPIRAN ... 96

(12)

xii

DAFTAR GAMBAR

Gambar 2.1 Sel Tumor ... 10

Gambar 2.2 Titik Ekuilibrium ... 24

Gambar 2.3 Potret Fase Kasus I ... 29

Gambar 2.4 Potret Fase Kasus II... 29

Gambar 2.5 Potret Fase Kasus III ... 30

Gambar 2.6 Potret Fase Kasus IV ... 31

Gambar 2.7 Potret Fase Kasus V ... 31

Gambar 2.8 Proses Pemodelan Matematika... 35

Gambar 2.9 Skema Reaksi Enzim ... 36

Gambar 2.10 Hubungan laju reaksi enzim dan konsentrasi substrat ... 38

Gambar 3.1 Roadmap Penelitian ... 42

Gambar 4.1 Diagram Transfer Pengaruh Imunoterapi ... 46

Gambar 4.2 Kondisi saat antigenitas tumor 0.05 ... 86

Gambar 4.3 Kondisi saat antigenitas tumor 0.03 ... 86

(13)

xiii

DAFTAR TABEL

Tabel 1.1 Tabel Tinjauan Pustaka ... 7

Tabel 2.1 Tabel Routh-Hurwitz ... 33

Tabel 2.2 Tabel contoh kriteria Routh-Hurwitz ... 34

Tabel 4.1 Tabel Nilai Parameter ... 45

Tabel 4.2 Nilai Parameter Simulasi ... 83

Tabel 4.3 Nilai titik ekuilibrium P₀ ... 83

Tabel 4.4 Nilai titik ekuilibrium P₁ ... 84

(14)

xiv

DAFTAR LAMBANG

E = Populasi sel Efektor

T = Populasi sel Tumor

I = Interleukin

 = Nilai eigen

J = Matriks Jacobian

 = Bilangan positif kecil

 = Bilangan positif kecil 1

P = Titik ekuilibrium bebas tumor

2,3

P = Titik ekuilibrium terinfeksi tumor

2,3

p = Laju poliferasisel efektor

2



= Half-life dari sel efektor

1,2,3

g = Half-saturation untuk pembersihan kanker

1,2

s = Parameter pengobatan

a = Parameter pembersihan kanker

b = Kapasitas sel tumor 2

r = Laju pertumbuhan tumor

 

i

e



(15)

xv

ABSTRACT

MATHEMATICAL MODELING OF IMMUNOTHERAPY ON TUMOR-IMMUNE DISEASES

By

The mathematical model of the influence of immunotherapy on tumor disease is a differential equation model. The problem in this immunotherapy is how to know when tumor cells will disappear. This paper studied how much influence immunotherapy on tumor cell cleaning based on assumptions that have been made. Research is solved mathematically by using the theory of stability.

The model analysis stage involves looking for equilibrium points, then analyzing the stability of the equilibrium point using Routh-Hurwitz criteria and numerically. Next gives a simulation as a model approach to the values of the given parameters.

The results of the model analysis it can be concluded that the use of immunotherapy in tumor treatment is still not effective, looking at the time period required until the tumor is in stable condition. The mathematical model of immunotherapy influence on tumor disease has three equilibrium points where one equilibrium point is a free equilibrium points and the other two are tumor-infected equilibrium points. The equilibrium condition of the equilibrium point is based on simulation 1, simulation 2 and simulation 3. In simulation 1 and simulation 2, the equilibrium points are unstable and have saddle point type, meaning the effector cell, tumor cells and iterleukin-2 will grow in constant condition, there are tumor cells in the body. In simulation 3, there is a stable equilibrium point of the tumor that is asymptotically stable and has a point type node, meaning the effector cell population and interleukin-2 will be constant at the equilibrium point whereas the tumor cell population will disappear over time.

Keywords: immunotherapy, equilibrium point, routh-hurwitz, modeling of tumor disease

(16)

xvi

INTISARI

PEMODELAN MATEMATIKA PENGATUH IMUNOTERAPI TERHADAP PENYAKIT TUMOR

Oleh

Model matematika tentang pengaruh imunoterapi terhadap penyakit tumor merupakan model berbentuk persamaan diferensial. Permasalahan yang timbul pada penggunaan imunoterapi ini adalah bagaimana mengetahui kapan sel tumor akan menghilang. Penelitian ini mempelajari seberapa besar pengaruh imunoterapi terhadap pembersihan sel tumor berdasarkan asumsi-asumsi yang telah dibuat. Penelitian diselesaikan secara matematis dengan menggunakan teori kestabilan.

Tahap menganalisis model meliputi mencari titik ekuilibrium bebas penyakit dan endemik, kemudian menganalisis kestabilan titik ekuilibrium menggunakan kriteria Routh-Hurwitz dan secara numerik. Selanjutnya memberikan simulasi sebagai bentuk pendekatan model terhadap nilai-nilai parameter yang diberikan.

Berdasarkan hasil dari analisis model dapat disimpulkan bahwa penggunaan imunoterapi dalam pengobatan kanker masih belum efisien, melihat jangka waktu yang dibutuhkan sampai tumor dalam kondisi stabil. Model matematika pengaruh imunoterapi terhadap penyakit tumor meiliki tiga titik ekuilibrium yang mana satu titik ekuilibrium merupakan titik ekuilibrium bebas tumor dan dua titik ekuilibrium yang lain merupakan titik ekuilibrium terinfeksi tumor. Kondisi kestabilan titik ekuilibrium berdasarkan simulasi 1, simulasi 2 dan simulasi 3. Pada simulasi 1 dan simulasi 2, ketiga titik ekuilibrium tidak stabil dan memiliki jenis titik saddle, artinya populasi sel efektor, sel tumor dan iterleukin-2 akan tumbuh secara beriringan, sehingga masih terdapat sel tumor dalam tubuh. Pada simulasi 3, terdapat satu titik ekuilibrium bebas tumor yang stabil asimtotik dan memiliki jenis titik node, artinya populasi sel efektor dan interleukin-2 akan konstan pada titik ekuilibrium sedangkan populasi sel tumor akan menghilang seiring bertambahnya waktu.

Kata kunci : imunoterapi, titik ekuilibrium, kriteria routh-hurwitz, pemodelan penyakit tumor

(17)

1

BAB I

PENDAHULUAN

Pada bab ini akan dijelaskan tentang latar belakang yang merupakan dasar dari penelitian ini dan merumuskan dalam suatu rumusan masalah. Batasan masalah dan rumusan masalah yang telah disusun kemudian digunakan untuk menentukan tujuan penelitian agar memiliki arahan yang jelas mengenai apa saja yang ingin dicapai. Selanjutnya pada bab ini juga dijelaskan manfaat penelitian, tinjauan pustaka, dan sistematika penulisan skripsi ini.

1.1. Latar Belakang Masalah

Tumor ganas atau yang sering dikenal dengan kanker merupakan salah satu penyebab kematian utama di seluruh dunia. Pada tahun 2012, kanker menjadi penyebab kematian sekitar 8,2 juta orang. Berdasarkan data GLOBOCAN, International Agency for Research on Cancer (IARC), diketahui bahwa pada tahun 2012 terdapat 14.067.894 kasus baru kanker dan 8.201.575 kematian akibat kanker di seluruh dunia. Pada kuisioner Riset Kesehatan Dasar (Riskesdas) yang dilaksanakan oleh Badan Penelitian dan Pengembangan Kesehatan, didapatkan prevalensi penderita kanker pada penduduk semua umur di Indonesia sebesar 1,4%. Prevalensi kanker tertinggi berada pada Provinsi DI Yogyakarta, yaitu sebesar 4,1%, jauh lebih tinggi dibandingkan dengan angka nasional. Tingginya kasus baru kanker dan sekitar 40% dari kematian akibat

(18)

2

kanker berkaitan erat dengan faktor resiko kanker yang seharusnya dapat dicegah (Kemenkes RI, 2015). Kanker yang diketahui sejak dini memiliki kemungkinan untuk mendapatkan penanganan lebih baik. Oleh karena itu perlu dilakukan upaya pencegahan untuk meningkatkan kesadaran masyarakat dalam mengenali gejala dan resiko penyakit kanker sehingga dapat menentukan langkah-langkah pencegahan dan deteksi dini yang tepat (LKKI,

http://www.lembagakonsultankankerindonesia.or.id/?Kanker diakses 22 Mei

2017).

Pengobatan kanker standar yang ada saat ini yaitu operasi, terapi radiasi, kemoterapi dan imunoterapi. Masing-masing pengobatan tersebut memiliki keuntungan dan kerugian, seperti pada kemoterapi yang memiliki efek samping yaitu selain membunuh sel tumor juga membunuh sel normal dan menyebabkan beberapa efek samping seperti mual, muntah dan anemia. Untuk beberapa kanker, pengobatan terbaik dilakukan dengan kombinasi dari operasi, terapi radiasi dan kemoterapi. Imunoterapi merupakan metode baru dalam pengobatan kanker, imunoterapi adalah upaya untuk meningkatkan sistem imunitas tubuh, untuk mengalahkan sel-sel kanker dengan cara meningkatkan reaksi kekebalan tubuh terhadap sel kanker (Radioterapi-Wikipedia, 2017).

Interaksi sel efektor dan sel tumor telah dimodelkan secara matematis oleh Kuznetsov, dkk (1994). Dalam penelitian tersebut dijelaskan aplikasi model matematika sederhana untuk menyelidiki dinamika pertumbuhan sel efektor dan sel tumor dengan tujuan memprediksi kombinasi optimal dari pendekatan yang mengarah ke pembersihan tumor. Pembentukan model matematika yang

(19)

3

dilakukan Kuznetsov berdasar pada model predator prey. Pada dasarnya model

predator prey diterapkan untuk penyakit kanker karena dalam penyakit kanker

sel-sel imun berkembang dengan cepat dan tidak terbatas sedangkan sel tumor terus memangsa sel imun sehingga terjadi mangsa-pemangsa dalam tingkatan penyakit kanker.

Dalam penelitian ini imunoterapi akan ditambahkan pada model, sehingga terdapat tiga kelas model. Kelas pertama sel efektor, kelas kedua sel tumor dan kelas ketiga imunoterapi yang berupa interleukin-2. Kemudian dibahas bagaimana pembentukan model matematika dan dianalisis kestabilan titik ekuilibrium pada model. Selanjutnya dengan software MATLAB dilakukan simulasi model sehingga dapat diketahui bagaimana pengaruh imunoterapi terhadap pertumbuhan sel tumor.

1.2. Rumusan Masalah

Secara terperinci dari latar belakang di atas, dapat dirumuskan beberapa masalah yang akan dibahas yaitu mencakup hal hal berikut :

1. Bagaimana bentuk model matematika pengaruh imunoterapi terhadap penyakit tumor?

2. Bagaimana analisis kestabilan di sekitar titik kesetimbangan dari model matematika untuk melihat pengaruh imunoterapi terhadap penyakit tumor? 3. Sejauh mana efektifitas imunoterapi dalam menyembuhkan penyakit tumor.

(20)

4

1.3. Batasan Masalah

Permasalahan yang dibahas dalam skripsi ini dibatasi pada: 1. Model hanya dipengruhi oleh imunoterapi dengan interleukin-2.

2. Analisis yang digunakan adalah analisis titik kesetimbangan dengan metode nilai karakteristik.

3. Analisis model matematika menggunakan parameter-parameter yang tersedia pada literatur.

4. Simulasi model menggunakan software MATLAB. 1.4. Tujuan Penelitian

Berdasar rumusan masalah di atas maka tujuan dari penelitian ini adalah sebagai berikut :

1. Memformulasikan model matematika tentang pengaruh imunoterapi terhadap penyakit tumor.

2. Menganalisis kestabilan titik kesetimbangan pada model matematika tentang pengaruh imunoterapi terhadap penyakit tumor.

3. Menganalisis titik ekuilibrium guna melihat sejauh mana efektifitas imunoterapi dalam menyembuhkan penyakit tumor.

1.5. Manfaat Penelitian

Mengacu pada tujuan penelitian di atas, maka manfaat penelitian yang diperoleh adalah :

1. Melengkapi hasil penelitian yang dilakukan para peneliti di bidang pengobatan tumor dengan imunoterapi.

(21)

5

2. Memberi kontribusi dalam pengembangan di bidang matematika terapan khususnya matematika biolog dan persamaan diferensial.

3. Sebagai dasar penelitian-penelitian selanjutnya yang berkaitan dengan penyakit tumor.

1.6. Tinjauan Pustaka

Tinjauan pustaka pada penelitian ini mengacu pada literatur-literatur yang tersebut dalam daftar pustaka. Penelitian dilakukan dengan mempelajari beberapa buku, jurnal, karya ilmiah dan penelitian sebelumnya yang berkaitan dengan penelitian ini. Dalam penulisan tugas akhir ini digunakan beberapa sumber pustaka. Untuk pengertian dasar aljabar linear tentang matriks, determinan matriks dan nilai eigen mengacu pada Aljabar Linear Elementer (Anton, 2004). Beberapa pengertian dasar persamaan diferensial mengacu pada

Differential Equation (Ross, 1984). Selanjutnya mengenai beberapa materi dasar

teori sistem, yaitu sistem nonlinear, pengertian matriks Jacobian, titik ekuilibrium, linearisasi, serta teorema penting tentang kestabilan sistem non linear mengacu pada Differential Equation and Dynamical System (Perko 1991),

Mathematical System Theory (Olsder, 2004), dan Mathematical Biology (Muray,

1993).

Adapun jurnal dan penelitian yang berkaitan dengan penelitian yang sekarang adalah D. Kirschner dan J. C. Panneta (1998) dalam papernya yang berjudul “Modelling Immunoterapy of the tumor-immune interaction”. Dalam paper tersebut dijelaskan bagian bagian dari imunoterapi seperti pengaruh

(22)

6

Kuznetsov (1994) dalam papernya yang berjudul “Nonlinear dynamics of

immunogenic tumors”. Dalam paper ini pemodelan matematika hanya dibatasi

pada sel efektor dan sel tumor saja. Selanjutnya Ratnasari Dwi Ambarwati (2014) dalam penelitiannya yang berjudul “Analisis Model Matematika Tentang Pengaruh Terapi Gen Terhadap Dinamika Pertumbuhan Sel Efektor dan Sel Tumor dalam Pengobatan Kanker”, paper ini membahas tentang bagaimana pengaruh terapi gen terhadap pertumbuhan sel tumor.

Dalam skripsi ini akan diuraikan dan dijabarkan pembahasan bagaimana pengaruh imunoterapi (Interleukin-2) terhadap penyakit tumor kemudian mengnalisis bagaimana kestabilan titik kesetimbangan pada model.

(23)

7

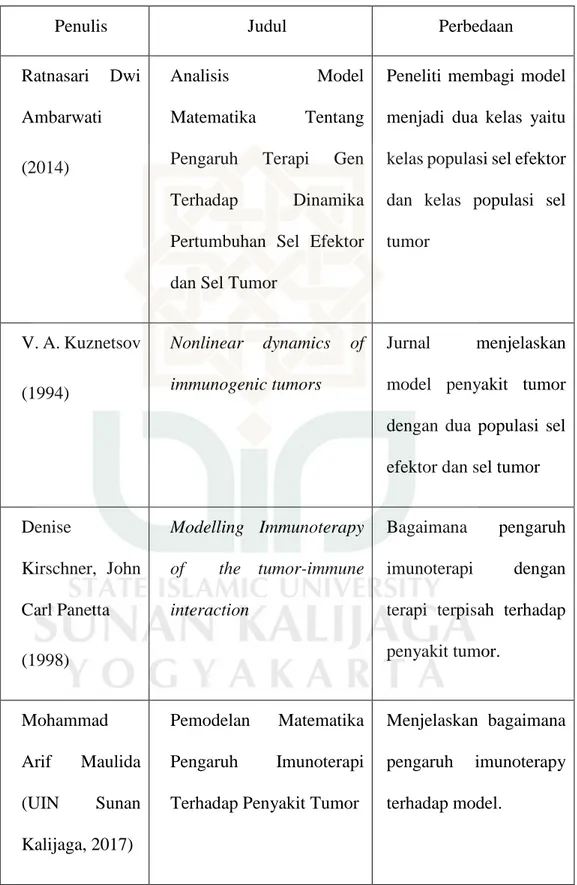
Tabel 1.1 Tinjauan Pustaka

Penulis Judul Perbedaan

Ratnasari Dwi Ambarwati (2014)

Analisis Model Matematika Tentang Pengaruh Terapi Gen Terhadap Dinamika Pertumbuhan Sel Efektor dan Sel Tumor

Peneliti membagi model menjadi dua kelas yaitu kelas populasi sel efektor dan kelas populasi sel tumor V. A. Kuznetsov (1994) Nonlinear dynamics of immunogenic tumors Jurnal menjelaskan model penyakit tumor dengan dua populasi sel efektor dan sel tumor

Denise Kirschner, John Carl Panetta (1998) Modelling Immunoterapy of the tumor-immune interaction Bagaimana pengaruh imunoterapi dengan terapi terpisah terhadap penyakit tumor. Mohammad Arif Maulida (UIN Sunan Kalijaga, 2017) Pemodelan Matematika Pengaruh Imunoterapi Terhadap Penyakit Tumor

Menjelaskan bagaimana pengaruh imunoterapy terhadap model.

(24)

8

1.7. Sistematika Penulisan

Secara garis besar sistematika pembahasan dalam penelitian ini sebagai berikut:

BAB I : PENDAHULUAN

Berisi latar belakang, rumusan masalah, batasan masalah, tujuan penelitian, manfaat penelitian, tinjauan pustaka dan sistematika penulisan.

BAB II : LANDASAN TEORI

Berisi tentang tori-teori penunjang yang akan digunakan dalam bab selanjutnya, meliputi teori-teori dasar aljabar linear, persamaan diferensial, dan teori sistem.

BAB III : METODE PENELITIAN

Berisi tentang proses atau cara ilmiah yang akan digunakan dalam penelitian ini meliputi kajian dalam bidang kedokteran dan matematika.

BAB IV : HASIL DAN PEMBAHASAN

Membahas model matematika penyakit tumor beserta kestabilannya berdasarkan titik ekuilibrium model tersebut yang selanjutnya dibuat simulasi numerik.

BAB V : PENUTUP

Berisi tentang kesimpulan dan saran yang dieroleh dari pembahasan yang telah dilakukan.

(25)

92 BAB V

PENUTUP

Pada bab ini akan diberikan kesimpulan dan saran-saran yang dapat diambil dari materi-materi yang telah dibahas pada bab-bab sebelumya.

5.1. Kesimpulan

Kesimpulan yang dapat diambil penulis setelah menyelesaikan pembahasan skripsi ini adalah :

1. Model matematika pengaruh imunoterapi terhadap penyakit tumor dibentuk atas tiga persamaan yaitu :

1 2 1 1 p EI dE cT E s dt   g I 





2 2 1 dT aET r T bT dt   g T 2 3 2 3 ET dI I s dt g T p _    

2. Model matematika pengaruh imunoterapi terhadap penyakit tumor memiliki tiga titik ekuilibrium yaitu titik ekuilibrium saat tidak ada tumor P0 



E T I0, 0, 0



dan titik ekuilibrium terinfeksi tumor P1



E T I1, ,1 1



dan P2 



E T I2, 2, 2



.

3. Berdasarkan pada simulasi 1 populasi sel efektor, sel tumor dan interleukin akan stabil stelah hari ke 1500, kemudian pada simulasi 2, ketiga titik ekuilibrium tidak memenuhi syarat keberadaan yang berarti sel efektor, sel tumor dan interleukin

(26)

93

berkembang secara fluktuatif seiring bertambahnya waktu t. Berdasarkan simulasi 3 terdapat dua titik ekuilibrium yang memenuhi syarat keberadaan yaitu P₀ dan

2

P yang berarti kondisi ketiga populasi berada pada titik kesetimbangan. Sehingga dapat diambil kesimpulan bahwa pengobatan kanker dengan metode imunoterapi kurang begitu efisien, karena membutuhkan waktu yang relatif cukup lama untuk menyembuhkan tumor.

5.2. Saran

Setelah membahas dan mengiplementasikan model pengaruh imunoterapi terhadap penyakit tumor, penulis menyarankan untuk penelitian selanjutnya membahas model terkait dengan penambahan variabel baru seperti kombinasi dengan terapi kanker lainnya. Kemudian juga membahas kestabilan global untuk titik ekuilibriumnya.

(27)

94

DAFTAR PUSTAKA

Anton, H & Rorres, C. 2004. Aljabar Linear Elementer. Jakarta:Erlangga.

Bender. 1978. An Introduction to Mathematical Modelling. USA: Jhon Wiley and Sons.

Haryanto, S & Nugroho, S. (2009). Terapi Pengobatan Tumor-Kanker. Yogyakarta: Kanisius.

International Agency for Research on Cancer (IARC) / WHO. (2012). GLOBOCAN 2012: Estimated cancer incidence, mortality, and prevalence

worldwide in 2012. Diakses melalui

http://globocan.iarc.fr/Pages/fact_sheets_population.aspx pada tanggal 15 Maret 2017.

Isanto, R.J. (2012). Pemodelan Matematika. Yogyakarta: Graha Ilmu.

Kementerian Kesehatan RI. (2013). Riset Kesehatan Dasar (RISKESDAS). Jakarta: Badan Litbang Kemenkes RI.

Kementerian Kesehatan RI. (2015). Buletin Jendela Data dan Informasi Kesehatan. Jakarta : Badan Litbang Kemenkes RI.

Kirschner, D & Panetta, JC. (1998). Modelling Immunotherapy of the Tumor-Immune Interaction. Journal of Mathematical Biology. 37(3). Hlm. 235-252. Kuznetsov, V.A. & Makalkin, I.A. (1994). Nonlinear Dynamics of Immunogenic Tumors: Parameter Estimation and Global Bifurcation Analysis. Bulletin of

Matheatical Biology. 56(2). Hlm. 295-321.

LKKI, (2015). Lembaga Konsultan Kanker Indonesia. Diakses melalui

http://www.lembagakonsultankankerindonesia.or.id/?Kanker pada tanggal 22 Mei 2017 Jam 20.38 WIB

Mamat, M, dkk. (2013). Mathematical Model of Cancer Treatments Using Immunotherapy, Chemotherapy and Biochemotherapy. Applied Mathematical Sciences, Vo. 7. Hlm. 247-261.

Masihi KN. (July 2001). “Fighting infection using immunomodulatory agents.” Expert Opin Biol Ther 1 (4). Hlm. 641.

Murray, J.D. (2001). Mathematical Biology: I. An Introduction. 3rd. New York: Springer.

Olsder, G.J. & van der Woude, J.W. 2004. Mathematical System Theory, Belanda: Deflt University Pers.

Perko, L. 1991. Differential Equations and Dynamical System. New York Springer Verlag.

(28)

95

Price et al., 2006. Bab 8 Gangguan Pertumbuhan, Proliferasi, dan Diferensiasi Sel. Jakarta: EGC, 150-158.

Sohail, A, dkk. (2015). Numerical Analysis of Fractional-order Tumor Model. International Journal of Biomathematics. 8(5). Hlm. 13.

Sehat Semua, http://sehatsemua.com/pengertian-kanker/ diakses pada 24 Mei 2017

Jam 19.05

Tsygvintsev, Alexei, dkk. (2012). A Mathematical Model of Gene Therapy for The Treatment of Cancer. Mathematical Models and Methods in Biomedicine. Springer-Verlag. Hlm. 357-373.

Widowati & Sutimin. (2007). Buku Ajar Pemodelan Mateatika. Semarang: FMIPA UNDIP.

Wikipedia. (2017). “Radioterapi”. https://id.wikipedia.org/wiki/Radioterapi.html diakses pada 7 Mei 2017 Jam 22.25 WIB.

World Health Organization. (2007). Prevention. cancer control: knowledge into action: WHO guide for effective programmes: module 2). Geneva: World Health Organization.

(29)

96

Lampiran 1

Program Simulasi 1

M-File 1

function dy = fungsi(t,y)%estimasi

p1=0.1245; p2=5; g1=2*10^7; g2=10^5; g3=10^3; m2=0.03; m3=10; A=1; b=10^-9; c=0.05; r2=0.18; s1=10^-3; s2=0.45; dy=[((c*y(2))-(m2*y(1))+((p1*y(1)*y(3))/(g1+y(3)))+s1);... ((r2*y(2))-(r2*y(2)*b*y(2))-((A*y(1)*y(2))/(g2+y(2))));... (((p2*y(1)*y(2))/(g3+y(2)))-(m3*y(3))+s2)]; end M-File 2 %Listing Program clear all

t = linspace(0,3500,100);%niliai t, jumlah titik %Equilibrium Point

%plot(1+0*t,0+0*t,'k*') %hold on

%Orbits

[t,y] = ode45('fungsi',t,[100 100 100]); plot(t,y(:,1),'b')% biru

hold on

[t,y] = ode45('fungsi',t,[100 100 100]); plot(t,y(:,2),'r')% red

hold on

[t,y] = ode45('fungsi',t,[100 100 100]); plot(t,y(:,3),'g')% green

hold on

(30)

97

Lampiran 2

M-File 1

p1=0.1245; p2=5; g1=2*10^7; g2=10^5; g3=10^3; m2=0.03; m3=10; A=0.9; b=10^-9; c=0.03; r2=0.18; s1=10^-3; s2=0.45; dy=[((c*y(2))-(m2*y(1))+((p1*y(1)*y(3))/(g1+y(3)))+s1);... ((r2*y(2))-(r2*y(2)*b*y(2))-((A*y(1)*y(2))/(g2+y(2))));... (((p2*y(1)*y(2))/(g3+y(2)))-(m3*y(3))+s2)]; end M-File 2 %Listing Program clear all

%Orbits

hold on

(31)

98

Lampiran 3

M-File 1

p1=0.1245; p2=5; g1=2*10^7; g2=10^5; g3=10^3; m2=0.03; m3=10; A=0; b=10^-9; c=00; r2=0.18; s1=0; s2=0; dy=[((c*y(2))-(m2*y(1))+((p1*y(1)*y(3))/(g1+y(3)))+s1);... ((r2*y(2))-(r2*y(2)*b*y(2))-((A*y(1)*y(2))/(g2+y(2))));... (((p2*y(1)*y(2))/(g3+y(2)))-(m3*y(3))+s2)]; end M-File 2 %Listing Program clear all

%Orbits

hold on

(32)

99

CURRICULUM VITAE

A. Data Pribadi

Nama Lengkap : Mohammad Arif Maulida

Umur : 24 Tahun

Tempat, Tanggal Lahir : Kudus, 23 November 1992

Agama : Islam

Status : Belum Nikah Jenis Kelamin : Laki-laki

Alamat : Jl. Masjid At Taqwa Gg. Kususma RT.03/RW.03 Loram Kulon No.591 Kecamatan Jati Kabupaten Kudus Jawa Tengah

Nomor HP : 083811133008

E-mail : arifmaulida@gmail.com

B. Latar Belakang Pendidikan Formal 1. SD Negeri 01 Loram Kulon (1998-2004) 2. MTs. NU TBS Kudus (2004-2007) 3. MA NU TBS Kudus (2007-2010)