BAB 4
HASIL SIMULASI DAN ANALISA
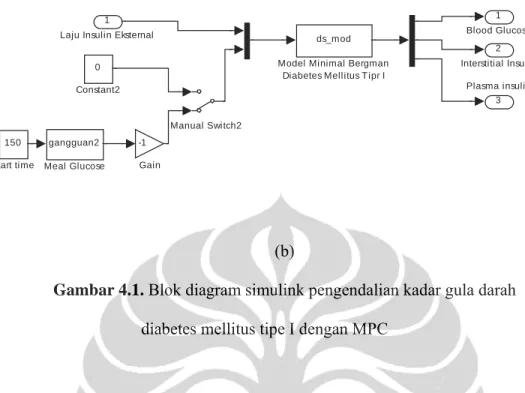
Bab ini membahas analisa dari uji eksperimen pengendalian kadar gula darah penderita diabetes mellitus tipe I dengan metode MPC dengan beberapa parameter penalaan yang berbeda. Simulasi dilakukan dengan menggunakan Simulink yang terdapat pada perangkat lunak MATLAB 7 seperti pada gambar 4.1.
Signal 2 trajectory blood glucose1
x3_out nilai insulin plasma
x2_out nilai insulin interstitial
x1_out nilai blood glucose z 1 Unit Delay u_kendali To Workspace3 set_point To Workspace2 150 Start time mpc_ani_3 S-Function
Output & SetPoint Blood Glucose gangguan2 Meal Glucose Manual Switch2 Manual Switch1 -1 Gain3 -1 Gain2 -1 Gain1 -1 Gain 0 Display1 Laju Insulin Ekste
Blood Glucose nterstitial Insulin Plasma insulin DIABETIC TYPE I SYSTEM
0 Constant2
0 Constant1
6.Output & SetPoint Blood Glucose 5.error 4.insulin interstitial 3.Meal_Glucose 2.Insulin Plasma 1.Sinyal Kendali
Laju insulin eksternal
3 Plasma insulin 2 Interstitial Insulin 1 Blood Glucose 150 Start time ds_mod
Model Minimal Bergman Diabetes Mellitus Tipr I
gangguan2 Meal Glucose Manual Switch2 -1 Gain 0 Constant2 1 Laju Insulin Eksternal
(b)
Gambar 4.1. Blok diagram simulink pengendalian kadar gula darah
diabetes mellitus tipe I dengan MPC
Tujuan dari uji eksperimen ini adalah untuk mengetahui kinerja MPC dengan parameter penalaan yang berbeda-beda. Model yang digunakan pada simulasi adalah persamaan ruang keadaan linier dari model minimal Bergman yang didiskritkan dengan waktu pencuplikan 5 menit yang terdapat pada persamaan (3.32).
4.1. PENGARUH NILAI CONTROL HORIZON DAN PREDICTION
HORIZON PADA HASIL PENGENDALIAN MPC
4.1.1. Hasil Uji Simulasi dengan Nilai Prediction Horizon Tetap dan Nilai
Control Horizon Bervariasi
Pengaruh control horizon (Hu) terhadap hasil pengendalian MPC dapat dilihat dengan melakukan uji simulasi pada nilai prediction horizon (Hp) tetap, yaitu sebesar 10, dan nilai control horizon dibuat bervariasi. Variasi control horizon yang digunakan pada uji simulasi adalah sebesar 2 dan 4. Faktor bobot kesalahan
(Q) yang digunakan adalah IHp sedangkan faktor bobot perubahan sinyal kendali
(R) yang digunakan adalah 0,0001IHu. Hasil uji simulasi dengan prediction
horizon tetap dan control horizon yang berbeda terdapat pada gambar 4.2 dan 4.3.
0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 Time (minutes) B lood G luc o s e ( m m o l/ L) set point keluaran Hu = 2 (a) 0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 Time (minutes) B loo d Gl u c o s e (m m o l/ L ) Set point Keluaran Hu = 4 (b)
0 100 200 300 400 500 600 0 10 20 30 40 50 60 Time (minutes) P las m a I ns ul in ( m U /L) Hu = 2 (c) 0 100 200 300 400 500 600 0 10 20 30 40 50 60 Time (minutes) P la s m a I n s u li n (m U/ L) Hu = 4 (d) 0 100 200 300 400 500 600 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 Time (minutes) In te rs ti ti a l In s u li n ( m U /L ) Hu = 2
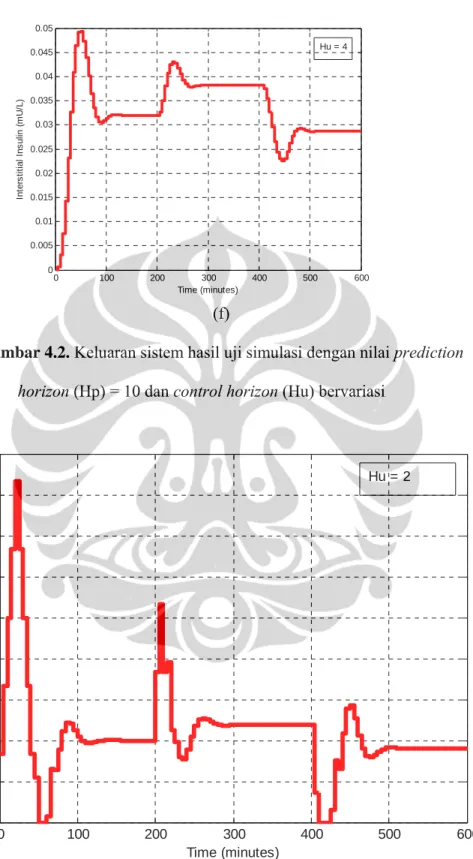
0 100 200 300 400 500 600 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 Time (minutes) In te rs ti ti a l In s u lin ( m U /L ) Hu = 4 (f)
Gambar 4.2. Keluaran sistem hasil uji simulasi dengan nilai prediction
horizon (Hp) = 10 dan control horizon (Hu) bervariasi
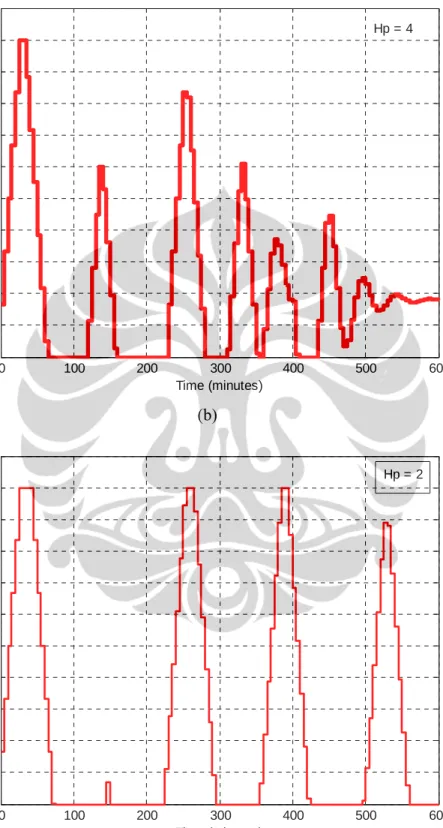
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 Time (minutes) Laj u I ns ul in E k s te rnal ( m U /m in ) Hu = 2 (a)
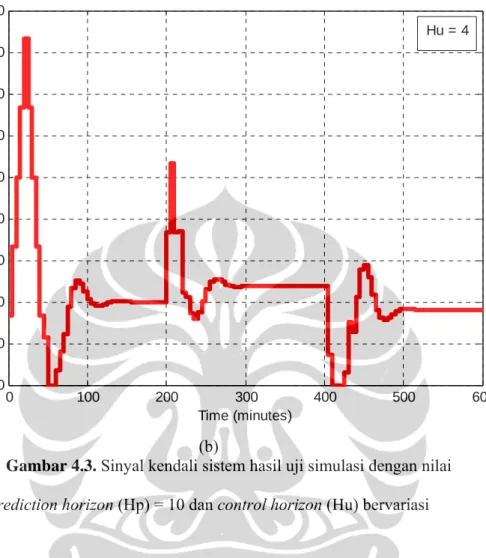
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 Time (minutes) Laj u I n s u lin E k s terna l (m U /m in) Hu = 4 (b)
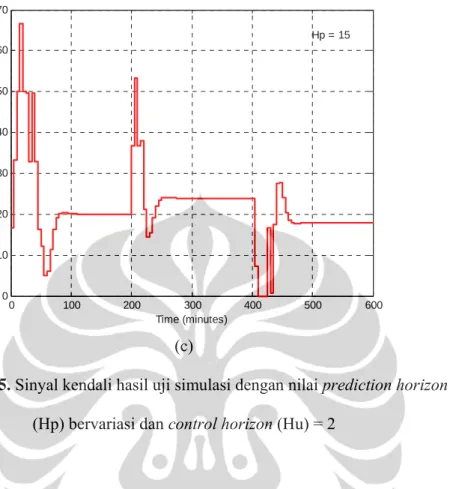
Gambar 4.3. Sinyal kendali sistem hasil uji simulasi dengan nilai
prediction horizon (Hp) = 10 dan control horizon (Hu) bervariasi
Berdasarkan gambar 4.2 dan 4.3 ternyata hasil pengendalian sama jika control horizon diubah-ubah baik mendekati maupun menjauhi prediction horizon. Keluaran sistem tidak jauh berbeda jika control horizon diubah-ubah, walaupun sinyal kendali terdapat sedikit perbedaan (gambar 4.3.(a) dan 4.3.(b)). Semakin kecil nilai control horizon, sinyal kendali semakin cenderung berubah secepatnya dan sebesar-besarnya agar nilai keluaran sistem dapat dengan segera mencapai nilai trayektori acuan, terlebih jika bobot perubahan sinyal kendali kecil yang berarti pembebanan pada sinyal kendali kecil sehingga pergerakan sinyal kendali lebih bebas. Pada menit ke-200 sampai menit ke-300 keluaran sistem mulai
bergerak menuju trayektori acuan yang naik dari 5 mmol/L menjadi 6 mmol/L (gambar 4.2.(a) dan (b)), karena itu laju insulin eksternal (sinyal kendali) berkurang agar keluaran sistem dapat mencapat trayektori acuan (gambar 4.3.(a) dan (b)). Laju insulin eksternal yang berkurang secara otomatis mengurangi volume insulin yang disuntikkan, sehingga membuat kadar glukosa darah bergerak naik.
4.1.2. Hasil Uji Simulasi dengan Nilai Control Horizon Tetap dan Nilai
Prediction Horizon Bervariasi
Untuk melihat pengaruh prediction horizon (Hp) terhadap hasil pengendalian MPC, dilakukan uji simulasi dengan nilai control horizon (Hu) tetap yaitu sebesar 2, dan nilai prediction horizon dibuat bervariasi. Variasi prediction horizon yang digunakan pada uji simulasi adalah sebesar 4, 8, dan 15. Faktor bobot kesalahan (Q) yang digunakan adalah IHp sedangkan faktor bobot perubahan sinyal kendali
(R) yang digunakan adalah 0,0001IHu.
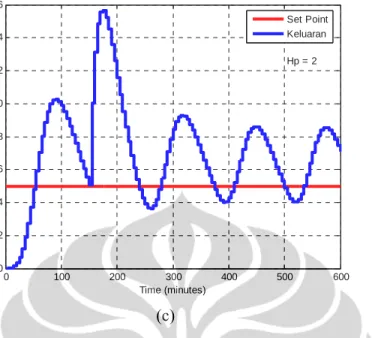
0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 9 10 Time (minutes) B loo d G luc os e ( m m ol /L) Set Point Keluaran Hp = 4 (a)
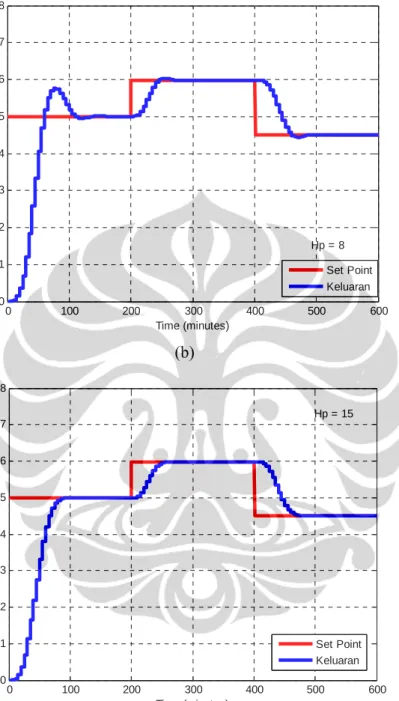
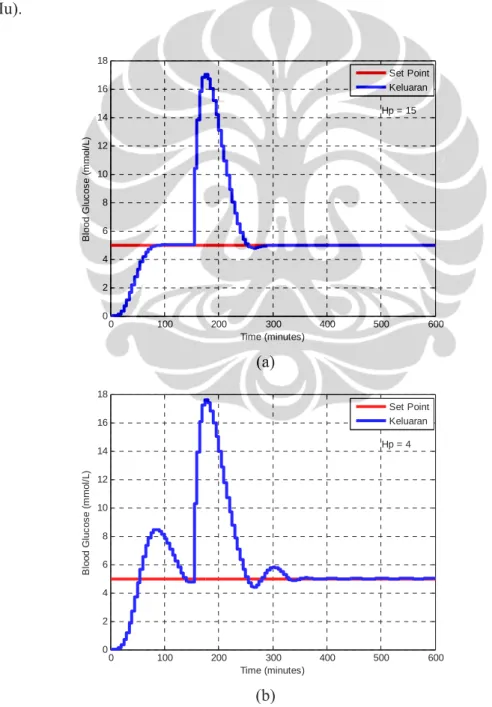
0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 Time (minutes) B lo od G lu c os e ( m m ol /L) Set Point Keluaran Hp = 8 (b) 0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 Time (minutes) B loo d G luc os e ( m m o l/ L ) Set Point Keluaran Hp = 15 (c)
Gambar 4.4. Keluaran sistem hasil uji simulasi dengan nilai prediction
horizon (Hp) bervariasi dan control horizon (Hu) = 2
Hasil uji simulasi dengan control horizon tetap dan prediction horizon bervariasi terdapat pada gambar 4.4 dan gambar 4.5. Dari hasil uji simulasi
terlihat bahwa untuk nilai faktor bobot perubahan sinyal kendali R yang kecil, maka hasil pengendali akan tetap bagus jika nilai prediction horizon dibuat menjauhi nilai control horizon. Hal ini sama seperti yang terjadi pada uji simulasi pertama (nilai Hu tetap dan nilai Hp bervariasi), di mana semakin dekat nilai control horizon dengan nilai prediction horizon, maka variansi perubahan sinyal kendali saat akan terjadi perubahan trayektori acuan semakin besar.
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 110 Time (minutes) Laj u I ns ul in E k s ter nal ( m U /m in) Hp = 4 (a) 0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 Time (minutes) Laj u I ns ul in E k s ter nal ( m U /m in ) Hp = 8 (b)
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 Time (minutes) Laj u I ns ul in E k s te rnal ( m U /m in) Hp = 15 (c)
Gambar 4.5. Sinyal kendali hasil uji simulasi dengan nilai prediction horizon
(Hp) bervariasi dan control horizon (Hu) = 2
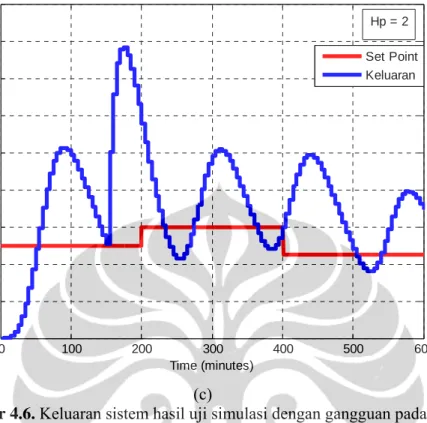
Hasil uji simulasi untuk nilai prediction horizon yang berbeda juga dilakukan saat sistem mendapat gangguan yaitu berupa sinyal eksponensial. Gangguan disimulasikan pada menit ke-150. Hasilnya seperti pada saat sistem bebas dari gangguan, yaitu jika prediction horizon dibuat sebesar-besarnya maka keluaran sistem lebih bagus dan variansi perubahan sinyal kendali lebih kecil (gambar 4.6 dan 4.7). Semakin kecil nilai Hp, semakin besar fluktuatif sinyal kendali hingga mencapai nilai batas maksimalnya yaitu 100 mU/min. Hal ini menyebabkan keluaran sistem menjadi fluktuatif jauh dari trayektori yang ditetapkan (gambar 4.6.(c)). Pada saat gangguan terjadi maka kadar glukosa darah meningkat (gambar 4.6), hal ini merespon sinyal kendali (laju insulin eksternal) bergerak meningkat
untuk menahan atau mengurangi kenaikan keluaran sistem (kadar glukosa darah) akibat gangguan berupa glukosa dari makanan (gambar 4.7.(b) dan (c)) .
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 20 Time (minutes) B lood G luc os e (m m ol /L ) Set Point Keluaran Hp = 15 (a) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 20 Time (minutes) B loo d G lu c os e ( m m o l/ L ) Set Point Keluaran Hp = 4 (b)
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood G luc os e (m m o l/ L) Set Point Keluaran Hp = 2 (c)
Gambar 4.6. Keluaran sistem hasil uji simulasi dengan gangguan pada nilai
prediction horizon (Hp) bervariasi dan control horizon (Hu) = 2
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 Time (minutes) L a ju I n s u li n E k s terna l (m U /m in) Hp = 15 (a)
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 110 Time (minutes) L a ju I n s u lin E k s te rn a l ( m U /m in ) Hp = 4 (b) 0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 110 Time (minutes) Laj u Ins ul in E k s ternal ( m U /m in) Hp = 2 (c)
Gambar 4.7. Sinyal kendali hasil uji simulasi dengan gangguan pada nilai
Gambar 4.8 dan 4.9 merupakan hasil uji simulasi untuk trayaktori acuan konstan pada level 5 mmol/L. Uji simulasi ini dilakukan karena pada kenyataannya kadar glukosa darah yang diharapkan adalah konstan. Seperti pada uji simulasi sebelumnya untuk nilai prediction horizon (Hp) bervariasi, uji simulasi dengan nilai trayektori acuan konstan juga menghasilkan keluaran sistem yang lebih baik jika prediction horizon (Hp) dibuat menjauhi nilai control horizon (Hu). 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B loo d G luc os e (m m ol /L ) Set Point Keluaran Hp = 15 (a) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood G luc o s e ( m m ol /L) Set Point Keluaran Hp = 4
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 Time (minutes) B loo d G luc os e (m m ol /L ) Set Point Keluaran Hp = 2 (c)
Gambar 4.8. Keluaran sistem hasil uji simulasi dengan gangguan dan set point
konstan 5 mmol/L pada nilai prediction horizon (Hp) bervariasi dan control horizon (Hu) = 2 0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 Time (minutes) L a ju I n s u lin E k s te rn a l (m U /m in ) Hp = 15 (a)
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 Time (minutes) L a ju I n s u lin E k s te rn a l (m U /m in ) Hp = 4 (b) 0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 Time (minutes) L a ju I n s u lin E k s te rn a l (m U /m in ) Hp = 2 (c)
Gambar 4.9. Sinyal Kendali hasil uji simulasi dengan gangguan dan set point
konstan 5 mmol/L pada nilai prediction horizon (Hp) bervariasi dan control horizon (Hu) = 2
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 20 Time (minutes) B loo d G luc os e ( m m ol /L)
Gambar 4.10. Hasil simulasi dengan gangguan dan tanpa pengendali
Gambar 4.10. merupakan hasil uji simulasi tanpa penegendalian saat sistem mendapat gangguan pada menit ke-100 dan mendapatkan masukan pada nilai setimbangnya (U = 16,667 mU/min). Ternyata nilai steady keluaran hanya mencapai 4 mmol/L dan dicapai relatif lebih lama dibandingkan jika menggunakan pengendali.
4.2. Pengaruh Nilai Faktor Bobot Perubahan Sinyal Kendali (R) dan
Batas Sinyal Kendali
4.2.1. Hasil Uji Simulasi dengan Nilai Faktor Bobot Kesalahan (Q) Tetap
dan Nilai Faktor Bobot Perubahan Sinyal Kendali (R) bervariasi
Pengaruh faktor bobot perubahan sinyal kendali R pada hasil pengendali dapat dilihat dengan melakukan uji simulasi pada sistem dengan membuat nilai diagonal matriks R berbeda-beda, yaitu 0; 0,01; dan 1, sedangkan nilai parameter
pengendali lainnya dibuat tetap, dengan Hu = 2, Hp = 10, dan Q = IHp. Hasil uji
simulasi ini dapat dilihat pada gambar 4.11 sampai dengan gambar 4.17.
0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 Time (minutes) B lood G luc o s e (m m o l/ L) Set Point Keluaran R = 0 (a) 0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 Time (minutes) B lood G luc os e ( m m ol /L) Set Point Keluaran R = 0.01 (b)
0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 Time (minutes) B loo d G luc o s e (m m o l/ L ) Set Point Keluaran R = 1 (c)
Gambar 4.11. Keluaran sistem hasil uji simulasi dengan nilai Q tetap yaitu IHp
danR bervariasi 0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 Time (minutes) Laj u In s ul in E k s ter n al ( m U /m in) R = 0 (a) 0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 Time (minutes) Laj u Ins ul in E k s ter nal ( m U/ m in) R = 0.01 (b)
0 100 200 300 400 500 600 0 5 10 15 20 25 30 Time (minutes) L a ju I n s u lin E k s te rn a l ( m m o l/ L ) R = 1 (c)
Gambar 4.12. Sinyal kendali hasil uji simulasi dengan nilai Q tetap yaitu IHp dan
R bervariasi
Dari hasil simulasi pada gambar 4.11 dan gambar 4.12 terlihat bahwa semakin besar nilai matriks R, perubahan sinyal kendali menjadi semakin ditekan sehingga menyebabkan keluaran sistem menjadi semakin halus. Dengan nilai matriks R yang besar (IHu), variansi perubahan sinyal kendali sangat kecil, bahkan saat akan
terjadi perubahan trayektori acuan. Hal ini menyebabkan keluaran sistem lebih lama mencapai nilai trayektori yang ditetapkan. Hasil uji simulasi ini sama jika sistem mendapat gangguan. Saat R diperbesar menjadi satu, sinyal kendali makin terbebani sehingga tidak dapat berubah secara cepat (gambar 4.14.(f)) dan hasil pergerakannya lebih halus, hal ini menyebabkan keluaran sistem mencapai level hypoglycemia yaitu di bawah 3,3 mmol/L (gambar 4.13.(f)). Batas nilai faktor bobot perubahan sinyal kendali R yang memungkinkan untuk mencapai kadar glukosa darah serendah-rendahnya agar tidak terjadi hypoglycemia adalah R = 0,35. Pada nilai R = 0,35 dicapai keluaran sistem (kadar glukosa darah) pada level normoglycemia terendah yaitu 3,3 mmol/L (gambar 4.13.(e)).
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 20 Time (minutes) B lood G lu c os e ( m m ol /L) Set Point Keluaran R = 0 (a) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood G luc os e (m m ol /L) Set Point Keluaran R = 0,001 (b) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lo od G luc os e ( m m o l/ L) Set Point Keluaran R = 0,01 (c)
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood Gl uc os e ( m m ol /L) Set Point Keluaran R = 0,1 (d) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 20 Time (minutes) B lood G luc os e (m m ol /L) Set Point Keluaran R = 0,35 (e) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 20 Time (minutes) B loo d G luc os e ( m m ol /L) Set Point Keluaran R = 1 (f)
Gambar 4.13. Keluaran sistem hasil uji simulasi dengan gangguan pada nilai Q
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 100 Time (minutes) Laj u I n s ul in E k s ter nal (m U /L) R = 0 (a) 0 100 200 300 400 500 600 -10 0 10 20 30 40 50 60 70 80 90 Time (minutes) Laj u I ns u lin E k s ternal ( m U /m in) R = 0,001 (b) 0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 Time (minutes) L aj u I n s ul in E k s ter na l ( m U /m in) R = 0,01 (c)
0 100 200 300 400 500 600 0 5 10 15 20 25 30 35 40 45 50 Time (minutes) La ju I ns ul in E k s terna l ( m m o l/ L) R = 0,1 (d) 0 100 200 300 400 500 600 0 5 10 15 20 25 30 35 Time (minutes) Laj u I n s ul in E k s ternal ( m U /m in) R = 0,35 (e) 0 100 200 300 400 500 600 0 5 10 15 20 25 30 35 40 45 50 Time (minutes) La ju I n s u li n E k s terna l (m U /L ) R = 1 (f)
Gambar 4.14. Sinyal kendali hasil uji simulasi dengan gangguan pada nilai Q
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood G luc os e (m m o l/ L) Set Point Keluaran R = 0 (a) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood G luc os e (m m o l/ L) Set Point Keluaran R = 0,0001 (b)
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood G luc os e ( m m ol /L) Set Point Keluaran R = 0,1 (c) 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lood G luc os e (m m ol /L) Set Point Keluaran R = 0,17 (d)
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lo od G luc os e ( m m ol /L ) Set Point Keluaran R = 1 (e)
Gambar 4.15. Keluaran sistem hasil uji simulasi dengan gangguan dan set point
konstan 5 mmol/L pada nilai Q tetap yaitu IHp danR bervariasi
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (minutes) B lo od G luc os e (m m ol /L) R = 0 Set Point R = 0,0001 R = 0,1 R = 0,17 R = 1
Gambar 4.16. Perbandingan keluaran sistem hasil uji simulasi dengan gangguan
Gambar 4.15 dan 4.16 menunjukkan keluaran sistem untuk variasi nilai R pada trayektori acuan yang dibuat konstan dengan gangguan pada menit ke-150. Pada gambar 4.16 terlihat jelas pergerakan keluaran sistem yang semakin jauh dari trayektori acuan jika nilai faktor bobot perubahan sinyal kendali R diperbesar. Nilai R yang semakin besar membuat laju insulin eksternal makin halus (gambar 4.17) karena pergerakannya terbebani dengan nilai R yang besar. Level normoglycemia terendah (yaitu 3,3 mmol/L) tercapai untuk nilai R sebesar 0,17. Jika nilai R diperbesar menjadi di atas 0,17 maka kadar glukosa darah memasuki hypoglycemia (di bawah 3,3 mmol/L).
0 100 200 300 400 500 600 -10 0 10 20 30 40 50 60 70 80 90 Time (minutes) La ju I ns ul in E k s ter na l (m U /m in) R = 0 (a)
0 100 200 300 400 500 600 0 10 20 30 40 50 60 70 80 90 Time (minutes) L a ju I n s u lin E k s te rn a l (m U /m in ) R = 0,0001 (b) 0 100 200 300 400 500 600 0 5 10 15 20 25 30 35 40 45 50 Time (minutes) L a ju I n s u lin E k s te rn a l (m U /m in ) R = 0,1 (c)
0 100 200 300 400 500 600 0 5 10 15 20 25 30 35 40 Time (minutes) L aj u I ns u li n E k s ter nal ( m U /m in) R = 0,17 (d) 0 100 200 300 400 500 600 0 5 10 15 20 25 Time (minutes) L a ju I n s u lin E k s te rn a l (m U /m in ) R = 1 (f)
Gambar 4.17. Sinyal Kendali hasil uji simulasi dengan gangguan dan set point
4.2.2. Hasil Uji Simulasi dengan Nilai Batas Mimimum Sinyal Kendali Tetap dan Nilai Batas Maksimum Sinyal Kendali Bervariasi
Pengaruh batas sinyal kendali pada hasil pengendali dapat dilihat dengan melakukan uji simulasi pada sistem dengan membuat nilai batas maksimum sinyal kendali berbeda-beda, yaitu 25 dan 20, sedangkan nilai parameter pengendali lainnya dibuat tetap, dengan Hu = 2, Hp = 10, R = 0,0001IHu, Q = IHp, dan Umin =
0. Hasil uji simulasi ini dapat dilihat pada gambar 4.18, 4.19 dan 4.20. Perubah batas maksimum disertai perubahan slew rate yaitu menjadi sebesar 5. Perubahan batas maksimum sinyal kendali yang makin kecil yang berarti mempersempit rentang sinyal kendali menyebabkan pergerakan sinyal kendali semakin kecil sehingga keluaran sistem tidak dapat mencapai trayektori acuan yang ditetapkan (gambar 4.18.(b)). 0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 Time (minutes) B loo d G lu c os e ( m m o l/ L ) Set point Keluaran U maks = 25 (a)
0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 Time (minutes) B loo d G luc o s e (m m ol /L) Set point Keluaran u maks = 20 (b)
Gambar 4.18. Keluaran sistem hasil uji simulasi dengan nilai batas sinyal kendali
minimum tetap (Umin = 0) danbatas sinyal kendali maksimum bervariasi
0 100 200 300 400 500 600 0 5 10 15 20 25 30 35 Time (minutes) L a ju I n s u li n E x te rn a l (m U /m in) Umaks = 25 (a)
0 100 200 300 400 500 600 0 5 10 15 20 25 Time (minutes) Laj u K el ua ran E x ter nal ( m U /m in) U maks = 20 (b)
Gambar 4.19. Sinyal kendali hasil uji simulasi dengan nilai batas sinyal kendali
minimum tetap (Umin = 0) danbatas sinyal kendali maksimum bervariasi
0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 16 18 Time (Minutes) B lo od G luc os e ( m m ol /L) Set point Keluaran U maks = 20 (a)
0 100 200 300 400 500 600 0 5 10 15 20 25 Time (Minutes) La ju I ns ul in E x ter n al ( m U /m in) U maks = 20 (b)
Gambar 4.20. Hasil simulasi dengan gangguan pada Umin =0 , Umax = 20 dan slew