09. Lipatan

(1)

Geologi Dinamik – Geologi ITB

9. Lipatan

9.1

Pendahuluan

Lipatan adalah hasil perubahan bentuk atau volume dari suatu bahan yang ditunjukkan sebagai lengkungan atau kumpulan dari lengkungan pada unsur garis atau bidang didalam bahan tersebut. Pada umumnya unsur yang terlibat di dalam lipatan adalah struktur bidang, misalnya bidang perlapisan atau foliasi. Lipatan merupakan gejala yang penting, yang mencerminkan sifat dari deformasi

; terutama, gambaran geometrinya berhubungan dengan aspek perubahan bentuk

(distorsi) dan perputaran (rotasi).

Lipatan terbentuk bilamana unsur yang telah ada sebelumnya terubah menjadi bentuk bidang lengkung atau garis lengkung. Perlipatan adalah deformasi yang tak seragam (inhomogeneous) yang terjadi pada suatu bahan yang mengandung unsur garis atau

bidang. Walaupun demikian, suatu deformasi

yang menghasilkan lipatan pada suatu keadaan, tidak selalu demikian pada kondisi yang lain. Suatu masa batuan yang tidak mempunyai unsur struktur garis atau bidang, tidak menunjukkan tanda perlipatan. Perlu juga dipertimbangkan bahwa, suatu unsur yang sebelumnya berbentuk lengkungan dapat berubah menjadi bidang atau garis lurus, atau suatu unsur dapat tetap sebagai struktur bidang atau garis lurus setelah terjadi deformasi.

9.2 Deskripsi geometri pada lipatan

Secara geometri suatu lipatan dapat dideskripsikan sebagai suatu permukaan bidang lengkung yang tunggal. Bentuk suatu lipatan sangat beragam, dari yang sederhana sampai sangat rumit, yang sulit dideskripsikan secara terinci. Untuk kegunaan praktis, disamping metoda matematik, dipakai metoda deskriptif lain seperti pembuatan kontur struktur dan sebagainya.

Sebagai penyederhanaan, suatu lipatan dapat dianggap sebagai suatu bentuk permukaan yang silindris dengan sumbu lipatan sebagai kerangka permukaan tersebut, dan unsur-unsurnya dapat ditunjukkan pada suatu penampang (profile) lipatan. Beberapa titik profil permukaan dideskripsikan seperti pada gambar 9.1.

- Hinge

point

Titik maksimum pelengkungan pada lapisan yang terlipat.

(2)

Geologi Dinamik – Geologi ITB

- Crest

Titik tertinggi pada lengkungan.

- Trough

Titik terendah pada pelengkungan.

- Inflection

point

Titik batas dari dua pelengkungan yang berlawanan.

(3)

78 Lipatan

p

Geologi Dinamik – Geologi ITB Gambar 9.1 Titik-titik yang dideskripsi pada profil permukaan lipatan silindris Pada gambaran tiga dimensi, tempat kedudukan dari hinge-point pada satu permukaan lipatan akan berupa garis yang disebut sebagai

hinge-line atau sumbu dari lipatan (fold-axis). Demikian pula titik-titik crest dan trough, yang merupakan perpotongan dari garis pada bidang profil, yaitu crestal-line, dan trough-line, yang sejajar dengan sumbu perlipatan.

Tempat kedudukan dari titik dan garis ini bergantung pada orientasi dari permukaan lipatan terhadap bidang horisontal. Unsur-unsur lipatan yang umumnya dapat dideskripsikan kedudukannya diantaranya adalah (Gambar 9.2) :

- Fold axis (sumbu lipatan/hinge line)

Garis maksimum pelengkungan pada suatu permukaan bidang yang terlipat.

- Axial plane (bidang

sumbu)

Bidang yang dibentuk melalui garis-garis sumbu pada satu lipatan. Bidang ini tidak selalu berupa bidang lurus (planar), tetapi dapat melengkung lebih umum dapat disebutkan sebagai Axial surface.

- Fold limb (sayap

lipatan)

Secara umum merupakan sisi-sisi dari bidang yang terlipat, yang berada diantara daerah pelengkungan (hinge-zone) dan batas pelengkungan (inflection line).

9.3 Dasar Klasifikasi Lipatan

(4)

Praktikum Geologi Struktur 79

Lipatan dapat diklasifikasikan dengan bermacam kriteria. Pada umumnya klasifikasi ini didasarkan pada sifat yang dapat dideskripsikan unsur-unsurnya secara geometri seperti yang telah dibahas sebelumnya. Klasifikasi dan penamaan

(5)

80 Lipatan

jenis lipatan umumnya juga secara tidak langsung akan mencerminkan sifat kejadian atau pembentukan lipatan secara tidak langsung kan mencerminkan sifat kejadian atau pembentukan lipatan tersebut dan jenis atau material yang terlibat. misalnya lipatan yang ketat (tight) mencerminkan deformasi yang kuat, lipatan yang sejajar (paralel) umumnya terjadi pada lapisan yang kompeten dan sebagainya.

Gambar 9.2 Unsur-unsur pada suatu lipatan

9.3.1 sudut antar say a p (interlimb

angle)

Sudut antar sayap adalah sudut yang terkecil yang dibentuk oleh sayap-sayap lipatan, dan diukur pada bidang profil suatu lipatan (gambar 9.3). Sudut ini mencerminkan sifat keketatan (tightness) dari lipatan. Fleuty (1964) membuat klasifikasi seperti pada tabel 9.1.

Gambar 9.3 Sudut antar sayap (interlimb angle)

(6)

A

Tabel 9.1 klasifikasi berdasarkan sudut antar sayap Sudut antar sayap Deskripsi lipatan 1800 _{- 120}0 _{Gentle (landai)} 1200 _{- 70}0 _{Open (terbuka)} 700 _{- 30}0 _{Close (tertutup)} 300 _-00 _{Tight (ketat)} 00 _{Isoclinal (isoklin)} 9.3.2 Sifat simetri

Simetri merupakan salah satu kriteria untuk menyatakan bentuk dari suatu permukaan silindris. Sifat simetri ditentukan oleh bidang yang melalui hinge-line dan membagi sama-besar sudut antar sayap lipatan, yang disebut bidang simetri. lipatan ini disebut sebagai lipatan

simetris, dan keseluruhan lipatan memiliki sifat simetri orthorhombic.

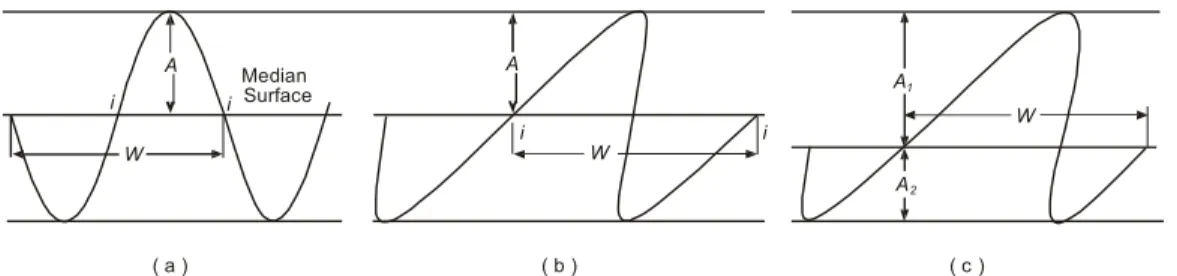
Suatu seri dari lipatan dikatakan simetri apabila masing- masing mempunyai sifat simetri, dan mempunyai pola yang periodik. Dalam hal ini, bidang-bidang yang membatasi permukaan lipatan akan berupa bidang yang lurus (planar) dan saling sejajar, dan bidang yang melalui titik-titik batas pelengkungan (inflection point) akan tepat terletak ditengah bidang-bidang tersebut yang disebut sebagai median. Pada lipatan simetri, besaran amplitude dan panjang gelombang (wavelenght), yang perbandingannya merupakan parameter untuk bentuk lipatan, akan mudah dideskripsi (gambar 9.4a).

A _Median A 1 i i Surface _W i i W W A2 ( a ) ( b ) ( c )

Gambar 9.4 Besaran suatu lipatan W = wavelenght, A = amplitude Apabila jejak dari bidang yang melalui hinge-line (hinge surface) bukan sebagai bidang simetri, lipatan tersebut disebut sebagai lipatan asimetris, yang hanya mempunyai sifat simetri monoklin. Untuk itu perlu ditambahkan sifat asimetrinya, umumnya disebutkan sifat arah miring bidang sumbunya (vergence), atau arah relatif puncak antiform terhadap puncak sinform nya (gambar 9.4 b,c), misalnya arah mata angin, kiri-kanan atau perputaran jarum jam bagi lipatan yang sumbunya menunjam.

(7)

82 Lipatan

Apabila sifat asimetri dari lipatan makin besar, deskripsi dapat diberikan dengan sifat-sifat seperti yang ditunjukkan pada gambar 9.4 b,c.

9.3.3 Kedudukan lipat a n

Berdasarkan bentuknya, lipatan yang kemiringan bidang sayapnya menuju ke arah yang berlawanan, disebut sebagai Antiklin, dan

synform, kemiringan bidang sayapnya menuju ke satu arah, disebut

sebagai Sinklin.

Kedudukan lipatan ditanyakan dari kedudukan sumbu lipatan (fold axis) dan

bidang sumbu lipatan (axial plane/axial surface).

Fleuty (1964) membuat klasifikasi yang didasarkan pada kedua sifat kedudukan tersebut, dan secara lebih tepat menyatakan besaran kecondongannya kemiringan dan penunjamannya. Deskripsi yang diberikan merupakan gabungan dari kedua kriteria yang ada, yaitu kemiringan dari bidang sumbu dan penunjaman dari garis sumbu (Tabel 9.2).

Tabel 9.2 Penamaan untuk kedudukan lipatan (Fleuty, 1964)

Sudut Istilah Kemiringan bidang sumbu Penunjaman garis

sumbu

0

1 - 10 HorizontalSubhorizontal Recumbent foldRecumbent fold Horizontal foldHorizontal fold

10 - 30 Gentle Gently inclined fold Gently plunging fold

30 - 60 Moderate Moderately inclined

fold Moderately plunging fold

60 - 80 Steep Steeply inclined fold Steeply inclined fold

80 - 89 90 Subvertical Vertical Upright fold Upright fold Vertical fold Vertical fold

Perlu dicatat bahwa beberapa gabungan untuk penamaan lipatan tidak dapat diberikan, karena garis sumbu posisinya berada pada bidang sumbu, misalnya, jenis lipatan gently - inclined, steeply - plungging fold tidak mungkin diberikan atau tidak ada. Klasifikasi ini agak sulit dipakai mengingat kerangka yang digunakan adalah kedudukan dari sumbu lipatan, yang penunjamannya terukur pada bidang vertikal yang tidak ada hubungannya dengan geometri lipatan. Untuk mengatasi ini dapat dipakai kriteria pitch garis sumbu dan kemiringan bidang sumbu. Kesulitannya adalah mengukur besaran pitch dilapangan.

Klasifikasi yang lebih sederhana dengan menggabungkan besaran penunjaman dan pitch, seperti bagan bentuk lipatan yang ditunjukkan pada gambar 9.5.

(8)

Rickard (1971), membuat diagram segitiga yang memperhitungkan tiga variabel, yaitu ; kedudukan bidang sumbu lipatan (kemiringan) dan sumbu lipatan (penunjaman dan pitch terhadap bidang sumbu lipatan), seperti ditunjukkan pada gambar 9.6.

(9)

84 Lipatan

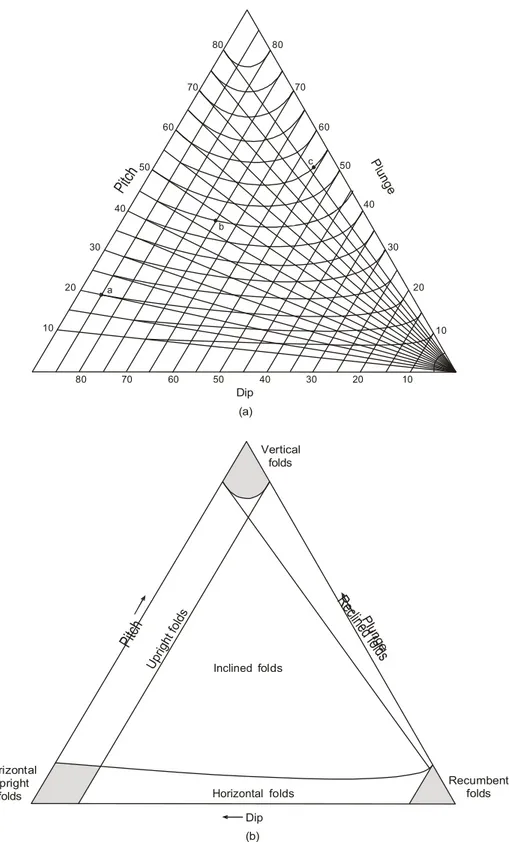
Pasangan kemiringan dan pitch dari suatu lipatan ditunjukkan sebagai titik pada perpotongan garis lurus, yang angkanya dibaca sepanjang tepi dasar dan kiri diagram (gambar 9.6a). Untuk penunjaman digunakan kurva dan angka pada tepi kanan diagram. Jenis-jenis kedudukan lipatan dapat ditentukan pada diagram gambar 9.6 b.

Untuk dapat memberikan kedudukan yang lebih pasti pada lipatan yang miring (inclined fold), Rickard mengusulkan untuk memberikan indeks besaran angka dari kemiringan (D) dan penunjaman dari (P), misalnya ; - Upright fold (D85P25), menurut klasifikasi Fleuty (Tabel 9.2)

adalah

Upright, gently, plunging fold.

- Inclined fold (D70P45), Steeply inclined,

moderately-plunging fold.

- Reclined fold (D56P55),

Moderately-inclined fold.

Diagram ini juga dapat digunakan untuk berbagai lipatan secara lebih terinci pada suatu wilayah, misalnya bila terdapat suatu perubahan kedudukan pada arah atau geometri lipatan-lipatan tersebut.

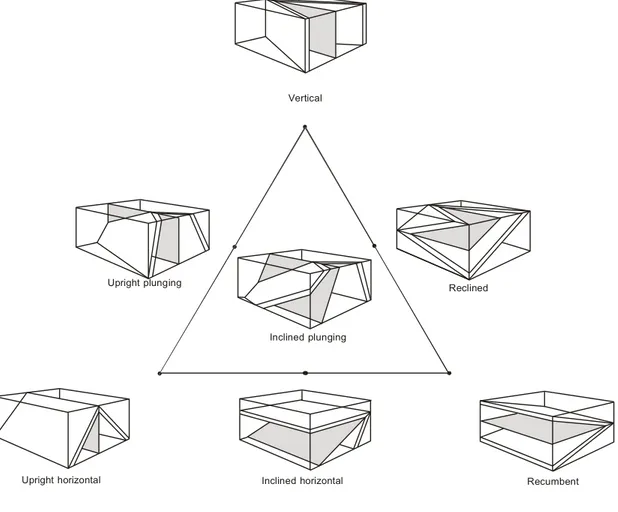
Vertical

Upright plunging _Reclined

Inclined plunging

(10)

(11)

80 80 70 70 60 60 50 c 50 40 40 b 30 30 20 a 20 10 ₁₀ 80 70 60 50 40 30 20 10 Dip (a) Vertical folds Inclined folds Horizontal Upright

folds Horizontal folds Dip (b)

Recumbent folds

Gambar 9.6 a. Diagram segitiga untuk menentukan kedudukan lipatan

(12)

9.3.4 Isogon

Pada umumnya, hampir semua lipatan terdiri lebih dari satu permukaan, untuk ini diperlukan cara untuk membahas hubungan ruang dan geometri antara bidang bidang lengkung yang membentuk lipatan. Tempat kedudukan dari semua hinge- line, yang disebut sebagai hinge

surface, merupakan unsur yang penting. Bidang permukaan ini seringkali

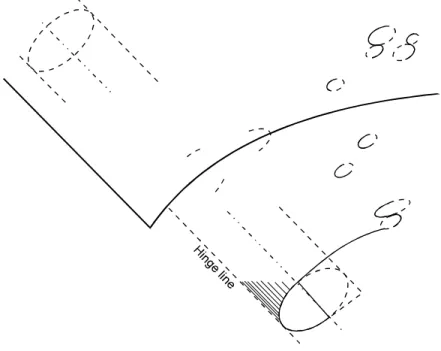
dianggap sama dengan bidang sumbu (axial plane) atau axial surface, akan tetapi tidak berhubungan langsung dengan sumbu. Suatu lipatan yang tidak silindris mempunyai bidang permukaan sejenis ini, tetapi tidak merupakan sumbu lipatan. Oleh karena itu lebih sesuai disebut sebagai hinge surface (gambar 9.7).

Gambar 9.7 Hinge surface pada lipatan silindris

Bidang sumbu lebih dikhususkan untuk bidang yang sejajar dengan hinge surface yang melalui keseluruhan dari lipatan silindris.

Dengan pengertian yang sama dengan hinge surface, akan terdapat inflection surface, yang merupakan tempat kedudukan dari garis batas lengkung, crestal surface dan trough surface.

Hubungan geometri dari dua permukaan lengkung tergantung

pada pelengkungan relatif dan jarak antara keduanya, Cara sederhana untuk menyatakan hubungan sumbu adalah dengan membuat garis dari titik-titik pada dua permukaan lipatan dimana

(13)

(14)

dibuat dari kerangka horisontal, pada suatu bidang profil. Garis-garis ini disebut Isogon. Isogon kemiringan merupakan suatu pola yang dapat dipakai untuk membedakan bentuk lipatan dan juga merupakan dasar untuk klasifikasi geometri lipatan yang mudah untuk diterapkan.

Cara membuat

isogon

Isogon dapat dibuat secara langsung dengan menggambarkan dari berbagai lengkungan dari suatu gambar atau foto yang diambil sepanjang sumbu lipatan.

Langkah pertama adalah memilih datum (kerangka horisontal). Pada masing- masing jejak dari dua permukaan lipatan yang berdekatan, dibuat suatu seri kemiringan yang menyinggung

permukaan lipatan. Hubungkan

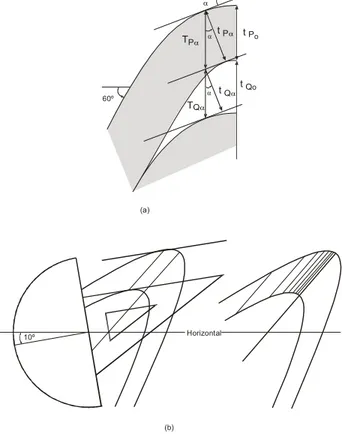
titik-titik singgung pada permukaan lipatan, dari kemiringan yang sama (gambar 9.8). Interval kemiringan 100 _{atau 20}0 _{cukup memadai untuk}

melihat pola isogonnya.

α TPα α t Pα t Po 60º TQα α t Qαt Qo (a) 10º Horizontal (b)

Gambar 9.8 Isogon kemiringan

a. Cara membuat isogon dengan kemiringan α dan β

(15)

Klasifikasi isogon

Dasar yang dipakai pada klasifikasi ini adalah sifat kesejajaran dari isogon serta arah dari sifat konvergensi dan divergensinya. Bagian dalam dari busur lipatan dipakai sebagai kerangka untuk arah konvergensi isogon.

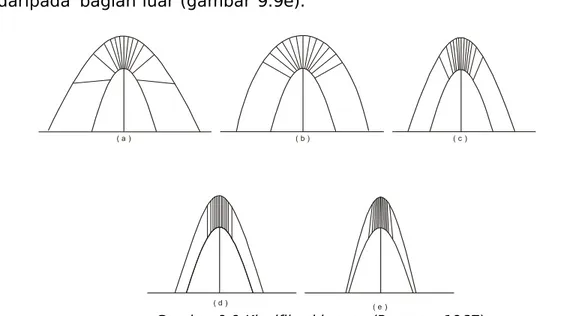
Didasarkan pada sifat ini, terdapat lima jenis lipatan (Ramsay, 1967), yaitu luar lebih kecil daripada bagian dalam, jarak terkecil dari dua permukaan lipatan terletak searah hinge surface (gambar 9.9) :

- lipatan dengan isogon konvergen kuat (1A), lenkungan pada busur luar

lebih kecil daripada bagian dalam, jarak terkecil dari dua permukaan lipatan terletak searah hinge surface (gambar 9.9a).

- lipatan paralel (1B), lengkungan pada busur dalam lebih besar,

jarak dari dua permukaan lipatan tetap, yang disebut sebagai

ketebalan ortogonal lapisan (gambar 9.9b).

- lipatan dengan isogon konvergen lemah (1C), lengkungan pada

busur luar lebih besar, jarak terbesar dari dua permukaan lipatan terletak pada hinge surface (gambar 9.9c).

- lipatan similar (2), kedua lengkungan lipatan identik, dan isogon

sejajar, jarak antara lengkungan yang diukur pada isogon tetap, yang disebut sebagai ketebalan bidang sumbu (gambar 9.9d).

- lipatan divergen (3), lengkungan pada busur dalam lebih kecil

daripada bagian luar (gambar 9.9e).

( a ) ( b ) ( c )

( d ) _{( e )}

(16)

D

at

um

Selain klasifikasi, dasar ini juga dipakai untuk mendeskripsi bentuk lipatan, dari pola isogonnya, pada satu lapisan tunggal. Berbagai cara dapat dilakukan, yaitu dengan memplot garis normal ortogonal dan ketebalan bidang sumbu sebagai fungsi dari kemiringan, α (Ramsay, 1967). Cara yang lebih sederhana adalah memperhitungkan besaran sudut isogon φ sebagai fungsi dari α (Hudleston,

1973). Gambar 9.10a menunjukkan cara membuat sudut isogon dari garis normal

setiap isogon kemiringan. Variasi dari φ dan α ditunjukkan sebagai kurva pada diagram 9.10b.

-90 α 3 -60 2 1A φ -30 1C A φ 0 1B 1B 1C +30 2 1A 2 1 +60 ( a ) +90 -90 -60 -30 0 +30 +60 +90 α ( b )

Gambar 9.10 Pola isogon pada satu lapisan tunggal a. Pembuatan sudut isogon φ

b. Diagram yang menunjukkan kurva φ terhadap α

9.4 Lipatan Sejajar

(parallel fold)

Lipatan paralel adalah bentuk lipatan yang ketebalan (ortogonal) lapisannya tetap. Pembentukan lipatan ini dapat dibayangkan sebagai susunan lapisan-lapisan yang saling bergeser (flexural slip) apabila dilipat (Gambar 9.11).

(17)

Gambar 9.11 Gambaran pergeseran lapisan (flexural slip) pada perlipatan

(18)

N

9.4.1 konstruksi pena m pang pada lipatan seja j ar

Dasar dari metoda ini adalah anggapan bahwa lipatan merupakan bentuk busur dari suatu lingkaran dengan pusatnya adalah perpotongan antara sumbu-sumbu kemiringan yang berdekatan (gambar 9.12). Metoda ini disebut sebagai metoda busur lingkaran (arc method).

A B _C O O₂ A B C A 30º O2 B 30º O₁ O₁ _O 1

Gambar 9.12 Cara pembuatan busur lipatan (Busk, 1929)

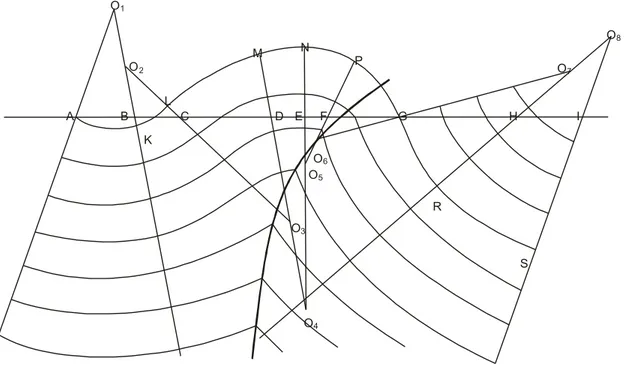
Dalam metoda ini rekonstruksi bisa dilakukan dengan menghubungkan busur lingkaran secara langsung (Gambar 9.13) apabila data yang ada hanya kemiringan dan batas lapisan hanya setempat.

O1 O8 M P O2 O7 L A B C D E F G H I K O6 O5 R O3 S O4

Gambar 9.13 Rekonstruksi lipatan sejajar dengan metoda busur, menunjukkan jejak dari hinge surface (Busk, 1929)

(19)

B IS E C T O R A B B IS E C T O R A B

Apabila batas-batas lapisan dijumpai berulang pada lintasan yang akan direkonstruksikan, maka pembuatan busur lingkaran dilakukan

dengan interp olasi.

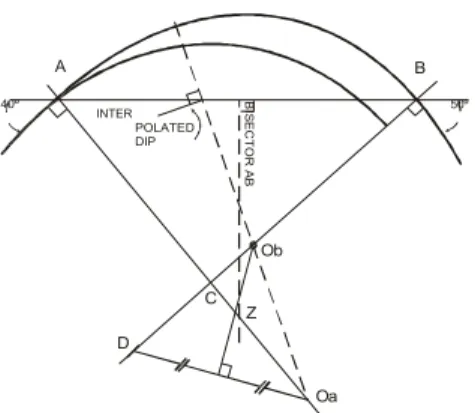
Metoda Higgins (1962) A B 40º INTER POLATED DIP 50º Ob C Z D Oa

Gambar 9.14 Interpolasi antara dua kemiringan terukur (Higgins, 1962) - tarik garis normal kemiringan di A dan B

- tentukan Oa sembarang di seberang bisector AB

- tentukan D dimana Aoa = BD, tarik sumbu Doa didapat Ob - Oa dan Ob adalah pusat lingkaran untuk interpolasi

Metoda Busk (1929) P A B 40º 50º Oc C Z Od

Gambar 9.15 Interpolasi antara dua kemiringan terukur (Busk,1929)

- tarik garis normal dan perpanjang kemiringan di A dan b

- tarik garis tegak lurus AB berpotongan di masing-masing garis normal di Oc dan Od - Oc dan Od adalah pusat lengkungan interpolasi

(20)

9.4.2 Cara konstruksi l i patan tak sejajar

Salah satu cara untuk mengkonstruksi lipatan yang tak sejajar yaitu dengan Metoda Boundary ray. Dasar dari metoda ini bahwa penipisan atau kompaksi lapisan batuan adalah fungsi dan kemiringan. (Coates, 1945 dan Gill, 1953). Dengan dasar ini, disusun suatu tabel untuk mendapatkan posisi boundary ray yang dipakai untuk batas rekonstruksi lipatan. Tabel tersebut dibuat untuk bermacam penipisan, tergantung pada sifat batuan.

Cara mendapatkan boundary ray

(gambar 9.16)

- Kemiringan lapisan adalah 550 _{dan 40}0_{. Posisi boundary ray}

didapatkan dari perpotongan perpanjangan kemiringan.

- Arah dari boundary ray didapatkan dengan menggunakan tabel. Misalnya digunakan tabel dengan maksimum penipisan 45%, kemiringan kecil (400_{) dipakai sebagai ordinat dan kemiringan}

besar (550_{) dipakai sebagai absis, didapatkan sudut 61}0 _{dan 40}0_.

- Untuk kemiringan yang berlawanan dipakai bagian yang bawah yaitu 40

dan diukurkan pada kemiringan yang besar 550_.

- Untuk kemiringan yang searah, dibuat lebih dulu garis bisectornya kemudian diukurkan pada garis yang sejajar dengan kemiringan yang besar.

- Untuk mendapatkan posisi boundary ray dari tabel kemiringan lapisan diinterpolasi dan dikelompokkan lebih dulu menjadi kelipatan 50 _{lihat tabel}

9.3. Vertical section 59º Boundary Ray Angle from tables Surface 59º 40º 40º 55º 40º 55º _40º _40º 55º 40º Boundary Ray Angle from tables

Boundary Ray Boundary Ray Boundary Ray

(a) (b) (c)

40º Boundary Ray Angle from tables

50º thinning tables used in these examples

Gambar 9.16 Cara perhitungan sudut Boundary ray (bedgley, 1965)

Apabila pembuatan penampang tidak tegak lurus jurus lapisan, maka yang dipakai adalah kemiringan yang telah dikoreksi (gambar

(21)

(22)

Gambar 9.17 Contoh rekonstruksi boundary ray pada penampang yang tidak tegak lurus jurus.

Dalam rekonstruksi lipatan seringkali arc method digabungkan dengan metoda tangan bebas (free hand method) apabila diketahui adanya penipisan pada daerah tertentu. Metoda ini juga dipakai apabila terdapat penipisan dan penebalan yang tidak teratur. Cara penggambarannya ialah dengan menghubungkan batas-batas lapisan mengikuti orientasi kemiringan.

(23)

G a n tl e D ip a t D ip d ir e ct io n P o in t (o rd in a te )0 5 10 50 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 0 87 84 82 79 76 74 71 68 65 63 60 58 55 33 50 47 45 42 87 84 82 79 76 74 71 68 65 63 60 58 55 32 50 47 45 42 5 87 84 81 79 76 73 70 68 65 62 60 57 34 52 49 47 44 82 80 77 74 71 69 66 63 61 58 55 53 30 47 45 42 40 10 86 84 81 78 75 72 70 67 64 62 59 37 54 52 49 47 77 75 72 69 66 64 61 58 56 53 50 48 45 43 40 38 15 86 83 80 77 74 72 69 66 64 61 59 56 54 51 49 72 70 67 64 61 69 56 53 51 48 46 43 40 38 35 20 85 83 80 77 74 72 69 66 64 61 59 56 54 51 67 65 62 59 56 54 51 49 46 43 41 38 36 33 25 85 82 79 77 76 71 69 66 64 61 58 56 53 62 40 57 54 52 49 46 44 41 38 36 33 31 30 84 82 79 76 74 71 68 66 63 61 58 56 57 55 52 49 47 44 41 39 36 34 31 29 35 84 81 79 76 73 71 68 65 63 60 58 52 50 47 44 42 39 36 34 31 29 26 40 63 81 78 76 73 70 68 65 63 60 47 45 42 39 37 34 32 29 26 24 45 83 81 78 34 73 70 67 65 64 42 40 87 78 32 29 27 24 22

50 Example when adjoining

Dips are 85° and 90° 91° for dip in the some direction

3° for opposed direction

83 80 37 75 72 70 67 65 37 85 80 30 27 24 22 19 55 82 35 77 75 72 69 67 32 82 27 25 22 20 17 60 27 80 77 74 71 69 25 22 20 17 15 65 82 80 77 74 72 22 20 17 15 12 70 82 79 77 74 17 15 12 10 75 82 79 77 12 10 7 80 81 79 8 5 85 81 2 Tabel 9.3 a Sudut Boundary Ray untuk penipisan 10% dan 25%

Boundary Ray Angles for Compactional Thinning of 10 Per Cent

Steeper Dip of Dip Intersection Point (Abscissa)

(24)

Steeper Dip of Dip Intersection Point (Abscissa) G a n tl e D ip a t D ip d ir e ct io n P o in t (o rd in a te )0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 0 87 84 81 74 76 71 68 65 62 59 56 54 51 48 45 42 40 37 87 84 81 74 76 71 68 65 62 59 56 54 51 48 45 42 40 37 5 86 83 79 76 73 70 67 64 61 58 55 52 50 47 44 41 39 82 79 76 73 70 66 63 60 57 55 52 49 46 43 40 38 35 10 84 81 78 75 72 69 66 63 60 57 54 51 49 46 43 41 77 74 71 68 65 62 59 56 53 50 47 44 41 39 36 33 15 83 80 77 74 71 68 65 62 59 56 53 50 48 45 42 72 69 66 63 60 57 54 51 48 45 42 39 37 34 31 20 82 79 76 73 70 67 64 61 58 55 52 49 47 44 67 64 61 58 55 52 49 46 43 40 38 35 32 30 25 81 78 75 72 69 66 63 60 57 54 51 49 46 62 59 56 53 50 47 44 41 38 36 33 30 28 30 80 77 73 71 67 65 62 59 36 53 50 48 57 54 51 48 45 42 39 37 34 31 28 26 35 78 75 72 69 64 63 61 58 55 52 50 52 49 46 43 40 37 35 32 29 27 24 40 76 74 71 68 65 62 60 57 54 51 47 44 41 38 35 33 30 27 25 22 45 76 73 70 67 64 62 59 56 53 42 39 36 33 31 28 25 27 20 50 75 72 69 66 63 61 58 55 37 34 31 29 26 23 21 18 55 0

69° for dips in the some direction 0

3 for opposed dips

74 71 68 65 63 60 57 32 29 27 24 21 19 16 60 73 70 67 65 62 59 27 24 22 19 16 14 65 72 69 67 64 61 22 20 17 15 12 70 71 69 66 63 17 15 12 10 75 71 68 65 12 10 7 80 70 67 7 5 85 69 3 Notes Angles shown in the table are those between the stepeer dip and the boundary

(25)

Tabel 9.3.b Sudut Boundary Ray untuk penipisan 40% dan 50%. Boundary Ray Angles for Compactional Thinning of 40

Per Cent

Steeper Dip of Dip Intersection Point (Abscissa) G a n tl e D ip a t D ip d ir e ct io n P o in t (o rd in a te )0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 0 87 83 80 76 73 69 66 62 59 56 52 49 46 43 40 37 34 31 87 83 80 76 73 69 66 62 59 56 52 49 46 43 40 37 34 31 5 85 81 78 74 71 67 64 60 57 54 51 47 44 41 36 35 32 82 78 75 71 68 64 61 58 54 51 48 45 41 38 35 33 30 10 83 79 76 72 69 65 62 59 55 52 49 46 43 39 37 34 77 73 70 66 63 59 56 53 49 46 43 40 37 34 31 28 15 81 77 74 70 67 63 60 57 53 50 47 44 41 38 35 72 68 65 61 58 55 51 48 45 42 39 36 33 30 27 20 79 75 72 68 65 61 50 55 52 48 45 42 39 36 67 63 60 56 53 50 47 43 40 37 34 31 28 26 25 77 73 70 66 63 60 56 53 50 47 44 40 38 62 58 55 52 48 45 42 39 36 33 30 27 24 30 75 71 68 64 61 58 54 51 48 45 42 39 57 53 50 47 43 40 37 34 31 28 25 23 35 73 69 66 62 59 56 53 49 46 43 40 52 48 45 42 39 36 33 30 27 24 21 40 71 67 64 61 57 54 51 48 45 41 47 43 40 37 34 31 28 25 22 20 45 69 66 62 58 55 52 49 46 43 42 39 35 22 29 26 23 21 18 50 67 64 60 37 54 50 47 44 37 34 31 28 25 22 19 16 55 65 62 58 55 52 49 46 32 29 26 23 70 17 15 60

55° for dips in the some direction 2° for opposed dips

63 60 57 53 50 47 27 24 21 18 15 13 65 61 58 55 52 48 22 19 16 14 11 70 60 56 53 50 17 14 12 9 75 58 55 51 12 10 7 80 56 53 7 5 85 55 2 Notes Angles shown in the table are those between the stepeer dip and boundary

(26)

Steeper Dip of Dip Intersection Point (Abscissa) G a n tl e D ip a t D ip d ir e ct io n P o in t (o rd in a te )0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 0 86 83 79 75 71 68 64 60 57 53 50 46 43 39 36 33 30 27 86 83 79 75 71 68 64 60 57 53 50 46 43 39 36 33 30 27 5 84 80 76 73 69 65 62 57 54 51 47 44 40 37 34 31 28 81 78 74 70 66 63 59 56 52 48 45 42 38 35 32 29 26 10 81 78 74 70 66 63 59 56 52 48 45 42 38 35 32 29 76 73 69 65 62 58 54 51 47 44 40 37 34 31 28 25 15 79 75 71 68 64 60 57 53 50 46 43 39 36 33 30 71 68 64 60 57 53 50 46 43 39 36 33 30 26 24 20 76 73 69 65 61 58 54 51 47 44 40 37 34 31 66 63 59 55 52 48 45 41 38 35 32 28 25 22 25 74 70 66 63 49 55 52 48 45 41 38 35 31 61 58 54 51 47 44 40 37 34 30 27 24 21 30 71 68 64 60 57 53 49 45 42 39 36 32 56 53 49 46 42 39 36 32 29 26 23 20 35 69 65 61 58 54 51 47 43 40 37 33 51 48 44 41 38 34 31 28 25 22 19 40 66 63 59 55 52 48 45 41 38 34 47 43 40 36 33 30 26 23 20 18 45 64 60 56 53 49 46 42 39 35 42 38 35 31 28 25 22 19 16 50 61 58 54 50 47 43 40 36 37 33 30 27 24 21 18 15 55 59 55 51 48 44 41 37 32 28 25 22 19 16 14

60 44° for dips in the some

direction

2 for opposed dips

56 53 49 45 42 38 27 24 20 18 15 12 65 54 50 46 43 39 22 19 16 13 10 70 51 48 44 40 17 14 11 9 75 49 45 42 12 9 7 80 46 42 7 5 85 44 2 Notes Angles shown in the table are those between the stepeer dip and boundary

(27)

Z

er

o

d

ip

d

a

tu

m

K on st ru ks ik an " di p Is og on " pa da in te rv al d ip 2 0, d is ku si ka n ge om et ri b en tu k li pa ta n da ri p ol a B og on

(28)

. . . . .. .. .. .. .. . . . . . . .. .. .. .. .. . . . . . . . . . . . . . . . F D E A B C D F E F G H I H F G J K e m ir in ga n s e m u B a ta s lit o lo g i S s _B C la y C S s _F S h G S s H S h _I G p J S s _D S h E C la y A S a ya ta n v er tik a l un tu k so a l n o : 1 R e ko n st ru ks ik a n lip a ta n i n i d e n ga n m et od a ga bu ng a n : " A re m et ho d d a n f re e h an d m e th o d " . . . . . . . . . . . .. . . .. . . . . . .. . . .. . ._{. . . . . .} . . . . . . . . . .. . . .. . .

(29)

9 8 L ip ata n G eo lo gi D in am ik – G eo lo gi IT B