BAB 2 SOLUSI NUMERIK PERSAMAAN

(1)

BAB 2

SOLUSI NUMERIK PERSAMAAN

Dalam sains dan rekayasa, kita seringkali harus mencari akar (solusi) dari persamaan f(x) 0. Jika f(x) merupakan fungsi polinomial linear atau kuadratis, solusi eksaknya mudah untuk didapatkan karena rumusnya sudah tersedia. Akan tetapi, persamaan aljabar lainnya, terutama persamaan fungsi transenden, rumus untuk mendapatkan solusinya jarang tersedia. Jadi, apa yang dapat kita lakukan untuk memecahkan persoalan tersebut?

Pada bab ini, kita akan mempelajari metode-metode untuk menentukan akar persamaan secara numerik, di antaranya adalah metode biseksi, metode regula falsi, metode iterasi titik tetap, Newton-Raphson, dan metode tali busur.

2.1 Metode Biseksi

Metode biseksi (bagi dua) diawali dengan menggambarkan grafik f(x), dengan asumsi sebagai fungsi kontinu, seperti diperlihatkan pada Gambar 2.1. Akar real dari f(x) = 0 adalah titik perpotongan kurva dengan sumbu x, sebut x0. Selanjutnya, ambil selang [a, b], dengan x0 berada di dalamnya.

Secara matematis, akar akan terdapat di dalam selang [a, b] jika f(a) dan f(b) berlawanan tanda atau dengan kata lain

0 ) ( ) (a f b f

Algoritma metode biseksi sebagai berikut. (1) Pilih an dan bn. (2) Hitung 2 n n n b a x

(3) Hitung f(xn). Jika f(xn) = 0, berhenti dan akarnya diperoleh x0 = xn. (4) Hitung galat 2 n n n a b e .

(5) Jika f(an) f(xn) 0, pilih an+1 = an dan bn+1 = xn. Jika f(an) f(xn) 0, pilih an+1 = xn dan bn+1 = bn.

(6) Ulangi (1) s.d. (5) hingga diperoleh en < galat yang diinginkan.

Jumlah iterasi yang diperlukan untuk menjamin hampiran yang diperoleh memiliki galat kurang dari e ditentukan menggunakan persamaan

2 ln | | ln e a b n . x y a b x0 Gambar 2.1

(2)

CONTOH 1

Tentukan akar real dari x3 – 3x – 5 = 0 dengan akurasi 0,000001.

Penyelesaian

Skets grafik f(x)= x3 – 3x – 5. Terlihat bahwa kurva memotong sumbu-x antara 2 dan 3. Tahap 1: Ambil a1 = 2 dan b1 = 3.

Tahap 2: 2,5 2 3 2 2 1 1 1 b a x Tahap 3: ( ) (2,5) (2,5)3 3(2,5) 5 3,125 1 f x f Tahap 4: 0,5 2 2 3 2 1 1 1 a b e Tahap 5: ( ) (2) 23 3(2) 5 3 1 f a f maka f(a₁) f(x₁) 3(3,125) 9,375 0

Karena f(a_n) f(x_n) 0, pilih a2 = a1 = 2 dan b2 = x1 = 2,5.

Ulangi Tahap 1 s.d. 5 terus-menerus sehingga diperoleh nilai x0 dengan galat yang diinginkan. Dalam hal ini, jumlah iterasi yang diperlukan adalah

25 , 23 2 ln 0000001 , 0 | 2 3 | ln 2 ln | | ln e a b n .

Dengan demikian, jumlah iterasi minimum yang diperlukan adalah 24. Hasil perhitungannya diperlihatkan pada Tabel 2-1.

Tabel 2-1

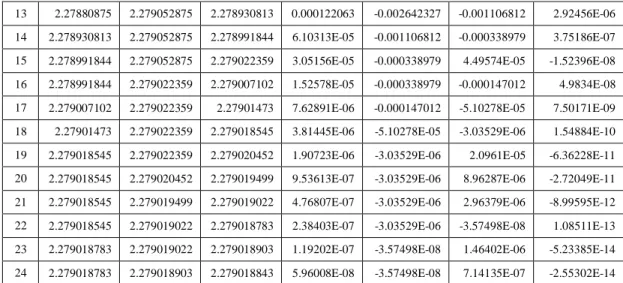
Iterasi untuk mendapatkan akar real dari persamaan x3 – 3x – 5 = 0 dengan galat 0,000001 menggunakan metode biseksi.

n an bn xn en f(an) f(xn) f(an) f(xn) 1 2 3 2.5 0.5 -3 3.125 -9.375 2 2 2.5 2.25 0.25 -3 -0.359375 1.078125 3 2.25 2.5 2.375 0.125 -0.359375 1.271484375 -0.456939697 4 2.25 2.375 2.3125 0.0625 -0.359375 0.428955078 -0.154155731 5 2.25 2.3125 2.28125 0.03125 -0.359375 0.028106689 -0.010100842 6 2.25 2.28125 2.265625 0.015625 -0.359375 -0.167293549 0.060121119 7 2.265625 2.28125 2.2734375 0.0078125 -0.167293549 -0.070009708 0.011712173 8 2.273438 2.28125 2.277344 0.003906 -0.070003456 -0.021052618 0.001473756 9 2.277344 2.28125 2.279297 0.001953 -0.021052618 0.003500954 -7.37043E-05 10 2.277344 2.279297 2.2783205 0.0009765 -0.021052618 -0.008782349 0.000184891 11 2.2783205 2.279297 2.27880875 0.00048825 -0.008782349 -0.002642327 2.32058E-05 12 2.27880875 2.279297 2.279052875 0.000244125 -0.002642327 0.000428906 -1.13331E-06

(3)

13 2.27880875 2.279052875 2.278930813 0.000122063 -0.002642327 -0.001106812 2.92456E-06 14 2.278930813 2.279052875 2.278991844 6.10313E-05 -0.001106812 -0.000338979 3.75186E-07 15 2.278991844 2.279052875 2.279022359 3.05156E-05 -0.000338979 4.49574E-05 -1.52396E-08 16 2.278991844 2.279022359 2.279007102 1.52578E-05 -0.000338979 -0.000147012 4.9834E-08 17 2.279007102 2.279022359 2.27901473 7.62891E-06 -0.000147012 -5.10278E-05 7.50171E-09 18 2.27901473 2.279022359 2.279018545 3.81445E-06 -5.10278E-05 -3.03529E-06 1.54884E-10 19 2.279018545 2.279022359 2.279020452 1.90723E-06 -3.03529E-06 2.0961E-05 -6.36228E-11 20 2.279018545 2.279020452 2.279019499 9.53613E-07 -3.03529E-06 8.96287E-06 -2.72049E-11 21 2.279018545 2.279019499 2.279019022 4.76807E-07 -3.03529E-06 2.96379E-06 -8.99595E-12 22 2.279018545 2.279019022 2.279018783 2.38403E-07 -3.03529E-06 -3.57498E-08 1.08511E-13 23 2.279018783 2.279019022 2.279018903 1.19202E-07 -3.57498E-08 1.46402E-06 -5.23385E-14 24 2.279018783 2.279018903 2.279018843 5.96008E-08 -3.57498E-08 7.14135E-07 -2.55302E-14

Dari tabel di atas, setelah iterasi ke-24, diperoleh x0 = 2,279018843 dengan galat e = 0,0000000596 < 0,0000001. Galat relatif hampirannya adalah

% 0000026 , 0 % 100 279018843 , 2 0000000596 , 0 % 100 0 x e erh

2.2 Metode Regula Falsi

Penentuan akar persamaan menggunakan metode regula falsi dilakukan dengan menarik garis antara dua titik, yaitu (a, f(a)) dan (b, f(b)) di sekitar lokasi akar, seperti diilustrasikan pada

Gambar 2.2. Perpotongan antara garis ini dengan sumbu-x merupakan taksiran akar (posisi palsu)

yang akan diperbaiki.

Gambar 2.2 Metode regula falsi.

Algoritma metode regula falsi sebagai berikut. (1) Pilih an dan bn dan cari f(an) dan f(bn). (2) Hitung ) ( ) ( ) ( ) ( n n n n n n n a f b f a f b b f a x

(3) Hitung f(xn). Jika f(xn) = 0, selesai.

(4) Hitung galat en | f(xn)| x y a b (b, f(b)) (a, f(a)) x

(4)

(5) Jika f(an) f(xn) 0, pilih an+1 = an dan bn+1 = xn. Jika f(an) f(xn) 0, pilih an+1 = xn dan bn+1 = bn.

(6) Ulangi (1) s.d. (5) hingga diperoleh en < galat yang diinginkan.

CONTOH

Tentukan akar real dari x3 – 3x – 5 = 0 dengan akurasi 0,000001 menggunakan metode regula falsi.

Penyelesaian

Ambil f(x) x3 3x 5.

Gunakan algoritma metode regula falsi. Hasilnya diperlihatkan pada Tabel 2-2.

Tabel 2-2

Iterasi untuk mendapatkan akar real dari persamaan x3 – 3x – 5 = 0 dengan galat 0,000001 menggunakan metode regula falsi.

n an bn f(an) f(bn) xn f(xn) f(an) f(xn) en 1 2 3 -3 13 2.1875 -1.094970703 3.284912109 1.094970703 2 2.1875 3 -1.094970703 13 2.25061923 -0.351825547 0.385238667 0.351825547 3 2.25061923 3 -0.351825547 13 2.270365691 -0.108360059 0.038123837 0.108360059 4 2.270365691 3 -0.108360059 13 2.276397202 -0.032937229 0.00356908 0.032937229 5 2.276397202 3 -0.032937229 13 2.278225912 -0.009971468 0.000328433 0.009971468 6 2.278225912 3 -0.009971468 13 2.278779115 -0.003015102 3.0065E-05 0.003015102 7 2.278779115 3 -0.003015102 13 2.278946349 -0.000911349 2.74781E-06 0.000911349 8 2.278946349 3 -0.000911349 13 2.278996894 -0.000275435 2.51018E-07 0.000275435 9 2.278996894 3 -0.000275435 13 2.27901217 -8.32414E-05 2.29276E-08 8.32414E-05 10 2.27901217 3 -8.32414E-05 13 2.279016787 -2.51568E-05 2.09409E-09 2.51568E-05 11 2.279016787 3 -2.51568E-05 13 2.279018182 -7.60272E-06 1.9126E-10 7.60272E-06 12 2.279018182 3 -7.60272E-06 13 2.279018604 -2.29764E-06 1.74684E-11 2.29764E-06 13 2.279018604 3 -2.29764E-06 13 2.279018731 -6.94379E-07 1.59544E-12 6.94379E-07 14 2.279018731 3 -6.94379E-07 13 2.279018769 -2.09851E-07 1.45716E-13 2.09851E-07 15 2.279018769 3 -2.09851E-07 13 2.279018781 -6.34196E-08 1.33086E-14 6.34196E-08

Dari tabel di atas, setelah iterasi ke-15, diperoleh x0 = 2,279018769 dengan galat e = 0,0000000634196 < 0,0000001. Galat relatif hampirannya adalah

% 0000027 , 0 % 100 279018769 , 2 196 0000000634 , 0 % 100 0 x e erh

(5)

2.3 Metode Iterasi Titik Tetap

Metode iterasi titik tetap merupakan metode sederhana karena prosedur iterasinya yang mudah. Hal pertama yang kita lakukan ketika menggunakan metode ini adalah membentuk persamaan x =

g(x) dari persamaan asalnya, yakni f(x) = 0.

Algoritmanya sebagai berikut.

1. Bentuk persamaan xn1 g(xn) dari f(x) = 0.

2. Taksir nilai awal, misal x1 = a.

3. Hitung xn1 g(xn).

4. Hitung |e xn 1 xn

5. Lakukan tahapan di atas secara berulang hingga dipenuhi e < galat yang diinginkan.

CONTOH

Tentukan akar real dari x2 – 4x – 5 = 0 menggunakan metode iterasi titik tetap dengan galat kurang dari 0,001.

Penyelesaian

Persamaan x2 – 4x – 5 = 0 dapat dibentuk menjadi sebagai berikut.

(1) x 4x 5 (2) 4 5 2 x x (3) 4 5 x x

Kita akan coba gunakan tiap-tiap persamaan di atas.

(1) x 4x 5

Ambil nilai awal: x1 = 3. Hasil iterasinya seperti diperlihatkan pada Tabel 2-3.

Tabel 2-3

Hampiran akar real dari x2 – 4x – 5 = 0 dengan metode iterasi titik tetap.

Iterasi ke - xn e 1 3 2 4.123106 1.123106 3 4.635992 0.512886 4 4.852213 0.216221 5 4.940531 0.088319 6 4.976156 0.035624 7 4.990453 0.014297 8 4.996180 0.005727 9 4.998472 0.002292 10 4.999389 0.000917

(6)

(2) 4 5 2 x x

Tabel 2-4

Iterasi ke - xn e 1 3 2 1 -2 3 -1 -2 4 -1 0 5 -1 0

Jadi, akar real persamaan x2 – 4x – 5 = 0 adalah x = –1.

(3)

4 5 x x

Tabel 2-5

Iterasi ke - xn e 1 3 2 -5 -8 3 -0.55556 4.444444444 4 -1.09756 -0.54200542 5 -0.98086 0.116699732 6 -1.00384 -0.022981215 7 -0.99923 0.004610361 8 -1.00015 -0.000921506 9 -0.99997 0.000184324 10 -1.00001 -3.68638E-05

Jadi, akar real persamaan x2 – 4x – 5 = 0 adalah x = –1.

Pemilihan x = g(x) dan nilai awal menentukan konvergensi akar yang dihasilkan. Bahkan, bisa jadi kita tidak mendapatkan hasil karena iterasinya divergen (nilainya terus membesar).

2.4 Metode Newton-Raphson

Dibandingkan dengan metode lain, untuk mendapatkan akar persamaan, metode Newton-Raphson merupakan metode yang paling cepat konvergensinya. Oleh karena itu, metode ini paling banyak digunakan dalam sains dan rekayasa.

Untuk mendapatkan metode ini, tinjau grafik y = f(x) seperti diperlihatkan pada Gambar 2.3. Misalnya f(x) terdiferensialkan maka grafik f(x) memiliki garis singgung pada setiap titik. Jika x1 merupakan hampiran pada akar sejatinya, hampiran yang lebih baik dari itu, x2, merupakan titik

(7)

potong garing singgung pada titik (x1, f(x1)) dengan sumbu-x. Dengan menggunakan hampiran x2, hampiran yang lebih baik lagi, x3, akan diperoleh. Demikian seterusnya sehingga hampiran yang mendekati nilai sejatinya, atau dengan kata lain galatnya lebih kecil dari yang disyaratkan, akan diperoleh.

Persamaan garis singgung pada grafik f(x) di titik (x1, f(x1)) adalah

) )( ( ' ) (x1 f x x x1 f y

dan titik potongnya dengan sumbu-x (y = 0) adalah

) ( ' ) ( 1 1 1 2 x f x f x x Catatan: f’(x1) 0.

Algoritma metode Newton-Raphson sebagai berikut. (1) Pilih x1 (2) Hitung xn+1 ) ( ' ) ( 1 n n n n x f x f x x (3) Hitung galat en | | _n₁ _n n x x e

(4) Ulangi (2) dan (3) sampai diperoleh en < galat yang diinginkan.

CONTOH

Gunakan metode Newton-Raphson untuk mendapatkan akar real dari x3 – 3x – 5 = 0 hingga tujuh desimal. Penyelesaian 5 3 ) ( 3 x x x f maka '( ) 3 2 3 x x f sehingga diperoleh 3 3 5 2 3 3 5 3 ) ( ' ) ( 2 3 2 3 1 n n n n n n n n n n x x x x x x x f x f x x

Pilih x1 = 2,5. Hasil iterasinya diperlihatkan pada Tabel 2-6 berikut.

Tabel 2-6

x y x2 (x1, f(x1)) x1 x0

(8)

Iterasi ke - xn e 1 2,5 2 2,30 0,20 3 2,2793 0,0207 4 2,2790188 0,0002812 5 2,2790188 0

2.5 Metode Tali Busur

Metode Newton sangat baik, tetapi menghitung turunan fungsinya kadang-kadang sulit. Keadaan ini mendorong pada gagasan untuk menggantikan turunan f’(xn) oleh hasil bagi selisih sebagai berikut. 1 1) ( ) ( ) ( ' n n n n n x x x f x f x f

Jika hasil ini dimasukkan pada rumus metode Newton, diperoleh

) ( ) ( ) ( ) ( 1 1 1 n n n n n n n x f x f x f x x x x .