Pelabelan Super Graceful Untuk Beberapa Graf Khusus

(1)

183 PELABELAN SUPER GRACEFUL_{UNTUK BEBERAPA}

GRAF KHUSUS 1

Primas Tri Anjar Anjani, 2Robertus Heri SU, 3Bayu Surarso 1,2,3

Jurusan Matematika Universitas Diponegoro Jl. Prof. Soedarto, SH, Tembalang, Semarang 54275

Abstract:

Given a graph G(V,E), super graceful labeling is bijective function f :V(G)E(G)



1,2,3,,pq



such that f(uv) f(u) f(v) for every edge uvE(G). A graph G that has a super graceful labeling called a super graceful graph. In this final paper discuss about super graceful labeling for special graphs graph 𝑃_𝑛, graph 𝑃_𝑚(𝑛), graph 𝑃_𝑛+− 𝑒₁, graph 𝐶_𝑛 𝑛 ≥3 graph 𝑃𝑛 1,2,…,𝑛 , graph 𝐾𝑚,𝑛, and graph Coconut tree.

Keywords: Graph labeling, super graceful labeling, super graceful graph. I. Pendahuluan

Graf merupakan salah satu cabang matematika yang berkembang pesat saat ini. Banyak penemuan-penemuan baru tentang graf seperti berbagai macam graf, macam-macam pelabelan graf dan cara melabelkannya. Pelabelan graf pertama kali dikenalkan oleh A.Kotsig dan Rosa (1967). Pelabelan pada graf G adalah pemberian nilai vertex dan edge pada grafG_.

Ada banyak pelabelan yang telah dikembangkan, diantaranya pelabelan

super graceful. Pelabelan super graceful merupakan pemetaan bijektif



p q



G E G V f : ( ) ( ) 1,2,3,4,,  sedemikian sehingga f(uv) f(u) f(v), untuk setiap sisi uvE(G). Sebuah graf G disebut graf super graceful jika merupakan pelabelan supergraceful.

II. Pembahasan Definisi 2.1 𝟖

Pelabelan graceful dari graf G(V,E) adalah pemetaan injektif



q



G V

f : ( ) 0,1,2,3,, , q E(G) sedemikian sehingga f(uv) f(u) f(v), untuk setiap uvE(G) sehingga label sisi yang dihasilkan berbeda.

Contoh 2.1 1 v v2 3 v 4 v 1 2 1 4 4 2 3 0

(2)

184 Definisi 2.2 𝟖

Pelabelan super graceful dari graf G adalah pemetaan bijektif



p q



G E G V f : ( ) ( ) 1,2,3,,  sedemikian sehingga f(uv) f(u) f(v), untuk setiap sisi uvE(G). Sebuah graf G yang memiliki pelabelan super graceful disebut graf supergraceful.

Contoh 2.2 3 5 1 6 7 2 4 v1 v2 v4 v3

Gambar 3.2 Graf supergraceful

Teorema 2.3 𝟖

Graf P_n adalah graf supergraceful. Bukti:

Misal Pn v1v2v3vn path dengan panjang n1, dengan V(Pn) n

dan E(P_n) n1.

Pelabelan titik untuk graf Pn(n1) didefinisikan dengan:

𝑓 𝑣𝑗 = ₂ _{𝑛 −}𝑗 −1, 1_𝑗_{, 1}_{≤ 𝑗}≤ 𝑗 ≤ 𝑛_{≤ 𝑛},_,𝑗 ≡_{𝑗 ≡}0(₁₍𝑚𝑜𝑑_𝑚𝑜𝑑2)₂₎

Pembuktian bahwa graf Pn adalah graf super graceful, akan dibagi menjadi dua

kasus.

Kasus 1,

n

adalah bilangan ganjil.

Himpunan label titik pada graf P_n, adalah: 𝑉1 = 𝑓 𝑣𝑗 𝑛 −1 𝑗=1 𝑗 ≡0(𝑚𝑜𝑑2) = 𝑗 −1 𝑛−1 𝑗=1 𝑗 ≡0(𝑚𝑜𝑑2) = 1, 3, 5,…,𝑛 −2 𝑉2 = 𝑓 𝑣𝑗 𝑛 𝑗=1 𝑗 ≡1(𝑚𝑜𝑑2) = 2𝑛 − 𝑗 𝑛 𝑗=1 𝑗 ≡1(𝑚𝑜𝑑2) = 2𝑛 −1, 2𝑛 −3,…,𝑛

Himpunan label sisi pada grafP_n, adalah: 𝐸1 = 𝑓 𝑣𝑗𝑣𝑗+1 𝑛 −1 𝑗=1 𝑗 ≡0 𝑚𝑜 𝑑2 = 2(𝑛 − 𝑗) 𝑛−1 𝑗=1 𝑗=0(𝑚𝑜𝑑2)

(3)

185 = 2 𝑛 −2 , 2 𝑛 −4 , 2 𝑛 −6 ,…,2 𝐸2 = 𝑓 𝑣𝑗𝑣𝑗+1 𝑛 −2 𝑗=1 𝑗 ≡1(𝑚𝑜𝑑2) = 2 𝑛 − 𝑗 𝑛 −2 𝑗=1 𝑗 ≡1 𝑚𝑜𝑑2 = 2(𝑛 −1), 2(𝑛 −3), 2(𝑛 −5),…,4

Terbukti untuk

n

bilangan ganjil,



1,2, ,

 

1,2, ,2 1



:VE pq  n

f   bijektif dan f(uv) f(u) f(v)

sehingga graf P_n merupakan graf supergraceful. Kasus 2,

n

adalah bilangan genap

Himpunan label titik pada graf P_n, adalah: 𝑉1 = 𝑓 𝑣𝑗 𝑛 𝑗=1 𝑗 ≡0(𝑚𝑜𝑑2) = 𝑗 −1 𝑛 𝑗=1 𝑗 ≡0(𝑚𝑜𝑑2) = 1, 3, 5,…,𝑛 −1 𝑉2 = 𝑓 𝑣𝑗 𝑛 −1 𝑗=1 𝑗 ≡1(𝑚𝑜𝑑2) = 2𝑛 − 𝑗 𝑛−1 𝑗=1 𝑗 ≡1(𝑚𝑜𝑑2) = 2𝑛 −1, 2𝑛 −3,…,𝑛+ 1

Himpunan label sisi pada grafPn, adalah:

𝐸1 = 𝑓 𝑣𝑗𝑣𝑗+1 𝑛 −2 𝑗=1 𝑗 ≡0(𝑚𝑜𝑑2) = 2 𝑛 − 𝑗 𝑛−1 𝑗=1 𝑗 ≡0 𝑚𝑜𝑑2 = 2 𝑛 −2 , 2 𝑛 −4 , 2 𝑛 −6 ,…,4 𝐸2 = 𝑓 𝑣𝑗𝑣𝑗+1 𝑛 −1 𝑗=1 𝑗 ≡1(𝑚𝑜𝑑2) = 2 𝑛 − 𝑗 𝑛 −1 𝑗=1 𝑗 ≡1 𝑚𝑜𝑑2 = 2(𝑛 −1), 2(𝑛 −3), 2(𝑛 −5),…,2

Terbukti untuk

n

bilangan genap,



1,2, ,

 

1,2, ,2 1



:VE pq  n

sehingga graf Pn(n1)merupakan graf super graceful. ∎

Dari kedua kasus diatas, dapat dilihat bahwa semua himpunan label titik memuat nilai ganjil dan semua himpunan label sisi memuat nilai genap. Terbukti, graf P_n adalah graf supergraceful.

Contoh 2.3

(4)

186 1

v v2 v3 v4 v5

9 8 1 6 7 4 5 2 3

Gambar 3.3 Graf P₅ b) Graf P₆adalah graf super graceful.

1 v v2 v3 v4 v5 9 8 7 6 1 3 4 2 6 v 5 10 11 Gambar 3.4 Graf P₆ Teorema 2.4 𝟖

Graf Pm(n)adalah graf supergraceful untuk m1dan n1.

Bukti:

Misal v1,v2,v3,,vm adalah titik dari path Pm dan ui,1,ui,2,,ui,n

adalah titik yang menggantung pada setiap vi, 1im. Dengan ) 1 ( )) ( (P n m n V _m dan E(P_m(n))m(n1)1. Pelabelan titik untuk path P_m(n)didefinisikan dengan:

𝑓 𝑣𝑖 = _𝑛_{+ 1}₂_𝑚_{+ 1} 𝑛+ 1_{− 𝑖 −} 𝑖 −_{1, 1}1, 1_{≤ 𝑖 ≤ 𝑚}≤ 𝑖 ≤ 𝑚_,,𝑖 ≡_{𝑖 ≡}₁₍0(_𝑚𝑜𝑑𝑚𝑜𝑑₂₎ 2)

Pelabelan titik untuk titik-titik yang menggantung pada setiap v_ididefinisikan dengan:

Untuk 1≤ 𝑖 ≤ 𝑚 dan 𝑖 ≡0 𝑚𝑜𝑑 2 ,

𝑓 𝑢𝑖,𝑗 = 𝑛+ 1 2𝑚+ 2− 𝑖 −(2𝑗+ 1), 1≤ 𝑗 ≤ 𝑛 dan

Untuk 1≤ 𝑖 ≤ 𝑚 dan 𝑖 ≡1 𝑚𝑜𝑑 2 ,

𝑓 𝑢𝑖,𝑗 = 𝑛+ 1 𝑖 −1 + 2𝑗 −1, 1≤ 𝑗 ≤ 𝑛.

Selanjutnya dikelompokkan himpunan label titik dan sisi sebagai berikut. Himpunan label titik pada graf Pm(n), adalah:

𝑉1 = 𝑓 𝑣𝑖 𝑚 𝑖=1 𝑖≡0 𝑚𝑜𝑑2 = 𝑛+ 1 𝑖 −1 𝑚 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

Untuk 𝑚 genap diperoleh

= 2𝑛+ 1, 4𝑛+ 3,…,𝑚 𝑛+ 1 −1 Untuk 𝑚 ganjil diperoleh

= 2𝑛+ 1, 4𝑛+ 3,…, 𝑚 −1 𝑛+ 1 −1 𝑉2 = 𝑓 𝑣𝑖 𝑚 −1 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 𝑛+ 1 2𝑚+ 1− 𝑖 −1 𝑚 −1 𝑖=1 𝑖≡1(𝑚𝑜𝑑2)

(5)

187 Untuk 𝑚 ganjil diperoleh

= 𝑛+ 1 2𝑚 −1, 𝑛+ 1 (2𝑚 −2)−1,…, 𝑛+ 1 (𝑚+ 1)−1 𝑉3 = 𝑓 𝑢𝑖,𝑗 𝑛 𝑗=1 𝑚 𝑖=1 𝑖≡0 𝑚𝑜𝑑2 = 𝑛+ 1 2𝑚+ 2− 𝑖 −(2𝑗+ 1) 𝑛 𝑗=1 𝑚 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

= 𝑛+ 1 2𝑚 −3, 𝑛+ 1 2𝑚 −5,…, 𝑛+ 1 2𝑚 −(2𝑛+ 1) ∪ 𝑛+ 1 2𝑚 −2 −3,…, 𝑛+ 1 2𝑚 −2 −(2𝑛+ 10) ∪ … ∪ 𝑛+ 1 𝑚+ 2 −3,…, 𝑛+ 1 𝑚+ 2 −(2𝑛+ 1) Untuk 𝑚 ganjil diperoleh

= 𝑛+ 1 2𝑚 −3, 𝑛+ 1 2𝑚 −5,…, 𝑛+ 1 2𝑚 −(2𝑛+ 1) ∪ 𝑛+ 1 2𝑚 −2 −3,…, 𝑛+ 1 2𝑚 −2 −(2𝑛+ 10) ∪ … ∪ 𝑛+ 1 𝑚+ 2 −3,…, 𝑛+ 1 𝑚+ 1 −(2𝑛+ 1) 𝑉4 = 𝑓 𝑢𝑖,𝑗 𝑛 𝑗=1 𝑚 −1 𝑖=1 𝑖≡1 𝑚𝑜𝑑2 = 𝑛+ 1 𝑖 −1 + 2𝑗 −1 𝑛 𝑗=1 𝑚−1 𝑖=1 𝑖≡1 𝑚𝑜𝑑2

= 1, 3, 5,…,2𝑛 −1 ∪ 2 𝑛+ 1 + 1, 2 𝑛+ 1 −3,…,2 𝑛+ 1 −2𝑛 −1

∪ … ∪ 𝑛+ 1 𝑚 −2 + 1,…, 𝑛+ 1 𝑚 −2 + 2𝑛 −1 Untuk 𝑚 ganjil diperoleh

= 1, 3, 5,…,2𝑛 −1 ∪ 2 𝑛+ 1 + 1, 2 𝑛+ 1 −3,…,2 𝑛+ 1 −2𝑛 −1

∪ … ∪ 𝑛+ 1 𝑚 −1 + 1,…, 𝑛+ 1 𝑚 −1 + 2𝑛 −1 Himpunan label sisi pada graf Pm(n), adalah:

𝐸1 = 𝑓 𝑣𝑖𝑣𝑖+1 𝑚 −2 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 𝑛+ 1 𝑖 −1−( 𝑛+ 1 2𝑚+ 1− 𝑖 −1) 𝑚 −2 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

= 2 𝑛+ 1 (𝑚 −2),2 𝑛+ 1 𝑚 −4 , 2 𝑛+ 1 𝑚 −6 ,…,4(𝑛+ 1) Untuk 𝑚 ganjil diperoleh

(6)

188 𝐸2 = 𝑓 𝑣𝑖𝑣𝑖+1 𝑚 −1 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 𝑛+ 1 2𝑚+ 1− 𝑖 −1 −( 𝑛+ 1 𝑖+ 1 −1) 𝑚 −1 𝑖=1 𝑖≡1 𝑚𝑜𝑑2

= 2 𝑛+ 1 (𝑚 −1),2 𝑛+ 1 𝑚 −3 , ,…,2(𝑛+ 1) Untuk 𝑚 ganji diperoleh

= 2 𝑛+ 1 (𝑚 −1),2 𝑛+ 1 𝑚 −3 , ,…,4(𝑛+ 1) 𝐸3 = 𝑓 𝑣𝑖𝑢𝑖,𝑗 𝑛 𝑗=1 𝑚 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 2 𝑛+ 1 𝑚 − 𝑖 −1 −1 ,…,2( 𝑛+ 1 𝑚 − 𝑖 −1 − 𝑛 𝑚 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

= {2((𝑛+ 1)(𝑚+ 1)−1),2((𝑛+ 1)(𝑚+ 1)−2),…,2((𝑛+ 1) (𝑚+ 1)− 𝑛)∪ … ∪{2((𝑛+ 1)−1),2((𝑛+ 1)−2),…,2} Untuk 𝑚 ganjil diperoleh

= 2(𝑛+ 1)(𝑚+ 1)−1),2((𝑛+ 1)(𝑚+ 1)−2),…,2((𝑛+ 1) (𝑚+ 1)− 𝑛)}∪ … ∪ 2 2 𝑛+ 1 −1 ,…,2𝑛+ 4 𝐸4 = 𝑓 𝑣𝑖𝑢𝑖,𝑗 𝑛 𝑗=1 𝑚 −1 𝑖=1 𝑖≡1 𝑚𝑜𝑑2 = 𝑛+ 1 2𝑚+ 1− 𝑖 −1−( 𝑛+ 1 𝑖 −1 + 2𝑗 −1) 𝑛 𝑗=1 𝑚−1 𝑖=1 𝑖≡1 𝑚𝑜𝑑2

= 2 𝑛+ 1 𝑚 −1 , 2 𝑛+ 1 𝑚 −2 ,…,2 𝑛+ 1 𝑚 − 𝑛 ∪ 2( 𝑛+ 1 𝑚 −2 −1,…,2( 𝑛+ 1 𝑚 −2 − 𝑛 ∪ … ∪ 2 2 𝑛+ 1 −1 , 2 2 𝑛+ 1 −2 ,…,2𝑛+ 4 Untuk 𝑚 ganjil diperoleh

= 2 𝑛+ 1 𝑚 −1 , 2 𝑛+ 1 𝑚 −2 ,…,2 𝑛+ 1 𝑚 − 𝑛 ∪ 2( 𝑛+ 1 𝑚 −2 −1,…,2( 𝑛+ 1 𝑚 −2 − 𝑛

∪ … ∪ 2 𝑛+ 1 −1 , 2( 𝑛+ 1 −2),…,2

Terbukti untuk

m

bilangan genap dan ganjil,



1,2, ,

 

1,2,3, ,( 1)2 1



:VE pq  n m f   bijektif dan ) ( ) ( ) (uv f u f v

(7)

189 Dari hasil diatas, dapat dilihat bahwa semua himpunan label titik memuat nilai ganjil dan semua himpunan label sisi memuat nilai genap. Terbukti, graf

) (n

Pm adalah graf supergraceful.

Contoh 2.4

Graf P₄(3) adalah graf super graceful.

v3 v1 v2 23 7 1 3 5 9 11 13 24 8 22 20 18 ₁₄ 10 12 6 4 v4 15 30 ₂₈ ₂₆ 31 16 29 27 25 21 19 17 1 , 1 u u1,2 u1,3 u2,1 u2,3 u2,3 u3,1 u3,2 u3,3 u4,1 u4,2 u4,3 2 Gambar 3.5 Graf P₄(3) Teorema 2.5 𝟖

Graf P_n e₁ dimana e₁v₁u₁ adalah super graceful untuk n1. Bukti:

Misal v1,v2,v3,,vn adalah titik dari path dengan panjang n1 dan n

u u u

u₁, ₂, ₃,, incident berturut-turut dengan titik v1,v2,v3,,vn. Dengan 1 2 ) (  1    _e _n P V _n dan (  1) 2 2  _e _n P E _n .

Pembuktian bahwa graf P_n e₁ adalah graf super graceful dibagi menjadi dua kasus.

Kasus 1, 𝑛 adalah bilangan ganjil

Pelabelan titik untuk graf P_n e₁definisikan dengan: 𝑓 𝑢𝑛 = 1 dan 𝑓 𝑣𝑛 = 4𝑛 −3

𝑓 𝑣𝑖 = ₃_{𝑛 −}𝑛+ 2_{3 +}− 𝑖_𝑖_{, 1}, 1_{≤ 𝑖 ≤ 𝑛 −}≤ 𝑖 ≤ 𝑛 −_1,1,_{𝑖 ≡}𝑖 ≡₁₍0(_𝑚𝑜𝑑𝑚𝑜𝑑₂₎ 2)

𝑓 𝑢𝑖 = ₃_{𝑛 −}₁𝑛_{− 𝑖}+𝑖_{, 2}, 2_{≤ 𝑖 ≤ 𝑛 −}≤ 𝑖 ≤ 𝑛 −_1,1,_{𝑖 ≡}𝑖 ≡₁0_𝑚𝑜𝑑 𝑚𝑜𝑑₂ 2

Selanjutnya dikelompokkan himpunan label titik dan sisi sebagai berikut. Himpunan label titik pada grafP_n e₁, adalah:

𝑉1 =𝑓 𝑢𝑛 = 1 dan 𝑉2 =𝑓 𝑣𝑛 = 4𝑛 −3 𝑉3 = 𝑓 𝑣𝑖 𝑛 −1 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 𝑛+ 2− 𝑖 = 𝑛,𝑛 −2,𝑛 −4,…,3 𝑛−1 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) 𝑉4 = 𝑓 𝑣𝑖 𝑛 −2 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 3𝑛 −3 +𝑖 𝑛−2 𝑖=1 𝑖≡1(𝑚𝑜𝑑2)

(8)

190 = 3𝑛 −2, 3𝑛, 3𝑛+ 2,…,4𝑛 −5 𝑉5 = 𝑓 𝑢𝑖 𝑛 −1 𝑖=2 𝑖≡0(𝑚𝑜𝑑2) = 𝑛+𝑖 𝑛−1 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 𝑛+ 2,𝑛+ 4,𝑛+ 6,…,2𝑛 −1 𝑉6 = 𝑓 𝑢𝑖 𝑛 −2 𝑖=2 𝑖≡1(𝑚𝑜𝑑2) = 3𝑛 −1− 𝑖 𝑛−2 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 3𝑛 −4,3𝑛 −6,…,2𝑛+ 1

Himpunan label sisi pada grafP_n e₁, adalah: 𝐸1 = 𝑓 𝑣𝑖𝑣𝑖+1 𝑛−1 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 2(𝑛+𝑖 −2) 𝑛−1 𝑖=1 𝑖≡0 𝑚𝑜𝑑2 = 2𝑛, 2𝑛+ 4,…,4𝑛 −6 𝐸2 = 𝑓 𝑣𝑖𝑣𝑖+1 𝑛 −2 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 2(𝑛+𝑖 −2) 𝑛−2 𝑖=1 𝑖≡1 𝑚𝑜𝑑2 = 2𝑛 −2, 2𝑛+ 4,2𝑛+ 6…,4𝑛 −8 𝐸3 = 𝑓 𝑣𝑖𝑢𝑖 𝑛 −1 𝑖=2 𝑖≡0(𝑚𝑜𝑑2) = 2𝑖 −2 𝑛−1 𝑖=2 𝑖≡0 𝑚𝑜𝑑2 = 2, 6,…,2𝑛 −4 𝐸4 = 𝑓 𝑣𝑖𝑢𝑖 𝑛 −2 𝑖=2 𝑖≡1(𝑚𝑜𝑑2) = 2𝑖 −2 𝑛−2 𝑖=2 𝑖≡1 𝑚𝑜𝑑2 = 4, 8,…,2𝑛 −6 𝐸5 = 𝑓 𝑢𝑛𝑣𝑛 = −4𝑛+ 4 = 4𝑛 −4

Terbukti untuk 𝑛 bilangan ganjil,



1,2, ,

 

1,2, ,4 3



:VE pq  n

sehingga graf P_n e₁ merupakan graf super graceful.

Kasus 2, 𝑛 adalah bilangan genap

Pelabelan titik untuk graf P_n e₁ definisikan: 𝑓 𝑢𝑛 = 1 dan 𝑓 𝑣𝑛 = 4𝑛 −3

(9)

191 𝑓 𝑢𝑖 = 3𝑛 −_𝑛1₊− 𝑖_𝑖_,2, 2_{≤ 𝑖 ≤ 𝑛 −}≤ 𝑖 ≤ 𝑛 −1,_1,_{𝑖 ≡}𝑖 ≡₁₍0(_𝑚𝑜𝑑𝑚𝑜𝑑₂₎ 2)

Selanjutnya dikelompokkan himpunan label titik dan sisi sebagai berikut. Himpunan label titik pada grafP_n e₁, adalah:

𝑉1 =𝑓 𝑢𝑛 = 1 dan 𝑉2 =𝑓 𝑣𝑛 = 4𝑛 −3 𝑉3 = 𝑓 𝑣𝑖 𝑛 −2 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 3𝑛 −3 +𝑖 𝑛−2 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 3𝑛 −1,3𝑛+ 1,3𝑛+ 3,…,4𝑛 −5 𝑉4 = 𝑓 𝑣𝑖 𝑛 −1 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 𝑛+ 2− 𝑖 𝑛−1 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 𝑛+ 1,𝑛 −1,𝑛 −3,…,3 𝑉5 = 𝑓 𝑢𝑖 𝑛 −2 𝑖=2 𝑖≡0(𝑚𝑜𝑑2) = 3𝑛 −1− 𝑖 𝑛−2 𝑖=2 𝑖≡0(𝑚𝑜𝑑2) = , 3𝑛 −3,3𝑛 −7,…,2𝑛+ 1 𝑉6 = 𝑓 𝑢𝑖 𝑛 −1 𝑖=2 𝑖≡1(𝑚𝑜𝑑2) = 𝑛+𝑖 𝑛−1 𝑖=2 𝑖≡1(𝑚𝑜𝑑2) = 𝑛+ 3,𝑛+ 5,…,2𝑛 −1

Himpunan label sisi pada grafP_n e₁, adalah:

𝐸1 = 𝑓 𝑣𝑖𝑣𝑖+1 = 2𝑛+ 2𝑖 −4 𝑛−2 𝑖=1 𝑖≡0 𝑚𝑜𝑑2 𝑛−2 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 2𝑛, 2𝑛+ 4,…,4𝑛 −8 𝐸2 = 𝑓 𝑣𝑖𝑣𝑖+1 𝑛 −1 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 2(𝑛+𝑖 −2) 𝑛−1 𝑖=0 𝑖≡1 𝑚𝑜𝑑2 = 2𝑛 −2, 2𝑛+ 2,…,4𝑛 −6 𝐸3 = 𝑓 𝑣𝑖𝑢𝑖 𝑛 −2 𝑖=2 𝑖≡0(𝑚𝑜𝑑2) = 2𝑖 −2 𝑛 −2 𝑖=2 𝑖≡0 𝑚𝑜𝑑2 = 2, 6, 10,…,2𝑛 −6

(10)

192 𝐸 4 = 𝑓 𝑣𝑖𝑢𝑖 𝑛 −1 𝑖=2 𝑖≡1(𝑚𝑜𝑑2) = 2𝑖 −2 𝑛−1 𝑖=2 𝑖≡1 𝑚𝑜𝑑2 = 4, 8,…,2𝑛 −4 𝐸5 = 𝑓 𝑢𝑛𝑣𝑛 = 𝑓 𝑢𝑛 − 𝑓 𝑣𝑛 = 4𝑛 −4

Terbukti untuk 𝑛 bilangan genap,



1,2, ,

 

1,2, ,4 3



:VE pq  n

sehingga graf P_n e₁ merupakan graf supergraceful. ∎

Dari kedua kasus diatas, dapat dilihat bahwa semua himpunan label titik memuat nilai ganjil dan semua himpunan label sisi memuat nilai genap. Terbukti, graf P_n e₁adalah graf supergraceful.

Contoh 2.5

a) Graf P₅ e₁adalah super graceful.

1 v v2 v3 v4 v5 16 13 6 2 4 15 8 11₁ 9 11 7 17 3 5 2 u u3 u4 u5 10 12 14 Gambar 3.6 Graf P₅ e₁ b) Graf P₆ e₁ adalah super graceful.

1 v v2 v3 v4 v5 8 7 6 2 4 6 v 5 10 1111 1 13 9 15 20 3 21 19 17 2 u u3 u4 u5 u6 12 14 16 18 Gambar 3.7 Graf P₆ e₁ Teorema 2.6 𝟖

(11)

193 Bukti:

Misal V(C_n)



u₁,u₂,u₃,,u_n



, dengan V(Cn) n dan E(Cn)n.

Pembuktian bahwa sikel C_n adalah graf supergraceful, akan dibagi menjadi dua kasus.

Kasus 1,

n

adalah ganjil, yaitu n2m1 untuk m1. Pelabelan titik untuk graf sikel C_n definisikan dengan:

𝑓 𝑢2𝑖−1 = 2𝑖 −1,1≤ 𝑖 ≤ 𝑚

𝑓 𝑢2𝑖 = 4𝑚+ 1−2𝑖,1≤ 𝑖 ≤ 𝑚 −1

𝑓 𝑢2𝑚 = 4𝑚 dan

𝑓 𝑢2𝑚+1 = 4𝑚+ 2

Selanjutnya dikelompokkan himpunan label titik dan sisi sebagai berikut. Himpunan label titik pada sikel C_n, adalah:

𝑉1 = 𝑓 𝑢2𝑖−1 𝑚 𝑖=1 = 2𝑖 −1 𝑚 𝑖=1 = 1,3,5,…,2𝑚 −1 𝑉2 = 𝑓 𝑢2𝑖 𝑚−1 𝑖=1 = 4𝑚+ 1−2𝑖 𝑚−1 𝑖=1 = 4𝑚 −1,4𝑚 −3,…,2𝑚+ 3 𝑉3 = 𝑓 𝑢2𝑚 = 4𝑚 𝑉4 = 𝑓 𝑢2𝑚+1 = 4𝑚+ 2

Himpunan label sisi pada sikel C_n, adalah: 𝐸1 = 𝑓 𝑢2𝑖−1𝑢2𝑖 𝑚−2 𝑖=1 = 4𝑚 −4𝑖 −2 𝑚−2 𝑖=1 = 4𝑚 −2,4𝑚 −6,4𝑚 −10,…,6 𝐸2 = 𝑓 𝑢2𝑖𝑢2𝑖+1 = 4(𝑚 − 𝑖) 𝑚−1 𝑖=1 𝑚−1 𝑖=1 = 4(𝑚 −1),4(𝑚 −2),…,4 𝐸3 = 𝑓(𝑢2𝑚−1𝑢2𝑚 = 2𝑚 −1 −4𝑚 = 2𝑚+ 1 𝐸4 = 𝑓(𝑢2𝑚𝑢2𝑚+1 = 4𝑚 −(4𝑚+ 2) = 2 𝐸5 = 𝑓(𝑢2𝑚+1𝑢1 = 4𝑚+ 2 −1 = 4𝑚+ 1

Terbukti untuk

n

bilangan ganjil,



1,2, ,

 

1,2, ,4 2



:VE pq  m

sehingga graf C_n merupakan graf super graceful

(12)

194 Pelabelan titik untuk graf sikel C_n definisikan dengan:

𝑓 𝑢2𝑖−1 = 2𝑖 −1, 1≤ 𝑖 ≤ 𝑚

𝑓 𝑢2𝑖 = 4𝑚 −1−2𝑖, 1≤ 𝑖 ≤ 𝑚 −1

𝑓 𝑢2𝑚 = 2 dan

𝑓 𝑢2𝑚+1 = 4𝑚

Selanjutnya dikelompokkan himpunan label titik dan sisi sebagai berikut. Himpunan label titik pada sikel Cn, adalah:

𝑉1 = 𝑓 𝑢2𝑖−1 𝑚−1 𝑖=1 = 2𝑖 −1 𝑚 𝑖=1 = 1,3,5,…,2𝑚 −3 𝑉2 = 𝑓 𝑢2𝑖 𝑚−1 𝑖=1 = 4𝑚 −1−2𝑖 𝑚−1 𝑖=1 = 4𝑚 −3,4𝑚 −5,…,2𝑚+ 1 𝑉3 = 𝑓 𝑢2𝑚−1 = 2 𝑉4 = 𝑓 𝑢2𝑚 = 4𝑚

Himpunan label sisi pada sikel C_n, adalah: 𝐸1 = 𝑓 𝑢2𝑖−1𝑢2𝑖 = 4(𝑚 − 𝑖) 𝑚−1 𝑖=1 𝑚−1 𝑖=1 = 4(𝑚 −1),4(𝑚 −2),…,4 𝐸2 = 𝑓 𝑢2𝑖𝑢2𝑖+1 = 4𝑚 −1−2𝑖 −(2𝑖+ 1) 𝑚−2 𝑖=1 𝑚−2 𝑖=1 = 4𝑚 −6,4𝑚 −10,…,6 𝐸3 = 𝑓(𝑢2𝑚−2𝑢2𝑚−1 = 𝑓 𝑢2𝑚−2 − 𝑓 𝑢2𝑚−1 = 2𝑚+ 1 −2 = 2𝑚 −1 𝐸4 = 𝑓(𝑢2𝑚−1𝑢2𝑚 = 𝑓 𝑢2𝑚−1 − 𝑓 𝑢2𝑚 = 4𝑚 −2 𝐸5 = 𝑓(𝑢2𝑚𝑢1 = 𝑓 𝑢2𝑚 − 𝑓 𝑢1 = 4𝑚 −1

Terbukti untuk

n

bilangan genap,



p q

 

m



E V

f :  1,2,,   1,2,,4 bijektif dan f(uv) f(u) f(v)

sehingga graf Cnmerupakan graf supergraceful. ∎

Dari kedua kasus diatas, diperoleh semua himpunan label titik dan semua label sisi berbeda. Terbukti, graf sikel C_n adalah graf super graceful.

Contoh 2.6

(13)

195 2 u 1 u 3 u 6 u 5 u 4 u 9 1 3 7 2 12 8 6 4 5 10 11 Gambar 3.8 Graf C₆ Teorema 2.7 𝟕

Graf Pn(1,2,,n) adalah graf super graceful untuk n1.

Bukti: Misal GPn(1,2,,n), dengan 2 ) 1 ( ) (G nn n V dan 2 ) 1 ( ) 1 ( ) (G  n nn E .

Pelabelan titik untuk graf G didefinisikan dengan: 𝑓 𝑣𝑖 = 𝑛2_{+ 3}_𝑛_{+ 1}₋1 2 𝑖+ 1 2_{, 1}_{≤ 𝑖 ≤ 𝑛}_,_{𝑖 ≡}₁₍_𝑚𝑜𝑑₂₎ 𝑖(𝑖+ 2) 2 −1, 1≤ 𝑖 ≤ 𝑛,𝑖 ≡0(𝑚𝑜𝑑 2) Untuk 1in dan i0(mod2)

𝑓 𝑢𝑖,𝑗 = 𝑛2+ 3𝑛+ 1− 𝑖2

2 −2𝑗, 1≤ 𝑗 ≤ 𝑖

Untuk 1in dan i1(mod2) 𝑓 𝑢𝑖,𝑗 =

𝑖−1 (𝑖+1)

2 −1 + 2𝑗, 1≤ 𝑗 ≤ 𝑖

Selanjutnya dikelompokan himpunan label titik dan sisi sebagai berikut. Himpunan label titik pada graf G, adalah:

𝑉1 = 𝑓 𝑣𝑖 𝑛 𝑖=1 𝑖≡1 𝑚𝑜𝑑2 = 𝑛2_{+ 3}_𝑛_{+ 1}₋_{1 2} 𝑖_{+ 1} 2 𝑛 𝑖=1 𝑖≡1(𝑚𝑜𝑑2)

Untuk 𝑛 ganjil diperoleh

= 𝑛2_{+ 3}_{𝑛 −}_1,_𝑛2_{+ 3}_{𝑛 −}_7,_𝑛2_{+ 3}_{𝑛 −}_17,_…_,𝑛

2_{+ 4}_𝑛_{+ 1}

2 Untuk 𝑛 genap diperoleh

= 𝑛2+ 3𝑛 −1,𝑛2+ 3𝑛 −7,𝑛2+ 3𝑛 −17,…,𝑛

2_{+ 6}_𝑛_{+ 2}

(14)

196 𝑉2 = 𝑓 𝑣𝑖 𝑛 −1 𝑖=1 𝑖≡0(𝑚𝑜𝑑2) = 𝑖(𝑖+ 2) 2 −1 𝑛−1 𝑖=1 𝑖≡0(𝑚𝑜𝑑2)

Untuk 𝑛 ganjil diperoleh = 3,11,23,…,𝑛

2₋₃

2 Untuk 𝑛 genap diperoleh = 3,11,23,…,𝑛 2_{+ 2n}₋₂ 2 𝑉3 = 𝑓 𝑢𝑖,𝑗 𝑖 𝑗=1 𝑛 −1 𝑖=1 𝑖≡0 𝑚𝑜𝑑2 = 𝑛2_{+ 3}_𝑛_{+ 1}₋𝑖 2 2 −2𝑗 𝑖 𝑗=1 𝑛 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

= 𝑛2+ 3𝑛 −1−2𝑗; 1≤ 𝑗 ≤2 ∪ 𝑛2+ 3𝑛 −7−2𝑗; 1≤ 𝑗 ≤4 ∪ … ∪ 𝑛2+ 8₂𝑛+ 1−2𝑗; 1≤ 𝑗 ≤ 𝑛 −1

Untuk 𝑛 genap diperoleh

= 𝑛2_{+ 3}_{𝑛 −}₁₋₂_𝑗_{; 1}_{≤ 𝑗 ≤}₂ ∪ 𝑛2_{+ 3}_{𝑛 −}₇₋₂_𝑗_{; 1}_{≤ 𝑗 ≤}₄ ∪ … ∪ 𝑛2+ 6₂𝑛+ 1 −2𝑗; 1≤ 𝑗 ≤ 𝑛 𝑉4 = 𝑓 𝑢𝑖,𝑗 𝑖 𝑗=1 𝑛 𝑖=1 𝑖≡1 𝑚𝑜𝑑2 = 𝑖 −1 (𝑖+ 1) 2 −1 + 2𝑗 𝑖 𝑗=1 𝑛 𝑖=1 𝑖≡1 𝑚𝑜𝑑2

= 2𝑗 −1;𝑗 = 1 ∪ 3 + 2𝑗; 1≤ 𝑗 ≤3 ∪ 11 + 2𝑗; 1≤ 𝑗 ≤5 ∪ … ∪ 𝑛2₂−3+ 2𝑗; 1≤ 𝑗 ≤ 𝑛

= 2𝑗 −1;𝑗 = 1 ∪ 3 + 2𝑗; 1≤ 𝑗 ≤3 ∪ 11 + 2𝑗; 1≤ 𝑗 ≤5 ∪ … ∪ 𝑛2−2₂𝑛 −2+ 2𝑗; 1≤ 𝑗 ≤ 𝑛 −1

(15)

197 Himpunan label sisi pada graf G, adalah:

𝐸1 = 𝑓 𝑣𝑖𝑣𝑖+1 𝑛−2 𝑖=1 𝑖≡1𝑚𝑜𝑑2) = 𝑛2_{+ 3}_𝑛_{+ 2} −₍_𝑖2_{+ 3}_𝑖_{+ 2)} 𝑛−2 𝑖=1 𝑖≡1 𝑚𝑜𝑑2

= 𝑛2+ 3𝑛 −4,𝑛2+ 3𝑛 −18,…,2𝑛+ 2 Untuk 𝑛 genap diperoleh

= 𝑛2_{+ 3}_{𝑛 −}_4,_𝑛2_{+ 3}_{𝑛 −}_18,_…_,4_𝑛_{+ 2} 𝐸2 = 𝑓 𝑣𝑖𝑣𝑖+1 𝑛−1 𝑖=1 𝑖≡0𝑚𝑜𝑑2) = 𝑖2+ 3𝑖+ 2 − 𝑛2+ 3𝑛+ 2 𝑛 −1 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

= 𝑛2_{+ 3}_{𝑛 −}_10,_𝑛2_{+ 3}_{𝑛 −}_28,_…_,2_𝑛_{+ 2}

= 𝑛2_{+ 3}_{𝑛 −}_10,_𝑛2_{+ 3}_{𝑛 −}_28,_…_,4_𝑛_{+ 2} 𝐸3 = 𝑓 𝑣𝑖𝑢𝑖,𝑗 𝑖 𝑗=1 𝑛 𝑖=1 𝑖≡1(𝑚𝑜𝑑2) = 𝑛2+ 3𝑛+ 2−2𝑗 − 𝑖(𝑖+ 1) 𝑖 𝑗=1 𝑛 𝑖=1 𝑖≡1 𝑚𝑜𝑑2

= 𝑛2_{+ 3}_{𝑛 −}₂ ∪ 𝑛2_{+ 3}_{𝑛 −}_12,_𝑛2_{+ 3}_{𝑛 −}_14,_𝑛2_{+ 3}_{𝑛 −}₁₆

∪ … ∪ 2𝑛, 2𝑛 −2,…,2 Untuk 𝑛 genap diperoleh

= 𝑛2 _{+ 3}_{𝑛 −}₂ ∪ 𝑛2_{+ 3}_{𝑛 −}_12,_𝑛2_{+ 3}_{𝑛 −}_14,_𝑛2_{+ 3}_{𝑛 −}₁₆ ∪ … ∪ 4𝑛, 4𝑛 −2,…,2𝑛+ 4 𝐸4 = 𝑓 𝑣𝑖𝑢𝑖,𝑗 𝑖 𝑗=1 𝑛 −1 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

(16)

198 = 𝑖 𝑖+ 1 + 2𝑗 −(𝑛2+ 3𝑛+ 2) 𝑖 𝑗=1 𝑛 −1 𝑖=1 𝑖≡0 𝑚𝑜𝑑2

= 𝑛2+ 3𝑛 −6,𝑛2+ 3𝑛 −8 ∪ … ∪ 4𝑛, 4𝑛 −2,…,2𝑛+ 4 Untuk 𝑛 genap diperoleh

= 𝑛2+ 3𝑛 −6,𝑛2+ 3𝑛 −8 ∪ … ∪ 2𝑛, 2𝑛 −2,2𝑛 −4,…,2

Terbukti untuk 𝑛 bilangan ganjil dan bilangan genap,



1,2,3, ,





1,2,3, , 3 1



:VE pq  n2 n f   bijektif dan ) ( ) ( ) (uv f u f v

f   sehingga graf P_n(1,2,,n) merupakan graf super graceful.

∎

Dari kedua kasus diatas, diperoleh semua himpunan titik bernilai ganjil dan semua himpunan sisi bernilai genap. Terbukti, graf P_n(1,2,,n)adalah graf

super graceful. Contoh 2.7

Graf P₄(1,2,3,4) adalah supergraceful.

v3 v1 v2 u1,1 u2,1 u2,2 u3,1 u3,2 u3,3 27 3 1 25 23 5 7 9 20 8 2 4 6 12 10 u4,1 u4,2 u4,3 u4,3 19 17 15 13 16 ₁₄ 24 22 26 21 11 v4 18 Gambar 3.9 Graf P₄(1,2,3,4) Teorema 2.8 𝟕

Setiap graf bipartit komplit K_m_,_n(m1,n1) adalah graf super graceful.

Bukti:

Misal VV₁V₂ dimana V1



u1,u2,u3,,um



dan



v v v vn



V₂  ₁, ₂, ₃,, . Dengan V(Km,n) mn dan E(Km,n) mn

Pelabelan titik untuk graf K_m_,_n didefinisikan dengan:

(17)

199 Selanjutnya dikelompokkan himpunan label titik dan sisi sebagai berikut.

Himpunan label titik pada graf K_m_,_n, adalah: 𝑉1 = 𝑓 𝑢𝑖 𝑚 𝑖=1 = 𝑖 𝑚 𝑖=1 = 1,2,…,𝑚 𝑉2 = 𝑓 𝑣𝑗 𝑛 𝑗=1 = 𝑚+ 𝑚+ 1 𝑗 𝑛 𝑗=1 = 𝑚+ 𝑚+ 1 ,𝑚+ 2 𝑚+ 1 ,…,𝑚+𝑛(𝑚+ 1) Himpunan label sisi pada graf K_m_,_n, adalah:

𝐸 = 𝑓 𝑢_𝑖𝑣_𝑗 𝑛 𝑗=1 𝑚 𝑖=1 = 𝑚+ 𝑚+ 1 𝑗 − 𝑖 𝑛 𝑗=1 𝑚 𝑖=1 = 𝑚+ 𝑚+ 1 −1,𝑚+ 2 𝑚+ 1 −1,…,𝑚+𝑛 𝑚+ 1 −1 ∪ 𝑚+ 𝑚+ 1 −2,𝑚+ 2 𝑚+ 1 −2,…,𝑚+𝑛 𝑚+ 1 −2 ∪ … ∪ 𝑚+ 1,2 𝑚+ 1 ,…,𝑛 𝑚+ 1 Terbukti f :VE



1,2,3,,pq

 

 1,2,3,,mn(m1)



_bijektif dan f(uv) f(u) f(v) sehingg graf K_m_,_n merupakan graf supergraceful. ∎

Diperoleh semua himpunan label titik dan himpunan label sisi berbeda dan gabungannya adalah



1,2,3,,mn(m1)



. Terbukti, graf K_m_,_n(m1,n1)

adalah graf supergraceful. Contoh 2.8

Graf K₃_,₃ adalah supergraceful. 1 u u2 u3 1 v v2 v₃ 1 2 4 3 5 6 7 8 10 14 11 12 9 13 15 Gambar 3.10 Graf K₃_,₃

(18)

200 Teorema 2.9 𝟕

Graf Coconut tree adalah graf supergraceful.

Bukti:

Pelabelan titik untuk graf G didefinisikan dengan:

𝑓 𝑣𝑗 = 2𝑖+ 1− 𝑗_𝑗_{, 1} ,1_{≤ 𝑗 ≤ 𝑖}≤ 𝑗 ≤ 𝑖_,,_𝑑𝑎𝑛𝑑𝑎𝑛_{𝑗 ≡}𝑗 ≡₁₍0(_𝑚𝑜𝑑𝑚𝑜𝑑₂₎ 2)

𝑓 𝑣𝑘 = 2𝑘 −1,𝑖+ 1≤ 𝑘 ≤ 𝑛.

Selanjutnya dikelompokkan himpunan label titik dan sisi sebagai berikut. Himpunan label titik graf G, adalah:

𝑉1 = 𝑓 𝑣𝑗 𝑖 𝑗=1 𝑗 ≡0 𝑚𝑜𝑑 2 = 2𝑖+ 1− 𝑗 𝑖 𝑗=1 𝑗≡0 𝑚𝑜𝑑 2

Untuk 𝑖 genap diperoleh = 2𝑖 −1, 2𝑖 −3,…,𝑖+ 1 Untuk 𝑖 ganjil diperoleh = 2𝑖 −1, 2𝑖 −3,…,𝑖+ 2 𝑉2 = 𝑓 𝑣𝑗 𝑖−1 𝑗=1 𝑗 ≡1 𝑚𝑜𝑑 2 = 𝑗 𝑖−1 𝑗=1 𝑗 ≡1 𝑚𝑜𝑑 2

Untuk 𝑖 genap diperoleh = 1, 3, 5 ,…,𝑖 −1 Untuk 𝑖 ganjil diperoleh = 1, 3, 5,…,𝑖 𝑉3 = 𝑓 𝑣𝑘 𝑛 𝑘=𝑖+1 = 2𝑘 −1 𝑛 𝑘=𝑖+1

Untuk 𝑖 genap diperoleh = 2𝑖+ 1,2𝑖+ 3,…,2𝑛 −1 Untuk 𝑖 ganjil diperoleh = 2𝑖+ 1,2𝑖+ 3,…,2𝑛 −1 Himpunan label sisi garf G, adalah:

𝐸1 = 𝑓 𝑣𝑗𝑣𝑗+1 𝑖−2 𝑗=1 𝑗 ≡0 𝑚𝑜𝑑2 = 2(𝑖 − 𝑗) 𝑖−2 𝑗=1 𝑗 ≡0 𝑚𝑜𝑑2

Untuk 𝑖 genap diperoleh = 2 𝑖 −2 , 2 𝑖 −4 ,…,4

(19)

201 Untuk 𝑖 ganjil diperoleh

= 2 𝑖 −2 , 2 𝑖 −4 ,…,2 𝐸2 = 𝑓 𝑣𝑗𝑣𝑗+1 𝑖−1 𝑗=1 𝑗 ≡1 𝑚𝑜𝑑2 = 2(𝑖 − 𝑗) 𝑖−2 𝑗=1 𝑗 ≡0 𝑚𝑜𝑑2

Untuk 𝑖 genap diperoleh = 2 𝑖 −1 , 2(𝑖 −3),…,2

Untuk 𝑖 ganjil diperoleh = 2 𝑖 −1 , 2(𝑖 −3),…,4 𝐸3 = 𝑓 𝑣𝑘𝑣1 𝑛 𝑘=𝑖+1 = 2𝑘 −2 𝑛 𝑘=𝑖+1

Untuk 𝑖 genap diperoleh = 2𝑖, 2𝑖+ 2, 2𝑖+ 4,…,2𝑛 −2 Untuk 𝑖 ganjil diperoleh

= 2𝑖, 2𝑖+ 2, 2𝑖+ 4,…,2𝑛 −2

Terbukti untuk bilangan i genap dan ganjil,



1,2,3, ,

 

1,2,3, 2 1



:VE pq  n

f   _{bijektif dan} f(uv) f(u) f(v)

sehingga graf Coconut tree merupakan graf supergraceful. ∎

Dari kedua kasus diatas, diperoleh semua himpunan label titik bernilai ganjil dan semua himpunan label sisi bernilai genap. Terbukti, graf Coconut tree

dalah graf supergraceful. Contoh 2.9

(20)

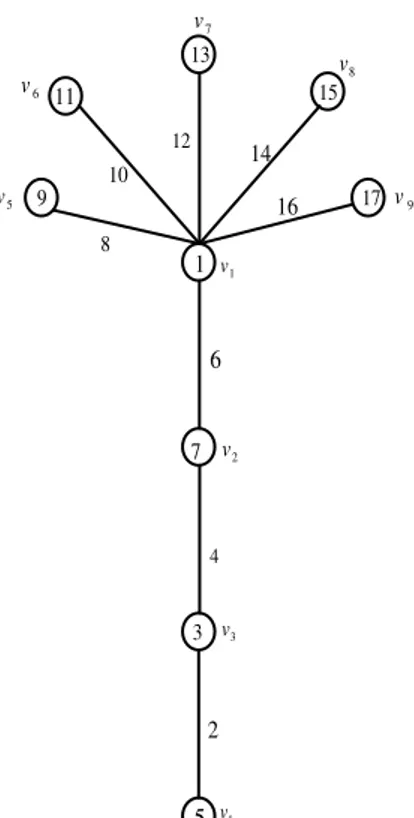
202 1 v 2 v 3 v 4 v 5 v 6 v 7 v 8 v 9 v 1 2 3 4 5 6 7 8 9 10 12 14 16 11 13 15 17

Gambar 3.11 Graf Coconut tree untuk i4dan n9 III. Kesimpulan

Berdasarkan pembahasan mengenai pelabelan super graceful untuk beberapa graf khusus, dapat diambil kesimpulan yaitu setiap himpunan titik berlabel ganjil dan himpunan sisinya berlabel genap, kecuali untuk graf Cn

dan graf K_m_,_n. Untuk graf C_n tidak memiliki himpunan label sisi genap dan himpunan label titik ganjil karena pada graf C_n jumlah banyaknya titik dan sisi bernilai genap, maka label titiknya tidak semuanya bernilai ganjil begitu juga dengan graf K_m_,_n yang memiliki jumlah banyaknya titik dan sisi dapat bernilai ganjil atu genap maka label titiknya tidak semuanya bernilai ganjil.

IV. Referensi

[1] Arifin, Achmad. 2000. Aljabar. Bandung: ITB.

[2] Bartle, Robert G dan Donald R. Sherbert. 2000. Introduction to Real Analysis Third Edition. New York:John Willey and Sons.

[3] Baskar Babujee, J. dan V. Vishnupriya. 2011. On A-Vertex Consecutive Edge Bimagic Labeling in Graphs. European Journal of Scientific Research, Vol.63, No.1, hal 84-89.

[4] Chartrand, G dan L. Lesniak. 1996. Graphs and Digraphs, 3𝑟𝑑 ed, Chapman & Hill. London.

(21)

203 [5] Dwi Asyani, Destian. 2012. Pelabelan 𝑄 𝑎 𝑃(𝑏)-super graceful-sisi pada graf kubus hiper 𝑄_𝑘 untuk 𝑘 ≤3. Semarang: FMIPA Universitas Diponegoro.

[6] Ghafur, Abdul. 2010. Pelabelan Super Edge-graceful pada path dan fan graph. Semarang: FMIPA Universitas Diponegoro.

[7] Perumal, M.A, Navaneethakrishnan, S, Arockiaraj, S dan Nagarajan.A. 2011. Super Graceful Labeling for Some Special Graphs. IJJRAS, Vol.9, hal 382-404.

[8] Perumal, M.A, Navaneethakrishnan, S, Arockiaraj, S dan Nagarajan.A.. 2012. Super Graceful Labeling for Some Simple Graphs. Journal of Mathematics and Soft Computing, Vol.2,No.1,hal 35-49.

[9] Rosen, Kenneth H. 2007. Discrete Mathematics and Its Application. edisi ke-7. New York: McGraw. Hill.

[10] Seputro, Theresia MH Tirta. 1992. Graf Pengantar. Surabaya :University Press IKIP.

[11] Susilo, Frans. 2006. Himpunan dan Logika Kabur serta Aplikasinya. Yogyakarta : Graha Ilmu

[12] Wilson, J. Robin and John J. Watskin. 1990. Graphs An Introductory Approach. New York : University Course Graphs, Network, and Design

[13] Yismianto, Bambang dan Irawanto, Bambang. 2003. Buku Ajar Matematika Diskret I. Semarang: FMIPA Universitas Diponegoro.