HUBUNGAN PELABELAN GRACEFUL PADA DIGRAF BIDIRECTIONAL G DAN GRAF UNDERLYING DARI G

HUBUNGAN PELABELAN GRACEFUL PADA

DIGRAF BIDIRECTIONAL G DAN GRAF UNDERLYING DARI G Kristiana Wijaya

Jurusan Matematika FMIPA Universitas Jember E-mail: kristiana_wijaya@yahoo.com

Diterima 12 Juni 2007, perbaikan 25 Januari 2008, disetujui untuk diterbitkan 28 Januari 2008

ABSTRACT

A graceful labelling of digraph D with n vertices and e arcs is a one to one function

λ ^{: V ( D )} → { ^{0 , 1 ,} L ^{, e} }

^such

that each arc

a = xy

in D is labelled with

λ ( a ) = λ ( xy ) = λ ( y ) − λ ( x )

^mod

⁽ e + ^{1 )}

, the resulting arc labels are distinct. A digraph D is called graceful if it admits any graceful labeling. In this paper we give the relation between a graceful labeling on bidirectional digraph

G

and underlying graph of

G

, i.e

G = G

^.

Keywords: graceful labeling, bidirectional digraph and underlying graph

1. PENDAHULUAN

Pelabelan graf merupakan pemberian nilai (biasanya bilangan bulat tak negatif) pada himpunan titik atau sisi graf yang memenuhi aturan tertentu. Pelabelan graf sudah dikenal sejak tahun 60-an. Sejak itu sudah lebih dari 300 tulisan yang dihasilkan mengenai pelabelan graf. Pelabelan graf menjadi topik yang banyak mendapat perhatian, karena model-model yang ada pada pelabelan graf mempunyai aplikasi yang luas, seperti dalam masalah teori koding, kristalografi sinar-X, radar, sistem alamat jaringan komunikasi dan desain sirkuit ¹⁾.

Salah satu jenis pelabelan graf yang telah dikenal adalah pelabelan graceful. Pelabelan graceful diperkenalkan oleh Rosa²⁾ pada tahun 1967 dengan nama valuasi-β, yang didefinisikan sebagai fungsi

λ

yang merupakan fungsi satu-satu dari himpunan titik graf G ke himpunan bilangan bulat {0, 1, 2,…,

) (G

E

}, sehingga setiap sisi (x, y) di G mendapat label |λ(x) − λ(y)| yang berbeda semua. Kemudian pada tahun 1972, Golomb menamakan pelabelan ini sebagai pelabelan graceful.

Pelabelan graceful pada graf telah banyak dikaji, diantaranya adalah sebagai berikut:

1. Rosa²⁾ membuktikan bahwa graf sikel Cn graceful jika dan hanya jika n ≡ 0 atau 3 (mod 4),

2. Hoede dan Kuiper³⁾ membuktikan bahwa graf roda Wn graceful untuk setiap

n ≥ 3

,

3. Golomb⁴⁾ membuktikan bahwa graf lengkap Kn

graceful jika dan hanya jika

n ≤ 4

; dan graf bipartit lengkap Km,n adalah graceful untuk setiap m dan n.

Hasil tentang graceful pada graf, selengkapnya dapat dilihat di Galian⁵⁾.

Sejalan dengan ide pelabelan graceful pada graf, Bloom dan Hsu⁶⁾ memperkenalkan pelabelan graceful pada digraf (graf berarah). Misalkan

D ( e n , )

digraf dengan n titik dan e arc. Pelabelan graceful pada digraf D adalah fungsi satu-satu:

{ ^e }

Z D

V ( )

_e

0, 1, 2, ,

: →

₊₁

= L

λ

^{, dengan}

setiap arc

( x , y )

di D mendapat label

λ ⁽ x ^, y ⁾ = λ ⁽ y ⁾ − λ ⁽ x ⁾ ( ^{mod (} e + ^{1 )} )

yang berbeda semua.

Sebuah digraf D disebut digraf graceful jika setiap titik dan arc pada digraf D dapat diberi labell menurut aturan pelabelan graceful.

Graf (tak berarah) G = |D| merupakan graf underlying dari digraf D, jika

V ( G ) = V ( D )

^{dan sisi}

( x , y )

adalah sisi di G jika arc

( x , y )

atau arc

( y , x )

adalah arc di D. Karena setiap sisi di |D| merupakan salah satu arah atau dua arah yang ada di D, maka ada 3^e digraf D yang berasosiasi dengan graf underlying |D|.

Jadi setiap digraf merupakan orientasi dari |D|.

Sedangkan digraf bidirectional

G

dari graf G adalah graf dengan himpunan titik

V ( G ) = V ( G )

^{dan arc}

simetri

( x , y )

dan

( y , x )

adalah arc di

G

jika sisi

) ,

( x y

adalah sisi di G. Dengan demikian jika G adalah graf dengan n titk dan e sisi, maka digraf bidirectional

G

adalah graf dengan n titik dan 2e arc.

Untuk selanjutnya, digraf bidirectional

G

akan disebut digraf

G

saja. Selebihnya mengenai konsep graf dan digraf dapat dibaca pada buku Graphs and Digraphs⁷⁾ dan Graph Theory⁸⁾.

Pada paper ini dibahas mengenai hubungan pelabelan graceful pada digraf bidirectional dan graf underlying- nya, yaitu apakah pelabelan graceful pada digraf

G

dapat diperoleh dari pelabelan graceful pada graf underlying dari

G

(yaitu

G = | G |

). Hubungan ini akan diterapkan pada beberapa kelas graf, khususnya kelas graf yang telah dikaji kegracefulannya, yaitu graf sikel, graf roda, graf lengkap dan graf bipartit lengkap.

2. METODE PENELITIAN

Penulisan paper ini dilakukan dengan metode teoritis, yaitu dengan cara mempelajari dan mengkaji karya- karya ilmiah yang telah ada mengenai pelabelan graceful, baik pelabelan graceful pada graf maupun pelabelan graceful pada digraf. Langkah selanjutnya adalah menyelidiki hubungan antara pelabelan graceful pada graf dan digraf, khususnya pelabelan graceful pada digraf bidirectional

G

dan graf underlying

|

| G

G =

, yaitu apakah untuk mendapatkan pelabelan graceful pada digraf bidirectional dapat diperoleh dari pelabelan graceful pada graf underlying-nya. Langkah terakhir, diselidiki perumusan pelabelan graceful pada kelas digraf bidirectional, yaitu digraf sikel dan digraf lengkap guna melihat hubungannya dengan pelabelan graceful pada graf sikel dan graf lengkap.

3. PEMBAHASAN

Pada bagian ini dibahas hubungan pelabelan graceful pada digraf

G

dengan pelabelan graceful pada graf

|

| G

G =

, yaitu bahwa pelabelan graceful pada digraf

G

bisa didapatkan dari pelabelan graceful pada graf G. Selanjutnya akan dibahas pelabelan graceful pada beberapa kelas digraf bidirectional, yaitu kelas digraf

G

dengan graf

G = | G |

yang telah diketahui graceful atau tidak. Kelas digraf yang dimaksud adalah digraf sikel

C

_n , digraf roda

W

_n , digraf lengkap

K

_n

dan digraf bipartit lengkap

K

_m,n.

Teorema 1. Jika graf G graceful, maka digraf

G

juga graceful dengan label titik yang sama dengan graf G ⁶⁾. Bukti: Jika G adalah graf dengan n titik dan e sisi, maka

G

adalah graf dengan n titik dan 2e arc. Dengan demikian pelabelan graceful pada digraf

G

menggunakan modulo

( 2 e + 1 )

. Misalkan G graceful dengan label titik λ(x) untuk setiap

x ∈ V (G )

^{, maka}

λ(x) juga menjadi label titik di

G

untuk setiap

) (G V

x ∈

. Dan untuk setiap sisi

( x , y )

di G mendapat label λ(x, y) = |λ(y) - λ(x)|. Karena label titik

pada digraf

G

sama dengan label titik pada graf G, maka kita tinggal menunjukkan bahwa label arc di

G

semuanya berbeda. Berdasarkan definisi

G

, jika (x, y) di E(G) maka arc

( x , y )

dan

( y , x )

di A(

G

). Tanpa mengurangi keumuman bukti, kita misalkan λ(y) > λ(x), sehingga setiap arc di

G

mendapat label

( )

) , (

) 1 2 ( mod ) ( ) ( ) , (

y x

e x

y y x

λ λ λ λ

=

+

−

= dan

( )

( )

) , ( 1 2

) 1 2 ( mod )

, (

) 1 2 ( mod ) ( ) ( ) , (

y x e

e y

x

e y

x x y

λ λ

λ λ λ

− +

=

+

−

=

+

−

=

.

Karena G graceful maka label sisi di G adalah

e , , 2 ,

1 L

. Dengan demikian sebanyak e arc di

G

yaitu arc

( x , y )

mempunyai label yang sama dengan e sisi di G, yaitu

1 , 2 , L , e

. Sedangkan e arc selebihnya di

G

yaitu arc

( y , x )

mempunyai label

)) 1 2 ( (mod ,

, 2 ,

1 − − +

− L e e

yang tidak lain

adalah

2 e , 2 e − 1 , L , e + 1

secara berturut-turut.

Dengan demikian sebanyak 2e arc di

G

mempunyai label yang semuanya berbeda. Jadi jika setiap titik di

G

diberi label sama dengan label titik di G, maka 2e arc di

G

mendapat label

1 , 2 , 3 , L , 2 e

^{. Jadi}

pelabelan pada digraf

G

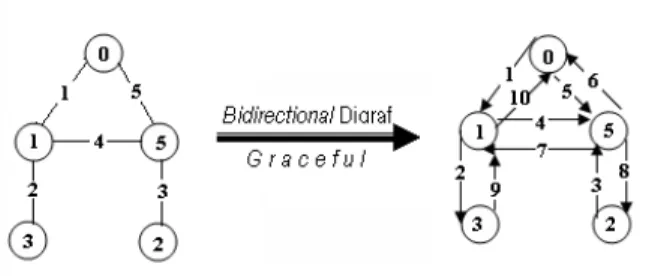
memenuhi sifat pelabelan graceful. ■

Sebagai contoh, pada Gambar 1 diperlihatkan pelabelan graceful pada bidirectional digraf yang dihasilkan dari pelabelan graceful graf underlying-nya.

Akibat 1

Berdasarkan Teorema 1 dan hasil dari garceful pada kelas graf, kita dapatkan:

1. Digraf sikel

C

_n graceful untuk n ≡ 0 atau 3 (mod 4),

2. Digraf roda

W

_n graceful untuk setiap n ≥ 3, 3. Digraf lengkap

K

_n graceful untuk

n ≤ 4

; dan

digraf bipartit lengkap

K

m,n graceful untuk setiap m dan n. ■

Sebagai contoh, Gambar 2 merupakan pelabelan graceful pada digraf lengkap

K

4 yang dihasilkan dari pelabelan graceful pada graf lengkap

K

₄.

Kebalikan dari Teorema 1, bahwa jika digraf

G

graceful maka graf G graceful, belum tentu benar. Hal

Gambar 1. Pelabelan Bidirectional Digraf Graceful Yang Dihasilkan Dari Pelabelan Graf Graceful

Gambar 2. Pelabelan Graceful Pada Graf K4 dan Digraf

K

4

ini akan dibahas pada digraf sikel

C

_n dan digraf lengkap

K

_n . Walaupun graf sikel Cn graceful ²⁾ jika dan hanya jika n ≡ 0 atau 3 (mod 4), tetapi digraf sikel

C

n graceful untuk setiap n. Hal ini dibahas pada teorema berikut.

Teorema 2 Digraf sikel

C

_n graceful untuk setiap n ⁶⁾. Bukti: Misalkan himpunan titik dari digraf sikel

C

_n

adalah

^V ( ) ^C

ⁿ

^{= { x}

¹

^{, x}

²

^{, L , x}

ⁿ

^}

dan himpunan arcnya adalah

( ) ^C

ⁿ

^{{ e e e}

ⁿ

^{a a a}

ⁿ

^}

A =

₁

,

₂

, L , ,

₁

,

₂

, L

^dengan

+1

=

_{i i}

i

x x

e

,

a

_i

= x

_i+1

x

_i ^untuk

1 , , 2 ,

1 −

= n

i L

^dan

e

_n

= x

_n

x

1,

a

_n

= x

₁

x

_n . Berdasarkan Akibat 1 diketahui bahwa digraf sikel

C

_n

graceful untuk

n ≡ 0

atau 3 (mod 4). Dengan demikian kita tinggal menunjukkan bahwa digraf sikel

C

n graceful untuk

n ≡ 1

atau 2

(mod 4 )

. Definisikan pelabelan titik pada digraf

C

_n dengan

) 4 (mod r

n ≡

untuk

r = 1

atau

r = 2

sebagai berikut :















= +

−

− +

= −

=

−

−

−

= −

=

−

+

= − +

=

=

. untuk ,

1

2 , , 4 , , 4 , 4

2 untuk ,

1

4 , , 4 , 2 , 1 ,

2 untuk ,

2 , , 4 , 1 , 0 , 1 2 untuk ,

) (

n i n

r n r n r j n j i j

n

r j n

j i j

n

r j n

j i j

x_i

L L

L λ

Dengan demikian arc di

C

_n mendapatkan label:

( )

( )























=

− + =

+

− − +

= − +

+

−

− − +

−

= −

−

−

−

= − +

−

−

= −

−

=

, untuk

, 1 untuk 2

2

, 2 , 2 , , 4 untuk 2

, ) 1 2 ( mod 1

, 1 , 2 , , 2 2 untuk 2 ,

1

2 , , 4 , 4 , 2 untuk ,

) 1 2 ( mod

2 , , 6 , 3 , 1 untuk ,

) (

n i n

n r i

n

r n n r i n n

i n

r n n r i n

i n

r i n

n n

i

r i n

i n

e_i

L L L

L

λ

dan

λ ^{( a}

i

^{) = −} λ ^{( e}

i

⁾ ( ^{mod( 2 n + 1 )} )

untuk setiap

i = 1 , 2 , L , n .

Dapat dibuktikan dengan mudah bahwa pelabelan titik di atas memenuhi fungsi satu-satu dan setiap arc di

C

n untuk

n ≡ 1

atau 2 (mod 4) mendapat label yang berbeda semua. Dengan demikian pelabelan di atas adalah pelabelan graceful. Jadi digraf sikel

C

_n

graceful untuk setiap n. ■

Contoh pelabelan graceful pada digraf

C

₅ diberikan pada Gambar 3.

Gambar 3. Pelabelan Graceful Pada Digraf Sikel

C

₅

Selanjutnya dibahas pelabelan graceful pada digraf lengkap

K

_n. Telah diketahui bahwa graf lengkap

K

_n

graceful ⁴⁾ jika dan hanya jika

n ≤ 4

. Sehingga graf lengkap

K

_n tidak graceful untuk

n ≥ 5

. Menurut Akibat 1, digraf lengkap

K

_n graceful untuk

n ≤ 4

. Bagaimana dengan digraf lengkap

K

_n untuk

n ≥ 5

? Dalam paper ini penulis mendapatkan bahwa digraf lengkap

K

_n untuk

n = 5

dan

n = 6

adalah digraf graceful. Sedangkan untuk

n ≥ 7

masih menjadi open problem. Pelabelan graceful digraf lengkap

K

_n untuk

= 5

n

dan

n = 6

disajikan dalam bentuk matriks

( ) ^K

ⁿ

^{= [ ] a}

^ij

λ

dengan entri

a

_ij menyatakan label arc

v

_i

v

_j sebagai berikut.

( )



 

 









 

 







=

0 2 7 8 11

19 0 5 6 9

14 16 0 1 4

13 15 20 0 3

10 12 17 18 0

11 9 4 3 0

11 9 4 3 0 titik label

K

5

λ

( )





























=

0 4 11 13 14 19

27 0 7 9 10 15

20 24 0 2 3 8

18 22 29 0 1 6

17 21 28 30 0 5

12 16 23 25 26 0

19 15 8 6 5 0

19 15 8 6 5 0 titik label

K6

λ

4. KESIMPULAN DAN SARAN

Dengan label titik yang sama, jika graf G graceful maka digraf

G

juga graceful. Sedangkan jika digraf

G

graceful maka graf G belum tentu graceful. Sebagai contoh, digraf sikel

C

_n dengan

n ≡ 1

atau 2 (mod 4) graceful, tetapi graf sikel Cn dengan

n ≡ 1

atau 2 (mod 4) tidak graceful. Demikian juga digraf lengkap

K

₅

dan

K

₆ graceful, tetapi graf lengkap

K

₅ dan

K

₆

tidak graceful.

Pada paper ini masih belum ditemukan apakah ada digraf

G

yang tidak graceful. Hal ini dapat diselidiki pada digraf lengkap

K

_n untuk

n ≥ 7

.

DAFTAR PUSTAKA

1. Bloom, G. S. and Golomb, S. W. 1977.

Applications of numbered undirected graphs. Proc.

of the IEEE, 65: 562-570.

2. Rosa, A. 1967. On certain valuations of the vertices of a graph, in Theory of Graphs (Internat.

Symposium Rome, July 1966). Gordon and Breach, N. Y. and Dunod Paris, 349-355.

3. Hoede, C. and Kuiper, H. 1978. All wheels are graceful. Utilitas Mathematica 14: 311.

4. Golomb, S. W. 1972. How to number a graph, in Graph Theory and Computing. New York, Academic Press, 23-37.

5. Gallian, J. A. 2007. A dynamic survey of graph labelings. Electronic J. Combinatorics 4.

6. Bloom, G. S. and Hsu, D. F. 1985. Graceful directed graphs. SIAM Journal on Matrix Analysis and Applications, 519-536.

7. Chartrand, G. and Lesniak, L. 1996. Graphs and Digraphs. Chapman & Hall, New York.

8. Harary, F. 1994. Graph Theory. Third Edition.

Addison-Wesley Publishing Company, Inc.

Philippine