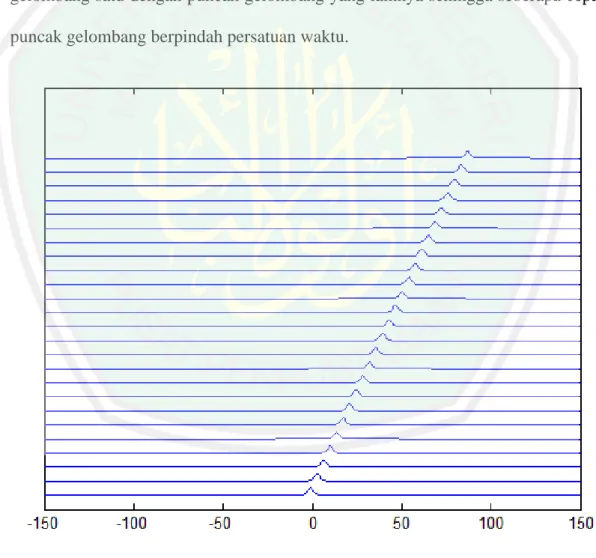
Model gelombang soliter yang dihasilkan oleh aliran yang melalui sebuah gundukan

MODEL GELOMBANG SOLITER YANG DIHASILKAN OLEH ALIRAN YANG MELALUI SEBUAH GUNDUKAN. SKRIPSI. Oleh: FARIDA MASLUCHAH NIM. 10610016. JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS ISLAM NEGERI MAULANA MALIK IBRAHIM MALANG 2014.

MODEL GELOMBANG SOLITER YANG DIHASILKAN OLEH ALIRAN YANG MELALUI SEBUAH GUNDUKAN. SKRIPSI. Diajukan kepada: Fakultas Sains dan Teknologi Universitas Islam Negeri Maulana Malik Ibrahim Malang untuk Memenuhi Salah Satu Persyaratan dalam Memperoleh Gelar Sarjana Sains (S.Si). Oleh: FARIDA MASLUCHAH NIM. 10610016. JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS ISLAM NEGERI MAULANA MALIK IBRAHIM MALANG 2014.

MODEL GELOMBANG SOLITER YANG DIHASILKAN OLEH ALIRAN YANG MELALUI SEBUAH GUNDUKAN. SKRIPSI. Oleh: FARIDA MASLUCHAH NIM. 10610016. Telah Diperiksa dan Disetujui untuk Diuji: Tanggal: 02 April 2014. Pembimbing I. Pembimbing II,. Mohammad Jamhuri, M.Si NIP. 19810502 200501 1 004. Dr. Abdussakir, M.Pd NIP. 19751006 200312 1 001. Mengetahui, Ketua Jurusan Matematika. Dr. Abdussakir, M.Pd NIP. 19751006 200312 1 001.

MODEL GELOMBANG SOLITER YANG DIHASILKAN OLEH ALIRAN YANG MELALUI SEBUAH GUNDUKAN. SKRIPSI. Oleh: FARIDA MASLUCHAH NIM. 10610016 Telah Dipertahankan di Depan Dewan Penguji Skripsi dan Dinyatakan Diterima sebagai Salah Satu Persyaratan untuk Memperoleh Gelar Sarjana Sains (S.Si) Tanggal: 10 April 2014. Penguji Utama. Ketua Penguji. Sekretaris Penguji. Anggota Penguji. : Dr. Usman Pagalay M.Si NIP. 19650414 200312 1 001. ________________. : H. Wahyu Henky Irawan, M.Pd NIP. 19710420 200003 1 003. ________________. : Mohammad Jamhuri, M.Si NIP. 19810502 200501 1 004. ________________. : Dr. Abdussakir, M.Pd NIP. 19751006 200312 1 001 ________________ Mengesahkan, Ketua Jurusan Matematika. Dr. Abdussakir, M.Pd NIP. 19751006 200312 1 001.

PERNYATAAN KEASLIAN TULISAN. Saya yang bertanda tangan di bawah ini: Nama. : FARIDA MASLUCHAH. NIM. : 10610016. Jurusan. : Matematika. Fakultas. : Sains dan Teknologi. Judul. : Model Gelombang Soliter yang Dihasilkan oleh Aliran yang Melalui Sebuah Gundukan. menyatakan dengan sebenarnya bahwa skripsi yang saya tulis ini benar-benar merupakan hasil karya saya sendiri, bukan merupakan pengambilan data, tulisan atau pikiran orang lain yang saya akui sebagai hasil tulisan atau pikiran saya sendiri, kecuali dengan mencantumkan sumber cuplikan pada daftar pustaka. Apabila di kemudian hari terbukti atau dapat dibuktikan skripsi ini hasil jiplakan, maka saya bersedia menerima sanksi atas perbuatan tersebut.. Malang, 02 April 2014 Yang membuat pernyataan,. Farida Masluchah NIM. 10610016.

MOTTO.          “Allah menghendaki kemudahan bagimu, dan tidak menghendaki kesukaran bagimu”.

HALAMAN PERSEMBAHAN. Dalam iringan doa dan rasa syukur yang teramat besar, sehingga penulis persembahkan karya tulis ini kepada: Bapak tercinta (Mustajab), Ibu tercinta (Mutmainah) dan Kakak tercinta (Amir Farhan) yang tidak pernah berhenti mencurahkan do’a dengan penuh ketulusan hati dan kesabaran jiwa demi keberhasilan penulis. Semoga engkau selalu mendapat perlindungan Allah SWT . Untuk orang terdekat penulis (Moh. Zainuddin Malik) yang selalu memberikan semangat, doa serta motivasi dalam menyelesaikan skripsi ini..

KATA PENGANTAR. Assalamu’alaikum Wr.Wb. Alhamdulillah puji syukur ke hadirat Allah SWT yang telah melimpahkan rahmat, taufiq, hidayah serta inayahnya penulis dapat menyelesaikan studi di Jurusan Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Maulana Malik Ibrahim Malang sekaligus menyelesaikan skripsi sebagai tugas akhir dengan judul “Model Gelombang Soliter yang Dihasilkan oleh Aliran yang Melalui Sebuah Gundukan” . Keberhasilan penulisan skripsi ini tidak lepas dari bimbingan dan pengarahan dari semua pihak, baik berupa motivasi, pikiran, tenaga maupun doa. Untuk itu, penulis mengucapkan terima kasih yang sebesar-besarnya kepada: 1. Prof. Dr. H. Mudjia Rahardjo, M.Si, selaku Rektor Universitas Islam Negeri Maulana Malik Ibrahim Malang. 2. Dr. drh. Hj. Bayyinatul Muchtaromah, M.Si, selaku Dekan Fakultas Sains dan Teknologi Universitas Islam Negeri Maulana Malik Ibrahim Malang. 3. Dr. Abdussakir, M.Pd, selaku Ketua Jurusan Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Maulana Malik Ibrahim Malang. 4. Mohammad Jamhuri, M.Si dan Dr. Abdussakir, M.Pd, selaku Dosen Pembimbing skripsi yang tulus ikhlas serta penuh kesabaran dalam membimbing dan mengarahkan dalam penyelesaian skripsi ini. 5. Evawati Alisah M.Pd, selaku Dosen Wali yang selalu memberikan motivasi dan bimbingan mulai semester satu hingga semester akhir.. viii.

6. Segenap sivitas akademika Jurusan Matematika, terutama seluruh dosen, terima kasih atas segenap ilmu dan bimbingannya. 7. Bapak Mustajab, Ibu Mutmainah dan Kakak Amir Farhan yang tidak pernah lelah memberikan do’a, kasih sayang serta semangat dan motivasi kepada penulis dalam menyelesaikan skripsi ini. 8. Sahabat-sahabat penulis (Chusnul Fathonah, Syifa’ul Amamah, Ayu Dewi Purwandini, Afidah Karimatul L., Siska Dwi O., Khafidho , Khuriatul Hawin, Binti tsamrotul, Fatma Mufidah, Rianti Mandasari, Masruroh, Nur Laili Arofah) dan mahasiswa Jurusan Matematika 2010 khususnya Matematika A yang selalu memotivasi penulis, terima kasih atas semua pengalaman berharga dan kenangan terindah saat menuntut ilmu bersama. 9. Semua pihak yang tidak dapat disebutkan satu-persatu, terima kasih atas do’a dan dukungan dalam kelancaran skripsi ini. Maka dengan iringan do’a semoga Allah SWT akan membalas semua amalan mereka dengan pahala yang berlipat ganda, di dunia dan akhirat. Semoga skripsi ini dapat bermanfaat bagi penulis pada khususnya dan bagi para pembaca pada umumnya, Amin ya Robbal ‘alamiin... Wassalamu’alaikum Wr. Wb. Malang, April 2014. Penulis. ix.

DAFTAR ISI. HALAMAN JUDUL HALAMAN PENGAJUAN HALAMAN PERSETUJUAN HALAMAN PENGESAHAN HALAMAN PERNYATAAN HALAMAN MOTTO HALAMAN PERSEMBAHAN KATA PENGANTAR ...................................................................................... viii DAFTAR ISI ..................................................................................................... x DAFTAR GAMBAR ........................................................................................ xii ABSTRAK ........................................................................................................ xiii ABSTRACT ...................................................................................................... xiv ‫ ملخص‬................................................................................................................... xv BAB I PENDAHULUAN 1.1 Latar Belakang ................................................................................ 1 1.2 Rumusan Masalah ........................................................................... 3 1.3 Tujuan Penelitian ............................................................................ 4 1.4 Asumsi Dasar ................................................................................... 4 1.5 Manfaat Penelitian .......................................................................... 4 1.6 Metode Penelitian ........................................................................... 4 1.7 Sistematika Penulisan ..................................................................... 5 BAB II KAJIAN PUSTAKA 2.1 Persamaan-persamaan Dasar .......................................................... 7 2.1.1 Persamaan Kontinuitas ......................................................... 8 2.1.2 Persamaan Momentum ......................................................... 12 2.1.3 Persamaan Bernoulli ............................................................. 18 2.1.3.1 Koordinat Cartesius ................................................. 19 2.1.4 Persamaan Laplace ............................................................... 22 2.2 Kajian Keagamaan ........................................................................ 23 BAB III PEMBAHASAN 3.1 Penurunan Persamaan forced KdV ................................................ 27 3.1.1 Kondisi-kondisi Batas pada Fluida ..................................... 27 3.1.1.1 Kondisi Batas pada Permukaan Fluida ................... 27 3.1.1.2 Kondisi Batas pada Dasar Fluida ............................ 29 3.1.2 Penskalaan Variabel ........................................................... 31 3.1.3 Aproksimasi Variabel-variabel yang Digunakan ............... 41 3.1.4 Peninjauan pada Tiap-tiap Orde dari Deret Asimtotik ....... 48 3.1.5 Penyederhanaan Solusi dari Deret Asimtotik ..................... 50 x.

3.2 Solusi Gelombang Soliter .............................................................. 55 3.2.1 Solusi Homogen ................................................................. 56 3.2.2 Solusi Non Homogen .......................................................... 66 3.3 Kajian Keagamaan ......................................................................... 72 BAB IV PENUTUP 4.1 Kesimpulan ................................................................................... 74 4.2 Saran ............................................................................................. 75 DAFTAR PUSTAKA ....................................................................................... 76 LAMPIRAN. xi.

DAFTAR GAMBAR. Gambar 2.1 Bentuk Saluran Fluida dalam Dua Dimensi ................................... 7 Gambar 2.2 Ilustrasi Keseimbangan Massa ....................................................... 9 Gambar 3.1 Persamaan (3.100) untuk .................................................... 62 Gambar 3.2 Persamaan (3.100) untuk .................................................... 62 Gambar 3.3 Persamaan (3.100) untuk ................................................. 63 Gambar 3.4 Solusi Persamaan (3.90) untuk ........................................... 63 Gambar 3.5 Solusi Persamaan (3.90) untuk ........................................... 64 Gambar 3.6 Solusi Persamaan (3.90) untuk ........................................ 65 Gambar 3.7 Solusi Persamaan (3.89) untuk ........................................... 69 Gambar 3.8 Solusi Persamaan (3.89) untuk ........................................ 70 Gambar 3.9 Solusi Persamaan (3.89) untuk ..................................... 71. xii.

ABSTRAK. Masluchah, Farida. 2014. Model Gelombang Soliter yang Dihasilkan oleh Aliran yang Melalui Sebuah Gundukan. Skripsi. Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Islam Negeri Maulana Malik Ibrahim Malang. Pembimbing: (I) Mohammad Jamhuri, M.Si (II) Dr. Abdussakir, M.Pd Kata Kunci: Gelombang Soliter, Persamaan forced KdV, Metode Koefisien Tak Tentu Penelitian ini membahas penurunan model gelombang permukaan yang dihasilkan oleh aliran yang melalui suatu gundukan, yang dilakukan dengan mengasumsikan aliran fluida berada pada saluran dua dimensi yang mempunyai kecepatan seragam dan dasar tidak rata, sehingga kecepatan aliran tersebut berubah dan menimbulkan gelombang pada permukaan fluida. Adapun langkah-langkah penurunan model gelombang permukaan tersebut sebagai berikut: menurunkan persamaanpersamaan dasar fluida, penskalaan, aproksimasi dengan deret asimtotik, peninjauan tiaptiap orde, menyederhanakan solusi ke dalam model matematika dan interpretasi dari model tersebut. Model gelombang yang dihasilkan berupa persamaan ketinggian permukaan, persamaan ketinggian tersebut berupa persamaan differensial parsial nonlinier yang dikategorikan ke dalam bentuk persamaan forced KdV, dengan bentuk forced-nya merupakan representasi dari gundukan. Kemudian persamaan tersebut diselesaikan menggunakan metode beda hingga skema eksplisit dan disimulasikan. Simulasi tersebut menunjukkan bahwa, dengan kecepatan aliran dan besar kecilnya gundukan yang berbeda menghasilkan ketinggian gelombang yang berbeda-beda. Untuk peneliti selanjutnya dapat melakukan aproksimasi deret asimtotik sampai orde kelima.. xiii.

ABSTRACT. Masluchah, Farida. 2014. The Solitary Wave Models Generated by Flow Passing a Bump. Thesis. Department of Mathematics, Faculty of Science and Tecnology, State Islamic University Maulana Malik Ibrahim Malang. Advisor: (I) Mohammad Jamhuri, M.Si (II) Dr. Abdussakir, M.Pd Keywords:. Solitery wave, forced Korteweg de Vries (fKdV) equation, Method of indeterminate coefficients. This study discusses about derivation of surface wave models generated by flow passing a bump. In the derivation, we assume a fluid flow is at two dimensional channel having a uniform speed and flat bottom, so that the flow velocity changed and generated waves on the fluid surface. The steps of a derivation surface wave models can be generated as follows: derive a governing equation of fluid, scale the variabels, approximat the system of equation using asymptotic series function, review the order of approximation, simplify the solution of the mathematical model and interprete the model. The obtained wave equation is an equation of surface height, the equation of height is in the form of nonlinear partial differential equations which are categorized into forced KdV equation, with the forcing term representing the bump. Then, the forced KdV equation is solved with explicit finite difference schemes and simulation. The simulation shows that, varied flow velocity and the size of bump generated different wave height. For further research one can perform an asymptotic series approximation to the fifth order.. xiv.

‫ملخص‬. ‫مصلحة‪،‬فريدة‪.٤١٠٢ .‬نماذج موجة االنفرادي منشأ بواسطة التدفق من خالل‬. ‫التلة‪.‬أطروحة ‪.‬قسم الرياضيات‪ ،‬كلية‬. ‫العلوم والتكنولوجيا‪ ،‬جامعة والية اإلسالمية موالنا مالك إبراهيم ماالنج‪.‬‬. ‫مستشار‪ .٠:‬حممد مجهوري‪ ،‬املاجستري‬ ‫‪ .٤‬د‪ .‬عبد الشكري‪ ،‬املاجستري‬. ‫كلمات البحث‪:‬موجة االنفرادي‪ ،‬أجربت كدف(‪ )KdV‬املعادلة‪ ،‬معامل الطريقة غري متأكد‬ ‫هذه البعثيناقش االخنفاض يف مناذج املوجات السطحية يعصلمن تدفق خالل التلة‪ ،‬واليت تتم عن طريق افرتاض تدفق السائل يف قناة‬ ‫ثنائية األبعاد وجود سرعة موحدة وقاعدة ليست مسطحة‪ ،‬حبيث تغري سرعة تدفق وموجات السبب على سطح السائل‪ .‬خطوات اخنفاضا يف‬ ‫منوذج املوجات السطحية على النحو التايل‪ :‬خفض املعادالت األساسية من السوائل‪ ،‬والتحجيم‪ ،‬وتقريب بالسلسلة املقاربة‪ ،‬واستعراض كل رتبة‪،‬‬ ‫وتبسيط حل النموذج الرياضي وتفسري النموذج‪.‬‬ ‫منوذج معادلة املوجةاليت يتم إنشاؤها يف شكل املعادلة ارتفاع السطح‪ .‬معادلة االرتفاع‪ .‬شكل املعادالت التفاضلية اجلزئية غري‬. ‫اخلطيةاليت تصنيفهايف شكل املعادلة ‪ KdV‬القسري‪ ،‬مما اضطر أشكاله هو متثيل من التل‪ .‬مث يتم حل املعادلة باستخدام طريقة الفروق احملددة‬ ‫مع خطة واضحة ومث حماكاة‪.‬احملاكاةيبني أنه مع سرعة املوجة وحجم املطبات من ارتفاعات خمتلفة تنتج موجة خمتلفة‪ .‬للباحث القادم‪ ،‬ميكن أن‬ ‫تؤدي سلسلة تقريب مقارب للرتتيب اخلامس‪.‬‬. ‫‪xv‬‬.

BAB I PENDAHULUAN. 1.1 Latar belakang Matematika merupakan salah satu cabang ilmu yang mendasari berbagai macam ilmu yang lain dan selalu menghadapi berbagai macam fenomena yang semakin kompleks sehingga penting untuk dipelajari. Matematika merupakan alat untuk menyederhanakan penyajian dan pemahaman masalah. Dalam bahasa matematika, suatu masalah dapat menjadi lebih sederhana untuk disajikan, dipahami, dianalisis, dan dipecahkan. Untuk keperluan tersebut, pertama dicari pokok masalahnya, kemudian dibuat rumusan atau model matematikanya (Purwanto, 1998).. Secara umum pengertian model merupakan usaha menciptakan suatu replika dari suatu fenomena alam. Kesesuaian model terhadap fenomena alam tergantung dari ketepatan formulasi persamaan matematis dalam mendeskripsikan fenomena alam tersebut. Abdussakir (2007) menyatakan bahwa alam semesta memuat bentukbentuk dan konsep matematika, meskipun alam semesta tercipta sebelum matematika itu ada. Alam semesta serta segala isinya diciptakan oleh Allah dengan ukuran-ukuran yang cermat dan teliti, dengan perhitungan-perhitungan yang mapan, dan dengan rumus-rumus serta persamaan yang seimbang dan rapi. Allah SWT berfirman dalam Al-Qur’an surat Al-Qomar ayat 49:. 1.

2.       Artinya: “Sesungguhnya Kami menciptakan segala sesuatu menurut ukuran.”. Ayat ini menjelaskan bahwa semua yang ada di alam ini, ada ukurannya, ada hitungannya, ada rumusnya atau ada persamaannya. Sebagaimana dalam skripsi ini bahwa fenomena alam yang terkait dengan gelombang permukaan yang dihasilkan oleh aliran yang melalui suatu gundukan akan menghasilkan model matematika dalam bentuk persamaan forced KdV (Korteweg-de Vries). Berbagai fenomena alam banyak yang terkait dengan gelombang, di antaranya adalah bunyi, cahaya, pergerakan air laut, aliran air sungai, riak pada air kolam, dan contoh-contoh lain yang banyak terjadi dalam kehidupan sehari-hari. Jika sekumpulan air dikenakan gaya, maka akan timbul gelombang yang disebut sebagai gelombang permukaan. Gelombang permukaan adalah fenomena yang dapat ditemui ketika mengamati permukaan air laut dan biasa disebut sebagai ombak. Jika suatu fluida yang memiliki kecepatan seragam mengalir pada sebuah saluran dengan dasar yang tidak rata, kemudian mengalami gangguan berupa gundukan pada dasar saluran, maka kecepatan aliran fluida tersebut akan berubah dan menimbulkan gelombang pada permukaan fluida. Wiryanto (2010) memodelkan gelombang permukaan yang muncul akibat gangguan yang terjadi pada dasar saluran. Model yang dihasilkan adalah persamaan Bousinessq dengan dasar saluran tak rata sebagai pembangkit gelombangnya. Solusi dari persamaan tersebut berupa gelombang soliter yang berjalan dalam dua arah. Gelombang soliter adalah gelombang yang memiliki satu puncak, dimana dalam.

3 perambatannya mempertahankan bentuk dan kecepatannya. Persamaan gerak yang dapat menggambarkan gerak gelombang soliter adalah persamaan Kortewegde Vries (KdV) (Hakim, 2009). Dalam penelitian ini diturunkan model gelombang permukaan untuk masalah yang sama dengan yang dikerjakan oleh Wiryanto (2010). Perbedaannya gelombang permukaan yang diobservasi kemudian diturunkan ke dalam bentuk persamaan KdV, yang diketahui sebagai bentuk dari perjalanan gelombang soliter yang berjalan satu arah. Dalam penurunan model, penulis menyelesaikan persamaan Laplace beserta kondisi-kondisi batasnya ke dalam bentuk persamaan ketinggian permukaan pada fluida. Kemudian persamaan ketinggian tersebut disederhanakan ke dalam persamaan forced KdV, dengan bentuk forced-nya merupakan representasi dari gangguan yang berada pada dasar saluran. Selanjutnya digunakan prosedur numerik dengan menggunakan metode beda hingga untuk menentukan solusi dari persamaan forced KdV tersebut. Berdasarkan latar belakang di atas maka penulis tertarik untuk melakukan penelitian dan menyajikannya dalam judul “Model Gelombang Soliter yang Dihasilkan oleh Aliran yang Melalui Sebuah Gundukan”.. 1.2 Rumusan Masalah Berdasarkan latar belakang di atas, maka rumusan masalah dalam penelitian ini adalah bagaimanakah model gelombang soliter yang dihasilkan oleh aliran yang melalui sebuah gundukan?.

4 1.3 Tujuan Penelitian Adapun tujuan penelitian ini adalah menurunkan model gelombang soliter yang dihasilkan oleh aliran yang melalui sebuah gundukan.. 1.4 Asumsi dasar Berikut beberapa asumsi dasar yang digunakan dalam membuat batasan masalah: 1. Permasalahan ditinjau sebagai masalah satu dimensi. 2. Fluida diasumsikan ideal, yaitu tak termampatkan atau tidak bergantung pada tekanan, tak kental dan mempunyai kerapatan konstan. 3. Fluida diasumsikan sebagai fluida tak berotasi atau tidak berputar terhadap sumbu aliran. 4. Fluida diasumsikan memiliki rapat massa yang homogen atau konstan atau tidak berubah terhadap waktu.. 5. Tekanan hidrostatiknya diasumsikan sangat kecil sehingga dapat diabaikan.. 1.5 Manfaat Penelitian Hasil penelitian ini diharapkan dapat digunakan sebagai model morfologi pantai yang mempunyai dasar tidak rata atau alirannya mengalami gangguan.. 1.6 Metode Penelitian Teknik kajian yang digunakan dalam pembahasanan skripsi ini adalah penelitian kepustakaan (Library Research). Penelitian kepustakaan merupakan penampilan argumentasi penalaran keilmuan yang memaparkan hasil kepustakaan.

5 berisi satu topik yang di dalamnya memuat beberapa gagasan yang berkaitan dan harus didukung oleh data yang diperoleh dari berbagai sumber kepustakaan. Metode yang digunakan dalam penelitian ini sebagai berikut: 1. Menurunkan persamaan-persamaan dasar dari hukum-hukum kesetimbangan yang terjadi pada aliran fluida. 2. Melakukan penskalaan yang bertujuan untuk mengecilkan variabel , , dan kecepatan. 3. Melakukan aproksimasi atau taksiran terhadap variabel-variabel yang digunakan. 4. Menyelesaikan sistem dengan melakukan peninjauan pada tiap-tiap orde dari deret, mulai dari orde yang paling rendah sampai orde yang dikehendaki. 5. Menyederhanakan solusi dari deret asimtotik ke dalam sebuah model matematika. 6. Memberikan interpretasi dari model yang dihasilkan.. 1.7 Sistematika Penulisan Secara umum penulisan penelitian ini terdiri dari empat bab. Masingmasing bab dibagi ke dalam beberapa subbab dengan rumusan sebagai berikut: Bab I. Pendahuluan Dalam bab ini dijelaskan mengenai latar belakang, rumusan masalah, tujuan masalah, asumsi dasar, manfaat penelitian, metode penelitian, dan sistematika penulisan..

6 Bab II. Kajian Pustaka Dalam bab ini terdiri atas persamaan-persamaan dasar fluida yang mendasari penulisan penelitian ini. Adapun persamaan-persamaan dasar fluida yang termuat di dalamnya adalah persamaan kontinuitas, persamaan momentum, persamaan Bernoulli, dan persamaan Laplace.. Bab III Pembahasan Dalam bab ini berisi tentang bagaimana model gelombang soliter yang dihasilkan oleh aliran yang melalui sebuah gundukan dengan melakukan penskalaan, melakukan aproksimasi atau taksiran terhadap variabel-variabel yang digunakan, menyelesaikan sistem dengan melakukan peninjauan pada tiap-tiap orde dari deret, mulai dari orde yang paling rendah sampai orde yang dikehendaki, menyederhanakan solusi dari deret asimtotik ke dalam sebuah model matematika, interpretasi dari model tersebut. Bab IV Penutup Dalam bab ini berisi tentang kesimpulan dari materi yang telah dibahas. pada. bab. sebelumnya. pengembangan selanjutnya.. dan. berisi. saran. untuk.

7.



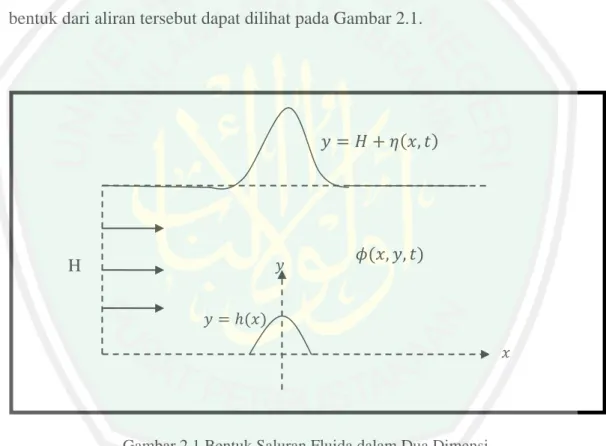
BAB II KAJIAN PUSTAKA. 2.1 Persamaan-persamaan Dasar Penelitian ini berkaitan dengan gelombang permukaan yang disebabkan oleh aliran fluida yang mengalami gangguan berupa gundukan pada dasar saluran, bentuk dari aliran tersebut dapat dilihat pada Gambar 2.1.. H. Gambar 2.1 Bentuk Saluran Fluida dalam Dua Dimensi. Untuk melihat bagaimana perilaku dari gelombang tersebut, dapat diturunkan model matematika yang merupakan representasi dari ketinggian gelombang pada permukaan tersebut. Dalam penurunan model digunakan persamaan-persamaan dasar yang berasal dari hukum-hukum kekekalan yang terjadi pada aliran fluida.. 7.

8 2.1.1. Persamaan Kontinuitas Persamaan kontinuitas mengungkapkan bahwa massa fluida bersifat kekal. yakni tidak dapat diciptakan ataupun dimusnahkan. Kekekalan massa fluida mempersyaratkan bahwa dalam suatu volume zat massa selalu konstan, karena itu laju perubahan massanya sama dengan nol. Berbagai bentuk persamaan kontinuitas untuk suatu volume kontrol diturunkan dengan menyatakan secara matematik, bahwa laju massa rata-rata ke dalam suatu daerah tertentu sama dengan laju perubahan massa di daerah tersebut (Olson, 1993). Volume kontrol adalah suatu daerah sembarang dalam ruang yang dipilih semata-mata untuk memudahkan pemecahan masalah-masalah aliran fluida, sedangkan permukaan kontrol adalah permukaan-permukaan yang membatasi volume kontrol (Olson, 1993). Hukum kekekalan massa menyatakan bahwa massa di dalam suatu sistem adalah tetap konstan terhadap waktu. Dalam bentuk persamaan. dimana. ialah massa total (Streeter, 1986). Douglas (2001), menyatakan massa jenis dinotasikan. yang didefinisikan. sebagai massa per satuan volume, yaitu. sehingga = =. (2.1).

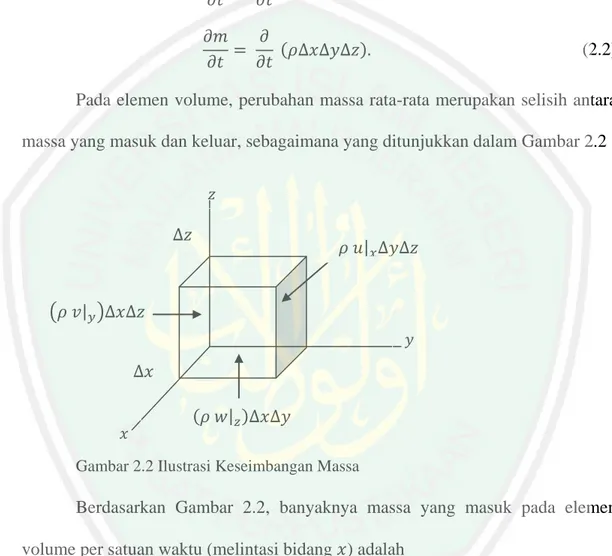
9 dimana. adalah massa jenis dan. adalah volume. .. Perubahan massa terhadap waktu dinyatakan dalam bentuk. (2.2) Pada elemen volume, perubahan massa rata-rata merupakan selisih antara massa yang masuk dan keluar, sebagaimana yang ditunjukkan dalam Gambar 2.2. Gambar 2.2 Ilustrasi Keseimbangan Massa. Berdasarkan Gambar 2.2, banyaknya massa yang masuk pada elemen volume per satuan waktu (melintasi bidang ) adalah . Banyaknya massa yang keluar melewati bidang. yaitu. , sehingga perubahan massa antara massa yang masuk dengan massa yang keluar dalam arah. adalah ..

10 Sebagai catatan. menyatakan komponen kecepatan dalam arah . Begitu juga,. banyaknya massa yang masuk dalam arah. dan arah adalah. dan banyaknya massa yang keluar melewati bidang. dan melewati bidang. yaitu. . Perubahan massa antara massa yang masuk dengan massa yang keluar dalam arah dan arah adalah. Sebagai catatan. menyatakan komponen kecepatan dalam arah. dan. menyatakan komponen kecepatan dalam arah . Oleh karena itu, perubahan massa persatuan waktu sama dengan perubahan massa dalam arah. plus perubahan massa dalam arah. plus. perubahan massa dalam arah (2.3). Bagi persamaan (2.3) dengan besaran sehingga menjadi. yaitu volume daerah yang diamati.

11 (2.4). Kemudian didekati dengan. diperoleh. Sehingga persamaan (2.4) perubahan massa persatuan waktu menjadi (2.5). Fluida dengan kerapatan massa ubah maka. relatif konstan artinya. tidak berubah-. , sehingga persamaan (2.5) menjadi (2.6). Persamaan (2.6) ini disebut sebagai persamaan kontinuitas. Dalam bentuk vektornya dapat dituliskan. dimana. Operator gradien sedangkan. menyatakan differensiasi terhadap berbagai komponen arah,. menyatakan vektor kecepatan dalam tiga dimensi..

12 Aliran yang kerapatan massanya dalam persamaan kontinuitas dianggap konstan disebut aliran tak dapat mampat, aliran dianggap tak dapat mampat bila perubahan kerapatan fluida dapat diabaikan. Sebetulnya semua fluida dapat dimampatkan walaupun sangat sedikit, tetapi pada umumnya yang dianggap tidak dapat mampat adalah fluida yang kerapatannya tidak tergantung pada tekanan (Olson, 1993). 2.1.2. Persamaan Momentum Dalam mekanika fluida, hukum Newton dinamakan kekekalan momentum. linier atau asas momentum. Hukum kedua Newton menyatakan bahwa gaya yang bekerja pada suatu massa tertentu sebanding dengan laju perubahan momentum linier massa tersebut terhadap waktu (Olson, 1993). Douglas (2001) menyatakan bahwa momentum linier (atau “momentum” untuk singkatnya dari sebuah benda didefinisikan sebagai hasil kali massa dan kecepatannya. Momentum jamaknya adalah “momenta”) biasanya dinyatakan dengan simbol. . Karena kecepatan merupakan vektor maka momentum. dinyatakan dalam bentuk vektor. Arah momentum adalah arah kecepatan, dan besar momentum adalah (2.7) Berdasarkan hukum kedua newton bahwa gaya total adalah perkalian massa dengan percepatan, maka hukum kedua newton dapat dinotasikan sebagai. Dengan menggunakan definisi percepatan sebagai turunan dari kecepatan terhadap waktu, persamaan tersebut dapat dinotasikan.

13. Apabila diintegralkan kedua ruas terhadap. diperoleh (2.8). ruas kanan dari persamaan (2.8) merupakan definisi dari momentum yang ditunjukkan pada persamaan (2.7). Dari persamaan (2.8), jika diturunkan terhadap t didapatkan. (2.9) yang berarti bahwa gaya total adalah rata-rata perubahan momentum persatuan waktu, karena. =. diperoleh hubungan sebagai berikut (2.10). Dalam tiga dimensi persamaan (2.10) dapat ditulis dalam bentuk. sehingga untuk rata-rata perubahan momentum persatuan waktu dapat dinotasikan. Olson (1993) menyatakan bahwa teorema momentum untuk mekanika fluida, yaitu gaya netto yang bekerja pada fluida sama dengan laju perubahan momentum fluida terhadap waktu plus laju gaya fluks atau pemindahan momentum ke luar dari volume kontrol melalui permukaannya. Teorema momentum dapat diterapkan pada aliran-aliran baik yang steady maupun yang tidak steady, berdimensi satu, dua, atau tiga, dapat mampat atau.

14 tidak dapat mampat. Aliran disebut steady bila kondisi-kondisi dalam aliran tidak berubah terhadap waktu, aliran yang tidak demikian tentu saja disebut aliran unsteady atau tidak steady. Aliran air yang konstan di dalam sebuah pipa bersifat steady, akan tetapi pada saat katup alirannya sedang dibuka, aliran itu tidak steady (Olson, 1993). Berdasarkan teorema momentum maka keseimbangan momentum pada elemen volume dapat dinyatakan dengan perubahan momentum = rata-rata momentum masuk – rata-rata momentum keluar + jumlah gaya-gaya. Gaya yang digunakan dalam pembahasan ini adalah gaya gravitasi dan gaya tekanan. Chorlton (1967) menyatakan bahwa gaya gravitasi pada massa diferensial di dalam volume kendali ialah. di sini. secara umum boleh mempunyai orientasi sebarang terhadap sistem. koordinat yang dipakai. Gaya tekanan fluida. didefinisikan sebagai gaya tekan yang diterima. persatuan luas fluida dan dinotasikan sebagai berikut. Dengan cara yang sama dalam menghasilkan persamaan kontinuitas maka dengan Gambar 2.2 juga dapat menghasilkan persamaan momentum, yaitu perubahan momentum untuk arah massa yang melintasi bidang. , momentum yang masuk bidang. adalah. dan kecepatan yang melintasi bidang . Fluida.

15 dengan rapat massa. dan bergerak dengan kecepatan. melintasi bidang. maka. dalam selang satuan waktu terdapat sebanyak. Sehingga momentum yang melintasi bidang. adalah. sedangkan momentum yang keluar bidang. adalah massa yang melintasi bidang. dan kecepatan yang melintasinya adalah. Maka resultan dari gaya-gaya tersebut dalam arah. yaitu. menyatakan tekanan pada bidang , sedangkan. menyatakan percepatan. akibat gravitasi dalam arah . Perubahan momentum untuk arah massa yang melintasi bidang melintasi bidang. , momentum yang masuk bidang. adalah. dan kecepatan yang melintasinya. Massa yang. dengan kecepatan. yang melintasi bidang. adalah. Sehingga momentum yang melintasi bidang. sebesar. sedangkan momentum yang keluar bidang. adalah massa yang melintasi bidang. dan kecepatan yang melintasinya adalah. Maka resultan dari gaya-gaya tersebut dalam arah. yaitu.

16. menyatakan tekanan pada bidang. , sedangkan. menyatakan percepatan. akibat gravitasi dalam arah . Perubahan momentum untuk arah , momentum yang masuk bidang massa yang melintasi bidang melintasi bidang. adalah. dan kecepatan yang melintasinya. Massa yang. dengan kecepatan. yang melintasi bidang adalah. Sehingga momentum yang melintasi bidang sebesar. sedangkan momentum yang keluar bidang. adalah massa yang melintasi bidang. dan kecepatan yang melintasinya adalah. Maka resultan dari gaya-gaya tersebut dalam arah. yaitu. menyatakan tekanan pada bidang , sedangkan. menyatakan percepatan. akibat gravitasi dalam arah . Berdasarkan keseimbangan momentum maka perubahan momentum untuk arah. dalam elemen volume. sama dengan momentum yang masuk. dikurangi momentum yang keluar plus jumlah gaya-gaya, yaitu.

17 (2.11) Kemudian bagi persamaan (2.11) dengan besaran. yaitu volume daerah. yang diamati sehingga menjadi. Kemudian didekati dengan. maka. Sehingga perubahan momentum dalam arah. diperoleh (2.12).

18 Dengan cara yang sama, perubahan momentum dalam arah. dan. adalah (2.13). (2.14) Persamaan (2.12)-(2.14) disebut sebagai persamaan momentum. Bentuk vektor persamaan (2.12)-(2.14) dapat dituliskan: (2.15). Kemudian kedua ruas persamaan (2.15) dibagi dengan. didapatkan. (2.16) dimana:. Operator gradien sedangkan. menyatakan differensiasi terhadap berbagai komponen arah,. menyatakan vektor kecepatan dalam tiga dimensi dan. merupakan. percepatan akibat gravitasi. 2.1.3. Persamaan Bernoulli Integrasi persamaan-persamaan Euler untuk aliran nonrotasi yang tidak. dapat mampat menghasilkan persamaan Bernoulli. Persamaan ini menghubungkan kecepatan, tekanan, dan perubahan ketinggian dalam fluida yang tidak viskous. Persamaan Bernoulli sering digunakan untuk aliran berdimensi satu yang efek-.

19 efek viskous dapat diabaikan. Persamaan Euler boleh juga diintegrasi untuk aliran rotasi yang tidak dapat mampat, sebagaimana halnya untuk aliran yang dapat mampat (Olson, 1993). Persamaan–persamaan. untuk. fluida-fluida. tidak. viskous. akan. dikembangkan baik dalam sistem koordinat natural (streamline atau garis arus) maupun dalam sistem koordinat Cartesius. Apabila diintegrasi, persamaanpersamaan tersebut akan menjadi persamaan-persamaan Bernoulli baik untuk aliran tak dapat mampat maupun aliran dapat mampat. Streamline atau garis arus adalah garis yang setiap saat menjadi tempat singgungan vektor-vektor kecepatan (Olson, 1993). Gaya-gaya yang bekerja pada sebuah elemen fluida secara umum ada dua macam: body forces dan gaya-gaya permukaan (surface forces). Body forces adalah gaya-gaya yang bekerja pada volume atau massa elemen fluida. Gaya-gaya ini meliputi gaya gravitasi dan gaya pada fluida penghantar dalam sebuah medan magnet. Untuk fluida-fluida tidak viskous, gaya-gaya permukaan pada sebuah elemen fluida tidak viskous yang terdapat di dalam fluida adalah gaya-gaya normal yang disebabkan oleh tekanan (Olson, 1993). 2.1.3.1 Koordinat Cartesius Misalkan X, Y, dan Z adalah body forces per satuan massa dalam arah-arah , , dan. sedemikian rupa sehingga resultanya adalah. misalkan vektor kecepatan adalah. (Olson, 1993).. , dan.

20 Olson (1993) menyatakan gaya-gaya permukaan pada sebuah elemen dengan sisi-sisi. ,. , dan. serta massa. hanya ditimbulkan oleh. tekanan, sehingga resultan gaya itu dalam arah x adalah. Ini sama dengan hasil kali antara massa dan percepatan dalam arah x, bila percepatan adalah. Karena jumlah komponen-komponen gaya dari luar persatuan volume sama dengan komponen percepatan (2.17). Demikian pula untuk arah-arah. dan (2.18). dan (2.19). Untuk persamaan (2.17)-(2.19) bentuk vektornya dapat dituliskan sebagai berikut (2.20). dengan.

21 Operator gradien sedangkan. menyatakan differensiasi terhadap berbagai komponen arah, menyatakan vektor kecepatan. sebagai medan vektor. konservatif, yaitu adanya fungsi skalar . Chorlton (1967) menyatakan perkalian vektor , maka hasil kali vektor untuk. adalah (2.21). Untuk aliran yang seragam dan fluida tak berotasi. maka. persamaan (2.21) diperoleh. Dengan. , persamaan (2.20) menjadi. (2.22) Dengan mengintegralkan persamaan (2.22) terhadap variabel , , dan. dengan. diperoleh. , sehingga menjadi.

22 (2.23). Persamaan (2.23) merupakan persamaan Bernoulli dan. merupakan fungsi. sebarang dari akibat integrasi yang dilakukan terhadap , , dan . 2.1.4. Persamaan Laplace Aliran potensial adalah aliran nonrotasi yang komponen-komponen. kecepatannya boleh diturunkan dari fungsi-fungsi potensial kecepatan. Kondisi ini berlaku untuk fluida tak dapat mampat dan karena aliran fluida tersebut nonrotasi, persamaan Bernoulli berlaku untuk medan aliranya secara keseluruhan. Variasivariasi kecepatan dan tekanan untuk sebuah medan aliran dapat diketahui dari pola arus dan dari penerapan Bernoulli (Olson, 1993). Olson (1993) menyatakan aliran rotasi atau nonrotasi tergantung apakah partikel-partikel dalam fluida berputar terhadap sumbu aliran. Untuk aliran nonrotasi terdapat sebuah fungsi. yang disebut potensial kecepatan. Fungsi ini. sedemikian rupa sehingga komponen-komponen kecepatan. dan. dapat. diperoleh dari. Dengan penggunaan tanda negatif pada fungsi. di atas menunjukkan. bahwa aliran bergerak ke arah berkurangnya potensial. Kalau fungsi potensial ini digabungkan dengan definisi untuk. (curl V) maka didapatkan.

23 Vortisitas. didefinisikan sebagai. curl V, yang besarnya sama dengan. kecepatan sudut atau rotasi. Pada umumnya, besaran vektor vortisitas merupakan fungsi posisi dan waktu dalam sebuah fluida. Kalau vortisitas di seluruh fluida yang bergerak sama dengan nol, aliran fluida itu disebut aliran nonrotasi. Dengan demikian curl V = 0 dan. ,. ,. yang didapatkan dengan. menetapkan koefisien-koefisien i, j, dan k dalam curl V masing-masing sama dengan nol (Olson, 1993). Dengan demikian, kondisi nonrotasi menjamin pendefinisian potensial kecepatan. Dari penggabungan di atas dengan persamaan kontinuitas. ,. diperoleh (2.23). atau dalam bentuk vektor. Aliran nonrotasi juga disebut aliran potensial, persamaan (2.23) merupakan persamaan Laplace dalam fungsi potensial. (Olson, 1993). Persamaan (2.23) ini. merupakan persamaan diferensial parsial orde-2 yang memerlukan syarat batas untuk memperoleh solusinya.. 2.2 Kajian Keagamaan Berdasarkan ayat sebelumnya bahwa semua yang ada di alam ini, ada rumusnya atau ada persamaannya. Ahli matematika tidak dapat membuat rumus sedikitpun, mereka hanya menemukan rumus atau persamaan. Albert Einstein.

24 tidak. membuat. rumus. tetapi. dia. hanya. menemukan. dan. menyimpulkannya. Archimedes menemukan hitungan mengenai volume benda melalui media air. Hukum Archimedes itu sudah ada sebelumnya dan dialah yang menemukan pertama kali melalui hasil menelaah dan membaca ketetapan Allah (Abdussakir, 2007). Matematika juga dapat digunakan dalam mengungkapkan kejadian menjadi ungkapan yang sistematis. Ditemukannya pemodelan-pemodelan matematika adalah salah satu keajaiban Allah. Pada hakikatnya manusia hanya mencari persamaan atau rumus-rumus yang berlaku pada suatu fenomena. Dalam penelitian ini fenomena alam yang terkait dengan gelombang permukaan akan menghasilkan model matematika dalam bentuk persamaan fKdV. Dalam menentukan rumus atau persamaan perlu adanya pembuktian kebenaran, apakah rumus atau persamaan tersebut benar atau salah. Allah berfirman dalam surat Al-Israa’ ayat 36 :.                   Artinya: “Dan janganlah kamu mengikuti apa yang kamu tidak mempunyai pengetahuan tentangnya. Sesungguhnya pendengaran, penglihatan dan hati, semuanya itu akan diminta pertanggungan jawabnya.”.. Kemudian apabila hal tersebut benar, maka tunjukkan bukti dari kebenaran tersebut. Allah SWT berfirman dalam surat Al-Baqarah ayat 111:.                .

25 Artinya: “Dan Dia mengajarkan kepada Adam Nama-nama (benda-benda) seluruhnya, kemudian mengemukakannya kepada Para Malaikat lalu berfirman: "Sebutkanlah kepada-Ku nama benda-benda itu jika kamu mamang benar orang-orang yang benar!".. Selain itu juga terdapat dalam surat Al-Baqarah ayat 111 sebagai berikut:.                       Artinya: “Dan mereka (Yahudi dan Nasrani) berkata: "Sekali-kali tidak akan masuk surga kecuali orang-orang (yang beragama) Yahudi atau Nasrani". demikian itu (hanya) angan-angan mereka yang kosong belaka. Katakanlah: "Tunjukkanlah bukti kebenaranmu jika kamu adalah orang yang benar".. Dalam ayat tersebut bahwa Allah SWT seakan-akan meminta bukti kebenaran. yang. menguatkan. anggapan. mereka. apabila. mereka. dapat. mengemukakan bukti-bukti yang benar maka dugaan mereka benar. Sebagaimana dalam skripsi ini dijelaskan mengenai model gelombang permukaan yang diturunkan ke dalam bentuk persamaan fKdV, yang diketahui sebagai bentuk dari perjalanan gelombang soliter yang berjalan satu arah. Dalam penurunan model tersebut, dengan menyelesaikan persamaan Laplace beserta kondisi-kondisi batasnya ke dalam bentuk persamaan ketinggian permukaan pada fluida kemudian persamaan ketinggian tersebut disederhanakan ke dalam persamaan forced KdV. Kebenaran persamaan yang diperoleh dilengkapi dengan bukti..

BAB III PEMBAHASAN. Dalam bab ini dijelaskan penurunan model gelombang permukaan yang dihasilkan oleh aliran yang melalui sebuah gundukan. Penurunan model dilakukan dengan mengasumsikan aliran fluida berada pada saluran dua dimensi yang mempunyai dasar tidak rata dan memiliki kecepatan seragam, kemudian aliran mengalami gangguan berupa gundukan pada dasar saluran, sehingga kecepatan aliran tersebut berubah dan menimbulkan gelombang pada permukaan fluida. Model gelombang permukaan diperoleh dengan menyederhanakan persamaanpersamaan kesetimbangan yang diturunkan dari hukum-hukum kekekalan yang terjadi pada aliran fluida berupa persamaan ketinggian permukaan fluida. Persamaan ketinggian tersebut berupa persamaan diferensial parsial nonlinier yang dapat dikategorikan ke dalam bentuk persamaan forced KdV. Adapun langkah-langkah penurunan model tersebut sebagai berikut: menurunkan persamaan-persamaan dasar fluida kemudian dilakukan penskalaan, aproksimasi variabel dengan deret asimtotik, peninjauan tiap-tiap orde dengan deret asimtotik, menyederhanakan solusi ke dalam sebuah model matematika, dan yang terakhir interpretasi dari model tersebut.. 26.

27 3.1 Penurunan Persamaan forced KdV 3.1.1. Kondisi-kondisi Batas pada Fluida Dalam gerak partikel fluida mempunyai kondisi batas yaitu kondisi batas. dinamik dan kondisi batas kinematik. Kondisi batas dinamik terjadi karena adanya gaya-gaya yang bekerja pada fluida sedangkan kondisi batas kinematik terjadi karena gerak partikel (Hakim, 2009). 3.1.1.1 Kondisi Batas pada Permukaan Fluida Pada permukaan fluida terdapat kondisi batas kinematik dan kondisi batas dinamik, yaitu: a) Kondisi batas kinematik Kondisi batas kinematik diturunkan berdasarkan ide dasar dari sifat kontinum fluida. Misalkan. adalah kurva yang membatasi air dan. udara dan dinyatakan oleh persamaan permukaan . Ketika suatu partikel di. dan partikel tersebut tetap pada permukaan maka. . Didefiniskan suatu operator untuk turunan total terhadap waktu , atau dinamakan turunan mengikuti gerakan dan dinotasikan sebagai. Karena telah didefinisikan untuk vektor kecepatan dalam dua dimensi maka turunan total tersebut dapat dituliskan sebagai. Adapun penurunan untuk kondisi batas kinematik pada permukaan fluida yaitu. ,.

28. dimana. , sehingga. (3.1). Dengan. menyatakan komponen kecepatan. menyatakan komponen kecepatan. dalam arah. dan. dalam arah , maka persamaan (3.1) menjadi. Jadi kondisi batas kinematik pada permukaan fluida adalah (3.2). b) Kondisi batas dinamik Kondisi batas dinamik diturunkan dari persamaan Bernoulli yang berlaku pada permukaan fluida. Adapun persamaan Bernoulli yaitu. dimana. merupakan fungsi sebarang dari t akibat integrasi yang dilakukan. terhadap. dan .. Diasumsikan bahwa fluida tak kental dan tekanan pada permukaan sama dengan tekanan pada udara adalah konstan maka Bernoulli menjadi. , sehingga persamaan.

29. Pada keadaan seragam (uniform) maka ruas kiri dari persamaan Bernoulli berlaku kecepatan vertikal dimana. , kecepatan horizontal. dan. merupakan kecepatan mula-mula, karena tidak ada perubahan terhadap. waktu, maka. Sehingga kondisi batas dinamik pada permukaan fluida yaitu. (3.3) 3.1.1.2 Kondisi Batas pada Dasar Fluida Pada dasar fluida hanya berlaku kondisi batas kinematik sedangkan kondisi batas dinamik tidak diamati karena partikel pada dasar fluida tidak bergerak. Nyatakan fungsi posisi untuk fluida yang tidak rata . Ketika suatu partikel di permukaan fluida maka. dan partikel tersebut tetap pada. . Didefinisikan suatu operator untuk turunan total. terhadap waktu , atau dinamakan turunan mengikuti gerakan dan dinotasikan sebagai.

30. Karena telah didefinisikan untuk vektor kecepatan dalam dua dimensi. ,. maka turunan total tersebut dapat dituliskan sebagai. Adapun penurunan untuk kondisi batas kinematik pada dasar fluida yaitu. (3.4). Dengan. menyatakan komponen kecepatan. menyatakan komponen kecepatan. dalam arah. dan. dalam arah , maka persamaan (3.4) menjadi. Jadi kondisi batas kinematik pada dasar fluida adalah (3.5). Berdasarkan persamaan Laplace beserta kondisi batas pada permukaan fluida dan kondisi batas pada dasar fluida akan dilakukan penskalaan variabel ( , c,. ,. , h, dan ). Penskalaan variabel tersebut bertujuan untuk mengecilkan variabel , , dan kecepatan c. Namun sebelumnya variabel tersebut akan digunakan tanda.

31 bar yang bertujuan untuk membedakan sebelum dilakukan penskalaan dengan setelah dilakukan penskalaan. 3.1.2. Penskalaan Variabel Skala disini didefinisikan sebagai perbandingan antara keadaan nyata. dengan model atau gambarnya dan penskalaan didefinisikan sebagai mengubah ukuran baik memperbesar atau mengecilkan. Sebagai gambarannya, ketika ingin mengambar sebuah rumah cukup sulit apabila mengambar sesuai keadaan aslinya, sehingga terlebih dahulu dilakukan penskalaan pada panjang dan lebarnya. Begitu juga sebelum diperoleh model gelombang soliter, terlebih dahulu dilakukan penskalaan terhadap persamaan Laplace beserta kondisi batas pada permukaan fluida dan kondisi batas pada dasar fluida. Suatu saluran fluida yang memiliki panjang L jauh lebih besar dibandingkan dengan kedalamannya H, sehingga dapat didefinisikan sebuah parameter yang sangat kecil. sebagai. . Dengan mengasumsikan. amplitudo dari gundukan sangat kecil dibandingkan dengan kedalaman dari saluran maka kita dapat menyatakan gundukan tersebut sebagai. ,. sehingga fungsi potensialnya dapat ditulis sebagai. ,. dimana. menyatakan kecepatan aliran fluida yang seragam. Sebagaimana dalam Wiryanto (2010), skala-skala lain yang digunakan di. antaranya satuan kecepatan dalam , dan. ,. ,. ,. ,.

32 dimana waktu,. menyatakan gravitasi, H menyatakan kedalaman fluida, menyatakan perbedaan kecepatan aliran,. gundukan, dan. menyatakan. menyatakan representasi. menyatakan ketinggian permukaan.. Selanjutnya dilakukan penskalaan dengan mensubstitusikan skala-skala ke persamaan (2.23), (3.2), (3.3) dan (3.5) sebagai berikut: Pertama, penskalaan variabel pada persamaan Laplace (2.23). Skala-skala. , disubstitusi ke. , diperoleh. ,. dan.

33. (3.6). Skala-skala. , disubstitusi ke. , diperoleh. ,. dan.

34. (3.7). Persamaan (3.6) dan persamaan (3.7) disubstitusi ke persamaan (2.23), sehingga diperoleh penskalaan pada persamaan (2.23). (3.8) Kedua, penskalaan pada persamaan (3.2). Skala-skala. , disubstitusi ke. , diperoleh. ,. dan.

35. (3.9). Skala-skala. dan. disubstitusi ke. diperoleh. (3.10). Skala-skala. dan. disubstitusi ke. diperoleh. (3.11).

36 Skala-skala. , disubstitusi ke. ,. ,. dan. diperoleh. (3.12) Persamaan (3.9)-(3.12) disubstitusi ke persamaan (3.2). (3.13).

37 Ketiga, penskalaan pada persamaan (3.3). Skala-skala. , disubstitusi ke. dan diperoleh. (3.14) Skala-skala. , disubstitusi ke. , diperoleh. ,. dan.

38. (3.15). (3.16) Skala-skala. , disubstitusi ke. , diperoleh. ,. dan.

39. (3.17) Persamaan (3.14)-(3.17) disubstitusi ke persamaan (3.3) diperoleh. (3.18) Keempat, penskalaan pada persamaan (3.5). Skala-skala. , disubstitusi ke. , diperoleh. ,. dan.

40. (3.19) Skala-skala. ,. disubstitusi ke. diperoleh. (3.20). Skala-skala. , disubstitusi ke. , diperoleh. ,. dan.

41. (3.21) Persamaan (3.19)-(3.21) disubstitusi ke persamaan (3.5). (3.22) Setelah dilakukan penskalaan, kemudian mencari solusi dari persamaan (3.8) beserta kondisi batas persamaan (3.13), persamaan (3.18) dan persamaan (3.22) dengan menggunakan deret asimtotik, dengan dilakukan aproksimasi (hampiran) terhadap variabel-variabel tak bebasnya dalam deret pangkat sampai orde ketiga. 3.1.3. Aproksimasi Variabel-variabel yang Digunakan Persamaan (3.8) beserta kondisi batas persamaan (3.13), persamaan (3.18). dan persamaan (3.22) sulit untuk diselesaikan secara langsung, sehingga dilakukan aproksimasi atau hampiran dengan menggunakan deret asimtotik. Hakim (2009) menyatakan deret asimtotik adalah suatu teknik yang digunakan untuk menentukan suatu fungsi yang merupakan penyelesaian dari.

42 suatu masalah nilai awal atau batas, dimana fungsi tersebut dinyatakan dalam deret pangkat terhadap parameter kecil . Dalam deret asimtotik, persamaan (3.8) beserta kondisi-kondisi batasnya diaproksimasi dengan memisalkan variabel-variabel tak bebasnya dalam bentuk deret asimtotik. Variabel-variabel tak bebas yang digunakan dalam bentuk deret asimtotik tersebut adalah a) Variabel tak bebas. (gundukan) dalam bentuk deret asimtotik dengan. menuliskan (3.23) dimana. ,. , dan. merupakan bentuk orde pertama, kedua, dan ketiga. dengan adalah parameter yang kecil. b) Variabel tak bebas. (tinggi permukaan) dalam bentuk deret asimtotik dengan. menuliskan.    (1)   2 ( 2)   3 (3)   dimana. ,. , dan. (3.24). merupakan bentuk orde pertama, kedua, dan ketiga. dengan adalah parameter yang kecil. c) Variabel tak bebas. (perbedaan kecepatan aliran) dalam bentuk deret. asimtotik dengan menuliskan. c  c (0)   1c (1)   2 ( 2)   dimana. ,. , dan. (3.25). merupakan bentuk orde pertama, kedua, dan ketiga. dengan adalah parameter yang kecil..

43 Adapun aproksimasi atau hampiran persamaan (3.8), (3.13), (3.18), (3.22) dengan memisalkan variabel-variabel tak bebasnya dalam bentuk deret asimtotik sebagai berikut a) Aproksimasi pada persamaan (3.8) Variabel tak bebas. (gundukan) pada persamaan (3.8) dalam bentuk deret. asimtotik (3.26). (3.27). (3.28) Substitusikan persamaan (3.27)-(3.28) ke persamaan (3.8) sehingga diperoleh hampiran dari persamaan (3.8) adalah. (3.29) b) Aproksimasi pada persamaan (3.13) Variabel tak bebas. (gundukan) dan. (ketinggian permukaan) pada persamaan. (3.13) dalam bentuk deret asimtotik (3.30) (3.31). (3.32).

44 (3.33). (3.34). (3.35). (3.36) Substitusikan persamaan (3.31)-(3.36) ke persamaan (3.15) sehingga diperoleh hampiran dari persamaan (3.15) adalah. (3.37).

45 c) Aproksimasi pada persamaan (3.18) Variabel tak bebas. (gundukan),. (ketinggian permukaan) dan c (perbedaan. kecepatan aliran) pada persamaan (3.18) dalam bentuk deret asimtotik (3.38). (3.39). (3.40). (3.41). (3.42). (3.43). (3.44). (3.45). (3.46) Substitusikan persamaan (3.39)-(3.46) ke persamaan (3.18) sehingga diperoleh hampiran dari persamaan (3.18) adalah.

46. kemudian diuraikan menjadi.

47. (3.47) d) Aproksimasi pada persamaan (3.22) Variabel tak bebas. (gundukan) dan c (perbedaan kecepatan aliran) pada. persamaan (3.22) dalam bentuk deret asimtotik (3.48). (3.49). (3.50). (3.51) Substitusikan persamaan (3.49)-(3.51) ke persamaan (3.22) sehingga diperoleh hampiran dari persamaan (3.22) adalah. (3.52) Setelah dilakukan aproksimasi variabel-variabel tak bebasnya kemudian didapatkan solusi dari masing-masing persamaan (3.8), (3.13), (3.18) dan (3.22) dengan melakukan peninjauan pada tiap-tiap orde sampai orde ketiga dari deret asimtotik..

48 3.1.4. Peninjauan pada Tiap-tiap Orde dari Deret Asimtotik Berdasarkan persamaan (3.29), (3.37), (3.47), dan persamaan (3.52) akan. ditinjau setiap orde untuk mendapatkan solusi dari deret asimtotik. a) Orde Berdasarkan orde. didapatkan solusi dari persamaan (3.29), (3.37), (3.47), dan. persamaan (3.52) yaitu (3.53). dan (3.54). (3.55) dan (3.56). b) Orde  2 Berdasarkan orde. didapatkan solusi dari persamaan (3.29), (3.37), (3.47), dan. persamaan (3.52) yaitu (3.57). dan (3.58).

49. (3.59). dan (3.60). c) Orde  3 Berdasarkan orde. didapatkan solusi dari persamaan (3.29), (3.37), (3.47), dan. persamaan (3.52) yaitu (3.61). dan (3.62). (3.63). dan (3.64). Selanjutnya dari persamaan (3.53) sampai dengan (3.64) disederhanakan ke dalam model matematika..

50 3.1.5. Penyederhanaan Solusi dari Deret Asimtotik Adapun langkah-langkah dalam penyederhanaan solusi dari deret. asimtotik ke dalam model matematika sebagai berikut: a) Pada orde diperoleh (3.65). Integralkan persamaan (3.65) terhadap. yaitu. (3.66) Dengan menggunakan kondisi batas (3.54) maka diperoleh , sehingga persamaan (3.66) menjadi (3.67). Untuk kondisi batas (3.56) sama seperti kondisi batas (3.54) didapatkan. Selanjutnya untuk kondisi batas (3.55) dengan. dihasilkan.

51. (3.68) Kemudian integralkan persamaan (3.67) terhadap. yaitu. (3.69). (3.70) Dengan menggunakan kondisi batas. pada persamaan (3.69) diperoleh (3.71). Dari persaman (3.68) dan persamaan (3.71) didapatkan. Maka persamaan (3.69) dan persamaan (3.70) menjadi. (3.72).

52 b) Pada Orde Substitusikan persamaan (3.72) ke persamaan (3.57) diperoleh. (3.73) Integralkan persamaan (3.73) terhadap. yaitu. (3.74). Dengan menggunakan kondisi batas (3.60) maka didapatkan (3.75). , sehingga persamaan (3.74) menjadi. (3.76). Kemudian dengan menggunakan kondisi batas (3.58) pada persamaan (3.76) akan diperoleh (3.77). . Dengan c ( 0)  1 , persamaan (3.76) menjadi. (3.78). Integralkan persamaan (3.78) terhadap. yaitu.

53. (3.79) Dengan menggunakan kondisi batas (3.59) untuk persamaan (3.79) didapatkan (3.80). sehingga persamaan (3.79) menjadi. (3.81). Dengan. maka persamaan (3.81) diperoleh (3.82). c) Pada orde. diperoleh.

54 (3.83). Substitusikan persamaan (3.82) ke persamaan (3.83) didapatkan (3.84). Integralkan persamaan (3.84) terhadap. yaitu. (3.85). Dengan menggunakan kondisi batas (3.64) pada persamaan (3.85) maka diperoleh (3.86). sehingga persamaan (3.85) menjadi (3.87). Kemudian dengan menggunakan kondisi batas (3.62) didapatkan.

55. Dengan. diperoleh. (3.88) Dengan mengabaikan tanda superscript. maka persamaan (3.88) dapat. disederhanakan menjadi (3.89). Persamaan (3.89) merupakan model matematika untuk gelombang permukaan yang berbentuk persamaan forced KdV, dimana permukaan fluida,. adalah ketinggian. adalah representasi dari gundukan pada dasar saluran,. adalah perbedaan kecepatan aliran. Grimshaw, dkk (2007) menyatakan perbedaan kecepatan aliran, dimana jika flow), jika. adalah. disebut aliran subkritis (subcritical. disebut aliran kritis (critical flow), jika. superkritis (supercritical flow). Pada keadaan. disebut aliran menunjukkan tidak. adanya gangguan pada dasar saluran yang dikenal dengan persamaan KdV dan mempunyai solusi analitik yang berbentuk secant-hiperbolik.. 3.2 Solusi Gelombang Soliter Penurunan model matematika untuk gelombang permukaan diperoleh dengan cara menyelesaikan persamaan Laplace beserta kondisi-kondisi batasnya ke dalam bentuk persamaan ketinggian permukaan fluida. Persamaan ketinggian.

56 tersebut disederhanakan ke dalam persamaan forced KdV. Adapun persamaan forced KdV yang dihasilkan yaitu. dengan. adalah ketinggian permukaan fluida,. gundukan pada dasar saluran dan. adalah representasi dari. adalah perbedaan kecepatan aliran. Persamaan. forced KdV dikenal sebagai salah satu bentuk persamaan diferensial parsial yang tidak memiliki solusi analitik, sehingga untuk menentukan solusinya dapat digunakan prosedur numerik. Namun sebelum itu ditinjau solusi untuk dasar saluran rata 3.2.1. dengan menggunakan metode koefisien tak tentu.. Solusi Homogen Pada bagian ini akan dijelaskan solusi untuk dasar saluran rata atau tidak. ada gundukan pada dasar saluran. . Untuk dasar saluran rata maka. persamaan (3.89) dapat dinyatakan sebagai (3.90). Model gelombang permukaan (3.90) merupakan representasi dari gelombang yang berjalan satu arah tanpa mengalami perubahan dan tanpa adanya interaksi antar satu gelombang dengan gelombang yang lain. Solusi persamaan (3.90) dapat diselesaikan dengan menggunakan metode koefisien tak tentu dengan memisalkan profil dari gelombang permukaan yang dihasilkan berbentuk secant hiperbolik, sehingga dapat diperoleh solusi persamaan (3.90) dalam bentuk fungsi secant hiperbolik juga. Misalkan solusi persamaan (3.90) dalam bentuk fungsi secant hiperbolik adalah.

57 (3.91) dengan. merupakan ketinggian permukaan, A merupakan amplitudo. gelombang, B merupakan lebar dari gelombang, C merupakan kecepatan aliran dari gelombang dan D merupakan sebarang konstanta. Konstanta-konstanta tersebut diperoleh dengan mensubstitusi persamaan (3.91) ke persamaan (3.90), tujuannya untuk memenuhi konstanta-konstanta A, B, dan C. Adapun langkahlangkahnya sebagai berikut: a) Hitung. ,. , dan.

58. b) Substitusi. ,. , dan dan. ke persamaan (3.90) dan kumpulkan koefisien , sehingga diperoleh.

59. (3.92) Persamaan (3.92) dapat diuraikan menjadi. Kemudian kumpulkan koefisien. dan menjadi. (3.93) Untuk memperoleh bentuk yang lebih sederhana bagi persamaan (3.93) dengan , sehingga diperoleh.

60 (3.94). Karena. maka persamaan (3.94). menjadi. (3.95) Persamaan (3.95) dapat diuraikan menjadi. Kumpulkan koefisien. dan. diperoleh. (3.96) Persamaan (3.96) dapat disederhanakan menjadi. Misalkan. .. (3.97). dan. sehingga. persamaan (3.97) menjadi (3.98) Kemungkinan persamaan (3.98) dapat dipenuhi dengan atau. dan. , apabila. dapat dipenuhi jika.

61 dan. . Sehingga digunakan. dan. untuk memenuhi persamaan (3.98) sebagai berikut dan menghasilkan. ,. . Dari. , dan. dan. .. Jadi dapat disimpulkan bahwa solusi dari persamaan (3.90) dalam bentuk fungsi secant hiperbolik adalah (3.99) dengan koefisien A, B, dan C harus memenuhi hubungan-hubungan sebagai berikut. , Misalkan. dan ,. ,. . ,. dan diberikan kondisi awal. , maka diperoleh solusi (3100). Berdasarkan persamaan (3.100) dapat dilustrasikan pada Gambar 3.1, Gambar 3.2, dan Gambar 3.3 dengan menggunakan perbedaaan kecepatan aliran dan. ,.

62. Tinggi Permukaan. 0.5 0.4 0.3 0.2 0.1 0 50 40 30 20 10 0. t. -150. -100. 0. -50. 50. 100. 150. x. Gambar 3.1 Persamaan (3.100) untuk. Tinggi Permukaan. 0.5 0.4 0.3 0.2 0.1 0 50 40 30 20. 0 -50. 10. t. 0. -150. -100. x. Gambar 3.2 Persamaan (3.100) untuk. 50. 100. 150.

63. Tinggi Permukaan. 0.5 0.4 0.3 0.2 0.1 0 50 40 100. 30 20 10. t. 0. -50 0. -150. 150. 50. -100. x. Gambar 3.3 Persamaan (3.100) untuk. Kemudian simulasi dari hasil solusi persamaan (3.90) dapat juga diilustrasikan pada Gambar 3.4, Gambar 3.5, dan Gambar 3.6 berikut. Gambar 3.4 Solusi Persamaan (3.90) untuk.

64 Solusi persamaan (3.90) dengan. dapat diilustrasikan pada gambar. 3.4 yang menunjukkan perambatan gelombang mengalami perubahan pada ketinggian gelombang. Hal ini terlihat, ketika. dan. gelombang 0.3932, sedangkan ketika. ketinggian gelombang. dan. ketinggian. 0.0013. Selain itu, perambatan gelombang berjalan menuju ke hulu dengan kecepatan fase sebesar. . Kecepatan fase dapat dilihat dari puncak. gelombang satu dengan puncak gelombang yang lainnya sehingga seberapa cepat puncak gelombang berpindah persatuan waktu.. Gambar 3.5 Solusi Persamaan (3.90) untuk. Selanjutnya solusi persamaan (3.90) dengan. dapat diilustrasikan. pada gambar 3.5 yang menunjukkan perambatan gelombang mengalami.

65 perubahan pada ketinggian gelombang. Hal ini terlihat, ketika. dan. ketinggian gelombang 0.3932, sedangkan ketika. ketinggian. gelombang. dan. . Selain itu, perambatan gelombang berjalan ke arah. hilir dengan kecepatan fase sebesar 0.9167. Kecepatan fase dapat dilihat dari puncak gelombang satu dengan puncak gelombang yang lainnya sehingga seberapa cepat puncak gelombang berpindah persatuan waktu. Sebaliknya solusi persamaan (3.90) untuk. dapat diilustrasikan. pada gambar 3.6 perambatan gelombang berjalan ke arah hulu dengan kecepatan fase sebesar 1.0833. Kecepatan fase dapat dilihat dari puncak gelombang satu dengan puncak gelombang yang lainnya sehingga seberapa cepat puncak gelombang berpindah persatuan waktu. Selain itu perambatan gelombang mengalami perubahan pada ketinggian gelombang. Hal ini terlihat, ketika dan. ketinggian gelombang 0.3932 sedangkan ketika. ketinggian gelombang. .. Gambar 3.6 Solusi persamaan (3.90) untuk. dan.

66 Selain perbedaan kecepatan aliran (c) yang mempengaruhi perambatan gelombang, amplitudo gelombang dan lebar dari gelombang juga mempengaruhi perambatan gelombang, semakin besar nilai amplitudo menyebabkan amplitudo gelombang semakin tinggi akibatnya lebar dari gelombang semakin kecil. 3.2.2. Solusi Non Homogen Bentuk tak homogen dari persamaan KdV disebut persamaan forced KdV. sebagaimana pada persamaan (3.89). Persamaan forced KdV dikenal sebagai salah satu bentuk persamaan diferensial parsial yang tidak memiliki solusi analitik, sehingga untuk menentukan solusinya digunakan prosedur numerik. Dalam skripsi ini metode yang digunakan adalah metode beda hingga skema eksplisit atau CTCS (central time central space). Adapun persamaan beda CTCS yang digunakan adalah (3.101). (3.102). (3.103). (3.104). Selanjutnya persamaan (3.101), (3.102), (3.103) dan (3.104) disubstitusi ke dalam persamaan (3.89) sebagai berikut.

67. (3.105) Persamaan (3.105) dapat diuraikan menjadi.

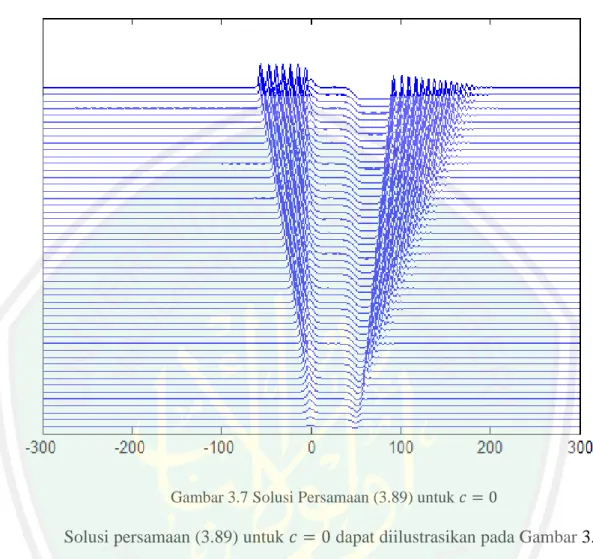
68. (3.106) Persamaan (3.106) adalah model pendekatan persamaan (3.89) dengan menggunakan metode beda hingga skema eksplisit atau CTCS (central time central space). Persamaan fKdV merupakan representasi dari gelombang yang dihasilkan oleh aliran yang melalui sebuah gundukan, maka dalam simulasi ini gaya luar yang digunakan sebagaimana yang terdapat dalam Grimshaw, dkk (2007), yaitu. Bentuk gaya luar yang digunakan di atas, berupa gundukan dengan puncak datar dengan lebar L dan tinggi gundukan sebesar kemiringan antara. , sedangkan. merupakan sudut. dan sebagai lebar kaki dari gundukan tersebut.. Kemudian dilakukan simulasi dengan menggunakan perbedaan kecepatan aliran yaitu. ,. dan. , serta. ,. dan. . Hasil. dari perhitungan numerik tersebut dapat diilustrasikan pada Gambar 3.7, Gambar 3.8 dan Gambar 3.8 sebagai berikut.

69. Gambar 3.7 Solusi Persamaan (3.89) untuk. Solusi persamaan (3.89) untuk. dapat diilustrasikan pada Gambar 3.7. yang menunjukkan bahwa adanya gangguan pada dasar saluran mengakibatkan timbulnya riak-riak gelombang pada permukaan. Pada saat gelombang berjalan ke arah hulu dan pada saat. riak-riak. riak-riak gelombang. berjalan ke arah hilir. Riak-riak gelombang berjalan dengan mengalami perubahan pada ketinggian riak-riak gelombang tersebut yaitu diperoleh tinggi gelombang sebesar 0.4695 sedangkan. ,. dan ,. dan. diperoleh tinggi gelombang sebesar 0.6874. Besar kecilnya gundukan.

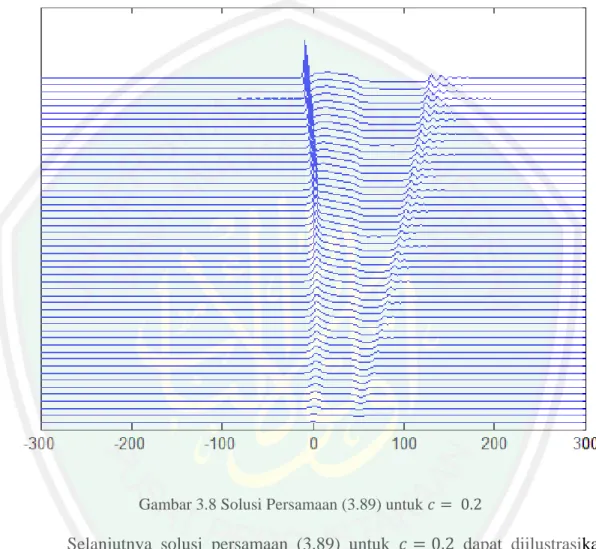
70 mempengaruhi tinggi gelombang permukaan. Semakin besar gundukan maka semakin besar pula amplitudo pada gelombang permukaan tersebut.. Gambar 3.8 Solusi Persamaan (3.89) untuk. Selanjutnya solusi persamaan (3.89) untuk. dapat diilustrasikan. pada Gambar 3.8 yang menunjukkan bahwa adanya gangguan pada dasar saluran mengakibatkan timbulnya riak-riak gelombang pada permukaan. Pada saat riak-riak gelombang berjalan ke arah hulu dan pada saat. riak-riak. gelombang berjalan ke arah hilir. Riak-riak gelombang berjalan dengan mengalami perubahan pada ketinggian riak-riak gelombang tersebut yaitu diperoleh tinggi gelombang sebesar 1.0581 sedangkan. ,. dan ,. dan.

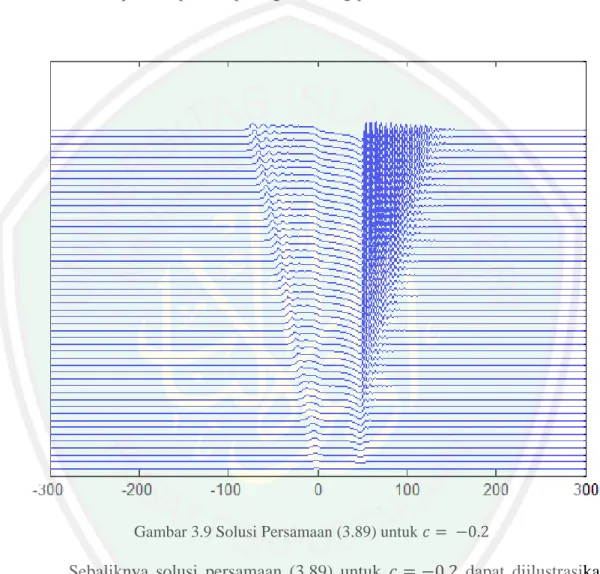
71 diperoleh tinggi gelombang sebesar 1.2499. Besar kecilnya gundukan mempengaruhi tinggi gelombang permukaan. Semakin besar gundukan maka semakin besar pula amplitudo pada gelombang permukaan tersebut.. Gambar 3.9 Solusi Persamaan (3.89) untuk. Sebaliknya solusi persamaan (3.89) untuk. dapat diilustrasikan. pada Gambar 3.9 menunjukkan bahwa adanya gangguan pada dasar saluran mengakibatkan timbulnya riak-riak gelombang pada permukaan. Pada saat riak-riak gelombang berjalan ke arah hulu dan pada saat gelombang berjalan ke arah hilir. Riak-riak gelombang berjalan dengan dan. diperoleh tinggi gelombang sebesar 0.2194.. riak-riak ,.

72 3.3 Kajian Keagamaan Model gelombang permukaan yang dihasilkan dalam bentuk persamaan forced KdV pada persamaan (3.89) adalah. Persamaan (3.89) diturunkan dari persamaan Laplace beserta kondisi batas pada permukaan fluida dan kondisi batas pada dasar fluida, sehingga membuktikan bahwa terdapat model matematika untuk fenomena alam yang terkait dengan gelombang permukaan. Adanya model matematika ini, dapat meningkatkan keimanan dan ketaqwaan kepada Allah SWT, sebab Allah SWT telah menciptaan alam semesta ini dengan perhitungannya masing-masing. Sebagaimana Allah berfirman dalam surat Al-Furqan ayat 2:.                     Artinya: “ Yang kepunyaan-Nya-lah kerajaan langit dan bumi, dan Dia tidak mempunyai anak, dan tidak ada sekutu baginya dalam kekuasaan(Nya), dan Dia telah menciptakan segala sesuatu, dan Dia menetapkan ukuran-ukurannya dengan serapi-rapinya”.. Selain itu, Allah berfirman dalam surat Al-Hijr ayat 21:.             Artinya: “Dan tidak ada sesuatupun melainkan pada sisi Kami-lah khazanahnya dan Kami tidak menurunkannya melainkan dengan ukuran yang tertentu”.. Namun demikian, perlu diingat bahwa apa yang diketahui sekarang, hanyalah sebagian kecil dari apa yang tidak diketahui. Oleh karena itu, Allah tidak.

73 membolehkan untuk bersikap sombong. Sebab sungguh amat luas apa yang diciptakan Allah SWT. Allah berfirman dalam surat Al-Isra’ ayat 37:.                Artinya: “Dan janganlah kamu berjalan di muka bumi ini dengan sombong, karena Sesungguhnya kamu sekali-kali tidak dapat menembus bumi dan sekali-kali kamu tidak akan sampai setinggi gunung”.. Selain itu, firman Allah di atas juga dipertegas dengan surat Lukman ayat 18:.                   Artinya: “Dan janganlah kamu memalingkan mukamu dari manusia (karena sombong) dan janganlah kamu berjalan di muka bumi dengan angkuh. Sesungguhnya Allah tidak menyukai orang-orang yang sombong lagi membanggakan diri”..

BAB IV PENUTUP. 4.1 Kesimpulan Skripsi ini membahas penurunan model matematika untuk gelombang permukaan yang dihasilkan oleh aliran yang melalui suatu gundukan. Model tersebut. dihasilkan. dengan. menyederhanakan. persamaan-persamaan. kesetimbangan yang diturunkan dari hukum-hukum kekekalan yang terjadi pada aliran fluida, kemudian dilakukan penskalaan, aproksimasi variabel, peninjauan tiap-tiap orde dengan deret asimtotik, menyederhanakan solusi ke dalam sebuah model matematika. Berdasarkan pembahasan diperoleh model gelombang permukaan dalam bentuk persamaan ketinggian permukaan yang disederhanakan ke dalam persamaan forced KdV sebagai berikut. dimana. adalah ketinggian permukaan fluida,. adalah representasi dari. gundukan pada dasar saluran, adalah perbedaan kecepatan aliran. Hasil simulasi untuk dasar tidak rata dengan menggunakan metode beda hingga skema eksplisit menunjukkan perambatan gelombang mengalami perubahan pada ketinggian gelombang. Perubahan pada ketinggian gelombang berjalan seiring dengan perubahan waktu. Selain itu, dalam simulasi tersebut digunakan perbedaan kecepatan aliran yaitu. 74. ,. , dan. ..

75 Hasil simulasi untuk dasar rata (. dengan menggunakan metode. koefisien tak tentu menunjukkan gelombang berjalan mengalami perubahan pada ketinggian gelombang. Selain itu, dalam simulasi tersebut digunakan perbedaan kecepatan aliran yaitu. ,. , dan. . Untuk. menunjukkan. perambatan gelombang berjalan menuju ke hilir dengan kecepatan fase sebesar , sedangkan untuk. menunjukkan perambatan gelombang menuju ke. arah hilir dengan kecepatan fase sebesar 0.9167 dan untuk. menunjukkan. perambatan gelombang ke arah hulu dengan kecepatan fase sebesar -1.0833.. 4.2 Saran Dalam penelitian ini dilakukan aproksimasi/hampiran dalam bentuk deret asimtotik sampai orde ketiga, sehingga peneliti menyarankan untuk melakukan aproksimasi deret asimtotik sampai orde kelima. Bertambahnya orde maka orde erornya semakin besar dan akurasinya semakin meningkat sehingga didapatkan hasil aproksimasi yang lebih baik..



DAFTAR PUSTAKA. Abdussakir. 2007. Ketika Kiai Mengajar Matematika. Malang: UIN Malang Press. Chorlton, F.. 1967. Textbook of Fuid Dynamics. London: D.Van Nostrand Company LTD London. Douglas, G.. 2001. Fisika Edisi kelima. Jakarta: Erlangga. Grimshaw, R.H.J., Zhang, D.H., & Chow, K.W.. 2007. Generation of Solitary Waves by Transcritical Flow Over a Step. J.Fluid Mech. Hal.235-254. Hakim, A.. 2009. Prediksi Kecepatan Phase Gelombang Soliter Terganggu. Thesis. Tidak diterbitkan. Bogor: Sekolah Pascasarjana Institut Pertanian Bogor. Olson, R.. 1993. Dasar-dasar Mekanika Fluida. Jakarta: PT Gramedia Pustaka Utama. Purwanto. 1998. Matematika Diskrit . Malang: IKIP Malang. Streeter, V.L.. 1986. Mekanika Fluida Edisi Delapan Jilid 1. Jakarta: Erlangga. Wiryanto, L.. 2010. A Solitary-like Wave Generated by Flow Passing a Bump. ICMSA 2010. Hal.1176-1183.. 76.

Lampiran 1 Program MATLAB untuk persamaan (3.100). ,. ,. 3.1, Gambar 3.2, dan Gambar 3.3. clc,clear,clf c=0 [x,t] = meshgrid(-150:0.6:150,0:0.2:50); z = (1/2)*sech((1/2)*x+(((1/12)-(c*(1/2)))*t)+2).^2; surf(x,t,z) xlabel('x') ylabel('t') zlabel('tinggi permukaan'). pada Gambar.

Lampiran 2 Program MATLAB untuk solusi persamaan (3.90). ,. Gambar 3.4, Gambar 3.5, dan Gambar 3.6. clc,clear,clf dx=0.5; dt=0.2; x=-150:dx:150; t=0:dt:50;. c=-2; Mx=length(x); Nt=length(t); z=sparse(Mx,Nt);. figure(1), clf k=0; for n=1:Nt for j=1:Mx z(j,n+1) = (1/2).*sech((1/2).*x(j)+(((1/12)c.*(1/2)).*t(n))+2).^2; end if mod(n,10)==0 k=k+1; plot(x,z(:,n)+k), hold on pause(0.01) n end end. ,. pada.

Lampiran 3 Program MATLAB untuk solusi persamaan (3.89). ,. ,. pada Gambar 3.7, Gambar 3.8, dan Gambar 3.9. clc,clear,clf dx=0.5; dt=0.2; x=-300:dx:300; t=0:dt:300; A=dt/dx; B=dt/(6*(dx.^3)); FM=0.1; gama=0.25; L=50; c=0; s=abs((dt/dx)*(gama-0.5)-dt/(3*(dx^3))) F=(FM/2)*(tanh(gama*x)-(tanh(gama*(x-L)))); Fx= diff(F);. Mx=length(x); Nt=length(t); u=sparse(Mx,Nt);. figure(1), clf k=0; for n=2:Nt-1 for j=3:Mx-2 C=(B*(u(j+2,n)-(2*u(j+1,n))+(2*u(j-1,n))-u(j-2,n))); D=(A*(((u(j+1,n)+u(j,n)+u(j-1,n))/3)-c)*(u(j+1,n)-u(j1,n)));. u(j,n+1)=u(j,n-1)+C+D+(dt*Fx(j)); end if mod(n,30)==0 k=k+1; plot(x,u(:,n)+0.2*k), hold on pause(0.01) end end.

KEMENTERIAN AGAMA RI UNIVERSITAS ISLAM NEGERI MAULANA MALIK IBRAHIM MALANG FAKULTAS SAINS DAN TEKNOLOGI Jl. Gajayana No. 50 Dinoyo Malang Telp./Fax.(0341)558933 BUKTI KONSULTASI SKRIPSI Nama NIM Fakultas/Jurusan Judul Skripsi. : Farida Masluchah : 10610016 : Sains dan Teknologi/ Matematika : Model Gelombang Soliter yang Dihasilkan oleh Aliran yang Melalui Sebuah Gundukan Pembimbing I : Mohammad Jamhuri, M.Si Pembimbing II : Dr. Abdussakir, M.Pd No Tanggal Hal Tanda Tangan 1. 31 Oktober 2013 Konsultasi BAB I dan BAB II 1. 2. 05 Nopember 2013 Revisi BAB I BAB II 2. Konsultasi BAB III 3. 14 Nopember 2013 ACC BAB I BAB II 3. Revisi BAB III 4. 12 Nopember 2013 Konsultasi Keagamaan 4. 5. 20 Nopember 2013 Revisi Keagamaan 5. 6. 03 Desember 2013 ACC Keagamaan 6. 7. 16 Januari 2014 Revisi BAB III 7. 8. 30 Januari 2014 Revisi BAB III 8. Konsultasi BAB IV 9. 20 Februari 2014 Revisi BAB IV 9. ACC BAB III 10. 27 Februari 2014 ACC Bab IV 10. 11. 05 Maret 2014 Konsultasi Abstrak 11. 12. 13 Maret 2014 Konsultasi Keagamaan BAB III 12. 13. 02 April 2014 ACC Keseluruhan 13. Malang, 03 April 2014 Mengetahui, Ketua Jurusan Matematika. Dr. Abdussakir, M.Pd NIP. 19751006 200312 1 001.