Gelombang Soliter Internal pada Laut Dalam untuk Aliran yang Tunak

GELOMBANG SOLITER INTERNAL PADA LAUT DALAM UNTUK

ALIRAN YANG TUNAK

INTAN RATNA NURJANAH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

GELOMBANG SOLITER INTERNAL PADA LAUT DALAM UNTUK

ALIRAN YANG TUNAK

INTAN RATNA NURJANAH

G54104009

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRACT

INTAN RATNA NURJANAH. Internal Solitary waves at Deep sea for the Steady-State. Under supervision by JAHARUDDIN and ALI KUSNANTO

ABSTRAK

INTAN RATNA NURJANAH. Gelombang Soliter Internal pada Laut Dalam untuk Aliran yang Tunak. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.

GELOMBANG SOLITER INTERNAL PADA LAUT DALAM UNTUK

ALIRAN YANG TUNAK

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

INTAN RATNA NURJANAH

G54104009

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul : Gelombang Soliter Internal pada Laut Dalam untuk Aliran yang

Tunak

Nama

: Intan Ratna Nurjanah

NIM :

G54104009

Menyetujui,

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Tanggal Lulus :

Pembimbing II

Drs. Ali Kusnanto, M. Si.

NIP. 131 913 135

Pembimbing I

Dr. Jaharuddin, M. Si.

NIP. 132 045 530

KATA PENGANTAR

Puji syukur penulis panjatkan kepada Allah SWT atas segala karunianya sehingga penulis dapat menyelesaikan karya ilmiah yang berjudul, Gelombang Soliter Internal Pada Laut Dalam Untuk Aliran yang Tunak. Shalawat dan salam semoga senantiasa tercurah kepada Rasulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman. Karya ilmiah ini saya persembahkan untuk keluarga tercinta : Apa, ibu, Teh Ageung, A Agung, Aden, Ua Bandung, Ua Jemah, D Sifa, Ibi Cikampek dll yang telah banyak memberikan motivasi, inspirasi dan doa, sehingga karya ilmiah ini dapat terselesaikan.

Keterbatasan dan ketidaksempurnaan membuat penulis membutuhkan bantuan, dukungan dan semangat dari orang-orang secara langsung ataupun tidak langsung berkontribusi besar dalam pembuatan karya ilmiah ini. Oleh karena itu penulis ingin mengucapkan rasa terima kasih yang sebesar-besarnya kepada Dr. Jaharuddin, M. Si dan Drs. Ali Kusnanto, M. Si masing-masing sebagai pembimbing pertama dan kedua yang dengan sabar telah membimbing dan mengarahkan selama penulisan karya ilmiah ini. Demikian juga kepada Drs. Siswandi, M. Si atas kesediaannya menjadi penguji dalam karya ilmiah ini, dan Yudi Surya Lesmana (Aa tersayang) atas bantuan, motivasi, saran, do’a dan kasih sayangnya.

Taklupa penulis juga mengucapkan terima kasih kepada Rina dan Roma, sahabat sekaligus teman seperjuangan. Endit, Mba Situl, dan Tia atas kesediaannya menjadi pembahas dalam seminar karya ilmiah ini, dan mahasiswa matematika angkatan 41 atas dukungan dan doanya. Seluruh dosen Departemen Matematika atas segala ilmu yang telah diberikan. Staf dan karyawan TU Matematika IPB, serta seluruh pihak yang tidak dapat penulis sebutkan satu per satu. Penulis menyadari bahwa karya ilmiah ini masih jauh dari kesempurnaan. Oleh karena itu, kritik dan saran sangat dibutuhkan. Semoga karya ilmiah ini dapat bermanfaat bagi khususnya penulis dan bagi pihak lain yang membutuhkan.

Bogor, Januari 2008

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 12 Nopember 1986 sebagai anak ketiga dari empat bersaudara. Anak dari Bapak Saepujar Hidayat dan Ibu Enok Warilah.

Pada tahun 1992 penulis menyelesaikan pendidikan di TK Assalam. Kemudian pada tahun 1998, penulis melanjutkan pendidikan di SD Negeri Cibungbulang II. Penulis melanjutkan pendidikan di SLTP Negeri 1 Cibungbulang pada tahun yang sama. Pada tahun 2000 penulis pindah sekolah ke SLTP Negeri 1 Wado sumedang utara, karena penulis mengikuti Orang Tua yang bekerja di Sumedang. Pada Tahun 2001 penulis melanjutkan pendidikan di SMU Negeri 1 Sumedang. Pada tahun 2004, penulis diterima di Institut Pertanian Bogor (IPB) melalui jalur Ujian Seleksi Masuk Institut Pertanian Bogor (USMI) di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam IPB.

vii

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

PENDAHULUAN Latar Belakang ... 1

Tujuan ... 1

Sistematika Penulisan ... 1

LANDASAN TEORI Persamaan Dasar Fluida ... 2

Syarat Batas ... 2

Aliran Fluida Tunak ... 3

Metode Asimtotik ... 4

PEMBAHASAN Formulasi Lagrange ... 5

Persamaan BO Tunak ... 6

Fluida Lapisan Atas ... 6

Fluida Lapisan Bawah ... 6

Solusi Persamaan BO ... 7

Contoh Kasus Fluida Dua Lapisan ... 8

SIMPULAN ... 10

DAFTAR PUSTAKA ... 10

viii

DAFTAR GAMBAR

Halaman

1. Domain Fluida dengan Kedalaman yang Besar ... 2

2. Perbandingan Solusi eksak MNA dengan Solusi MNA Metode Asimtotik ... 5

3. Simpangan Gelombang pada Fluida Dua Lapisan Untuk Orde Rendah ... 9

DAFTAR LAMPIRAN

Halaman 1. LAMPIRAN A ... 12

2. LAMPIRAN B ... 17

3. LAMPIRAN C ... 21

4. LAMPIRAN D ... 24

PENDAHULUAN

Latar Belakang

Laut dapat dianggap sebagai fluida ideal yang bersifat takmampat dan takkental serta terdiri atas beberapa lapisan air. Munculnya lapisan ini disebabkan perbedaan rapat massa. Perbedaan rapat massa di setiap lapisan disebabkan adanya kadar garam (salinitas) dan suhu. Kadar garam di lapisan bawah lebih besar dibandingkan di atasnya, dan suhu di lapisan atas lebih panas dibandingkan di bawahnya karena dipengaruhi oleh sinar matahari. Berdasarkan perbedaan tersebut, terjadi aliran partikel di bawah permukaan laut sehingga terjadi suatu gelombang yang disebut dengan gelombang internal. Gelombang internal ini tidak terlihat secara kasat mata tetapi dapat terdeteksi di permukaan laut dengan menggunakan foto satelit. Gelombang internal yang banyak dipelajari adalah gelombang soliter internal.

Pengetahuan mengenai gelombang soliter berasal dari hasil pengamatan gelombang di laut dangkal, teluk yang curam, danau, dan lapisan atmosfer. Gelombang soliter adalah gelombang internal yang mempertahankan bentuk dan kecepatannya. Pada karya ilmiah ini hanya mengkaji gelombang soliter internal pada laut dalam. Laut dalam menggunakan asumsi bahwa kedalaman laut lebih besar dibandingkan dengan panjang gelombang yang ditinjau.

Gelombang soliter internal dapat terdeteksi melalui Synthetic Aperture Radar (SAR) sebagai pola gelap terang (riak gelombang) yang tampak teratur di permukaan laut dan hanya terjadi pada daerah perairan tertentu. Misalnya di Laut Andaman (Thailand), dan Laut Sulu (Philipina). Gelombang soliter yang terjadi di Laut Andaman menyebar luas beberapa mil dengan gerakan yang sangat lambat kurang lebih 10 km per jam [Herman, 1992].

Beberapa peneliti meneliti berbagai dampak yang ditimbulkan oleh gelombang soliter internal, seperti naiknya polutan dari dasar laut ke permukaan laut dan robohnya tiang penyangga anjungan minyak yang dibangun di laut. Hal ini perlu memperhatikan besarnya kekuatan gelombang soliter ini. Selain itu, gelombang ini juga dapat mempengaruhi kehidupan habitat laut [Garkema, 1994]. Dampak yang ditimbulkan oleh gelombang ini memotivasi penulis untuk lebih mengenali karakteristik dan besarnya kekuatan gelombang soliter internal.

Karya ilmiah ini dimulai dengan menurunkan suatu persamaan dasar fluida ideal (takmampat dan takkental) yang irrotasional dari hukum kekekalan massa dan kekekalan momentum. Kemudian dengan asumsi aliran tunak diperoleh suatu persamaan yang dinyatakan dalam fungsi arus. Persamaan ini disebut persamaan Long. Selanjutnya, persamaan Long yang diperoleh disederhanakan dengan menggunakan peubah Lagrange sehingga diperoleh persamaan dasar dalam formulasi Lagrange. Berdasarkan persamaan dasar ini, diturunkan persamaan gerak gelombang internal dengan menggunakan metode asimtotik. Asumsi yang digunakan dalam penurunan ini adalah asumsi fluida dalam. Persamaan gerak gelombang internal yang diperoleh merupakan suatu persamaan Benjamin-Ono (BO). Persamaan BO selanjutnya diselesaikan dengan memisalkan penyelesaiannya dalam bentuk gelombang soliter, yaitu suatu gelombang berjalan yang memiliki ciri khusus. Berdasarkan formulasi gelombang soliter persamaan BO, maka dikaji suatu contoh kasus. Contoh kasus yang dibahas dalam karya ilmiah ini adalah kasus fluida dua lapisan. Fluida dua lapisan adalah fluida yang terdiri atas dua lapisan yang masing-masing memiliki rapat massa konstan.

Tujuan

Berdasarkan latar belakang di atas, karya ilmiah ini adalah menurunkan persamaan gerak gelombang internal dengan menggunakan metode asimtotik, dan menentukan penyelesaiannya dalam bentuk gelombang soliter. Selain itu, menggunakan formulasi gelombang soliter internal pada fluida dalam untuk mengkaji kasus fluida dua lapisan.

Sistematika Penulisan

LANDASAN TEORI

Teori-teori yang digunakan pada bab ini

disarikan dari pustaka [David dkk, 1994], [Grimshaw, 1997], [Long, 1953], [Jaharuddin, 2004], dan [Hinch, 1992]. Bagian pertama membahas penurunan persamaan dasar fluida ideal yang takberotasi pada fluida dalam dengan aliran tunak dan bagian kedua dibahas konsep dasar metode asimtotik.

Persamaan Dasar Fluida

Penurunan persamaan dasar fluida menggunakan hukum kekekalan massa dan kekekalan momentum. Hukum kekekalan massa pada suatu sistem adalah laju perubahan massa suatu sistem dalam elemen luas sama dengan selisih antara massa yang masuk ke dalam sistem dengan massa yang meninggalkan sistem pada elemen luas tersebut.

Misalkan ρ adalah rapat massa, u adalah kecepatan partikel dalam arah horizontal dan w adalah kecepatan partikel dalam arah vertikal. Karena diasumsikan aliran partikel fluida dalam dua dimensi, maka ρ, ,u dan w bergantung pada koordinat horizontal x dan koordinat vertikal z yang merupakan fungsi dari waktu t. Berdasarkan hukum kekekalan massa, persamaan kontinuitas fluida yang takmampat adalah:

0 0.

t x z

x z

u w

u w

ρ + ρ + ρ = ⎫

⎬

+ _{= ⎭} (1)

Hukum kekekalan momentum pada suatu sistem adalah laju perubahan momentum sama dengan selisih dari momentum yang masuk pada sistem dengan momentum yang meninggalkan sistem ditambah gaya-gaya yang bekerja pada elemen luas. Sehingga, diperoleh persamaan momentum berikut:

(

)

(

)

0

0,

t x z x

t x z z

u uu wu P

w uw ww P g

ρ

ρ ρ

+ + + _{= ⎫⎪}

⎬

+ + + + _{= ⎪⎭} (2)

dengan Padalah tekanan dan g adalah gaya gravitasi. Dengan demikian persamaan fluida ideal diberikan sebagai berikut:

(

)

(

)

0 0

0

0

t x z

x z

t x z x

t x z z

u w

u w

u uu wu P

w uw ww P g

ρ ρ ρ

ρ

ρ ρ

+ + = ⎫

⎪

+ _{= ⎪}

⎬

+ + + _{= ⎪}

⎪

+ + + + _{= ⎭}

(3)

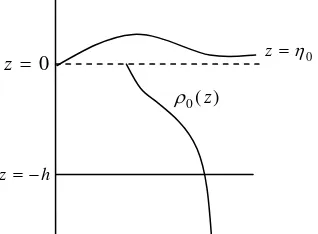
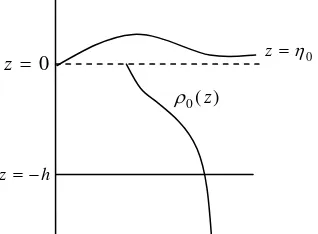
Syarat Batas

Syarat batas pada gerak partikel fluida terdiri atas dua jenis, yaitu syarat batas dinamik dan

kinematik. Syarat batas dinamik terjadi karena adanya gaya-gaya yang bekerja pada fluida. Sedangkan syarat batas kinematik terjadi karena gerak partikel.

Gambar 1. Domain fluida dengan kedalaman yang besar

Asumsi syarat batas dinamik adalah tekanan di udara sama dengan nol. Jika tekanan di permukaan sama dengan tekanan udara, maka tekanan di permukaan sama dengan nol

(

P=0

)

. Sedangkan syarat batas kinematik yaitu di z=η0

( )

x t, , kurva yang membatasi

antara udara dan permukaan yang diilustrasikan pada Gambar 1.

Misalkan z=η₀ merupakan persamaan permukaan. Jika S= −z η0 =0, maka

0

S= −z η dengan asumsi tidak ada satupun partikel fluida yang menembus permukaan, diperoleh

0 DS

Dt = di z=η0

( )

x t, , (4) dengan

, D

u w

Dt t x z

∂ ∂ ∂

= + +

∂ ∂ ∂

yaitu turunan total terhadap waktu. Persamaan (4) menjadi

0t 0x

w=η +uη di z=η₀. (5) Selanjutnya, jika diasumsikan fluida memiliki kedalaman yang besar, maka diperoleh

0

w= di z→ −∞. (6) Jadi, pada kedalaman yang besar kecepatan partikel fluida dalam arah vertikal adalah nol. Sehingga syarat batas fluida diperoleh sebagai berikut:

0

w= diz→ −∞

0t 0x

w=η +uη diz=η₀ 0

P= diz=η0.

0

z=η

0 z =

z= −h

0( )z

3

Berikut ini akan diturunkan syarat batas dinamik. Dalam notasi vektor, persamaan (2) dapat ditulis

, D

P Dt

ρ q= −∇ +ρg (7)

dengan g=

(

0,−g

)

, dan q=

(

u w,

)

.

Jika menggunakan notasi turunan total, diperoleh

( . ) .

t

D

Dt = ∂ + ∇

q

q q q (8) Persamaan (8) dapat ditulis

2 1 (( ) ) 2 t D Dt ⎛ ⎞ = ∂ + ∇× × + ∇⎜ ⎟ ⎝ ⎠ q

q q q q (9)

Berdasarkan asumsi partikel fluida takberotasi

(∇ ×q)=0, maka terdapat suatu fungsi skalar

(

x z t, ,

)

φ yang disebut kecepatan potensial dan memenuhi ∇ =φ q, (u=φx dan w=φz).

Persamaan (9) menjadi

( )

1

(

2 2

)

2

t x z

D

Dt φ φ φ

⎛ ⎞

= ∂ ∇ + ∇_⎜ + _⎟

⎝ ⎠

q

. (10) Selanjutnya, persamaan (10) disubstitusi- kan ke persamaan (7), setelah itu diintegralkan terhadap koordinat ruang, maka diperoleh

(

2 2

)

1

( ) 2

t x z

P

gz C t

φ φ φ

ρ

+ + + + = , (11)

dengan C t( ) fungsi sembarang dari t, peubah

z merupakan ketinggian partikel yang diamati dari dasar. Karena P=0 di z=η0

dan misalkan C t( )=0, maka persamaan (11) memberikan:

(

2 2

)

0

1

0 2

t x z g

φ + φ +φ + η = diz=η0

( )

x t, . (12)

Persamaan (12) disebut syarat batas dinamik pada permukaan fluida.

Aliran Fluida Tunak

Berikut ini akan dibahas persamaan dasar untuk aliran yang tunak. Ilustrasi aliran tunak adalah sebagai berikut. Misalkan suatu gelombang difoto dan gelombang tersebut bergerak seperti bingkai foto yang bergerak. Sehingga kecepatan gelombang sama dengan kecepatan bingkai. Misalkan gelombang tersebut hanya bergerak ke arah kanan dengan kecepatan c>0, maka koordinat foto X

dapat ditulis X = −x ct sehingga

x X

∂ = ∂ , ∂ = − ∂t c X.

Selanjutnya, bentuk tunak dari persamaan (3a) dapat ditulis

0.

X X z

cρ uρ wρ

− + + = (13)

Misalkan U= −u c, maka persamaan (13) menjadi

0.

X z

Uρ +wρ = Persamaan (3b) menjadi

0.

X z

U +w =

Kemudian persamaan (3c) dan (3d) dapat ditulis menjadi

ρ

(

Uu_X +wu_z

)

+P_x =0

(

UwX wwz

)

Pz g 0.

ρ + + +ρ =

Untuk memudahkan penulisan, notasi X dan U pada setiap persamaan ditulis dalam notasi x dan u. Sehingga persamaan dasar fluida ideal untuk aliran tunak adalah:

(

)

(

)

0 0 0 0. x z x z

x z x

x z z

u w

u w

uu wu P

uw ww P g

ρ ρ ρ ρ ρ + = ⎫ ⎪ + _{= ⎪} ⎬ + + _{= ⎪} ⎪ + + + _{= ⎭} (14)

Misalkan 2 2 2

u w

= +

q dan ξ =w_x−u_z. Persamaan (14c) dan (14d) dapat ditulis menjadi

2

1

0

2 w Px

x

ρ ∂ ⎛_⎜ ⎞ −_⎟ ρξ + =

∂ ⎝ q ⎠ (a)

2

1

0.

2 u Pz g

z

ρ ∂ ⎛_⎜ ⎞ +_⎟ ρξ + +ρ =

∂ ⎝ q ⎠ (b)

Eliminasi P pada persamaan (a) dan (b) dengan terlebih dahulu persamaan (b) diturunkan terhadap x dan persamaan (a) diturunkan terhadap z. Kemudian, persamaan (b) yang baru dikurangi oleh persamaan (a) yang baru. Sehingga diperoleh

2 2

1 1

2 2

x ρ z z ρ x

∂ ⎛ ∂ ⎛ ⎞⎞ ∂ ⎛ ∂₋ ⎛ ⎞⎞₊

⎜ ⎜ ⎟⎟ ⎜ ⎜ ⎟⎟

∂ ⎝ ∂ ⎝ q ⎠⎠ ∂ ⎝ ∂ ⎝ q ⎠⎠

(

u

)

(

w

)

xg 0,

x ρξ z ρξ ρ

∂ ₊ ∂ _{+ =}

∂ ∂ (15)

dengan

. D

u w

Dt x z

∂ ∂

= +

∂ ∂

Persamaan (15) dapat ditulis sebagai berikut

(

2 2

)

1 1

2 D

u w

Dt x z

ξ ρ

ρ

∂ ∂ ⎛ ⎞

+ _⎜ + _⎟−

∂ ∂ ⎝ ⎠

(

2 2

)

1 1

0. 2

g

u w

z x x

ρ ρ

ρ ρ

∂ ∂ ⎛ ₊ ⎞₊ ∂ ₌

⎜ ⎟

∂ ∂ ⎝ ⎠ ∂ (16)

Selanjutnya, misalkan ψ merupakan fungsi arus (stream function) yang memenuhi

z

u= −ψ dan w=ψx. (17) Berdasarkan persamaan (14a), diperoleh

0, D

Dt

ρ ₌

Jika persamaan (17) disubstitusikan ke persamaan (16) kemudian diintegralkan terhadap koordinat ruang, maka diperoleh

(

2 2

)

1 1

( ), 2

zz xx z x

d z H d ρ ψ ψ σ ψ ψ ψ σρ ψ ⎛ ⎞ + + _⎜ + + _⎟= ⎝ ⎠ (18) dengan H( )ψ adalah konstanta yang diperoleh berdasarkan kondisi upstream

(

x→ ±∞

)

, dan σ suatu parameter. Kondisi upstream adalah kondisi dimana garis arus hampir berupa garis lurus jauh di kanan dan di kiri. Misalkan rapat massa fluida dalam keadaan setimbang dinyatakan ρ0

( )

z ,

sehingga dalam kondisi upstream

( )

0 z .

ρ→ρ Diasumsikan pada kondisi upstream kecepatan partikel fluida pada arah horizontal usama dengan c, dan kecepatan partikel fluida pada arah vertikal w sama dengan 0, maka ψ →cz sehingga persamaan (18) memberikan

( )

0 2

0 1 . 2 d H c d c ρ σ ψ ψ ρ σ ψ ⎛ ⎞ = _⎜ + _⎟

⎝ ⎠ (19)

Dengan demikian persamaan (18) menjadi

(

2 2

)

0 0

1 1

2

zz xx z x

d z d ρ ψ ψ σ ψ ψ σρ ψ ⎛ ⎞ + + _⎜ + + _⎟= ⎝ ⎠ 2 0 0 1 , 2 d c d c ρ σ ψ ρ σ ψ ⎛ ₊ ⎞ ⎜ ⎟

⎝ ⎠ (20)

atau 0 0 1 zz xx d d ρ ψ ψ σρ ψ + +

(

2 2 2

)

1

0.

2 z x c z c

ψ

σ ψ ψ

⎛ _{+ − +}⎛ ₋ ⎞⎞₌

⎜ ⎜ ⎟⎟

⎝ ⎠

⎝ ⎠ (21)

Persamaan (21) disebut persamaan Long.

Selanjutnya diperkenalkan variabel takberdimensi berikut: ' ' ' . ch x x h z z h ψ ψ = ⎫_⎪ ⎪ ⎪ = _⎬ ⎪ ⎪ = _⎪⎭ (22)

Berdasarkan peubah baru tersebut, persamaan (21) menjadi

(

2 2

)

0 0

1 1

1 2

zz xx x z

d d ρ ψ ψ ψ ψ ρ ψ ⎛ ⎞ + + _⎜ + − _⎟ ⎝ ⎠

(

)

0 2 0 1

+ d z 0,

d c

ρ _ψ

ψ

σρ − = (23)

setelah tanda aksen dihilangkan. (Penurunan persamaan (5), (6), (7), (8), (9), (11), (16), (18), dan (23) dapat dilihat pada Lampiran A).

Metode Asimtotik

Metode asimtotik merupakan salah satu cara untuk menyelesaikan masalah nilai batas atau masalah nilai awal. Penyelesaian dengan metode ini dinyatakan dalam bentuk uraian asimtotik.

Misalkan f t x

(

, ,σ

)

kontinu pada t∈\

dan x∈\n,σ >0 merupakan parameter kecil. Fungsi f mempunyai uraian terhadap parameter kecil σ . Untuk kasus khusus f

mempunyai uraian Taylor terhadap σ, yaitu

(

)

(

)

( )

( )

2

1 2

, ; , ; 0 , ,

f t xσ = f t x + f t x σ+ f t x σ

( )

... fn t x, σn + +

dengan koefisien f f1, 2,...,fn bergantung

pada t dan x.

Misalkan masalah nilai awal diberikan

2 0

x− σx+ =x

(24) dengan syarat awal x

( )

0 =1,x

( )

0 =0. Solusi eksak yang diperoleh adalah

( )

(

2

)

2

1 cos 1

1

t t

x t eσ σ t σ eσ

σ

= − −

−

(

2

)

sin 1−σ .t

Selanjutnya, persamaan (24) akan ditentukan solusinya dengan metode asimtotik. Misalkan solusi persamaan (24) dinyatakan dalam bentuk uraian asimtotik berikut

2

0 1 2

( ) ( ) ( ) ( ) ...

x t =x t +σx t +σ x t + (25) Jika persamaan (25) disubstitusikan ke persamaan (24), maka koefisien untuk σ0 memberikan persamaan

0 0 0

x +x =

Sedangkan koefisien σ1

memberikan persamaan

1 1 2 0 0.

x + −x x =

Sedangkan koefisien σn

adalah

1 2 1 0,

n n

x + −x x− =

(26)

1, 2,...

n=

dan kondisi awal berikut

( )

0 0 1,

x = x₀

( )

0 =0

( )

0 0,

n

x = xn

( )

0 =0, n=1, 2,... Solusi persamaan diferensial untuk x0 dan x1

adalah

x t0

( )

=cost

( )

1 cos sin cos .

x t = t− t+t t

Jadi solusi masalah nilai awal (24) dengan menggunakan metode asimtotik adalah

( )

cos

(

cos sin cos ... .

)

5

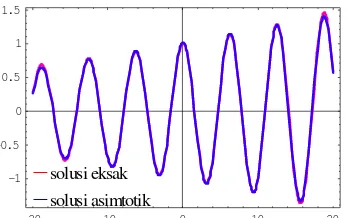
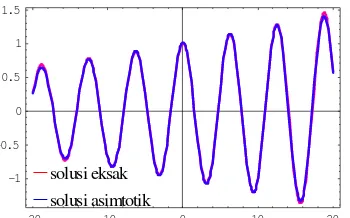
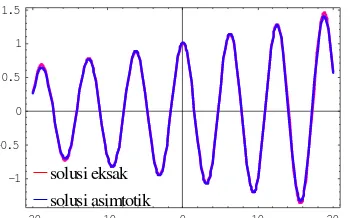
Solusi eksak dan solusi dengan metode asimtotik diilustrasikan pada Gambar 2, dengan menggunakan σ =0.02.

Pada Gambar 2, terlihat bahwa solusi eksak dan solusi dengan metode asimtotik tidak jauh berbeda. Sehingga dapat digunakan untuk menyelesaikan suatu masalah nilai awal.

-20 -10 0 10 20

-1 -0.5 0 0.5 1 1.5

Gambar 2. Perbandingan solusi eksak MNA dengan solusi MNA dengan metode asimtotik.

PEMBAHASAN

Bagian ini akan membahas penurunan

persamaan gerak gelombang internal dengan menggunakan metode asimtotik. Sebelumnya persamaan dasar fluida diformulasikan dalam formulasi Lagrange.

Formulasi Lagrange

Misalkan z= f x

(

,ψ

)

dengan menggunakan prinsip aturan rantai diperoleh

1 1 1 z x x zz

x x x

xx

f

f f

f f

f f f

x f f f

ψ ψ ψ ψ ψ ψ ψ ψ ψ ψ ψ ψ ψ ⎫ = _⎪ ⎪ ⎪ = − _⎪ ⎪⎪ ⎬ ⎛ ⎞ ∂ _⎪ = ⎜_⎜ ⎟_{⎟ ⎪} ∂ ⎝ ⎠ _⎪ ⎪ ⎛ ⎞ ⎛ ⎞ ∂ ∂ = −_∂ ⎜_⎜ ⎟_⎟+ _∂ ⎜_⎜ ⎟⎪_⎟ ⎪ ⎝ ⎠ ⎝ ⎠⎭ (27)

Jika persamaan (27) disubstitusikan ke persamaan (23), maka diperoleh

2 2 2 2 0 0 1 1 1 2 x x x f f c c

f_ψ f_ψ f_ψ

ψ ρ ⎛ ⎞ ⎛⎜ρ ⎛⎜ ⎜⎛⎛ ⎞ ⎛ ⎞ ⎞⎟⎞⎟⎟⎞ − ⎜_{⎜ ⎟}⎟ + _{⎜ ⎜} ⎜_⎜ ⎟_⎟ +⎜_⎜ ⎟_⎟ − _⎟⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ _{⎝ ⎝ ⎝}⎝ ⎠ ⎝ ⎠ _⎠⎠⎠

0

(

)

1 0. z ψ ρ ψ σ

+ − = (28)

Khususnya

(

,

)

(

,

)

z= f x Z = +Z η x Z (29) dengan Z =ψ, persamaan (23) menjadi

(

)

(

)

2 2

2 2

0 0 2

1 2

1 ₁

Z Z x

x

Z x Z

Z c c η η η η ρ ρ η η ⎛ ⎛ _{+ −} ⎞⎞ ⎜ ⎜ ⎟⎟ ⎛ ⎞ + ⎜ ⎜ ⎟⎟ ⎜ ₊ ⎟ + ⎜ ⎟ ⎝ ⎠ _⎜ ⎜_⎜ ⎟_⎟⎟ ⎝ ⎠ ⎝ ⎠

+ρ0N2η=0. (30)

Persamaan (30) berlaku pada daerah 0.

Z

−∞ < < Pada kedalaman yang semakin

besar (Z → −∞), maka gelombang yang terjadi cukup kecil sehingga w=0. Jadi untuk

Z→ −∞ nilai η =0. Sedangkan untuk 0,

Z= yaitu di permukaan fluida, diasumsikan tekanan permukaan sama dengan tekanan atmosfer (yaitu sama dengan nol), sehingga

(

2 2 2

)

1

0

2 ψx +ψz −c +gz= di Z =η. (31) Selanjutnya persamaan (27) dan (29) disubstitusikan ke persamaan (31), maka diperoleh

(

)

(

)

2 2 2 2 1 2 . 1

Z Z x

Z c η η η η σ η ⎛ _{+ −} ⎞ ⎜ ⎟ ⎝ ⎠ =

+ (32)

Sehingga persamaan dasar fluida ideal untuk aliran tunak dalam formulasi Lagrange adalah

(

)

(

)

2 2

2 2

0 0 2

1 2

1 1

Z Z x

x

Z x Z

Z c c η η η η ρ ρ η _η ⎛ ⎛ _{+ −} ⎞⎞ ⎜ ⎜ ⎟⎟ ⎛ ⎞ + ⎜ ⎜ ⎟⎟ ⎜ ₊ ⎟ + ⎜ ⎟ ⎝ ⎠ _⎜ ⎜_⎜ ⎟_⎟⎟ ⎝ ⎠ ⎝ ⎠ 2

0N 0

ρ η

+ = (33) dengan syarat batas

(

)

(

)

2 2 2 2 1 2 1

Z Z x

Z c η η η η σ η ⎛ _{+ −} ⎞ ⎜ ⎟ ⎝ ⎠ =

+ di Z =0. (34)

Persamaan (33) akan ditentukan solusinya dengan metode asimtotik berdasarkan syarat batas pada persamaan (34), (penurunan persamaan (27), (28), (30), (31) dan (32) dapat dilihat pada Lampiran B).

solusi eksak solusi asimtotik

Persamaan BO Tunak

Fluida Lapisan Atas

Misalkan lapisan atas didefinisikan pada 0.

h Z

− < ≤ Jika persamaan (33) diuraikan,

maka diperoleh

2

0 ₂

(1 )

(1 )

xx Z x xZ

Z

c ρ η η η η

η ⎛ + − ⎞ ⎜ ⎟ ⎜ ₊ ⎟ ⎝ ⎠

(

)

(

(

(

)

)

)

2 2 2 1 0 2 2

1 Z Z x Z

Z

c _{ρ η η η}

η + + − +

(

)

(

)

2 2 1 2 2 0 3 2 1

Z Z x ZZ

Z c η η η η ρ η + − − +

2 0. N ρ η

+ =

(35) Kemudian kedua ruas pada persamaan (35) dikalikan dengan

(

1+ηZ

)

3, diperoleh

(

)

(

(

)

)

2

0 1 Z xx 1 Z x xZ

c ρ +η η +η −η η

2

(

)

(

(

1

(

2 2

)

)

)

0 2

1 Z Z Z x

Z

c η ρ η η η

+ + + −

2

(

1

(

2 2

)

)

0 2

2c ρ η ηZZ Z ηZ ηx

− + −

+ρ₀N2η

(

1+ηZ

)

3 =0. (36)

Misalkan η dan c menyatakan dalam bentuk uraian asimtotik sebagai berikut:

(

)

2 3

1 2 3

, ...

X Z

η =αη α η α η+ + + (37)

2

0 1 2 ...,

c=c +αc +α c + (38) dengan α adalah suatu parameter kecil yang mengukur amplitudo gelombang dan X =αx

menyatakan koordinat horizontal yang ditinjau cukup panjang. Jika persamaan (37) dan (38) disubstitusikan ke persamaan (36), maka koefisien α memberikan masalah nilai batas berikut

2 2

0 0 1 0 1

2

1 0 1

( ) 0 , 0

0 , 0.

Z Z

Z

c N h Z

c Z

ρ η ρ η

η σ η

⎫

+ = _{− < < ⎪}

⎬

− = = _⎪⎭ (39)

Dengan metode pemisahan peubah , misalkan

( ) ( )

1 A X Z

η = φ (40)

dengan A adalah fungsi sembarang dan

( )

Z

φ memenuhi masalah nilai eigen berikut:

2 2

0 0 0

2 0

( ) 0 , 0

0 , 0.

Z Z

Z

c N h Z

c Z

ρ φ ρ φ

φ σ φ

⎫

+ = _{− < < ⎪}

⎬

− = = _⎪⎭ (41)

Selanjutnya koefisien α2

memberikan

2 2

0 0 2 0 2

2

2 0 2

( ) 0 , 0

0 , 0.

Z Z

Z

c N F h Z

c G Z

ρ η ρ η

η σ η

⎫

+ + = _{− < < ⎪}

⎬

− + = = _⎪⎭

(42)

dengan

(

2

)

2 2

1Z 0 0 1Z _Z 2 0 0 1ZZ 1Z 3 0 1 1Z

F=η c ρ η − c ρ η η + ρ Nη η

2 2 0 1 0 1 0 0 1

1

2 .

2

Z Z

Z

c cρ η c ρ η

⎛ ⎞

+_⎜ + _⎟

⎝ ⎠ (43)

dan

2 2

1 1 0 1 1 0 1

1

2 2 .

2

Z Z Z

G= η η − σc cη − σ ηc (44) Jika η1 pada persamaan (40)

disubstitusikan ke persamaan (43) dan (44), maka diperoleh

(

)

(

)

2 2 2 2 2

0 0 0 2 0 3

Z Z _Z Z ZZ

F= Aφ c ρ φ +ρ Aφ − cφ + N φ

0 0 1 0

1 2

2

Z Z

Z

cρ φA c c Aφ

⎡ ⎛ ⎞⎤

+_{⎢ ⎜} + _⎟⎥

⎝ ⎠

⎣ ⎦

(45)

dan

2

0 1 0

1

2 2 .

2

Z Z

G=Aφ _⎜⎛ Aφ− σc c − σc Aφ ⎞_⎟

⎝ ⎠ (46)

Sehingga diperoleh dua masalah nilai eigen yaitu untuk φ pada persamaan (41) dan untuk

2

η pada persamaan (42) (penurunan persamaan (35), (36), (39), (42), (43) dan (44) dapat dilihat pada Lampiran C).

Masalah nilai batas pada persamaan (42) akan mempunyai penyelesaian jika memenuhi kondisi terselesaikan (Solvability condition) [Stokgold, hal 198], berikut

(

)

0

0 2

0 0 2 2 .

Z

Z Z _{Z h}

h

F dZφ c ρ η φ η φ =₌₋

−

⎤

= − _⎦

∫

(47)

Nilai φ dan η2 serta turunannya di Z =0

telah diperoleh pada lapisan atas. Sedangkan nilai φ dan η2 serta turunannya di Z = −h

perlu memperhatikan lapisan bawah. Fluida Lapisan Bawah

Misalkan lapisan bawah didefinisikan pada .

H Z h

− ≤ ≤ − Misalkan η αη θ=

( )

,Z

dengan Z =αZ, rapat massa ρ₀

( )

z =ρ_∞

diasumsikan konstan, dan θ=x. Jika pemisalan tersebut disubstitusikan ke persamaan (36), maka koefisien α menghasilkan persamaan berikut:

0.

ZZ

θθ

η +η = (48) Jika dimisalkan X =αθ, maka diperoleh MNB berikut:

2

0

XX ZZ

α η +η = (49) dengan kondisi batas

0 0 di di . Z H Z h η η η = = − ⎫ ⎬

7

Dengan menggunakan integral Fourier, solusi masalah nilai batas pada persamaan (49) dan (50) adalah

(

)

0

(

(

(

(

)

)

)

)

sinh 1 ˆ , sinh 2 ikX

k H Z

X Z e dk

k H h

α η η α π ∞ −∞ + = −

∫

(51) dengan

( )

0 0 1 ˆ . 2 ikX

X e dX

η η

π ∞

−

−∞

=

∫

(52)

Turunan pertama η terhadap Zdi

Z = −h adalah

(

,

)

coth

(

(

)

)

ˆ0 .

2

ikX

Z X h k k H h e dk

α η α η π ∞ −∞ − =

∫

− (53) Untuk memperoleh nilai φ dan η₂ serta turunannya terhadap Z di Z= −h, maka penyelesaian η dan turunannya terhadap Zdi lapisan atas dan di lapisan bawah sama sampai

( )

2

, O α yaitu

(

)

(

)

(

)

(

)

(

)

(

)

2 1 2 2 1 2 , , , , , ,

Z Z Z

X h X h X h

X h X h X h

αη αη α η αη αη α η ⎫ − = − + − ⎪ ⎬ − = − + _{− ⎪⎭} (54) Berdasarkan koefisien α dan α2

pada persamaan (54a) memberikan

( ) ( )

0 A X h

η = φ − dan η₂

(

X,− =h

)

0.

Sedangkan koefisien α dan α2 untuk persamaan (54b) memberikan η_1Z =0dan

2Z Z.

αη =η Karena η_Z =O

( )

α , maka dari persamaan (53), diperoleh φZ

( )

− =h 0 dan

(

)

(

)

2 0 1 ˆ coth . 2 ikX

Z k k H h e dk

η α η π ∞ −∞ =

∫

− (55) Jika dinormalkan φ

( )

− =h 1, maka diperoleh

( )

0 A X ,

η = (56)

sehingga

(

)

(

(

)

)

2 1 , coth 2 ikX

Z X h k k H h e

η α

π ∞

−∞

− =

∫

−

F A dk

( )

, (57) dengan

( )

1

( )

. 2

ikX

F A A X e dX

π ∞

−

−∞

=

∫

(58)

Jika nilai φ dan η2 serta turunannya terhadap

Z di Z= −h disubstitusikan ke persamaan (47), maka diperoleh

2 1

1 2

c A μA δ

− + − L

( )

_A =_{0 (59)}

dengan

L

( )

1 _coth

(

(

)

)

2

ikX

A k αk H h e

π ∞

−∞

=

∫

−

F A dk

( )

(60) dan koefisien μ dan δ adalah

(61)

Misalkan T =α(H−h), jika T → ∞ maka persamaan (60) menjadi

L

( )

1

( )

_.

2

ikX

A k e F A dk

π ∞

−∞

=

∫

(62)

dengan menggunakan integral kompleks diperoleh

( )

sgn . ikX ikX e

dX i k e

X X π

∞ − −∞ = ⎡_⎣ ⎤_⎦ −

∫

Jadi k F A

( )

∞

−∞

=

∫

[

( )

_{A e}−ikX_dX

dengan

[ _{( )A} 1 A X( )_dX.

X X π ∞ −∞ = −

∫

(63)

[

( )

_{A merupakan transformasi Hilbert dari}

.

A Sehingga persamaan (62) dapat ditulis menjadi

L

( )

_{A =} [

( )

A (64) dan persamaan (59) menjadi

2 1

1 2

c A μA δ

− + − [

( )

A =_0, (65) dengan koefisien μ dan δ telah diberikan pada persamaan (61). Persamaan (59) dan (65) berturut-turut disebut persamaan ILW (Intermediate Long Waves) dan persamaan BO (Benjamin-Ono).

Solusi Persamaan BO

Jika persamaan (65) dilakukan transformasi Fourier dan menggunakan teorema konvolusi dan transformasi Fourier dari ,A maka diperoleh

(

)

( ) (

' '

)

'

1

2

c δ k A μ A k A k k dk

∞

−∞

+ =

∫

− (66)

( )

1 . 2

b k

A k = abe (67) Jika persamaan (67) disubstitusikan ke persamaan (66), diperoleh

(

)

( ) 2 2 ( ) 1

1

,

2 8

b k b k

ab

c k e a b k e

b μ δ ⎛ ⎞ + = _⎜ + _⎟ ⎝ ⎠ atau

( ) 2 2 2 2 ( ) 1

1

.

2 2 8 8

b k b k

ab ab

c k e a b a b k e

b μ μ δ ⎡ ₊ ⎤ ₌⎡ ₊ ⎤ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦

P

ersamaan di atas terpenuhi jika dan hanya jika

(68)

Selanjutnya balikan transformasi Fourier dari persamaan (67) adalah

( )

1

, 2

ikX

A A k e dk

π ∞

−∞

=

∫

(69)

yang merupakan solusi dari persamaan (65). Jika persamaan (67) disubstitusikan ke persamaan (69) dan menggunakan rumus integral kompleks berikut

( )

2 ₂

1 2

, 2

b k ikX b

e dk X b π ∞ + −∞ = +

∫

(70)

maka diperoleh

( )

2 2 2.

ab A X

X b

=

+ (71)

Jadi persamaan (71) merupakan solusi dari persamaan (65) dengan

1

4c a

μ

= dan b 4 . a

δ μ =

Persamaan (71) merupakan solusi persamaan gerak gelombang internal (penurunan persamaan (48), (51), (53), (59), (60), (61), (62), (63), (64), dan (66) dapat dilihat pada Lampiran D).

Parameter c₁ menyatakan kecepatan phase gelombang. Sedangkan parameter a dan b

berturut-turut merupakan amplitudo dan panjang gelombang internal. Sedangkan μ dan δ adalah koefisien persamaan BO. Untuk mengetahui simpangan, panjang gelombang, dan kecepatan phase gelombang internal, harus diketahui data fisis, seperti rapat massa dan kedalaman fluida. Adapun langkahnya sebagai berikut. Langkah pertama menentukan fungsi eigen φ dan nilai eigen c0 berdasarkan

persamaan (41), langkah kedua menghitung koefisien persamaan BO yaitu μ dan δ berdasarkan persamaan (61). Kemudian

langkah ketiga menentukan bentuk A X

( )

dengan a dan b dari persamaan (68). Untuk lebih jelasnya diberikan contoh kasus berikut ini.

Contoh Kasus Fluida Dua Lapisan

Contoh kasus yang dibahas dalam karya ilmiah ini adalah masalah fluida dua lapisan. Fluida dua lapisan ialah fluida yang terdiri atas dua lapisan yang masing-masing memiliki rapat massa konstan. Gelombang internal yang muncul dikatakan sebagai gelombang interfacial. Salah satu contoh gelombang interfacial adalah aliran air dan minyak dalam pipa, serta aliran lumpur di suatu perairan.

Misalkan rapat massa dua lapisan yang akan dibahas diberikan sebagai berikut :

( )

1 0 2 , 0 , h Z Z Z h ρ ρ ρ − ≤ ≤ ⎧

= ⎨ _{−∞ < < −}

⎩ (72)

dan

(

2 1

)

2 1 2 . ρ ρ σ ρ ρ − =

+ (73)

Jadi penyelesaian masalah nilai eigen pada persamaan (41), yaitu fungsi eigen φ

( )

Z

berbentuk:

( )

2 0 2 2 0 0 0 1 , c Z h Z

Z c h c h

Z h σ φ σ σ ⎧ + − ≤ ≤ ⎪ =⎨ − −

⎪ _{−∞ < < −}

⎩ atau

( )

2 0 2 0 , 0 1

1 , , c

Z

h h _{h Z}

Z c h Z h σ φ σ ⎧ + ⎪ ⎪ − ≤ ≤ ⎪ = ⎨ ₋ ⎪ ⎪

−∞ < < − ⎪⎩

(74)

Sedangkan nilai eigen c0 diperoleh dengan

mengintegralkan persamaan (41a) dari − −h λ ke − +h λ, kemudian dibuat λ →0. Sehingga diperoleh persamaan untuk c₀2 berikut :

(

)

2

0 2 2 0.

c h

σ +σ − σ = (75)

Untuk menginterpretasikan parameter-parameter tersebut, maka diberikan suatu contoh data sebagai berikut.

Misalkan 0.1,σ = dan a= −0.1. Berdasarkan dari persamaan (75), diperoleh

0 0.976 .

c = h

9

Jika dimisalkan Z' Z, h

= dan h=1, maka nilai eigen φ berbentuk

( )

0.905( ' 0.095) , 1 ' 0

'

1 , ' 1.

Z Z

Z

Z

φ _{= ⎨}⎧− + − ≤ ≤

− ∞ < < − ⎩

(76) Sedangkan koefisien persamaan BO, yaitu μ dan δ, diperoleh dari persamaan (61) yaitu:

1.618 h

μ= − dan δ =_0.442h32 ₍₇₇₎

Untuk a= −0.1, maka dari persamaan (68) diperoleh

1

0.040 c

h

= dan b=10.927 .h (78)

Oleh karena itu bentuk A X

( )

pada mode internal adalah

( )

₂ 2 2

11.940 . 119.401

h A X

h X

= −

+ (79)

Jika X =θh, maka

( )

2

11.940 . 119.401

A θ

θ = −

+ (80)

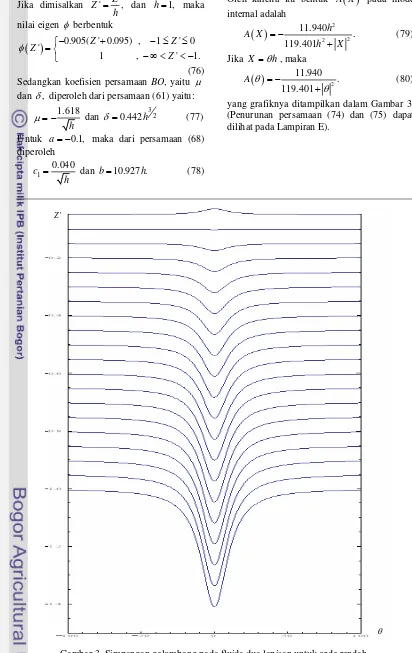
yang grafiknya ditampilkan dalam Gambar 3. (Penurunan persamaan (74) dan (75) dapat dilihat pada Lampiran E).

Gambar 3. Simpangan gelombang pada fluida dua lapisan untuk orde rendah.

θ

'

Berdasarkan Gambar 3, kecepatan phase gelombang adalah 1.016, panjang gelombang internal 10.927, dan amplitudo 0.1.

Amplitudo terbesar berada antara dua lapisan,

' 1.

Z = −

SIMPULAN

Persamaan gerak gelombang internal pada

fluida dengan kedalaman yang cukup besar dengan aliran tunak berbentuk persamaan Benjamin-Ono (BO) yang berbentuk tunak. Persamaan BO ini diturunkan dari persamaan dasar dalam bentuk tunak (berupa persamaan Long). Persamaan Long diturunkan berdasarkan hukum kekekalan massa dan kekekalan momentum dengan menambahkan asumsi irrotasional. Dengan metode asimtotik diperoleh persamaan BO dari persamaan Long. Persamaan BO tersebut menghasilkan penyelesaian persamaan dalam bentuk gelombang soliter.

Formulasi gelombang soliter digunakan untuk menjelaskan gerak gelombang soliter internal pada kasus fluida dua lapisan untuk fluida dalam. Dalam formulasi ini, diperoleh

tiga parameter yaitu kecepatan phase gelombang, amplitudo, dan panjang gelombang internal. Jika salah satu parameter tersebut diketahui, maka dua parameter lainnya dapat ditentukan. Dalam contoh kasus ini, untuk batas kedua lapisan pada kedalaman satu satuan panjang dengan amplitudo 0.1

memberikan kecepatan phase gelombang sebesar 1.016 dan panjang gelombang

10.927 satuan panjang. Simpangan

gelombang soliter internal yang memiliki amplitudo terbesar dicapai di batas antar dua fluida (pada kedalaman satu satuan panjang). Sedangkan di permukaan, amplitudo gelombang relatif kecil.

DAFTAR PUSTAKA

David, H. dan Robert R. 1994. Fisika.

Erlangga.

Duff. GFC. 1966. Differential Equation Of Applied Mathematics. A Willey International Edition. Canada.

Gerkema, T. 1994. Nonlinear Dispersive Internal Tide : Generations Models For A Rotating Ocean. Phd-Thesis. Univ. of Utrecht, Netherlands.

Grimshaw, R. 1980. A Second-Order Theary For Solitary Waves In Deep Fluids. University of Mebourne, Parkuille, Victoria 3052, Australia.

Grimshaw, R. 1997. Internal Solitary Waves “Advances in Coastal and Ocean Engineering”, Ed. P. L. F Liu World Scientific Pub. Company, 3, 1-30.

Herman, Russell. 1992. Solitary waves. American Scientist, 80-350.

Hinch, E. J. 1992. Perturbation Methods. Cambridge Univ. Press, Cambridge.

Jaharuddin, Pudjaprasetya, S. R. 2001. Gelombang Soliter Interfacial Pada Aliran Tunak. MIHMI, Vol 7, No.1, 31-38.

Jaharuddin. 2004. Gelombang Soliter di Selat Lombok dan Simulasi Numeric Fenomena Morning Glory. PhD-Thesis. ITB, Bandung.

Long, R.R. 1953. Some Aspecta of The Flow of Stratified Fluids, Tellus, 5, 42-58. Saidah. 2007. Gelombang Soliter Internal

Pada Aliran Tunak [Skripsi]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Spiegel, M. R. 1981. Advanced Calculus. McGraw-Hill International Book Company, Singapore.

LAMPIRAN A

Penurunan persamaan (5)

Dengan menggunakan persamaan D u w ,

Dt t x z

∂ ∂ ∂

= + +

∂ ∂ ∂ persamaan (4) menjadi

0 DS

Dt = di z=η0

( )

x t,

0

( )

0 D z

Dt η −

=

(

0

)

0

u w z

t x z η

∂ ∂ ∂

⎛ _{+ +} ⎞ _{− =}

⎜_{∂ ∂ ∂} ⎟

⎝ ⎠

0 0 0

0

z z z

u w u w

t x z t x z

η η η

∂ ∂ ∂

∂ ₊ ∂ ₊ ∂ _{− − − =}

∂ ∂ ∂ ∂ ∂ ∂

0t 0x 0

w−η −uη =

0t 0x

w=η +uη di z=η0.

Penurunan persamaan (6)

Dengan menggunakan persamaan D u w ,

Dt t x z

∂ ∂ ∂

= + +

∂ ∂ ∂ dan persamaan (4) serta diasumsikan

bahwa fluida memiliki kedalaman yang besar, maka diperoleh

• DS 0,

Dt = jika z= −h x

( )

. Sehingga

( )

( )

0

D z h x

Dt +

=

( )

(

)

0

u w z h x

t x z

∂ ∂ ∂

⎛ _{+ +} ⎞ _{+ =}

⎜_{∂ ∂ ∂} ⎟

⎝ ⎠

( )

( )

( )

0

h x h x h x

z z z

u w u w

t x z t x z

∂ ∂ ∂

∂ ∂ ∂

+ + − − − =

∂ ∂ ∂ ∂ ∂ ∂

0,

x

w uh− =

• DS 0,

Dt = jika z= −h. Sehingga

( )

0

D z h

Dt

+ =

(

)

0

u w z h

t x z

∂ ∂ ∂

⎛ _{+ +} ⎞ _{+ =}

⎜_{∂ ∂ ∂} ⎟

⎝ ⎠

0

z z z h h h

u w u w

t x z t x z

∂ ₊ ∂ ₊ ∂ ₋∂ ₋ ∂ ₋ ∂ ₌

∂ ∂ ∂ ∂ ∂ ∂

0,

w=

• DS 0,

Dt = jika z= −∞. Sehingga

( ) 0 D z

Dt =

( )

0

u w z

t x z

∂ ∂ ∂

⎛ _{+ +} ⎞ ₌

⎜_{∂ ∂ ∂} ⎟

⎝ ⎠

0

z z z

u w

t x z

∂ ₊ ∂ ₊ ∂ ₌

∂ ∂ ∂

0.

13

Jadi pada fluida dengan kedalaman yang besar kecepatan partikel dalam arah vertikal adalah nol.

Penurunan persamaan (7) Dari persamaan (2), diperoleh

(

)

(

)

(

)

(

)

(

)

(

)

0 0

0

, , , ,

t x z x

t x z z

t x z t x z x z

u uu wu P

w uw ww P g

u uu wu w uw ww P P g

u w u u w w u w

t x z x z

ρ

ρ ρ

ρ ρ

ρ

+

+ + + =

+ + + + =

+ + + + + + + + =

∂ ∂ ∂ ∂ ∂

⎛ _{+ +} ⎞ ⎛₊ ⎞

⎜_{∂ ∂ ∂} ⎟ ⎜_{∂ ∂} ⎟

⎝ ⎠ ⎝ ⎠ 0

0

P g

u w P g

t x z

D

P Dt

ρ

ρ ρ

ρ ρ

+ =

∂ ∂ ∂

⎛ _{+ +} ⎞_{+ ∇ + =}

⎜_{∂ ∂ ∂} ⎟

⎝ ⎠

= −∇ +

q q q

q

g

dengan g=

(

0,−g

)

.

Penurunan persamaan (8)

Dengan menggunakan notasi turunan total, diperoleh

D

u w

Dt t x z

∂ ∂ ∂

= + +

∂ ∂ ∂

q q q q

= q_t+uq_x+wq_z

_t u _x w _{z t} u w

x z

∂ ∂

= ∂ + + = ∂ + +

∂ ∂

q q

q q q q

x z

t t

x z

u u

u u

u w u w

w w

w w

x z

⎛ ⎞ ⎛ ⎞

⎛ ⎞ ⎛ ⎞

∂ ∂

= ∂ + _{⎜ ⎟}+ _{⎜ ⎟}= ∂ + _{⎜ ⎟}+ _{⎜ ⎟}

∂ _{⎝ ⎠} ∂ _{⎝ ⎠ ⎝ ⎠ ⎝ ⎠}

q q

x z x z

t t

x z x z

uu wu uu wu

uw ww uw ww

+

⎛ ⎞ ⎛ ⎞ ⎛ ⎞

= ∂ +_{⎜ ⎟}+_{⎜ ⎟}= ∂ +_{⎜ ⎟}

+

⎝ ⎠

⎝ ⎠ ⎝ ⎠

q q

t t

( )

. .

u

u w

w

x z

⎛ ⎞

∂ ∂

⎛ ⎞

= ∂ +_⎜ + _{⎟⎜ ⎟}= ∂ + ∇

∂ ∂

⎝ ⎠⎝ ⎠

q q q q

Jadi persamaan (8) ditulis t ( . ) D

Dt = ∂ + ∇

q

q q q.

Penurunan persamaan (9) Dari persamaan (8), diperoleh

( . )

t

D

Dt = ∂ + ∇

q

q q q = ∂ +_tq uq_x+wq_{z t} x z

x z

uu wu

uw ww

+

⎛ ⎞

= ∂ + ⎜ ₊ ⎟

⎝ ⎠

q _t z x x x

z x z z

wu ww uu ww

uu uw uu ww

− +

⎛ ⎞ ⎛ ⎞

= ∂ +_{⎜ ⎟ ⎜}+ _⎟

− + _⎝ + _⎠

⎝ ⎠

q

t

(

(

z x

)

0

(

z x

)

)

x x

z z

uu ww

wu ww i j uu uw k

uu ww

+

⎛ ⎞

= ∂ + − + + − + _{+ ⎜ ⎟}

+

⎝ ⎠

q

(

)

(

(

)

)

(

0

)

x x

t z x z x

z z

uu ww

w u w i j u u w k

uu ww

+

⎛ ⎞

= ∂ + − + − − _{+ ⎜ ⎟}

+

⎝ ⎠

q

(

)

0 0

0

x x

t z x

z z

i j k

uu ww

u w

uu ww

u w

+

⎛ ⎞

= ∂ + − _{+ ⎜ ⎟}

+

⎝ ⎠

q

(

)

(

)

(

)

(

)

1 2 1 2

0 0 ,

2 2

t i uz wx j k x z u w

⎛ ⎛ ⎞⎞

= ∂ + − × + ∂ ∂_{⎜ ⎜} + _⎟⎟

⎝ ⎠

⎝ ⎠

2

1

0 , ,

2 0

t

i j k

u w

x z x z

u w

⎛ ⎞

⎜ _{∂ ∂} ⎟ _{⎛ ∂ ∂ ⎞}

⎛ ⎞⎛ ⎞

⎜ ⎟

= ∂ + × _{+ ⎜⎜ ⎟⎜ ⎟⎟}

⎜∂ ∂ ⎟ ⎝⎝∂ ∂ ⎠⎝ ⎠⎠

⎜ ⎟

⎝ ⎠

q q

2

1

(( ) )

2

t

⎛ ⎞

= ∂ + ∇× × + ∇⎜q q q _⎝ q ⎟_⎠.

Penurunan persamaan (11)

Jika persamaan (10) disubstitusikan ke persamaan (7), maka

( )

1

(

2 2

)

2

t x z P

ρ⎛_⎜∂ ∇ + ∇φ ⎛_⎜ φ +φ ⎞_⎟⎞_⎟= −∇ +ρ

⎝ ⎠

⎝ ⎠ g

( )

1

(

2 2

)

0. 2

t x z P

ρ⎛ φ ⎛ φ φ ⎞⎞ ρ

∇ _⎜∂ +_⎜ + _⎟⎟+ ∇ − =

⎝ ⎠

⎝ ⎠ g

Jika kedua ruas dibagi ,ρ maka

( )

1

(

2 2

)

0, 2

t x z

P

φ φ φ

ρ

⎛ ⎛ ⎞ ⎞

∇ ∂_⎜ +_⎜ + _⎟+ _⎟− =

⎝ ⎠

⎝ ⎠ g

Kemudian kedua ruas diintegralkan terhadap koordinat ruang, diperoleh

( )

1

(

2 2

)

( ) 2

t x z

P

gz C t

φ φ φ

ρ

⎛_{∂ +}⎛ ₊ ⎞₊ ⎞_{+ =}

⎜ ⎜ ⎟ ⎟

⎝ ⎠

⎝ ⎠ .

Dengan ( )C t adalah konstanta integral. Penurunan persamaan (16)

Dari persamaan (14c) dan (14d) dan D u w ,

Dt x z

∂ ∂

= +

∂ ∂

2 2 2

,

u w

= +

q serta ξ =wx−uz, diperoleh:

• ρ

(

uux+wuz

)

+Px=0

2 2

1 1

0 2u 2w wuz wwx Px x

ρ ∂ ⎛_⎜ + ⎞_⎟+ρ −ρ + =

∂ ⎝ ⎠

2

1

0

2 w Px

x

ρ ∂ ⎛_⎜ ⎞ −_⎟ ρξ + =

∂ ⎝ q ⎠ (i)

• ρ

(

uw_x+ww_z

)

+P_z+ρg=0

2 2

1 1

0 2u 2w uux uwx Pz g z

ρ ∂ ⎛_⎜ + ⎞_⎟−ρ +ρ + +ρ =

∂ ⎝ ⎠

2

1

0.

2 u Pz g

z

ρ ∂ ⎛_⎜ ⎞ +_⎟ ρξ + +ρ =

∂ ⎝ q ⎠ (ii)

Jika pada persamaan (i) dan (ii) P dieliminasi, maka

(

)

(

)

2

2

2

1

0 2

1

0 2

1 1

2 2

xz x xz

u P g

x z x

w P

z x z

x z z x

ρ ρξ ρ

ρ ρξ

ρ ρ

−

∂ ⎛ ∂ ⎛ _{⎞ +}⎞ ∂ _{+ + =}

⎜ ⎜ ⎟⎟

∂ ⎝ ∂ ⎝ ⎠⎠ ∂

∂ ⎛ ∂ ⎛ _{⎞ −}⎞ ∂ _{+ =}

⎜ ⎜ ⎟⎟

∂ ⎝ ∂ ⎝ ⎠⎠ ∂

∂ ⎛ ∂ ⎛ _{⎞ −}⎞ ∂ ∂

⎜ ⎜ ⎟⎟

∂ ⎝ ∂ ⎝ ⎠⎠ ∂ ∂

q

q

q q

(

)

(

)

(

)

(

)

2

2 2 2 2

0

1 1

0.

2 2

x

u w g

x z

u w u w u w g

x z x z z x x

ρξ ρξ ρ

ξ ξ ρ ρ ρ

ρ

⎛ ⎛ _{⎞ +}⎞ ∂ ₊ ∂ _{+ =}

⎜ ⎜_⎝ ⎟_⎠⎟ _{∂ ∂}

⎝ ⎠

∂ ∂ ∂ ∂ ∂ ∂ ∂

⎛ ₊ ⎞₊ ⎛ ₊ ⎞₋ ⎛ ₊ ⎞_{+ =}

⎜ _{∂ ∂} ⎟ _{∂ ∂} ⎜ ⎟ _{∂ ∂} ⎜ ⎟ _∂

⎝ ⎠ ⎝ ⎠ ⎝ ⎠

15

(

2 2

)

(

2 2

)

1 1 1 1

0.

2 2

D g

u w u w

Dt x z z x x

ξ ρ ρ ρ

ρ ρ ρ

∂ ∂ ⎛ ⎞ ∂ ∂ ⎛ ⎞ ∂

+ _⎜ + _⎟− _⎜ + _⎟+ =

∂ ∂ ⎝ ⎠ ∂ ∂ ⎝ ⎠ ∂

Penurunan persamaan (18)

Persamaan (17) disubstitusikan ke persamaan (16), dan

z

u= −ψ dan w=ψx, diperoleh

(

2 2

)

(

2 2

)

1 1 1 1

0,

2 2

D g

u w u w

Dt x z z x x

ξ ρ ρ ρ

ρ ρ ρ

∂ ∂ ⎛ ⎞ ∂ ∂ ⎛ ⎞ ∂

+ _⎜ + _⎟− _⎜ + _⎟+ =

∂ ∂ ⎝ ⎠ ∂ ∂ ⎝ ⎠ ∂

menjadi

(

2 2

)

(

2 2

)

1 1 1 1

0

2 z x 2 z x

D g

Dt x z z x x

ξ ρ _{ψ ψ} ρ _{ψ ψ} ρ ψ

ρ ρ ρ ψ

∂ ∂ ⎛ ⎞ ∂ ∂ ⎛ ⎞ ∂ ∂

+ _⎜ + _⎟− _⎜ + _⎟+ =

∂ ∂ ⎝ ⎠ ∂ ∂ ⎝ ⎠ ∂ ∂

2 2 2 2

1 1 1 1 1 1

0

2 z 2 x 2 z 2 x

D g

Dt x z z x x

ξ ρ ψ _{ψ ψ} ρ ψ _{ψ ψ} ρ ψ

ρ ψ ρ ψ ρ ψ

∂ ∂ ∂ ⎛ ⎞ ∂ ∂ ∂ ⎛ ⎞ ∂ ∂

+ _⎜ + _⎟− _⎜ + _⎟+ =

∂ ∂ ∂ ⎝ ⎠ ∂ ∂ ∂ ⎝ ⎠ ∂ ∂

2 2 2 2

1 1 1 1 1

0

2 z 2 x 2 z 2 x

D g

Dt x z z x x

ξ ρ ψ _{ψ ψ} ψ _{ψ ψ} ρ ψ

ρ ψ ρ ψ

⎛ ∂ ⎛ ∂ ∂ ⎛ ⎞ ∂ ∂ ⎛ ⎞⎞⎞ ∂ ∂

+_{⎜ ⎜ ⎜} + _⎟− _⎜ + _⎟⎟⎟+ =

∂ ⎝ ∂ ∂ ⎝ ⎠ ∂ ∂ ⎝ ⎠⎠ ∂ ∂

⎝ ⎠

2 2

1 1 1

0 2 z 2 x

D g

Dt x z z x x

ξ ρ _{ψ ψ} ψ ψ ρ ψ

ρ ψ ρ ψ

⎛ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ ∂ ∂ ⎞ ∂ ∂

+_{⎜ ⎜} + _{⎟ ⎜⎟} − _⎟+ =

∂ ⎝ ⎠ ⎝ ∂ ∂ ∂ ∂ ⎠ ∂ ∂

⎝ ⎠

( )

( )

2 2

1 1 1 1 1

0. 2 z 2 x

D

gz gz

Dt x z z x x z z x

ξ ρ _{ψ ψ} ψ ψ ρ ψ ρ ψ

ρ ψ ρ ψ ρ ψ

⎛ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ ∂ ∂ ⎞ ∂ ∂ ∂ ∂ ∂ ∂

+_{⎜ ⎜} + _{⎟ ⎜⎟} − _⎟+ − =

∂ ⎝ ⎠ ⎝ ∂ ∂ ∂ ∂ ⎠ ∂ ∂ ∂ ∂ ∂ ∂

⎝ ⎠

Misalkan 1

( )

gz 0,

z x

ρ ψ ρ ψ

∂ ∂ ∂

=

∂ ∂ ∂ maka

( )

2 2

1 1 1 1

0 2 z 2 x

D

gz

Dt x z z x x z z x

ξ ρ _{ψ ψ} ψ ψ ρ ψ ψ

ρ ψ ρ ψ

⎛ ∂ ⎛ ⎞ ⎛⎞ ∂ ∂ ∂ ∂ ⎞ ⎛ ∂ ⎞⎛∂ ∂ ∂ ∂ ⎞

+_{⎜ ⎜} + _{⎟ ⎜⎟} − _⎟+_{⎜ ⎟⎜} − _⎟=

∂ ⎝ ⎠ ⎝ ∂ ∂ ∂ ∂ ⎠ ∂ ⎝ ∂ ∂ ∂ ∂ ⎠

⎝ ⎠ ⎝ ⎠

2 2

1 1 1

0 2 z 2 x

D D

gz

Dt Dt

ξ ρ _{ψ ψ}

ρ ψ

⎛ ∂ ⎛⎛ ⎞ ⎞⎞

+ ⎜ _∂ ⎜⎜_⎝ + ⎟_⎠+ ⎟⎟=

⎝ ⎠

⎝ ⎠

2 2

1 1 1

0. 2 z 2 x

D

gz Dt

ρ

ξ ψ ψ

ρ ψ

⎛ ₊⎛ ∂ ⎛⎛ ₊ ⎞₊ ⎞⎞⎞₌

⎜ ⎜ ⎜⎜ ⎟ ⎟⎟⎟

⎜ _{⎝ ∂ ⎝⎝ ⎠ ⎠⎠}⎟

⎝ ⎠

jika integralkan terhadap koordinat ruang, maka

(

)

2 2 2 2

1 1 1 1 1

( ),

2 z 2 x zz xx 2 z x

d

gz gz H

d

ρ ρ

ξ ψ ψ ψ ψ ψ ψ ψ

ρ ψ ρ ψ

⎛ ∂ ⎛⎛ ⎞ ⎞⎞ ⎛ ⎞

+_{⎜ ⎜⎜} + _⎟+ _⎟⎟= + + _⎜ + + _⎟=

∂ ⎝⎝ ⎠ ⎠ ⎝ ⎠

⎝ ⎠

jika 1 . gh

σ= Sehingga persamaan terakhir menjadi

(

2 2

)

1 1

( ). 2

zz xx z x

d

z H

d ρ

ψ ψ σ ψ ψ ψ

σρ ψ

⎛ ⎞

+ + _⎜ + + _⎟=

⎝ ⎠

Penurunan persamaan (23) Dari persamaan (21) diperoleh

(

2 2 2

)

0 0

1 1

0, 2

zz xx z x

d

c z

d c

ρ ψ

ψ ψ σ ψ ψ

σρ ψ

⎛ ⎛ ⎞⎞

+ + _⎜ + − +_⎜ − _⎟⎟=

⎝ ⎠

⎝ ⎠

( )

(

( )

)

( )

(

( )

)

(

)

(

( )

)

(

( )

)

(

) ( )

(

)

2 2

2 0

0

0 0

' ' 1 1 ' '

' ' ' ' ' 2 ' '

' 1

' 0 '

ch ch d ch ch

c

z h z h x h x h d ch x h z h

ch d

z h

d ch c

ψ ψ ρ ψ ψ

ρ ψ

ψ ρ

ρ ψ

⎛ ⎛_{⎛ ⎞ ⎛ ⎞} ⎞⎞

∂ ∂ ∂ ∂

∂ ∂ _{⎜ ⎜ ⎟⎟}

+ + _{⎜ ⎜}⎜_⎜ ⎟_⎟ +⎜_⎜ ⎟_⎟ − _⎟⎟

∂ ∂ ∂ ∂ _{⎜ ⎝} ∂ _{⎠ ⎝} ∂ _{⎠ ⎟}

⎝ ⎠

⎝ ⎠

⎛ ⎞

+ ⎜_⎜ − ⎟_⎟=

⎝ ⎠

atau

(

2 2

)

0 0

' ' ' ' ' '

2 2 2

0 0

1 1 1 ' '

' ' ' ' 1 0,

' 2 '

z z x x x z

d d

ch z

d d

h c c

ρ ρ ψ

ψ ψ ψ ψ

ρ ψ σρ ψ

⎛ _{+ +} ⎛ _{+ −} ⎞₊ ⎛ ₋ ⎞⎞₌

⎜ ⎜ ⎟ ⎜ ⎟⎟

⎝ ⎠ ⎝ ⎠

⎝ ⎠

karena

2 0

ch

h ≠

.

Sehingga

(

2 2

)

(

)

0 0

' ' ' ' ' ' 2

0 0

1 1 1

' ' ' ' 1 ' ' 0

' 2 '

z z x x x z

d d

z

d c d

ρ ρ

ψ ψ ψ ψ ψ

ρ ψ σρ ψ

⎛ ⎞

+ + _⎜ + − _⎟+ − =

⎝ ⎠

dengan 1 . gh

σ =

Untuk memudahkan penulisan maka tanda aksen dihilangkan menjadi

(

2 2

)